Simulations of hydro-fracking in rock mass at meso-scale using fully coupled DEM/CFD approach

Abstract

The paper deals with two-dimensional (2D) numerical modelling of hydro-fracking (hydraulic fracturing) in rocks at the meso-scale. A numerical model was developed to characterize the properties of fluid-driven fractures in rocks by combining the discrete element method (DEM) with computational fluid dynamics (CFD). The mechanical behaviour of the rock matrix was simulated with DEM and the behaviour of the fracturing fluid flow in newly developed and pre-existing fractures with CFD. The changes in the void geometry in the rock matrix were taken into account. The initial 2D hydro-fracking simulation tests were carried out for a rock segment under biaxial compression with one injection slot in order to validate the numerical model. The qualitative effect of several parameters on the propagation of a hydraulic fracture was studied: initial porosity of the rock matrix, dynamic viscosity of the fracking fluid, rock strength and pre-existing fracture. The characteristic features of a fractured rock mass due to a high-pressure injection of fluid were realistically modelled by the proposed coupled approach.

1 Introduction

Hydro-fracking (hydraulic fracturing) is a well stimulation technique to increase the productivity of petroleum, gas or heat reservoirs in which rocks are fractured by a pressurized fluid [11, 16]. The process involves the high-pressure injection of fluid (primarily water, containing sand or other proppants suspended with the aid of thickening agents) into a wellbore to create cracks in the deep-rock formations or to increase the connectivity of the pre-existing fracture network through which natural gas and petroleum will flow more freely. When the hydraulic pressure is removed from the well, small grains of hydraulic fracturing proppants hold the fractures open. Hydro-fracking has been seen as one of the key methods of extracting unconventional oil and unconventional petroleum, gas and heat resources. In the last decade, exploration and drilling activities in shale gas and shale oil reservoirs were intensified in a number of countries. The economic production from the gas and heat reservoirs greatly depends on the effectiveness of hydraulic fracturing stimulations that are affected by a realistic theoretical description of fracture in brittle crustal rocks. The fracture pattern may be very complex in rocks since it is strongly affected by different coupled mechanical, thermal and hydraulic processes at the meso-scale [39, 45]. Rocks have a very complicated heterogeneous structure, and they are strongly anisotropic due to naturally existing pre-discontinuities, such as joints, faults, veins and bedding planes which are ubiquitous and may greatly vary in appearance, dimensions and arrangement. These naturally occurring pre-discontinuities often include complex networks and dominate the geomechanical, thermal and hydrological behaviour of subsurface rocks. Our topic is a strong understanding of how hydraulic fractures propagate through rocks and how fluid flows through hydraulically stimulated fractures between wells. The ultimate objectives of our research works, dedicated to simulations of a dynamic hydro-fracking process in rock masses are:

• (a) explanation of the complex mechanism of the initiation and propagation of fractures in rocks due to the activity of the high fluid pressure (higher than the tensile strength of rocks) during hydro-fracking (by taking the existing pre-discontinuities and voids into account) and

• (b) description of this mechanism at the meso-scale by applying an advanced mathematical model, based on the three-dimensional (3D) discrete element method (DEM) fully coupled with fluid flow (the so-called a coupled discrete-continuum method-discrete and continuous domains coexist in one system).

Since hydraulic fracturing strongly depends on the heterogeneous meso-structure of rocks, the discrete element method (DEM) is a suitable numerical tool for investigating a non-uniform formation process of complex fracture patterns at the mesoscopic level. The fracturing fluid system is assumed to be continuous and is described by locally volume-averaged Navier–Stokes equations to be solved by computational fluid dynamics (CFD). In general, the numerical coupled calculations will be carried out for a two-phase (fluid and gas) turbulent flow of incompressible viscous fluid by taking the mass, momentum and heat transport into account in existing and newly developing fractures in rocks. In the first research step, we developed a simplified dynamic hydro-mechanical meso-scale model of hydro-fracking, based on DEM and CFD to characterize the properties of fluid-driven fractures in rocks. DEM was used to capture the mechanical behaviour of the rock mass that was represented by a set of representative discrete spherical elements interacting through elastic-brittle bonds that can break to form fractures. It was coupled with fluid mechanics via the computational fluid dynamics (CFD) to describe laminar fracturing fluid flow in voids and channels between discrete elements using a novel so-called Virtual Pore Network (VPN) approach.

The aim of the current paper is to present simulation results on checking the capability of the fully coupled simplified approach DEM/CFD to describe the process of hydro-fracking in rocks at the meso-level. The approach was formulated for laminar incompressible viscous one-phase fluid flow in isothermal conditions. A series of simple two-dimensional (2D) hydraulic fracturing simulations were performed on a small rock segment subjected to a pressurized fracturing fluid under biaxial compression conditions. This small rock segment had a very simplified particulate meso-structure and contained solely one injection slot. The qualitative effect of the following parameters on the hydraulic fracture geometry, fracturing fluid velocity and pressure was studied in 2D simulations: initial micro-porosity of the rock matrix, rock matrix strength, dynamic viscosity of the fracking fluid and presence of a pre-existing macro-crack. The innovative elements of our approach with respect to other existing DEM/CFD models in the literature are the following: (1) co-existence of two domains (a discrete and continuous one) in one physical system (the sum of domain geometries creates a complete physical system), (2) precise determination of the geometry and topology change of voids and fractures during hydro-fracking, (3) remeshing method of voids and fractures, (4) transformation schema of computation results from the old grid (before remeshing) to the new grid (after remeshing) and (5) detailed tracking of the fluid volume fraction in voids and fractures (rock voids can be fully or partially filled with the fluid). In our approach, every single pore is discretized by a number of triangles. Thus, the pressure field in a single pore is spatially variable while in existing DEM/CFD models, the pressure field in a single pore is constant. The flow path is also reproduced in a single pore in contrast to existing DEM/CFD models. In addition, the huge pressure gradients in a single pore are captured while in existing DEM/CFD models the pressure gradient in a single pore is equal to zero. Thus, the resulting forces from the fluid are more realistic on our approach (magnitude and direction). The hydraulic fracture propagation can be investigated in our approach in rocks that are initially partially filled with the fluid (what is more realistic). In addition, the particles floating (e.g. proppant particles) in fractures pre-filled with the fluid may precisely be traced.

The modelling of the fluid-driven fracture propagation in rocks comprises the coupling of different physical mechanisms including deformation of the solid skeleton induced by the fluid pressure on fracture surfaces, flow of the pore fluid along new fractures and through the region of surrounding existing fractures and pronounced temperature changes. Hydraulic fracturing results in complex fracture patterns composed of pre-existing and new ones that greatly influence the process at the global scale [40]. Due to difficulties in performing experimental works on the fracture network propagation in situ and at the laboratory scale, the numerical modelling becomes an essential tool in analyses of hydraulic fracturing [61].

Micro-seismic measurements suggest that the creation of complex intersecting and branching fracture networks during hydraulic fracturing is a common occurrence in many rock reservoirs [56]. A significant temperature difference between the wellbore fluid and rock formation introduces additional compressive or tensile stresses, depending on whether the fluid temperature is higher or lower than the surrounding rock [64]. De Simone et al. [10] suggested that decreasing temperatures induced a significant perturbation to the stress field even in intact rocks. The size changes of fractures also provide a distinctive response to thermal stresses [18, 22]. In view of natural pre-discontinuities in rocks, the physical models become very complex. The major challenges in numerical modelling of complex hydraulic fractures are:

• multiphase fluid flow in both macro-voids, micro-voids and pre-discontinuities of rocks (faults, veins, bedding planes) that may be partially filled with both a fluid- and gas-phase. The rock pressure is close to the hydrostatic pressure at the borehole depth,

• non-isothermal conditions, wherein both the temperature difference between the wellbore fluid and rocks and rapid size changes of fractures cause pronounced thermal stresses,

• high velocity of a hydraulic fracture propagation process that contributes to extremely large and rapid topology changes of voids and fractures.

There are two main approaches for modelling the propagation of hydraulically driven complex fracture patterns: (1) continuum-based models and (2) discontinuous meso-scale models at the grain level. The continuum-based models [5, 21, 41, 57] use continuum formulations and coarse-grid meshing for the fluid part. The fluid flow and solid–fluid interactions are defined at the meso-scale using empirical relations (e.g. Darcy’s law). There is no direct coupling at the local scale: forces acting on the individual particles are defined as a function of a meso-scale averaged fluid velocity obtained from permeability–porosity-based estimates. The solution of the continuum problem provides a fluid velocity and momentum exchange between two phases at each node of the mesh. The individual particle behaviour is not accurately reproduced, and this fact limits their application to problems such as strain localization, micro-cracking, local heterogeneities in porosity and internal erosion by transport of fines that are all inherently heterogeneous on the micro-scale. The solutions can be obtained with classical numerical methods such as finite differences, finite elements and finite volumes. A great advantage of the continuum-based models is an affordable CPU cost. However, they need a series of phenomenological assumptions that rely on a number of empirical relationships. In consequence, they require a new calibration procedure for each new type of rock meso-structure. The continuum-based meso-scale models are obviously unable to fully describe meso-scale coupled thermal, hydraulic and mechanical effects [5]. In addition, continuum models usually assume a homogeneous and an isotropic rock structure that is not realistic [9] and thus, the models do not capture interaction between the hydraulic fracturing and discrete fracture network. It is of major importance to take into account a heterogeneous meso-structure of rocks and a realistic pattern of pre-existing discontinuities that affect the shape and range of hydraulic fracture propagation. Summing up, the main drawback of currently used continuum hydraulic-mechanical models [5, 9, 10, 15, 18, 21, 41, 56, 57, 61, 64] is the lack of the detailed treatment of the geometry at the meso-structural level. In addition, the rock system is initially fully pre-filled with the fluid and only one-phase fluid flow is taken into account. Simple approaches are used to track fluid flow in voids and fractures.

As compared with usual continuum mechanics methodologies in most of existing numerical studies, discontinuous meso-scale models at the grain level [such as the discrete element method (DEM)] are more realistic since they allow for a direct simulation of the meso-structure and are very useful for studies of local physical phenomena at the meso-level such as the mechanism of the initiation, growth and formation of cracks [37, 40, 54]. DEM allows for a better understanding of local meso-structural phenomena that evidently affect a macroscopic rock behaviour. The strength and deformational features of rock masses are strongly affected by persistence, spacing, orientation and mechanical properties of geological structures. It is thus essential to accurately describe the fundamental behaviour of pre-existing structures when studying the stability of a rock mass. The first DEM model for rocks was formulated by Potyondy and Cundall [43]. Rock fracturing was captured by the rupture of bonds whose strength was characterized by a constant maximum acceptable force in tension and a cohesive-frictional maximum acceptable force in shear. Different types of bonds were proposed to simulate discontinuities [31, 35, 45]. The most universal contact formulation was proposed by Scholtès and Donze [45], based on the identification and re-orientation of each discrete element interaction that crossed the plane representing a discontinuous surface.

Various methods were developed to model fluid flow in pores and fractures at the grain level when using DEM. The commonly used approach to describe fluid flow and predict interaction mechanisms between flowing fluid and particles is the pore network modelling. It assumes that fluid flows through channels connecting pores that accumulate pressure. A simplified laminar viscous Poiseuille flow is assumed in channels [32, 47, 60] and no flow or Stokes flow is taken in pores [4, 40, 55]. The Poiseuille flow in channels describes laminar Newtonian fluid flow between two plates (in general non-parallel) and is based on Reynold’s equations of a classical lubrication theory. The Stokes flow takes place in pores when advective inertial forces are small as compared with viscous forces (the Reynolds number less than 1). The pore network model is built through a weighted Delaunay triangulation over the discrete element packing. Pre-existing fractures and hydraulically driven fractures are treated as a series of channels connected face-to-face or by cell grids, depending on fluid flow model. The finite volume method is applied to solve the governing equations of motion. In this approach, the edges of triangles connect the gravity centres of discrete elements. The geometry of a fluid domain (voids) is thus not accurately reproduced. The triangles do not reproduce a geometry but volumes of voids. A single triangle covers partially particles and a void. The void volumes are the difference between the areas of triangles and areas of particles in triangles and next multiplied by 1 m (in the z-direction). One pore is always discretized by one triangle. This approach is also called the pore-scale finite volume (PFV) method [4, 55]. The model may describe either incompressible or compressible fluid. Due to its simplicity, PFV overcomes the problem of the high computational cost of meso-scale models without introducing all phenomenological assumptions of continuum-based methods [23]. The models meet the following simplifying assumptions [4, 32, 40, 47, 55, 60]: (a) the single-phase fluid flow (full saturation) in voids and fractures; the only phase is a fluid (the gas-phase is neglected), (b) the incompressible viscous laminar fluid flow (turbulent flow conditions are neglected) and (c) isothermal conditions in rock and flowing fluid (thermal stresses are not taken into account).

There exist also several combined solutions using DEM connected to the Smooth Particle Hydromechanics (SPH) approach to describe the fluid behaviour [2, 14, 34, 44, 53]. Other coupled approaches which were successfully applied to fluid-particle system simulations is DEM combined with the lattice Boltzmann method [3, 33] that comes from the kinetic theory of gases. However, this approach requires huge computation time and is rarely employed in modelling of hydro-fracking. Recently several coupled DEM/CFD simulation results were described in different hydro-mechanical engineering problems [12, 30, 46, 58, 59, 62, 63].

The paper is arranged as follows. After Introduction (Sect. 1) and a brief overview of existing continuous and discontinuous approaches for simulating hydro-fracking in rocks, the discrete element method is summarized in Sect. 2 and the fluid flow model in Sect. 3. The coupling of DEM/CFD is discussed in Sect. 4 and the model calibration in Sect. 5. Section 6 reports on numerical study results of hydro-fracking in a rock specimen. Finally, some concluding remarks are offered in Sect. 7.

2 DEM for rocks

The advantage of the meso-scale modelling (in particular under 3D conditions) is that it directly simulates meso-structure and thus may be used to comprehensively study the mechanism of the initiation, growth and formation of localized zones and cracks that greatly affect the macroscopic behaviour of frictional-cohesive materials. It may also be used for studying different local phenomena at the aggregate level (e.g. force chains and vortex-structures) to predict the early fracture process [24, 36]. The disadvantages are the huge computational cost.

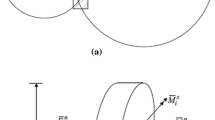
In order to describe the mechanical behaviour of rocks at the meso-scale, DEM was used. The calculations were performed with the three-dimensional open-source spherical explicit discrete element model YADE which was developed at the University of Grenoble [25, 49]. DEM considers a material as consisting of particles interacting with each other through a contact law and Newton’s second law via an explicit time-stepping scheme [8]. Outstanding advantages of DEM include its ability to explicitly handle the modelling of particle-scale properties including size and shape which play an important role in the fracture behaviour of frictional-cohesive materials [37]. The disadvantage is an enormous computational cost. The DEM model was successfully used for describing the behaviour of granular materials by taking shear localization into account [26,27,28,29, 38]. It demonstrated also its usefulness for both local and global fracture simulations in concrete under bending (2D and 3D analyses) [37, 48], uniaxial compression (2D and 3D simulations) [50] and splitting tension (2D analyses) [51, 52]. The 3D spherical discrete element method takes advantage of the so-called soft-particle approach (i.e. the model allows for particle deformation that is modelled as an overlap of particles) (Fig. 1). A linear normal contact model under compression was used (Fig. 1b). The interaction force vector representing the action between two spherical discrete elements in contact was decomposed into the normal and tangential components. A cohesive bond was assumed at the grain contact exhibiting brittle failure under the critical normal tensile load. The tensile failure initiated contact separation and the shear cohesion failure initiated contact slip and sliding obeying the Coulomb friction law under normal compression (Fig. 1a). The linear elastic response was assumed before reaching the fracture condition. The contact forces were linked to the displacements through the normal and tangential stiffness moduli K_n and K_s (Fig. 1a–c) [25]

$$\vec{F}_{\text{n}} = K_{\text{n}} U\vec{N}$$

(1)

$$\vec{F}_{\text{s}} = \vec{F}_{\text{s,prev}} + K_{\text{s}} \Delta \vec{X}_{\text{s}} ,$$

(2)

where U is the overlap between elements, $\vec{N}$ denotes the unit normal vector at the contact point, $\vec{X}_{\text{s}}$ is the increment of the relative tangential displacement, and $\vec{F}_{\text{s,prev}}$ is the tangential force from the previous iteration. The normal and tangential stiffness moduli K_n and K_s were computed as the functions of the modulus of elasticity E_c and Poisson’s ratio υ_c of the grain contact and two contacting grain radii R_A and R_B (to determine the tangential stiffness K_s), respectively [25]

Fig. 1

Mechanical response of DEM: a tangential contact model, b normal contact model, c loading and unloading path in tangential contact model and d modified Mohr–Coulomb model [25, 49]

$$K_{\text{n}} = E_{\text{c}} \frac{{2R_{\text{A}} R_{\text{B}} }}{{R_{\text{A}} + R_{\text{B}} }}\quad {\text{and}}\quad K_{\text{s}} = \upsilon_{\text{c}} E_{\text{c}} \frac{{2R_{\text{A}} R_{\text{B}} }}{{R_{\text{A}} + R_{\text{B}} }}$$

(3)

If two grains in contact had the same size (R_A= R_B= R), the numerical stiffnesses were equal to: K_n= E_cR and K_s= υ_cE_cR, respectively (thus K_s/K_n= υ_c). The contact forces $\vec{F}_{\text{s}}$ and $\vec{F}_{\text{n}}$ in the limit states were assumed to satisfy the Coulomb condition for the cohesive failure and frictional sliding states (Fig. 1d)

$$\left\| {\vec{F}_{\text{s}} } \right\| - {F_{ \hbox{max} }^{\text{s}} } - \left\| {\vec{F}_{\text{n}} } \right\| \times \tan \mu \le 0\quad ({\text{before}}\;{\text{contact }}\;{\text{breakage}})$$

(4)

and

$$\left\| {\vec{F}_{\text{s}} } \right\| - \left\| {\vec{F}_{\text{n}} } \right\| \times \tan \mu_{\text{c}} \le 0\quad \left( {{\text{after}}\;{\text{ contact }}\;{\text{breakage}}} \right),$$

(5)

where μ_c denotes the inter-particle friction angle. Moreover, if any contact between grains after failure re-appeared, the cohesion between them was not taken into account (Eq. 5). The motion of fragments (mass-spring systems with cohesion) was similar to the rigid body motion. A choice of a very simple constitutive law was intended to capture on average various contact possibilities in a real material. The critical cohesive $F_{ \hbox{max} }^{\text{s}}$ and tensile forces $F_{ \hbox{min} }^{\text{n}}$ were assumed as a function of the cohesive stress C_c (maximum shear stress at pressure equal to zero), tensile normal stress T_c and element radius R [13, 25]

$$F_{ \hbox{max} }^{\text{s}} = C_{\text{c}} R^{2} \quad {\text{and}}\quad F_{ \hbox{min} }^{\text{n}} = T_{\text{c}} R^{2} .$$

(6)

A crack occurred when the normal force between elements in Eq. (1) reached its minimum value $F_{ \hbox{min} }^{\text{n}}$ (Eq. 6) or the cohesive force between grains (Eq. 4) disappeared after reaching the critical threshold value $F_{ \hbox{max} }^{\text{s}}$ (Eq. 6). For two discrete elements in contact, the smaller values of C_c, T_c and R were used. A local non-viscous damping scheme was applied [7] in order to dissipate excessive kinetic energy in a discrete system and facilitate convergence towards quasi-static equilibrium. The damping parameter α_d was introduced to reduce the forces acting on elements

$$\vec{F}_{\text{damped}}^{k} = \vec{F}^{k} - \alpha_{\text{d}} \cdot \text{sgn} \left( {\vec{v}_{\text{p}}^{k} } \right) \left\| \vec{F}^{k} \right\| ,$$

(7)

where $\vec{F}^{k}$ are the kth components of the residual force and translational particle velocity v_p, respectively. A positive damping coefficient α_d was assumed smaller than 1 (sgn(·) to preserve the sign of the kth component of velocity). The equation could be separately applied to each kth component of the 3D vector x, y and z. Note that material softening was not assumed in the DEM model. The crack was not allowed to propagate through grains, i.e. the grain breakage has not been taken into account yet. The following five main local material parameters are needed for our discrete simulations: E_c, υ_c, μ_c, C_c and T_c. In addition, the particle radius R, particle mass density ρ and damping parameters α_d were required. In general, the shape of interacting discrete elements may be arbitrary [27].

In general, the DEM material constants are calibrated with the aid of simple laboratory tests on the material (uniaxial compression, uniaxial tension, shear, biaxial compression). The detailed calibration procedure for frictional-cohesive materials (e.g. concrete) was described in [36, 37] based on real simple standard laboratory tests (uniaxial compression and uniaxial tension) of concrete specimens. The calibration process consisted of running several uniaxial tension and uniaxial compression simulations on a given assembly of discrete elements with the same material constants to reproduce the selected experimental behaviour.

3 Fracturing fluid flow model

Hydro-fracking in rocks involves a high-pressure injection of fluids (over 70 MPa). The dominating fluid flow driving factor is thus pressure. After hydro-fracking initiates, fracture starts to propagate in rocks and to affect a topology of all voids (including micro- and macro-voids, pre-existing fractures and newly forming hydraulic fractures) that results in large volume and velocity changes of the fracking fluid. The basic concept of the virtual pore network (VPN) assumed in current calculations was a division of the entire physical system into two domains which together co-existed and did not overlay each other (Fig. 2). The 2D concept was the following: (1) the system of discrete particles described the rock matrix behaviour and (2) the continuous domain included all voids wherein the fracking fluid moved. The voids were discretized into a grid of non-regular triangles [called here virtual pores (VPs)] (Fig. 2) to precisely capture their changing geometry (shape, area and location). The vertices of triangles were on the surfaces of spheres (but not at the gravity centres of spheres as in the PFV method). The triangles accurately reproduced the geometry of voids between the discrete elements. The grid density could be changed by a user. The denser the grid, the more accurate were the results.

Fig. 2

Specimen divided into: (A) continuous domain representing fluid and (B) discrete domain composed of particles representing rock mass

The gravity centres of grid triangles were connected by channels composed of two parallel plates that created a fluid flow network (Fig. 3a). One assumed two channel types: 1) those running between discrete elements of the rock matrix in contact (called the ‘S2S’ channels) (detail ‘A’ in Fig. 3b) and 2) those connecting triangles that touched each other by a common edge (called the ‘T2T’ channels) (detail ‘B’ in Fig. 3b). The pronounced changes of both the geometry and topology were continuously tracked in detail. In contrast to existing pore network models for rocks, VPs accumulated pressure and stored both the fluid fraction and density. We assumed incompressible laminar one-phase fluid flow under isothermal conditions in the rock matrix. The mass change in VPs was related to a fluid density change that resulted in pressure variations. The fluid initially might exist in both the rock matrix and pre-existing fractures. It might fully or partially fill in the voids. The fluid moved flow from VP to another one when it was already fully filled. The pressure increased in fully filled VPs but it did not change in partially filled VPs. To simplify the fluid flow model, the fluid flow network approach was assumed wherein the fluid flow solely took place in the network of channels. The fluid domain was divided into the triangles. The volumetric parameters in each triangle were reduced to the points that were located in their gravity centres. The fluid could solely flow in the fluid flow network and was driven by a pressure difference between the adjacent VPs. In general, the pressure in the points connecting channels did not solely depend on mass flow rates in channels but also on volume changes. Since there was no fluid flow in triangles by assumption (flow regime was stagnant and Re ≪ 1), the fluid velocity was close to zero. As a result, the equation of momentum conservation was neglected in triangles. However, the mass was still conserved in the entire volume of triangles. The volume changes, mass sources and mass flow rates were taken into account in channels to compute the pressure in triangles. The fluid flow (for a stagnant flow regime) was separately considered in VPs and in the channels connecting VPs.

Fig. 3

Fluid flow network in rock matrix with triangular discretization of voids: a fluid flow network (in blue) and b channel types: (A) ‘S2S’ (red colour) and (B) ‘T2T’ (red colour) (color figure online)

3.1 Fluid flow model in channels

The full one-phase laminar fluid flow was assumed in channels without transitional zones. The capillary pressure was neglected due to a huge injection pressure. The fluid moved in channels through a thin film region that was separated by two closely spaced parallel plates according to a classical lubrication theory [19] (based on the Poiseuille flow law [1]):

$$h\frac{\partial \rho }{\partial t} = \frac{{\partial M_{x} }}{\partial x},$$

(8)

where h denotes the hydraulic channel aperture (its perpendicular width) (m), ρ is the fluid density (kg/m³), t is the time (s), $M_{x}$ denotes the mass fluid flow rate (per unit length) across the film thickness in the x-direction [kg/(m s)]. The mass fluid flow rate was computed from Eq. (8) as

$$M_{x} = \rho \frac{{h^{3} }}{12\mu }\frac{\partial P}{\partial x},$$

(9)

where μ denotes the dynamic fluid viscosity (Pa s) and P is the fluid pressure (Pa). The mass fluid flow rate depends on the channel length L and its hydraulic aperture h. The channel length was assumed to be equal to the distance between the gravity centres of adjacent grid triangles (Fig. 3).

In real 3D problems, the fluid flows around the spheres in contact. However, in 2D problems, there is no free space for fluid flow. Therefore, the concept of virtual channels, called S2S, was introduced. The S2S channels connected the centres of gravity of two triangles which were separated by the spheres in contact (Fig. 5b). They were located along a contact line between two neighbouring deformed or non-deformed spheres. Usually, the S2S channels did not coincide with the contact lines between spheres (they intersected one triangle’s edge only). However, if the S2S channel crossed the vertices of triangles, the flow rate was uniformly divided into adjacent edges. The S2S channel existed in the system until the contact between the spheres was lost. After that, free space occurred that was next discretized by the new triangles.

The hydraulic aperture h of the channel type ‘S2S’ was related to the normal stress by the slightly modified empirical formula of Hökmark et al. [20]:

$$h = \beta \left( {h_{ \inf } + \left( {h_{0} - h_{ \inf } } \right){\text{e}}^{{ - 1.5 \cdot 10^{ - 7} \sigma_{\text{n}} }} } \right),$$

(10)

where $h_{ \inf }$ is the hydraulic aperture for the infinite normal stress (m), $h_{0}$ denotes the hydraulic aperture for the zero normal stress (m), $\sigma_{\text{n}}$ is the effective normal stress at the particle contact (N/m²) and β denotes the aperture coefficient (to be determined in a macroscopic permeability test, Sect. 6.2). The hydraulic aperture of the channel type ‘T2T’ was directly connected to the geometry of adjacent triangles (Fig. 4) as

$$h = \gamma e\cos \left( {90^\circ - \omega } \right),$$

(11)

where e the length of the edge between two adjacent triangles (m), ω the angle between the edge with the length e and the centre line of the channel that connects two adjacent triangles and γ the reduction factor, necessary to fit the intensity of fluid flow to real complex fluid flow conditions in rocks (Sect. 6.2). The reduction factor γ was determined in parametric studies so that the maximum Reynolds number Re along the main flow path was always lower than the critical one for in a turbulent flow regime. Experimentally, Pfenninger [42] maintained laminar pipe flow up to Re = 10⁵. Hence, the critical number of Re = 10⁵ was chosen in the current computations.

Fig. 4

‘T2T’ channel (red colour denotes channel width h) (color figure online)

For the ‘S2S’ channels located between overlapping discrete elements, a special discretization procedure was used (Fig. 5a). The 3D spherical particles were projected onto the 2D plane and next discretized into the 2D polygons. Next a remeshing procedure discretized overlapping circles, determined contact lines and deleted overlapping areas (Fig. 5b).

Fig. 5

‘S2S’ channels between deformed spheres: a overlapping spheres ‘A’ and ‘B’ and b deformed spheres ‘A’ and ‘B’ after discretization

The shear stress along the boundary of the channel occurred due to viscous fluid flow. For non-movable parallel plates with no-slip boundary conditions (zero velocity), the shear stress profile in the fluid was triangular (the positive sign is for y = 0 and the negative sign is for y = h). The shear stress $\tau_{f0}$ at the channel surface for y = 0 was calculated as

$$\tau_{f0} = \frac{h}{2}\frac{{P_{i}^{n} - P_{j}^{n} }}{L}.$$

(12)

3.2 Fluid flow model in VPs

For fluid in VPs, two additional assumptions were met:

• flow regime was stagnant (the Reynolds number Re ≪ 1) and

• fluid was barotropic ($\rho = \rho (P)$).

The integral form of the mass conservation equation in VPs is (by neglecting the grid velocity)

$$\frac{\text{d}}{{{\text{d}}t}}\mathop \int \limits_{V} \rho {\text{d}}V + \mathop \int \limits_{\partial V} \rho \vec{v} \cdot d\vec{A} - {\dot{Q}}_{v} = 0.$$

(13)

Equation (13) may be expressed next in terms of the sum of volume fluxes along VP edges as

$$\frac{\text{d}}{{{\text{d}}t}}\mathop \int \limits_{V} \rho {\text{d}}V + \mathop \sum \limits_{f} \left({\rho_{f} U_{f}^{n}} \right) - {\dot{Q}}_{v} = 0,$$

(14)

where f is the triangle edge number, $U_{f}^{n}$ the volume flux through the edge f (m³/s) based on the channel average velocity, t the time step (s), n the time increment, i the VP number (–), ${\acute{Q}}_{v}$ the internal source (kg/s) and $\rho_{f}$ the fluid density through the edge f. The internal source ${\acute{Q}}_{v}$ was used to define boundary conditions only, e.g. the mass flow rate at the injection point. The explicit formulation did not require an iterative solution of the transport equation during each time step. The product $\rho_{f} U_{f}^{n}$ in Eq. (14) was the mass flow rate $M_{f}$ of the fluid flowing through the edge f of VP_s. It was equal to (based on Eq. 9)

$$M_{f} = \rho_{f}^{n} \frac{{h^{3} }}{12\mu }\frac{{P_{i}^{n} - P_{j}^{n} }}{L},$$

(15)

where i is the VP number, j the adjacent VP number, P the pressure, L the channel length (m) and f the edge number of the triangle in VP. The linear relationship between the density and pressure was assumed for a fluid [5]

$$\rho_{i}^{n + 1} = \rho_{0} \left( {1 + C\left( {P_{i}^{n + 1} - P_{0} } \right)} \right),$$

(16)

where $P_{0}$ is the reference pressure (Pa), $\rho_{0}$ the density for the reference pressure (kg/m³) and $C$ the fluid compressibility (1/Pa). Substituting Eq. (16) into Eq. (14) and transforming it with respect to ${\partial P}/{\partial t}$, the pressure change in VPs was expressed as

$$\mathop \int \limits_{V} \frac{\partial P}{\partial t}{\text{d}}V = K\left({\mathop \sum \limits_{j = 1}^{k} ({q_{j}}) - {\dot{V}} + Q_{v}} \right),$$

(17)

where $V$ is the volume of VP (m³), $K$ the fluid bulk modulus (Pa), $q_{j}$ the volumetric flow rate of the fluid (m³/s), k the number of VP edges (for 2D problems it is equal to 3), ${\acute{V}}$ the time derivative of the virtual pore volume (m³/s) and $Q_{v}$ the internal source (m³/s). By using a first-order backward difference time integration scheme, Eq. (17) was replaced by a discrete form

$$P_{i}^{n + 1} = \Delta t\frac{K}{{V_{i}^{n}}}\left({\mathop \sum \limits_{j = 1}^{k} \left({q_{j}} \right) - {\dot{V}} + Q_{v}} \right) + P_{i}^{n},$$

(18)

where $\Delta t$ is the time step (s), $V_{i}^{n}$ the volume of VP_i (m³), j the channel number and n the time increment. The volumetric fluid flow rate $q_{j}$ was computed from Eq. (15) as

$$q_{j} = \frac{{h^{3} }}{12\mu }\frac{{P_{i}^{n} - P_{j}^{n} }}{L}.$$

(19)

There exist 3 terms affecting the pressure (Eq. 19): the sum of the volumetric fluid flow rates in the channels, the time derivative of the volume and the internal source. The sum of the volumetric fluid flow rates in the channels was the result of fluid flow and was computed in CFD. The time derivative of the volume was due to the counter forces acting on the fluid. It was computed in DEM and next transferred to CFD. The internal source was solely used to define boundary conditions (volumetric flow rate) in boundary pores.

Fluid flow between VPs was allowed only when VP was fully saturated. Thus, the pressure in VP solely increased when the fluid volume/area fraction was $\alpha = 1$. In partially filled VPs ($\alpha < 1$), the pressure was equal to its initial value. The fluid volume fracture $\alpha_{i}^{n + 1}$ in VPs was computed as

$$\alpha_{i}^{n + 1} = \frac{{V_{w,i}^{n + 1} }}{{V_{p,i}^{n + 1} }},\quad {\text{with}}\quad V_{w,i}^{n + 1} = V_{w,i}^{n} + \Delta V_{i} ,$$

(20)

where $V_{p,i}^{n + 1}$ is the volume of VP_i for the n + 1 time increment, $V_{w,i}^{n}$ the fluid volume VP_i for the time increment n and $\Delta V_{i}$ the fluid volume that was transported from the adjacent VPs into VP_i during the time step $\Delta t$. The transported fluid volume $\Delta V_{i}$ was computed as

$$\Delta V_{i} = \frac{{\Delta m_{i} }}{{\rho_{i} }},\quad {\text{with}}\quad \Delta m_{i} = \Delta t \cdot \mathop \sum \limits_{f} \rho_{f}^{n} \frac{{h^{3} }}{12\mu }\frac{{P_{i}^{n} - P_{j}^{n} }}{L}.$$

(21)

Putting Eqs. (16) and (21) into Eq. (20), the transported fluid volume $\Delta V_{i}$ was

$$\Delta V_{i} = \frac{1}{{\rho_{0} (1 + C(P_{\text{init}} - P_{0} ))}}\Delta t \cdot \mathop \sum \limits_{f} \rho_{f}^{n} \frac{{h^{3} }}{12\mu }\frac{{P_{i}^{n} - P_{j}^{n} }}{L},$$

(22)

where $P_{\text{init}}$ denotes the initial pressure in the rock mass (Pa).

3.3 Discretization and large grid deformations

The discrete and continuous domains were discretized into a triangular grid. The triangular grid of the continuous domain was used to model fluid flow. The algorithm of discretization was based on the Delaunay triangulation. In the first step, the circumference of spheres and voids was discretized. The number of vertices along the circumference was a parameter set by the user. In the second step, the contact lines (Fig. 5b) between the deformed spheres were identified and the additional vertices of triangles were generated. When the distance between some vertices was too small (defined by a critical value), one of those vertices was removed to avoid too small triangles in the final mesh. Finally, the S2S and T2T channels were generated (Figs. 3, 4). The discretization algorithm directly influenced the fluid flow network. The denser was the grid, the more precise fluid flow path was reproduced.

When the hydraulic fracture started to propagate, the pore triangular grid significantly deformed. The triangle vertices in VPs changed their location, and the triangles changed their volumes. The volume changes in Eq. (18) were transferred to CFD. The grid remeshing was automatically performed when topological properties of the grid geometry changed (e.g. two spheres lost contact or the triangle was deformed due to a sphere rotation, Fig. 6). To identify the change in topological geometry properties, the remeshing procedure was applied based on two criteria: the loss of the contact between two spheres or the excessively distorted shape of triangles. The contact between two spheres was lost when the normal force in contact was equal to zero (the crack occurred). The triangle was considered to be too distorted when the ratio of its area to the circumference was below a certain limit value (e.g. 1 mm). Those two criteria were checked in each iteration. In contrast to the existing DEM/CFD models (e.g. in YADE), the grid reproduced the geometry of voids between the discrete elements (Fig. 3). The topology of the grid reproducing the geometry of voids (number of triangles, location of triangle vertices and shape of triangles) could strongly vary after each remeshing and the grids did not match each other (old and new ones). Thus, the computational results (e.g. pressures, fluid fractions) had to be accurately transformed from the old grid to the new one (modified by the remeshing procedure). After remeshing, the pressure and fluid phase fraction in VPs were transformed from the old grid to the new one, based on the assumption that mass was a topological invariant. The triangles that had changed the volume only were not transformed (the volume changes were taken into account in Eq. 18). However, after remeshing, there might happen that, e.g. VP located in the new grid overlapped some VPs that were located in the old grid (Fig. 7) or the new VP appeared in the new grid at the place where previously was a sphere in the old grid. If the VP configuration changed and the grid was remeshed, a transformation procedure was performed and the new grid was projected onto the old grid. Figure 7 presents a transformation of the new remeshed grid when one sphere rotated. The new VP1 (Fig. 7b) in the new grid was projected onto the old grid. The new VP1 (continuous green line) overlapped partially two VPs in the old grid (dotted red line). The volume part I of VP1 and volume part II of VP2 in the old grid were taken over by the new VP1. The fluid mass which was taken over was computed as

$$\mathop \sum \limits_{j = 1}^{J} \left( {V_{j}^{n} \alpha_{j}^{n} \rho_{j}^{n} } \right) = m_{T,i}^{n} ,$$

(23)

where j is the VP-number in the old grid, i the VP number in the new grid, J the number of VPs in the old grid from which VP_i in the new grid took over the mass, $V_{j}^{n}$ the fluid volume taken over from VP_j in the old grid, $\alpha_{j}^{n}$ the fluid volume fraction in VP_j, $\rho_{j}^{n}$ the fluid density in VP_j, and $m_{T,i}^{n}$ the total fluid mass taken over by VP_i in the new grid. If there was no volume change in VP_i (when applying the mass quantities in Eq. (15) instead of mass flow rates), Eq. (20) was used to find the fluid volume fraction. Similarly, Eq. (16) was used to calculate the new pressure after a transformation in VPs that were fully saturated.

Fig. 6

Topological changes of grid void geometry: (A) before deformation, (B) after deformation and (C) after remeshing a contact loss of two spheres and b deformation due to sphere rotation)

Fig. 7

VP in new grid overlapping some VPs in old grid (e.g. after sphere rotation): a overall view of deformed region, b zoomed view (A) mass transferred to new VP1 located in new grid (green colour) from two VPs (volume I from old VP1 and volume II from old VP2) located in old grid (red d dotted line) (color figure online)

The following material constants are needed for the CFD simulations: reference pressure $P_{0}$ (Pa), fluid density $\rho_{0}$ for the reference pressure $P_{0}$ (kg/m³), fluid bulk modulus K and dynamic fluid viscosity μ (Pa s). The inverse of the bulk modulus gives a fluid compressibility C (1/Pa).

4 Hydro-mechanical coupling

The coupling scheme of DEM with CFD involved two sets of discrete equations to be solved: the flow rule defined in Eqs. (18) and (19) for all VPs and the law of motion defined in DEM for all discrete elements. The two-way coupling scheme (Fig. 8) was based on a transfer of pressure and shear stress forces from CFD to DEM and the time derivative of the Virtual Pore volume from DEM to CFD. The pressure and shear forces from the fluid caused the displacements of spheres in DEM that changed the coordinates and volumes of triangles in VPN. The term ${\dot{V}}$ was computed in DEM and next transferred to CFD. The volume change was taken into account in Eq. (19) that included the term ${\dot{V}}$. As a result, the volume change in DEM affected the pressure change in the fluid in CFD. The fluid pressures in VPs and channels were next converted into the forces acting on spheres in DEM. Two-time steps were distinguished: the fixed time step $\Delta t_{\text{D}}$ in DEM and the varying time step $\Delta t_{\text{C}}$ in CFD ($\Delta t_{\text{C}} \le \Delta t_{\text{D}}$). The CFD time step was limited by the Courant–Friedrichs–Lewy condition (for 1D channel flow) [6]

$$\Delta t_{\text{C}} = C_{ \hbox{max} } \frac{{L_{ \hbox{min} } }}{{v_{ \hbox{max} } }},$$

(24)

where $C_{ \hbox{max} }$ the Courant number (–), $L_{ \hbox{min} }$ the minimum channel length (m) and $v_{ \hbox{max} }$ the maximum fluid channel velocity (m/s). The Courant number $C_{ \hbox{max} }$ was limited to 0.1. The rock pressure field and shear stresses in the ‘S2S’ channels were calculated by CFD in each time step $\Delta t_{\text{C}}$. They were, however, transferred from CFD to DEM in each time step $\Delta t_{\text{D}}$. They were used to compute the fluid forces which were added to the contact forces F before the time integration to update the displacements of each discrete element.

Fig. 8

DEM-CFD coupling schema (m is current time sub-increment and n_c is number of sub-increments in CFD)

The discrete domain (DEM) was modelled as a 3D system while the fluid domain (CFD) was modelled as a 2D system. The discrete domain consisted of one layer of spheres whose centres were located in the XY plane. The fluid pressures in VPs and ‘S2S’ channels were converted into the forces $\vec{F}_{P,j}$ acting on spheres (Fig. 9b)

$$\vec{F}_{P,j} = - P_{i} \vec{n}A_{k} ,$$

(25)

where $\vec{n}$ is the unit vector normal to the discretized sphere’s edge, $P_{i}$ the pressure in VP, i the VP number, j the sphere number and $A_{k}$ the contact area between the fluid in VP_i and sphere

$$A_{k} = 2r_{j} e_{k} ,$$

(26)

where $r_{j}$ is the sphere radius and $e_{k}$ the sphere edge length. The shear stresses were converted into the forces acting on spheres in the ‘S2S’ channels (Fig. 9c) as

$$\vec{F}_{S,j} = \tau_{f0,i} \vec{I}A_{k} \quad {\text{with}}\quad A_{k} = 2r_{j} L_{k} ,$$

(27)

where $\vec{I}$ is the unit vector parallel to the channel wall and oriented in the fluid flow direction, $\tau_{f0,i}$ the shear stress in the channel (Eq. 12), i the channel number, j the sphere number and $A_{k}$ the contact area between the channel fluid and sphere and $L_{k}$ the channel length. The DEM/CFD coupling technique was implemented into the platform YADE. The developed method of the fluid domain discretization and hydro-mechanical coupling enabled to simulate floating of particles in fractures. The floating particles in fractures were usually surrounded by triangles of a CFD domain only. Owing to the novel remeshing and transformation procedure, the interaction between the floating particle and the surrounding fluid was reproduced. Thus, the particle movement might be observed and tracked.

Fig. 9

Schema of converting fluid pressure and shear stress into force acting on discretized sphere: a original sphere, b pressure conversion on discretized sphere and c shear stress conversion on discretized sphere

The extension of the VPN model from 2D into 3D is straightforward. The discrete and continuous domains are discretized using tetrahedrons under 3D conditions (instead of triangles in 2D conditions). The S2S virtual channels are not required (the T2T channels exist only). In 3D, the width of channels is related to the geometry of tetrahedron’s faces (in 2D, the width of S2S and T2T channels is equal to 1 m). The mathematical model of fluid flow is the same under 2D and 3D conditions.

5 Model calibration

5.1 Pure DEM calibration

The real meso-structure of the rock mass was not taken into account. Instead an extremely simple 2D DEM one-phase mesoscopic model with spheres was assumed to approximately reproduce the rock mass behaviour at the meso-scale. The specimen included one row of spherical particles in depth. The spheres’ diameter was between 0.7 and 1.3 mm (with the mean diameter equal to d₅₀= 1 mm). An arbitrary micro-porosity can be achieved in DEM due to that the particles may overlap. The initial micro-porosity was assumed as p = 1% (corresponding, e.g. to shale rocks). The spheres were put into the box that corresponded to the rock specimen size and shape (with the inter-particle friction angle of μ_c= 0°) until the desired initial micro-porosity was obtained. The spheres were allowed to settle until their total kinetic energy became insignificant. Next, all forces between the spheres were deleted due to the particle penetration U and μ_c was set on the target value [37]. In order to take the starting configuration into account, the initial overlap was subtracted in each calculation step when determining the normal forces ($\vec{F}_{\text{n}} = K_{\text{n}} \left( {U_{n} - U_{0} } \right)\vec{N}$, where U_o is the initial overlap and U_n the overlap in the calculation n-steps). The following material constants were mainly used in all DEM analyses for rock specimens (Sect. 4): E_c= 3.36 GPa, υ_c= 0.3, C_c= 170 MPa and T_c= 34 MPa (C_c/T_c= 5), μ_c= 18° and ρ = 2.6 kG/m³. The damping parameter α_d= 0.10 did not affect the results [27, 28, 50, 51]. The material constants were calibrated in order to approximately describe laboratory test results for shale rock [17] during quasi-static both uniaxial compression and tension splitting. About 10,000 spheres were used in calculations. For uniaxial compression, the quadratic specimen 100 × 100 mm² was assumed. The bottom and top of specimen were smooth. The prescribed vertical displacement was applied along the top boundary with the constant load velocity of 2 mm/s. For tension splitting, the circular specimen was used with the diameter of D = 100 mm. The vertical displacement was prescribed along the specimen top and bottom boundary by two rigid cylinders to eliminate the effect of boundaries [51] (with the constant load velocity of 2 mm/s).

Figure 10 shows the 2D stress–strain or stress–displacement curves and fracture patterns during some simple strength tests for the rock specimen (uniaxial compression and tension splitting). The calculated maximum compressive normal stress was σ = 47 MPa for the vertical normal strain ε = 1% (Fig. 10Aa), and the maximum tensile stress was σ = 8 MPa for the displacement of u = 0.75 mm (Fig. 10Ba) (the values are in agreement with, e.g. the experiment [17]). Note that the displacements shown in [17] also included the piston displacement until the specimen’s compression started. The numerical post-peak response of the rock specimen was too brittle in both the cases due to some simplifications met (simple one-phase material, narrow particle diameter size range, 2D analyses and small number of spheres) [36]. The failure mode was characterized during uniaxial compression by the occurrence of few almost vertical and skew macro-cracks (Fig. 10Ab) and during tension splitting by one vertical macro-crack (Fig. 10Bb) as in experiments [17]. In addition, Fig. 11 demonstrates the effect of micro-porosity p on strength and brittleness of the specimen for p = 1%, p = 5% and p = 10%. The strength, initial stiffness and brittleness of rock specimens decreased with increasing micro-porosity. The maximum vertical normal stress was σ = 16-47 MPa (uniaxial compression) and σ = 3.7-8.0 MPa (tension splitting).

Fig. 10

2D pure DEM: a stress–strain or stress-displacement curves and b fracture patterns for uniaxial compression (A) and splitting test (B) with specimen initial micro-porosity 1% (displacements were was magnified by factor 100)

Fig. 11

2D pure DEM: stress–strain curves for uniaxial compression (A) and stress-displacement curves for tension splitting (B) with initial micro-porosity p: ap = 1%, bp = 5% and cp = 10%

5.2 CFD calibration

Two types of rocks were chosen to study the physical correctness of the VPN model: fresh limestone and sandstone. The calibration was performed for average rock permeability values. The aperture constant β in Eq. (10) was calibrated by means of a numerical permeability test (Fig. 12). The quadratic specimen 10 × 10 mm² was chosen. All spherical discrete elements of the rock specimen were fixed so that the rock matrix was non-deformable. The test was performed until the equilibrium was reached. The specimen was fully saturated. The zero-flux conditions ($q_{\text{BC}} (t) = 0$) were imposed on vertical walls. The pressures $P_{\text{UP}} (t)$ and $P_{\text{BT}} (t)$ were imposed along horizontal walls of the specimen (Fig. 12a). The uniform initial conditions were assumed for the water pressure $P_{0} (t = 0) = 10\;{\text{MPa}}$. The initial micro-porosity of the rock specimen was again p = 1%, and the fluid properties were as follows: dynamic viscosity $\mu = 4.06 \cdot 10^{ - 4}$ Pa s (water at the temperature of 70 °C), compressibility $C = 4.0 \cdot 10^{ - 10}$ Pa⁻¹ and fluid density $\rho_{0} = 977.36\;\frac{\text{kg}}{{{\text{m}}^{ 3} }}$ for the reference pressure $P_{0} = 0.1\;{\text{MPa}}$. The channel apertures in Eq. (10) were $h_{ \inf } = 2.5 \cdot 10^{ - 8}$ m and $h_{0} = 3.25 \cdot 10^{ - 7}$ m (Eq. 10). The reduction factor was $\gamma = 0.01$ (Eq. 11). The calibration procedure was performed for two different aperture coefficients β: β = 0.9 (case ‘1’) and β = 1.2 (case ‘2’). Assuming that the volumetric flow rate at horizontal walls was the same at the equilibrium state, the macroscopic permeability coefficient κ of the rock specimen was calculated using the Darcy’s law:

$$\kappa = \frac{Q}{A}\mu_{q} \frac{L}{\Delta P},$$

(28)

where Q is the volumetric flow rate at the equilibrium (m³/s), A the specimen cross section (m²), L the specimen height and $\Delta P$ the pressure difference between the bottom and top wall (Pa).

Fig. 12

Permeability CFD test for rock specimen (case ‘2’ with β = 1.2): a geometry and boundary conditions, b pressure distribution at equilibrium state and c pressure isolines (scale denotes pressure)

The equilibrium state was reached for the fluid velocity of 0.016 m/s for the case ‘1’ and 0.008 m/s for the case ‘2’. The calculated permeability coefficients of the rock matrix were: $\kappa = 1.092 \cdot 10^{ - 17}$ m² for the case ‘1’ (value typical for rocks like fresh limestone and dolomite) and $\kappa = 2.165 \cdot 10^{ - 15}$ m² for the case ‘2’ (value typical for sandstone). A realistic one-dimensional fluid flow was obtained at the macroscopic level (Fig. 12b). The pressure isolines (Fig. 12c) were almost parallel to the bottom and top wall of the rock specimen (they were qualitatively the same for the cases ‘1’ and ‘2’). The aperture constant β = 0.9 (corresponding to fresh limestone) was chosen for further simulations. Note that the calibration of β has to be always carried out for the specified rock.

5.3 Dependence on time step

Three fixed DEM time steps were analysed: $\Delta t_{\text{D}} = 5 \cdot 10^{ - 8}$, $\Delta t_{\text{D}} = 1 \cdot 10^{ - 8}$ and $\Delta t_{\text{D}} = 1 \cdot 10^{ - 9}$ (Fig. 13). The adaptive CFD time step was varying with the fixed $C_{ \hbox{max} }$ = 0.1. The quadratic specimen 10 × 10 mm² was chosen (Fig. 13a). The initial fluid fraction in voids of the rock matrix was α = 1 (full saturation). The initial porosity of the specimen was p = 1%. The fluid and rock properties were as in Table 1. The grain diameter varied between 0.75 and 1.30 mm. The initial vertical and horizontal normal stresses were equal to 30 MPa, respectively. The impermeable walls were assumed. The pressure was applied on the specimen through smooth (frictionless) rigid walls. The walls were free to move (except the bottom one, which was fixed). One injection slot was located at the bottom mid-point of the rock specimen. The initial fluid pressure of 30 MPa was assumed in all pores. The fracking fluid with the constant pressure of 60 MPa was injected.

Fig. 13

Effect of time step in coupled DEM/CFD calculations: a rock specimen and b fluid pressure along main flow path

Table 1 Basic material constants assumed for rock matrix and fluid in coupled DEM/CFD calculations of hydro-fracking

The fluid pressure along the main flow path in the hydraulic fracture is shown in Fig. 13b. The maximum pressure difference of 2.54 MPa (4.2% of the maximum pressure in the main fluid flow path in the hydraulic fracture) was obtained between the time step $\Delta t_{\text{D}} = 5 \cdot 10^{ - 8}$ and $\Delta t_{\text{D}} = 1 \cdot 10^{ - 9}$. However, a significant difference in the computing time t_c was registered (t_c= 2 h for $\Delta t_{\text{D}} = 5 \cdot 10^{ - 8}$ and t_c= 23 h for $\Delta t_{\text{D}} = 1 \cdot 10^{ - 9}$). The computing time was not directly proportional to $\Delta t_{\text{D}}$ due to the use of the adaptive algorithm in CFD calculations (the shorter the DEM time step $\Delta t_{\text{D}}$, the less CFD time sub-steps were needed). The DEM time step of $1 \cdot 10^{ - 8}$ s was always assumed in the simulations. The CFD time step was about 2–10 times smaller.

6 Coupled DEM/CFD simulation results

The processes of initiation and propagation of hydraulic fracture in the rock specimen were studied for the different initial micro-porosity, rock strength, fracking fluid dynamic viscosity and the presence of a pre-existing fracture. In order to significantly reduce the computation time, a small quadratic rock specimen 30 × 30 mm² was assumed (with 1500 spheres). The specimen was subjected to biaxial compression (Fig. 14). The diameter of spheres was again in the range of 0.7 mm and 1.3 mm (Sect. 6.1). In order to more realistically distribute stresses along boundaries, a row of small spheres with the diameter of 0.5 mm was added. The initial vertical and horizontal normal stresses of 10 MPa were prescribed and kept constant. The rigid impermeable specimen edges were assumed to be smooth (frictionless). The boundaries were free to move except of the fixed bottom. The initial fluid pressure of 10 MPa was assumed in all pores. One injection slot was located at the bottom mid-point of the rock specimen with the width of 0.5 mm. To simulate the fluid flow conditions at one injection point, the constant pressure of 70 MPa was assumed instead of, e.g. the constant flow rate in the wellbore that lead in simulations to an uncontrolled pressure increase at the injection point. Thus, the magnitude of the flow rate should be defined according to the experimental data. In general, different boundary conditions in the fluid domain were implemented in our VPN model: constant pressure, variable pressure, constant flow rate, variable flow rate and controlled flow rate. They enabled us to reproduce arbitrary boundary conditions in the wellbore. The initial fluid volume fraction in the entire specimen was α = 0.98. The basic material constants for the fracking fluid and rock matrix in coupled DEM/CFD calculations are given in Table 1.

Fig. 14

Geometry and boundary conditions of rock specimen subjected to hydraulic fracturing with one injection slot at bottom (‘P1’—horizontal pressure, ‘P2’—vertical pressure, red arrow—injection of fracturing fluid) (color figure online)

6.1 Initiation and propagation of hydraulic fracture in rock matrix

The evolution of hydraulic fracture and fluid pressure is shown in Fig. 15. The results are presented for the advancing flow time t: t = 0.08 ms, t = 2.80 ms, t = 4.82 ms and t = 5.51 ms. The red colour denotes the maximum water pressure of 70 MPa and the cyan colour the minimum water pressure of 10 MPa. Figure 16 presents the evolution of the fluid parameters: pressure, velocity and Reynolds number along the main flow path in the moving hydraulic fracture.

Fig. 15

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) for time tat = 0.08 ms (initial stage), bt = 2.80 ms, ct = 4.82 ms and dt = 5.51 ms (final stage) (scales denote pressure)

Fig. 16

2D DEM/CFD simulations: propagation of single hydraulic fracture (A) pressure along main flow path l, (B) velocity along main flow path, (C) Reynolds number along main flow path: at = 0.08 ms, bt = 2.80 ms, ct = 4.82 ms and dt = 5.51 ms (red colour—fitting line obtained with distance weighted least squares method) (color figure online)

The hydraulic fracture occurred at the injection slot and propagated in a vertical direction up to the specimen top with some branches in the upper region caused by the specimen heterogeneity (Fig. 15). The final crack width for t = 5.51 ms varied between 0.75 mm and 1.3 mm. Initially, no fluid flow occurred since the fluid needed some time to flood first the micro-voids. The clear hydraulic fracture initiated for t = 0.29 ms. The fluid started to damage the rock matrix for t = 2.80 ms, when the pressure was higher than the rock strength and initial confining pressure. The mean fluid velocity was 0.5 m/s (R_e= 0–400) (Fig. 16). In the final stage of the hydraulic fracture process (t = 5.51 ms), some large fluid velocity jumps were obtained. The mean fluid velocity was 3.8 m/s; the fluid velocity locally increased up to 11.5 m/s. The maximum and mean Reynolds numbers were 20,300 and 4000 (Fig. 16dC), respectively, i.e. below the limit value of 10⁵. The fluid zone width was higher than the macro-crack width (up to 5 mm at the maximum in some regions) since the fluid slightly leaked out beyond the hydraulic fracture.

6.2 Effect of initial micro-porosity of rock matrix

Four different initial micro-porosities of the rock matrix p were chosen for comparative simulations: 1%, 5%, 10% and 15% (Fig. 17). The results of the hydraulic fracture were shown for the same time t = 2.57 ms for each different p. For this time, the macro-crack reached a left vertical specimen boundary for p = 15%. The height, inclination and width of the main crack and fluid path increased with the higher micro-porosity (Fig. 17). The height of the crack was measured in the vertical direction between its maximum point and bottom. The inclination of the crack was defined as the angle of the crack path to the horizontal. The width of the crack was the distance between the discrete elements without contact.

Fig. 17

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) with different initial micro-porosity p for time t = 2.57 ms: ap = 15%, bp = 10%, cp = 5% and dp = 1% (scales denote pressure, horizontal pink line denotes coordinate axis) (color figure online)

The fluid leakage became also higher with growing initial micro-porosity. The branching of the macro-crack already happened at the specimen bottom for the high p (p = 10–15%, Fig. 17a, b). The secondary macro-crack was almost horizontal for those cases. The fracture width was about 7 mm for p = 15%.

6.3 Effect of dynamic viscosity of fracking fluid

The effect of different viscosities of fluids in the conditions of the partially saturated rock matrix was investigated. Three different dynamic viscosities of the fracking fluid were chosen: μ = 0.4·10⁻⁴ Pa s (low fluid viscosity), μ = 0.7·10⁻⁴ Pa s (medium fluid viscosity) and μ = 1.0·10⁻⁴ Pa s (high fluid viscosity). Figure 18 presents the geometry of the hydraulic fracture with the approximate length of 20 mm in the specimen for different dynamic viscosities μ in the varying time t.

Fig. 18

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) with different dynamic viscosities of fracking fluid, aμ = 0.4·10⁻⁴ Pa s (t = 1.50 ms), bμ = 0.7·10⁻⁴ Pa s (t = 2.58 ms) and c μ = 1.0·10⁻⁴ Pa s (t = 3.06 ms) (scale denotes pressure, horizontal pink line denotes coordinate axis) (color figure online)

The results show that the smaller the dynamic viscosity, the faster the hydraulic fracture propagates. The macro-crack length of 20 mm was reached for t = 1.50 ms with μ = 0.4·10⁻⁴ Pa s and for t = 3.06 ms with μ = 1.0·10⁻⁴ Pa s (Fig. 18). The smallest width of the hydraulic fracture was 1.5 mm for μ = 0.4·10⁻⁴ Pa s, and the largest was 2.2 mm for μ = 1.0·10⁻⁴ Pa s. The strongest fluid leakage was obtained for the smallest viscosity μ = 0.4·10⁻⁴ Pa s and the weakest one for the highest dynamic viscosity μ = 1.0·10⁻⁴ Pa s. The highest fluid velocity (23 m/s) took place for μ = 0.4·10⁻⁴ Pa s and the lowest fluid velocity (17 m/s) for μ = 1.0·10⁻⁴ Pa s.

6.4 Effect of rock strength

The effect of three different (proportionally scaled) cohesive and tensile normal stresses in the rock matrix were investigated: (1) C_c= 17 MPa and T_c= 3.4 MPa, (2) C_c= 170 MPa and T_c= 34 MPa and (3) C_c= 340 MPa and T_c= 68 MPa. Figure 19 shows the results of the propagating hydraulic fracture for a final stage when it reached the specimen top boundary.

Fig. 19

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) with different rock strength: aC_c= 17 MPa, T_c= 3.4 MPa (t = 4.71 ms), bC_c= 170 MPa and T_c= 34 MPa (t = 5.51 ms) and cC_c= 340 MPa and T_c= 68 MPa (t = 8.74 ms) (scales denote pressure, horizontal pink line denotes coordinate axis) (color figure online)

When the rock specimen was the strongest, the hydraulic fracture developed during the longest time and it was the least curved. In addition, no secondary macro-cracks were created (that are visible for two weakest specimens). The fluid pressures and velocities of along the main path were similar for all specimens.

6.5 Effect of pre-existing fracture

A single pre-existing fracture was formed in the rock specimen with the length of 20 mm and width of 0.5 mm. It was located 10 mm (case ‘I’) and 15 mm (case ‘II’) above the specimen bottom (Figs. 20, 21). It was artificially created by removing several dozen spherical particles.

Fig. 20

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) with pre-existing single horizontal macro-crack (case ‘I’ at = 1.82 ms, bt = 1.94 ms, ct = 2.44 ms and dt = 3.71 ms, scales denote pressure)

Fig. 21

2D coupled DEM/CFD simulations: evolution of hydraulic fracture with pressure distribution (A) and evolution of pressure distribution in specimen (B) with pre-existing single horizontal macro-crack (case ‘II’) at = 1.97 ms, bt = 2.74 ms, ct = 3.36 ms and dt = 5.42 ms, scales denote pressure)

In the case ‘I’, the hydraulic fracture started to propagate towards the pre-existing fracture (Fig. 20aA). It reached the pre-existing fracture for t = 1.94 ms (Fig. 20bA). The fracking fluid started next to fill in the pre-existing fracture (Fig. 20bA). For t = 2.44 ms, the pre-existing fracture was totally filled in with the fluid (Fig. 20cA) and the fluid pressure started to grow there (Fig. 20cB). Later the fluid pressure sufficiently increased to damage the rock matrix and the hydraulic fracture slightly moved upwards at both the ends of the pre-existing fracture (Fig. 20dA). The moderate fluid leakage from the hydraulic fracture to the rock matrix was obtained during the entire simulation (Fig. 20B). Several single floating particles (separated from the rock mass) appeared in the hydraulic fracture (Fig. 20dA). Thus the VPN model makes it possible to study the effect of proppant particles on the hydraulic fracture opening/closure.

In the case ‘II’, the hydraulic fracture initiated and started to propagate also towards the pre-existing fracture (Fig. 21aA). After t = 2.43 ms, it reached the pre-existing fracture and the fracking fluid started to flood it (Fig. 21bA). The fracking fluid fully flooded the pre-existing fracture for t = 3.26 ms and next the fluid’s pressure began to grow (Fig. 21cA). On the right and left end of the pre-existing fracture, the fluid pressure increased enough to damage the rock matrix and extended slightly the pre-existing fracture. However, unlike the case ‘I’, the highest fluid pressure’s increase was obtained at the intersection of both fractures. It resulted in the huge damage of the pre-existing fracture near this intersection region. The hydraulic aperture of the pre-existing fracture increased near the intersection rather than at its ends as in the case ‘I’. After the relatively long time (1.8 ms), the hydraulic fracture damaged the pre-existing fracture at the intersection region and resumed the propagation way upwards. In the final stage of the simulation, the hydraulic fracture propagated upwards from the intersection region (Fig. 21dA). Before the pre-existing fracture was damaged and totally flooded with the fluid, no floating single particles grains appeared. However, after a significant increase of the fluid pressure, the grains began to separate from the rock matrix and to float. This process was more intensive than in the case ‘I’. The leakage of the fracking fluid in the rock matrix was pronounced during almost the entire simulation (Fig. 21aB–cB). The relative long-time damage of the pre-existing fracture (about 2.8 ms) caused a huge fluid’s leak in the rock matrix and consequently the significant pressure loss (Fig. 21dB).

7 Conclusions

This study focused on a hydro-fracking (hydraulic fracturing) process in the rock mass at the meso-level with the use of one injection slot. The novel two-way coupled CFD/DEM approach was used to simulate this complex process by discretizing the geometry of voids in the rock mass during laminar fracturing fluid flow. The model realistically depicted the development of a hydraulic fracture and fracturing fluid velocity and pressure.

The results showed significant effects of the initial porosity of the rock matrix, rock matrix strength, dynamic viscosity of the fracking fluid and presence of a pre-existing fracture on the fracture initiation and propagation. The height of the hydraulic fracture and its velocity strongly increased with increasing initial micro-porosity of the rock matrix and decreasing dynamic viscosity of the fracturing fluid and rock strength, and the lack of a pre-existing fracture.

The Virtual Pore Network model enabled to study the effect of floating grains separated from the rock matrix in a hydraulic fracture.

The developed method of tracking fluid fractions in voids allowed for investigating the effect of the fluid’s leakage from the hydraulic fracture into the rock matrix. The fluid’s leakage was in particular pronounced in the case of high rock micro-porosity and presence of a pre-existing macro-crack.