1 Introduction

Many advanced constitutive models for sand have been proposed (e.g. [12, 14, 16, 18, 30, 31, 33,34,35]). These models can capture the state-dependent dilatancy and strain-softening of single sand elements under various loading conditions. But a sand model with strain-softening can give highly mesh-dependent results when used in finite element analysis of boundary value problems. For instance, the model gives non-unique force and displacement relationship for plane strain compression on dense sand with strain-softening [7, 21]. The computed thickness and orientation of shear bands is also mesh-dependent. The shear band thickness decreases as the element size decreases and the shear band direction may follow the direction of element edges [7]. When a sand model with strain-softening is used in practical boundary value problems, the solution can become unreliable due to the mesh-dependency. For instance, the bearing capacity predicted by a strain-softening sand model can change dramatically when the mesh size or orientation changes [3, 19]. The mesh-dependency is caused by the assumption used in standard elastoplastic models that the stress–strain relationship at an integration point is dependent on the local stress, strain and state variables only.

Many methods for regularizing the mesh-dependence of finite element solutions of strain-softening models have been developed, including the nonlocal theories [2, 6, 7, 21], viscous plasticity [23, 26], strain-gradient plasticity [1, 4, 13] and mico-polar theories [5, 29, 32]. These methods can significantly reduce the mesh sensitivity of the finite element solutions. In particular, the nonlocal method is found effective and convenient in regularizing strain-softening models for soils (e.g. [7, 21, 22, 25, 27, 28]). In a fully nonlocal constitutive model, the stress, strain and state variables should all be considered as nonlocal variables. Since a fully nonlocal model makes the constitutive equations complex, the partially nonlocal approach has been used in most cases. In a partially nonlocal model, some of the state variable (e.g. plastic shear strain, void ratio or yield surface size) are assumed nonlocal [7]. Indeed, the partially nonlocal approach is found sufficient for regularizing most soil models with strain softening. For instance, Galavi and Schweiger [7] and Summersgill et al. [27] have assumed that the strain softening is controlled by the nonlocal plastic shear strain. Lu et al. [20] have proposed to use nonlocal plastic multiplier which controls the increment of plastic strain to regularize soil models with strain-softening.

The nonlocal method has mainly been used in soil models with simple strain-softening rule. For instance, the variable controlling the strain softening is a function of the plastic shear strain only in Galavi and Schweiger [7], Summersgill et al. [28] and Mánica et al. [22]. Therefore, the model can be easily regularized by assuming that strain-softening variable is dependent on the nonlocal plastic shear strain. But the strain-softening of real sand is dependent on several variables, such as the void ratio, mean effective stress, fabric anisotropy and plastic strain. The hardening parameter of an advanced sand model which describes the strain-softening cannot be expressed by these variables explicitly. Instead, the increment of the hardening parameter is given in terms of these variables. This makes the nonlocal regularization of these models challenging. Mallikarachchi and Soga [21] are among the first to propose a nonlocal regularization method for an advanced sand model considering the effect of void ratio and mean effective stress on the soil behaviour. Specifically, the void ratio increment is assumed to depend on the void ratio increment at the local and neighbouring integration points. It is found that this method can effectively reduce the mesh-dependency of the model prediction for drained and undrained plane strain compression tests. But this method has not be used in a practical geotechnical problem. In addition, the integration of this regularization method with the explicit/implicit stress integration methods have not been discussed.

This paper presents a method for regularizing an anisotropic critical state sand model based on the work by Mallikarachchi and Soga [21]. The paper is organized as follows. The original constitutive model and regularization method are first introduced. Implementation of the nonlocal model using the explicit stress integration method is then presented. The nonlocal model is finally used to simulate strain localization in plan strain compression and the response of a strip footing on dry sand. The practicality of this regularization method in real geotechnical engineering problems is discussed.

2 The original constitutive model

The model used in this study was developed based on the anisotropic critical state theory which considers fabric evolution of sand during loading [17]. A detailed discussion of the model can be found in Gao et al. [31] and Gao et al. [8]. This model accounts for the plastic deformation of sand under shear only. Therefore, a Mohr–Coulomb type yield function is used

$$f=R/g\left(\theta \right)-{H}_{d}=0$$
(1)

where \(R=\sqrt{3{r}_{ij}{r}_{ij}/2}\), \({r}_{ij}=\left({\sigma }_{ij}-p{\delta }_{ij}\right)/p\) is the stress ratio tensor, \({\sigma }_{ij}\) is the stress tensor, \(p={\sigma }_{ii}/3\) is the mean effective stress, \({\delta }_{ij}\) is the Kronecker delta (\(=1\) for \(i=j\), and \(=0\) for \(i\ne j\)), \({H}_{d}\) is the hardening parameter and \(g\left(\theta \right)\) is an interpolation function which describes the variation of critical state stress ratio with the Lode angle \(\theta\) of \({r}_{ij}\) [12, 31] The hardening law for the yield function is expressed as

$$d{H}_{d}=\langle L\rangle {r}_{H}=\frac{G{h}_{1}\mathrm{exp}({h}_{2}A)}{{\left(1+e\right)}^{2}\sqrt{p{p}_{a}}R}\left[{M}_{c}g\left(\theta \right)\mathrm{exp}(-n\zeta )-R\right]$$
(2)

where \(L\) is the loading index, \(\langle \rangle\) are the Macaulay brackets which make \(\langle L\rangle =L\) for \(L>0\) and \(\langle L\rangle =0\) for \(L\le 0\), \({h}_{1}\), \({h}_{2}\) and \(n\) are model parameters, \(G\) is the elastic shear modulus, \(A\) is the anisotropic variable [17, 31], \(e\) is the void ratio, \({p}_{a}\) is the atmospheric pressure, \({M}_{c}\) is the critical state stress ration in triaxial compression and \(\zeta\) is the dilatancy state parameter [17]. This hardening law can capture the strain-softening response of dense sand.

The plastic shear strain increment \({de}_{ij}^{p}\) is expressed as

$${de}_{ij}^{p}=\langle L\rangle {m}_{ij}=\langle L\rangle \frac{\frac{\partial g}{\partial {r}_{ij}}-\left(\frac{\partial g}{\partial {r}_{mn}}{\delta }_{mn}\right){\delta }_{ij}/3} {\left\| { \frac{\partial g}{\partial {r}_{ij}}-\left(\frac{\partial g}{\partial {r}_{mn}}{\delta }_{mn}\right){\delta }_{ij}/3} \right\| }$$
(3)

where \(g\) is the plastic potential function in the \({r}_{ij}\) space

$$g=R/g\left(\theta \right)-{H}_{g}{e}^{-{k}_{h}{(1-A)}^{2}}=0$$
(4)

where \({k}_{h}\) is a model parameter and \({H}_{g}\) is determined based on the current stress state and \(A\). The term involving \(A\) in Eq. (4) enables the model to capture the non-coaxial response of sand caused by fabric anisotropy [9, 31]. The total plastic strain increment \(d\varepsilon_{ij}^{p}\) as below

$$d\varepsilon_{ij}^{p} = de_{ij}^{p} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}d\varepsilon_{v}^{p} \delta_{ij} =\langle L\rangle\left( {m_{ij} + \sqrt {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 {27}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${27}$}}} D\delta_{ij} } \right)$$
(5)

where \(d\varepsilon_{v}^{p}\) is the plastic volumetric strain increment and \(D\) is the dilatancy function (see [8]). In this model, the fabric evolution with plastic shear strain is considered

$$dF_{ij} = \langle L\rangle k_{f} \left( {n_{ij} - F_{ij} } \right)$$
(6)

where \(dF_{ij}\) is the increment of \(F_{ij}\), \(k_{f}\) is a model parameter and \(n_{ij}\) is the loading direction defined as

$$n_{ij} = \frac{\frac{\partial f}{\partial {r}_{ij}}-\left(\frac{\partial f}{\partial {r}_{mn}}{\delta }_{mn}\right){\delta }_{ij}/3} {\left\| { \frac{\partial f}{\partial {r}_{ij}}-\left(\frac{\partial f}{\partial {r}_{mn}}{\delta }_{mn}\right){\delta }_{ij}/3} \right\| }$$
(7)

3 Nonlocal formulation of the constitutive model

In previous studies, some of the state variables affecting the strain-softening and flow rule are assumed to evolve with the nonlocal plastic strain. This is called the partially nonlocal approach [7, 28]. Though it is less rigorous than the fully nonlocal method which assume that both stress strain are nonlocal, it is found effective in regularizing most soil models with strain-softening. The strain-softening of this model is mainly affected by \(e\), \(F_{ij}\) and \(H_{d}\). It is inconvenient to use nonlocal \(F_{ij}\) and \(H_{d}\) in the hardening law. There are several reasons for this. First, the evolution of \(F_{ij}\) and \(H_{d}\) is dependent on the plastic shear strain increment, but their full form cannot be expressed explicitly in terms of the total plastic shear strain. It is therefore impossible to use the nonlocal plastic shear strain to get the nonlocal \(F_{ij}\) and \(H_{d}\). Secondly, the plastic shear strain increment has to be calculated before the averaging calculation is carried out if the increment of \(F_{ij}\) and \(H_{d}\) is assumed nonlocal. Since the original model is complex, it has to be implemented using some advanced stress integration methods such as the explicit or implicit methods [9, 36]. In these stress integration methods, the plastic strain increment can only be obtained at the end of each step when the stress and state variables are already updated. This means that the nonlocal increment of \(F_{ij}\) and \(H_{d}\) has to be calculated at the end of each step. If the nonlocal increment of \(H_{d}\) is used without changing the previous stress integration (e.g. the stress increment), the condition of consistency for the yield function cannot always be satisfied. The evolution of \(F_{ij}\) is dependent on the loading direction \(n_{ij}\) which can change during the stress integration. It is thus inappropriate to simply take the average of \(dF_{ij}\) at the end of the step. But the evolution of \(e\) is deponent on the total volumetric strain only, and therefore, it is convenient to make it nonlocal. Following Mallikarachchi and Soga [21], the increment of void ratio \(de\) is assumed to be nonlocal as below

$$de = \left( {1 + e} \right)d\varepsilon_{vn}$$
(8)

where positive \(de\) is associated with volume contraction and \(d\varepsilon_{vn}\) is the nonlocal volumetric strain increment

$$d\varepsilon_{vn} = \frac{{\mathop \sum \nolimits_{k = 1}^{N} w_{i} v_{i} d\varepsilon_{vi} }}{{\mathop \sum \nolimits_{k = 1}^{N} w_{i} v_{i} }}$$
(9)

where \(N\) is the number of integration points within the averaging area, \(w_{i}\), \(v_{i}\) and \(d\varepsilon_{vi}\) represent the weight function, volume and local volumetric strain increment of integration point \(i\). The weight function proposed by Galavi and Schweiger [7] is used

$$w_{i} = \frac{{r_{i} }}{{l^{2} }}{\text{exp}}\left( { - \frac{{r_{i}^{2} }}{{l^{2} }}} \right)$$
(10)

where \(l\) is the internal length, \(r_{i}\) is the distance between the current integration point and the \(i\)-th integration point used for calculating the averaged value in Eq. (8). Note that several other weight functions have also be proposed in the literature but one in Galavi and Schweiger [7] is found to give the best regularization results for soils with strain softening [28].

3.1 Implementation of the nonlocal method

The original model has been implemented in Abaqus using the explicit stress integration method with automatic sub-stepping [8]. The total strain increment needs to be divided into several sub-increments in this method. Strictly speaking, the nonlocal averaging of void ratio increment should be done at each sub-increment for all the integration points. But this would dramatically increase the computational time. Therefore, a simplified method has been used in implementing the nonlocal method. At the start of each increment, the nonlocal volumetric strain increment for each integration point is calculated using Eqs. (8) and (9). A scaling variable \(r_{v}\) defined as the ratio of the nonlocal and local volumetric strain increment is then obtained

$$r_{v} = \frac{{d\varepsilon_{vn} }}{{d\varepsilon_{vl} }}$$
(11)

where \(d\varepsilon_{vl}\) is the total local volumetric strain increment for that step. The stress integration is then carried out following that for a local model, but the void ratio is updated as below at the end of each sub-increment

$$de = \left( {1 + e} \right)d\varepsilon_{\varepsilon l}^{s} r_{v}$$
(12)

where \(d\varepsilon_{\varepsilon l}^{s}\) is the local volumetric strain increment for the sub-increment.

Two user subroutines, USDFLD (user-defined field variables) and UMAT (user-defined materials), are needed for implementing the nonlocal method in Abaqus. The subroutine USDFLD is used to get the volume of each integration point (IVOL) using the utility routine GETVRM. This variable IVOL is then returned as a common block array VOLINT (NEL, NIP, 1), where NEL is the total number of elements in a problem and NIP is the number of integration points in each element. Specifically, the volume of each integration point (NPT in Abaqus) of the associated element (NOEL in Abaqus) is obtained and then stored as a component VOLINT (NOEL, NPT, 1) in the USDFLD. Since VOLINT is defined as a common block, it can be used in the other subroutines of Abaqus like UMAT. The nonlocal averaging is carried out at the beginning of each increment in the UMAT. First, the local volumetric strain increment \(d\varepsilon_{vl}\) for each integration point is calculated. The nonlocal strain increment \(d\varepsilon_{vn}\) and scaling variable \(r_{v}\) are then calculated using Eqs. (8)–(10). The integration points within the radius of \(4l\) are considered for Eq. (9) to reduce the computational time because \(w_{i}\) becomes negligible when \(r_{i} > 4l\). A common block array ENCD (NEL, NIP, 4) is used in UMAT to return the coordination [ENCD (NEL, NIP, 1–3)] and \(d\varepsilon_{vl}\) [ENCD(NEL, NIP, 4)] of each integration point (Mallikarachchi and Soga, 2020). Similar to the VOLINT, the components of ENCD are obtained in the UMAT for each integration point, which can then be used for the UMAT of the other integration points. The remaining part of the UMAT is the same as that for a local model, except that the void ratio is updated using Eq. (12) at the end of each sub-increment. Since the shear strain in the shear band can be very large and the geometrical nonlinearity should also be considered (e.g. [8, 9, 11]). But previous studies on nonlocal regularization have mainly used the small strain formulation (e.g. [7, 21]). We have thus neglected the geometrical nonlinearity here for easy comparison with these studies.

4 Strain localization under plane strain compression

The strain localization under plane strain compression will be simulated in this section. The model parameters (Table 1) are the same as those in Gao et al. [8]. The sample size (60 mm × 120 mm) and boundary conditions are shown in Fig. 1. A confining pressure of \(p_{0} = 200\) kPa is applied on the two vertical sides. Vertical displacement is applied on the top side with the horizontal displacement unconstrained. The bottom side is pinned at the left and free to move to the right. The strain localization is triggered by assigning a ‘weak’ area (12 mm × 12 mm) with inclined bedding plane orientation (\(\alpha = 45^\circ\)). Horizontal bedding plane orientation (\(\alpha = 0^\circ\)) is specified for the remaining area (Fig. 2). The 8-noded plan strain elements with reduced integration are used in the simulations. The initial void ratio of the sample is \(e_{0} = 0.65\) (relative density \(D_{r} = 88\%\)) and the initial degree of anisotropy is \(F_{0} = 0.4\).

Table 1 Model parameters for Toyoura sand
Full size table
Fig. 1
figure 1

The boundary conditions and bedding plan orientation for the plane strain test simulations

Full size image
Fig. 2
figure 2

The location of the ‘weak’ area with \(\alpha = 45^\circ\): a mesh size 6 mm and 200 elements, b mesh size 3 mm and 800 elements

Full size image

4.1 The effect of internal length

The internal length \(l\) is an important parameter for nonlocal soil models, as it is used for the weight function of Eq. (10). Bigger \(l\) means that the stress–strain relationship of the current integration point is affected by that of integration points further away. Wider shear band and a slower rate of strain-softening will be predicted as \(l\) increases. Experimental evidence shows that the shear band thickness \(t_{s}\) is about \(10 - 20d_{50}\) for most sand, where \(d_{50}\) is the mean particle size [7]. For the Toyoura sand used here, \(d_{50} \approx 0.2\) mm and \(t_{s} \approx 2 - 4\) mm. The predicted \(t_{s}\) is very close to \(l\) when the Galavi and Schweiger [7] weight function is used, which will be shown in the subsequent sections. Therefore, \(l \approx 2 - 4\) mm has to be used if realistic prediction of \(t_{s}\) is required. But the maximum mesh size must always be smaller than \(l\). While it is feasible to use very small \(l\) to simulate the response of small soil samples, it is impractical to use \(l \approx 2 - 4\) mm in most real boundary value problems. There are two major reasons. First, small mesh size causes numerical convenience issues for advanced soil models which give a highly nonlinear stress–strain relationship. Secondly, the computational time will be significantly increased when a small mesh size is used for a nonlocal model. Therefore, \(l\) is typically chosen based on the size of the boundary value problem rather than \(d_{50}\). Figure 3 shows the effect of \(l\) on the \(s - R_{v}\) relationship predicted by the nonlocal model, where \(s\) is the vertical displacement and \(R_{v}\) is the total vertical reaction force measure on the top surface of the sample. The mesh size is 4 mm \(\times\) 4 mm (450 elements). The nonlocal model always gives higher peak \(R_{v}\) and slower rate of strain-softening than the local model. This is due to that the nonlocal model makes the stress and strain distribution more uniform in the soil. For the nonlocal model, the peak \(R_{v}\) shows little variation with \(l\) but the rate of strain-softening is slower at bigger \(l\).

Fig. 3
figure 3

Effect of internal length on the force–displacement relationship in plane strain compression

Full size image

4.2 Simulation of the strain localization

Figure 4 shows the \(s - R_{v}\) relationship predicted by the local and nonlocal models with different mesh sizes. The same internal length of \(l =\) 12 mm is used. The \(s - R_{v}\) relationship predicted by the nonlocal model is insensitive to the mesh size. Visible difference can only be observed at \(s > 0.1H\), where \(H\) is the initial height of the sample (Fig. 4a). The local model gives mesh-dependent \(s - R_{v}\) relationship with higher peak \(R_{v}\) and slower rate of strain-softening at a bigger mesh size (Fig. 4b).

Fig. 4
figure 4

Force–displacement relationship predicted by the a original model and b nonlocal model for the tests with horizontal bedding plane

Full size image

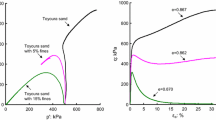
Figures 5 and 6 show the shear strain localization predicted by the local and nonlocal models, where SDV11 represents the total shear strain. The shear band thickness \(t_{s}\) measured at \(s = 0.09H\) is shown in Fig. 7. When the mesh size \(h < l\), the location and thickness of shear bands predicted by the nonlocal model are independent of the mesh size (Fig. 7a). When \(h = l\), the shear band predicted by the nonlocal model locates at a lower position (Fig. 5c). The shear band thickness is also close to that predicted by the local model (Fig. 7a). This means that the regularization method works when \(h < l\). When the mesh size is the same, the shear band thickness predicted by the nonlocal model increases with \(l\) (Fig. 7b). But there is not a linear relationship between \(h\) and \(l\), which has been reported in previous research [7]. The shear band thickness predicted by the local model increases with the mesh size, which is in agreement with existing studies (Fig. 7b). The shear band orientation predicted by the nonlocal model varies between 47 ° (50 elements) and 51 ° (800 elements), and that predicted by the local model varies between 47 ° (50 elements) and 53 ° (800 elements) (Figs. 5 and 6). This indicates that shear band orientation predicted by the nonlocal model is not sensitive to the mesh size.

Fig. 5
figure 5

Shear band predicted by the nonlocal model in plane strain compression at \(s/H\) = 0.09 (SDV11 is the total shear strain) a 800 elements, b 200 elements and c 50 elements

Full size image
Fig. 6
figure 6

Shear band predicted by the local model in plane strain compression at \(s/H\) = 0.09 (SDV11 is the total shear strain) a 800 elements, b 200 elements and c 50 elements

Full size image
Fig. 7
figure 7

The effect of a mesh size and b internal length on the shear band thickness. The internal length \({\varvec{l}}\) is 12 mm for the nonlocal model in a

Full size image

Based on these results, it can be concluded that the nonlocal model can give mesh-independent force–displacement relationship for different mesh sizes. But mesh-independent strain localization pattern can only be observed when the mesh size is smaller than the internal length. To improve the regularization method for larger mesh sizes, more state variables which control the strain-softening (e.g. \(F_{ij}\) and \(H_{d}\)) should be assumed nonlocal. But this would significantly increase the model complexity and computational time, which has been discussed before.

Figure 8 shows the evolution of void ratio and anisotropic variable \(A\) of an element in the ‘weak’ area. Both elements are within the shear band. The prediction of the local and nonlocal models is the same before strain-softening (\(s < 0.028H\)). Volume expansion is predicted by both the local and nonlocal models as the soil is dense. But the nonlocal model gives less volume expansion due to the assumption made in Eqs. (8)–(10). It is well known that there is much smaller plastic deformation and less volume expansion outside the shear band. Since the void ratio evolution is assumed to depend on the volumetric strain increment of local and neighbouring integration points in the nonlocal model, the increase in void ratio becomes smaller than that predicted by the local model. There is also difference in the evolution of \(A\) during strain softening. This is due to that the nonlocal treatment of void ratio evolution has effect on the plastic hardening and plastic shear strain increment, which affect the evolution of fabric anisotropy (Eq. 6). Both the local and nonlocal models predict higher void ratio and anisotropic variable \(A\) within the shear band due to the shear strain concentration. This has been discussed in more details in Gao and Zhao [9] and will not be repeated here.

Fig. 8
figure 8

Evolution of the a void ratio and b anisotropic variable in the ‘weak’ area (800 elements)

Full size image

5 Simulation of the response of a strip footing on sand

The loading condition (e.g. the stress path) in a plane strain compression is relatively simple. But the soil elements can be subjected to much more complex loading conditions in a practical geotechnical engineering problem. It is thus important to further investigate the effectiveness of the nonlocal regularization method in larger-scale boundary value problems. The response of a strip footing on sand with different densities and bedding plane orientation (horizontal and vertical) will be simulated in this study.

This simulation is based on the centrifuge tests reported in Kimura et al. [15]. The size of the problem is shown in Fig. 9. Uniform vertical pressure of 1 kPa is applied on the top surface and uniform vertical deformation is applied on the footing (width B = 0.9 m). The effective weight of Toyoura sand is \(\gamma {^{\prime}} = 16{\text{kN}}/{\text{m}}^{3}\) and the initial lateral earth pressure coefficient \(K_{0} = 0.4\) [24]. More details of the simulation can be found in Gao et al. [8]. The mesh size in the rectangle area beneath the footing is \(w\) (Fig. 9). The maximum mesh size is 0.5 m (at the two vertical sides and the bottom). Four different values of \(w\) (0.15 m, 0.2 m, 0.25 m and 0.35 m) have been used in the simulation. The mesh distribution with \(w = 0.35\) m and \(w = 0.15\) m is shown in Fig. 10.

Fig. 9
figure 9

The boundary conditions and used in the simulations

Full size image
Fig. 10
figure 10

The mesh size used in the simulations: a minimum element size w = 0.35 m and 1156 elements, b minimum element size w = 0.15 m and 2881 elements

Full size image

Figure 11 shows the effect of internal length on the force–displacement relationship of the strip footing (\(w = 0.25\) m and 1648 elements). Higher peak vertical load is predicted with bigger \(l\), because the stress and strain distribution in the soil becomes more uniform at bigger \(l\). The change of strain-softening rate with \(l\) is not obvious, but Summersgill et al. [27] have shown that \(l\) has a dramatic influence on the strain-softening rate. This is due to the difference in the original constitutive models. The settlement at peak vertical load is insensitive to the internal length. It should be mentioned that this observation is based on the internal length chosen in Fig. 11. The nonlocal model prediction could change significantly if a smaller \(l\) is used. But that would require smaller mesh sizes which will cause convergence issues. The simulations below show that reasonable prediction of the centrifuge test data can be obtained with \(l = 0.6\) m (Figs. 12 and 13). Therefore, it is acceptable to use the internal length shown in Fig. 11 when the peak vertical load and the corresponding settlement is of concern, though the exact thickness of shear band will not be captured.

Fig. 11
figure 11

The effect of internal length on the predicted force–displacement relationship of the strip footing

Full size image
Fig. 12
figure 12

The local and nonlocal model prediction for the strip footing response on sand with horizontal bedding plane: a and b dense sand, c and d medium dense sand

Full size image
Fig. 13
figure 13

The local and nonlocal model prediction for the strip footing response on sand with vertical bedding plane: a and b dense sand, c and d medium dense sand

Full size image

Figures 12 and 13 show the local and nonlocal model predictions for the strip footing response on Toyoura sand. The internal length \(l = 0.6\) m is used for the nonlocal model. The force–displacement relationship predicted by the nonlocal is not completely mesh-independent. But the result shows much less mesh sensitive than that predicted by the local model. For instance, the difference in the maximum and minimum bearing capacity (peak \(Q\)) predicted by the anisotropic model in Fig. 12a is about 8%. But the local model gives a difference of 18%. The nonlocal model also gives more mesh-insensitive results when the bedding plane is vertical, where the strain-softening is less significant (Fig. 13). Both the local and nonlocal models have convergency issues as the mesh size becomes smaller. Some of the simulations are aborted before \(s = 0.25B\) because the force equilibrium cannot be reached. But it is worth noticing that the nonlocal regularization can help improve the convergency of the model, especially when the bedding plane is vertical. This is due to that the nonlocal treatment makes the stress distribution more uniform in the soil.

The test data is also shown in Figs. 12 and 13 for comparison. In general, the nonlocal model gives reasonable prediction of the test results at different mesh sizes. But the local model prediction is only acceptable at \(w = 0.35\) m. There is underprediction of the bearing capacity at other mesh sizes. Indeed, the mesh size has to be chosen by best fitting the test data when the local models are used [3, 8]. The nonlocal method can reduce the mesh sensitivity of the numerical results but does not always improve the model prediction of the force–displacement relationship. For instance, both the local and nonlocal model are not capable of capturing the force–displacement relationship before failure when \(D_{{\text{r}}} = 85.6\%\) and the bedding plane is horizontal. There two main reasons for this. First, the void ratio of sand may not be uniform at the initial state. There may be some areas with lower void ratio which makes the slope of the force–displacement relationship higher. Secondly, the model needs to be improved to capture the sand response with initially anisotropic stress state. It is found that the constitutive model used in this study can give reasonable prediction of sand behaviour with an initially isotropic stress state but tends to underestimate the stiffness when the initial stress state is anisotropic [10]. It is well known that the initial stress state of sand in the centrifuge tests is anisotropic.

The shear strain localization predicted by the nonlocal model for the strip footing on dense sand (\(D_{r} = 85.6\%\)) with horizontal bedding plane is shown in Fig. 14. The location of the slip surfaces indicated by the solid red lines are independent of the mesh size. Note that the slip surfaces are those which can fully develop if the simulations can continue to a larger strain level [11]. Similar slip surfaces have been reported in Kimura et al. [15]. Therefore, it can be concluded that the regularization method proposed here is proper for practical geotechnical engineering problems.

Fig. 14
figure 14

The shear strain localization predicted by the nonlocal model at \({\varvec{s}} = 0.18{\varvec{B}}\) (SDV11 is the total shear strain): a \({\varvec{w}} = 0.2\) m with 2097 elements, b \({\varvec{w}} = 0.25\) m with 1648 elements, c \({\varvec{w}} = 0.35\) m with 1156 elements

Full size image

6 Conclusion

Nonlocal regularization of an anisotropic critical state sand model is presented. The evolution of void ratio is assumed to depend on the volumetric strain increment at the local and neighbouring integration points [21]. The nonlocal model has been implemented for finite element analysis using the explicit stress integration method. The nonlocal model has been used to simulate the strain localization in drained plane strain compression and the response of a strip footing on sand. The main conclusions are:

  1. a.

    The nonlocal model gives mesh-independent force–displacement relationship in plane strain compression with strain localization. The location and thickness of the shear band are mesh-independent when the mesh size is smaller than the internal length. Better regularization results for the strain localization can be obtained if the two variables \(F_{ij}\) and \(H_{d}\) which affect the strain-softening are made nonlocal. But this would significantly increase the model complexity and the computational time.

  2. b.

    The nonlocal regularization method can effectively reduce the mesh-dependency of the force–displacement relationship of a strip footing on sand. Reasonable prediction of the bearing capacity of the strip footing can be obtained with different mesh sizes. The nonlocal model gives mesh-independent strain localization beneath the strip footing. The regularization method is thus proper for solving practical geotechnical engineering problems.