1 Introduction

Anisotropy has long been acknowledged to be a salient feature of sand [8]. Sand deposited under gravity or subjected to anisotropic stress inevitably exhibits anisotropy in strength and deformation (e.g., [1, 3, 42, 61, 77, 79, 80]). As possible consequences of such anisotropic characteristics, the bearing capacity and earth pressure of sand can be significantly directional dependent [4, 7, 49]. Yoshimine et al. [88] showed that under undrained monotonic shearing in various directions, sand behavior can range from mostly dilative hardening to strongly contractive, approaching static liquefaction.

Due to its significance and unavoidable nature, a myriad of studies have been focused on various aspects of sand anisotropy. Research on strength anisotropy has been carried out to establish mathematical formulations for the anisotropic strength criterion of sand (e.g., [18, 20, 27, 33, 39, 53]). The influence of anisotropy on dilatancy has been analyzed (e.g., [25, 43, 69, 88]), with strong evidence indicating dilatancy to be directional dependent. Anisotropy in the small strain behavior of sand has also been investigated [21, 24, 32]. These important advances in different facets of anisotropic sand behavior undoubtedly contribute to the development of anisotropic constitutive models.

The origin of the anisotropic behavior of sand lies within the microstructural fabric of the material [13, 46, 56]. Two approaches for constitutive model development have been adopted to incorporate the anisotropic fabric and microstructure of soil. One approach introduces assumptions for the kinematic and mechanical characteristics of sand at the microlevel, such as the particle, particle group, or generically oriented plane levels [29, 30, 40]. The microlevel behavior is then integrated to obtain the macrolevel stress–strain relationship (e.g., [9, 10, 44, 50]). Although this approach avoids most of the assumptions at the macrolevel, the assumptions made at the microlevel, which serves as an intermediary between actual granular sand and the continuum constitutive model, are nonetheless difficult to validate and calibrate. Another approach is to introduce a statistical representation of the microstructural fabric of sand to the continuum constitutive formulations (e.g., [15, 35, 47, 64, 65, 79, 85]), often making assumptions for the dependency of stress–strain relationship on the fabric tensor [57]. This approach requires quantification of the fabric tensor and its evolution and more importantly understanding of its role in various continuum constitutive components.

Although measuring fabric in physical tests is still technically challenging, virtual numerical tests through methods such as DEM (discrete element method [14]) have become an important means complementary to physical tests in the quantification and understanding of fabric in sand [17, 22, 31, 34, 45, 62, 71]. Aided by observations from DEM tests, Li and Dafalias [36] proposed the anisotropic critical state theory (ACST). ACST adds a fabric anisotropy condition to the classical critical state theory and introduces the influence of fabric anisotropy and its evolution on the state of sand. These advances have promoted rapid development in fabric tensor-based anisotropic plasticity models. Such models have been upgraded from only being able to consider inherent anisotropy with fixed fabric tensors [15, 35, 47] to incorporating the evolution of fabric [19, 51, 52, 78, 91].

Due to limitations in physical test measurement, fabric tensor-based anisotropic plasticity models have mostly only been validated indirectly against physical test results on the macrostress–strain relationship level, while quantitative validation of the micromechanical assumptions for fabric evolution and its influence on important constitutive components such as modulus and dilatancy has rarely been conducted [26]. DEM numerical test data can be adopted to validate the fabric anisotropy-related assumptions made for these models. On the other hand, existing anisotropic plasticity models have mostly been formulated and applied for monotonic loading, with little consideration for the influence of fabric anisotropy on the cyclic behavior of sand. However, evidence has suggested that fabric anisotropy can significantly affect the liquefaction resistance of sand and should be considered in the modeling of cyclic sand behavior [75, 76, 80, 86, 87].

This study aims to develop a plasticity model incorporating fabric evolution for monotonic and cyclic sand behavior and utilizes quantitative micromechanical information obtained through DEM numerical tests in the development and validation of the continuum-based constitutive model. Section 2 of this paper discusses the influence of fabric anisotropy and its evolution on the strength, shear modulus, and dilatancy of sand using DEM test data. Based on these understandings, the detailed multiaxial formulation of the proposed model is presented in Sect. 3. In Sect. 4, the model is validated for both macrolevel stress–strain relationships and microlevel fabric evolution against DEM numerical and laboratory physical test data and is then used to analyze the influence of fabric anisotropy on the liquefaction behavior of sand. The stress and strain in this study follow conventional soil mechanics sign conventions with compression being positive. Tensors are denoted by bold letters to distinguish them from plain scalars.

2 Observations on anisotropic behavior of sand in DEM

DEM is a powerful tool in assisting to bridge the gap between macroscopic anisotropic behavior of sand and its microscopic fabric origins. Results from 3D DEM triaxial tests conducted using the widely adopted open-source code Yade [60] are used to illustrate the influence of fabric and its evolution on several key constitutive components in this section, namely strength, modulus, and dilatancy. Four tests are conducted on samples with almost the same initial void ratio of 0.657 ± 0.005 but different bedding plane angles of 0°, 30°, 60°, and 90°, respectively. The bedding plane angle δ here refers to the angle between the major principal stress in triaxial loading and the deposition direction, as illustrated in Fig. 1a. The vertical axis is the major principal stress axis. Over 200,000 particles (Table 1) are first randomly generated and deposited under gravity. Four samples consisting of approximately 40,000 particles each are cut out from the deposit after rotating it by 0°, 30°, 60°, and 90° angles, respectively, and are isotropically consolidated under mean effective stress p = 100 kPa. Constant p drained triaxial numerical test is then conducted on each sample through strain-controlled servomechanism loading using rigid walls.

Fig. 1
figure 1

Influence of bedding plane angle on the strength of granular material: a schematic illustration of triaxial loading on a sample with bedding plane angle δ; b peak and critical state deviatoric stress ratio η in constant p = 100 kPa drained triaxial 3D DEM numerical tests on for four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°

Full size image
Table 1 DEM test parameters
Full size table

3D clumped particles with aspect ratio of 1.5:1 formed by two rigidly connected identical overlapping spherical particles are used in the numerical tests. Linear elastic–plastic contact is used with contact parameters in Table 1, and the loading walls are frictionless to limit boundary effects. The loading rate guarantees quasi-static conditions with the inertial number smaller than 1.0 × 10−5 [41]. The homogeneity of the samples is evaluated by comparing the state of the sample at various subdomains following the procedures proposed by Fu and Dafalias [18].

Figure 1b plots the measured [5] deviatoric stress ratio η at both the peak and critical states for the four samples with different bedding plane angles. Here, the deviatoric stress ratio η = q/p, with q = σ1–σ3 and p = (σ1 + σ2 + σ3)/3, while σ1, σ2, and σ3 are the principal stress values. The peak η shows clear dependency on bedding plane angle, which reflects initial fabric orientation. The peak η for samples with lower δ is significantly greater, agreeing with existing laboratory and DEM test results [23, 46, 64, 83]. At the critical state, η becomes the same under triaxial compression regardless of the initial bedding plane angle, conforming to the critical state theory. The critical state is determined according to its definition, as the state when the sample approaches constant void ratio while continuing to deform in shear under constant stress [55, 58]. The macroscopic stress–strain response of the tests is in more detail in Sect. 4 in comparison with constitutive model simulations.

The influence of fabric anisotropy on the shear modulus of sand can also be investigated using the numerical tests. An equivalent shear modulus, represented by the deviatoric stress increment divided by the deviatoric strain increment dq/dεq, at different deviatoric strain values, is plotted in Fig. 2. The deviatoric strain εq = (2/9((ε1 − ε2)2 + (ε2 − ε3)2 + (ε1 − ε3)2))1/2, where ε1, ε2, and ε3 are the three principal strain values. At the initial state, the equivalent shear modulus decreases with increasing δ, agreeing with the test observations by Yang et al. [82] on sand. As deviatoric strain increases, not only does the equivalent shear modulus decrease, the difference in equivalent shear modulus between the four samples also reduces. At εq = 0.1, the difference becomes almost indistinguishable. At the critical state, the equivalent shear modulus becomes zero, irrespective of the bedding plane angle.

Fig. 2
figure 2

Influence of bedding plane angle δ on the shear modulus, reflected by dq/dεq, at various states in constant p = 100 kPa drained triaxial 3D DEM numerical tests on for four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°

Full size image

The dilatancy D at different deviatoric strain values is plotted in Fig. 3. The dilatancy D = dε pv /dε pq , where the superscript p indicates plastic strain. The plastic strain is calculated by subtracting the elastic strain increment from the total strain in DEM, following Wan and Pinheiro [67]. The dilatancy at the initial state shows strong bedding plane angle dependency, with dilatancy increasing with increasing bedding plane angle, indicating stronger contraction. As loading progresses, the samples become dilative with negative dilatancy, and the samples with lower δ become dilative at smaller deviatoric strain values. The difference in dilatancy for samples with different δ gradually diminishes after reaching the dilative phase. At the critical state, the dilatancy of all four samples becomes zero. The observed influence of δ on D agrees with the implications from the test results of Yoshimine et al. [88] and Nakata et al. [43] and qualitatively supports the dependency of dilatancy on fabric anisotropy proposed by Li and Dafalias [36].

Fig. 3
figure 3

Influence of bedding plane angle δ on dilatancy D, at various states in constant p = 100 kPa drained triaxial 3D DEM numerical tests on for four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°

Full size image

The analysis on strength, shear modulus, and dilatancy indicates that these key constitutive components are significantly dependent on the bedding plane angle during the early stage of loading, but this dependency disappears as the samples approach the critical state. The origin of such behavior lies within the samples’ fabric states and their evolution, the quantification of which is a major advantage of DEM numerical testing. Fabric tensors of sand can be defined based on different particle-scale features, including contact normal directions, particle orientations, and void orientations. In this study, we mainly focus on the contact normal fabric tensor, which has been found to be closely related to dilatancy anisotropy [69]. The deviatoric contact normal fabric tensor F is calculated based on Satake’s formulation [57]:

$$ {\mathbf{F}} = \frac{1}{{\left( {1 + e} \right)}}\left( {\frac{1}{N}\mathop \sum \limits_{k = 1}^{N} {\mathbf{v}}^{k} \otimes {\mathbf{v}}^{k} - \frac{1}{3}{\mathbf{I}}} \right) $$
(1)

N is the number of contacts within the domain, \( {\mathbf{v}}^{k} \) is the unit norm vector in the normal direction of the kth contact, I is the 2nd-order identity tensor, and e is the void ratio. The term 1 + e is introduced as a per-volume measure, achieving thermodynamic consistency with the continuum definition of fabric [37]. The anisotropic critical state theory suggests that a critical state fabric tensor exists as functions of the lode angle and mean effective stress, irrespective of the initial void ratio and fabric anisotropy [36]. This has been supported by evidence from DEM investigations [18, 23, 34, 71, 83]. Hence, F can be normalized by its norm ||Fc|| at the critical state, resulting in a unit norm tensor Fn at the critical state:

$$ {\mathbf{F}}_{\text{n}} = \frac{{\mathbf{F}}}{{||{\mathbf{F}}_{\text{c}} ||}} $$
(2)

Figure 4 presents the fabric orientation θn, norm ||Fn||, and ||Fn|| − An at different deviatoric strain values for samples with different δ. An is an invariant of the fabric tensor Fn and the tensor-valued unit norm deviatoric loading direction tensor n in terms of An = Fn:n = tr(Fnn); in triaxial loading, it is assumed \( {\mathbf{n}} = \frac{\sqrt 6 }{6}\left[ {\begin{array}{*{20}c} { - 1} & 0 & 0 \\ 0 & { - 1} & 0 \\ 0 & 0 & 2 \\ \end{array} } \right] \). An reflects the combined development of both fabric norm and the relative orientation of fabric and loading directions. Its value is between − ||Fn|| and ||Fn||, and hence 0 ≤ ||Fn|| − An ≤ 2||Fn||. θn is the angle between the major principal fabric orientation and the horizontal plane. The average ||Fc|| at the critical state is used to obtain the normalized fabric in Eq. (2).

Fig. 4
figure 4

Fabric at various states in constant p = 100 kPa drained triaxial 3D DEM numerical tests on for four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°: a contact normal fabric orientation θn, i.e., the angle between the major principal contact normal fabric and the horizontal plane; b normalized contact normal fabric norm ||Fn||; c ||Fn|| − An, An = Fn:n = tr(Fnn)

Full size image

At the initial state, θn ≈ δ + 90°, while ||Fn|| ≈ 0.4. ||Fn|| − An is distinctly different for samples with different bedding plane angles at the initial state (Fig. 4c). As deviatoric strain increases, the fabric orientation θn of each sample gradually evolves toward 90°, and the difference in θn between the four samples gradually reduces. Difference in norm ||Fn|| between the four samples is generated at low deviatoric strain levels, with ||Fn|| greater for samples with lower δ. This difference in ||Fn|| reduces again at low deviatoric strain levels. The difference in ||Fn|| − An between the four samples gradually reduces with increasing deviatoric strain. At the critical state, the fabric orientation becomes the same as the loading direction, while ||Fn|| reaches unity, and ||Fn|| − An reaches zero, irrespective of the bedding plane angle. During its evolution, the norm of the fabric tensor ||Fn||, and subsequently An, can reach a peak beyond its critical state value (e.g., samples with δ = 0° and 30° in Fig. 4b), similar to the peak deviatoric stress ratio being greater than that at the critical state for dense sand. The evolution of fabric is the origin of the anisotropic behavior of sand observed in Figs. 1, 2, and 3. In particular, the evolution of ||Fn|| − An for samples with different δ shows strong resemblance to the strength and evolution of shear modulus and dilatancy. The initial difference in ||Fn|| − An of the four samples is associated with the initial differences in stress–strain relationships. As fabric evolves toward the same critical state, the differences in stress–strain relationship diminish along with the difference in ||Fn|| − An. Under the same conditions, a greater value of ||Fn|| − An corresponds to smaller modulus and stronger contraction. This feature of ||Fn|| − An makes it extremely useful in the formulation of constitutive models considering fabric anisotropy.

||Fn|| − An adopted in this study is different from the term 1 − An adopted to reflect anisotropy in many ACST-based constitutive models. This choice is made with considerations of two very appealing characteristics of the term ||Fn|| − An: (1) ||Fn|| − An decouples the influence of fabric anisotropy intensity and fabric orientation on anisotropic behavior, as \( \left\| {{\mathbf{F}}_{n} } \right\| - A_{n} = \left\| {{\mathbf{F}}_{n} } \right\|\left( {1 - {\mathbf{n}}_{\text{F}} :{\mathbf{n}}} \right) \). This formulation allows for more control over anisotropic behavior when adopted in constitutive models; (2) the decoupling of the influence of fabric anisotropy intensity and fabric orientation on anisotropic behavior results in ||Fn|| − An = 0 when the loading direction is the same as that of the fabric tensor (Fig. 4). This is very appealing for the calibration of constitutive models, where many parameters unrelated to anisotropy can be determined via traditional tests without the need to consider the coupled influence of fabric anisotropy, which will be discussed in more detail in Sect. 4. However, it should be noted that this choice neglects the influence of fabric anisotropy intensity on soil behavior when the loading direction is the same as that of the fabric tensor, which is a compromise.

3 Constitutive model formulation

3.1 Basic equations and elasticity

Based on the anisotropic behavior of sand and its fabric origins observed in the previous section, an anisotropic plasticity model is proposed. The model builds on the framework proposed by Wang et al. [73], which has been proven to be highly effective in providing a unified description of sand of different conditions from pre- to postliquefaction under both monotonic and cyclic loading [11, 68, 70], but does not consider anisotropy. Here, the evolution of the fabric tensor and its influence on the strength, shear modulus, and dilatancy of sand is incorporated into the model. The basic equations in incremental form for the model in multiaxial stress space are:

$$ d\varepsilon_{v}^{e} = \frac{dp}{K};\quad d{\mathbf{e}}^{e} = \frac{{d{\mathbf{s}}}}{2G} $$
(3)
$$ d{\mathbf{e}}^{p} = \left\langle L \right\rangle {\mathbf{m}};\quad d\varepsilon^{p}_{v} = \left\langle L \right\rangle D $$
(4)
$$ d{\varvec{\upvarepsilon}} = \frac{1}{2G}pd{\mathbf{r}} + \left( {\frac{1}{2G}{\mathbf{r}} + \frac{1}{3K}{\mathbf{I}}} \right)dp + ({\mathbf{m}} + \frac{D}{3}{\mathbf{I}})\left\langle L \right\rangle $$
(5)

\( {\varvec{\upvarepsilon}} \) is the strain tensor, the volumetric strain is denoted by \( \varepsilon_{v} = {\text{tr(}}{\varvec{\upvarepsilon}}) \), and the deviatoric strain tensor is \( {\mathbf{e}} = {\varvec{\upvarepsilon}} - \varepsilon_{v} /3{\mathbf{I}} \). Superscripts e and p represent elastic and plastic, respectively. \( {\varvec{\upsigma}} \) is the effective stress tensor, \( p = {\text{tr(}}{\varvec{\upsigma}})/3 \) is the mean effective stress, and \( {\mathbf{s}} = {\varvec{\upsigma}} - p{\mathbf{I}} \) is the deviatoric stress. The deviatoric stress ratio tensor is here defined as \( {\mathbf{r}} = \frac{{\mathbf{s}}}{p} \), and \( q = \sqrt {\frac{3}{2}{\mathbf{s:s}}} \), \( \eta = \frac{q}{p} \). K and G are the elastic bulk and shear moduli, respectively, L is the loading index, \( {\mathbf{m}} \) is the deviatoric strain flow direction, and D is the dilatancy. In this model, the dilatancy is decomposed into a reversible and an irreversible part, following Zhang and Wang [87]. 〈 〉 are the Macaulay brackets with \( \langle x \rangle = x \) for \( x > 0 \) and \( \left\langle x \right\rangle = 0 \) for \( x \le 0 \).

K and G are defined following Richart et al. [54]:

$$ K = \frac{1 + e}{\kappa }p_{a} \left( {\frac{p}{{p_{a} }}} \right)^{{\frac{1}{2}}} $$
(6)
$$ G = G_{o} \frac{{\left( {2.973 - e} \right)^{2} }}{1 + e}p_{a} \left( {\frac{p}{{p_{a} }}} \right)^{{\frac{1}{2}}} $$
(7)

Go and \( \kappa \) are material constants, and pa = 101 kPa is the atmospheric pressure. Anisotropy in elastic modulus is not considered in this study.

3.2 Plasticity

Plastic loading occurs when the load index L is greater than zero:

$$ L = \frac{{pd{\mathbf{r:n}}}}{H} $$
(8)

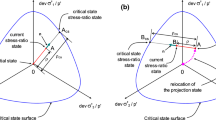
\( {\mathbf{n}} \) is a unit norm deviatoric tensor representing the loading direction, which can be determined following the mapping rule in Fig. 5. H is the plastic modulus. Figure 5 shows the three surfaces and corresponding mapping rule of the proposed model in the π plane of the stress ratio space. The maximum stress ratio surface serves as the bounding surface of the model. The critical state surface determines the ultimate critical state stress ratio. The reversible dilatancy surface determines the stress ratio beyond which reversible dilatancy occurs. The shape of these three homothetic surfaces is determined by a function g(θ) of the load angle θ, for which the formulation of Zhang and Wang [90] is adopted, defined as:

Fig. 5
figure 5

Schematic of the maximum stress ratio surface, critical state surface, reversible dilatancy surface, and mapping rule of the proposed model in the π plane of the stress ratio space

Full size image
$$ g(\theta ) = \frac{1}{{1 + M_{c} (1 + \sin 3\theta - \cos^{2} 3\theta )/6 + (M_{c} - M_{o} )\cos^{2} 3\theta /M_{o} }} $$
(9)

where Mc = M and Mo are the critical state deviatoric stress ratio at triaxial compression and simple shear, which follow the relationship between these two values in the Mohr–Coulomb criteria. The formulation of g(θ) can be replaced based on the needs to reflect different features of the influence of intermediate stress coefficient b, which is not the primary focus of this study, and does not affect the overall concept of the model. The size of each surface at θ = − 30° is determined by the maximum, critical state, and reversible dilatancy stress ratios, respectively, at the triaxial compression state, which will be presented in the following formulations.

For the mapping rule, \( {\mathbf{n}} \) is the unit norm deviatoric tensor normal to the maximum stress ratio surface at \( {\bar{\mathbf{r}}} \), which is the projection of \( {\mathbf{r}} - {\varvec{\upalpha}}_{in} \) on the surface (Fig. 5). Here, \( {\varvec{\upalpha}}_{{{\mathbf{in}}}} \) is the previous load reversal point and is updated upon each load reversal to the current \( {\mathbf{r}} \), i.e., when L in Eq. (8) becomes negative.

The plastic modulus H is defined using bounding surface plasticity [16]:

$$ H = \frac{2}{3}hg\left( \theta \right)G\exp ( - n^{p} \varPsi )\left( {\frac{{M\exp ( - n^{p} \varPsi )}}{{M_{m} }}\frac{{||{\bar{\mathbf{r}}} - {\varvec{\upalpha}}_{\text{in}} ||}}{{||{\mathbf{r}} - {\varvec{\upalpha}}_{\text{in}} ||}} - \frac{1}{{\exp ( - \Delta_{\;1} (||{\mathbf{F}}_{n} || - A_{n} )^{1/2} )}}} \right) $$
(10)

h is a model parameter for plastic modulus, M is the stress ratio at critical state in triaxial compression, and is also a model parameter. The state parameter Ψ = e − ec proposed by Been and Jefferies [6] is used for state dependency behavior. The critical state void ratio ec is a function of the mean effective stress, which is determined as \( e_{c} = e_{0} - \lambda_{c} (p_{c} /p_{at} )^{\xi } \) following Li and Wang [38], where e0, λc, and ξ are model parameters. np is a model parameter dictating the sensitivity of the plasticity modulus to changes in void ratio. Mm is the equivalent maximum stress ratio at the triaxial compression state. When the current equivalent stress ratio η/g(θ) is smaller than Mexp(− npΨ), Mm is the maximum stress ratio that has occurred during loading. If η/g(θ) > Mexp(− npΨ), Mm = η/g(θ) until η/g(θ) < Mexp(− npΨ) again. Δ1 is the positive-valued modulus anisotropy model parameter.

3.3 Influence of fabric anisotropy on plastic modulus

The influence of fabric anisotropy on both the strength and shear modulus anisotropy of sand is introduced in Eq. (10) through the term exp(− Δ1(||Fn|| − An)1/2). As discussed in Fig. 4, 0 ≤ ||Fn|| − An ≤ 2||Fn||, with An = Fn:n. In Eq. (10), greater ||Fn|| − An leads to a smaller exp(− Δ1(||Fn|| − An)1/2), which results in smaller peak deviatoric stress ratio and also smaller H, in accordance with the DEM results shown in Figs. 1, 2, and 4. In the constitutive model, Fn is a normalized deviatoric fabric tensor corresponding to the fabric tensor in Eq. (2), the norm of which is 1 at the critical state. The fabric evolution equation for the model builds on the incremental formulation by Li and Dafalias [36]:

$$ d{\mathbf{F}}_{n} = < L > c({\mathbf{n}} - (1 + D){\mathbf{F}}_{n} ) $$
(11)

This incremental fabric evolution formulation guarantees that at the critical state, the normalized fabric tensor Fn becomes the same as n, as suggested by the results in Fig. 4 and many other studies [18, 23, 34, 71, 83]. c is a fabric evolution rate model parameter. The incorporation of the dilatancy D following Yang et al. [84] allows ||Fn|| to reach beyond 1, as observed for dense sand and in the DEM results in Fig. 4b. The use of D to capture the fabric evolution of sand with different densities has been shown to be effective when simulating DEM test results on samples with various densities [75]. For dense sand, peak ||Fn|| exceeds its critical state value, while for loose sand, ||Fn|| gradually increases toward its critical state value. Only one model parameter is introduced in Eq. (11) to try and keep the fabric evolution formulation as simple as possible for the current model.

In the proposed model, it is assumed that the deviatoric strain flow direction m = n, for simplicity. If the influence of fabric anisotropy on the noncoaxiality between the strain increment and stress is to be considered, a linear combination between n and the direction of Fn in the form of \( {\mathbf{m}} = ({\mathbf{n}} - x{\mathbf{F}}_{n} /||{\mathbf{F}}_{n} ||)/||({\mathbf{n}} - x{\mathbf{F}}_{n} /||{\mathbf{F}}_{n} ||)|| \) may serve as possible solution, with x being a positive parameter less than 1. Calibration and validation of such noncoaxial behavior should ideally be conducted for radial loading in the π plane in different directions with respect to the fabric orientation and more importantly, for loading with rotation of the principal stress axes, which is not within the scope of the current study.

3.4 Dilatancy

The dilatancy's \( D \) is a combination of a reversible part \( D_{re} \) and an irreversible part \( D_{ir} \) following the findings of Shamoto et al. [59] and Zhang [89]:

$$ D = D_{\text{re}} + D_{\text{ir}} $$
(12)

This decomposition has two major benefits: (1) It allows for separate control over contraction and dilation, which is very important when working with cyclic loading; (2) using the formulation of the model, it allows for the generation and eventual saturation of the postliquefaction shear strain during undrained cyclic loading. According to its definition, the volumetric strain \( \varepsilon^{p}_{v,re} \) caused by reversible dilatancy is always nonpositive [87], generating during loading and releasing after load reversal. Hence, Dre is determined separately for generation and release following Wang et al. [73]:

$$ D_{\text{re}} = \left\{ {\begin{array}{*{20}l} {D_{\text{re,gen}} ,} \hfill & {{\mathbf{(r}}_{{\mathbf{d}}} - {\mathbf{r):n}} < 0} \hfill \\ {D_{\text{re,rel}} ,} \hfill & {{\mathbf{(r}}_{{\mathbf{d}}} - {\mathbf{r):n}} > 0} \hfill \\ \end{array} } \right. $$
(13)

rd is the intersection of \( {\bar{\mathbf{r}}} \) and the reversible dilatancy surface, i.e., \( {\mathbf{r}}_{{\mathbf{d}}} = \frac{{M_{d} }}{{M_{m} }}{\bar{\mathbf{r}}} \). Md = Mexp(ndΨ) is the deviatoric stress ratio beyond which reversible dilatancy is generated in triaxial compression. nd is a model parameter for state-dependent dilatancy. The reversible dilatancy generation Dre,gen follows:

$$ D_{\text{re,gen}} = \sqrt {\frac{2}{3}} d_{{{\text{re}},1}} \left( {{\mathbf{r}}_{{\mathbf{d}}} - {\mathbf{r}}} \right){\mathbf{:n}} $$
(14)

\( d_{{{\text{re}},1}} \) is a reversible dilatancy parameter. After load reversal, reversible is released until \( \varepsilon^{p}_{{v,{\text{re}}}} \) becomes zero again. The reversible dilatancy release Dre,rel is:

$$ D_{\text{re,rel}} = \left( {d_{{{\text{re}},2}} \chi } \right)^{2} /p $$
(15)

\( d_{{{\text{re}},2}} \) is a model parameter. The function \( \chi = \hbox{min} \left( { - d_{ir} \frac{{\varepsilon_{{v,{\text{re}}}}^{p} }}{{\varepsilon_{{v,{\text{ir}}}}^{{p,{\text{pr}}}} }},1} \right) \) is introduced to guarantee Dre,rel = 0 after \( \varepsilon_{\text{vd,re}} \) is completely released, where \( \varepsilon_{{v,{\text{ir}}}}^{{p,{\text{pr}}}} \) is the irreversible dilatancy-induced volumetric strain \( \varepsilon_{{v,{\text{ir}}}}^{p} \) at previous load reversal. \( d_{\text{ir}} \) is a irreversible dilatancy model parameters. Prior to the first load reversal, \( \chi \) remains zero.

By definition, irreversible dilatancy induces nonnegative contractive volumetric strain \( \varepsilon_{{v,{\text{ir}}}}^{p} \) only. Zhang and Wang [90] showed that \( \varepsilon_{{v,{\text{ir}}}}^{p} \) accumulates asymptotically during cyclic loading, while its accumulation rate also decreases during every single monotonic shearing event. Based on these observations, Wang et al. [73] proposed an isotropic formulation for the irreversible dilatancy Dir,iso:

$$ D_{\text{ir,iso}} = d_{\text{ir}} \exp (n^{d} \varPsi - \alpha \varepsilon_{\text{vd,ir}} )( < M_{d} - \eta > \exp (\chi ) + \left( {1 + \frac{{\gamma_{mono} }}{{\gamma_{d,r} < 1 - \exp (n^{d} \varPsi ) > }})^{ - 2} } \right) $$
(16)

\( \alpha \) is another irreversible dilatancy model parameter. The term \( \left( {1 + \frac{{\gamma_{\text{mono}} }}{{\gamma_{d,r} < 1 - \exp (n^{d} \varPsi ) > }}} \right)^{ - 2} \) reflects the decrease in \( \varepsilon^{p}_{{v,{\text{ir}}}} \) accumulation rate during a monotonic shearing event. \( \gamma_{\text{mono}} \) is the accumulated shear strain since the last stress reversal. \( \gamma_{d,r} \) is a model parameter that can be assumed to be 0.05 by default. χ is introduced to enhance contraction upon load reversal.

3.5 Influence of fabric anisotropy on dilatancy

Figure 3 indicates that the dilatancy of sand is significantly anisotropic, especially during contraction. To take dilatancy anisotropy into consideration, the irreversible dilatancy Dir in this model is proposed as:

$$ D_{\text{ir}} = \frac{{d_{\text{ir}} + (||{\mathbf{F}}_{n} || - A_{n} )\Delta_{\;2} }}{{d_{\text{ir}} }}D_{\text{ir,iso}} $$
(17)

Δ2 is the positive-valued irreversible dilatancy anisotropy model parameter. By adding the fabric anisotropy term (||Fn|| − An)Δ2 to the isotropic irreversible dilatancy Dir,iso in Eq. (13), the irreversible dilatancy Dir in Eq. (14) increases in contraction with increasing ||Fn|| − An, as indicated by the results in Figs. 3 and 4. Figures 3 and 4 also show that the bedding plane angle has only little influence on the dilatancy during the dilative phase, which has also been discussed in Wang et al. [75]. These observations suggest that dilatancy anisotropy should be able to be reflected by the anisotropic irreversible dilatancy alone in the proposed model. Hence, the influence of fabric anisotropy on Dre is neglected.

The development of total, irreversible, and reversible dilatancy during a typical undrained triaxial loading and reverse loading path is plotted in Fig. 6, to visualize the performance of the dilatancy formulation. The model parameters for Toyoura sand, discussed later in Sect. 4, are used here, under the undrained stress path shown in Fig. 6a. In the model, the total dilatancy D is the sum of the irreversible dilatancy Dir and the reversible dilatancy Dre. At the initiation of loading, Dre remains inactive at zero and D = Dir, being positive, i.e., contractive (Fig. 6b). When the stress ratio exceeds the reversible dilatancy surface in Fig. 5, reversible dilatancy Dre is generated following Eq. (14). Also, as loading continues, Dir decreases gradually according to Eq. (16). When the sum of Dir and Dre becomes negative, the model exhibits overall dilatancy, causing the undrained stress path to show increase in mean effective stress p in Fig. 6a. Upon reverse loading, Dir increases significantly due to the combined effects of Eq. (16) and fabric anisotropy in Eq. (17), while Dre follows Eq. (15) and becomes strongly contractive. Dre quickly falls back to zero during reverse loading, and D once again becomes the same as Dir until the stress state reaches beyond the reversible dilatancy surface again.

Fig. 6
figure 6

Development of total, irreversible, and reversible dilatancy during undrained triaxial loading and reverse loading: a stress path, q versus p, b dilatancy D versus deviatoric stress ratio η

Full size image

3.6 Liquefaction state

A distinct feature of the models by Zhang and Wang [90] and Wang et al. [73] is the formulation for the generation of large yet bounded shear strain at the liquefaction state of zero effective stress, which uniquely captures the cyclic liquefaction behavior of sand. This formulation was proposed based on the insights obtained from test observations of cyclic drained and undrained loading of sand by Shamoto et al. [59] and Zhang [89], and is adopted here. At the liquefaction state, as the increments of p and s are zero, no elastic strains are assumed to be generated. However, dr is not zero and the dilatancy equations are still assumed functional. As the model reaches liquefaction state, it is initially contractive. During the contractive phase, a “virtual” elastic volumetric strain is generated due to \( (d\varepsilon^{e}_{v} )_{\text{virtual}} = d\varepsilon_{v} - d\varepsilon^{p}_{v} \). This is to offset the inconsistency between the plastic volumetric strain with the volumetric strain boundary condition, which has been shown to be caused by the change in internal structure of the material [70]. As shear strain continues to occur at the liquefaction state, r increases and the model eventually becomes dilative. During the dilative phase, the “virtual” elastic volumetric strain must be fully erased before the model exists liquefaction. Hence, according to Eq. (4), sufficient shear strain must occur at the liquefaction state to facilitate the dilatancy process, which accumulates asymptotically with increasing number of load cycles due to the asymptotic accumulation of irreversible dilatancy-induced volumetric strain \( \varepsilon^{p}_{{v,{\text{ir}}}} \). This “virtual” elastic volumetric strain is fully released when sand leaves liquefaction state, and does not come into the model in nonliquefaction states, where the sum of the elastic and plastic volumetric strain is consistent with the volumetric strain boundary condition.

4 Model validation and application

4.1 Model parameters

The proposed model has a total of 17 parameters, as listed in Table 2. In total, 14 of these parameters are identical to those in the isotropic model by Wang et al. [73], the calibration of which can also follow the same procedure as stated in the previous work. Two of these 14 parameters, namely dre,2 and γd,r, can generally use default values of 30 and 0.05, respectively. Three new fabric anisotropy-related parameters, Δ1, Δ2, and c, are introduced in the proposed anisotropic model. Two of the three new parameters, Δ1 and Δ2, can be calibrated based on results from triaxial or torsional shear tests on samples with different bedding plane angles, such as the tests by Oda [46] and Yoshimine et al. [88]. The fabric evolution parameter c and the normalized initial fabric tensor should ideally be obtained by measuring the fabric of sand during loading. Though measuring the microstructure of sand is now possible (e.g., [2, 66]), the application of such technology is still not yet common. For now, the determination of the initial fabric tensor and the calibration of all three fabric anisotropy parameters for actual sand without microscopic measurement would still need to rely on an indirect trial-and-error process using tests on samples with different bedding plane angles. In this study, the initial fabric tensor Fn,in is not considered as a model parameter along the same logic as that of the initial void ratio e not being considered a model parameter, although many existing ACST models use initial fabric as a model parameter. The initial fabric of soil is its inherent property and is independent of the constitutive model. Although direct measurement of fabric in laboratory tests is still difficult compared with void ratio, DEM already allows “real measurements” of initial fabric. The current development of DEM can provide a valuable means to evaluate ACST-based models’ simulation of the true material fabric, rather than treating fabric as an idealized concept. The detailed model parameter calibration process is described as follows:

Table 2 Model parameters for various numerical simulations
Full size table
  1. 1.

    Monotonic drained tests on samples with bedding plane angle of 0° and different densities and mean effective stress values are first used to calibrate 10 model parameters G0, κ, h, M, dir, np, nd, λc, e0, and ξ following the conventional method described in Wang et al. [73]. Here, the advantage of using ||Fn|| − An to reflect anisotropic behavior is highlighted. When the bedding plane angle is 0°, ||Fn|| − An is always 0 and does not affect the calibration of these 10 parameters.

  2. 2.

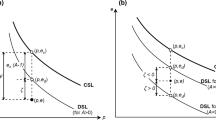
    Monotonic drained tests on dense sand samples with bedding plane angle of 90° are then used to determine the two fabric anisotropy influence parameters Δ1 and Δ2. In the proposed model, the peak deviatoric stress ratio \( \eta_{{\;f,90^{ \circ } }} \) and maximum volumetric strain in contraction \( \varepsilon_{{v,\hbox{max} ,90^{ \circ } }} \) for dense sand samples with bedding plane angle of 90° are influenced by Δ1 and Δ2, respectively. Therefore, Δ1 and Δ2 can be determined via \( \eta_{{\;f,90^{ \circ } }} \) and \( \varepsilon_{{v,\hbox{max} ,90^{ \circ } }} \) through an iterative approach:

    $$ \left\{ {\begin{array}{*{20}l} {\frac{{\Delta_{{\;1,{\text{n}}}} - \Delta_{{\;1,{\text{n}} - 1}} }}{{\Delta_{{\;1,{\text{n}} - 1}} - \Delta_{\;1, 0} }} = \frac{{\eta_{{\;f,90^{ \circ } }} - \eta_{{\;f,{\text{n}} - 1}} }}{{\eta_{{\;f,{\text{n}} - 1}} - \eta_{{\;f,{\text{n}} - 2}} }}} \hfill \\ {\frac{{\Delta_{{\;2,{\text{n}}}} - \Delta_{{\;2,{\text{n}} - 1}} }}{{\Delta_{{\;2,{\text{n}} - 1}} - \Delta_{\;2, 0} }} = \frac{{\varepsilon_{{v,\hbox{max} ,90^{ \circ } }} - \varepsilon_{{v,\hbox{max} ,{\text{n}} - 1}} }}{{\varepsilon_{{v,\hbox{max} ,{\text{n}} - 2}} - \varepsilon_{{v,\hbox{max} ,{\text{n}} - 1}} }}} \hfill \\ \end{array} } \right. $$
    (18)

    where n is an iteration index. The initial iterative values can generally be taken as \( \left\{ \begin{aligned} \Delta_{\;1, 0} = 0 \hfill \\ \Delta_{\;2, 0} = 0 \hfill \\ \end{aligned} \right. \) and \( \left\{ \begin{aligned} \Delta_{\;1,1} = 0.5 \hfill \\ \Delta_{\;2, 1} = 0.5 \hfill \\ \end{aligned} \right. \). In most cases, adequate convergence is achieved after two to three iterations, i.e., \( \left\{ \begin{aligned} \Delta_{\;1} = \Delta_{\;1,4} \hfill \\ \Delta_{\;2} = \Delta_{\;2,4} \hfill \\ \end{aligned} \right. \). Figure 7 shows an example of this iterative approach. Starting with \( \left\{ \begin{aligned} \Delta_{\;1, 0} = 0 \hfill \\ \Delta_{\;2, 0} = 0 \hfill \\ \end{aligned} \right. \) and \( \left\{ \begin{aligned} \Delta_{\;1,1} = 0.5 \hfill \\ \Delta_{\;2, 1} = 0.5 \hfill \\ \end{aligned} \right. \), convergence toward the peak deviatoric stress ratio and maximum volumetric strain in contraction of the sample with bedding plane angle of 90° is achieved at \( \left\{ \begin{aligned} \Delta_{\;1,4} { = 0} . 6\hfill \\ \Delta_{\;2,4} { = 1} . 0\hfill \\ \end{aligned} \right. \).

    Fig. 7
    figure 7

    Determination of two fabric anisotropy influence parameters Δ1 and Δ2

    Full size image
  3. 3.

    The remaining parameters dre,1, α, and the fabric evolution rate parameter c are then calibrated through a trial-and-error process via fitting the simulation curves with test results for undrained cyclic shearing. dre,1 mainly controls the postliquefaction shear strain generation during each undrained load cycle, and greater dre,1 results in smaller postliquefaction shear strain. α affects the asymptotic saturation of the postliquefaction shear strain, and greater α results in faster saturation of the postliquefaction shear strain. The fabric evolution rate parameter c mainly determines how quickly the stress and strain response of samples with different bedding plane angles converges.

The previous isotropic model by Wang et al. [73] uses step 1 and 3 (without parameter c) to complete model parameter calibration. Step 2 is unique to the current proposed model.

The original isotropic model has been validated against a wide range of tests on sand of different void ratios and under different confining stresses [70, 73], allowing for the evaluation of the proposed anisotropic model performance in this study to focus on the influence of fabric anisotropy. The model is first scrutinized against DEM numerical monotonic drained triaxial tests on samples with different initial void ratio and bedding plane angle, including the four presented in Sect. 2, and then against undrained triaxial tests on samples with different bedding plane angles and undrained cyclic simple shear tests, on both macro- and microlevels. Though several plasticity models incorporating fabric tensors have been developed, quantitative validation of their fabric-related formulations on the micromechanical level has rarely been reported, especially under cyclic loading. Undrained and drained monotonic tests [46, 88] and undrained cyclic tests [12, 28] on various sand samples are also simulated, validating the model against physical tests. Numerical analysis is also performed to investigate the influence of fabric anisotropy on the liquefaction behavior of sand.

4.2 Validation against DEM tests

The four DEM constant p = 100 kPa triaxial tests on samples with ein = 0.657 ± 0.005 and δ = 0°, 30°, 60°, and 90°, discussed in Sect. 2, along with two other constant p triaxial tests on samples with ein = 0.693 and 0.690 and δ = 0° and 90°, two undrained conventional triaxial compression tests on samples with ein = 0.655 and 0.661 and δ = 0° and 90°, and four undrained cyclic simple shear test on samples with ein = 0.655 and δ = 0°, and ein = 0.693 and δ = 0°are used to validate the model. In the simulations for these tests with various stress paths on samples with various void ratio and initial fabric using the proposed constitutive model, a single set of model parameters is used, while the initial normalized fabric tensor Fn of each sample obtained from the DEM tests is used directly as the input of the simulations. The 17 model parameter values used for these simulations are provided in Table 2.

Figure 8 shows the overall deviatoric stress ratio–deviatoric strain and void ratio–deviatoric strain relationships from both the DEM tests and the constitutive model simulations for the constant p triaxial tests on samples with ein = 0.657 ± 0.005. The proposed model is able to reproduce the anisotropy in both strength and void ratio evolution observed in the DEM tests. The peak η is greater for samples with lower δ. Samples with greater δ initially experience stronger contraction. Both the stress and void ratio converge to each respective unique value at the critical state.

Fig. 8
figure 8

Stress and deformation results from DEM numerical tests and constitutive model simulations of constant p = 100 kPa triaxial loading on four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°: DEM numerical test results for a deviatoric stress ratio η versus deviatoric strain εq; b void ratio e versus deviatoric strain εq; constitutive model simulation results for c η versus εq; d e versus εq

Full size image

The equivalent shear modulus dq/dεq and dilatancy D for these DEM tests and constitutive model simulations on the four samples with ein = 0.657 ± 0.005 are plotted against the deviatoric stress ratio η in Fig. 9. For the equivalent shear modulus, the constitutive model simulations agree with the DEM test results in terms of samples with higher δ having lower dq/dεq. The model simulations show faster degradation of equivalent shear modulus with respect to the η, which is due to the specific formulation of the plastic modulus in Eq. (10). For the dilatancy, the simulated results agree well with the DEM results. Both the simulated and DEM results show greater initial contraction for samples with higher δ. Also, as dilation occurs, the D − η plots for the different samples tend to cluster, while the samples with higher δ have smaller absolute values of peak dilation.

Fig. 9
figure 9

Shear modulus dq/dεq and dilatancy D results from DEM numerical tests and constitutive model simulations of constant p = 100 kPa triaxial loading on four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°: DEM numerical test results for a shear modulus dq/dεq versus deviatoric stress ratio η; b dilatancy D versus deviatoric stress ratio η; constitutive model simulation results for c dq/dεq versus η; d D versus η

Full size image

A significant advantage of validating the proposed model against DEM data is the accessibility of the fabric information. Figure 10 plots the fabric orientation θn and norm ||Fn|| against the deviatoric stress ratio η for samples with different δ, for both DEM tests and constitutive model simulations. The simulations are generally able to reflect the evolution of the fabric tensor during loading. The simulations show a similar evolution of θn toward the loading direction with the DEM results, reaching 90° at the critical state. The simulation results for ||Fn|| also evolve toward the same value of 1 at the critical state. Due to the incorporation of the dilatancy D in Eq. (11), the constitutive model is able to reflect the peak of ||Fn|| reaching beyond 1 for dense sand.

Fig. 10
figure 10

Contact normal fabric results from DEM numerical tests and constitutive model simulations of constant p = 100 kPa triaxial loading on four samples with ein = 0.657 ± 0.005 and bedding plane angles of 0°, 30°, 60°, and 90°: DEM numerical test results for a contact normal fabric orientation θn versus deviatoric stress ratio η; b normalized contact normal fabric norm ||Fn|| versus deviatoric stress ratio η; constitutive model simulation results for c θn versus η; d ||Fn|| versus η

Full size image

It should be acknowledged that the simulation of fabric evolution based on the relatively simple form of Eq. (11) is far from perfect, especially for the results in Fig. 10b, d. Recently, through detailed analysis of DEM test data, Wang et al. [74] showed that the contact normal fabric evolution is not only dependent on its own state but also is affected by other particle-scale features, including particle and void orientations. More realistic simulation of fabric evolution can be achieved with formulations incorporating a few extra model parameters. However, considering the current state of the art for fabric measurement and model calibration, the current model still adopts the simple formulation in Eq. (11), to limit the number of model parameters.

Corresponding to the tests with ein = 0.657 ± 0.005 and δ = 0°, 30°, 60°, and 90°, two other constant p triaxial tests on looser samples with ein = 0.693 and 0.690 and δ = 0° and 90° are also simulated using the model. Using the same set of parameters, the model is also able to simulate the behavior of the looser samples under triaxial loading, which exhibit lower peak η and stronger initial contraction (Fig. 11). The anisotropic behavior due to different initial δ is again well reflected.

Fig. 11
figure 11

Stress and deformation results from DEM numerical tests and constitutive model simulations of constant p = 100 kPa triaxial loading on two samples with ein = 0.693 and 0.690, bedding plane angles of 0° and 90°: DEM numerical test results for a deviatoric stress ratio η versus deviatoric strain εq; b void ratio e versus deviatoric strain εq; constitutive model simulation results for c η versus εq; d e versus εq

Full size image

Two undrained conventional triaxial compression DEM tests on the dense samples, with ein = 0.655 and 0.661 and δ = 0° and 90°, are also conducted and simulated, again with the same set of model parameters. Undrained loading is achieved in DEM through applying constant volume constraint. The simulation from the constitutive model can capture the difference in stress path and stress–strain relationships for the two samples with different bedding plane angles to a good extent (Fig. 12). Stronger initial contraction is observed for the 90° sample, evident from the more significant initial decrease in p. The simulations show slight underestimation of the deviatoric stress compared with the DEM results. These results show that the proposed model is not only valid for drained triaxial tests on samples with various void ratio and initial fabric, but also for undrained tests as well.

Fig. 12
figure 12

Stress and deformation results from DEM numerical tests and constitutive model simulations of undrained conventional triaxial compression loading on two samples with ein = 0.655 and 0.661, bedding plane angles of 0° and 90°: DEM numerical test results for a deviatoric stress q versus mean effective stress p; b deviatoric stress q versus deviatoric strain εq; constitutive model simulation results for c q versus p; d q versus εq

Full size image

Few anisotropic models have been validated against cases of undrained cyclic loading. Here, an undrained cyclic simple shear DEM test on a sample with ein = 0.655, δ = 0°, and ||Fn,in|| = 0.43 is conducted and used to validate the capability of the model in capturing the cyclic liquefaction behavior of anisotropic sand, on both macroscopic and microscopic levels. The cyclic simple shear DEM tests are conducted on samples isotropically consolidated at p = 100 kPa, and the bedding plane angle δ refers to the angle between the deposition direction and the vertical direction, and shear is then applied to the horizontal plane. Figure 13 shows the stress path, stress–strain relationship, and fabric evolution during undrained cyclic loading in both DEM test and constitutive simulation.

Fig. 13
figure 13

Stress, strain, and fabric evolution results from DEM numerical tests and constitutive model simulations of undrained cyclic simple shear loading on a sample with e = 0.655, δ = 0°, and ||Fn,in|| = 0.43: DEM numerical test results for a shear stress τ versus mean effective stress p; b shear stress τ versus shear strain γ; c shear stress τ versus shear strain γ for the first six load cycles; d contact normal fabric norm ||Fn|| times the sign of Fzz − Fxx − Fxz versus mean effective stress p; constitutive model simulation results for e τ versus p; f τ versus γ; for the first six load cycles; h ||Fn||sign(Fzz − Fxx − Fxz) versus p

Full size image

The proposed constitutive model is able to capture the decrease in effective stress during undrained cyclic loading, eventually leading to initial liquefaction and the “butterfly orbit” of the stress path after similar number of load cycles as that in DEM (Fig. 13a, e). The accumulation of large shear strain at liquefaction during each load cycle is well reproduced by the constitutive model, though generation of shear strain in the constitutive simulations is slower (Fig. 13b, f). Figure 13c, g also zooms in on the shear strain in the first six load cycles. The key features of fabric evolution are also surprisingly well simulated by the constitutive model (Fig. 13d, h), considering that the fabric evolution formulation has yet to be directly compared to that in actual physical or numerical tests.

In Fig. 13d, h, the contact normal fabric norm ||Fn|| is multiplied by the sign of Fzz − Fxx − Fxz to reflect not only the value of ||Fn|| but also the direction of the fabric tensor, for visual clarity, especially after initial liquefaction. Prior to initial liquefaction, relatively mild evolution of fabric is observed in both DEM test and constitutive simulation, where the oscillation of fabric in simulation results within each cycle is less significant than that in the DEM results. After initial liquefaction, the fabric tensor is found to evolve abruptly at the liquefaction state within each loading cycle, from one direction to another, reflected by the oscillation of ||Fn||sign(Fzz − Fxx − Fxz) from positive to negative and vice versa. As with the development of shear strain, the evolution of fabric in cycles after initial liquefaction predicted by the constitutive model is slower than that in the DEM test and shows slower achievement of the saturated level. These quantitative differences between model simulation and DEM results suggest that further studies on fabric evolution under cyclic loading should be conducted.

Further undrained cyclic simple shear DEM test is conducted on the sample with ein = 0.655, δ = 0°, and ||Fn,in|| = 0.43 for two other cyclic stress ratios (CSR = τmax/p0′), and on another sample with ein = 0.693, δ = 0°, and ||Fn,in|| = 0.41, and are simulated using the proposed model. Figure 14 shows the stress path (τ − p) and stress–strain relationship (τ − γ) during undrained cyclic loading in both DEM test and constitutive simulation. The increase in number of load cycles needed to reach initial liquefaction with decreasing CSR is well reflected, while the amplitude of postliquefaction shear strain is unaffected by CSR, as was found in Wang et al. [72]. The number of load cycles required to reach initial liquefaction for the sample with ein = 0.655, δ = 0°, and ||Fn,in|| = 0.43 under CSR of 0.1, 0.2, and 0.3 is 46, 8, and 4 in DEM, and 40, 8, 4 in constitutive modeling, respectively. Decrease in liquefaction resistance and increase in postliquefaction shear strain amplitude with increase in void ratio is also well modeled.

Fig. 14
figure 14

Stress and strain results from DEM numerical tests and constitutive model simulations of undrained cyclic simple shear loading on a sample under various cyclic stress ratios (CSR) and with void ratios (δ = 0°): a DEM e = 0.655, CSR = 0.1, τ versus p; b constitutive e = 0.655, CSR = 0.1, τ versus p; c DEM e = 0.655, CSR = 0.1, τ versus γ; d constitutive e = 0.655, CSR = 0.1, τ versus γ; e DEM e = 0.655, CSR = 0.3, τ versus p; f constitutive e = 0.655, CSR = 0.3, τ versus p; g DEM ein = 0.655, CSR = 0.3, τ versus γ; h constitutive e = 0.655, CSR = 0.3, τ versus γ; i DEM e = 0.655, CSR = 0.3, τ versus p; j Constitutive e = 0.655, CSR = 0.3, τ versus p; k DEM e = 0.655, CSR = 0.3, τ versus γ; l Constitutive e = 0.655, CSR = 0.3, τ versus γ

Full size image

4.3 Validation against laboratory tests

Although DEM test results may show quantitative differences to real sand due to the difference in particle shape and contact, they can be qualitatively representative of sand and offer the benefit of direct measurement of fabric quantities. This benefit allows for the direct validation of fabric anisotropy-based constitutive models. With the aid of DEM tests, direct evaluation of the dependency of shear modulus and dilatancy on fabric anisotropy, and the evolution of fabric can be achieved, as in this study. Nonetheless, it is still very important to apply the model to real sand. In the case of physical tests, there are not enough data corresponding to all the DEM test stress paths for the same sand and no corresponding measurement of microscopic fabric quantities. Consequently, the macroscopic results of several classical test results on two types of sand are simulated, using model parameters in Table 2. Both undrained monotonic and cyclic torsional shear tests on the widely used Toyoura sand are first simulated using the same set of model parameters.

The simulations for undrained monotonic loading on Toyoura sand with e = 0.825 ± 0.004 and bedding plane angle δ of 15°, 30°, 60°, and 75° are presented in Fig. 15. The tests were conducted by Yoshimine et al. [88] using a hollow cylinder torsional apparatus, with pin = 100 kPa and b = (σ2 − σ3)/(σ1 − σ3) = 0.5. The model parameters for the simulations are listed in Table 2. As the fabric information is not available, the initial fabric tensor orientation is assumed to be δ + 90°, and the initial fabric norm is assumed as ||Fnin|| = 0.4, similar to that those in the DEM tests. The three fabric-related model parameters are estimated. Both the simulated stress paths and stress–strain curves for the different samples agree well with the test data. The sample with δ = 15° shows mostly dilative behavior, while the δ = 75° shows strong initial contraction, almost reaching static liquefaction. Figure 15e, f also plots the evolution of dilatancy D and contact normal fabric norm ||Fn|| obtained from the constitutive simulations. As the samples in these tests are relatively loose, the samples are initially strongly contractive, and dilatancy D is initially greater for samples with greater bedding plane angles. The evolution of contact normal fabric of the different samples also shows different features, ||Fnin|| gradually increases toward 1 for the sample with δ = 15°, while it initially decreases and then increases toward 1 for the sample with δ = 75°. It should be noted that by introducing the dilatancy in the fabric evolution Eq. (11), for a strongly contractive loose sample, the initial fabric increment direction may become opposite to the current loading direction. Whether this feature is realistic still requires justification from further test evidence.

Fig. 15
figure 15

Stress and strain results from laboratory tests and constitutive model simulations of undrained monotonic hollow cylinder torsional shear loading on four samples with bedding plane angles of 15°, 30°, 60°, and 75°: laboratory test results for a deviatoric stress σ1 − σ3 versus mean effective stress p; b deviatoric stress σ1 − σ3 versus deviatoric strain ε1 − ε3; constitutive model simulation results for c σ1 − σ3 versus p; d σ1 − σ3 versus ε1 − ε3; e ε1 − ε3 versus dilatancy D; f ε1 − ε3 versus ||Fn||. Laboratory test results from Yoshimine et al. [88]

Full size image

Using the exact same model parameters and initial fabric state, the undrained monotonic triaxial tests reported by Yoshimine et al. [85] are also simulated. These tests are conducted under different initial confining pressures, under both triaxial compression (TC) and extension (TE). Overall good agreement between simulation and test results is achieved for both initial confining pressures. Stronger contraction under TE is observed in both simulation and test results, with the TE tests reaching static liquefaction, and generating significant shear strain at liquefaction state (Fig. 16c, d). The TC results show initial contraction followed by subsequent dilatancy and increase in p (Fig. 16a, b). The constitutive model simulations overestimate the increase in deviatoric stress with increasing deviatoric strain (Fig. 16c, d), which may be due to the simple g(θ) function in Eq. (9), which does not introduce any parameters other than M. If necessary, an alternative function form may be used for g(θ).

Fig. 16
figure 16

Stress and strain results from laboratory tests and constitutive model simulations of undrained triaxial compression (TC) and triaxial extension (TE) loading on samples with e = 0.876, 0.878, 0.888, and 0.890 under initial p = 100 kPa and 50 kPa, laboratory test: a σ1 − σ3 versus p; b σ1 − σ3 versus ε1 − ε3; constitutive simulation: c σ1 − σ3 versus p; d σ1 − 3 versus ε1 − ε3. Laboratory test results from Yoshimine et al. [88]

Full size image

The simulations for undrained cyclic hollow cylinder torsional shear tests on Toyoura sand with e = 0.846 under CSR = 0.16 and e = 0.768 under CSR = 0.182 are presented in Fig. 17, and the tests were conducted by Chiaro et al. [12] and Koseki et al. [28], respectively. The model parameters are the same as those used to simulate the monotonic tests by Yoshimine et al. [88], listed in Table 2. The initial fabric norm is again assumed as ||Fnin|| = 0.4, as the sample preparation technique was largely consistent for these tests. The good agreement between simulation and test results under undrained cyclic loading again highlights the model’s ability to capture both monotonic and cyclic behavior of sand, reproducing the decrease in effective stress during undrained cyclic loading and also the postliquefaction shear strain generation. Both test and simulation results exhibit similar increase in number of load cycles to liquefaction with decreasing void ratio and decrease in postliquefaction shear strain with decreasing void ratio.

Fig. 17
figure 17

Stress and strain results from laboratory tests and constitutive model simulations of undrained cyclic hollow cylinder torsional shear loading on two samples with various void ratios under different CSR: a laboratory test [12] e = 0.846, CSR = 0.16, τ versus p; b constitutive e = 0.846, CSR = 0.16, τ versus p; c laboratory test [12] e = 0.846, CSR = 0.16, τ versus γ; d constitutive e = 0.846, CSR = 0.16, τ versus γ; e laboratory test [28] e = 0.768, CSR = 0.182, τ versus p; f constitutive e = 0.768, CSR = 0.182, τ versus p; g laboratory test [28] e = 0.768, CSR = 0.182, τ versus γ; h constitutive e = 0.768, CSR = 0.182, τ versus γ

Full size image

A drained cyclic torsional test on Toyoura sand with e = 0.730 reported by Zhang and Wang [90] is also simulated using the model with the same set of model parameters listed in Table 2. The initial fabric norm is assumed to be the same as those of the previous tests as ||Fnin|| = 0.4. As shown in Fig. 18, the stress–strain loop is well captured using the model and its parameters and the accumulation of contractive volumetric strain from constitutive simulation agree well with the laboratory test results.

Fig. 18
figure 18

Stress and strain results from laboratory tests and constitutive model simulations of drained cyclic hollow cylinder torsional shear loading on a sample with e = 0.730 under cyclic shear strain amplitude of 0.01: a laboratory test γ versus τ; b laboratory test τ versus εv; c constitutive γ versus τ; d constitutive test τ versus εv. Laboratory test results from Zhang and Wang [90]

Full size image

It should be noted that different batches of even the standard Toyoura sand may show large inconsistencies in terms of material behavior and different preparation methods would result in significantly different initial state of the samples. Therefore, it should not be expected that this exact same set of parameters and initial state values will always be applicable to all existing tests using Toyoura sand.

The drained triaxial compression tests on a quartz sand at 65% relative density and pin = 100 kPa with bedding plane angle δ of 0°, 30°, 60°, and 90° by Oda [46] are also simulated using the proposed model (Fig. 19), to evaluate the model’s performance for drained loading, using the parameters in Table 2. Again, the initial fabric tensor orientation is assumed as δ + 90°, while ||Fnin|| = 0.4. Similar to the simulations of the DEM triaxial tests, the model is able to capture the anisotropic deviatoric stress and volumetric strain development for the four different samples.

Fig. 19
figure 19

Stress and strain results from laboratory tests and constitutive model simulations of conventional drained triaxial compression loading on for four samples with bedding plane angles of 0°, 30°, 60°, and 90°: laboratory test results for a deviatoric stress σ1 − σ3 versus axial strain ε1; b volumetric strain εv versus axial strain ε1; constitutive model simulation results for c σ1 − σ3 versus ε1; d εv versus ε1. Laboratory test results from Oda [46]

Full size image

4.4 Influence of fabric anisotropy on liquefaction behavior

As exhibited in the validations against DEM data, one of the main strength of the model framework adopted in this study is its capability in reflecting the cyclic and especially liquefaction behavior of sand. Here, undrained cyclic simple shear simulations are conducted to investigate the influence of fabric anisotropy on liquefaction resistance and liquefaction-induced shear strain. Simulations on samples of ein = 0.655 with bedding plane angle δ = 0° and initial fabric norm ||Fnin|| = 0.01 and with δ = 45° and ||Fnin|| = 0.43 are carried out and compared with the results for the simulation in Sect. 4.1 on the sample with ein = 0.655, δ = 0°, and ||Fn,in|| = 0.43.

The shear stress τ versus mean effective stress p and shear stress τ versus shear strain γ results for the simulations are plotted in Fig. 20. These simulation results, along with that in Fig. 13, clearly depict the significant influence of fabric anisotropy on the liquefaction behavior of sand. Comparison of Fig. 20a, b with Fig. 13d, e indicates that greater fabric anisotropy can lead to a significant decrease in liquefaction resistance. The number of load cycles needed to reach initial liquefaction reduces from 12 to 7 as ||Fnin|| increases from 0.01 to 0.43. These results corroborate the observations from laboratory tests [48, 81, 86, 87] and DEM numerical tests [72, 74, 76]. The results from the simulations on samples with the same ||Fnin|| but different δ show that the fabric anisotropy orientation significantly affects the shear strain accumulation (Fig. 20c, d and Fig. 13d, e). When the initial fabric orientation is symmetric with respect to the cyclic shearing direction, the postliquefaction shear strain accumulation is also symmetric with respect to zero (Fig. 13e). When the initial fabric orientation is asymmetric with respect to the cyclic shearing direction, accumulation of postliquefaction shear strain in one direction occurs (Fig. 20d).

Fig. 20
figure 20

Stress and strain results from simulation of undrained cyclic simple shear loading using the proposed constitutive model on samples of the same granular material with different initial fabric anisotropy levels and bedding plane angles: a shear stress τ versus mean effective stress p for the sample with initial contact normal fabric norm ||Fnin|| = 0.01 and δ = 0°; b shear stress τ versus shear strain γ for the sample with ||Fnin|| = 0.01 and δ = 0°; c τ versus p for the sample with ||Fnin|| = 0.43 and δ = 45°; d τ versus γ for the sample with ||Fnin|| = 0.4 and δ = 45°

Full size image

The influence of initial fabric on liquefaction resistance is a result of its influence on dilatancy. When the fabric tensor Fn and loading direction n are not proportional, greater ||Fn|| can lead to greater irreversible dilatancy, according to Eq. 17. Figure 21 shows the dilatancy for the two simulations with the same δ = 0 but different ||Fnin||. Increase in ||Fnin|| causes the positive dilatancy to increase, indicating stronger contraction tendency.

Fig. 21
figure 21

Dilatancy results from simulation of undrained cyclic simple shear loading using the proposed constitutive model on samples of the same granular material with initial contact normal fabric norm ||Fnin|| = 0.01 and ||Fnin|| = 0.43

Full size image

5 Conclusions

Based on existing understanding of the anisotropic behavior of sand from laboratory tests and micromechanical DEM numerical test data, an anisotropic plasticity model incorporating fabric evolution is proposed in this study. The development and validation of the proposed model using macro- and microlevel data from DEM numerical tests on granular materials provides a paradigm for the formulation and evaluation of models incorporating micromechanical features of sand, aiding the endeavor to bridge the gap between micro and macro.

The proposed model builds on an isotropic model that can achieve a unified description of sand of different conditions from pre- to postliquefaction under both monotonic and cyclic loading. A normalized fabric tensor and its evolution rule are introduced in the model. By incorporating the fabric tensor and its invariant with the loading direction in the formulation for plastic modulus and dilatancy, the model is able to reflect the influence of fabric on the strength, shear modulus, and dilatancy of sand.

The model is directly validated against DEM test results, using the fabric information obtained from the numerical tests, exhibiting good performance for both the macrolevel stress–strain relationships and the microlevel fabric features. This validation process using DEM numerical test results provides a new means of validating micromechanical-based constitutive models on both micro- and macroscales. Validation of the model against a wide range of different laboratory tests is also carried out, showing good agreement with the laboratory test results, highlighting the model’s adaptability to different stress paths.

The influence of fabric anisotropy on the undrained cyclic behavior of sand is investigated using the proposed model. Initial fabric tensor norm and orientation are found to significantly affect the liquefaction resistance and postliquefaction shear strain, respectively. Greater initial fabric norm leads to weaker liquefaction resistance, which is due to the influence of fabric anisotropy on dilatancy, agreeing with observations from laboratory and DEM tests.

In the proposed model, a relatively simple formulation for the evolution of fabric is currently used. Though the simple formulation is able to capture the overall fabric evolution observed in DEM tests, distinct difference still exists between the model simulation and DEM test fabric evolution results. Further studies should be carried out to investigate the evolution of and the relationship between fabric tensors based on various particle-level characteristics, such as the contact normal, particle orientation, and void orientation, under both monotonic and cyclic loading. More accurate formulations for fabric evolution and its influence on the mechanical behavior can be developed based on such analysis. Also, the influence of intermediate stress coefficient b on the evolution and the effects of fabric should be further investigated and considered in constitutive model formulations.

Although the current model mainly focuses on the influence of fabric anisotropy on the shear strength, shear modulus, and dilatancy of sand, it should be acknowledged that fabric anisotropy can also affect other behaviors as well, which should also be explored in future studies. In applications where the small strain behavior of sand is important, anisotropic elasticity should be considered. For loading with a significant rotation of principal stress axes, fabric anisotropy induced noncoaxiality between strain increment and total stress may also be important.