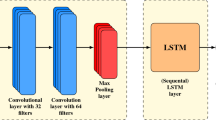
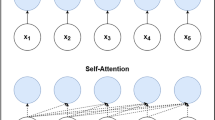
Abstract
Precise carbon price forecasting matters a lot for both regulators and investors. The improvement of carbon price forecasting can not only provide investors with rational advice but also make for energy conservation and emission reduction. But traditional methods do not perform well in prediction because of the nonlinearity and non-stationarity of carbon price. In this study, an innovative multiscale nonlinear integration model is proposed to improve the accuracy of carbon price forecasting, which combines optimal feature reconstruction and biphasic deep learning. For one thing, the optimal feature reconstruction, including variational mode decomposition (VMD) and sample entropy (SE), is used to extract different features from the original carbon price effectively. For another thing, biphasic deep learning based on deep recurrent neural network (DRNN) and gate recurrent unit (GRU) is applied to predict carbon price. DRNN, a novel framework of deep learning, is applied to predict each component. Meanwhile, GRU is used for nonlinear integration, and the final prediction of carbon price can be acquired through this procedure. For illustration and comparison, this study takes carbon price from Beijing, Hubei, and Shanghai in China as sample data to examine the capability of the proposed model. The empirical result proves that the new hybrid model can improve the carbon price predictive accuracy in consideration of statistical measurement. Hence, the novel hybrid model can be considered as an efficient way of predicting carbon prices.















Similar content being viewed by others
Data availability
The datasets analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- ARIMA:
-
Autoregressive integrated moving average
- EMD:
-
Empirical mode decomposition
- EEMD:
-
Ensemble empirical mode decomposition
- DRNN:
-
Deep recurrent neural network
- ANN:
-
Artificial neural network
- GRU:
-
Gate recurrent unit
- BDS test:
-
Brock-Decher-Scheikman test
- AE:
-
Approximate entropy
- BP:
-
Back propagation
- GARCH:
-
Generalized autoregressive conditional heteroskedasticity
- GJR:
-
Gap junction remodeling
- WT:
-
Wavelet transform
- LSTM:
-
Long short-term memory
- MAE:
-
Mean absolute error
- MAPE:
-
Mean absolute percentage error
- RNN:
-
Recurrent neural network
- RMSE:
-
Root mean squared error
- SE:
-
Sample entropy
- ADF test:
-
Augmented Dickey-Fuller test
- VMD:
-
Variational mode decomposition
- GA:
-
Genetic algorithm
- SVM:
-
Support vector machine
- LSSVM:
-
Least square support vector machine
- XGBoost:
-
eXtreme gradient boosting
References
Atsalakis GS (2016) Using computational intelligence to forecast carbon prices. Appl Soft Comput 43:107–116. https://doi.org/10.1016/j.asoc.2016.02.029
Babazadeh R (2017) A hybrid ARIMA-ANN approach for optimum estimation and forecasting of gasoline consumption. Rairo-Oper Res 51(3):719–728. https://doi.org/10.1051/ro/2016059
Byun SJ, Cho H (2013) Forecasting carbon futures volatility using GARCH models with energy volatilities. Energy Econ 40:207–221
Carolina G, Rodriguez J, Sanchez MJ (2013) Modelling and forecasting fossil fuels, CO2 and electricity prices and their volatilities. Appl Energy 101:363–375. https://doi.org/10.1016/j.apenergy.2012.03.046
Chevallier J (2011) Wavelet packet transforms analysis applied to carbon prices. Econ Bull 31(2):1731–1747
Chien FS, Chau KY, Ady SU, Zhang YQ, Tran QH, Aldeehani TM (2021) Does the combining effects of energy and consideration of financial development lead to environmental burden: social perspective of energy finance? Environ Sci Pollut Res 28:40957–40970. https://doi.org/10.1007/s11356-021-13423-6
Cui H, Dou X (2018) Carbon price forecasts in Chinese carbon trading market based on EMD-GA-BP and EMD-PSO-LSSVM. Oper Res Manag Sci 148:137–147
Dimitriadis D, Katrakilidis C, Karakotsios A (2021) Investigating the dynamic linkages among carbon dioxide emissions, economic growth, and renewable and non-renewable energy consumption: evidence from developing countries. Environ Sci Pollut Res 28:40917–40928. https://doi.org/10.1007/s11356-021-13613-2
Dragomiretskiy K, Zosso D (2014) Variational mode decomposition. IEEE Trans Signal Proces 62:531–544. https://doi.org/10.1109/TSP.2013.2288675
Dutta A (2018) Modeling and forecasting the volatility of carbon emission market: the role of outliers, time-varying jumps and oil price risk. J Clean Prod 172:2773–2781. https://doi.org/10.1016/j.jclepro.2017.11.135
E. J, Jimin Y, He L, Jin HH (2019) Energy price prediction based on independent component analysis and gated recurrent unit neural network. Energy 189:116278. https://doi.org/10.1016/j.energy.2019.116278
El-Danaf TS, Hadhoud AR (2014) Computational method for solving space fractional Fisher's nonlinear equation. Math Methods Appl Sci 37:657–662. https://doi.org/10.1002/mma.2822
Fan XH, Li SS, Tian LX (2015) Chaotic characteristic identification for carbon price and a multi-layer perception network prediction model. Expert Syst Appl 42:3945–3952
Hao Y, Tian CS, Wu CY (2020) Modelling of carbon price in two real carbon trading markets. J Clean Prod 244:118556. https://doi.org/10.1016/j.jclepro.2019.118556
Hu GB, Ye SR, Chen DZ, Zhao L, Xia FY, Dai X, Jiang P (2020) Extracting unmodeled systematic errors from BDS orbit determination residuals and application in SPP/PPP. Navigation-US 67:275–289. https://doi.org/10.1002/navi.365
Huang YM, Dai XY, Wang QW, Zhou DQ (2021) A hybrid model for carbon price forecasting using GARCH and long short-term memory network. Appl Energ 285. https://doi.org/10.1016/j.apenergy.2021.116485
Hussain I, Rehman A (2021) Exploring the dynamic interaction of CO2 emission on population growth, foreign investment, and renewable energy by employing ARDL bounds testing approach. Environ Sci Pollut Res 28:39387–39397. https://doi.org/10.1007/s11356-021-13502-8
Jia PT, Liu HD, Wang SJ, Wang P (2020) Research on a mine gas concentration forecasting model based on a GRU network. IEEE Access 8:38023–38031. https://doi.org/10.1109/ACCESS.2020.2975257
Kim HY, Won CH (2018) Forecasting the volatility of stock price index: a hybrid model integrating LSTM with multiple GARCH-type models. Expert Syst Appl 103:25–37. https://doi.org/10.1016/j.eswa.2018.03.002
Lee M, Cho MS, Lee H, Jeong C, Kwak J, Jung J, Kim SS, Yoon SM, Song SY, Lee SW, Kim JH, Choi EK, Cho S, Cho B (2021) Geometric and dosimetric verification of a recurrent neural network algorithm to compensate for respiratory motion using an articulated robotic couch. J Korean Phys Soc 78(1):64–72. https://doi.org/10.1007/s40042-020-00013-x
Lin Y, Yang N, Bao B, Wang L, Chen J, Liu J (2020) Luteolin reduces fat storage in Caenorhabditis elegans by promoting the central serotonin pathway. Food Funct 11:730–740. https://doi.org/10.1039/c9fo02095k
Liu H, Shen L (2020) Forecasting carbon price using empirical wavelet transform and gated recurrent unit neural network. Carbon Manag 11(1):25–37. https://doi.org/10.1080/17583004.2019.1686930
Mujtaba A, Jena PK, Joshi DPP (2021) Growth and determinants of CO2 emissions: evidence from selected Asian emerging economies. Environ Sci Pollut Res 28:39357–39369. https://doi.org/10.1007/s11356-021-13078-3
Naghibi Z, Sadrossadat SA, Safari S (2019) Time-domain modeling of nonlinear circuits using deep recurrent neural network technique. Aeu-Int J Electron C 100:66–74. https://doi.org/10.1016/j.aeue.2018.12.010
Noh J, Park HJ, Kim JS, Hwang SJ (2020) Gated recurrent unit with genetic algorithm for product demand forecasting in supply chain management. Mathematics 8(4), 565. https://doi.org/10.3390/math8040565
Paolella MS, Taschini L (2008) An econometric analysis of emission allowance prices. J Bank Financ 32:2022–2032
Perfecto C, Elbamby MS, Ser JD, Bennis M (2020) Taming the latency in multi-user VR 360 degrees: a QoE-aware deep learning-aided multicast framework. IEEE Trans Commun 68:2491–2508. https://doi.org/10.1109/TCOMM.2020.2965527
Popoola SI, Adebisi B, Ande R (2021) Memory-efficient deep learning for botnet attack detection in IoT networks. Electronics 10:1104. https://doi.org/10.3390/electronics10091104
Qin QD, He HD, Li L, He LY (2020) A novel decomposition-ensemble based carbon price forecasting model integrated with local polynomial prediction. Comput Econ 55(4):1249–1273. https://doi.org/10.1007/s10614-018-9862-1
Richman JS, Moorman JR (2000) Physiological time-series analysis using approximate entropy and sample entropy. Am J Phys Heart Circ Phys 278:2039–2049
Song Y, Liang D, Liu T (2018) How China’s current carbon trading policy affects carbon price? An investigation of the Shanghai Emission Trading Scheme pilot. J Clean Prod 181:374–384
Sun W, Wang YW (2020) Factor analysis and carbon price prediction based on empirical mode decomposition and least squares support vector machine optimized by improved particle swarm optimization. Carbon Manag 11:315–329. https://doi.org/10.1080/17583004.2020.1755597
Sun H, Yu B (2020) Forecasting Financial Returns Volatility: A GARCH-SVR Model. Comput Econ 55:451–471. https://doi.org/10.1007/s10614-019-09896-w
Sun GQ, Chen T, Wei ZN, Sun YH, Zhang HX, Chen S (2016) A carbon price forecasting model based on variational mode decomposition and spiking neural networks. Energies 9(1):54. https://doi.org/10.3390/en9010054
Sun W, Sun CP, Li ZQ (2020) A hybrid carbon price forecasting model with external and internal influencing factors considered comprehensively: a case study from China. Pol J Environ Stud 29(5):3305–3316. https://doi.org/10.15244/pjoes/114261
Tang L, Yu LA, Wang S, Li JP, Wang SY (2012) A novel hybrid ensemble learning paradigm for nuclear energy consumption forecasting. Appl Energy 93(1):432–443. https://doi.org/10.1016/j.apenergy.2011.12.030
Tasyurek M, Celik M (2020) RNN-GWR: A geographically weighted regression approach for frequently updated data. Neurocomputing 399:258–270. https://doi.org/10.1016/j.neucom.2020.02.058
Wang J, Li X, Hong T, Wang SY (2018) A semi-heterogeneous approach to combining crude oil price forecasts. Inf Sci 460:279–292. https://doi.org/10.1016/j.ins.2018.05.026
Wang S, E. JW, Li SG (2019) A novel hybrid carbon price forecasting model based on radial basis function neural network. Acta Phys Pol A 135(3):368–374. https://doi.org/10.12693/APhysPolA.135.368
Wu QL, Liu ZT (2020) Forecasting the carbon price sequence in the Hubei emissions exchange using a hybrid model based on ensemble empirical mode decomposition. Energy Sci Eng 8:2708–2721. https://doi.org/10.1002/ese3.703
Wu Z, Rincon D, Christofides PD (2020) Process structure-based recurrent neural network modeling for model predictive control of nonlinear processes. J Process Control 89:74–84. https://doi.org/10.1016/j.jprocont.2020.03.013
Xu H, Wang MG, Jiang SM, Yang WG (2020) Carbon price forecasting with complex network and extreme learning machine. Physica A 545:122830. https://doi.org/10.1016/j.physa.2019.122830
Zhang YJ, Wei YM (2010) An overview of current research on EU ETS: evidence from its operating mechanism and economic effect. Appl Energy 87(6):1804–1814. https://doi.org/10.1016/j.apenergy.2009.12.019
Zhang J, Li DZ, Hao Y, Tan ZF (2018) A hybrid model using signal processing technology, econometric models and neural network for carbon spot price forecasting. J Clean Prod 204:958–964. https://doi.org/10.1016/j.jclepro.2018.09.071
Zhao X, Han M, Ding LL, Kang WL (2018) Usefulness of economic and energy data at different frequencies for carbon price forecasting in the EU ETS. Appl Energy 216:132–141. https://doi.org/10.1016/j.apenergy.2018.02.003
Zhou JG, Yu XC, Yuan XL (2018) Predicting the carbon price sequence in the Shenzhen Emissions Exchange using a multiscale ensemble forecasting model based on ensemble empirical mode decomposition. Energies 11. https://doi.org/10.3390/en11071907
Zhu BZ (2012) A novel multiscale ensemble carbon price prediction model integrating empirical mode decomposition, genetic algorithm and artificial neural network. Energies 5:355–370. https://doi.org/10.3390/en5020355
Zhu BZ, Wei YM (2013) Carbon price forecasting with a novel hybrid ARIMA and least squares support vector machines methodology. Omega 41(3):517–524. https://doi.org/10.1016/j.omega.2012.06.005
Zhu BZ, Shi XT, Chevallier J, Wang P, Wei YM (2016) An adaptive multiscale ensemble learning paradigm for nonstationary and nonlinear energy price time series forecasting. J Forecast 2:633–651
Zhu BZ, Han D, Chevallier J, Wei YM (2017a) Dynamic multiscale interactions between European carbon and electricity markets during 2005-2016. Energy Policy 107:309–322
Zhu BZ, Han D, Wang P, Wu ZC, Zhang T, Wei YM (2017b) Forecasting carbon price using empirical mode decomposition and evolutionary least squares support vector regression. Appl Energy 191:521–530. https://doi.org/10.1016/j.apenergy.2017.01.076
Zhu BZ, He SX, Wang P, He KJ, Zhang T, Wei YM (2018a) A novel multiscale nonlinear ensemble leaning paradigm for carbon price forecasting. Energy Econ 70:143–157
Zhu BZ, Ma SJ, Xie R, Chevallier J, Wei YM (2018b) Hilbert spectra and empirical mode decomposition: a multiscale event analysis method to detect the impact of economic crises on the European carbon market. Comput Econ 52(1):105–121
Zhu BZ, Ye SX, He KJ, Chevallier J, Xie R (2019a) Measuring the risk of European carbon market: an empirical mode decomposition-based value at risk approach. Ann Oper Res 281:373–395
Zhu J, Wu P, Chen H, Liu J, Zhou L (2019b) Carbon price forecasting with variational mode decomposition and optimal combined model. Physica A 519:140–158. https://doi.org/10.1016/j.physa.2018.12.017
Zhu BZ, Jiang MX, Zhang SF et al (2020) Resource and environment economic complex system: models and applications. Science Press, Beijing
Zhu BZ, Ye SX, Wang P, Chevallier J, Wei YM (2021a) Forecasting carbon price using a multi-objective least squares support vector machine with mixture kernels. J Forecast. https://doi.org/10.1002/for.2784
Zhu QN, Zhou XF, Tan JL, Guo L (2021b) Knowledge base reasoning with convolutional-based recurrent neural networks. IEEE Trans Knowl Data Eng 33(5):2015–2028. https://doi.org/10.1109/TKDE.2019.2951103
Acknowledgements
This research was supported by the National Natural Science Foundation of China (Grant No. 71971122 and 71501101).
Author information
Authors and Affiliations
Contributions
Jujie Wang, Qian Cheng, and Xin Sun: conceived of the presented idea, developed the theory and performed the computations, discussed the results, wrote the paper, and approved the final manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Responsible Editor: Ilhan Ozturk
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Wang, J., Cheng, Q. & Sun, X. Carbon price forecasting using multiscale nonlinear integration model coupled optimal feature reconstruction with biphasic deep learning. Environ Sci Pollut Res 29, 85988–86004 (2022). https://doi.org/10.1007/s11356-021-16089-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11356-021-16089-2