Experimental Identification of Frictional Effects on Interlaminar Toughness of Composite Laminates in 4ENF Test

Abstract

Background

Understanding and characterizing delamination in composite laminates is fundamental for analysing their structural integrity, since operational loads may promote the propagation of interlaminar defects. Propagation often occurs in mode II and is driven by shear stress. However, the methods used to characterise this propagation mode are affected by frictional effects between crack surfaces.

Objective

This work aims to build up an experimental method to identify the effect of friction in a 4 points End Notched Flexure test, which does not require the use of analytical or numerical models of the specimen.

Methods

This goal is achieved by performing a series of loading–unloading cycles before the delamination test, which helps to calibrate an analytical expression that estimates the energy dissipated by friction, and the analytical expression is then inserted into the formulation of the Irwin-Kies equation. Experimental validation is carried out considering tests on different materials and different friction conditions between the crack surfaces, as well as validation by means of a virtual experiment being performed for comparison with an analytical model presented in literature. The novelty of this method lies in the fact that it does not require the development of any analytical or numerical model of the specimen and consequently no calibration between models and the experiment is required.

Results

Tests on composite specimens show good results, the friction contribution estimated by the method is comparable with those presented in the literature. Moreover, the virtual experiment shows that there is a good match between the results obtained using this method and those obtained using an analytical model presented in the literature.

Conclusions

This method seems to provide satisfactory results for both real and virtual experiments, moreover, the procedure is relatively simple, making it a suitable method for the evaluation of frictional effects in the 4 point End Notched Flexure test.

Introduction

Composite materials exhibit excellent properties when loaded along the fibres, but they are also subjected to stresses in different planes and directions, which are characterised by much poorer strength properties. In particular, it is fundamental to investigate the properties of interlaminar layers, which cannot be reinforced by fibres in conventional lamination technologies. Characterization of interlaminar toughness is a key aspect in the evaluation of the damage tolerance of a composite structure and it plays an important role in the design process and in the definition of the maintenance/inspection plan. Mode I and mode II delamination are the most common propagation modes. Mode I is typically studied by performing the Double Cantilever Beam (DCB) test, as exemplified in [1, 2], which can be carried out following the standard presented in [3]. Mode II, which is the mode investigated in this work, is typical of composite laminates subjected to transverse and bending loads. The experimental characterization of mode II propagation can be carried using different test methods ([4, 5]), but it is usually performed by means of two tests: the 3 point End Notched Flexure test (3 point ENF), and the 4 point End Notched Flexure test (4 point ENF). Currently, the 3 point ENF is easier to perform, more diffused ([6,7,8]), and regulated by an ASTM standard [9], although it is characterised by unstable crack propagation. On the contrary, in the 4 point ENF test stable crack propagation is obtained, but the test response is affected much more by the friction between the crack surfaces [10]. Another advantage of the 4 point ENF is that, ideally, the toughness evaluation is independent of the crack length, when the crack tip is between the two inner pins [11]. In open literature, different approaches to modelling the friction between the sliding surfaces in mode II are discussed, based on both numerical and analytical models, such as in [12,13,14,15,16,17]. Indeed, it is well known that the effect of the friction is to increase the toughness, G_IIc, leading to a wrong measurement of the toughness called "perceived toughness" (see, for instance [12, 18]). The numerical approaches presented in literature may be used to identify a real toughness, correlating numerical models and experimental tests in order to identify the friction coefficient, by matching experimental and numerical force vs. opening (or crack advance) response [19]. Analytical approaches are typically developed by defining an analytical model of the specimen, which takes into account the friction between the sliding crack surfaces [12, 16, 17]. This work proposes an experimental procedure able to identify the real toughness without knowing the coefficient of friction, but linking the energy dissipated by friction during crack propagation with the energy dissipated during hysteresis cycles performed without propagating the crack. A simplified analytical formulation of the energy dissipated by the work of frictional forces is presented and then inserted into the Irwin-Kies equation as a dissipative term. Thereafter, an experimental activity is presented on carbon fibre reinforced and glass fibre reinforced composite specimens. In this phase, loading–unloading cycles on the specimen without propagating the crack are performed, so that the dissipative term can be calibrated. The method is validated by artificially changing the friction between the crack surfaces in different tests, proving that the same real toughness is obtained. A further verification is carried out considering the model proposed in [12] and performing a virtual experiment. The advantage of this method lies in the fact that the frictional effects are evaluated directly on the specimen being examined without developing any analytical or numerical model of the test.

Simplified Expression of the Energy Dissipated by Friction During a 4ENF Test

Role of Friction in Loading–unloading Cycles

In the 4 point ENF test, mode II delamination is studied by applying a bending moment to a pre-cracked specimen. The specimen is supported by two external pins and is loaded by two internal pins. Actually, the two internal loading pins are connected to a stiff support, which can rotate about a central pin fixed to the test machine. In Fig. 1(a), a schematic representation of the test is shown. Thanks to the loading mechanism, all the pins have a reaction force equal to half of the load applied by the test machine. Moreover, the central part of the specimen is characterised by a constant bending moment. When the specimen is loaded, the two faces of the crack are in contact and undergo relative sliding during the test, which gives rise to distribution of frictional tractions, f(z), where z is the coordinate along the specimen’s axis, shown in Fig. 1(a).

Fig. 1

a) Schematic representation of the 4 point ENF test b) sketch of specimen model presented in [12]

The relative sliding between the two crack surfaces ξ occurs in the opposite direction to the frictional tractions f. As a consequence, this phenomenon dissipates energy. Referring to the problem presented in Fig. 1(a), the external work performed for an infinitesimal deflection du, without crack propagation, is balanced by the increment in the elastic energy stored in the specimen and the work dissipated by the frictional forces, distributed from z = 0 and z = z_a, at the crack tip. Relative sliding dξ occurs along the crack surfaces, and so the energy balance can be represented as shown in equation (1).

$$Pdu=kudu+{\int }_{0}^{{z}_{a}}\left|f\left(z\right)d\xi \left(z\right)\right|bdz$$

(1)

where k is the stiffness of the specimen and b is the width of the specimen. The modulus is applied to the work done by friction because the dissipation is positive both during loading (where Pdu > 0) and unloading (where Pdu < 0). Assuming a linear relationship between the distribution of dξ and du, and between the distribution of f and P, the relationship can be written as:

$$d\xi ={C}_{u}\left(z\right)du$$

(2)

$$f\left(z\right)={C}_{F}\left(z\right)P$$

(3)

where C_u(z) and C_F(z) determine the distributions of relative sliding and frictional force, respectively, given a displacement of the central pin and the load P. These distributions depend on the characteristics of the specimens. By substituting them in equation (1), equation (4) is obtained:

$$Pdu=kudu+Pdu\frac{\left|Pdu\right|}{Pdu}{\int }_{0}^{{z}_{a}}{C}_{F}{C}_{u}bdz$$

(4)

Considering C_Fu to be the results of the definite integral in equation (4) and an arbitrary displacement du ≠ 0, the following relation is obtained:

$$P=ku+P{C}_{Fu}\frac{\left|Pdu\right|}{Pdu}$$

(5)

So the expression of the load versus displacement can be achieved for both loading (equation (6)) and unloading (equation (7)) phases.

$$P=\frac{k}{1-{C}_{Fu}}u$$

(6)

$$P=\frac{k}{1+{C}_{Fu}}u$$

(7)

The result obtained points out that, under the simplified assumption of a constant friction coefficient and linear system, the friction affects the stiffness of the specimen by increasing it in the loading phase and reducing it in the unloading phase.

Analogous results can be obtained considering the model of the specimen shown in Fig. 1(b), which is introduced in [12] to study frictional effects in a 4 ENF specimen. The specimen is modelled with three beams (one for each arm and one for the non-cracked region) and is subjected to bending by means of four rollers, which are represented by their reaction forces. The friction contribution is modelled by considering a friction coefficient that generates the frictional forces F and bending moments C. The comparison between the results obtained in [12] and those in equations (6) and (7) may provide an analytical expression of the coefficient C_Fu. To accomplish this objective, one must start from the equation found by [12], which relates the applied load P to the displacement of the central pin u.

$$u=\frac{3a\left(3{L}_{a}-4h\alpha \right)+{L}_{a}\left(3L-10{L}_{a}+9h\alpha \right)}{8{h}^{3}b{E}_{xx}/\eta }{L}_{a}P$$

(8)

where, α is the friction coefficient, La is the distance between the external pin and the internal pin, L is the distance between the two external pins, η accounts for plane stress or plane strain condition, h is the thickness of the specimen’s arms, which corresponds to half of the total laminate thickness, Exx is the elastic modulus in the direction of the specimen’s axis, and a is the crack length, which is measured from the external support pin to the crack tip. Solving equation (8) in order to express the load P function of displacement u, and collecting the terms multiplied by the friction coefficient, leads to:

$$P=\frac{8{h}^{3}b{E}_{xx}/\eta }{{L}_{a}\left[\left(9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}\right)+\alpha \left(9{L}_{a}h-12ah\right)\right]}u$$

(9)

Equation (9) can be transformed into the following form:

$$P=\frac{8{h}^{3}b{E}_{xx}/\left[\eta {L}_{a}\left(9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}\right)\right]}{1-\alpha \frac{12ah-9{L}_{a}h}{9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}}}u$$

(10)

Equation (10) obtained has the same form as equation (6) and it shows that the term C_Fu can be expressed as indicated in equation (11).

$${C}_{Fu}=\alpha \frac{12ah-9{L}_{a}h}{9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}}$$

(11)

It can be seen that the parameter C_Fu depends on the friction coefficient, geometrical properties of the specimen and geometrical properties of the test fixture.

In Fig. 2 the loading–unloading cycle is shown, under the assumption of a constant frictional coefficient both in loading and unloading and of linearity. It is possible to find the analytical expression of the work dissipated in a cycle until a generic maximum displacement u_max by evaluating the area between the loading and unloading curves.

Fig. 2

loading–unloading cycle

By applying equations (6, 7), the ΔP term has the following expression:

$$\Delta P=\frac{2{C}_{Fu}}{\left(1-{C}_{Fu}\right)\left(1+{C}_{Fu}\right)}k{u}_{max}$$

(12)

After performing some algebraic passages, the area is found to be:

$$dissipated\ work=\frac{{u}_{max}\Delta P}{2}=\frac{{C}_{Fu}\left(1-{C}_{Fu}\right)}{\left(1+{C}_{Fu}\right)}\frac{{P}_{max}^{2}}{k}$$

(13)

where P_max corresponds to the maximum load applied in the loading phase. The compliance C can be introduced as the inverse of the specimen’s stiffness k. Moreover, since the first term of the equation is a combination of coefficients, it can be rewritten as a single coefficient H, leading to the expression of the dissipated work given in equation (14).

$$dissipated\ work=HC{P}_{max}^{2}$$

(14)

The work dissipated during a loading–unloading cycle turns out to be related to three different contributions:

• Load, represented by the maximum applied load P in the cycle.

• Geometry, material and boundary conditions, which determine the compliance C.

• Sliding surface properties, given by the coefficient H.

Since compliance during the loading phase can be measured experimentally, the evaluation of the area enclosed in a loading–unloading cycle performed up to the load P_max can be used to identify the coefficient H, which provides an analytical expression of the energy dissipated by the frictional effects.

Modification of the Irwin-Kies Equation

The expression for the dissipated work obtained in Eq. 14 can be introduced into the Irwin-Kies equation. Indeed, by considering the energy balance for an infinitesimal crack advancement da in a specimen with a width equal to b, the energy balance can be written as:

$$Pdu=\int Pdu+bGda+dUd$$

(15)

where Pdu is the external work required to propagate the crack, the integral of Pdu is the elastic stored energy, bGda is the energy spent to open the crack by an infinitesimal value da, and dU_d is the energy dissipated during an infinitesimal crack advancement da. Now, differentiating with respect to a on both sides and moving the bG term to the left side:

$$bG=P\frac{\partial{u}}{\partial{a}}-\frac{\partial}{\partial{a}}\int Pdu-\frac{\partial{U}_{d}}{\partial{a}}$$

(16)

By dividing by the width b and introducing the compliance C, which is defined as the ratio between the displacement u and the corresponding load P, the previous equation becomes:

$$G=\frac{1}{b}\frac{u}{C}\frac{\partial u}{\partial a}-\frac{1}{b}\frac{\partial }{\partial a}\int \frac{u}{C}du-\frac{1}{b}\frac{\partial {U}_{d}}{\partial a}$$

(17)

Assuming linear behaviour and applying the expression for the dissipated work in equation (14) for U_d, equation (18) is obtained.

$$G=\frac{1}{b}\frac{u}{C}\frac{\partial u}{\partial a}-\frac{1}{b}\frac{\partial }{\partial a}\frac{1}{2}\frac{{u}^{2}}{C}-\frac{1}{b}\frac{\partial HC{P}^{2}}{\partial a}$$

(18)

The derivatives of u²/C and HCP² are calculated, thus leading to:

$$G=\frac{1}{b}\frac{u}{C}\frac{\partial u}{\partial a}-\frac{1}{b}\frac{u}{C}\frac{\partial u}{\partial a}+\frac{1}{2b}\frac{{u}^{2}}{{C}^{2}}\frac{\partial C}{\partial a}-\frac{1}{b}\frac{\partial C}{\partial a}H{P}^{2}$$

(19)

Since u²/C² is equal to P², simplifications lead to:

$$G=\frac{1}{2b}{P}^{2}\frac{\partial C}{\partial a}-\frac{1}{b}\frac{\partial C}{\partial a}H{P}^{2}$$

(20)

Finally, by rearranging all the terms of equation (20), equation (21) is obtained:

$$G=\frac{{P}^{2}}{2b}\frac{\partial C}{\partial a}\left(1-2H\right)$$

(21)

Equation (21) can be considered to be a modified Irwin-Kies equation with an explicit dissipation term. This term can be calibrated experimentally, by performing a series of loading–unloading cycles at different load steps, without propagating the crack and measuring the work dissipated. It can be seen that, since H is positive, it tends to decrease the value of the energy release rate evaluated by applying the Irwin-Kies equation in the conventional form.

When a crack propagates, applying equation (21) makes possible to correct the "perceived toughness", G’_c which is affected by the contribution of the friction, to provide a real toughness, which depends only on the energy required to propagate the crack in mode II.

Equation (21) can be rewritten considering the classical Irwin-Kies equation, which is:

$${G}_{c}^{^{\prime}}=\frac{{P}^{2}}{2b}\frac{\partial C}{\partial a}$$

(22)

As said before, the Irwin-Kies equation (equation (21)) doesn't take into account the friction effect, thus, it calculates a perceived value of toughness if friction effects occur. The modified Irwin-Kies equation can be written as a function of the Irwin-Kies equation leading to equation (23).

$${G}_{c}={G}_{c}^{^{\prime}}\left(1-2H\right)$$

(23)

Both equations (21, 22) only hold in a static condition, without considering dynamic effects. The tests carried out in the next section were conducted consistently at a low crosshead velocity.

Experimental Validation

A series of tests was performed to evaluate the capability of the previously proposed formulation to evaluate the contribution of friction in 4 point ENF tests. Tests were conducted on different materials and included cases in which the friction between the crack faces was artificially modified; an interlaminar friction coefficient of 0.35–0.37 is expected without artificially changing the friction properties as reported in [10]. The parameter H was evaluated by means of loading–unloading cycles and then used to evaluate the toughness of the interlaminar layers.

Test Setup

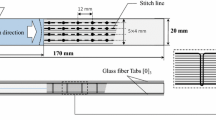
All the tests were carried out by using a MTS Mini Bionix II test system, with a cross-head velocity of 1 mm/min, at room temperature and in a dry environment. A fixture was adopted to connect the loading pins to the test machine, allowing rotation about a central pin. The test setup is shown in Fig. 3. The distance between the internal pins was set to 80 mm, while the distance between the external pins was set to 145 mm. The crack tip position was between the two inner pins, as prescribed by the test procedure.

Fig. 3

Test setup: a) front view b) bottom view

Test performed considering different materials and crack surface conditions

Two types of specimens were tested, one made of carbon fibre UD and the other made of glass fibre UD. The carbon fibre UD material has a longitudinal elastic modulus E_xx = 130,000 MPa, a Poisson coefficient ν₁₂ = 0.3, a fibre volumetric fraction of 56.4% and a density of 1.53 g/cm³. Glass fibre UD has a longitudinal elastic modulus E_xx = 45,300 MPa, a Poisson coefficient ν₁₂ = 0.33, a fibre volumetric fraction of 50% and a density of 1.85 g/cm³.

Both the types of specimens had the fibres oriented at 0°, along the specimen’s axis and a nominal width of 25 mm. For the carbon fibre specimens, the nominal total thickness was 4 mm and the layup consisted of 28 plies, in agreement with the dimension prescribed in [9]. For the glass fibre specimens, the nominal total thickness was 9 mm, with a layup of 40 plies. Considering the compliance of the glass fibre reinforced plies, this thickness was adopted to minimize the effect of geometrical nonlinearity, which is known to affect the value of the toughness measured in ENF tests [13]. The length of all the specimens was 220 mm. In both the specimen types the pre-crack was obtained by means of a Polytetrafluoroethylene (PTFE) insert with a thickness of 0.06 mm, set in the middle of the lamination sequence.

The specimen manufacturing procedure was carried out according to [9]. Specimens were obtained from a composite panel with the proper layup, which was laminated and then cured in an autoclave with a curing pressure of 3 bar and a temperature of 120 °C for 3 h. After curing, the panel was removed from the mould and the specimens were cut from the panel.

Crack propagation tests were performed after a pre-opening test, to achieve a condition at the crack tip that could be considered representative of realistic delamination induced by manufacturing defects or by loads experienced under operational conditions. In these pre-openings, unstable crack propagation was obtained. Then, crack propagation tests were performed with three types of conditions affecting the friction forces between the crack surfaces. Considering that friction forces are typically developed at the external pin and the first internal pin ([19]), the three conditions are:

• A) in condition A, the test was performed with the PTFE insert still in the zone between the external pin and the first internal one.

• B) In condition B, the test result was recorded after an initial opening, in order to have direct contact between the surfaces of the composite material in the zone between the external pin and the first internal one.

• C) In condition C, a folded sheet of sandpaper (grit 400) was introduced between the crack faces, to obtain a very high friction coefficient.

Three specimens were considered for the data processing presented in this paper. The test conditions for each specimen are indicated below:

• UD-CFRP#1: tested in conditions A and C.

• UD-CFRP#2: tested in conditions A and B.

• UD-GFRP#1: tested in conditions A and C.

These conditions were defined with the aim of obtaining different levels of frictional effects during crack propagation. In the first case, the PTFE layer used to produce the pre-crack was left in place. In this case, friction could have been influenced by several factors, which could be competitive to some extent, such as the low frictional coefficient of the PTFE layer as well as the development of potential adhesion and wrinkles during the manufacturing process. In the second case, the PTFE was successfully removed, so that it was possible to measure the frictional effects during the development of a crack under operational conditions in a real-world structure. Finally, a condition with a high frictional coefficient was examined, by artificially introducing a layer of sandpaper between the crack faces. Crack propagation in a carbon fibre reinforced specimen was studied in all the three conditions. The tests performed on the glass-reinforced specimen allowed further assessment of the method, considering both a low friction condition (with PTFE) and a high friction condition (with sandpaper). The objective was to test the method on the two composite materials most utilized in the aerospace field to validate it in a more general way. Since the tests on the carbon specimens shown a small difference in the behaviour of interfaces A and B, we focused on interfaces A and C for glass specimen.

Crack propagation tests were performed until the crack advanced a few millimetres. It is worth noting, that the force required to open the crack in the 4 point ENF is theoretically constant with the crack length ([18]), so that a comparison between the different force vs. displacement curves immediately provided a direct indication of the different “perceived toughness”.

The force vs. displacement responses, are exemplified in Figs. 4 and 5, which show the load–displacement curves for the UD-GFRP #1 and UD-CFRP#1 specimens respectively, in conditions A and C.

Fig. 4

Load–displacement curves with crack propagation of the UD-GFRP#1 specimen in conditions A and C

Fig. 5

Load–displacement curves with crack propagation of the UD-CFRP#1 specimen in conditions A and C

As can be observed, the propagations performed with the sandpaper between the crack surfaces occurred at a higher load, thus leading to a higher perceived toughness. This behaviour was also obtained for the other specimens. It indicates that the higher the roughness of the sliding surfaces, the higher the load required for crack propagation and consequently the perceived toughness.

Data Reduction and Identification of Frictional Effects

The perceived toughness was calculated by using the Irwin-Kies equation, calibrating the compliance by means of the results from loading–unloading cycles, after having performed some preliminary tests. In particular, this compliance calibration was carried out by loading the specimen up to half of the crack propagation load obtained in the preliminary tests, with a crack length a = 38 mm. Then, the specimen was shifted to reach a crack length a + Δa = 48 mm and loaded up to half of the crack propagation load. Since the compliance is linear with the crack length in the 4ENF test, its derivative in relation to the crack length is constant and was easily calculated using the following expression:

$$\frac{\partial C}{\partial a}=\frac{\Delta C}{\Delta a}=\frac{C\left(a+\Delta a\right)-C\left(a\right)}{\Delta a}$$

(24)

Then, the “perceived toughness” was calculated using equation (22).

The identification of frictional effects was carried out following the procedure described below, with the goal of identifying the coefficient H, to be inserted in the modified Irwin-Kies equation (equation (21)).

• Step 1: Positioning the specimen so as to obtain the desired initial crack length.

• Step 2: A series of loading-unloading cycles was performed at the crack length previously fixed, each cycle having a different maximum load reached at the end of loading, which was performed monotonically at a constant cross-head speed of 1 mm/min.

• Step 3: Calculation of the work dissipated in each cycle by measuring the area enclosed between the loading and unloading curves.

• Step 4: Plotting of the result of the work dissipated vs. the maximum load on a graph and fitting the points that correspond to the cycles with a second order polynomial.

• Step 5: Dividing the coefficients of the polynomial by the compliance, which corresponds to the position of the crack defined in Step 1, in order to evaluate the coefficient H, to be used in the modified Irwin-Kies equation (equation (21)).

• Step 6: After evaluating the coefficient H, calculation of the real toughness using the modified Irwin-Kies equation (equation (21)).

In Fig. 6 an example of loading–unloading cycles is provided.

Fig. 6

Loading–unloading cycles performed on the UD-GFRP#1 specimen in condition C

All the cycles were performed at the same crack length, as can be seen from the slope of the loading curve, and the energy dissipated, which is represented by the area between loading and unloading curves, increases with the maximum load reached.

In Tab. 1, the values of critical energy release rate are shown for each specimen and interface condition, without taking into account the values related to preopening. As said before, marker A indicates the interface with pins over the PTFE insert, marker B indicates the interface with pins over the opened crack and marker C indicates the interface with pins over the sandpaper.

Table 1 Experimental results for toughness, friction contribution and derivative of compliance

The first row of Tab. 1 shows the value of the derivative of the compliance calculated experimentally. The second row shows the value of the mode II perceived toughness, calculated using the Irwin-Kies equation (equation (22)). The third row shows the values of the mode II real toughness calculated according to equation (21). The fourth row represents the percentage of perceived toughness attributed to the friction, which was subtracted from the perceived toughness to obtain the real toughness. One can observe that the perceived toughness increases as the roughness of the sliding surfaces increases. For instance, in specimen UD-GFRP#1, the perceived toughness increased from 1.386 kJ/m² to 1.530 kJ/m² when sandpaper was inserted between the two sliding surfaces, with a friction contribution that increased from 6.0% to 14.4%. Similar results were obtained for the UD-CFRP#1 specimen. The UD-CFRP#2 specimen exhibited a slight reduction in the perceived toughness, passing from condition A to condition B. This behaviour can be attributed to the fact that the pre-cracked surface, in which the PTFE sheet was inserted, presented an irregular, but visible, waviness originating from the manufacturing process.

The analysis results indicate that the proposed method provides a value that is almost identical to the real toughness that is independent of the surface conditions. The G_IIc value for the Carbon UD material obtained from the different specimens and surface conditions varies from 0.800 kJ/m² to 0.830 kJ/m², while the perceived G’_IIc value varied from 0.860 kJ/m² for condition B to a maximum of 0.925 kJ/m² for condition C. For the Glass UD material, the toughness obtained using the method was 1.303 kJ/m² and 1.310 kJ/m² for the two conditions A and C, though the perceived values were very different.

The effect of variation of the friction coefficient is analysed in Fig. 7, which provides the ratio of the work dissipated to the compliance during a hysteresis cycle. It is interesting to note that the upper curves, which relate to the UD-CFRP#1 and UD-GFRP#1 specimens, with interface condition C, with sandpaper, obtained the greatest values for the work dissipated by frictional effects.

Fig. 7

Dissipated work per unit of compliance versus maximum applied load in the cycle

Verification with the Results of an Analytical Model

The method proposed is based on the assumption of a constant friction coefficient and linear behaviour. The same assumptions are considered for the analytical model presented in [12], and so the method can be also verified by means of a virtual experiment, based on application of that analytical model.

In particular, a virtual loading–unloading cycle was considered by applying the analytical formulation. The stiffness in both the loading and the unloading phase was evaluated and then the area between the two curves was obtained. The coefficient H was identified and used in the modified Irwin-Kies equation (equation (21)). Finally, the result was compared with the value of toughness calculated by directly applying the analytical model in [12], which leads to the expression given in equation (25).

$${G}_{II c}^{analytical}=\frac{{\left(3{L}_{a}-4h\alpha \right)}^{2}}{16{h}^{3}{b}^{2}{E}_{xx}}\eta {P}^{2}$$

(25)

In order to plot the loading curve, equation (10) was used, while the unloading curve was calculated by reversing the sign of the term multiplied by α, in order to obtain:

$$P=\frac{8{h}^{3}b{E}_{xx}/\left[\eta {L}_{a}\left(9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}\right)\right]}{1+\alpha \frac{12ah-9{L}_{a}h}{9a{L}_{a}+3L{L}_{a}-10{L}_{a}^{2}}}u$$

(26)

The test conditions adopted in the experiments presented in "Experimental Validation" were applied. As regards the parameters used for the specimens, h was set equal to 2 mm, E_xx was equal to 130,000 MPa, η was set equal to 1 for a plane stress condition. The friction coefficient α was set equal to 0.4, which is a value that is used by the author in [12] and is close to that mentioned in [10], and a = 38 mm was chosen. A load P equal to 850 N was considered for determining the hysteresis area and the coefficient H was found using equation (27) below, which is equivalent to polynomial fitting in the experimental procedure.

$$H=\frac{hysteresis\,area}{C{P}^{2}}=0.0088$$

(27)

The analytical derivative was found by using equation (24), considering a crack advancement from 38 mm to 48 mm, as in the tests, which led to:

$$\frac{\partial C}{\partial a}=4.57\times {10}^{-5}{\mathrm{N}}^{-1}$$

(28)

Finally, substituting the values in the modified Irwin-Kies equation (equation (21)) we get:

$${G}_{II c}=0.627 \mathrm{kJ}/{\mathrm{m}}^{2}$$

(29)

While using equation (25) proposed in [12] gives us:

$${G}_{II c}^{analytical}=0.619 \mathrm{kJ}/{\mathrm{m}}^{2}$$

(30)

The result obtained by applying the proposed method is 1.3% higher than that derived from direct application of the analytical model. However, the differences induced by this variation seem negligible, thus verifying the substantial equivalence between the proposed approach and the analytical one.

Conclusions

The method proposed in this paper aims to evaluate the frictional effects in mode II delamination propagation by performing a preliminary series of loading–unloading cycles on a 4 point ENF specimen. The data obtained in these cycles is used in the data reduction method to calibrate the correction term that represents the contribution of the frictional effects.

The formulation adopted is based on the assumptions of a constant friction coefficient and completely linear behaviour. Under such assumptions, the force vs. displacement response obtained in the loading–unloading cycles is represented by a simplified triangular response. The experimental validation of the method indicates that this simplification is acceptable and leads to consistent results in the evaluation of the real toughness, obtained by removing the contribution of frictional forces from the work required for the crack to advance in the test. This conclusion is supported by the results obtained under very different conditions, including cases in which frictional effects were artificially increased by interposing rough sandpaper between the crack faces.

Moreover, the analytical formulation and subsequent verification show that the method is equivalent to the application of an analytical test model, but it does not need explicit identification of the friction coefficient obtained by correlating the modelled and the experimental force vs. displacement response in the tests.

Accordingly, the proposed method can be considered to be a promising approach to identifying frictional effects in delamination propagation by means of a simple experimental procedure and data reduction.