Analytical corrections for double-cantilever beam tests

Abstract

Double-cantilever beams (DCBs) are widely used to study mode-I fracture behavior and to measure mode-I fracture toughness under quasi-static loads. Recently, the authors have developed analytical solutions for DCBs under dynamic loads with consideration of structural vibration and wave propagation. There are two methods of beam-theory-based data reduction to determine the energy release rate: (i) using an effective built-in boundary condition at the crack tip, and (ii) employing an elastic foundation to model the uncracked interface of the DCB. In this letter, analytical corrections for a crack-tip rotation of DCBs under quasi-static and dynamic loads are presented, afforded by combining both these data-reduction methods and the authors’ recent analytical solutions for each. Convenient and easy-to-use analytical corrections for DCB tests are obtained, which avoid the complexity and difficulty of the elastic foundation approach, and the need for multiple experimental measurements of DCB compliance and crack length. The corrections are, to the best of the authors’ knowledge, completely new. Verification cases based on numerical simulation are presented to demonstrate the utility of the corrections.

1 Introduction

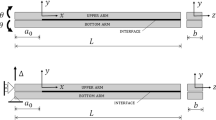
Double cantilever beams (DCBs) (Fig. 1a) are widely used to study mode-I fracture behavior and to measure mode-I fracture toughness. Several standard test methods were developed for the quasi-static testing of DCBs and subsequent post-processing of experimental data, to measure mode-I fracture toughness. These include ASTM D5528 (2014) for interlaminar fracture toughness of carbon-fiber-reinforced plastics and ISO 25217 (2009) for fracture toughness of adhesives.

The beam-theory-based data-reduction method in these standards assumes an effective boundary condition to calculate the energy release rate (ERR), whereby each DCB arm is perfectly built-in at the crack tip (Fig. 1b). Clearly, however, the beam is not perfectly built-in, and rotation may occur at the crack tip. So, the assumption leads to overestimation of the ERR. One correction that can be introduced to overcome this is to replace the crack length a with an effective crack length $a_\text {eff}=a+\varDelta$, where $\varDelta$ is an additional crack length (Hashemi et al. 1989). When the cube root of the compliance $C^{1/3}$ is plotted versus $a_\text {eff}$, linear regression should give an intercept of zero, thus providing one means to determine $\varDelta$. This is sometimes called the modified beam theory (MBT) method (ASTM D5528 2014).

Another data-reduction method is to introduce an elastic foundation to model the uncracked region of the DCB (Fig. 1c) (Kanninen 1973). This analytical method of introducing an elastic foundation to model DCBs was also used in various other research works, for example, Kondo (1995), Abbaszadeh et al. (2017), Škec et al. (2019). The advantage of using an elastic foundation over an effective boundary condition is that it automatically allows rotation at the crack tip, and no correction is needed. One issue with the elastic foundation, however, is its significant complexity and difficulty of use in comparison to the effective-boundary-condition method.

The authors have recently developed analytical solutions for DCBs under dynamic loads with consideration of structural vibration and wave propagation using both above methods, namely, with an effective boundary condition (Chen et al. 2020a) and with an elastic foundation (Chen et al. 2020b). Analytical corrections for quasi-static and dynamic DCB tests, afforded by combining both these methods, are presented in this letter. To the best of the authors’ knowledge, these corrections are completely new. A convenient and easy-to-use relationship between the additional crack length for crack-tip rotation $\varDelta$ and the elastic foundation stiffness k is obtained. Therefore, with knowledge of the foundation stiffness k, which is often known with reasonable accuracy, the appropriate $\varDelta$ required for post-processing the experimental data can be determined immediately without the need for multiple measurements of a and the subsequent linear regression of $C^{1/3}$ as a function of a.

For instance, for adhesively bonded DCBs under plane-stress conditions, the foundation stiffness k is simply twice the Young’s modulus of the adhesive $E_\text {adhesive}$ (Chen et al. 2020b). For mono-material or co-cured fiber-reinforced-polymer (FRP) DCBs, there is no unanimous agreement on the appropriate foundation stiffness. Kanninen (1973) claimed that the selection of foundation stiffness was ‘arbitrary’ and required experimental confirmation. Nevertheless, for these types of DCB, the foundation stiffness is usually reckoned as being of the same order as the DCB material’s Young’s modulus (Wang et al. 2013). For DCBs made of one isotropic material, Kanninen (1973) used $k=2Eb/h$ (where E is the Young’s modulus, b is the DCB width, and h is the thickness of each DCB arm). For co-cured FRP DCBs, Turon et al. (2007) argued by mechanical considerations that the foundation stiffness is $k=b E_{nn}$ where $E_{nn}=\alpha E_3/h_0$ is the interface stiffness, and $E_3$ is the transverse modulus, $h_0$ is the thickness of the adjacent sub-laminate, and $\alpha$ is a parameter that may be taken as 50.

Fig. 1

a DCB schematic; b DCB arm with effective boundary condition; c DCB arm with uncracked region resting on elastic foundation

As stated above, for adhesively bonded DCBs under plane-stress conditions, the relationship between the Young’s modulus of the adhesive $E_\text {adhesive}$ and the foundation stiffness k is $E_\text {adhesive}=0.5k$, which can be readily explained as follows: With reference to Fig. 1a, the force applied to the DCB is $E_\text {adhesive} \int _{0}^{L} 2 w(x,t) \, dx$, where 2w(x, t) is the relative displacement between the two DCB arms. (The force would be $E_\text {adhesive} b \int _{0}^{L} 2 w(x,t) \, dx/h_0$, but as per Diehl (2008), the adhesive thickness $h_0$ is taken as a unity constitutive thickness, ensuring that the strain equals the relative separation displacement; and b is also unity under plane-stress conditions.) By comparison, with reference to Fig. 1c, the force required to produce the same deflection w(x, t) in the half DCB model is $k \int _{0}^{L} w(x,t) \, dx$. The cases are equivalent, and so the relationship $E_\text {adhesive}=0.5k$ is a result of equating the two force expressions, with the coefficient’s value of 0.5 being due to the symmetric deformation of the DCB and its interface. Cabello et al. (2016) reported a general analytical model for the relationship between the Young’s modulus of the adhesive $E_\text {adhesive}$ and the foundation stiffness k under plane-strain conditions.

It is worth noting the difference between the foundation modulus $k_0$ (with SI units of $\text {N}\,\text {m}^{-3}$) seen in some works, and the foundation stiffness k (with SI units of $\text {N}\,\text {m}^{-2}$) used by Kanninen (1973) and in this letter. Since $k=2E_\text {adhesive}$ under plane-stress conditions with unity DCB width, k, in general, depends on the DCB width and is not purely a material property. The foundation modulus $k_0$, however, is defined as k/b and so can be considered a material parameter.

The format of this letter is as follows: The theory is presented in Sect. 1. Verification cases are presented in Sect. 3. Conclusions are given in Sect. 4.

2 Theory

Consider the DCB configuration shown in Fig. 1, where a is the crack length, L is the uncracked length, 2h is the thickness of the DCB, with h being the thickness of each DCB arm, and vt is the opening displacement suddenly applied at time $t=0$ with v being the constant-opening rate. The width of the DCB is b, and so for each arm the cross-sectional area is $A=bh$ and its second moment is $I=bh^3/12$. The Young’s modulus of the DCB material is E and its density is $\rho$. As discussed in the introduction, there are two methods of data reduction using the beam theory, namely, by employing an effective boundary condition with each DCB arm perfectly built-in at the crack tip, as shown in Fig. 1b; or, by using an elastic foundation to model the uncracked region, as shown in Fig. 1c.

2.1 Dynamic ERR using effective boundary condition

The dynamic ERR of the DCB shown in Fig. 1a, based on the effective boundary condition shown in Fig. 1b, is (Chen et al. 2020a)

$$\begin{aligned} G=\frac{9EIv^2t^2}{ba^4}+\frac{12\sqrt{\rho AEI}v^2t}{ba^2}\sum _{i=1}^{\infty }\frac{\varLambda _i}{\lambda _i}\sin \left( \omega _it\right) , \nonumber \\ \end{aligned}$$

(1)

where $\omega _i=\lambda _i^2a^{-2}\sqrt{EI/(\rho A)}$ is the angular frequency of the ith vibration mode, and $\lambda _i$ is the ith solution of the frequency equation $\tan (\lambda _i)-\tanh (\lambda _i)=0$, and $\varLambda _i\approx (-1)^i\sqrt{2}$. The first term in Eq. (1) is the ERR due to the strain energy of quasi-static motion, and the second term is the ERR due to the kinetic energy of coupling between quasi-static motion and local vibration. To account for rotation at the crack tip, the crack length a should be replaced with the effective crack length $a_\text {eff}$ by including the additional crack length $\varDelta$, determined below. This may or may not be implemented by direct substitution of $a_\text {eff}$ for a in Eq. (1), as discussed as follows.

One way to determine the additional crack length $\varDelta$ under quasi-static loading is by using the standardized MBT method (ASTM D5528 2014). The compliance C of the DCB is the ratio of the load-point displacement to the applied load. When the cube root of the compliance $C^{1/3}$ is plotted as a function of the crack length a, the negative intercept with the a axis of the line of best fit is the additional crack length $\varDelta$.

The MBT method cannot, however, be directly applied to dynamic loading cases due to strong oscillation of the external load, as observed in many experiments, for example, those by Blackman et al. (1995). This leads to oscillating compliance, and so no linear relationship between $C^{1/3}$ and a can be obtained. Note that under dynamic loads without correction for the additional crack length $\varDelta$, the frequency of the ERR may not be accurately predicted, and this is confirmed by the first verification case study in Sect. 3.

The oscillating compliance based on the effective boundary condition is (Chen et al. 2020a, c)

$$\begin{aligned} C=\frac{a^3}{3EI-\frac{a^5}{t}\sqrt{\rho AEI}\sum _{i=1}^{\infty }\frac{\varLambda _i}{\lambda _i^3}\phi _i^3(a)\sin {(\omega _it)}} , \end{aligned}$$

(2)

where $\phi _i(x)$ is the mode shape of the ith vibration mode, which can found in Chen et al. (2020a, 2020c), but which is not critical for this discussion. Although the compliance oscillates with respect to time, it oscillates around the mean value of its quasi-static compliance, $a^3/(3EI)$. This suggests that the additional crack length $\varDelta$ for the dynamic case may be the same as that determined with the MBT method for quasi-static loads. This is confirmed by the second verification case study in Sect. 3.

Under quasi-static loads, there are two equivalent ways to implement the effective crack length $a_\text {eff}=a+\varDelta$, as laid out in ASTM D5528 (2014) (1) by direct substitution of $a_\text {eff}$ for crack length a in the expression for ERR; or (2) by direct substitution of an effective flexural modulus $E_\text {eff}$ for E, where $E_\text {eff}=a^3E/{(a+\varDelta )^3}$. Under dynamic loads, however, these two implementations of the effective crack length $a_\text {eff}$ are not equivalent in terms of the natural frequency. Substituting the effective crack length $a_\text {eff}$ gives the natural frequencies as $\omega _i=\lambda _i^2(a+\varDelta )^{-2}\sqrt{EI/(\rho A)}$, whereas substituting the effective flexural modulus $E_\text {eff}$ gives the natural frequencies as $\omega _i=\lambda _i^2(a+\varDelta )^{-2}\sqrt{EI(a+\varDelta )/(\rho Aa)}$. These two expressions for the natural frequencies are clearly not equal. The second verification case study in Sect. 3 shows that substituting the effective crack length provides the more accurate dynamic ERR in terms of natural frequency, and so

$$\begin{aligned} G&=\frac{9EIv^2t^2}{ba_\text {eff}^4}\nonumber \\&\quad +\frac{12\sqrt{\rho AEI}v^2t}{ba_\text {eff}^2} \sum _{i=1}^{\infty }\frac{\varLambda _i}{\lambda _i}\sin {\left( \frac{\lambda _i^2}{a_\text {eff}^2}\sqrt{\frac{EI}{\rho A}}t\right) } . \end{aligned}$$

(3)

2.2 Dynamic ERR using elastic foundation

The dynamic ERR of the DCB shown in Fig. 1c, based on the use of an elastic foundation to model uncracked region, is (Chen et al. 2020b)

$$\begin{aligned} G=\frac{9EIv^2t^2f_\text {st}^\text {U}}{ba^4}-\frac{v^2t}{b}\sum _{i=1}^{\infty }\sqrt{\frac{\omega _1}{\omega _i}}H_i\frac{d\omega _i}{da}\sin {(\omega _it)} , \nonumber \\ \end{aligned}$$

(4)

where $H_i$, which is defined in Chen et al. (2020b), represents the coupling of free vibration and the applied quasi-static motion, an inherent property of the DCB configuration, and

$$\begin{aligned} f_\text {st}^\text {U}=\frac{4a^4\gamma ^4(a\gamma +1)^2}{(2a^3\gamma ^3+6a^2\gamma ^2+6a\gamma +3)^2} , \end{aligned}$$

(5)

where $\gamma =\root 4 \of {k/(4EI)}$. Equation (5) applies under the assumption that $\gamma L\ge 3$, and $f_\text {st}^\text {U}$ is the reduction factor of the quasi-static motion component of the ERR $G_\text {st}^\text {U}$ due to the elastic foundation. When the foundation stiffness becomes very large, so that k and $\gamma$ approach infinity, then $f_\text {st}^\text {U}=1$ and $G_\text {st}^\text {U}=9EIv^2t^2/(ba^4)$, which is the same as the first term in Eq. (1). An infinite foundation stiffness or rigid interface is therefore equivalent to the effective boundary condition.

2.3 Relationship between effective boundary condition and elastic foundation models

The two methods of data reduction using the beam theory described above should be equivalent and produce the same results once appropriate values of the interface stiffness k and additional crack length $\varDelta$ have been determined. Equations (3) and (4) should therefore be equal, and by extension, their quasi-static components should also be equal, giving

$$\begin{aligned} \frac{9EIv^2t^2}{ba_\text {eff}^4}=\frac{9EIv^2t^2f_\text {st}^\text {U}}{ba^4} . \end{aligned}$$

(6)

Solving Eq. (6) together with Eq. (5) and substituting $a_\text {eff}=a+\varDelta$, the additional crack-length correction for crack-tip rotation $\varDelta$ is

$$\begin{aligned}&\varDelta =a_\text {eff}-a\nonumber \\&=\frac{1}{\gamma }\root 4 \of {\frac{(2a^3\gamma ^3+6a^2\gamma ^2+6a\gamma +3)^2}{4(a\gamma +1)^2}}-a . \end{aligned}$$

(7)

Equation (7) provides a convenient relationship between the additional crack length for crack-tip rotation $\varDelta$ and the elastic foundation stiffness k. Moreover, it also provides an analytical correction for DCB tests without using the MBT method to measure multiple compliances and crack lengths for regression. The foundation stiffness for interfaces of adhesive, mono-material and co-cured FRP can be found in Chen et al. (2020b), Kanninen (1973), Turon et al. (2007), respectively, as elaborated in Sect. 1.

To the best of the authors’ knowledge, this is the first time that Eq. (7) has been reported. The relationship is applicable to both stationary and propagating cracks under quasi-static loads, and to stationary cracks under dynamic loads. It cannot, however, be used for propagating cracks under dynamic loads since in this case $\varDelta$ is rate-dependent due to the influence of ‘stick-slip’ crack propagation, as shown by experimental investigations (Blackman et al. 1996). In contrast, the foundation stiffness is a material property and is rate-independent.

3 Verification

Verification case studies were conducted using finite-element-method (FEM) simulation of the DCB shown in Fig. 2 (its width is 1 mm). An isotropic elastic material was used, with the Young’s modulus of 10 GPa, the Poisson’s ratio of 0.3, and the density of $10^3$ kg m$^{-3}$.

Fig. 2

Geometry of DCB for verification

A 2D FEM model was built using plane-stress elements (CPS4R) in Abaqus/Explicit, which include the inertia effects. All viscous parameters were set to zero to avoid unnecessary damping. The virtual crack closure technique was used to determine the dynamic ERR. The nodes of the two DCB arms were shared along the uncracked interface, and no contact was modelled. A uniform mesh size of 0.1 mm was used.

3.1 Effective boundary condition without correction for crack-tip rotation

Results from Eq. (1) for ERR based on the effective boundary condition without any correction for crack-tip rotation are shown in Fig. 3 alongside FEM simulation results. Eq. (1) agrees with the FEM except for being out of phase. This indicates that the frequency is not accurately predicted by this approach without correction for crack-tip rotation. Moreover, the analytical model is stiffer than the FEM model. Comparison between Fig. 3a, b also demonstrates that by including more vibration modes, the analytical results become closer to the FEM simulation results.

Fig. 3

Comparison of ERR results from FEM (gray line) and from analytical theory without compensating for crack-tip rotation: a first vibration mode; b first five vibration modes

3.2 Effective boundary condition with correction for crack-tip rotation

Following the MBT method for quasi-static loading, the additional crack length $\varDelta$ is determined by calculating the compliance C for various crack lengths a and performing linear regression of $C^{1/3}$ with respect to a to find the negative intercept with the a axis. Abaqus/Standard, which does not include the inertia effects, was used to conduct quasi-static FEM simulations of the DCB in Fig. 2 with several different crack lengths to find the respective external force and displacement at the load point. Linear regression as per the MBT method is shown in Fig. 4, and the additional crack length was determined as $\varDelta =1.34$ mm.

Fig. 4

Cube-root compliance regression with respect to crack length by results from quasi-static FEM simulation

The additional crack length of $\varDelta =1.34$ mm was then implemented in Eq. (1) by the two methods discussed in Sect. 2.1, namely, by (1) direct substitution of effective crack length $a_\text {eff}=a+\varDelta$ for crack length a, and (2) direct substitution of effective flexural modulus $E_\text {eff}=a^3E/(a+\varDelta )^3$ for the Young’s modulus E. Note that the former corresponds to Eq. (3). The analytical ERR results from these two methods are presented in Fig. 5a, b, respectively (black lines) alongside the FEM simulation results (gray lines). Apparently, although both methods agree with the FEM, the method of directly substituting $a_\text {eff}$ for a in Eq. (1) is more accurate for predicting the frequency of the ERR.

Fig. 5

Implementation of additional crack length $\varDelta$ by the effective crack length $a_\text {eff}$ (a) and the effective flexural modulus $E_\text {eff}$ (b)

3.3 Effective crack length versus foundation stiffness

The DCB can also be analytically modelled by resting the uncracked region of one DCB arm on an elastic foundation, as described in Sect. 2.2. The foundation stiffness is required (just as the effective crack length is required for the effective-boundary-condition model). It is reported in Chen et al. (2020b) that a foundation stiffness of $k=0.35E$ gives an excellent agreement with FEM simulation. Results for ERR from Eq. (4) with $k=0.35E$ are shown in Fig. 6 (black line) alongside FEM simulation results (gray line). As expected, there is a very close agreement between the theory and the FEM as the elastic foundation automatically accounts for the crack-tip region.

Fig. 6

Comparison of ERR results from FEM (gray line) and from analytical theory with elastic foundation (black line)

According to Eq. (7), the additional crack-length correction for crack-tip rotation $\varDelta$ that corresponds to a foundation stiffness $k=0.35E$ is $\varDelta =1.66$ mm, which is very close to the value of $\varDelta =1.34$ mm, determined with the MBT method.

Now the ERR is calculated using Eq. (3), based on the effective boundary condition, but using the additional crack length of $\varDelta =1.66$ mm. The results are plotted in Fig. 7b (black line). For convenient side-by-side comparison, Fig. 5a, based on the additional crack length of $\varDelta =1.34$ mm, is repeated in Fig. 7a (black line). The difference between the values of $\varDelta$ are not significant, but $\varDelta =1.66$ mm (derived with the elastic-foundation model) gives a marginally more accurate result in terms of the frequency than $\varDelta =1.34$ mm (obtained with the MBT method).

Fig. 7

Comparison of ERR results from FEM (gray line) and from analytical theory with effective boundary condition (black line). Effective crack-length determined with MBT method (a) and relating to elastic foundation (b)

4 Conclusion

Analytical corrections for the crack-tip rotation of DCBs under quasi-static and dynamic loads were suggested. They can be readily applied in beam-theory-based data reduction of DCB test results to determine the ERR. The corrections are, to the best of the authors’ knowledge, completely new. When using an effective boundary condition, whereby each DCB arm is perfectly built-in at the crack tip, a correction for rotation at the crack tip should be introduced. The frequency of the oscillating dynamic ERR and the compliance of the DCB are not accurate without correcting for crack-tip rotation.

The standardized MBT method for quasi-static loading uses experimental measurements of compliance and crack length to determine the additional crack length required to correct for crack-tip rotation. It was shown that the MBT method can also be applied to dynamic cases with stationary cracks by direct substitution of the effective crack length for the crack length in the analytical theory. Furthermore, although the compliance oscillates with respect to time in dynamic loading cases, it oscillates around the mean value of its quasi-static compliance, and so the additional crack length for dynamic loads is the same as that under quasi-static loads. The MBT method cannot, however, be used for cases of propagating cracks under dynamic loads since the additional crack length is then rate-dependent due to the influence of ‘stick-slip’ crack propagation.

Although the MBT method can be applied to the results of quasi-static experiments or FEM simulations to determine the required additional crack length, this letter presents a convenient and easy-to-use analytical correction that gives the additional crack length in terms of the interface stiffness. The correction was obtained by relating the dynamic ERR of a DCB with the effective boundary condition to the dynamic ERR of a DCB with its uncracked interface, represented by an elastic foundation. The elastic foundation allows the crack tip to rotate automatically, and no further correction is needed. Therefore, with knowledge of the interface stiffness, which is often known with reasonable accuracy, the additional crack length required for post-processing experimental data can be determined immediately without the need for multiple measurements of DCB compliance and crack length.

Verification studies were conducted using the FEM. It was shown that the two beam-theory-based data-reduction methods, namely, using an effective built-in boundary condition at the crack tip, and employing an elastic foundation to model the uncracked interface of the DCB, are equivalent if their respective additional crack length or interface stiffness are related by the reported analytical relationship. This conclusion is valid for both quasi-static and dynamic loading cases, provided there is no ‘stick-slip’ crack propagation.