1 Introduction

Mobile communications systems are affected by what is known as fading, which is a well-known problem largely studied for decades. The fading comes from the fact that there is no direct radio path between the emitter (the antenna) and the mobile terminal (the receptor), therefore the radio signal is scattered by surrounding elements (buildings, trees, cars, and so) and more scattered even in the vicinity of the receptor (receptors are commonly far from the emitters). As a consequence of these so complex stochastic scattering mechanisms, the signal exhibits rapid signal level fluctuations. The direct consequence of fading is the complete loss of signal (or a large decrease of the received power). For a mobile radio channel characterized with a fixed gain and a linear phase response across the bandwidth greater than the bandwidth of the transmitted wave (what is the common real situation), the received signal will show what is known as at flat fading [1]. This is the most common situation and consequently the most researched and also the one accounted for in this paper.

As mentioned above, fading is associated to wireless communications. UAV (unmmanned aerial vehicles extensively use wireless signals for many purposes (i.e., transmission of acquired data from on-board systems, transmission of guidance parameters, among others). Due to UAVs operate in complex scenarios, frequently urban areas and following 3D arbitrary trajectories, correct modeling of fading is of great interest. Several works have been published, see for instance [2] for a modeling multiple-input multiple-output (MIMO) channel for UAV to vehicle (U2V) communications considering UAV heaving motion or [3] for a complete modeling of a non-stationary UAV to ground MIMO channel regarding 3D pose estimation of the UAV.

Rayleigh fading is a reasonable model for wireless channels that contain many objects that scatter the radio signal between the emitter and the receiver [4]. In such a case, the envelope of the channel response will be Rayleigh distributed, with probability density function (PDF) and cumulative distribution function (cdf),

$$\begin{aligned} g_R(r;\beta )= & {} 2\, \beta \, r\exp \left( -\beta \,r^2\right) ,\quad r\ge 0, \end{aligned}$$
(1)
$$\begin{aligned} G_R(r;\beta )= & {} 1-\exp (-\beta r^2),\quad r\ge 0, \end{aligned}$$
(2)

respectively, where \(\mathrm{I\hspace{-2.2pt}E}(R^2) = 1/\beta\) is the expected value of \(R^2\) being \(\beta >0\). In this situation we will denote \(R\sim \mathcal{R}(\beta )\).

Several alternatives to the Rayleigh modelling have been published such as the Nakagami-m distribution [5,6,7], the K distribution (a mixture of the Rayleigh distribution with the gamma one) [8], the Rician distribution (a mixture of the Rayleigh distribution with the lognormal one) [9] and the mixture Rayleigh-inverse Gaussian distribution [10]; among others. Most of these alternatives pretend to compare with the first one which was initially proposed in the early 1940’s [11].

However, as pointed out in [5], it is generally accepted that the Nakagami-m distribution is more versatile, allowing to modeling a variety of fading environments (including those modeled by one-sided Gaussian distributions and by the standard Rayleigh distribution). So, the need for a new mathematical formulation of this fading distribution is justified.

Thus, using a mixture of the Rayleigh distribution in fading literature is generally accepted. As it is known, this procedure facilitates computations of the average BER (Bit Error Rate) for DPSK (Differential Phase Shift Keying) and MSK (Minimum-Shift Keying) modulations of the resulting distribution obtained by mixing, which is of great applicability to modeling wireless fading channels. In a similar way as the K, Rician, and Rayleigh-inverse Gaussian are received in this work, we derive the well-known Nakagami-m distribution by a composite (mixture) argument from the classical Rayleigh distribution. Based on an exponential decay hat function, [12] presents a simple and highly efficient rejection method for generating independent Nakagami sequences with an arbitrary fading parameter. The methodology proposed here is different; it is based on a mixture procedure, and as in [12], the fading parameter can take arbitrary values.

The rest of the work is structured as follows. First, in Sect. 2, we obtain here the Nakagami-m distribution by mixture the Rayleigh distribution with a PDF which is not well-known in the literature. This facilitates computations of the BER for DPSK and MSK for the Nakagami-m distribution (see Sect. 2.1). Section 3 is concerning with the proposal of a multivariate version of the Nakagami-m distribution. Here, we pay special attention to the bivariate case. Some further results, extending the previous methodology to the three-parameter generalized Nakagami-m distribution and its bivariate version are also discussed herein. Main numerical results are shown in Sect. 4 and some conclusions and future lines of research are drawn in Sect. 5.

2 The composite Nakagami-m distribution

The Nakagami distribution (also called Nakagami-m distribution) with shape or fading parameter \(m\ge 1/2\) and scale parameter \(\Omega >0\) has PDF given by

$$\begin{aligned} h_R(r;m,\Omega )= \frac{2 m^m}{\Gamma (m)\Omega ^m}r^{2m-1}\exp \left( -\frac{m}{\Omega }r^2\right) ,\quad r\ge 0, \end{aligned}$$
(3)

where \(\Gamma (\cdot )\) is the Euler gamma function. It is well-known that this distribution becomes Rayleigh distribution when \(m=1\) and the half-normal density for \(m=1/2\). Furthermore, for \(m = (k+1)^2/(2k+1)\) the distribution in (3) is approximately Rician fading with parameter k. Thus, the Nakagami-m distribution can model Rayleigh and Rician distributions, as well as more general ones. It is also well-known that for support values of the m parameter lower than one the Nakagami-m fading causes more severe performance degradation than Rayleigh fading. As [11] has pointed out the Nakagami-m distribution is able to fit empirical data in a better way than either the Rayleigh, Rician, or lognormal distributions. Its cdf is written in terms of the incomplete gamma function as

$$\begin{aligned} H_R(r;m,\Omega )=\frac{\Gamma (m,m r^2/\Omega )}{\Gamma (m)}. \end{aligned}$$

For a comprehensive study of the Nakagami-m distribution see [13, 14] and [15], among others.

Consider now the PDF given by

$$\begin{aligned} \pi (x)=\frac{a^m}{x(x-a)^{m} \Gamma (\bar{m})\Gamma (m)},\quad 0<m< 1,\;a>0,\; x>a, \end{aligned}$$
(4)

where \(\bar{m} =1-m\). This PDF was introduced with different parameters by [16] in order to write the gamma distribution as a composite of the exponential distribution. Since the Nakagami-m distribution is related with the gamma one and the Rayleigh distribution with the exponential one, this suggests that the Nakagami-m distribution can also be written as a composite of the Rayleigh distribution when (4) is used as a mixing PDF.

The next result will be needed later.

Proposition 1

Let \(\varphi >0\) and \(k>0\). Then, the following relation is satisfied,

$$\begin{aligned} \int _a^{\infty } z^k\exp (-\varphi z)\pi (z)\,dz=\frac{{a^k}\exp (-\varphi a)}{\Gamma (m)}\,\mathcal{U}\left( \bar{m},k+\bar{m},\varphi a\right) , \end{aligned}$$
(5)

where \(\mathcal{U}(\delta ,\sigma ,\tau )\), \(\delta >0\), \(\tau >0\),

$$\begin{aligned} \mathcal{U}(\delta ,\sigma ,\tau )=\frac{1}{\Gamma (\delta )}\int _0^{\infty } t^{\delta -1}(1+t)^{-\delta +\sigma -1}\exp (-\tau t)\,dt \end{aligned}$$
(6)

is the confluent hypergeometric function (see for instance, [17]) and \(\bar{m} = 1-m\).

Proof

We have that

$$\begin{aligned}&\int _a^{\infty } z^k\exp (-\varphi z)\pi (z)\,dz=\frac{a^m}{\Gamma (\bar{m})\Gamma (m)}\nonumber \\&\int _a^{\infty }z^{k-1}(z-a)^{-m}\exp (-\varphi z)\,dz. \end{aligned}$$
(7)

Now, by making the change of variable \(z=\omega +a\) we get that (7) can be rewritten as

$$\begin{aligned} \frac{a^m}{\Gamma (\bar{m})\Gamma (m)}\int _0^{\infty } (\omega +a)^{k-1}\omega ^{-m}\exp \left[ -\varphi (\omega +a)\right] \,d\omega \end{aligned}$$
(8)

and by taking \(\omega = a t\) we have that (8) is written as

$$\begin{aligned}{} & {} \frac{a^k \exp (-\varphi a)}{\Gamma (\bar{m})\Gamma (m)}\int _0^{\infty } t^{-m} (1+t)^{k-1}\exp (-\varphi a t)\,dt \\{} &\quad {} ={\frac{a^k \exp (-\varphi a)}{\Gamma (\bar{m})\Gamma (m)}}\\{} &\quad \times {\int _0^{\infty }t^{1-m-1}(1+t)^{-1+m+k+1-m-1} \exp (-\varphi a t)\,dt}\\{} & \quad ={\frac{a^k \exp (-\varphi a)}{\Gamma (\bar{m})\Gamma (m)}\Gamma (\bar{m})\,\mathcal{U}(\bar{m}, k+\bar{m},\varphi a),} \end{aligned}$$

where we have compared the last integral with (6). From here, (5) is easily obtained. \(\square\)

Specifically, assume that in (1)\(, \beta>a>0\) and that this \(\beta\) parameter is not constant and varies according to the continuous and non-negative PDF given in (4), say \(\pi (\beta )\). Then, we have next stochastic representation,

$$\begin{aligned} R|\beta\sim & {} \mathcal{R}(\beta ),\quad (\text{ Rayleigh } \text{ PDF}),\end{aligned}$$
(9)
$$\begin{aligned} \beta\sim & {} \pi (\beta ). \end{aligned}$$
(10)

Then, we have the following result.

Theorem 1

Let \(g_R(r;\beta )\) the PDF of the Rayleigh distribution with parameter \(\beta >a\), and \(a=m/\Omega\). Then, the composite of this PDF with the PDF given in (4) is the PDF of the Nakagami-m distribution given in (3).

Proof

Assume that for the PDF in (1) \(\beta >m/\Omega\). Then, having into account the stochastic representation given in (9)-(10) we have

$$\begin{aligned} \int _{m/\Omega }^{\infty }g_R(r;\beta )\pi (\beta )\,d\beta = 2 r\int _{m/\Omega }^{\infty } \beta \exp (-\beta r^2)\pi (\beta )\,d\beta . \end{aligned}$$
(11)

Now, using (5) with \(k=1\) we have that (11) results

$$\begin{aligned}{} & {} 2 r\int _{m/\Omega }^{\infty } \beta \exp (-\beta r^2)\pi (\beta )\,d\beta \nonumber \\{} & {} =\frac{2 r m/\Omega \exp (-m r^2/\Omega )}{\Gamma (m)}\,\mathcal{U}\left( \bar{m},1+\bar{m},\frac{m}{\Omega }r^2\right) \end{aligned}$$
(12)

and having into account that \(\mathcal{U}(\bar{m},\bar{m}+1,m r^2/\Omega )=(m r^2/\Omega )^{-\bar{m}}\) we can write (12) as

$$\begin{aligned}{} & {} 2 r\int _{m/\Omega }^{\infty } \beta \exp (-\beta r^2)\pi (\beta )\,d\beta \nonumber \\{} & {} =\frac{2r m/\Omega \exp (-m r^2/\Omega )}{\Gamma (m)}\left( \frac{m r^2}{\Omega }\right) ^{-\bar{m}}\nonumber \\{} & {} =\frac{2 r^{2m-1}m^m}{\Omega ^m \Gamma (m)}\exp \left( -\frac{m}{\Omega }r^2\right) =h_R(r;m,\Omega ). \end{aligned}$$
(13)

Hence the result. \(\square\)

In word of [8] the mixture representation above describes local and global spatial variations of a signal envelope, and/or short-term and long-term temporal fluctuations of a signal envelope in fading-shadowing wireless channels.

Observe that in practise the parameter m in (13) is allowed to take values larger than 1.

2.1 Metrics to characterize the fading channel

This mixture representation of the Nakagami-m distribution facilitates computations of its moments and other features. For example, as it was expected, the squared envelope for the Nakagami-m distribution can be computed for its corresponding for the Rayleigh distribution as the unconditional mean, \(\mathrm{I\hspace{-2.2pt}E}[\mathrm{I\hspace{-2.2pt}E}(r^2;\beta )]=\Omega\). In particular and connecting with signal processing we can compute in an easy way moments of order \(k\in \{1,2,\dots \}\) of the BER for different modulation schemes, say \(\mathcal{M}\). Let \(\gamma =E_b/N_0\), being \(E_b\) the transmitted energy per bit and \(N_0\) accounts for the spectral density of the noise power. Then, the moments of order \(k\in \{1,2,\dots \}\) of the BER for the Rayleigh distribution provided in (1) will be a function of the parameter \(\beta\), say \(P_{b,\mathcal{M}}(\beta )\), and using the composite argument we have that the corresponding moments of the BER for the Nakagami-m distribution can be computed as

$$\begin{aligned} \mathrm{I\hspace{-2.2pt}E}\left\{ \left[ P_{b,\mathcal{M}}(\Omega ,m)\right] ^k\right\} =\int _{m/\Omega }^{\infty }\left[ P_{b,\mathcal{M}}(\beta )\right] ^k\pi (\beta )\,d\beta , \end{aligned}$$
(14)

where \(\pi (\beta )\) is given in (4).

In particular, the BER of DPSK (differential phase shift keying) and MSK (minimum shift keying) for the Nakagami-m distribution with PDF given by (3) will be obtained. This measures have been on interest in the last decades [18]. Recall that the BER is defined as the ratio between the number of bits in error between the total number of bits sent. Both measures are tools widely used in signal processing (see  [19, 20] and [21]; among others). In order to compute these metrics for the Nakagami-m distribution we need previously the following result.

Proposition 2

Let \(k>0\) and \(p>0\). Then, the following expectations with respect to the PDF given in (4) are sustained:

$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left[ \left( \frac{\beta }{p+\beta }\right) ^k\right] = \,_2F_1(k,m;1;-p\Omega /m),\end{aligned}$$
(15)
$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left[ \frac{1}{(p+\beta )^k}\right] \nonumber \\{} & {} =\left( \frac{\Omega }{m}\right) ^k\frac{\Gamma (k+m)}{\Gamma (m)\Gamma (k+1)}\,_2F_1(k,k+m;1+k;-p\Omega /m). \end{aligned}$$
(16)

where \(_2F_1\) is the hypergeometric function given by

$$\begin{aligned}{} & {} _2F_1(a,b;c;z)=\frac{\Gamma (c)}{\Gamma (b)\Gamma (c-b)}\nonumber \\{} & {} \int _0^{\infty } t^{-b+c-1}(t+1)^{a-c}(t-z+1)^{-a}\,dt. \end{aligned}$$
(17)

Proof

We have that by using (14) we get,

$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left[ \left( \frac{\beta }{p+\beta }\right) ^k\right] =\int _{m/\Omega }^{\infty } \left( \frac{\beta }{p+\beta }\right) ^{k}\frac{(m/\Omega )^m}{\beta \left( \beta -\frac{m}{\Omega }\right) \Gamma (m)\Gamma (\bar{m})}\\{} & {} =\frac{(m/\Omega )^m}{\Gamma (m)\Gamma (\bar{m})}\int _0^{\infty }\left( z+\frac{m}{\Omega }\right) ^{k-1}\left( z+\frac{m}{\Omega }+p\right) ^{-k} z^{-m}\,dz, \end{aligned}$$

where we have made the change of variable \(z=\beta -m/\Omega\). Now, after the change of variable \(t=z\Omega /m\) we get

$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left[ \left( \frac{\beta }{p+\beta }\right) ^k\right] =\frac{1}{\Gamma (m)\Gamma (\bar{m})}\int _0^{\infty }(t+1)^{k-1}\\{} & {} \left( t+\frac{p\Omega }{m}\right) ^{-k}t^{-m}\,dt \end{aligned}$$

and identifying this with (17) and by taking \(a=k\), \(b=m\), \(c=1\) and \(z=-p\Omega /m\) we get directly (15). In order to get (16) we have that

$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left[ \frac{1}{(p+\beta )^k}\right] = \frac{(m/\Omega )^m}{\Gamma (m)\Gamma (\bar{m})}\int _{m/\Omega }(p+\beta )^{-k}\beta ^{-1}\\{} & {} \left( \beta -\frac{m}{\Omega }\right) ^{-m}\,d\beta , \end{aligned}$$

from which by making the same changes of variables defined above we get (16) after some algebra. \(\square\)

This last result can be used for getting moments of the BER of DPSK and MSK for the Nakagami-m distribtion. This is shown in the following Proposition.

Proposition 3

Let \(\gamma =E_b/N_0\), being \(E_b\) the transmitted energy per bit and \(N_0\) accounts for the spectral density of the noise power. Then, the moments of order \(k\in \{1,2,\dots \}\) of the measures BER of DPSK and MSK for the Nakagami-m distribution with PDF given by (3) result,

$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left\{ \left[ P_{b,DPSK}(\beta )\right] ^k\right\} = \frac{1}{2^k}\,_2F_1(k,m;1;-\gamma \Omega /m),\end{aligned}$$
(18)
$$\begin{aligned}{} & {} \mathrm{I\hspace{-2.2pt}E}\left\{ \left[ P_{b,MSK}(\beta )\right] ^k\right\} = \frac{1}{2^k}\sum _{j=0}^{k}{k\atopwithdelims ()j}(-1)^{j}\left( \frac{\gamma \Omega }{m}\right) ^{(k-j)/2}\nonumber \\{} & {} \frac{\Gamma ((k-j)/2+m))}{\Gamma (m)\Gamma ((k-j)/2+1)}\times _2F_1\left( (k-j)/2,(k-j)/2\right. \nonumber \\{} & {} \left. +m;(k-j)/2+1,-\gamma \Omega /m\right) , \end{aligned}$$
(19)

Proof

Taking into account that for the Rayleigh distribution with PDF as in (1) the BER of DPSK conditioned by \(\beta\) see [19] is given by

$$\begin{aligned} P_{b,DPSK}(\beta ) = \frac{\beta }{2(\gamma +\beta )}, \end{aligned}$$

expression (18) follows by compounding using (15) and taking \(p=\gamma\).

Also, for the Rayleigh distribution, the BER of MSK see [19] and [11, eq. 5.72] is given by

$$\begin{aligned} P_{b,MSK}(\beta ) = \frac{1}{2}\left[ 1-\sqrt{\frac{\gamma }{\gamma +\beta }}\right] . \end{aligned}$$

Thus, making use of the Newton binomial expansion we have that

$$\begin{aligned} \left[ P_{b,MSK}(\beta )\right] ^k=\frac{1}{2^k}\sum _{j=0}^{k}{k\atopwithdelims ()j}(-1)^{j}\left[ \frac{\gamma }{\gamma +\beta }\right] ^{(k-j)/2}. \end{aligned}$$

Now, by compounding, using (16) and taking \(p=\gamma\) we get (19). \(\square\)

Corollary 1

Let \(\gamma =E_b/N_0\), being \(E_b\) the transmitted energy per bit and \(N_0\) accounts for the spectral density of the noise power. Then, the average BER of DPSK and MSK and their variance for the Nakagami-m distribution with PDF given by (3) result,

$$\begin{aligned}{} & {} \bar{P}_{b,DPSK}(\Omega ,m) =\frac{1}{2}\left( \frac{m}{m+\gamma \Omega }\right) ^m,\end{aligned}$$
(20)
$$\begin{aligned}{} & {} \bar{P}_{b,MSK}(\Omega ,m)\nonumber \\{} & {} =\frac{1}{2}\left[ \sqrt{\frac{\gamma \Omega }{m}}\frac{_2F_1\left( 1/2,m+1/2;3/2;-\gamma \Omega /m\right) }{2^{2m-1}B(m,m+1)}-1\right] ,\end{aligned}$$
(21)
$$\begin{aligned}{} & {} var\left[ P_{b,DPSK}(\beta )\right] =\frac{1}{4}\left( \frac{m}{m+\gamma \Omega }\right) ^{2m}\nonumber \\{} & {} \left[ \left( \frac{m}{m+\gamma \Omega }\right) ^{1-m} \frac{m+\gamma \Omega \bar{m}}{m}-1\right] ,\end{aligned}$$
(22)
$$\begin{aligned}{} & {} var\left[ P_{b,MSK}(\beta )\right] =\frac{1}{4}\left[ 1-\left( \frac{m}{m+\gamma \Omega }\right) ^m\right] \nonumber \\{} & {} -m\gamma \Omega \left( \frac{_2F_1(1/2,m+1/2;3/2;-\gamma \Omega /m)}{2^{2m}(2m+1)B(m+1,m+1)}\right) ^2, \end{aligned}$$
(23)

respectively, where \(B(a,b)=\int _0^1 t^{a-1}(1-t)^{b-1}\,dt\) is the Euler Beta function.

Proof

Expressions (20) and (21) are obtained from (18) and (19), respectively by replacing k by 1 and taking into account that \(_2F_1(0,b;c;z)=1\) and

$$\begin{aligned} \frac{\Gamma (m+1/2)}{\Gamma (m)\Gamma (3/2)}=\frac{1}{2^{2m-1}B(m,m+1)}. \end{aligned}$$

Now, (22) and (23) are derived by using the well-known expression for the variance of a random variable, \(var(Z)=\mathrm{I\hspace{-2.2pt}E}(Z^2)-(\mathrm{I\hspace{-2.2pt}E}(Z))^2\), by replacing k by 2 in (20) and (21) which together with the square of (20) and (21) provide the result after some straightforward algebra. \(\square\)

3 Multivariate version of the Nakagami-m distribution

In some occasions wireless communications involve analysis using bivariate and correlated two random variables. In this sense, Rayleigh and Nakagami-m distribution have been used as appropriate distributions (see, for instance [22] and [23]). In this case, the target is to compute the effect of correlation in fading between diversity branches in dual-diversity systems ([24] and [25]; among others). Based on the methodology provided in the previous section we propose a bivariate Nakagami-m distribution which can be considered as an alternative to the bivariate Nakagami-m distribution appearing in [22]. The advantage of our proposal is that does not depends on any special function.

We propose the next definition of a bivariate Nakagami-m distribution which is a natural extension of definition (9)–(10). The bivariate Nakagami-m distribution can be considered as the composite of independent \(R(r_i,\beta )\), \(i=1,2\) combined with the distribution given in (4).

Definition 1

A multivariate Nakagami-m distribution \((r_1,r_2,\dots ,r_s)\) is defined by the stochastic representation,

$$\begin{aligned} R_i|\beta\sim & {} \mathcal{R}(r_i,\alpha _i\beta ),\;i=1,2,\dots ,s\,\, {\text{ independent }},\\ \beta\sim & {} \pi (\beta ), \end{aligned}$$

where \(\alpha _i>0\), \(i=1,2,\dots ,s\). Observe that \(R_i\) (\(i=1,\dots , s\)) share the same parameter \(\beta\).

With this definition, and using similar arguments to those used in Theorem 1 we get that the joint multivariate PDF is given by,

$$\begin{aligned}{} & {} f_{R_1,R_2,\dots , R_s}(r_1,r_2,\dots ,r_s)\nonumber \\{} & {} \quad=\int _{m/\Omega }^{\infty }\prod _{i=1}^{s}\left[ 2\alpha _i\beta r_i \exp \left( -\alpha _i\beta r_i^2\right) \right] \,d\beta \nonumber \\{} &\quad {} =\frac{\left( \prod _{i=1}^{s}2 \alpha _i r_i\right) (m/\Omega )^s \exp (-\tilde{r} m/\Omega )}{\Gamma (m)}\,\mathcal{U}\nonumber \\{} &\quad {} \left( \bar{m},k+\bar{m},\frac{m \tilde{r}}{\Omega }\right) ,\nonumber \\{} &\quad {} r_1>0,\;r_2>0,\dots , r_s>0, \end{aligned}$$
(24)

where \(\tilde{r}=\sum _{i=1}^s\alpha _i r_i^2\).

As a special case, from (24) and by tanking \(s=2\) we get the bivariate PDF which can be written as

$$\begin{aligned}{} & {} f_{R_1,R_2}(r_1,r_2)\nonumber \\{} & {}\quad =\frac{\left( \prod _{i=1}^{2}2 \alpha _i r_i\right) (\tilde{r})^{m-2}m^m \left[ 1+(m/\Omega )(\tilde{r}-\Omega )\right] }{\Gamma (m)\Omega ^m}\nonumber \\{} & \quad{} \exp \left( -\frac{m\tilde{r}}{\Omega }\right) ,\nonumber \\{} \quad & {} r_1>0,\;r_2>0, \end{aligned}$$
(25)

where \(\tilde{r}=\sum _{i=1}^2\alpha _i r_i^2\) and provided that \(1+(m/\Omega )(\tilde{r}-\Omega )\ge 0\). Its cumulative distribution function (CDF) is written in terms of the incomplete gamma function as

$$\begin{aligned} F_{R_1,R_2}(r_1,r_2)=\frac{\Gamma (m,m \tilde{r}^2/\Omega )}{\Gamma (m)}. \end{aligned}$$

The marginal distributions obtained from (25) are obviously Nakagami-m distributions with PDF’s as in (3), but with parameters m and \(\Omega /\alpha _i\) (\(i=1,2\)). Because the marginal distributions have an explicit expression, the conditional distributions are obtained directly. Thus, marginal moments are the same of the Nakagami-m distribution and cross moment, covariance and correlation are given by,

$$\begin{aligned} \mathrm{I\hspace{-2.2pt}E}(R_1 R_2)= & {} \frac{\pi \,\Omega }{4\sqrt{\alpha _1\alpha _2}},\\ cov(R_1,R_2)= & {} \frac{\Omega }{\sqrt{\alpha _1\alpha _2}}\left\{ \frac{\pi }{4}-\frac{1}{m}\left[ \frac{\Gamma (m+1/2)}{\Gamma (m)}\right] ^2\right\} ,\\ \rho (R_1,R_2)= & {} {\frac{m \pi \Gamma (m)^2-4 \Gamma (m+1/2)^2}{4[m\Gamma (m)^2-\Gamma (m+1/2)^2]}}, \end{aligned}$$

respectively. Note that the correlation depends only on m being a decreasing function and taking values approximately between 0.008 and 0.785. A graph of this expression is displayed in Fig. 1.

Fig. 1
figure 1

Correlation of the bivariate distribution in front of the m parameter

Full size image

Values of the covariance and correlation for selected values of these parameters are shown in Table 1 and some graphics of the bivariate Nakagami-m distribution given in (25) are displayed in Fig. 2 for these parameters. Specifically, graphical representation of the bivariate case are plotted for values of m which provide a wide range of the correlation, near to zero, middle and near to 0.8. Values of the rest of parameters were selected in order to get a wide range of the covariance.

Table 1 Values of the covariance and correlation for selected values of the parameters of the bivariate Nakagami-m distribution
Full size table
Fig. 2
figure 2

Bivariate PDF corresponding to the expression given in (25) for the following parameter values reading from left to right and from top to bottom for the cases 1–6 provided in Table 1

Full size image

4 Numerical experiments

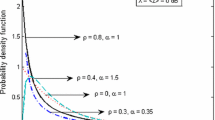
First, we show the numerical agreement between the original Nakagami-m distribution (3) and the one obtained through the Rayleigh composite. In Fig. 3, two cases are illustrated. The integral has been numerically solved by the adaptive Simpson quadrature (Simpson’s rule), which is done in Matlab with the method quad(\(\cdot\)). As it can be seen, as expected, the fitting between the analytical distribution and its composite version is acceptable. Note that, the small differences are due to errors from the numerical approximation of the integral (Theorem 1 assures the exactness of both distributions).

Fig. 3
figure 3

Comparison of the analytic Nakagami-m distribution and the composite one for two sets of parameters. The RMS error is 9.4593e−05 for the left plot and 6.6438e−04 for the right plot

Full size image

In order to apply the distribution to modelling a fading channel, it is necessary to know how to simulate the distribution. In this case, although the composite version can be used to get the random variables, it is computationally more efficient to simulate the original Nakagami-m distribution. By using Matlab, a \(N\times 1\) vector with samples following the Nakagami-m distribution with parameters ‘mu’ and ’omega’ is easily obtained by “pd = makedist(‘Nakagami’,‘mu’,m,‘omega’,omega)” and, “random(pd,N,1)”. If Matlab is not available, in the literature there is a plethora of methods to simulate a random variable following a statistical distribution. We follow the same method used in [20], applying the standard inverse transform method. This method can be efficiently programmed. In Algorithm 1 a simplified version of the inverse transform method is summarized. The cdf (cumulative density function) is given by,

$$\begin{aligned} F(r;m,\Omega )= P\left( m,\frac{m}{\Omega }r^2\right) , \end{aligned}$$

where P is the regularized (lower) incomplete gamma function. Indeed what is used is \(1 - F(r;m,\Omega )\), which is obtained at low computational cost and can be even pre-calculated for a set of m and \(\Omega\) parameters to speed up the numerical simulation.

Algorithm 1
figure c

Simulating the Nakagami-m distribution

Full size image

In Fig. 4, it can be seen the comparison for the Nakagami-m PDF’s (evaluating directly its PDF) and the one obtained from Monte Carlo simulations, which clearly shows a good fit. Apart from the visual evaluation, a measure of its excellent fitting is provided by comparing the analytic mean (0.6094) and variance (0.1286) values and the corresponding ones from the numerical simulation (0.6046 and 0.1284, respectively). As expected, the error is significantly small (\(\approx 0.7\%\) and \(\approx 0.1\%\)) for both statistical measures. It is remarkable to note that, deep fading mechanisms (larger than 60 dB) are present, what, as it well-known assures that the Nakagami-m distribution naturally accounts for the presence of large fading, which implies that minimum power is reaching the receiver.

Fig. 4
figure 4

Comparison of the analytic Nakagami-m distribution and the numerical simulation (left) and, (right) simulated samples (200 000)

Full size image

In Fig. 5, it can be seen the comparison for the MSK BER in Nakagami-m distribution AWGN (Additive White Gaussian Noise) fading for the theoretical case (using (21)) and the numerical simulation of the fading channel. The bit length of the simulated signal is 200 000 and the bit energy is \(E_b = 1\). This figure clearly shows consistent fitting along the whole range for both curves.

Fig. 5
figure 5

Comparison of the analytic BER for MSK modulation and the numerical simulation in Nakagami-m distribution AWGN fading channel

Full size image

5 Conclusion and further results

A three parameter generalization of the Nakagami-m distribution was studied by [26] and also  [27] obtained from the latter by the change of variable \(r\rightarrow r^{1/s}\), \(s>0\). This distribution can be obtained also by composite the Rayleigh distribution, after the previous change of variable, and calculate the integral

$$\begin{aligned} f_R(r;\Omega ,m,s)= & {} \int _{m/\Omega }^{\infty }2\beta s r^{2s-1}\exp \left( -\beta r^{2s}\right) \pi (\beta )\,d\beta \nonumber \\= & {} \frac{2s m^m r^{2ms-1}}{\Gamma (m)\Omega ^m}\exp \left( -\frac{m r^{2s}}{\Omega }\right) , \quad r>0. \end{aligned}$$
(26)

Finally, a bivariate generalized Nakagami-m distribution can be built in a similar way by using the same argument that the one provided in Sect. 3, but replacing in (25) \(2\beta s r^{2s-1}\exp \left( -\beta r^{2s}\right) \pi (\beta )\) by \(\prod _{i=1}^{2}2\beta s_i r^{2s_i-1}\exp \left( -\beta r^{2s_i}\right) \pi (\beta )\) in order to get a bivariate version of (26) with marginals being again generalized Nakagami-m distributions. This new formulations is going to fit experimental data in the tail better that the bivariate Nakagami-m distribution.