Abstract
Climate change and drought phenomena impacts have become a growing concern for water resources engineers and policy makers, mainly in arid and semi-arid areas. This study aims to contribute to the development of a decision support tool to prepare water resources managers and planners for climate change adaptation. The Hydrologiska Byråns Vattenbalansavdelning (The Water Balance Department of the Hydrological Bureau) hydrologic model was used to define the boundary conditions for the reservoir capacity yield model comprising daily reservoir inflow from a representative example watershed with the size of 14,924 km2 into a reservoir with the capacity of 6.80 Gm3. The reservoir capacity yield model was used to simulate variability in climate change-induced differences in reservoir capacity needs and performance (operational probability of failure, resilience, and vulnerability). Owing to the future precipitation reduction and potential evapotranspiration increase during the worst case scenario (−40% precipitation and +30% potential evapotranspiration), substantial reductions in streamflow of between −56% and −58% are anticipated for the dry and wet seasons, respectively. Furthermore, model simulations recommend that as a result of future climatic conditions, the reservoir operational probability of failure would generally increase due to declined reservoir inflow. The study developed preparedness plans to combat the consequences of climate change and drought.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
It is expected that climate variability will intensify the water resources stress (IPCC, 2014) such as the alteration in the river flow seasonality (Vicuna and Dracup, 2007; Minville et al. 2009) as well as reservoir planning properties (capacity) and performance (reliability, resilience and vulnerability). Such change is likely to lead to a negative effect on water resources management.
A growing number of researchers have explored climate change impacts on reservoirs (Fowler et al. 2003; Li et al. 2010; Park and Kim 2014). The majority of these scientists argued that due to climate change, there will be an increase in the storage capacity requirements in addition to the deterioration of its performance. Only a few researchers have focused on reservoir management adaptation to climate variability (McMahon et al. 2006; Li et al. 2010; Minville et al. 2009) and confirmed that the impact of such change on streamflow should be considered through a re-examination of reservoir operating rules.
The vast majority of researchers have investigated climate change impacts based on the results of large-scale general circulation models (GCM) that have been downscaled to the basin-scale applying statistical or regional (i.e. dynamical) downscaling procedures. However, Chen et al. (2011) claimed that there are many sources of uncertainty involved in climate change studies and the major sources of uncertainty are linked to GCM and greenhouse gasses emissions scenarios (GGES) in addition to the uncertainties that stem from a downscaling method. Therefore, to avoid the GCM and downscaling uncertainties and challenges, many studies (e.g., Tigkas et al. 2012; Vangelis et al. 2013; Reis et al. 2016) proposed delta perturbation (change factor) concepts, in which plausible alterations in meteorological variables are assumed. Then, by using a suitable rainfall-runoff model, the impacts of these changes on the streamflow can be predicted.
1.2 Aim, Objectives and Novelty
The aim of this research is to develop a methodology that can be used as part of a decision support tool to enable engineers and policy makers to prepare effectively for climate change adaptation, particularly in arid and semi-arid regions. The prime objectives are to (1) estimate the anticipated climate change impacts on runoff; (2) calculate the probable relative alteration in the annual streamflow availability of the downstream country under the collective impacts of climate change; (3) predict standardised reconnaissance drought index (RDIst) and streamflow drought index (SDI) values under the collective climate change impacts; (4) derive the anticipated relationships that link RDIst and SDI with the potential future variations of precipitation (P) and potential evapotranspiration (PET); (5) evaluate the reservoir operational probability of failure (OPOF) under the collective climate change impacts; and (6) develop relationships that integrate capacity-yield-reliability.
This research characterises the climate change impact uncertainties linked to the planning of reservoirs utilising a methodology similar to that described by Soundharajan et al. (2016). The main variations between the two studies are that a rainfall-runoff model is used to simulate the streamflow series rather than stochastic modeling that as used by Soundharajan et al. (2016). In addition, Soundharajan et al. 2016 did not take into consideration the reservoir capacity-yield-reliability relationships, which have been considered here. Consequently, the key purpose of this study is to assess the potential impacts of climate change on basin hydrology by considering the impacts of the reservoir operational probability of failure and storage in the water resources system on a typical example reservoir, which is the Dokan multi-purpose dam located in northern Iraq. The study attempts to answer the following question: How well would the adaptation measures, whether they are structural or non-structural, work across the range of climate change uncertainty? Successful adaptation measures may subsequently be used as supporting tools in mitigating climate change impacts on water resources. This is a first attempt to derive the capacity-yield-reliability relationships that can be used as part of an adaptation strategy for climate change by characterising the variability of reservoir storage and performance indices.
1.3 Case Study Description
The Lower Zab River (also known as Little and Lesser Zab) is one of the main streams of the Tigris River in the Erbil governorate located in the north-east of Iraq. The river and its tributaries are situated between latitudes 36°50′ N and 35°20′ N, and longitudes 43°25′ E and 45°50′ E (Mohammed and Scholz 2016); Fig. 1. The River originates from the Zagros Mountains in Iran and flows about 370 km southeast and southwest through north-western Iran and northern Iraq before joining the Tigris near Fatha city, which is located about 220 km north of Baghdad (Mohammed and Scholz 2016), with a total length of approximately 302 km. The catchment area of the River is approximately 19,254 km2 with nearly 76% located in Iraq. The mean annual storage of the river at Dokan and Altun Kupri-Goma is about 6 billion cubic meters (BCM) and 7.8 BCM in this order (Mohammed et al. 2017); Fig. 1. Dokan is the main dam that has been constructed within the upstream portion of the basin. The main function of the dam is to control the discharge of the Lower Zab, store water for irrigation purposes and to provide hydroelectric power.
2 Material and Methods
2.1 Identification of Drought
Drought is considered one of the leading water-related hazards (Mohammed and Scholz 2017). For drought identifying and quantifying there are many recommended approaches. However, indices are considered as one of the most popular methods (Vangelis et al. 2013; Mohammed and Scholz 2017). A high number of meteorological drought indices with different intricacy have been utilised in various climatic conditions (Mohammed and Scholz 2017). Latest drought trend studies (Sheffield et al. 2012; Vicente-Serrano et al. 2014) and drought scenarios under possible climate change predictions (e.g., Cook et al. 2014) depend on indices that take into consideration evapotranspiration and precipitation such as the reconnaissance drought index (RDI), which is considered in this study.
2.1.1 Reconnaissance Drought Index
The RDI is a newly developed meteorological drought index, which is mainly applied in arid and semi-arid geographical regions. The RDI is based on P, which is observed, and the PET, which is estimated. Tigkas et al. (2015) introduced a brief overview of the theoretical basis of RDI together with some practical applications with a specialised software package called drought indices calculator (DrinC).
This RDI can be formulated as the alpha (RDIαk), normalised (RDIn) and standardised (RDIst) forms. The RDIst is frequently applied for drought severity evaluations, whereas RDIαk can be applied as an aridity index, which is mainly founded on the aggregated P and PET theories (Vangelis et al. 2013; Mohammed and Scholz 2017). The RDI is normally estimated using Eq. (1).
where Pij and PETij represent precipitation and potential evapotranspiration of the jth month of the ith water year, which in Iraq starts in October, and N is the climate data total year number.
The values of RDIαk match both the gamma and the lognormal distributions in various positions for a variety of examined time scales. Through applying the former distribution, RDIst can be calculated applying Eq. (2).
where yi is the ln(αki), \( \overline{\mathrm{y}} \)ӯ is its arithmetic mean and σy is the corresponding standard deviation.
Equation (3) can be applied to compute RDIst in the gamma distribution application.
where γ and β are the shape and scale parameters, respectively, and Γ(γ) is the gamma function. The spatiotemporal extent of the gamma probability distribution parameters γ and β can be predicted for 3, 6, 9 and 12 months. The γ and β are estimated by the maximum likelihood method as shown in Eqs. (4) to (6).
When the cumulative precipitation data sets for the selected reference period contains zeros, the gamma function cannot be defined for x = 0. Therefore, a composite cumulative probability function (Eq. (7)) might be utilised.
where q is the likelihood of zero precipitation and G(x) is the gamma distribution cumulative probability. The probability of zero precipitation (q) can be computed by m/N if m is zero in the αk time series. The gamma distribution cumulative probability G(x) is replaced by the cumulative probability H(x).
A positive value of RDIst relates to a wet period. On the other hand, a negative value is indicative of a dry period in comparison to the natural conditions of the region. Drought severity phenomena increase when RDIst values are minimal. The severity of drought can be classified into (extremely, severely, moderately) dry, near normal, normal, (moderately, very and extremely) wet classes based on the corresponding boundary RDIst value ranges ≤ −2.00, −1.5 to −1.99, −1 to −1.49, 0.00 to −0.99, 0.99 to 0.00, 1.49 to 1.00, 1.99 to 1.5, and ≥2.00, respectively (Tigkas et al. 2012; Vangelis et al. 2013; Mohammed and Scholz 2017).
2.1.2 Hydrological Drought Index
Given a monthly time series streamflow storage Vij for a specific water year, the corresponding cumulative value can be obtained according to Eq. (8), which was developed by Nalbantis (2008).
where Sij is the aggregate streamflow storage for the ith water year and the kth reference period, k = 1 for the period October–December, k = 2 for October–March, k = 3 for October–June, and k = 4 for October–September.
The SDI founded on the discharge aggregated capacities Si , k for each period k of the ith water year can be defined according to Eq. (9).
where \( {\overline{\mathrm{M}}}_{\mathrm{k}} \) and SDk are the cumulative streamflow storage means and the standard deviation of the period k, respectively, since they are calculated over a long time. Although many values founded on logical criteria could be used, the truncation level is set to \( {\overline{\mathrm{M}}}_{\mathrm{k}} \) in this definition.
For most small basins, the streamflow follows a skewed probability distribution. This can be estimated by gamma distribution functions. The distribution is then converted into normal. Appling the two-parameter lognormal distribution, the SDI index is defined as shown in Eq. (10).
where the natural logarithms of cumulative streamflow with mean \( \overset{\_}{{\mathrm{y}}_{\mathrm{k}}} \)and standard deviation Sik can be estimated according to Eq. (11).
A value of SDI greater than zero relates to a non-drought period. In comparison, a negative value is indicative of a drought period in comparison to the natural conditions of the study region. The hydrological drought severity phenomena increase when SDI values are minimal, and it follows that the same classification for drought severity can be used as the one for the RDI index. Usually, an integer number from 0 (non-drought) to 4 (extreme drought) is considered.
2.1.3 Reservoir Capacity-Yield Simulation and Performance Indices
As a first step for reservoir capacity-yield (RCY) performance evaluation, the Hydrologiska Byråns Vattenbalansavdelning (HBV) rainfall-runoff models were calibrated depending on the recorded dataset of the baseline period. The HBV is an example of a semi-distributed conceptual model simulating daily discharge depending on daily rainfall, temperature, and potential evaporation as input. Air temperature data are used for calculating snow accumulation. Subsequently, the RCY simulation was performed applying Eq. (12) (McMahon and Adeloye 2005)
where St+1 and St are reservoir storage volumes at the end and beginning of a time period t, respectively; Qt is the inflow over period t; Dt is the actual water yield over the period t; ΔEt is the reservoir net evaporation loss within the period t; Lt represents other losses; and C is the reservoir active capacity.
During the simulation procedures, the reservoir So is typically assumed to be full (McMahon and Adeloye 2005), and the downstream demand is usually considered as a specific fraction of the mean inflow. The usual period is one month, but any other period can be used. The calculation of the reservoir OPOF can be summarised as follows: (a) assume the reservoir is initially full (So = C); (b) apply Eq. (12) month by month on the historical flows; (c) plot (St+1) against time on a monthly time scale; and (d) compute the OPOF by using Eq. (14).
The storage size estimated through RCY analysis varies little with the starting month. By the RCY analysis, the vulnerability of the reservoir is estimated by ignoring the constraint on Eq. (12) and then choosing the maximum negative value of (St+1) during the analysis period, whereas the resilience is estimated by computing the maximum consecutive number of empty months during the analysis (Moy et al. 1986).
Following simulation, three appropriate performance measures were assessed (McMahon and Adeloye 2005; McMahon et al. 2006): (1) The time-based reliability (Re) can be defined as the percentage of the entire period under investigation during which a reservoir is capable of providing the full demand without any deficiencies, as indicated in Eq. (13).
where Re is the reservoir reliability (%) and OPOF is the operational probability of failure (%), which is defined as the ratio of time units during which the reservoir is effectively empty to the total number of time units applied in the analysis (Eq. (14)).
where Ne is the time unit number during which the reservoir is empty, and N is the total number of time units in the streamflow time series. There is no limitation on the OPOF but many studies considered 5% to be an acceptable limitation (McMahon and Adeloye 2005).
(2) The resilience ρ describes the reservoir’s ability to recover from failure and can be expressed based on Eq. (14) as discussed previously (Fowler et al. 2003; Park and Kim 2014). Moy et al. (1986) defined it as the maximum number of consecutive periods of shortage that occur prior to recovery.
where Yt is the number representing the continuous shortage indicator, Yt = 1, if there is a shortage during period t, Yt = 0, and t = 1, 2, …, N, which is the total number of time units in the stream flow time series sequence of failure periods.
(3) The vulnerability ν is a criterion to determine the significance of failure. Mathematically, it is expressed by Eq. (16) as shown in the past (Fowler et al. 2003; Park and Kim 2014).
where v is the system vulnerability, and Dft is the deficit at time t (McMahon and Adeloye 2005; McMahon et al. 2006).
2.1.4 Data Availability and Methodology Application
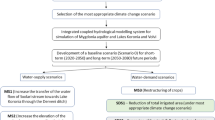
Figure 2 reveals the considered methodology and visualises how the research objectives can be integrated, which can be summarised in the following seven steps:
-
(1)
Thirty-five hydrological years (1979–2013) were utilised to estimate the RDIst values, specify the normal climatic conditions and then evaluate the regression coefficients a1, b1, a2, and b2 of Eqs. (17) and (18).
where RDIst, RDIα12, and SDI are the RDI standardised form, the RDI alpha representation, and the streamflow drought index, respectively.
-
(2)
Using daily P, T, and PET, the HBV model was calibrated and validated for the normal water years.
-
(3)
For assessing the model performance, the following criteria have been used (Eqs. (19) to (22)):
where RMSE is the root mean square error (dimensionless), IoA is the index of agreement (dimensionless), r is the correlation coefficient (dimensionless), MAE is the mean absolute error, Robs(i) is the recorded streamflow (mm/month) at time step i, Rsim(i) is the predicted streamflow (mm/month) at time step i, \( {\overline{\mathrm{R}}}_{\mathrm{obs}} \) is the average amount of the recorded values (mm/month), and n is the data point number.
-
(4)
The delta perturbations in P (dP) of 0–40% (2% step) and PET perturbations (dPET) of 0–30% (2% step) were used for the streamflow alteration analysis. Twelve years (1988–2000), which are characterised by an average value of RDIst close to zero, were applied for running the climate change scenarios. Although the delta perturbations method does not accommodate future alterations in the probability distribution of climatic characteristics and seasonality (and therefore the streamflow), it is, however, an effective technique in detecting tipping points at which a water storage structure such as a reservoir is expected to fail disastrously in providing water demand.
-
(5)
The expected relative alteration in the annual streamflow (%) depends on each climate change scenario, which was estimated relative to the reference average annual streamflow.
-
(6)
The predicted streamflow series input to the RCY model. The corresponding outputs of the model are evaluated using the indicators of reliability, resilience, and vulnerability, with reference to the imposed demands.
-
(7)
The RCY model has been utilised to develop the capacity-yield-reliability relationship for the selected time period (the 2020s). The first relation linked yield (%) with OPOF (%), and the second linked capacity(106 × m3) with yield(%). These relations can be applied to test various adaptation strategies, whether they are structural or non-structural, against the range of different future scenarios to select the most effective adaptation measures.
3 Results and Discussion
3.1 Rainfall–Runoff Simulation
In this section, the obtained results will be identified and discussed. Descriptions of the hydrological simulation results, drought and climate change impacts, and basin water supply future performances will be provided.
The HBV model has been calibrated and validated for the periods of 1988–1999 and 1979–1986, respectively. The statistical performance indicators RMSE, IoA, r and MAE during calibration were 0.73, 0.99, 0.93 and 0.65 in this order. The corresponding values were 0.68, 0.99, 0.84 and 0.60 during the validation period. Simulation results show promising outcomes emphasising that the simulation can be confidentially applied for more studies such as simulating the artificial climatic scenarios and estimating the relative alteration (%) in the average annual streamflow relative to the normal climatic conditions. The simulated runoff for the studied period against the observed one is visualised in Fig. 3a. The coefficients associated with Eqs. (17) and (18) are shown in Fig. 3b and c in that order.
a Observed against simulated streamflow time series using the Hydrologiska Byråns Vattenbalansavdelning model (Note that there was an outlier (1570 m3/s), which has been removed.); b The Lower Zab River Basin (LZRB) anticipated relationship of the standardised reconnaissance drought index (RDIst) and RDI alpha form; c The LZRB anticipated relationship of streamflow drought index (SDI) and runoff; d The selected simulation period for climate change scenarios; and e The LZRB anticipated (%) streamflow change for selected climate change scenarios
3.2 Drought and Climate Change Impacts
Figure 3d shows the period of time that has been selected for the simulation. Based on the simulation results, Fig. 3e reveals that there will be a substantial reduction in the streamflow due to the potential impacts of climate change, which in turn would result in a dramatic alteration on the LZRB water resources availability. For example, a change of almost −21% in terms of streamflow is expected to result in an anticipated climate condition of −10% P and +30% PET. The research outcomes indicated that there is a crucial requirement for pro-active strategies and actions to mitigate climate change influences, anthropogenic interventions, and drought events. Furthermore, Fig. 4a and b demonstrate that the anticipated RDIst and SDI relationships are subject to the potential impact of future P reduction under the collective effects of PET. Fig. 4c demonstrates that both RDIst and SDI changes depend on drought severity in the same way.
3.3 Future Performance of Water Supply
Figure 5 shows the reservoir inflow magnitude and timing, which prove how climate change will strongly lead to the reduction in the reservoir inflow. In the worst case scenario, substantial variations in inflow between −56% and −58% are anticipated for the dry and wet seasons, respectively. The inflow peak will decline, and there will be a marked shift in their magnitude, which can result in a dramatic effect on basin water resources availability.
One of the research objectives is an evaluation of water supply performance sensitivity on water scarcity brought about by climate change. For all considered scenarios, the future demand for water is assumed to continue without major change with respect to the baseline period. The climate change influence on the Dokan dam operation and its water system were assessed by entering modeled future inflows into the RCY model while maintaining the existing operating procedures. In order to simulate the operations of the Dokan reservoir, the HBV simulations of daily streamflow were applied to mimic water resources in the RCY model. The delta perturbations of climate change scenarios were applied. Then, the RCY model was run to assess the potential impacts of climate change on water resources availability, indicators and water supply capacity. After that, indicators were used for both the climate change scenarios and the baseline periods (Fig. 6a).
Table 1 presents a summary of the potential performance of the water resources system. It is important to note that the reliability of the water supply system is generally high during the baseline scenario. The reliability and resilience will decline, while the vulnerability will increase as a result of P reduction. However, Fig. 6b and Table 2 show that the volume required to meet the increase in water demand due to the decline of P and runoff. A 4% P decrease can mean that the existing volume is too little (by as much as 29% for a water yield of 82%), as an example. Moreover, the uncertainty or variability of the reservoir performance is characterised by Cv; i.e. the standard deviation divided by the mean. The uncertainty (Cv) of the OPOF, resilience, vulnerability and the required capacity varied between 0.78–0.07, 0.55–0.40, 0.87–0.47 and 0.46–0.10, respectively, which indicate that their uncertainty/variability increase as the basin become drier.
The so-called ‘operational failure’ rates have been determined for each model run and climate change scenario, which led to an amount of OPOF/reliability for each unit time per scenario. The successive range of OPOF involves the possible range of climate change impacts upon the water resources system over the chosen period. As the simulation results indicate that through combining adaptation measures, whether they are structural or non-structural, into water resources simulation (supply side), their effectiveness will be determined across a range of climate change and climate change variability by evaluating how each of the simulations react to a given adaptation strategy in terms of decrease (or otherwise) of OPOF, and how much of the distribution is moved away from a pre-determined and undesirable level of hazard. The developed approaches can be used to evaluate how well an adaptation measure would work within the uncertainty of a climate change range, and can, therefore, be used as a support tool for managing water resources.
Based on the results of this representative case study, an adaptation operational approach can be inferred, where the policy makers, in particular, in the semi-arid and arid regions, adjust the reservoir operating rules based on inflow estimations and the current state of reservoir capacity at each specified period, which can result in a more effective and viable management of reservoirs. In order to achieve this, the RCY model has been utilised to derive the capacity-yield-reliability relations for the 2020s period. The first one concerns the yield-OPOF relationships (Table 2), and the second considers the capacity-yield (Table 2). These relationships can be used to test various options against the range of different future scenarios to select the most effective adaptation measure or measures, whether they are structural or non-structural. For example, if the decision-makers target is to supply water for the downstream within 5% OPOF, then by using the first graph they can obtain two values of the expected rate of yield within the range of climate change scenarios. Then, using the second operational tool, they can investigate whether there will be a need to adapt either a structural or non-structural measure.
4 Conclusions and Recommendations
Based on the representative case study for arid and semi-arid regions results, it can be inferred that an adaptation operational method, where the policy makers adjust the reservoir operating rules, based on the predicted inflow and the current state of reservoir capacity at each specified period. This can result in a more effective and viable management of the reservoir. This study tried to estimate the potential impacts of climate change on the Dokan reservoir operation, which is located in a semi-arid region using the HBV and RCY models under delta perturbations of climate change scenarios.
One of the most important impacts of the anticipated climate variation in the reservoir area is the alteration of the hydrologic environment and the performance of the water resources system if the present operation modes remain to be used. The HBV model outputs recommend a critical decrease in the values of the Dokan reservoir inflow due to a decrease in P and increase in the PET, which in turn decreases the current capacity. For instance, a reduction of about 21% in streamflow is expected to result in 10% P reduction and 30% PET increase. Additionally, for the worst case scenario, a substantial decline in inflow ranged between 56% and 58%, are estimated for the dry and wet seasons in this order. The inflow maximum magnitude will decrease, and there will be a noticeable shift in their values, which can cause a dramatic effect on basin water resources availability. Moreover, a 4% P decrease can mean that the existing capacity is too little (by as much as 29% for a water yield of 82%). Variations in reservoir inflow will impact on water utilisation purposes such as water supply, hydropower, irrigation, downstream water quality enhancement and recreational uses. Accordingly, to moderate the negative hydrologic influences and to apply the positive effects, the potential climate change impact should be examined by water resources organisations in the future.
Alterations in future monthly reservoir inflows require modifications of some of the reservoir management processes to use water more efficiently. If existing operational rules continue to be operated unchanged, projected climate change would further lead to a decline in the ability to supply water to all stakeholders. In addition, the research results show potential decreases in the water supply reliability and increases in the resilience to nearly 22% and 86%, respectively, due to dam inflow decreases. However, with higher mean temperatures and extended crop growing periods, it is expected that the demands for irrigation would also rise, which will intensify the increasing demand, owing to an increase in population. Therefore, any alteration that would improve the ability of the system to accomplish the water needs for one sector would essentially require compromises from other stakeholders. Subsequently, it is essential to assess the monthly water supply to get the most out of profit, which means that the supply system organised by the multi-purpose reservoir should have operating policies that can be adjusted to potential hydrological and climatic alterations. The inflow increase will provide the chance to reallocate preservation storage under a climate change scenario.
The estimation of the existing water demand in the RCY model is a study limitation. Despite the fact that water demand prediction is vital to evaluate water resources systems in the future, this project and its outcomes should be seen as an initial examination of the climate change impacts on the dam water supply reliability. In order to facilitate adaptation to climate change, basin managers ought to have a quantitative basis for establishing the adaptation strategies. Accordingly, results provide a basis for enabling future water resources system managers and planners of the Dokan reservoir and similar case studies, in particular, in arid and semi-arid regions to adapt to climate change.
References
Chen J, Brissette FP, Leconte R (2011) Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J Hydrol 401(3–4):190–202. doi:10.1016/j.jhydrol.2011.02.020
Cook BI, Smerdon JE, Seager R, Coats S (2014) Global warming and 21st century drying. Clim Dyn 43(9–10):2607–2627. doi:10.1007/s00382-014-2075-y
Fowler HJ, Kilsby CG, Connell PEO (2003) Modeling the impacts of climatic change and variability on the reliability, resilience, and vulnerability of a water resource system. Water Resour Res 39(8):1222. doi:10.1029/2002WR001778
IPCC (2014) Intergovernmental panel on climate change. Climate change 2014: impacts, adaptation, and vulnerability. http://www.ipcc.ch/report/ar5/wg2. Accessed 15 May 2015
Li L, Xu H, Chen X, Simonovic SP (2010) Streamflow forecast and reservoir operation performance assessment under climate change. Water Resour Manag 24:83–104
McMahon TA, Adeloye AJ (2005) Water resources yield. Water Resources Publications, Littleton
McMahon TA, Adeloye AJ, Zhou SL (2006) Understanding performance measures of reservoirs. J Hydrol 324:359–382
Minville M, Brissette F, Krau S, Leonte R (2009) Adaptation to climate change in the management of a Canadian water resources system exploited for hydropower. Water Resour Manag 23:2965–2986
Mohammed R, Scholz M (2016) Impact of climate variability and streamflow alteration on groundwater contribution to the base flow of the Lower Zab River (Iran and Iraq). Environ Earth Sci 75:1392. doi:10.1007/s12665-016-6205-1
Mohammed R, Scholz M (2017) The reconnaissance drought index: a method for detecting regional arid climatic variability and potential drought risk. J Arid Environ (in press)
Mohammed R, Scholz M, Zounemat-Kermani M (2017) Temporal hydrologic alterations coupled with climate variability and drought for transboundary river basins. Water Resour Manag 31:1489–1502. doi:10.1007/s11269-017-1590-0
Moy W, Cohon JL, ReVelle CS (1986) A programming model for analysis of the reliability, resilience, and vulnerability of a water supply reservoir. Water Resour Res 22(4):489–498
Nalbantis Ι (2008) Drought and streamflow. Eur Water 23(24):65–76
Park JY, Kim SJ (2014) Potential impacts of climate change on the reliability of water and hydropower supply from a multipurpose dam in South Korea. J Am Water Resour Assoc (JAWRA) 50(5):1273–1288
Reis J, Culver TB, Block PJ, McCartney MP (2016) Evaluating the impact and uncertainty of reservoir operation for malaria control as the climate changes in Ethiopia. Clim Chang 136:601–614. doi:10.1007/s10584-016-1639-8
Sheffield J, Wood EJ, Roderick ML (2012) Little change in global drought over the past 60 years. Nature 491:435–438
Soundharajan BS, Adeloye AJ, Remesan R (2016) Evaluating the variability in surface water reservoir planning characteristics during climate change impacts assessment. J Hydrol 538:625–639. doi:10.1016/j.jhydrol.2016.04.051
Tigkas D, Vangelis H, Tsakiris G (2012) Drought and climatic change impact on streamflow in small watersheds. Sci Total Environ 440:33–41
Tigkas D, Vangelis H, Tsakiris G (2015) DrinC: a software for drought analysis based on drought indices. Earth Sci Inform 8(3):697–709. doi:10.1007/s12145-014-0178-y
Vangelis H, Tigkas D, Tsakiris G (2013) The effect of PET method on reconnaissance drought index (RDI) calculation. J Arid Environ 88:130–140
Vicente-Serrano SM, Lopez-Moreno JI, Beguería S, Lorenzo-Lacruz J, Sanchez-Lorenzo A, García-Ruiz JM, Azorin-Molina C, Morán-Tejeda E, Revuelto J, Trigo R, Coelho F (2014) Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ Res Lett 9(4):044001. doi:10.1088/1748-9326/9/4/044001
Vicuna S, Dracup JP (2007) The evolution of climate change impact studies on hydrology and water resources in California. Clim Chang 82:327–350. doi:10.1007/s10584-006-9207-2
Acknowledgements
The research has been financed by the Iraqi government via a Ph.D. scholarship for the lead author via Babylon University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mohammed, R., Scholz, M. Adaptation Strategy to Mitigate the Impact of Climate Change on Water Resources in Arid and Semi-Arid Regions: a Case Study. Water Resour Manage 31, 3557–3573 (2017). https://doi.org/10.1007/s11269-017-1685-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11269-017-1685-7