Abstract
An adhesive elliptical contact is normally found in microscale applications that involve cylindrical solids, crossing at an angle between 0° and 90°. Currently, only one model is available to describe the elliptical contact’s surface interaction: the approximate Johnson–Kendall–Roberts (JKR) model which is limited to soft materials. In this paper, a new adhesive elliptical model is developed for a wide range of adhesive contacts by extending the double-Hertz theory, where adhesion is modeled by the difference between two Hertzian pressure distributions. Both Hertzian pressures are assumed to have an equivalent shape of contact areas, the only difference being in size. Assuming that the annular adhesive region is obtained by the area difference between the two Hertzian contact areas, the pull-off force curves can be calculated. In the limiting case of an adhesive circular contact, the results are very close to results from the existing models. However, for an adhesive elliptical contact in the JKR domain, lower pull-off forces are predicted when compared to the JKR values. Unlike the developed model, the shape of the JKR contact area varies throughout contact. Results show, particularly for conditions close to the JKR domain, that it is important to take into account that the adhesive region is the result of the two Hertzian contact areas having a non-equivalent shape.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Surface adhesion is important in the mechanics of surface contacts, in particular at microscale [1,2,3,4], as a result of high surface area-to-volume ratios [5]. Various models have been developed to describe the adhesive contact between surfaces. In the context of modeling smooth surfaces, three important adhesive contact theories exist: (1) the Johnson–Kendall–Roberts (JKR) model [6]; (2) the Derjaguin–Muller–Toporov (DMT) model [7], which was later corrected by Muller et al. [8]; and (3) the Maugis–Dugdale (MD) model [9]. In the case of a circular contact, the JKR model relies on the assumption that short-range adhesion forces act within the contact area. Conversely, in the DMT model, long-range adhesion forces are assumed to act outside the contact area. Later, it was found that the DMT model and the JKR model had different pull-off predictions. This debate continued until a finding by Tabor [10] revealed that both theories were actually complementary. Solid materials with low surface energy are particularly suited to using the DMT model, while the JKR model is suitable for soft materials with high surface energy values. The important criterion to distinguish between the DMT model and the JKR model is the neck formation outside the contact area. The Tabor parameter μ is used to measure the ratio of neck height to the equilibrium separation [10]. For high values of μ, the adhesion forces outside the contact area can be disregarded as the surfaces are totally separated. This behavior perfectly describes the JKR contact [6]. As in the case of small μ values, the presence of adhesion forces is significant outside the contact area, as shown by the DMT model [7].
The transition between the DMT model and the JKR model is completed by the intermediate MD model that befits a wider range of common materials. Solutions from the MD model can be obtained analytically by solving a set of equations simultaneously. Greenwood and Johnson developed another transition model known as the double-Hertz (DH) model [11]. Not only has that model been proven to be feasible by producing similar results to those from the MD model, but it is also more straightforward in terms of mathematical formulations. All the models mentioned above have been extended for the application of line contacts, as shown by [12] with a JKR-based foundation and [13, 14] for cohesive MD models. The extension of the DH model was developed in [15]. Since its development, the DH model has been extended to various applications such as random multi-asperity contacts [16] and a sinusoidal wavy surface [17].
At present, there is only one contact model that can describe the mechanics of an adhesive elliptical contact, namely the approximate JKR model [18]. The model is built on the assumption that both major and minor axes have identical values of the stress intensity factor at the edges of the contact. This assumption is to avoid the separation at both ends of the major axis, while the stress intensity factor at both edges of the minor axis remains lower than the critical value. The shape of the elliptical contact area is shown to vary with the applied load. This behavior is different from that predicted by the Hertz theory in which the ellipse’s growth rate remains radially constant as the load varies. Validations for the elliptical JKR model have been conducted by several researchers, either by experimental or numerical studies. A finding in [19] shows that the difference between the pull-off forces from the experimental data and the model becomes prominently greater as the contact area approaches a slim elliptical shape. The same result was also reported in numerical simulations in [20]. It is found that in contrast to the JKR elliptical theory, the pull-off forces decrease as the skew angles become smaller in the numerical simulations.
For circular contacts, prediction of the contact behavior in the adhesive region is straightforward with constant deformations throughout the periphery. In the case of elliptical contacts, it is clearly a complex contact, involving various contact geometries, ranging from nearly circular to slim elliptical contacts. The ellipticity ratio β is introduced to illustrate the deviation of the ellipse from the circular shape, given as:
From Eq. (1), the values of the ellipticity ratios are found to be within the range of 0 < β < 1 where β values closer to one have nearly circular contact areas, which are equivalent to having a nearly 90° angle between the cylinders. β values closer to zero have contact areas with shapes that resemble line forms, due to really small skew angles. The shape variations of an elliptical contact are shown schematically in Fig. 1.
The current work focuses on extending the DH model for adhesive elliptical contacts with high initial ellipticity ratios β 0 ranging from 0.8 to 0.99. The developed model is expected to behave similarly to the current adhesive models in the limiting case of circular contacts within the range of 0.5 ≤ μ ≤ 5. In this paper, both contact and adhesive ellipses which bound the adhesive annular region are assumed to have identical, fixed ellipticity ratios throughout the contact, though the limit of this assumption must be evaluated. The developed model is also expected to follow the behavior of the JKR elliptical model in the JKR domain. It is shown that the pull-off behavior in the JKR domain is influenced by the unequal growth rate of its contact area in both the major and minor axes directions. However, the question of whether the adhesive region of the developed model is also subjected to the unequal growth rate, inside and outside the JKR domain, needs to be investigated. These aspects are explored in this paper.
2 Model Development
2.1 Non-adhesive Elastic Contact
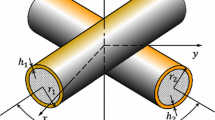
The Hertz model, described in [21], was the pioneer of contact models. An elliptical contact is produced from crossed cylinders with skew angle, θ skew , between 0° to 90°. The contact area is an ellipse, with semimajor axis a and semiminor axis b, as shown in Fig. 2.
Formulations for the non-adhesive elliptical contact model are given in [21], in Cartesian coordinates. In this paper, all the equations are expressed in a polar coordinate system, where geometrical parameters are defined in “Appendix 1”.
The initial gap, z, in polar coordinates is given in [21] by the general expression:
where R′ and R′′ are the first and the second principal relative radii of curvature for the cylinders. r is the radial coordinate and θ p is the angular coordinate of the chosen point in the contact region. R′ and R′′ are related to the angle between the crossing cylinders, θ skew , by:
where the cylinders in contact are assumed to have the same radius R c .
The effective radius, R, is given by:
and the effective Young’s modulus is:
where ϑ is the Poisson’s ratio and E* is the Young’s modulus for each cylinder.
When the adhesion effect is neglected, the Hertzian pressure distribution, P, acting in the elliptical contact area as obtained by [21] can be expressed as follows:
For this pressure distribution, the maximum pressure in the contact ellipse, Po ab , is given as:
where K(k) and E(k) are the complete elliptic integral of the first and second kind, and k is the elliptic modulus (eccentricity of the ellipse). The value of β throughout the contact is equal to β 0 , the initial ellipticity ratio at initial loading that can be expressed as:
The total load compressing the cylinders, W, is related to the contact area as follows:
where
Due to the pressure in Eq. (7), the surface displacement within the ellipse of two bodies, ω, is expressed in [21] as:
where l is the positive root to \(\frac{{\left( {r\cos \theta_{p} } \right)^{2} }}{{a^{2} + l}} + \frac{{\left( {r\sin \theta_{p} } \right)^{2} }}{{b^{2} + l}} = 1\).
Solutions for Eq. (12a) were obtained from [21]. Equation (12b) was solved in [22] and is applied here in our model. Further solutions for Eq. (12b) can be found in “Appendix 2.” Surface displacements in Eq. (12) are then rewritten as:
where
and
F(φ, k) and E(φ, k) are the incomplete elliptic integral of the first and second kind. k′ is the complementary elliptic modulus and φ is the second argument of the incomplete elliptic integrals.
2.2 Extension of the Double-Hertz Theory to Adhesive Elliptical Contacts
We developed the adhesive elliptical contact model by extending the DH theory by [11], originally created for an adhesive circular contact. The basis of the DH model is that the adhesive tensile stresses are represented by the difference between two Hertzian pressure distributions of different radii (radial coordinates). The equations describing the adhesive stresses are given by:
where r ab and r cd are the radial coordinates for the contact and the adhesive ellipses, respectively, such that r ab < r cd . The contact ellipse is the Hertzian contact area that is due to the applied load. The additional pressure distribution creates the adhesive ellipse with semimajor axis c and semiminor axis d. Contact and adhesive ellipses bound the adhesive region, an annular elliptical-shaped area where the adhesion forces act. In this paper, it is assumed that both contact and adhesive ellipses have equal values of ellipticity ratio during contact, which is expressed as:
which at the pull-off moment, the relation in Eq. (17) becomes:
Following the Hertzian assumption for elliptical contacts, the relation of
is maintained throughout the adhesive contact.
The maximum pressure in the adhesive ellipse, Po cd , is given as:
which is similar in form as Eq. (8) of the contact ellipse.
The surface displacements are:
Figure 3a shows the normalized pressure P/P 0 curves, obtained using Eqs. (8), (16) and (20) at β 0 = 0.99, which corresponds to θ skew ≈ 90°. From Fig. 3a, the maximum adhesive stress can be seen to occur at r ab and then decreases to approach a zero value at r cd . Surface displacements at β 0 = 0.99 are also presented in Fig. 3b, using Eq. (21). The results of the original DH model for a circular contact are also included. A uniform displacement over the contact region is annulled by a rigid-body displacement over the adhesive region of r ab ≤ r ≤ r cd to leave a gap. It can be observed that the surface deformations for the current model at β 0 = 0.99 closely resemble those of the DH model for a circular contact.
In a similar way as in the original DH model, the pressure expressions in Eq. (16) are scaled by ʋ to model the adhesive tensile stresses over the adhesive region, r ab ≤ r ≤ r cd , which produces the final stresses distribution when combined with an unscaled Hertzian pressure. The scaling factor, ʋ, is determined by the surface forces, which will be further discussed in Sect. 2.3. The pressure equations are now expressed as:
From Eq. (22b), it can be seen that the distribution of the tensile stress over the adhesive annular region is given by:
Then, at r = a and θ p = 0°, the maximum adhesive stress is given by:
The combined load, including the load in Eq. (10), is expressed as:
To include the scaling factor ʋ, surface displacements in Eq. (21) are rewritten as:
The gap, h, for the area outside the contact where r ab ≤ r ≤ r cd is then given by:
2.3 Work of Adhesion
The work needed to break the intermolecular bonds at pull-off moment is termed work of adhesion. This work is required to create new surfaces when separating two bodies attached together due to the presence of the adhesion forces. The work of adhesion from [11] can be expressed as:
which becomes
where σ ac is dependent on the separation h. For an elliptical contact, h is a function of both r and θ p , as shown in Eq. (27). Using the Jacobian of the transformation, the work of adhesion for an adhesive elliptical contact from Eq. (29) can be expressed as:
where the scaling factor ʋ is chosen such that the values of σ 0 and Δγ are fixed.
In this paper, only the results for the angular coordinate at θ p = 0° are shown, resulting in the model having a one-dimensional solution for the contact problem. The expression for the work of adhesion in Eq. (30) for θ p = 0° can be rewritten as:
3 Results
Previous results are summarized in non-dimensional form following the work of [11, 23] by:
and
Further, the Tabor parameter is defined in [10] as:
Using the equations above, the normal load in Eq. (25) is now expressed in non-dimensional form as:
The effects of changing the normalized load W* on the semimajor axes of contact and adhesive ellipses, a* and c*, are shown in Figs. 4 and 5. We obtained the values of c* and the factor ʋ by solving Eqs. (31) and (35) simultaneously in MATLAB. Due to incomplete elliptic integrals in Eq. (31), it cannot be solved directly in the same manner as in the DH circular contact. Both c* and ʋ values were then used in Eq. (36) to calculate the corresponding load. At a nearly circular contact, the model is compared to the original DH model for an intermediate case of μ = 1 and the JKR circular model for the soft material comparison at μ = 5. A β 0 value of 0.99 follows the behavior of a circular contact accurately for all μ values. At μ = 0.5, the pull-off moment occurs at a near-zero contact with a high pull-off force. It is shown that the deformations due to adhesion forces are negligible, which is in agreement with the predictions of the DMT model. For μ = 5, the surface separation involves a low pull-off force at an apparent nonzero contact, which is similar to those predicted by the JKR model. In Fig. 5, c* values are shown to be highly influenced by the value of μ, such that they become smaller with increasing μ. As the μ values approach the JKR domain where materials are easily deformed, the adhesive ellipse becomes smaller, while the contact ellipse becomes larger, resulting in a narrow adhesive region. This is in close agreement with the adhesive behavior in the JKR domain, where adhesion is contained within the contact area.
The performance of the developed model is further investigated for particular μ groups, as shown in Figs. 6 and 7. Both graphs plot the semimajor axes of contact and adhesive ellipses, a* and c*, versus the normalized load W*. Results are shown for various β 0 values at μ = 0.5 and μ = 5, respectively. At μ = 0.5, it is shown that with decreasing β 0 values, the gap between a* and c* becomes considerably wider. This shows that, outside the contact area, an expansion of the adhesive region along the major axis is predicted for contacts which deviate from a circular shape. However, there is barely any effect at μ = 5, as shown in Fig. 7. At μ = 5, a* values are nearly equal to c* values, indicating a narrow adhesive region.
In Fig. 8, the model is compared to the JKR elliptical model at its adhesive domain of μ = 5. Only the curve of β 0 = 0.99 has a close fit to the JKR elliptical model. The difference in pull-off force values between both models is more apparent with decreasing β 0 . Although both models show similar deformations, the pull-off forces predicted by the developed model at β 0 values of 0.8 and 0.9 are considerably low for β 0 values that are considered to be close to one.
As previously shown in Fig. 8, the initial assumption of an adhesive region with both contact and adhesive ellipses having equal ellipticity ratios that remain constant as the load varies, as given in Eqs. (17) and (19), is not realistic for β 0 values of 0.8 and 0.9. To further analyze the behavior of the adhesive region during contact, the pull-off moment results from the assumption of Eq. (19) are compared to when the model employed JKR-like behavior, in which its ellipticity ratio is constantly changing as the load varies. At the pull-off moment, both results employ Eq. (18) for the relation between the contact and adhesive ellipses. For the JKR-like behavior, the ellipticity ratios of both contact and adhesive ellipses are made equal as the ellipticity ratio of the contact area obtained from the JKR elliptical model, which is expressed as β (pull-off) = β JKR(pull-off) , for all β 0 values of 0.8, 0.9 and 0.99.
The variation of the normalized pull-off force W max * with the Tabor parameter μ is shown in Fig. 9a. Results from both assumptions employed in the developed model are compared with the existing adhesive circular and elliptical models. Both results from the developed model produce curves which lie close to the other adhesive circular and elliptical models at β 0 = 0.99. At β 0 values of 0.8 and 0.9, the assumption of Eq. (19) produces results which clearly deviate from the JKR elliptical model. With the new assumption of JKR-like behavior, the gap between the predicted pull-off forces of the developed model and the JKR values is slightly improved for β 0 values of 0.8 and 0.9, as shown in the relative errors graph in Fig. 9b. It must be noted that a perfect fit between the JKR curves and the developed model cannot be expected in the JKR domain. The adhesive force for the JKR model is restricted within its contact area, which is different from the adhesive behavior outside the JKR domain, where the adhesive region is present outside the contact ellipse. This is an important characteristic of the developed model that must be taken into consideration.
4 Discussion
At β 0 values of 0.8 and 0.9, results from the developed model show an apparent deviation for the nearly circular contact comparison. Using the initial assumption of β = β (pull-off) = β 0 throughout the contact until the pull-off moment, the adhesive region becomes smaller as the load decreases, but it maintains its annular elliptical shape. This is due to a constant deformation rate along the major and minor axes directions for both the contact and adhesive ellipses. As for the JKR contact, which assumes a constantly changing β during contact (β (pull-off) ≠ β 0 ), the shape of the contact area that contains the adhesive stresses slowly changes from an ellipse to a nearly circular shape at the pull-off moment. From the initial load, the deformation rate along the minor axis of the elliptical contact slowly increases, the shape of which eventually turns into a nearly circular contact area during pull-off. Adhesion that acts within a nearly circular contact area requires a higher pull-off force for the separation compared to a narrow annular elliptical-shaped adhesive region. Figure 10 illustrates the evolution of the adhesive region and the contact area for the developed model with β = β (pull-off) = β 0 assumption, including the JKR contact area as a comparison. The assumption of identical, fixed ellipticity ratios throughout the contact for the contact and adhesive ellipses which bounded the adhesive region is shown to be unsuitable for the pull-off force prediction, as seen in the limiting JKR case where the pull-off force is underestimated.
At the JKR domain, pull-off moment results from the new assumptions (β (pull-off) = β JKR(pull-off) ) are closer to the JKR elliptical model, compared to those from the initial assumption of β = β (pull-off) = β 0 . The results provide insight into how the developed model should behave near the JKR domain, which has ellipticity ratios that are continuously changing as the load varies. At μ = 5, a smooth transition cannot be expected between the developed model with either the initial or the new assumption and the JKR elliptical model, because the developed model cannot model the adhesion inside the contact area, which is the foundation of the JKR model.
Additionally, assuming an equal value of β for both contact and adhesive ellipses (β = β ab = β cd ) over a wide range of μ is also unrealistic. It is important to find the real geometrical behavior of both contact and adhesive ellipses to improve the model’s prediction, regardless of material types and crossing angles. It is expected that the adhesive ellipse has the same ellipticity ratio as the contact ellipse for low μ values, while nearly circular adhesive regions are expected for high μ values that are closer to the JKR domain. Further work is essential to predict realistic geometrical behavior of contact and adhesive ellipses to enable accurate prediction for an adhesive elliptical contact. Numerical simulations such as [20, 24] have been shown to be able to model adhesive contact accurately, which can help us to predict the behavior of both contact and adhesive ellipses.
5 Conclusions
A model has been developed for predicting the adhesive elliptical contact by extending the DH model. Both contact and adhesive ellipses have identical, fixed ellipticity ratios, following the Hertzian assumption. Based on this, the geometry of the adhesive contact can be modeled, allowing pull-off force predictions for adhesive elliptical contacts. The results are in agreement with those obtained using existing adhesive circular and elliptical models, but only at nearly circular contacts. Mildly elliptical contacts have better results when the adhesive region is assumed to be constantly changing, as taken into account in the JKR model. This behavior is also expected for non-JKR contacts, based on the transition from the JKR model to the developed model in the pull-off prediction.
Abbreviations
- a, b :
-
Semimajor and semiminor axes of the contact ellipse
- c, d :
-
Semimajor and semiminor axes of the adhesive ellipse
- \( \beta_{0}\) :
-
Ellipticity ratio at initial loading
- \( \beta_{{\left( {\text{pull-off}} \right)}}\) :
-
Ellipticity ratio at pull-off moment
- \( \beta_{{{\text{JKR}}\left( {\text{pull-off}} \right)}}\) :
-
Ellipticity ratio at pull-off moment from JKR elliptical model
- \(\beta\) :
-
Ellipticity ratio throughout contact
- \(\beta_{ab} = b/a\) :
-
Ellipticity ratio of the contact ellipse
- \(\beta_{cd} = d/c\) :
-
Ellipticity ratio of the adhesive ellipse
- r :
-
Radial coordinate
- \(\theta_{p}\) :
-
Angular coordinate
- \(r_{ab}\) :
-
Radial coordinate of the contact ellipse
- \(r_{cd}\) :
-
Radial coordinate of the adhesive ellipse
- \(\theta_{skew}\) :
-
Angle between crossing cylinders
- \(E^{*}\) :
-
Reduced Young’s modulus
- \(E_{1} ,E_{2}\) :
-
Young moduli of the contacting materials
- \(R_{c}\) :
-
Radius of cylinder
- \(R^{\prime } ,R^{\prime \prime }\) :
-
Principal relative radii of curvature
- \(R = \sqrt {R^{\prime}R^{\prime\prime}}\) :
-
Equivalent radius
- \(\vartheta\) :
-
Poisson’s ratio
- \(\mu\) :
-
Tabor parameter
- \(k = \left( {1 - \beta^{2} } \right)^{1/2}\) :
-
Elliptic modulus (eccentricity)
- \(k^{\prime} = \left( {1 - k^{2} } \right)^{1/2}\) :
-
Complementary elliptic modulus
- \(\varphi = \sin^{ - 1} \left( {a/\sqrt {l + a^{2} } } \right)\) :
-
Second argument of the incomplete elliptic integrals
- \(\varvec{K}\left( k \right)\) :
-
Complete elliptic integral of the first kind
- \(\varvec{E}\left( k \right)\) :
-
Complete elliptic integral of the second kind
- \(\varvec{F}\left( {\varphi ,k} \right)\) :
-
Incomplete elliptic integral of the first kind
- \(\varvec{E}\left( {\varphi ,k} \right)\) :
-
Incomplete elliptic integral of the second kind
- \(v\) :
-
Scaling factor to keep σ0 and Δγ at a constant value
- \(W\) :
-
Applied load of single asperity
- \(\Delta \gamma\) :
-
Work of adhesion
- \({Po}_{ab}\) :
-
Maximum pressure of the contact ellipse
- \({Po}_{cd}\) :
-
Maximum pressure of the adhesive ellipse
- \(\sigma_{0}\) :
-
Maximum adhesive stress
- \(\omega_{{{in}_{ab} }}\) :
-
Surface displacement within the contact ellipse
- \(\omega_{{{out}_{ab} }}\) :
-
Surface displacement outside the contact ellipse
- \(\omega_{{{in}_{cd} }}\) :
-
Surface displacement within the adhesive ellipse
- \(\omega_{0ab}\) :
-
Combined surface displacement for 0 ≤ r ≤ r ab
- \(\omega_{abcd}\) :
-
Combined surface displacement for r ab ≤ r ≤ r cd
- \(\delta\) :
-
Approach of distant points
- \(z\) :
-
Initial gap in contact area
- \(h\) :
-
Separation between surfaces in the adhesive region
References
Shi, Q., Wong, S., Ye, W., Hou, J., Zhao, J., Yin, J.: Mechanism of adhesion between polymer fibers at nanoscale contacts. Langmuir 28(10), 4663–4671 (2012)
Lai, T., Huang, P.: Study on microscale adhesion between solid surfaces with scanning probe. Sci. China Technol. Sci. 56, 2934–2952 (2013)
Lai, T., Chen, R., Huang, P.: Temperature dependence of microscale adhesion force between solid surfaces using an AFM. J. Adhes. Sci. Technol. 29(2), 133–148 (2014)
Hanrahan, B., Misra, S., Beyaz, M., Feldman, J., Waits, C., Ghodssi, R.: An adhesion-dominated rolling friction regime unique to micro-scale ball bearings. Tribol. Lett. 56(2), 215–221 (2014)
Kendall, K.: Adhesion: molecules and mechanics. Science 263(5154), 1720–1725 (1994)
Johnson, K.L., Kendall, K., Roberts, A.D.: Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. Ser. A 324, 301–313 (1971)
Derjaguin, B.V., Muller, V.M., Toporov, Y.P.: Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–325 (1975)
Muller, V.M., Derjaguin, B.V., Toporov, Y.P.: On two methods of calculation of the force of sticking of an elastic sphere to a rigid plane. Colloids Surf. 7, 251–259 (1983)
Maugis, D.: Adhesion of spheres: the JKR–DMT transition using a Dugdale model. J. Colloid Interface Sci. 150(1), 243–269 (1992)
Tabor, D.: Surface forces and surface interactions. J. Colloid Interface Sci. 58(1), 2–13 (1977)
Greenwood, J., Johnson, K.: An alternative to the Maugis model of adhesion between elastic spheres. J. Phys. D Appl. Phys. 31(22), 3279–3290 (1998)
Barquins, M.: Adherence and rolling kinetics of a rigid cylinder in contact with a natural rubber surface. J. Adhes. 26(June), 1–12 (1988)
Baney, J., Hui, C.: A cohesive zone model for the adhesion of cylinders. J. Adhes. Sci. Technol. 11(3), 393–406 (1997)
Johnson, K., Greenwood, J.: Maugis analysis of adhesive line contact. J. Phys. D Appl. Phys. 41(19), 199802 (2008)
Jin, F., Zhang, W., Zhang, S., Guo, X.: Adhesion between elastic cylinders based on the double-Hertz model. Int. J. Solids Struct. 51(14), 2706–2712 (2014)
Zhang, W., Jin, F., Zhang, S., Guo, X.: Adhesive contact on randomly rough surfaces based on the double-Hertz model. J. Appl. Mech. 81(5), 051008 (2014)
Jin, F., Wan, Q., Guo, X.: A double-Westergaard model for adhesive contact of a wavy surface. Int. J. Solids Struct. 102–103, 66–76 (2016)
Johnson, K., Greenwood, J.: An approximate JKR theory for elliptical contacts. J. Phys. D Appl. Phys. 38(7), 1042–1046 (2005)
Sümer, B., Onal, C., Aksak, B., Sitti, M.: An experimental analysis of elliptical adhesive contact. J. Appl. Phys. 107(11), 113512 (2010)
Jin, C., Jagota, A., Hui, C.: An easy-to-implement numerical simulation method for adhesive contact problems involving asymmetric adhesive contact. J. Phys. D Appl. Phys. 44(40), 405303 (2011)
Johnson, K.: Contact Mechanics. Cambridge University Press, Cambridge (1985)
Byrd, P., Friedman, M.: Handbook of Elliptic Integrals for Engineers and Scientists, 2nd edn. Springer, Berlin (1971)
Israelachvili, J.N.: Intermolecular and Surface Forces, 3rd edn. Academic Press, Amsterdam (2011)
Bazrafshan, M., Rooij, M.B., Valefi, M., Schipper, D.: Numerical method for the adhesive normal contact analysis based on a Dugdale approximation. Tribol. Int. 112, 117–128 (2017)
Acknowledgements
The authors gratefully acknowledge support from the Ministry of Education Malaysia, Universiti Teknikal Malaysia Melaka and Green Tribology and Engine Performance (G-TriboE) research group.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Coordinate System for Governing Equations
See Fig. 11.
where
Appendix 2: Solutions for Incomplete Elliptic Integrals
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zini, N.H.M., de Rooij, M.B., Bazr Afshan Fadafan, M. et al. Extending the Double-Hertz Model to Allow Modeling of an Adhesive Elliptical Contact. Tribol Lett 66, 30 (2018). https://doi.org/10.1007/s11249-017-0976-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-017-0976-8