An Approximate JKR Model of Elliptical Contact Between Thin Incompressible Elastic Coatings Covering Rigid Cylinders

Abstract

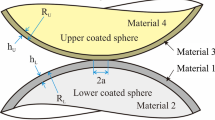
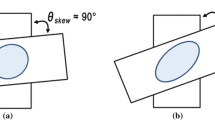
In the framework of the Johnson–Kendall–Roberts (JKR) theory, the adhesive contact between thin incompressible elastic coatings covering rigid cylinders is studied. The leading-order asymptotic model of three-dimensional non-axisymmetric JKR-type adhesive contact for a thin incompressible coating bonded to a rigid substrate is applied, and an approximate solution has been obtained under the assumption that the contact area remains elliptical.

Appendix: Nearly Circular Contacts

Let the interface gap be represented in the form

$$\begin{aligned} \varphi ({x,y})=\frac{x^2+y^2}{2R}+\mu \frac{y^2-x^2}{2R}, \end{aligned}$$

(31)

where we have introduced the notation

$$\begin{aligned} R=\frac{2R_1 R_2}{R_1+R_2},\quad \mu =\frac{R_1-R_2}{R_1+R_2}. \end{aligned}$$

(32)

On the other hand, we will have

$$\begin{aligned} R_1=\frac{R}{1-\mu },\quad R_2=\frac{R}{1+\mu }. \end{aligned}$$

(33)

The two-term asymptotic expansion for the solution of the adhesive contact problem under the assumption that $\mu$ is a small positive parameter was constructed in [18]. In particular, the polar equation for the contact contour was obtained in the form $r\simeq a_0+\mu a_2\cos 2\theta$, where $r,\theta$ are polar coordinates, so that the major and minor semi-axes are

$$\begin{aligned} a\simeq a_0+\mu a_2, \quad b\simeq a_0-\mu a_2, \end{aligned}$$

(34)

respectively, whereas the aspect ratio of the contact area is given by

$$\begin{aligned} s\simeq 1-2\mu \frac{a_2}{a_0}. \end{aligned}$$

(35)

Here, $a_0$ is the leading-order approximation as $\mu \rightarrow 0$, and $a_2$ is given by the formula

$$\begin{aligned} a_2=\frac{a_0}{3}\biggl (1-\frac{4R}{a_0^3}\sqrt{\frac{2\Delta \gamma }{m}} \biggr )^{-1}, \end{aligned}$$

(36)

while (see also Eq. (22))

$$\begin{aligned} \delta =\frac{a_0^2}{4R}-\frac{2}{a_0}\sqrt{\frac{2\Delta \gamma }{m}}. \end{aligned}$$

(37)

Let us now compare the asymptotic solution (36) with the approximate solution constructed above. First, from the second and third equations (15), we derive the equation

$$\begin{aligned} \frac{R_2}{R_1}=\frac{s^2\bigl [6s^2+s+1+2\xi (1+3s^2)\bigr ]}{s(s^2+s+6)+2\xi (3+s^2)}, \end{aligned}$$

which, in view of (33) and (35), implies

$$\begin{aligned} \xi \simeq \frac{9a_2-4a_0}{4(a_0-3a_2)}. \end{aligned}$$

(38)

At the same time, the first equation (15) can be rewritten as

$$\begin{aligned} \frac{1}{a_0\delta }\sqrt{\frac{2\Delta \gamma }{m}}\simeq \frac{ s^2\eta (s)(1+\mu a_2/a_0)}{s(1+s)+2\xi (1+s^2)}, \end{aligned}$$

(39)

where the first formula (34) was already taken into account.

The substitution of (35) and (38) into Eq. (39) results in the equation

$$\begin{aligned} \frac{a_2}{a_0}=\biggl ( \frac{2}{a_0\delta }\sqrt{\frac{2\Delta \gamma }{m}}+1\biggr )\biggl ( \frac{3}{a_0\delta }\sqrt{\frac{2\Delta \gamma }{m}}+3\biggr )^{-1}, \end{aligned}$$

which, after eliminating $\delta$ by means of Eq. (37), reduces to Eq. (36).

Thus, in the case of a nearly circular area of contact, the obtained approximate solution agrees with the asymptotic solution up to the second-order terms. This, in particular, means that the adopted approximation for the contact pressure (5) is asymptotically exact for nearly circular contacts. On the other hand, the asymptotic ansatz developed in [18], which was established for an arbitrary smooth gap function close to a paraboloid of revolution, may suggest a more elaborate approximation (incorporating more free parameters) in order to extend the analytical approach to the range of smaller values of the ratio $\rho$.