1 Introduction

In tribological systems operating in the boundary or mixed lubrication regime, protection of the surfaces from severe wear is frequently obtained by so-called anti-wear (AW) additives added to the base lubricant. Zinc dialkyldithiophosphate (ZDDP) is one of the most widely used additives [1].

So far, it is well known that the anti-wear mechanism of ZDDP is related to the formation of a protective layer—generally called `tribo-film.’ It is formed through the chemical decomposition of ZDDP, it has a heterogeneous structure, and it is up to 200 nm thick [2]. The ZDDP tribo-film is typically observed at the surfaces of steels, but was also found on the surfaces of other materials, such as aluminum–silicon alloys [3], DLC [4], silicon [5], tungsten carbide [6], and ceramics [7]. The structure of the films formed on various materials was reported to be similar [5, 6, 8]. In the case of steels, it mainly consists of oxygen, phosphate, sulfide, zinc, and iron, with an increase in the concentration of iron closer to the bulk material [1, 9]. The top surface may be covered by an iron-free zinc polyphosphate glass, which has a highly amorphous structure, while the bulk is composed of pyro- or orthophosphate glasses [10].

There is consensus on the fact that the tribo-film is continuously worn and replenished and has a sacrificial function [11, 12]. The exact mechanism of its growth and anti-wear action is however still under debate [10]. According to the hard and soft acids and bases theory (HSAB), hard abrasive iron oxide wear particles react with phosphate glasses to form softer less abrasive iron sulfides [13], thus preventing severe wear. Due to continuous generation and subsequent digestion of the oxide particles (or surface oxide layers), the tribo-film is replenished [14]. The theory, however, may not explain the generation of a tribo-film on nonferrous surfaces, such as DLC [4], silicon [5], other metals [6], and ceramics [7], although it was recently hypothesized that HSAB may be applied in nonferrous cases as well [15]. Based on molecular dynamic simulations, Mosey et al. [16] concluded that a tribo-film is formed due to the pressure-induced cross-linking of ZDDP molecules at pressures higher than 7 GPa. However, such high pressures are higher than the yield stress of most materials used in common engineering applications, so this is not realistic. It was also observed that tribo-films can grow at high temperatures (>150 °C) without any contact, suggesting that the chemical reactions also take place due to the thermal activation. However, in the case of rubbing, the growth rate is much higher [17].

Initially, the tribo-film growth was described using an Arrhenius equation [17, 18]. However, Bulgarevich et al. [19] showed that this leads to very low (unrealistic) activation energies. In a different paper, Bulgarevich et al. [20] introduced a stress dependence to the Arrhenius equation by means of a multiplication factor [20]. Very recently, Gosvami et al. [5] employed an Arrhenius equation where the activation energy was made stress-dependent. The equation was found to fit the growth of the ZDDP tribo-film observed in AFM measurements, while the obtained values for the activation energies were now similar to those typically found in thermo-activated reactions. Zhang and Spikes [6] confirmed the stress-activated Arrhenius relation for ZDDP film growth in a series of macroscale experiments. They also showed that the growth rate is governed by the shear stress, rather than the normal stress. This fact is confirmed by experiments showing that tribo-films do not grow in pure rolling contacts, not even at high pressures [21].

There are a number of wear models that include the presence of a tribo-film. Bosman and Schipper [11, 22] developed a mechano-chemical model to calculate wear rates in the mild wear regime. It was assumed that the growth of the tribo-film can be described with a diffusion type of process, while the wear was calculated from the volume of plastic deformation of the tribo-film. Andersson et al. [23] only included the influence of temperature and employed Arrhenius’ equation, following So et al. [24]. Ghanbarzadeh et al. [25] proposed a semi-deterministic model for tribo-film growth following Bulgarevich et al. [20]. The influence of the stress was taken into through a correction factor.

One of the characteristics of the tribo-film growth is its self-limitation. The ZDDP molecules react with material on the surface. With the growth of the tribo-film, the concentration of this material decreases and so will the growth of the film. Ultimately, the growth rate will be equal to the wear rate. To model this behavior, a maximum tribo-film thickness was introduced in previously developed models as a fitting parameter to the growth equation. In the current work, the concept of `stress-activated growth,’ recently proposed by Gosvami et al. [5], was adopted. This approach is closer to the physics and chemistry of tribo-film growth and wear, which makes the application of the model outside the domain in which the various parameters have been fitted more reliable. They assumed that the self-limitation is a result of the evolution of the mechanical properties. When sliding starts, there is no tribo-film and the contact pressure (and therefore tangential stress) at the asperity level is determined by the hardness and Young’s modulus of the bulk material of the bodies in contact. Since typically the substrates are harder and less compliant than the tribo-film, relatively high pressures are generated. According to the stress-activated growth concept, high contact pressure decreases the effective activation energy of the reaction and results in a high reaction rate, i.e., a high tribo-film growth rate. With further development of the film, the lower tribo-film hardness and/or Young’s modulus start to become relevant and gradually reduce the contact pressure until the growth rate is balanced by the wear rate. By using this concept, it is possible to build a model to predict the growth of the tribo-film up to its steady-state value.

In the current paper, a mechano-chemical model was developed to simulate the tribo-film growth and concurrent wear in the presence of a ZDDP additive. The growth rate of the tribo-film was calculated using a stress-activated Arrhenius equation. A layered elastic-fully plastic model was used to include the influence of the tribo-film on the contact stress and its growth rate. The model was developed based on the experimental data available in the literature, i.e., measurements of tribo-film growth under an AFM tip and in a macroscale contact. The software for the simulation is available online [26].

2 Numerical Model and Tribo-Film Growth

2.1 Layered Elastic-Fully Plastic Contact Models

In the current work, a layered elastic-fully plastic contact model was used for the simulation of the tribo-film growth. The contact pressures can be obtained by solving the following system of equations [27]:

$$\left\{ {\begin{array}{*{20}l} {u\left( {x,y} \right) = z\left( {x,y} \right) - h_{s} \left( {x,y} \right), \forall x,y \in A_{c} } \\ {p\left( {x,y} \right) > 0,\forall x,y \in A_{c} } \\ {p\left( {x,y} \right) \le H} \\ {F_{C} = {\iint }p\left( {x,y} \right) dxdy} \\ \end{array} ,} \right.$$
(1)

where the deflection \(u\left( {x,y} \right)\) can be calculated using the half-space approximation [28]. The model was implemented using the discrete fast Fourier transformation technique (DC-FFT) [29], since the deflection \(u\left( {x,y} \right)\) is a discrete convolution:

$$u\left( {x,y} \right) = \left( {K + S} \right) \otimes p,$$
(2)

where K and S are the influence matrices for normal and tangential stresses (tangential stress is \(f_{C}^{b} \cdot p\)). For a layered body, expressions for K + S are given in the frequency domain [30, 31]. The model assumes elastic-fully plastic behavior, i.e., a cutoff pressure is applied in the numerical solver.

2.2 Tribo-Film Growth and its Mechanical Model

Following Gosvami et al. [5] and Zhang and Spikes [6], a stress-activated Arrhenius model was employed to calculate the growth of the tribo-film. The growth rate of the tribo-film is given by the following equation:

$$\left( {\frac{\partial h}{\partial t}} \right)_{g} = \tilde{\varGamma }_{0} e^{{\frac{{\Delta U_{\text{act}} - \tau \cdot \Delta V_{\text{act}} }}{{k_{B} T}}}} ,$$
(3)

where \(\Delta U_{\text{act}}\) is the internal activation energy (in the absence of stress), \(\Delta V_{\text{act}}\) is the activation volume, \(\tilde{\varGamma }_{0}\) is a pre-factor,\(k_{B}\) and \(T\) are the Boltzmann’s constant and absolute temperature. The value of \(\tilde{\varGamma }_{0} = 10^{ - 2} \frac{m}{s}\) was taken from [5], while \(\Delta V_{\text{act}}\) and \(\Delta U_{\text{act}}\) were used to fit experimental data. The shear stress was obtained from \(\tau = \mu p\), where \(\mu\) is the friction coefficient and P is the contact pressure. The friction coefficient of ZDDP films varies only slightly within a range of 60–100 °C [32], and a constant value of \(\mu = 0.1\) was used in all simulations.

According to Eq. (3) and assuming a constant coefficient of friction, the growth rate depends on pressure. The contact pressure is determined by Young’s modulus and by the hardness of the tribo-film and substrate. It is reported [33] that, due to the underlying substrate, the hardness of the tribo-film varies with the height of the tribo-film and plastic penetration depth. Unfortunately, it was not possible to calculate the plastic penetration depth using the available simulation tools. It was therefore chosen to use the empirical variation of the hardness with the tribo-film height from [33], as shown in Fig. 1.

Fig. 1
figure 1

Hardness evolution with thickness, [33]

Full size image

It should be noted that Young’s modulus was found to be largely independent of the temperature [33, 34], i.e., within 25–200 °C (at 220 °C, the ZDDP tribo-film will start to degrade [35]), while the hardness does depend on temperature [33]. Bosman and Schipper [36] proposed a compensation factor for the hardness as a function of temperature. The hardness at a given temperature can then be obtained by using the initial hardness given in Fig. 1 multiplied by a compensation factor from Fig. 2.

Fig. 2
figure 2

Compensation factor [36]

Full size image

It should be noted that the hardness evolution of a tribo-film as a function of film thickness and temperature is likely to be dependent on the ZDDP molecule type and the substrate properties. It may be then too simplistic to combine the results of Figs. 1, 2, since they were obtained at different experiments. However, for the general simulations as considered in the current work, the proposed hardness evolution model is suitable since it follows the trends of the tribo-film hardness decay with film thickness and temperature. To get better quantitative description, one would need to evaluate the hardness at various temperatures and thicknesses at particular experimental conditions and incorporate it to the model.

The temperature increase was calculated using the approach of Bosman and De Rooij [37], and it was found to be less than 1 °C for both micro- and macroscale simulations. This is consistent with the findings of Fujita and Spikes [17]. Temperature variations due to frictional heating were therefore neglected in the current simulations.

2.3 Tribo-Film Wear Model

One of the most widely used wear equations is the linear Archard wear equation [38]. This relation does not take into account the presence of a tribo-film. This may be the reason for it to fail to fit experimental data in some cases [39–41]. In the current work, a simple linear relation of tribo-film wear to its height \(h\) was used. The wear rate was calculated using the following equation:

$$\left( {\frac{\partial h}{\partial t}} \right)_{w} = \alpha h,$$
(4)

where \(\alpha\) is a fitting parameter and H is the tribo-film thickness. According to this relation, wear rate increases with the growth of the tribo-film. This is consistent with experimental observation of Fujita and Spikes [42]. This is ascribed to a difference in wear resistance between the fraction of the film close to the surface (low wear resistance) compared and that of the bulk of the film (higher wear resistance). Equation (4) shows the same behavior.

2.4 Evolution of the Tribo-Film and the Flowchart of the Model

The evolution of the tribo-film was calculated from the balance of growth and wear. The change in the tribo-film thickness was calculated by the following equation:

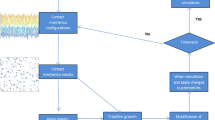
$$\frac{\partial h}{\partial t} = \left( {\frac{\partial h}{\partial t}} \right)_{g} - \left( {\frac{\partial h}{\partial t}} \right)_{w} ,$$
(5)

The flowchart of the simulation algorithm is shown in Fig. 3. Input are the mechanical properties, temperature, macroscale geometry, and roughness. Initially, the tribo-film does not exist (H = 0). After the calculation of contact pressures and shear stresses, the local growth of the tribo-film and subsequent wear are obtained from Eqs. (3) and (4), respectively. The tribo-film thickness is then updated, and the average tribo-film thickness is calculated. The average thickness is then used as a thickness of the (uniform) layer in the model. The hardness is recalculated based on the updated tribo-film thickness and the algorithm continues.

Fig. 3
figure 3

Flowchart of the tribo-film growth calculation

Full size image

3 Results and Discussion

3.1 Microscale Contact

The model was tested using the measurements of the tribo-film growth under an AFM tip from Gosvami et al. [5]. The contact consists of a DLC-coated (15 nm thick) silicon AFM tip with a radius of 53 nm and an iron-coated (10 nm thick) silicon substrate. First, the tribo-film growth at 600 nN was calculated.

By performing an elastic simulation with a layered model, it was found that the coatings are thick enough to neglect the influence of the underlying silicon. Therefore, only the iron film—DLC AFM tip contact—was taken into account.

The Young modulus and hardness of the tribo-film were reported to increase with the indentation depth in the range of 15–130 GPa and 2–4 GPa, respectively [33]. The lowest values of the Young modulus and hardness were used in the simulations, as discussed below. It was assumed that the tribo-film grows only on the substrate (iron-coated), as schematically shown in Fig. 4.

Fig. 4
figure 4

Schematic diagram of the contact model

Full size image

A semi-analytical contact model developed by Bosman and Schipper [22] indicated that the indentation depth of the tribo-film under considered conditions (assuming 2 GPa hardness) would be less than 0.5 nm. Since the plastic penetration depth was found to be less than 0.5 nm, the hardness of the substrate will not affect the contact pressure and the maximum contact pressure will be determined by the hardness of the tribo-film only. For the current simulations, the hardness of the tribo-film was assumed to be constant. On the other hand, the Young modulus of the substrate does influence the contact pressure even with thick films. The simulation of the tribo-film growth was therefore performed using the layered elastic-fully plastic contact model with a constant hardness of 2 GPa, see Fig. 4.

Initially, wear of the tribo-film was not taken into account and the growth was compared to the data published in Ref. [5]. This was done to test the hypothesis in [5] that the self-limiting behavior is based on the stress relaxation by the tribo-film, see Fig. 5a. It should be mentioned that the initial phase of the tribo-film growth is relatively slow, as discussed in detail in Ref. [5]. This phase of growth is not well understood but can also be regarded as not relevant for engineering problems. In practice, it can be assumed that a tribo-film already exists after running-in, i.e., when mild wear starts. The simulation data could therefore be shifted in time to correspond to the onset of the fast growth phase. As can be seen in Fig. 5a, the calculations correspond well with the experimental results, except for the last part of the curve where a significant deviation occurs. The mean contact pressure evolution is shown in Fig. 5b. Initially, a high contact pressure is developed due to the high elastic modulus of the iron substrate. With a rapid growth of the tribo-film with relatively low Young’s modulus and hardness, the pressure drops. However, the level of this contact pressure remains sufficiently high for steady growth of the tribo-film. It can thus be stated that the stress relaxation is not sufficient to limit the growth and wear should be included.

Fig. 5
figure 5

Contact between AFM tip and steel substrate. a Simulation and experimental data (data reconstructed from [5]) at 600 nN load of the tribo-film growth neglecting tribo-film wear, b corresponding mean pressure as a function of the tribo-film thickness

Full size image

This was done in the second calculation, shown in Fig. 6a, where the growth measurement data were used to find the values of \(\Delta U_{\text{act}}\) and \(\Delta V_{\text{act}}\). The rapid growth and the steady-state tribo-film thickness can be well predicted by the model. However, an important feature, i.e., an overshoot of the tribo-film thickness in the experimental data, cannot be reproduced. This overshoot is frequently observed in macroscale contacts as well [1, 2, 21]. The fact that it occurs on both micro- and macroscale makes is an intriguing feature of the tribo-film growth, which needs to be studied further.

Fig. 6
figure 6

Same case as from Fig. 4. The simulations now include both tribo-film growth and wear using a Eq. (4), b using a time lag, Eq. (6), with \(t_{\text{lag}} = 7\)

Full size image

The exact reason of the overshoot is not clear. Fujita and Spikes [42] reported an experimental investigation of this phenomenon. They first let the tribo-film grow until it stabilized after an overshoot. At this point, they added fresh ZDDP. They repeated this experiment several times, and every time after the addition of fresh ZDDP, they observed an overshoot of the tribo-film thickness. Interestingly, after each overshoot, the tribo-film stabilized toward the same value. From this, it can be concluded that the overshoot is related to certain processes within fresh ZDDP during rubbing. In order to include this behavior into the model, a delay between growth and removal was introduced in the wear equation:

$$\left( {\frac{\partial h}{\partial t}} \right)_{w} = \alpha h\left( {t - t_{lag} } \right),$$
(6)

This delay time T LAG can then be considered as a characteristic time for stabilization of the growth rate. The results obtained by using Eq. (6) are shown in Fig. 6b. It can be seen that almost the full curve, with the exception of the initial nucleation phase, can be described by the model. The parameters that were used in the simulations are given in Table 2. It should also be noticed that since the overshoot is not always observed and it does not influence the steady-state thickness of the tribo-film, Eq. (4) can be used to calculate wear of the tribo-film.

Next, the load was decreased to 340 nN. Figure 7b shows the result of the simulation using exactly the same input parameters as for the higher load case (see Table 2). The figure also shows the experimental results. The experiment stopped before the point of self-limitation was reached. However, it can be seen that the linear growth of the tribo-film thickness is again well predicted. The simulation was also performed with \(t_{\text{lag}} = 0\) to confirm that the time lag is also needed here. The results are shown in Fig. 7a. Unfortunately, there was no more data available to further test the performance of the model.

Fig. 7
figure 7

Contact between AFM tip and steel substrate simulation and experimental data (reconstructed approximately from [5]) at 340 nN load using a Eq. (4), b Eq. (6) with \(t_{\text{lag}} = 3000\varvec{ }\;{\text{cycles}}\)

Full size image

3.2 Macroscale Contact with Roughness

The model was further applied to a macroscale contact consisting of two rough steel surfaces. The physical properties of the steel, radius of curvature of the contact, and roughness are listed in Table 1. The applied load was 60 N, entrainment speed was 0.1 m/s, and the slide-to-roll ratio was 5 %. The growth of the tribo-film was recorded at 60, 80, and 100 °C. The variation of the effective Young modulus due to the presence of the tribo-film was found to have a negligible effect on the growth rate. On the other hand, the influence of the hardness was found to be very high.

Table 1 Properties of the macroscale contact
Full size table

The data from Ghanbarzadeh et al. [25] were used to fit the model parameters \(\Delta U_{\text{act}}\), \(\Delta V_{\text{act}}\), and \(\alpha\). Equation (4) was used for wear simulation. The simulation and test data are shown in Fig. 8a. A reasonable agreement at various temperatures can be obtained. It should be noted that including the stress dependency in the Arrhenius growth equation was a prerequisite to get a good fit of the three curves using the same constants. Figure 8a shows a saturation of the tribo-film thickness growth at higher temperatures, an effect that will not occur if only Arrhenius behavior is assumed. The stress-activated equation with the described mechanical model made it possible to also capture this effect.

Fig. 8
figure 8

a Comparison of simulation and experimental data [25], b evolution of the wear rate with temperature

Full size image

The set of optimum parameters for the macroscopic steel–steel contact is given in Table 2. The values of \(\Delta U_{\text{act}}\) and \(\Delta V_{\text{act}}\) are close to the ones reported by Gosvami et al. [5], see Table 2. This suggests that the proposed model is effective for a wide range of contact conditions, emphasizing the validity of the model.

Table 2 Parameters used in the simulations and found in the literature
Full size table

Wear of the tribo-film as a function of time is shown in Fig. 8b. As expected, the wear rate is larger for thicker films. It should be noted that the wear of the tribo-film leads to wear of the substrate material as well, in this case iron. This is caused by diffusion of the iron atoms into the tribo-film [9], which are subsequently removed if the tribo-film wears. Wear is measured by the removal of the substrate material (steel) and not by the removal of part of the tribo-film! The loss of substrate material due to tribo-film wear is calculated from the wear volume and the concentration of the substrate material atoms in the tribo-film. The concentration in the tribo-film will be highest close to the ‘interface with the substrate material’ and lower close to the ‘free surface.’ The loss of substrate material due to tribo-film wear will therefore decrease with increasing film thickness [9, 36]. The following relation was used to calculate the concentration as a function of the tribo-film thickness \(h\):

$$C\left( h \right) = e^{{ - C_{1} h}} ,$$
(7)

where \(C\left( h \right)\) is the concentration of substrate material, C 1 is an unknown constant. The wear of the substrate material can then be calculated from:

$$h_{w}^{m} = \mathop \smallint \limits_{0}^{t} C\left( h \right) \cdot \left( {\frac{\partial h}{\partial t}} \right)_{w} {\text{d}}t,$$
(8)

where \(h_{w}^{m}\) is the accumulated wear depth (wear of the substrate material). The constant \(C_{1}\) needs to be determined experimentally. In this case, the data from Ghanbarzadeh et al. [25] were used. They measured the wear depth after 45 and 120 min, at 60 and 100 °C. By taking the difference in wear depth between 120 and 45 min, the running-in period was excluded, see Table 3. Running-in was excluded here, since only mild tribo-chemical wear data were needed. As it can be seen in Table 3, a remarkable agreement of the simulation and experiment was achieved.

Table 3 Wear depth data as \(C_{1} = 1.24 \times 10^{7}\) derived from the measurements of Ghanbarzadeh et al. [25] and model calculations
Full size table

The evolution of the substrate material wear is shown in Fig. 9a. Figure 8 shows that the film thickness increases with increasing temperature. Hence, the substrate material concentration will be decreasing with increasing temperature, see Fig. 9b. The substrate material loss (wear) will therefore also decrease with increasing temperature. The highest wear of the substrate material is therefore found at 60 °C.

Fig. 9
figure 9

a Wear of a substrate material (wear depth), b concentration of the substrate material in a tribo-film

Full size image

4 Conclusion

A new mechano-chemical model was developed for the calculation of the tribo-film evolution. It was shown that the use of a stress-activated Arrhenius model makes it possible to calculate the tribo-film development up to its steady-state value. In addition, a mild tribo-chemical wear model was introduced based on the growth and wear of tribo-films. The models were validated using data from the literature. The results support the theory of stress- and temperature-driven growth and self-limitation of tribo-films.

Inputs for the model are, in addition to the traditional mechanical properties of the substrate materials, the constants in the stress-activated Arrhenius equations and the constants \(\alpha\) and C 1 in the wear equations. These constants depend on the type of additive, base oil, and concentration of ZDDP molecules [21, 43]. It is important to notice that these constants may be independent of load or temperature. This implies that the number of experiments that are required to calibrate the model is relatively small, which makes it relatively easy to apply the model to engineering problems. The test data that could be found for the validation of the model was limited. It is recommended to further perform tribo-film thickness evolution measurements at various stresses and temperatures at macroscale to advance the model.