1 Introduction

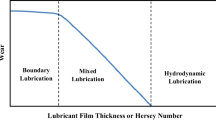
Wear is a topic that received a lot of attention in the past decades; however, still the most commonly used wear model is the linear wear law of Archard [1]. To model wear in more detail, Archard’s original model is combined with numerical methods to obtain the local variation in contact conditions and wear, see, for example, [2–4]; however, the basic principle is the same. And as an input, these methods use empirical determined values that are determined for one combination of bodies, lubricant and a limited load, and velocity range, and thus lack a predictive nature as there is no descriptive nature in the treatment of wear. In this study, a hypothesis for a wear model based on observed phenomena in mild wearing boundary-lubricated systems is suggested. This lubrication region is of increasing importance because many systems are running under starved conditions because of the increasing demand for smaller efficient components. To optimize systems running under these conditions without loss of lifetime, it is of crucial importance to understand the wear mechanism dominant in these systems and what kind of mechanical principle is causing the wear. Therefore, this article discusses a general hypothesis how to deal with mild (oxidative) wear in boundary-lubricated systems lubricated by additive-rich oils and running under mild conditions, which is applicable in a very wide range of applications and conditions.

The thought behind the model is the protection provided by the additive package originates from the chemical deposit/reaction it leaves on the surface, which acts as a sacrificial layer and is typically an amorphous glassy type of layer [5]. This layer is in chemical balance, which is then disturbed by mechanical removal of a part of the layer. To restore the chemical balance, base material is used. A commonly used additive is ZDDP, which is used as an antiwear agent in most engine lubricants. Because of the fact that the environmental regulations are becoming more restrictive concerning phosphorous and sulphur containing additives [6], the usage of ZDDP is restricted more and more. This results in the fact that a lot of research is currently done in understanding the mechanism behind the excellent antiwear properties of this additive [7–22] to eventually produce a more environment-friendly additive with the same excellent wear protection like ZDDP. These studies give a good overview of the film formed by this specific additive package; however, up to now, only little of this information is indeed used to model mild wear present in systems lubricated using a lubricant containing ZDDP.

2 Model

The model discussed here is based on some basic assumptions made in [23], where it is assumed that a boundary-lubricated system’s main protection mechanism is the chemical reaction layer on top of the surface in a system schematically depicted in Fig. 1. If it is now assumed that for only mild wear to take place, it is necessary that the shearing, which is needed for the accommodation of the velocity difference between the two contacting bodies, is located mainly in the chemically/physically adsorbed layer as well as the chemical reaction layer a first step in modeling mild wear can be made. This assumption concurs very well with TEM studies done on particles originating from systems running under mild conditions in the boundary lubrication regime; see, for example, [9]. Here, the thickness of the wear particles is less than the overall thickness of the chemical layer and the main components of the wear particles are chemical products originating from the additive packages present in the lubricant, rather than from wear particles “broken” out of the surface supporting the suggested wear mechanism proposed here. For a schematic representation of the proposed hypothesis, see Fig. 2. At the instant of first contact is it assumed that the system is chemical-balanced, after which the amount of plasticity in the thickness direction of the layer is assumed to be the thickness decrease because of contact. As mentioned before, lubricant to protect the surface the growth rate of the chemical layer should be larger than the removal rate:

$$ \mathop X\limits^{ \bullet } \ge \mathop W\limits^{ \bullet } . $$
(1)

In this paper, only the removal rate \( \mathop W\limits^{ \bullet } \)will be discussed and it is assumed that the growth rate is of such a magnitude it satisfies Eq. 1 and thus, the system is in a mild wear situation. To calculate the volume removed during wear, a removal model needs to be formulated. This will be done on the basic assumptions discussed in studies [23, 24], which will shortly be repeated here for brevity and the interested reader is referred to the indicated references for details. First, the representation of the system is given in Fig. 1, which suggests modeling of a layered system is required; however, this is not necessary if the right assumptions are made. First, a general impression is given about the mechanical properties of the chemical reaction layer. In typical systems, this layer has only a limited thickness (100 nm) and is reasonably rigid (E = 80 GPa), see Table 1. These properties combined with the input microgeometry/surface roughness used in this paper, which are interference microscopy measurements with a lateral resolution in the range of 1 micron, it can be concluded that the influence of the chemical layer in the normal direction can be neglected [23]. The major effect of the chemical reaction layer on the tribological system is lowering of the coefficient of friction. This ensures that plasticity is confined deep inside the bulk material rather than reaching the surface. The model thus assumes that the “environmental” conditions the chemical layer has to withstand, e.g., which mechanical and thermal stress the layer is put to, are determined by the properties of the bulk material.

Fig. 1
figure 1

Layers present at the surface of a run in system. The top layer is a physically/chemically adsorbed layer that only withstands very mild operational conditions. The second layer is a chemical layer that is a mixture of oxides and chemical products of the lubricant. The third layer is a nanocrystalline layer formed at the top of the bulk material by severe plastic deformation under large hydrostatic pressure

Full size image
Fig. 2
figure 2

a Asperities come into contact. b Part of the chemical layer is sheared of c Removed film is build up again from bulk and additives. d The geometry is changed and wear has occurred

Full size image
Table 1 Results for thickness and Young’s modulus for the chemical reaction layer retrieved from literature resulting from rubbing experiments in ZDDP rich oils
Full size table

The contact model used is a CGM-based elasto-plastic single-loop model first used by Keer and Polonsky [25]; here, the numerical efficiency was improved using the multigrid multisummation (MGMS) method. The MGMS method was later on replaced by Liu and Wang [26] with the DC-FFT algorithms not only decreasing the computational burden and improving accuracy but also most of all making the algorithm more comprehensive. The thermal model used is the model discussed in [27] with the adaption of interchanging the direct matrix inversion method combined with the moving grid method to solve the thermal inequality with the same numerical schemes as used for the contact solver rendering it possible to use larger grids without memory problems.

From the contact simulation, the stresses and displacements at the surface of the bulk material are known. The chemical layer is formed by the additives that reacted with the surface material and thus it can be assumed that the layer is mechanically bonded to the surface. Therefore, a nonslip condition at the interface between the base material and the chemical reaction layer is assumed. Because of the very limited thickness of the layer, the layer is in the plain stress condition, i.e. \( {{\partial \sigma_{ij} } \mathord{\left/ {\vphantom {{\partial \sigma_{ij} } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}} = 0 \). Using these assumptions and the strain at the surface of the bulk material, the stresses put on the chemical layer by the deformation of the bulk material can be expressed as follows:

$$ \sigma^{*}_{{ii_{\text{layer}} }} = {\frac{{E_{\text{layer}} }}{{\left( {1 + \nu_{\text{layer}} } \right)}}}\varepsilon_{{ii_{\text{bulk}} }} + {\frac{{\nu_{\text{layer}} E_{\text{layer}} }}{{\left( {1 + \nu_{\text{layer}} } \right)\left( {1 - 2\nu_{\text{layer}} } \right)}}}\left( {\varepsilon_{{ii_{\text{bulk}} }} + \varepsilon_{{jj_{\text{bulk}} }} + \varepsilon_{{kk_{\text{bulk}} }} } \right). $$
(2)

The stress put on the layer by the “environment” are the stress and shear because of the contact conditions giving:

$$ \sigma_{{zz_{\text{layer}} }} = \sigma^{*}_{{zz_{\text{layer}} }} + p_{{}} , $$
(3)
$$ \sigma_{{xz_{\text{layer}} }} = \mu \,p. $$
(4)

Using these conditions, the plastic yield of the layer can be calculated using a return-mapping algorithm.

Now, the contact conditions can be determined, the response of the chemical layer to these conditions is known if the mechanical properties of the layer are evaluated. To retrieve these parameters, a wide literature research was done on the properties of the chemical-reacted layer and a short summary is given in Table 1.

Table 1 gives a good first representation of the properties of a tribo-chemical layer present in a run-in system; however, there are some important effects missing. At first, the effect of the hydrostatic pressure on the properties will be discussed followed by the effect of the temperature.

The effect of the normal pressure on the Young’s modulus is depicted in Fig. 3. After a threshold pressure of 2 GPa, the equivalent modulus of the layer shows a linear increase with a slope of 35. Also the hardness is influenced by the effect of the normal pressure put on the film; however, the exact value is hard to obtain, and in Sect. 3, a first estimation will be made.

Fig. 3
figure 3

Young’s modulus of the chemical film as a function of the hardness (E = E 0 + 35(H – H 0) for H > H 0) (e.g. the maximum pressure applied to it). Figure is reproduced using the data presented in [42]

Full size image

A second effect is the effect temperature has on the mechanical properties [18, 36]. In both studies, it is shown that the influence of the temperature on the equivalent modulus is limited up to temperatures in the range of 100 °C, as shown in Fig. 4. However, in [36], a more pronounced temperature effect on the hardness is reported. Here, it is reported that at 80 °C, the hardness is already reduced to half of the value measured at 24 °C for low-indentation depths. The typical “indentation” during the wear process is also in the range of a few nano meters, suggesting this behavior is typical during the wear process. For this reason, an arctan function is used as depicted in Fig. 5 for the yield stress as a function of the temperature.

Fig. 4
figure 4

Equivalent Young’s modulus E * as a function of the temperature, measurement data are reproduced from [18]

Full size image
Fig. 5
figure 5

Proposed compensation factor C[–] as a function of the temperature for the yield stress of the chemical reaction layer

Full size image

The volume which will be removed from the chemical layer can be calculated using the contact solver and the assumptions made in Sect. 3. However, the amount of base material in this volume still needs to be determined. To do so, the first step is to get the chemical composition of the layer as a function of the depth. Different XPS studies were investigated [13, 15, 37, 38] and from these measurements, it can be concluded that the different conditions do not affect the iron concentration versus depth profile significantly. For this study, the profiles originating from [38] are used, see Fig. 6a. As discussed earlier, the structure of the film is amorphous suggesting a random molecule orientation and this enables the use of the atomic radius of different molecules to calculate the volumetric percentage of iron as a function of depth from the XPS signal, see Fig. 6b, which then can be used to calculate the amount of iron removed, which is fitted by the function:

$$ W_{\text{perc}} (\delta ) = {\frac{{4.5 \times 10^{19} \delta^{4} - 2.83 \times 10^{13} \delta^{3} + 1.75 \times 10^{ - 7} \delta^{2} + 0.001\delta }}{{h_{\text{balance}} }}} $$
(5)

Here, \( \delta = \varepsilon_{\text{plzz}}^{l} h_{\text{balance}} \)is the plastic penetration depth of the layer in which \( \varepsilon_{\text{plzz}}^{l} \)is the plastic strain in the chemical reaction layer in thickness direction and h balance is the thickness of the layer at which the system is in chemical balance. The next step is defining the “wear cycle” to estimate the rate the film is removed. For doing so, either a characteristic length or time is needed. Here, a length is chosen so that the wear loss parameter becomes dimensionless:

$$ K_{\text{wear}} (x,y) = {\frac{{h_{\text{inst}} (x,y)}}{l}} = {\frac{{W_{\text{wear}} }}{\Updelta x\Updelta yl}} = {\frac{{W_{\text{perc}} \left( {\varepsilon_{\text{plzz}}^{l} h_{\text{balance}} } \right)\varepsilon_{\text{plzz}}^{l} h_{\text{balance}} }}{l}}. $$
(6)

Here, W perc(x) is the percentage volumetric wear function presented in Fig. 6, Δx and Δy are the element sizes in x/y direction, and l is a characteristic wear length to be determined. If it is now assumed that for the system to wear volume W wear, the contact needs to be lost and then regained, e.g. the contact needs to be “opened” for the wear particle to detach, the average microcontact length in direction of sliding can be used as the characteristic length l. However, this would also imply that the sliding increment step would be of the same size yielding large computational times for longer sliding distances. To increase the numerical effectiveness, the specific wear coefficient is calculated from Eq. 6 and set constant over one sliding increment, as it is shown in [39] that this does not affect the results if the increment is chosen correctly:

$$ k(x,y) = {\frac{K(x,y)}{p(x,y)}}. $$
(7)

Giving the height loss for each increment:

$$ h_{\text{increment}} (x,y) = k(x,y)p(x,y)\Updelta s = K(x,y)\Updelta s. $$
(8)
Fig. 6
figure 6

Chemical composition of chemical reaction layer with a thickness of 70 nm. a XPS profile and b volume percentage of iron as a function of the depth

Full size image

3 Results

To validate the proposed wear model, two different tests were performed and reproduced in simulations: First, a new smooth ball and disk are used and second, a barrel-shaped specimen with a disk (elliptical contact) are simulated. The interference microscopy of the smooth new ball and disk are presented in Fig. 7a and b. The ball, disk, and barrel-shaped roller originate from roller bearings and are made of AISI-52100. The material parameters and geometrical entities and are presented in Tables 2 and 3.

Fig. 7
figure 7

a Surface topography of the ball and b of the disk used during the experiments and simulations. c Resulting pressure field and d temperature field. e Wear volume after 10 m of sliding

Full size image
Table 2 Geometrical entities and test conditions
Full size table
Table 3 Material parameters
Full size table

The first test is done using the new ball and disk on a CSM standard ball on disk setup under very mild conditions, F n = 10 N and V =0.005 m/s, using an commercially available ZDDP-rich lubricant of which some properties are given in Table 4 [40]. The test was run for ½ h after which the specific wear rate was determined. Under the given conditions, it is safe to assume that the main wear mechanism will be very mild oxidational wear. The measured coefficient of friction in this situation is 0.134 conforming that the contact is indeed running under boundary-lubricated conditions. The normal pressure in the test was under the threshold value of 2 GPa and thus the equivalent modulus of the film will be in the range of 35–40 GPa, because the “anvil effect” is not triggered at this pressure. The temperature rise inside the contact is less then 1 °C as shown in Fig. 7d, e.g. the reference hardness of 1 GPa [5] can be used for the chemical layer, because the contact conditions are very mild.

Table 4 Properties of commercial oil
Full size table

The measured specific wear rate during the test was found to be 8 × 10−9 mm3 N m−1. If the same sliding distance is modeled using 100 increment steps and the layer thickness (h balance) is set to 70 nm, as measured for this type of system, the specific wear rate calculated is 4 × 10−9 mm3 N m−1, which is determined using the calculated wear profile shown in Fig. 7e. This value is in the same range as the measured one, indicating the proposed wear model is capable of determining the specific wear rate for mild wearing point contacts.

The next step is to determine the specific wear rate of the run in elliptical contact, the surface geometry of which is presented in Fig. 8a. The run in procedure is the same as for the ball. However, in the roller-disk combination, the roughness of the roller used is significantly higher than the ball used in the previous test. This is also quite well represented by the clear roughening of the disk inside the wear track as shown in Fig. 8b. The roughening, e.g. running-out, of the disk is currently not incorporated in the model because the responsible mechanism will be plowing. Because of this increase in roughness, it is clearly shown in Fig. 8d that the pressure exceeds the threshold value of 2 GPa and the anvil effect needs to taken into consideration. However, as discussed in Sect. 2, not only the equivalent modus is a function of the pressure above the threshold but also the hardness starts to be affected by the pressure, as can be seen in Fig. 4 in [36]. To compensate this effect, the yield strength is defined as follows:

$$ \sigma_{y} (x,y) = \sigma_{y0} + \alpha p(x,y)\;\;\;\;for\;p(x,y) > p_{\text{tresh}} . $$
(9)

In the simulation, the threshold pressure is set to 2 GPa, e.g. equal to the threshold for the Young’s modulus and α = 0.1, which is in a realistic range for amorphous polymer glasses [41]. Using these values, the calculated specific wear rate becomes 9 × 10−9 m3 N m−1 for a sliding distance of 1 m, whereas the measured one is 1.6 × 10−8 m3 N m−1. As for the smooth ball-disk combination, both calculated and measured values are in close range with each other, using values readily obtained either from experiments or dedicated literature.

Fig. 8
figure 8

a Surface profile of a roller run for 8 h under the conditions given in Table 2. b Counter surface topography. c Temperature field in the contact and d Pressure field in the contact. e Resulting wear depth

Full size image

4 Wear Map

To increase the potential of the model even further, it can be combined with the theory presented in [39], where the transition from mild to severe wear is discussed. The hypothesis presented in this study states that if more than 10% of the contacting surfaces transcend, a predefined critical temperature severe adhesive wear will occur. In principle, this theory is inline with the current model, which states that the chemical layer softens under the influence of increasing temperature. If now the temperature is increased to far, the chemical layer will not be able to protect the surface against metal to metal contact and local adhesive wear will occur, increasing the temperature in the contact even further introducing complete failure of the whole contact. Using this hypothesis, a F – V failure diagram can be constructed as depicted in Fig. 9, which can now be extended by “iso-k” lines using the model presented in this paper. To do so, the input geometries from the previous study are used, see Fig. 10 for the disk surface topography. The counter surface is a cylindrical pin with a length effective contact length of 3.4 mm and a radius of 2 mm with a smooth surface creating a line contact situation. The disk is a hard-turned disk made of case-hardened steel, for the material parameters, see Table 3.

Fig. 9
figure 9

Failure diagram for a boundary-lubricated contact, reproduced from [39]

Full size image
Fig. 10
figure 10

a Measured disk and b filtered part of the surface used for the calculations

Full size image

To reduce calculation time without a significant loss of accuracy, the surface is reduced to a 240 × 240 grid using an average-moving filter as discussed in [39]. If the new surface is used for both cylinder and disk and it is assumed the load is put on instantaneously, the resulting calculated wear diagram is depicted in Fig. 11. This wear diagram shows realistic values for a boundary-lubricated contact; however, the validation of this diagram is a subject of further research and we would like to emphasize that the wear diagram presented here is to show the potential of the model. Further research on the effect the different operational conditions have on the chemical layer is needed to improve the wear diagram. Also the running-in under these conditions needs to be modeled using, for example, a model as discussed in [23]. To show the effect a change in roughness has, the simulation is also run with a smooth pin and smooth disk combination as well as a rough–rough combination, the results of which are shown in Fig. 12. Here, it is clearly shown that the change in roughness has a limited effect on the specific wear rate. However, the effect of the roughness change on the location of the transition line from mild to severe wear is pronounced.

Fig. 11
figure 11

Wear diagram with the different iso-wear lines for the combination of the smooth new cylinder and new rough disk if the force is put on instantaneously

Full size image
Fig. 12
figure 12

a Wearmap for the combination of a rough disk and rough pin (Ra = 0.27). b Wearmap if both the disk and pin are assumed to be smooth (Ra = 0.08 microns)

Full size image

5 Conclusions

In this paper, a model for mild wearing systems is proposed that is based on physical properties and phenomena observed in boundary-lubricated systems. A general model is proposed and to validate the model, two model tests were conducted to validate the model. The numerical results concur very well with the experiments validating the model. One of the next steps in modeling wear of this type would be including a growth model for the additive layer, this would not only include the thickness of the layer but also the effect the different additives have on the properties of the chemical layer. In this way, in near future, it might become possible to predict the lifetime of a component without the need to do countless wear experiments over a wide range of contact conditions. As an example, a theoretical wear diagram of a model system consisting of a smooth cylinder sliding over a rough disk is presented. In this simulation, the hypothesis that the transition from mild to severe wear is a thermal phenomenon is used. This is done to set the regime in which the mild wear model is valid. The results are not validated and this is a next step in the current research project; however, the potential of the model in which both the mild wear model and the transition prediction are combined is shown.