Abstract
The dynamics of catechol in zeolite Beta was studied using quesielastic neutron scattering (QENS) experiments and molecular dynamics simulations at 393 K, to understand the behaviour of phenolic monomers relevant in the catalytic conversion of lignin via metal nanoparticles supported on zeolites. Compared to previous work studying phenol, both methods observe that the presence of the second OH group in catechol can hinder mobility significantly, as explained by stronger hydrogen-bonding interactions between catechol and the Brønsted sites of the zeolite. The instrumental timescale of the QENS experiment allows us to probe rotational motion, and the catechol motions are best fit to an isotropic rotation model with a \(D^{rot}\) of 2.9 × 10\(^{10}\) s\(^{-1}\). While this \(D^{rot}\) is within error of that measured for phenol, the fraction of molecules immobile on the instrumental timescale is found to be significantly higher for catechol. The MD simulations also exhibit this increased in ‘immobility’, showing that the long-range translational diffusion coefficients of catechol are lower than phenol by a factor of 7 in acidic zeolite Beta, and a factor of \(\sim\)3 in the siliceous material, further illustrating the significance of Brønsted site H-bonding. Upon reproducing QENS observables from our simulations to probe rotational motions, a combination of two isotropic rotations was found to fit the MD-calculated EISF; one corresponds to the free rotation of catechol in the pore system of the zeolite, while the second rotation is used to approximate a restricted and rapid “rattling”, consistent with molecules anchored to the acid sites through their OH groups, the motion of which is too rapid to be observed by experiment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Lignin is a primary constituent of biomass, with the potential to become a dominant source of fuel and fine chemicals [1]. Lignin is a three-dimensional polymer of phenolic monomers, which has to be catalytically degraded into smaller components in order to maximise the returns of its utilization [2, 3].
A combination of mechano-catalysis and solvent extractions [4,5,6] is usually followed by a hydro-deoxygenation (HDO) process that aims to transform the lower molecular-weight phenolics obtained after the de-polymerization of lignin. The HDO of lignin-derived compounds, catalysed by metal nanoparticles supported on zeolites, is highly effective at increasing the elemental ratios of H:C and C:O, consequently enhancing the energy content of the produced fuel [1]. In the HDO transformation, the transition metal guides the hydrogenation and further de-polymerization of the soluble derivatives of the lignin degradation, with the resulting products going through additional dehydration, alkylation and coupling reactions at the internal acid sites of the zeolite [7,8,9]. As such, the acid sites of the zeolite, together with its topology and pore dimension, play an important role in the selectivity and yield of the overall conversion [10, 11]. To understand the selectivity and any potential rate-limiting steps, it is thus essential to analyse the dynamical behaviour of relevant molecules in the micropore system of zeolite catalysts. Of recent interest for use in HDO catalysis has been zeolite Beta (framework type BEA) [12,13,14], which features relatively large pore windows of 12 tetrahedral sites (T-sites), allowing the relatively unhindered entry of phenolic monomers into the micropore system [10]. However, a full understanding of factors governing the activity and selectivity of the catalytic system is hindered by the complexity of both the catalyst and the sorbates involved, and multiple techniques are required to understand the behaviour on a range of scales.
The unique ability of neutron spectroscopy to probe inorganic microporous catalytic systems [15] has been demonstrated a number of times for both the study of adsorbed hydrogenous species [16, 17] and active sites on the catalyst surface [18, 19]. In terms of probing sorbate mobility, quasielastic neutron scattering (QENS) can probe motions over a wide range of timescales, with different instruments covering a timescale range of 2 ps–100 ns [20]. This enables the probing of rotational motions local to the active site, or in the pore system [21,22,23,24] and longer range diffusion processes throughout the pore network, providing both qualitative and quantitative insights [25,26,27,28].
A particularly powerful combination for these systems is that of QENS experiments coupled with molecular dynamics simulations, which are able to model motion over the same time and length scales [29]. Unique insight has been gained in a range of systems relevant to microporous catalysis [25, 30, 31]. In addition, the development of simulation-led data analysis tools is a priority for neutron spectroscopy research across fields [32] where QENS observables, such as the intermediate scattering function and dynamical structure factor, may be calculated for direct comparison between theory and experiment [27, 33, 34].
Our previous work has studied the motions of adsorbed phenol in zeolite Beta with this combination [35]. The study showed that, on the timescale probed by experiment, only isotropic rotational motion is observed, with a fraction of the molecules remaining static. This finding was supported by MD calculations, which showed that a proportion of immobile molecules engaged in strong hydrogen-bonding with the acid sites, while the mobile fraction rotates relatively freely in the micropores when located farther away from the acidic protons.
In the present work, we compare our previous observations with that of catechol, which is another commonly observed compound in the conversion of lignin [36,37,38]. Catechol has an additional OH group at the ortho position compared to phenol, and thus we aim to analyse how differences in mass, steric interactions and extra H-bonding capability affect the molecular motion of phenol and catechol inside zeolite Beta, using both QENS and MD simulations.
2 Methods
2.1 Experimental
As in our previous work studying phenol [35], the commercial zeolite Beta samples used were obtained from Zeolyst International (CP814E*, Si/Al = 12.5) and received originally in the NH\(_4\) form. These samples were activated into the catalytic H-Beta form by heating from room temperature to 798 K for 4 h, with a heating rate of 5 K min\(^{-1}\), and then dried for 10 h under vacuum at 170 \(^\circ\)C. Next, the samples were ground using a pestle and mortar with 10% weight of catechol (approximately 4 molecules per unit cell) in a glovebox under argon. Finally, the samples (3.3 g in total for catechol mixed samples) were transferred to thin-walled aluminium cans of annular geometry, where a 1 mm annulus was used to avoid multiple scattering from the sample. The catechol-mixed samples were then heated to 393 K for 2 h in order to melt the catechol and ensure its adsorption into the zeolite pores.
QENS experiments were carried out using the time-of-flight backscattering neutron spectrometer OSIRIS [39] at the ISIS Pulsed Neutron and Muon Source. The cells were placed in a top-loading closed cycle refrigerator. The samples were then cooled to a base temperature of 10 K and a resolution measurement was taken, after which they were heated to 393 K, where the QENS spectra were measured. This temperature was selected by considering the temperatures used during the hydro-processing of phenolic compounds and also to avoid any molecular decomposition associated with pyrolytic processes.
Pyrolitic graphite 002 analyser crystals were used, giving an energy resolution of 24.5 μeV with energy transfers measured in a window of ±0.55 meV; the detector covered measurements over a Q range of 0.2–1.8 Å\(^{-1}\). The measurement was taken of the empty zeolite Beta sample and the signal was then subtracted from the signal of the catechol-loaded Beta, so that only the signal from the catechol could be extracted. In this way any scattering from the aluminium container, which is very low in comparison with the zeolite is also subtracted. No further corrections were necessary. All QENS spectra were fitted using the neutron scattering analysis softwares packages DAVE [40] and MANTID [41].
2.2 Computational Simulations
The molecular dynamics simulations complementing the QENS experiments were performed with the code DL_POLY [42, 43]. The pairwise atomic forces in the zeolite structure are represented by Coulombic interactions and classical potentials, according to the Born model of ionic solids [44]. The system energy comprises a combination of Coulombic contributions [45], short-range repulsions and dispersion forces in the form of Buckingham and Lennard–Jones potentials [46, 47], and harmonic potentials to represent covalent bonds and bond-bending angles. Full ionic charges are employed for the framework atoms Si\(^{4+}\), Al\(^{3+}\) and non-protonated O\(^{2-}\), while the fractional charges proposed by Schröder et al. are used for the OH group of the Brønsted acid site, i.e. − 1.426 and +0.426 e\(^-\) for the O and H atoms, respectively [48]. The inter-atomic interactions in acidic zeolite Beta are represented by the classical parameters originally proposed by Sanders et al. [49] and further expanded in following works to account for the replacement of Si\(^{4+}\) by Al\(^{3+}\) [50], and the parametrization of the acidic OH group [48]. The full set of parameters are compiled in Table 1 of Ref. [35].
In our previous work, [35] we adapted the parametrization proposed by Mooney et al., which has been used to study liquid phenol over the range of temperatures 333–523 K, [51] to define the intra- and inter-molecular interactions in phenol. Since phenol and catechol differ only by the addition of a second OH group, we decided to continue using these parameters, modifying only the atomic charges for catechol. A linear regression is applied to the relationship between the atomic charges of phenol reported by Mooney et al. and the corresponding Mulliken charges at the B3LYP/cc-pVTZ level, as calculated by the code NWChem [52]. The Mulliken charges are also computed for catechol, and the derived linear equation is then used to estimate the catechol charges employed in the classical model. The harmonic parameters reported by Sastre et al. describe the C–C and C–H bonds of the aromatic ring [61], while the C–O and O–H bonds remain fixed as originally proposed by Mooney and collaborators [51]. The full set of parameters is compiled in Table 1.
The interactions of the O atoms of catechol with Si\(^{4+}\) and Al\(^{3+}\) are based on the Buckingham potentials defining the framework pairs (Si\(^{4+}\), O\(^{2-}\)) and (Al\(^{3+}\), O\(^{2-}\)), where the pre-exponential factor A is re-scaled following a procedure analogous to the protocol employed by Schröder and co-workers [48]. Only the Coulombic contribution is used to describe the interaction between the acidic proton and the O atoms of catechol, in similar fashion to the equivalent inter-molecular interaction in catechol [51]. The remaining interactions between the O and H atoms of the zeolite framework and the catechol molecule are defined by the Lennard–Jones potentials reported by Vetrivel and collaborators [53]. The full set of interatomic parameters is compiled in Table 2.
The polymorph A of zeolite Beta, with symmetry \(P4_122\), is employed in the simulations. Zeolite Beta has a three-dimensional pore system, with inter-connected straight pores along the a and b directions. After optimization, the lattice parameters of the crystal have values of \(a=12.465\, \AA\) and \(c=26.224\, \AA\), in close agreement with the experimental values of 12.5 \(\AA\) and 26.6 \(\AA\), respectively [54]. The Al atoms are placed at the T6 sites, with the protons bound to the O12 bridging oxygens [35]. A Si/Al ratio of 15 is achieved by adding four Al atoms to the unit cell of zeolite Beta, with one Al per straight pore out of four present in the unit cell. The all-silica structure is also included in the calculations in order to examine the effect of the acid sites on the diffusion of catechol.
The simulation supercell is constructed by expanding the unit cell of zeolite Beta to a \(4\times 4\times 2\) cell along the directions a, b and c. Afterwards, 128 molecules of catechol (4 molecules per unit cell) are added to the system, obtaining a concentration that is very similar to the loading of 10 wt% used in the QENS experiments. The MD simulations are carried out at a temperature of 393 K, with an initial equilibration of 1 ns employing a micro-canonical ensemble (NVE), followed by another 1 ns using a canonical (NVT) ensemble; in this case, the temperature is controlled with a Berendsen thermostat applying a time constant for thermal energy exchange of 1.0 ps [55]. The production run consists of 6 ns of NVE ensemble. An integration time step of 0.5 fs is employed during the simulations, saving the atomic coordinates every 2000 steps.
We obtain mean-squared displacement (MSD) plots with satisfactory linearity and statistics by applying the method of multiple initial times \(t_0\); the trajectory over 6 ns is averaged into 1 ns, shifting \(t_0\) every 25 ps. The MSD of the catechol molecules is calculated from the movement of their center of mass, deriving the self-diffusion coefficients from the Einstein relationship:
The QENS observables are calculated by averaging the 6 ns of trajectory into 100 ps, shifting \(t_0\) every 50 ps, the methodology of reproducing these observables is further outlined in Sect. 3.2.
3 Results and Discussion
3.1 Quasi-elastic Neutron Scattering Experiments
QENS spectra as a function of Q at 393 K for catechol in zeolite Beta are shown in Fig. 1. The QENS spectra at Q = 0.56 and 1.58 \(\AA ^{-1}\) were omitted due to the presence of a significant Bragg peak in zeolite Beta at these Q values, which caused issues upon subtraction of the empty zeolite signal from that of the loaded zeolite. The spectra were fitted to a delta function convoluted with the resolution measurement taken at 10 K, a single Lorentzian function (which could describe the data satisfactorily) and a flat background function. Figure 1 contains the data points, the total fit (black), and the quasielastic component of the spectra (red) given by a Lorentzian function.
As observed for phenol, we note that the Lorentzian component is very small, particularly at low Q values, and the elastic component is very large at all Q values (though the increase in the intensity of the Lorentzian component relative to the elastic component as a function of Q appears to be lower in catechol compared to phenol). This suggests that we are either observing localised motions (rotation or confined diffusion), or that a large proportion of the molecules are static on the timescales probed by the instrument. The need for only one Lorentzian function to fit the broadening of the spectra suggests that only one dominant mode of motion is observed on the timescale of the instrument, as was observed with phenol, though its prevalence may be less.
We now analyse the possible localised motions present which can be characterised using the elastic incoherent structure factor (EISF), which is given by:
and is the proportion of the total scattered intensity that is elastic. The experimental EISF at 393 K is shown in Fig. 2.
a Isotropic rotation of a catechol molecule with a radius of rotation r. b Rotational motions of catechol bound to the zeolite surface by one or two hydroxyl groups; (b, left) uniaxial rotation through the O–C\(_1\) bond axis of catechol bound by one hydroxyl, H-bonded to the Brønsted site, with rotational radii of \(r_{u1}\) and \(r_{u2}\) for the differing protons; (b, right) 2-site symmetrical rotation of the protons around the C\(_2\) axis of catechol bound through its two oxygens, H-bonded to the Brønsted site with rotational diameters of \(d_{1-3}\) for the 6 protons. c Translational motion of catechol confined to a sphere of radius \(r_{conf}\)
A number of models are available to characterise the localised motions of catechol, related to the geometries of motion of the protons in the molecule. We outline the models used to fit the experimental EISF now.
Isotropic rotation is characterised by a molecule whose reorientation takes place through a series of small angle, random rotations so that no ‘most probable’ orientation exists on a time average, as depicted in Fig. 3a. The scattering law as derived by Sears [56] for this form of rotation has an EISF, \(A_0(Q)\), given as:
where r is the radius of rotation, and \(j_0\) is the 0th order spherical Bessel function.
The average radius of rotation of the 6 protons as calculated from the catechol center of mass is 2.9 \(\AA\). The theoretical EISF for isotropic rotation with a radius of rotation of 2.9 \(\AA\) is plotted against the experimental EISF in Fig. 2 as the dashed black line. We note that the model falls far below all experimental points.
Our next consideration is that of a catechol molecule, which is hydrogen-bonded by one of its OH groups to the zeolite surface, with a rotating hydroxylbenzyl group (shown in Fig. 3b, left). A model which reasonably describes this motion is that of uniaxial rotation of these protons around the O-C\(_1\) bond axis. The 3 protons belonging to the aromatic ring (on C\(_3\), C\(_5\) and C\(_6\)) share the same radius of rotation (r\(_{u1}\)) of 2.16 \(\AA\) and the proton of the non-H-bonded hydroxyl group has the radius of rotation (r\(_{u2}\)) of 3.2 \(\AA\). This model cannot be used for powder samples that are typically used in studies of porous materials, because no expression exists for the average angle \(\theta\) between the axis of rotation and the direction of Q. However, with a sufficiently large N (> 7), the scattering function does not change as N increases. The approximation of jump rotation over N sites may then be used, given in Eq. 4a. This model necessitates the incorporation of an immobile fraction to account for the H-bonded hydroxyl proton and the proton attached to C\(_4\) being static, such that only 4/6 protons are mobile, shown in Eq. 4b.
The uniaxial rotation model is plotted as the dotted line in Fig. 2, but while it appears to fit the data points at low Q, it falls below the data points at mid and higher Q values.
In addition to this mode of adsorption, we may also consider a catechol molecule which is adsorbed via H-bonding of both hydroxyl oxygens to the same Brønsted acid site proton. If this form of adsorption were to take place, the most likely mode of motion would be rotation with two-fold symmetry between equivalent sites, i.e. the symmetrical flipping of the catechol molecule through its C\(_2\) axis, as depicted in Fig. 3b (right). There are 3 diameters of rotation relevant to this flipping, marked as \(d_{1-3}\) (\(d_1\) = 4.7, \(d_2\) = 5.0, \(d_3\) = 4.9 \(\AA\)) in Fig. 3b. We note that in previous DFT calculations, the out-turned hydroxyl’s orientation in this structure was found to be less favourable by 67 kJ/mol. However, we consider it to be a reasonable orientation when the molecule is adsorbed by both oxygens to a Brønsted site where the catechol hydroxyl protons would likely be repelled. The theoretical EISF of this 2-site jump rotation model is given by Eq. 5, where \(j_0\) is the 0th order spherical Bessel function in Eq. 3b, and d in this case is the average diameter of \(d_{1-3}\).
This model (shown in Eq. 5) is plotted against the experimental EISF in Fig. 2 as the dot-dashed black line. The line falls on the experimental points at the lowest Q values, but it falls below the experimental points at mid and higher Q values. The shape of the model function is also not in agreement with the shape of the experimental EISFs.
We now consider translational motion of the catechol localised to a confined volume. Volino and Dianoux [57] developed a model to describe a scattering molecule undergoing translational motions in a confined spherical volume of radius \(r_{conf}\) (shown in Fig. 3c). This scattering model is based on the general event of a particle diffusing in a potential field of spherical symmetry, where the potential is low inside the sphere’s volume but infinite outside of it.
The EISF of this model is given as:
where \(j_1\) is the spherical Bessel function of the first kind, order 1, and \(r_{conf}\) is the radius of the sphere to which the diffusion is confined. In this study we consider the radius of a micropore in zeolite Beta, i.e. 3.2 \(\AA\). The Volino model for confined diffusion is plotted in Fig. 2 as the solid black line, showing that the model falls below the experimental points at all Q values. For a detailed discussion on the derivation and implementation of all aforementioned models for localised motion, we refer the reader to the referenced resources [59, 60].
The localised models of motion alone are clearly not suitable to fit the EISF. However, we may also consider that only a fraction of molecules are mobile and undergoing such localised motions on the timescale of the instrument, as was observed for phenol, where a significant population of molecules was immobile, either sterically hindered by the Beta channels, or strongly interacting with the pore walls/acid sites. We can calculate an effective EISF which takes this situation into consideration, given by:
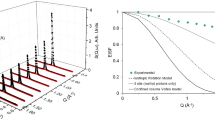
where \(p_x\) is the fraction of mobile molecules, and \(A_0(Q)\) is each EISF, as shown in Eqs. 3a, 4b, 5 and 6a. In Fig. 4 we have plotted these effective EISFs against the experimental data obtained at 393 K with the optimal \(p_x\) (as obtained by a least squares fitting procedure). The only model which is able to fit within all the experimental error bars is that of isotropic rotation with \(p_x\) = 0.39, suggesting that it is most likely that we are observing catechol rotating isotropically in the zeolite Beta pores with \(\sim\)61% of the molecules static on the timescale of the instrument (1–100 ps). We note that this is a significantly higher immobile fraction than that observed for phenol in the same zeolite, which had a static population of \(\sim\)40%. We consider that the reasons for this difference include the extra hydroxyl group on catechol allowing for an extra opportunity to strongly interact with the zeolite pore wall/Brønsted sites, or that the larger molecular radius of catechol could lead to more significant steric hindrance to its rotation, resulting in more molecules appearing to be static on the timescale of the instrument.
The full width at half maxima (FWHM) of the Lorentzian components of the QENS spectra as a function of Q at 393 K are plotted in Fig. 5. Crucially, the plot shows that the broadenings are independent of Q, which justifies our fitting of the EISF to a rotational model. We may now calculate the rates of rotation using the broadening of the Lorentzian components, with the isotropic rotational diffusion coefficient calculated as outlined in Ref. [23].
The rotational diffusion coefficients and mobile fractions are listed in Table 3. We note that, perhaps counter-intuitively, the calculated D\(^{rot}\) for catechol is slightly higher than that calculated for phenol in the same catalyst sample. However, the listed errors overlap for these values, and the mobile fraction \(p_x\) is significantly lower (by roughly 1/3) for catechol. We can therefore conclude that, compared to phenol, significantly more catechol is immobile over the timescale of the instrument, either owing to strong interactions with the acidic sites or the zeolite pore walls (due to the extra hydroxyl group of the molecule allowing for more H-bonding opportunities, and/or the generally increased molecular dimensions). However, we observe that the catechol molecules that are mobile undergo similar isotropic rotation to phenol with a similar (within error) rate of rotation.
3.2 Molecular Dynamics Simulations
The QENS experiments showed that phenol and catechol rotate at very similar rates (within error) in H-Beta, but with a significant difference in the amount of molecules that are visibly mobile to the spectrometer (39% of catechol compared to 60% of phenol molecules). This significant decrease in total mobility for the catechol system (despite the rates of rotation being similar) is reflected in the MD simulations, when we consider the longer-range translational mobility of both molecules in the zeolite, as shown by the MSD plots in Fig. 6. The highest translational diffusivity corresponds to phenol in all-silica Beta, with a diffusion coefficient of 8.04 × 10\(^{-10}\) m\(^2\)s\(^{-1}\) [35]. In comparison, the diffusion of catechol is slower by a factor of \(\sim\)3 compared to phenol in the siliceous zeolite, with a value of 2.51 × 10\(^{-10}\) m\(^2\)s\(^{-1}\), probably as a result of a higher recurrence of inter-molecular H-bonding interactions in catechol, which slows down the molecules, combined with more pronounced steric effects inside the micropore. In the presence of Brønsted acid sites, the translational motion is further constrained owing to the strong H-bonds formed between the OH groups of the molecules and the acidic protons. The Brønsted acid sites reduce the diffusion coefficient by a factor of approximately 5 and 10 for phenol and catechol in H-Beta, respectively (see Table 3). The fact that the catechol diffusivity is a factor of \(\sim\)7 lower in H-Beta than that of phenol illustrates the significance of the extra H-bonding capability of the diol.
We now proceed with the direct reproduction of QENS observables from our MD data. Equation 8 represents a Fourier transformation in the frequency domain, which allows one to obtain the incoherent dynamical structure factor \(S_{inc}({\varvec{Q}},\omega )\) from the self-part of the intermediate scattering function (ISF) \(F_s({\varvec{Q}},t)\) [29]:
\(S_{inc}({\varvec{Q}},\omega )\) is directly measured in experiment, as shown in Fig. 1. However, preserving the time-domain is better suited for the computation of the QENS parameters during the processing of the simulation data. Additionally, we have to consider that the QENS measurements are performed with polycrystalline samples, which justifies the use of the powder average expression of the function \(F_s({\varvec{Q}},t)\) [33, 58]:
In Eq. 9, N is equal to the number of H atoms in phenol and catechol, and \({\varvec{d}}_i\) represents the coordinate vector of the ith H atom with respect to the center of mass of the molecule and is thus sampling rotational motions. The modulus of the momentum transfer vector \(|{\varvec{Q}}|\) is represented by Q. To improve the statistics of the \(F_s(Q,t)\) sampling, we take the micro-canonical ensemble average over a set of initial times \(t_0\), which is denoted by the angular brackets in Eq. 9.
Powder average of the intermediate scattering function (ISF) obtained by feeding into Eq. 9 the proton coordinate changes with respect to the center of mass of catechol in all-silica Beta. The ISF curves are plotted for values of Q within the range 0.126 (top curve) to 2.016 \(\AA ^{-1}\) (bottom curve), at regular steps of 0.126 \(\AA ^{-1}\)
Figure 7 shows an example of the ISF curves obtained from Eq. 9 using the MD data for the adsorption of catechol in all-silica Beta. The ISF decays can be fitted with a combination of exponential functions, with each exponential describing a rotation in a specific frequency domain [27]. We are able to achieve a satisfactory fitting of the simulation data of catechol employing two exponentials, which was also the case for phenol [35]:
Schematic representation of an ideal, completely free isotropic rotation (grey circle with radius r), and a restricted rotation (blue circle with radius \(r'\)) with increasing level of constraint when moving from left to right in the scheme. The arrows represent the amplitude of the rotation over a period of time spanning from \(t_0\) to t
The decay factor \(\Gamma _n\) is equivalent to the half-width at half-maximum of a Lorentzian employed to fit the quasielastic component in a QENS experiment. The contribution of each exponential is expressed by the pre-exponential factor \(C_n\); for each value of Q, \(C_1(Q)+C_2(Q)+B(Q)=1\). The parameter B(Q) corresponds to the atomic arrangement in the momentum space when \(t\rightarrow \infty\), thus providing the molecular rotation symmetry. Therefore, the curve of B(Q) versus Q corresponds to the EISF, represented in Eq. 2, leading to a direct comparison between MD simulations and experiment.
Elastic incoherent structure factor (EISF) for phenol (red circles) and catechol (blue circles) in all-silica Beta (open circles) and H-Beta (full circles). The EISF is obtained after the fitting of the ISF curves with Eq. 10 and equating the parameter B(Q) to \(A_0(Q)\). The values of B(Q) for each system are represented by circles; the solid lines correspond to the best fitting of the isotropic model in Eq. 11 to the B(Q) data
The B(Q) parameter obtained from the MD data carries information from all the rotational motions present in the system. In this case, since two exponentials are needed for the fitting of the ISF curves, we should expect that the rotational model applied to the description of B(Q) should include information from two motions. We consider a combination of two isotropic rotations to fit the curves of B(Q) versus Q:
where \(c_n\) provides the contribution of the motion to the overall value of B(Q), with \(r_n\) representing the radius of rotation, or equivalently, the average molecular radius. The combination of two isotropic rotations proves suitable for the description of B(Q) over the entire range of Q values analysed in this study, as shown in Fig. 8. The values of \(c_n\) and \(r_n\) obtained after the fitting with Eq. 11 are listed in Table 3.
Phenol and catechol in all-silica Beta and H-Beta zeolites show \(r_1\) values that range between 2.4 and 2.7 \(\AA\), matching the radii employed to fit the experimental QENS data [35]. However, the second isotropic rotation included in the model of Eq. 11 reveals \(r_2\) values within the interval 0.7–1.4 \(\AA\) for phenol and catechol, which are too short for the size of these molecules. We can explain this discrepancy on the basis of a restricted motion that is approximated here as an isotropic rotation with a radius shorter than the one corresponding to a motion free of any constraint, as represented in Scheme 1.
In the present methodology, the amplitude of the rotation is represented by the displacement \(\Delta d=|{\varvec{d}}_i(t)-{\varvec{d}}_i(t_0)|\) in Eq. 9, which is averaged over all the molecules in the system. If there are no restrictions, the amplitude of the rotation reaches its maximum possible value, and the set of atomic displacements \(\Delta d\) in Eq. 9 leads to a B(Q) that, when fitted with an isotropic model, provides the expected rotation radius r, consistent with the dimension of the molecule. This case is represented by the grey circle in Scheme 1. However, constraints to the molecular movement may arise, for example, the strong H-bonds established between the molecular OH groups and the acidic protons of the zeolite. In this case, we could expect a motion characterized by a rapid rattling of restricted amplitude, with the molecule anchored through its O atom to the acid site. It is important to note that, during the processing of the MD data, the atomic coordinates of each molecule are referenced to its center of mass in order to take out the translational movement and exclusively deal with rotational motion. Thus, this rapid, hindered rattling of short amplitude is transformed into a restricted molecular rotation, as shown in Scheme 2. Additionally, we have to consider that this rattling should be random, which means that the corresponding restricted rotation is suitably described by an isotropic model when averaged over the entire set of molecules. Nevertheless, since the movement is constrained and hence the average atomic displacements \(\Delta d\) do not reach the maximum possible amplitude expected from the molecular dimension, the fitted rotational radius \(r'\) would be smaller than the ideal r obtained from a fully unrestricted isotropic rotation. We can conclude that the stronger the constraint on the molecular motion, the smaller the value of \(r'\) compared to r, whose case is represented by the set of blue circles in Scheme 1. This procedure allows us to decompose B(Q) into isotropic components, accounting for the most relevant rotational motions occurring in the MD simulations.
Q-Dependence of the rotational diffusion coefficients \(D_1^{rot}\) (blue circles) and \(D_2^{rot}\) (green circles) derived from the fitting of the ISF curves of each system with Eq. 13. The average values of \(D_1^{rot}\) and \(D_2^{rot}\) are represented by blue or green dashed lines; these average values are listed in Table 3. The lower and upper limits of \(D_1^{rot}\) are represented by grey dashed lines, with the numeric values stated in each plot (s−1). From left to right, phenol in all-silica Beta, catechol in all-silica Beta, phenol in H-Beta and catechol in H-Beta
In the present work, we have observed that the powder average of the ISF function is satisfactorily fitted by two exponentials. The first of these exponentials has a decay constant of \(\Gamma _1\) with a value within the experimental window of 0.55 meV, which we attribute to the isotropic rotation observed in the QENS experiments. Meanwhile, the decay constant \(\Gamma _2\) for the second exponential is above the 0.55 meV threshold, indicating a motion too fast to be observed in experiments. It is important to note that the QENS data are best described by an isotropic rotation model with a radius within the range 2.5–3.0 \(\AA\), consistent with an unrestricted isotropic rotation, and a fraction of immobile molecules. Therefore, upon considering the combination of two isotropic rotations necessary to fit the B(Q) function (the MD-generated EISF), we can conclude that the motion with rotation radius \(r_1\) between 2.4 and 2.7 \(\AA\) corresponds to the quasielastic signal detected in experiment, and thus with the first exponential. The second isotropic rotation with radius \(r_2\) between 0.7 and 1.4 \(\AA\) then most likely represents a rapid, restricted rattling of molecules anchored to the acid sites, too fast to be detected, and thus more likely to produce a flat background in the experimental scattering function.
Upon inspecting the coefficients weighing the contribution of the exponentials to the overall rotation, we note that the coefficient \(c_1\), which accounts for the unrestricted (long amplitude) isotropic rotation with radius \(r_1\), can be considered in terms of the fraction \(p_x\) of mobile molecules obtained from the QENS experiments. The value of \(c_1\) remains above 0.85 for phenol and catechol in all-silica Beta, with the contribution of the second isotropic motion lying below 0.15. This indicates that these molecules have a high degree of freedom in the all-silica zeolite, although there is a low but measurable level of constraints, which may arise from inter-molecular and/or molecule-zeolite interactions. When phenol dynamics is measured in H-Beta, the value of \(c_1\) drops from 0.91 to 0.82, with \(c_2\) consequently increasing to 0.18. Additionally, the rotational radius describing the rapid rattling decreases from 1.37 to 0.85 \(\AA\), suggesting an increase in hindrance caused by the strong H-bond interactions between phenol and the acid sites. The presence of a second OH group in catechol increases the level of observed constraints. The coefficient \(c_1\) for catechol in H-Beta shows a significant decrease, down to 0.56 from its value of 0.85 in the siliceous structure. We note that the experimental mobile fractions for phenol and catechol in H-Beta were measured at 0.60 and 0.39, respectively; 0.2 fractional units smaller than the calculated absolute values of \(c_1\) from the MD simulations (0.82 and 0.56, respectively), but retaining the same trends with a consistent offset. We therefore conclude that \(c_1\) can be compared directly to the \(p_x\) obtained by the QENS experiments, as they are describing the contribution of the same motion to the overall signal observed both experimentally and from the MD calculations.
The isotropic model can then be used to fit directly the \(F_s(Q,t)\) functions and calculate the rotational diffusion coefficient [33]:
where r is the rotational radius and \(D^{rot}\) is the rotational diffusion coefficient. As a development to our previous work on phenol, Eq. 12 can be further modified to consider the contribution of two isotropic rotations:
In Eq. 13, the 0th order spherical Bessel function, \(j_0\), is removed from the summation in Eq. 12 and treated independently from the rest of the expression. Two different sets of coefficients, \(\{c_n\}\) and \(\{C'_n\}\), are separately employed to weigh the contribution of both isotropic motions in the first and second summations of Eq. 13. Note that the summation \(\sum _{n=1}^{2}c_nj_0^2(Qr_n)\) in Eq. 13 is equivalent to Eq. 11, used to fit B(Q). Therefore, the parameters \(\{c_n\}\) and \(\{r_n\}\) already derived from the fitting of B(Q) are input in Eq. 13 and kept fixed during the fitting of \(F_s(Q,t)\), while the parameters \(\{C'_n\}\) and \(\{D_n^{rot}\}\) are allowed to vary. The first seven terms of the inner summation over l in Eq. 13 are retained during the fitting. We have to note that the addition of a second isotropic rotation in the fitting of the \(F_s(Q,t)\) curves will inevitably modify the value of the calculated \(D_n^{rot}\) compared to our previous work on phenol, which used a single isotropic motion during this procedure [35].
The calculated \(D^{rot}\) values are listed in Table 3. Figure 9 presents the variation of \(D_n^{rot}\) with Q. The diffusion coefficient \(D_1^{rot}\), corresponding to the long amplitude rotation with radius \(r_1\), shows a magnitude within the range \(10^{9}\) to \(10^{10}\) s\(^{-1}\), while \(D_2^{rot}\) remains at approximately \(10^{12}\) s\(^{-1}\), for phenol and catechol in all-silica Beta and H-Beta. Although tending to be smaller, the value of \(D_1^{rot}\) is comparable to the rotational diffusion coefficients derived from the QENS studies. The MD calculated values for the \(D^{rot}\) of catechol and phenol are relatively close, (that of catechol being \(\sim\)75% that of phenol) in a manner comparable to our experimental observations which have overlapping error bars. We note that the upper limit of our \(D_1^{Rot}\) values are also approaching those of experiment, with that of phenol lower than the experimental value by a factor of \(\sim\)2, and that of catechol lower by a factor of \(\sim\)3. We also note that \(D_2^{rot}\) is approximately two orders of magnitude larger than \(D_1^{rot}\), thus providing further evidence that the restricted molecular rattling is too fast to be observed by experiment.
4 Conclusions
The dynamical behaviour of catechol was studied in zeolite Beta (Si/Al = 12.5) using quasielastic neutron scattering at 393 K with a loading of 4 molecules per unit cell. Similarly to previous work probing phenol, a significant elastic component in all spectra was observed. Subsequent fitting of the EISF to the relevant models of localised catechol motion—including isotropic rotation and diffusion confined to a sphere matching dimensions of the zeolite Beta channels, along with dynamics of adsorbed molecules such as uniaxial rotation and 2-site flipping around the C\(_2\) axis—has suggested that on the instrumental timescale we are observing isotropic rotation of the catechol molecules in the zeolite pores, with a rotational diffusion coefficient of 2.9 × 10\(^{10}\) s\(^{-1}\). While this coefficient is slightly higher than that measured previously for phenol in the same zeolite, the values are within the experimental error of each other. The amount of catechol observed to be immobile on the instrumental timescale was significantly higher than that observed for phenol (~60% immobile catechol molecules compared to ~40% immobile phenol molecules). The molecular dynamics simulations agreed with this observation, first through a significant decrease in the long range diffusion coefficient calculated for catechol with a value of 0.25 × 10\(^{-10}\) m\(^2\) s\(^{-1}\) (a factor of \(\sim\)7 lower than that found previously for phenol). The MD simulations were then used to reproduce the experimental \(F_s(Q,t)\) and EISF, where it was found that two forms of isotropic rotation were necessary to fit the EISF calculated from the MD simulations. The first rotation corresponded to an unrestricted isotropic motion as observed experimentally, showing the same trend in terms of mobile fractions as in the QENS analysis, where a larger contribution of this unconstrained isotropic rotation could be attributed to the dynamics of phenol in H-Beta compared to catechol, with weighting (i.e. \(c_1 \equiv p_x\)) values of 0.82 and 0.56, respectively; the calculated rotational diffusion coefficients \(D_1^{rot}\) were also of similar magnitude to those measured experimentally. The second rotation fitted to the MD calculated EISF was considered to be a rapid rattling of restricted amplitude, corresponding to phenol and catechol molecules interacting via hydrogen-bonding with the acid sites of the zeolites. This motion had a higher contribution in the catechol system relative to phenol, consistent with more frequent interactions with the acid sites promoted by its extra OH group. The \(D_2^{rot}\) associated with this localised and very restricted second motion was calculated to be of the order of 10\(^{12}\) s\(^{-1}\), which is too fast to be observed within the experimental time window.
References
Rinaldi R, Schuth F (2009) Energy Environ Sci 2:610–626
Li C, Zhao X, Wang A, Huber GW, Zhang T (2015) Chem Rev 115:11559–11624
Ennaert T, Van Aelst J, Dijkmans J, De Clercq R, Schutyser W, Dusselier M, Verboekend D, Sels BF (2016) Chem Soc Rev 45:584–611
Schuth F, Rinaldi R, Meine N, Kaldstrom M, Hilgert J, Rechulski MK (2014) Catal Today 234:24–30
Kaldstrom M, Meine N, Fares C, Schuth F, Rinaldi R (2014) Green Chem 16:3528–3538
Calvaruso G, Clough MT, Rechulski MDK, Rinaldi R (2017) ChemCatChem 9:2691–2700
Hong DY, Miller SJ, Agrawal PK, Jones CW (2010) Chem Commun 46:1038–1040
Zhang W, Chen J, Liu R, Wang S, Chen L, Li K (2014) ACS Sustain Chem Eng 2:683–691
Kasakov S, Shi H, Camaioni DM, Zhao C, Barath E, Jentys A, Lercher JA (2015) Green Chem 17:5079–5090
Zhao C, Camaioni DM, Lercher JA (2012) J Catal 288:92–103
Zhao C, Kasakov S, He J, Lercher JA (2012) J Catal 296:12–23
Zhu X, Lobban LL, Mallinson RG, Resasco DE (2011) J Catal 281:21–29
Zhao C, Song W, Lercher JA (2012) ACS Catal 2:2714–2723
Zhu X, Nie L, Lobban LL, Mallinson RG, Resasco DE (2014) Energy Fuels 28:4104–4111
O’Malley AJ, Parker SF, Catlow CRA (2017) Chem Commun 53:12164–12176
Zachariou A, Hawkins A, Parker S, Lennon D, Howe R (2020) Catal Today. https://doi.org/10.1016/j.cattod.2020.05.030
O’Malley AJ, Parker SF, Chutia A, Farrow MR, Silverwood IP, Garcia-Sakai V, Catlow CRA (2016) Chem Commun 52:2897–2900
Lundie DT, McInroy AR, Marshall R, Winfield JM, Jones P, Dudman CC, Parker SF, Mitchell C, Lennon D, Phys J (2005) Chem B 109:11592–11601
Potter ME, Chapman S, O’Malley AJ, Levy A, Carravetta M, Mezza TM, Parker SF, Raja R (2017) ChemCatChem 9:1897–1900
Jobic H (2002) Curr Opin Solid State Mater Sci 6:415–422
Mitra S, Tripathy A, Gupta N, Mukhopadhyay R (2002) Appl Phys A 74:s1308–s1310
Jobic H, Bee M, Dianoux AJ (1989) J Chem Soc Faraday Trans 1L:2525–2534
Matam SK, O’Malley AJ, Catlow CRA, Suwardiyanto S, Collier P, Hawkins AP, Zachariou A, Lennon D, Silverwood I, Parker SF et al (2018) Catal Sci Technol 8:3304–3312
Jobic H, Renouprez A, Bee M, Poinsignon C (1986) J Phys Chem 90:1059–1065
Borah BJ, Jobic H, Yashonath S (2010) J Chem Phys 132:144507
O’Malley AJ, Garcia Sakai V, Silverwood IP, Dimitratos N, Parker SF (2016) Catlow CRA. Phys Chem Chem Phys 18:17294–17302
Sayeed A, Mitra S, Anil Kumar AV, Mukhopadhyay R, Yashonath S, Chaplot SL (2003) J Phys Chem B 107:527-533
O’Malley AJ, Catlow CRA, Monkenbusch M, Jobic H (2015) J Phys Chem C 119:26999–27006
Jobic H, Theodorou DN (2007) Micropor Mesopor Mater 102:21–50
Sharma VK, Gautam S, Mitra S, Mukhopadhyay R (2010) Zeitschrift fur Physikalische Chemie 224:133–152
O’Malley AJ, Hitchcock I, Sarwar M, Silverwood IP, Hindocha S, Catlow CRA, York APE, Collier PJ (2016) Phys Chem Chem Phys 18:17159–17168
Armstrong J, O’Malley AJ, Ryder MR, Butler KT (2020) J Phys Commun 4:072001
Mukhopadhyay R, Sayeed A, Mitra S, Anil Kumar AV, Rao MN, Yashonath S, Chaplot SL (2002) Phys Rev E 66:061201
O’Malley AJ, Sarwar M, Armstrong J, Catlow CRA, Silverwood IP, York APE, Hitchcock I (2018) Phys Chem Chem Phys 20:11976–11986
Hernandez-Tamargo C, O’Malley AJ, Silverwood IP, de Leeuw NH (2019) Catal Sci Technol 9:6700–6713
Furimsky E (2000) Appl Catal A 199:147–190
Patil PT, Armbruster U, Richter M, Martin A (2011) Energy Fuels 25:4713–4722
Barta K, Warner GR, Beach ES, Anastas PT (2014) Green Chem 16:191–196
Telling MTF, Andersen KH (2005) Phys Chem Chem Phys 7:1255–1261
Azuah RT, Kneller LR, Qiu Y, Tregenna-Piggott PL, Brown CM, Copley JR, Dimeo RM (2009) J Res Natl. Inst Stand Technol 114:341–358
Arnold O, Bilheux J, Borreguero J, Buts A, Campbell S, Chapon L, Doucet M, Draper N, Ferraz Leal R, M. Gigg et al. (2014) Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 764, 156-166
Todorov IT, Smith W, Trachenko K, Dove MT (2006) J Mater Chem 16:1911–1918
Bush I, Todorov I, Smith W (2006) Comput Phys Commun 175:323–329
Born M, Huang K (1988) Dynamical theory of crystal lattices. Oxford University Press, Oxford
Ewald PP (1921) Annalen der Physik 369:253–287
Buckingham RA (1938) Proc R Soc Lond A 168:264–283
Jones JE (1924) Proc R Soc Lond A 106:463–477
Schroder KP, Sauer J, Leslie M, Richard C, Catlow A, Thomas JM (1992) Chem Phys Lett 188:320–325
Sanders MJ, Leslie M, Catlow CR (1984) J Chem Soc Chem Commun 1271–1273
Catlow CR, James R, MacKrodt WC, Stewart RF (1982) Phys Rev B 25:1006–1026
Mooney DA, Muller-Plathe F, Kremer K (1998) Chem Phys Lett 294:135–142
Valiev M, Bylaska EJ, Govind N, Kowalski K, Straatsma TP, Van Dam HJ, Wang D, Nieplocha J, Apra E, Windus TL et al (2010) Comput Phys Commun 181:1477–1489
Vetrivel R, Catlow CRA, Colbourn EA (1989) J Chem Soc Faraday Trans 2 85:497–503
Newsam JM, Treacy MMJ, Koetsier WT, Gruyter CBD (1988) Proc R Soc Lond A 420:375–405
Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR (1984) J Chem Phys 81:3684–3690
Sears VF (1966) Can J Phys 44:1279–1297
Volino F, Dianoux A (1980) Mol Phys 41:271–279
Herwig KW, Wu Z, Dai P, Taub H, Hansen FY (1997) J Chem Phys 107:5186–5196
O’Malley AJ, Catlow CRA (2017) Chapter 6 - Sorbate Dynamics in Zeolite Catalysts. In: Fernandez-Alonso F, Price DL (eds) Neutron Scattering - Applications in Biology, Chemistry, and Materials Science, Experimental Methods in the Physical Sciences. Academic Press, 49, pp 349–401
Beé M (1988) Quasielastic Neutron Scattering, Adam Hilger
Sastre G, Raj N, Catlow CR, Roque-Malherbe R, Corma A (1998) Selective diffusion of C8 aromatics in a 10 and 12 MR zeolite. A molecular dynamics study. J Phys Chem B 102(17):3198–3209
Acknowledgements
This work was performed using the computational facilities of the Advanced Research Computing @ Cardiff (ARCCA) Division, Cardiff University, and HPC Wales. Via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC [Grant Number: EP/L000202], this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). The authors acknowledge EPSRC [Grant Number: EP/K009567/2] and NERC [Grant Number: NE/R009376/1] for funding. A.J.O.M acknowledges the Ramsay Memorial Trust for the provision of a Ramsay Memorial Fellowship, and Roger and Sue Whorrod for the funding of the Whorrod Fellowship. The STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities; the data from our experiment RB1720221 can be found at https://doi.org/10.5286/ISIS.E.87772570. Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalogue at http://doi.org/10.17035/d.2020.0120956733.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hernandez-Tamargo, C., Silverwood, I.P., O’Malley, A.J. et al. Quasielastic Neutron Scattering and Molecular Dynamics Simulation Study on the Molecular Behaviour of Catechol in Zeolite Beta. Top Catal 64, 707–721 (2021). https://doi.org/10.1007/s11244-020-01400-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11244-020-01400-1