Transport of Organic Volatiles through Paper: Physics-Informed Neural Networks for Solving Inverse and Forward Problems

Abstract

Transport of volatile organic compounds (VOCs) through porous media with active surfaces takes place in many important applications, such as in cellulose-based materials for packaging. Generally, it is a complex process that combines diffusion with sorption at any time. To date, the data needed to use and validate the mathematical models proposed in literature to describe the mentioned processes are scarce and have not been systematically compiled. As an extension of the model of Ramarao et al. (Dry Technol 21(10):2007–2056, 2003) for the water vapor transport through paper, we propose to describe the transport of VOCs by a nonlinear Fisher–Kolmogorov–Petrovsky–Piskunov equation coupled to a partial differential equation (PDE) for the sorption process. The proposed PDE system contains specific material parameters such as diffusion coefficients and adsorption rates as multiplication factors. Although these parameters are essential for solving the PDEs at a given time scale, not all of the required parameters can be directly deduced from experiments, particularly diffusion coefficients and sorption constants. Therefore, we propose to use experimental concentration data, obtained for the migration of dimethyl sulfoxide (DMSO) through a stack of paper sheets, to infer the sorption constant. These concentrations are considered as the outcome of a model prediction and are inserted into an inverse boundary problem. We employ Physics-Informed Neural Networks (PINNs) to find the underlying sorption constant of DMSO on paper from this inverse problem. We illustrate how to practically combine PINN-based calculations with experimental data to obtain trustworthy transport-related material parameters. Finally we verify the obtained parameter by solving the forward migration problem via PINNs and finite element methods on the relevant time scale and show the satisfactory correspondence between the simulation and experimental results.

Article Highlights

• A mathematical model to describe transport of polar volatile organics through paper is proposed.

• Based on experimental data, the deep learning method of physics-informed neural networks (PINNs) is used to solve the inverse problem of finding the sorption time constant.

• Solutions for the forward problem are obtained by the standard finite element method (FEM) and PINN methods.

• These solutions are compared with each other as well as with the experimental data to verify the model.

1 Introduction

Paper is a porous cellulose-based material. Structurally it can be pictured as a network of fibers held together by various types of chemical and physical interactions (Hirn and Schennach 2015).

To date, there is a lack of context-based numerical models that provide guidance to characterize and predict concentrations of volatile organic compounds (VOCs) during their transport through cellulose-based materials, i.e., paper. The interest to the named processes comes from the packaging industry. VOCs are compounds that readily sublimate or evaporate at normal conditions and therefore are prone to migrate through porous structures. On the one side, VOCs can be seen as essential aroma chemicals desired to be preserved in certain food products such as, e.g., the well known vanillin in pastry. On the other hand, some organic volatiles can be a cause of undesired contamination in products if migrated from or through the packaging and adsorbed by food. Therefore, it is of particular interest to be able to predict changes in concentrations of VOCs in paper and its adjacent layers over time.

This work focuses on a mathematical model suitable to predict the transport of polar VOCs through paper in thickness direction. Below, a particular VOC transported through a sheet of paper will be referred to as “migrant.” The sought mathematical model shall reflect the dependence of the migration process on the material properties of the paper/migrant pair. To understand which physical laws describe the processes relevant for a given pair, it is important to define the types of forces that drive the migration of the VOCs through paper. Generally, depending on the nature of migrants and pressure fields present, the transport through porous materials can be driven by various forces. In viscous or Knudsen flow it is the pressure gradient that drives the transport process. On the other hand, for the systems where the main transport process is described by diffusion laws, it is the spatial gradient of chemical potentials that controls the migration. In the latter case, chemical potentials are often substituted by the concentration values as they are more easily measurable in an experiment (Mehrer 2007).

Earlier it was shown on an example of water vapor transport through paper materials that in absence of pressure gradients the migration of volatile vapors is rather complex (Ramarao et al. 2003; Gupta and Chatterjee 2003a, b). It involves diffusion through the pore space as well as the diffusion through the solid fibrous phase of the paper matrix. Parallel to the diffusion also adsorption and desorption of the migrant take place on the surface of the paper fibers (Bandyopadhyay et al. 2000).

The aforementioned model of water vapor transport through paper was presented in Bandyopadhyay et al. (2000), Bedane et al. (2016) in a form of a nonlinear Fisher–Kolmogorov–Petrovsky–Piskunov parabolic partial differential equation (PDE) coupled to a PDE for the sorption process. In the present work we will use this approach as the starting point. On an example of dimethyl sulfoxide (DMSO), we will extend the ideas of Ramarao, Bandyopadhyay et al. toward the migration process of polar organic volatiles prone to strongly sorb onto the fibrous matrix of cellulose-based materials.

Since each particular volatile substance migrating through paper of a particular type will establish a unique complex of interactions with the paper material, diffusion and adsorption will be characterized by a set of material properties that is specific for the given “VOC/paper type” pair. In this sense it is crucial to find the way to determine the diffusion coefficients and sorption constants of a given system.

Various measurement techniques have been developed in order to determine the material parameters relevant for diffusion processes in porous materials (Poças et al. 2011; Li et al. 2019; Zülch and Piringer 2010). Typically, these are either methods based on empirical dependencies as, e.g., in Sakintuna et al. (2005) and Sakintuna et al. (2006) or indirect methods aiming to solve a so-called inverse problem (Crank 1975). An inverse problem seeks to identify unknown, not directly observable parameters in a PDE system by calibration of a macroscopic mathematical model to experimental data.

If the given mathematical model allows to obtain analytical solutions, the inverse problem takes the form of a regression model applied to known solutions represented by experimental data. In the absence of analytical solutions, building the regression model becomes a time-consuming challenge because every unique set of initial and boundary conditions requires a thorough mathematical investigation. More on the described issues can be found in Crank 1975, Isakov (2017), Keung and Zou (1998), Wang and Zou (2010), Prilepko and Kostin (1993) and Kunisch and White (1985). These methods, however, are generally cumbersome to use in practice as they require large amount of data points to achieve satisfying accuracy of the estimated parameters.

In the past few years, physics informed neural networks (PINNs) have been developed to solve forward and inverse PDE problems. In this context, “solving PDE problems forwardly” refers to directly solving the system of PDEs subjected to certain initial and boundary conditions without any further calibration. PINNs are neural networks that are trained to solve supervised learning tasks while respecting any given law of physics described by general nonlinear partial differential equations (Raissi et al. 2017). PINNs have demonstrated a great potential to significantly outperform traditional brute force computations and function-fitting methods in solving inverse problems (Lu et al. 2020; Depina et al. 2022). It was demonstrated that solving inverse problems becomes possible even for cases in which only a sparse amount of reliable experimental data is available (Karniadakis et al. 2021).

PINN methods require the independent variables as input, in our case of one dimensional transport the spatial coordinate x, time, and the free parameters. The entered coordinates form a pool of so-called collocation points, which can be selected either randomly or to suit the problem best. To solve an inverse problem, the experimental data are attached to the respective input coordinates and passed as anchor points to the PINN. Subsequently, the PINN method simultaneously optimizes (i) the weight and bias parameter associated to a neural network (NN) and (ii) the values of the desired parameters in order to approximate the solution of the PDEs with the NN prediction in each collocation point as best as possible. This objective is enforced by a regularized loss function (Pakravan and A. Mistani P, Aragon-Calvo MA, 2021). The loss function assesses whether the derivatives of the output of the neural network with respect to its input variables are consistent with the relations between these derivatives prescribed by the PDEs. The necessary numerical differentiation is realized with automatic differentiation (Lu et al. 2021) which does not require meshes and, hence, obliterates common issues related to mesh-based differentiation in, for example, finite element methods (FEM). For in-depth descriptions of the PINN method we refer the reader to Raissi et al. 2017, Yuan et al. (2022), Bischof and Kraus (2021), Lu et al. (2021) and Pakravan and A. Mistani P, Aragon-Calvo MA, (2021).

In this work we employ the latest generation of PINNs from the DeepXDE library (Lu et al. 2021) to implement the proposed mathematical model. We combine this model with experimentally obtained data on concentration fields of DMSO inside a stack of paper layers. The experimental setup allows us to track changes in DMSO concentrations over time and space during its transport through the paper layers. Taking advantage of the advanced optimization capabilities of PINNs, we solve an inverse problem to determine sorption kinetic constant that is a crucial parameter in the proposed transport model.

To verify our model, we solve the forward problem via the FEM simulations carried out via the pdepe function in MATLAB and compare these FEM solutions to the solutions obtained by PINNs. A close correspondence of these two solutions verifies that the PINN approach is suitable for solving the PDE system both inversely and forwardly.

2 Transport Model

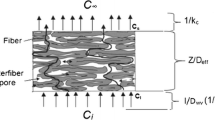
Firstly, in this work the discussion will be limited to diffusion in isothermal ($T < 50^\circ$), isobaric systems with no external force field gradients; the convective transfer is neglected. Secondly, we consider the transport process taking place along thickness direction x for a volatile migrant in concentrations below the saturation point. That is, in the following model the process never reaches the stage of condensation, therefore no capillary effects are taken into account. Lastly, we make a distinction between the part of the migrant in the gas phase of paper pores, and the part of the migrant which is sorbed onto the solid fibrous matrix (Fig. 1).

Fig. 1

Schematics of VOCs transport through paper. A VOC enters the pore space of a paper sheet. Parallel to diffusion through the gas phase of the pores sorption onto the fibers also takes place. After reaching the opposite side of the paper sheet, the VOC is released

2.1 Migration in the Gas Phase

The mass conservation equation for the vapor part of the migrant in the gas phase is given by:

$$\begin{aligned} \epsilon \frac{\partial c}{\partial t} = \epsilon \frac{\partial }{\partial x}\left( D_p \frac{\partial c}{\partial x}\right) - (1-\epsilon ) \frac{\partial q}{\partial t} \end{aligned}$$

(1)

where c is the vapor concentration of the migrant (mol/m$^3$) and $\epsilon$ the volume fraction of pores (porosity). The first term on the right-hand side accounts for the change in the gas phase concentration due to the diffusion. The diffusion coefficient $D_p$ is a binary diffusion coefficient of a mixture “migrant VOC vapor—air.” $D_p$ characterizes mutual diffusion of the mixture components inside the pore space of the paper material (m$^2$/s). The methodology to find $D_p$ will be described in Sect. 2.6.

For the present work we will consider $D_p$ being constant with respect to time and space, thus reducing Eq. (1) to:

$$\begin{aligned} \epsilon \frac{\partial c}{\partial t} = \epsilon D_p \frac{\partial ^2 c}{\partial x^2} - (1-\epsilon ) \frac{\partial q}{\partial t} \end{aligned}$$

(2)

The second term on the right side of equations (1) and (2) keeps track of local concentration changes caused by the binding of part of the migrant q to the solid part of the paper matrix.

2.2 Bound Migrant

Analogously to moisture transport in wood walls (Krabbenhøft 2004) and paper fibers (Bandyopadhyay et al. 2000) the flow of the migrant bound in and on the surface of paper fibers is assumed to be a diffusive process, that is governed by the following continuity equation:

$$\begin{aligned} \frac{\partial q}{\partial t} = \frac{\partial }{\partial x}\left(D_q \frac{\partial q}{\partial x}\right) + \dot{m} \end{aligned}$$

(3)

where q is the amount of the migrant bound to fibers per unit volume of paper (mol/m$^{3}$); $D_q$—the diffusion coefficient of the bound migrant through the solid matrix (m$^2$/s). The sorption term $\dot{m}$ accounts for the interchange between bound migrant and the gas phase (mol/m$^{3}$s), i.e., the adsorption and desorption of the migrant from/to the fibers. In case of adsorption $\dot{m}$ is positive. For the diffusion coefficient $D_q$ it is expected to depend on actual concentration of the migrant in the fibers and temperature. Bandyopadhyay et al. (2000) showed that $D_q$ is 3–4 orders of magnitude lower than $D_p$ for moisture transport in paper materials. That fact was attributed to high polarity of water molecules [$\mu = 1.85$ Debye (Zhu and Van Voorhis 2021)], that allows them to build strong bonds to the lignocellulosic fibers. In turn, these bonds hinder further diffusion within the solid phase of paper.

Since the dipole moment of a DMSO molecule has an even larger value of $\mu = 3.96$ Debye (Itoh and Ohtaki 1987), we will make an assumption for DMSO diffusion coefficients in paper: $D_q$ $<<$ $D_p$. With that the complexity of (3) can be reduced by neglecting the term related to the intrafibrous diffusion and taking only sorption processes into account:

$$\begin{aligned} \frac{\partial q}{\partial t} = \dot{m} \end{aligned}$$

(4)

2.3 Sorption Term $\dot{m}$

The sorption term $\dot{m}$ will be idealized as an uptake of the migrant by the fibers at a specific location x as a linear relaxation process:

$$\begin{aligned} \dot{m}(x,t) = k(q_{sat}-q(x,t)) \end{aligned}$$

(5)

where k is internal sorption rate constant (s$^{-1}$), $q_{sat}$ is the volumetric saturation concentration in the fibers (mol/m$^{3}$).

2.4 Initial and Boundary Conditions

The initial conditions are given as zero concentration in the porous and solid regions of the paper sheets:

$$\begin{aligned} q(x,t=0)=c(x,t=0)=0 \end{aligned}$$

(6)

Symmetrical Dirichlet boundary conditions are assumed:

$$\begin{aligned}&c(x=0,t)=c_{sat} \nonumber \\&q(x=0,t)=q_{sat} \nonumber \\&\frac{\partial c}{\partial x} (x=L,t) = 0 \nonumber \\&\frac{\partial q}{\partial x} (x=L,t) = 0 \end{aligned}$$

(7)

in which L is the length of the transportation path in transversal direction, i.e., thickness of the paper layer, and $c_{sat}$ is saturation concentration of the migrant in the gas phase. The last two equations enforce zero flux at the right boundary of the transportation path along the x-axis. This particular condition corresponds to the experimental setup described in the next sections.

2.5 Normalized PDEs System

Collecting the contributions from the previous subsections, the proposed mathematical model for the transport of a polar migrant through paper consists of the system of PDEs (2), (4), and (5) accompanied by the initial and boundary conditions from (6) and (7).

For the calculations employed in this work, the PDEs are reformulated in dimensionless quantities. We rearrange the PDE system such that the time-space domain becomes $0 \le X \le 1$; $0 \le T \le 1$. The concentration functions are normalized to their maximum values $q_{sat}$, $c_{sat}$ such that C and $Q \in [0;1]$.

The final system of PDEs is expressed as follows:

$$\begin{aligned}&\frac{1}{\alpha } \frac{\partial C}{\partial T} = \gamma \frac{\partial ^2 C}{\partial X^2} - \frac{(1-\epsilon )}{\epsilon } \frac{\partial Q}{\partial T} \nonumber \\&\frac{\partial Q}{\partial T} = \theta * k * (1-Q(X,T))\nonumber \\&C(X,T=0)=Q(X,T=0)=0\nonumber \\&C(X=0,T)=Q(X=0,T)=1\nonumber \\&\frac{\partial C}{\partial X} (X=1,T) = 0 \nonumber \\&\frac{\partial Q}{\partial X} (X=1,T) = 0 \end{aligned}$$

(8)

in which the dimensionless coordinates are defined as:

C:

$c/c_{sat}$

Q:

$q/q_{sat}$

X:

x/L

T:

$t/\theta$

and the parameters become:

$\theta$:

characteristic time, s

$\alpha$:

$q_{sat}/c_{sat}$, a.u.

$\gamma$:

$\frac{\theta D_p}{\alpha L^2}$, a.u.

For the full list of definitions, consult the Nomenclature section in Appendix A.

2.6 Diffusion Coefficient $D_p$

The well-developed theory to describe diffusion in binary gas mixtures at low to moderate pressures, usually credited to Chapman and Enskog (Poling et al. 2001), results from solving the Boltzmann equation. Based on the Chapman-Enskog equation, Brokaw (Chalykh 1987) proposed a refined relation if one or both components of a gas mixture are polar. Further, based on ideas of Enskog, Chapman and Brokaw, among other authors, Wilke and Fuller (Fuller et al. 1966) proposed their empirically derived relations for diffusion coefficients of binary gas systems. A detailed descriptions of all these methods can be found in Chap. 11 of Poling et al. (2001). Here we will refer mainly to the empirical equation of Fuller. This equation was derived by regression of the experimental results from a large number of binary systems:

$$\begin{aligned} D_p = 10^{-3} T^{1.75} \frac{ (1/M_A + 1/M_B)^{1/2} }{P\left[ \left( \sum v\right) _A^{1/3} + \left( \sum v\right) _B^{1/3} \right] ^2}. \end{aligned}$$

(9)

Therein, $M_A$ and $M_B$ being the molecular masses of A and B, g/mol; P—pressure [atm], $(\sum v)_A$, $(\sum v)_B$ represent the sum of dimensionless diffusion volume increments of atoms and structural elements constituting compounds A and B, respectively. The values $v_i$ for atomic and structural constituents relevant for organic compounds as well of some simple inorganic molecules and air can be found in Chap 11. of Poling et al. (2001) and in Chalykh (1987). According to Poling et al. (2001), Eq. (9) was applied to a broad range of binary systems and gave predictions with an average absolute error of about 4%.

Therefore, the diffusion coefficient $D_p$ used in this work will be calculated as the binary diffusion coefficient for the mixture “volatile migrant—air.”

3 Materials and Methods

In order to obtain experimental data to model the transport of VOCs through paper, two analytical procedures were developed and are described in the following section.

3.1 Paper Samples and Model Compounds

The experiments were carried out using an unbleached, sized Kraft pulp based paper sample. In order to determine the sorption of volatile organic compounds on paper, dimethyl sulfoxide (DMSO) (67-68-5), b.p. 189 $^{\circ }$C, was used as a model compound. DMSO was purchased from Sigma-Aldrich (USA). The paper samples were extracted in acetone (pesticide grade) purchased from Chem-Lab (Belgium).

3.2 Analytical Procedure to Determine Sorption Maximum

The maximum amount, $q_{sat}$, of DMSO which can be taken up by paper was determined by exposing a sheet of paper with defined dimensions and mass ($\sim$ 120 mg) to DMSO vapor above 10 mL liquid DMSO in a sealed 60 mL screw vial. The experiment was carried out at ambient conditions. The sheet of paper was weighed regularly until mass consistency was reached and subsequently extracted as described in the following paragraph. A threefold determination was carried out with the exact value for the sorption maximum determined with gas chromatography coupled to a flame ionization detector (GC/FID) via an external calibration.

3.3 Analytical Procedure to Obtain Concentration Profiles

In order to obtain concentration profiles, q, of DMSO over time and space on a paper sample, the following experimental setup using migration cells (MigraCell$^{\circledR }$ MC 60; testing area $\sim$ 0.5 dm$^2$; FABES Forschungs-GmbH, Germany) was employed. The paper was cut into disks of $\sim$ 0.5 dm$^2$ testing area using a laser cutter. A stack of five paper disks was placed in the migration cell (Fig. 2). To avoid permeation of DMSO through the paper stack, the top paper sheet was covered with a metal plate. The cell was closed as described by the manufacturer. To ensure that a sufficient amount of DMSO is available to be taken up by the paper sheets, the amount of DMSO added into the lower chamber of the cell was 500 $\upmu$L, applied with a Gilson m1000 pipette (Gilson, Inc, USA). The chosen amount of DMSO is assumed to be sufficient to maintain a saturated atmosphere of the model compound inside the migration cell. During the sorption process the cells were placed on a magnetic stirrer to ensure convection of the DMSO inside the cell. The experiments were carried out at ambient conditions, i.e., about 23 $^{\circ }$C and 50% RH.

In order to obtain the time-resolved sorption of DMSO on the paper stack, an array of migration cells was simultaneously prepared as described above with paper disks from the same paper sample. At certain pre-defined times within the range of 15 min to 120 h, the paper stack was removed from the cell and extracted in acetone. For that purpose, each paper disk was cut into smaller pieces and placed into a 30-mL glass vial with screw cap. 10 mL of acetone was added, and the sample was vortexed for 5 min. An aliquot of the extract was transferred into a 2-mL glass vial with screw cap and analyzed with GC/FID. In order to consider the paper matrix for external calibration, paper samples ($\sim$ 0.5  dm$^2$) were directly spiked with a defined amount of DMSO for a calibration between 44 $\upmu$g DMSO/g paper and 220 mg DMSO/g paper. The paper samples were extracted immediately in 10 mL acetone for 5 min on a Vortex. The extraction recovery of the model compound directly spiked on paper samples followed by extraction was proven to be good in previous experiments. All determinations were carried out at least in duplicate.

Fig. 2

Experimental setup to determine concentration profiles

3.4 GC/FID Analysis

The GC unit was a Shimadzu GC-2010 plus gas chromatograph equipped with a AOC-20i Shimadzu auto injector and a flame ionization detector. The used column was a Zebron ZB-Wax (30 m $\times$ 0.32 mm $\times$ 0.25 $\upmu$m) purchased from Phenomenex (USA). The following GC parameters were kept constant: detector temperature, 250 $^{\circ }$C; injector temperature, 220 $^{\circ }$C; injection mode, splitless; injection volume, 1 $\upmu$L. The column temperature program was from 50 $^{\circ }$C (1 min) to 220 $^{\circ }$C (1 min) in 10 $^{\circ }$C/min. The carrier gas was helium with a total flow rate of 36.1 mL/min. Data were evaluated using “LabSolutions” Version 5.92.

3.5 PINNs as Method to Solve Forward and Inverse PDE System Problem

PINNs can be seen as a universal function approximator based on compositional functions, named deep neural networks (DNNs). During the training of neural networks, the DNNs are optimized to satisfy a given PDE problem (Yuan et al. 2022).

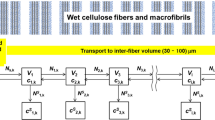
The scheme in Fig. 3 illustrates the logic of the application of PINNs on the example of the DeepXDE library from Lu et al. (2021). The “deep neural network” block in Fig. 3 suggests a solution $u_i$ of the PDE at a set of so-called collocation points with the coordinates ($x_i$, t). The $u_i$ is a compositional function and contains a large number of adjustable parameters. If these parameters are appropriately adjusted, $u_i$ will correctly represent the solution of the PDE. This adjustment takes place iteratively. At first the deep neural network makes a suggestion for the $u_i$ at an arbitrary chosen set of collocation points.

At the next step the validity of the $u_i$ proposed by the DNN is checked. An automatic differentiation straight-forwardly calculates the values of the partial derivatives of $u_i$, that are inserted into the equations of the physical problem as shown in the block of “physics information” (Fig. 3). Deviations from the PDE-prescribed relations among these derivatives of the neural network functions $u_i$ at any of the coordinates gives rise to a non-vanishing residual. Additional discrepancies between the network prediction and the initial and boundary conditions as well as experimental data are also cast into residuals. The weighted summation of the $L^2$ norm of residuals (mean square errors—MSE) of the PDEs and equations of boundary and initial constraints forms the loss function. Based on value of the loss function, the so-called loss, the parameters inside $u_i$ are altered (Fig. 3). With such adjusted parameters the process cycles anew beginning with the now updated DNN prediction.

The iterative process of optimization takes place until the total loss falls under a predefined threshold value. According to the state of the art (Sacchetti et al. 2022), the total loss typically needs to be smaller than $10^{-3} - 10^{-4}$ to achieve the solution accuracy comparable to classical FEM schemes.

The inverse problem is defined as a searching procedure for unknown parameters contained in a PDEs system by applying regression methods to experimentally obtained data and the PDEs solutions. As it was described in the Introduction section, PINNs are capable to solve inverse problems by optimizing its set of neural network functions so that these functions simultaneously satisfy the experimentally measured values serving as the PDEs solutions and provide unknown values at the chosen set of collocation points.

The experimental data are introduced to the PINNs as a set of pre-defined PDEs solutions at fixed collocation points, the so-called anchor points. Further, the validation check takes place for the losses encountered in the forward problem in combination with the losses obtained for experimental data. The parameters of the PDEs are being optimized together with the parameters of DNNs in order to achieve minimal losses.

Fig. 3

The framework of PINNs to solve the inverse problem of PDEs. Adapted from Lu et al. (2021)

Deep neural networks typically operate in the phase space $[0;1]^R$, where R is the dimension of the spatial domain. Therefore, the original PDE systems and the measurement data require a respective normalization procedure. Typical optimizers used in DeepXDE are adam and $L{-}BFGS{-}B$. The latter allows to significantly reduce calculation times and to obtain better results for the forward problem. However, $L{-}BFGS{-}B$ is not perfectly suitable for inverse problems as, for the moment, it does not allow an intermittent tracking of the values found for the optimized PDE parameters.

4 Results and Discussion

4.1 Large Time Scale Sorption and Sorption Maximum

The determination of the sorption concentration of DMSO on a paper sample allows us to (i) determine the maximum amount of DMSO [mmol/l] which can be adsorbed by a given volume of paper and (ii) the time needed to achieve the saturation state. This data is required to set the boundary conditions of the proposed transport model.

The large time scale sorption and the sorption maximum of around 650 mg DMSO/g paper were determined by exposing a paper strip to DMSO vapor and weighing it regularly until mass consistency was reached (Fig. 4). For more details see Sect. 3.2. This gravimetrically determined saturation concentration was independently corroborated via GC/FID analysis; after $\sim$ 12 weeks of exposing the paper to DMSO vapor a value of 593 ± 13 mg DMSO/g paper was determined. This confirms the paper samples take up large amounts of DMSO, what is consistent with previous studies that demonstrated a high affinity of paper samples toward polar model compounds (Chami Khazraji and Robert 2013).

Fig. 4

Results of one gravimetrical measurement for DMSO sorption amounts in paper vs time

Remarkably, it takes almost three months to reach the sorption maximum with this setup, which is an extremely long period compared to the time scale in the 5 layer paper stack experiments described in the Sect. 4.3.

Table 1 compares the saturation concentrations of DMSO found in a paper sample to the saturation concentration $c_{sat}$ of DMSO that can be reached in the gas phase at the same ambient conditions. The value of $q_{sat}$ = 11,800 mol/m$^3$ was converted from the previously found value of maximum sorption content of 660 mg DMSO/1 g paper for the given paper type of the known density $\rho = 1.4 \, \mathrm{g/cm}^3$. The DMSO saturation concentrations were estimated based on the partial pressures at the saturated state found experimentally in Ghazoyan et al. (2014). The time needed to reach saturation in the gas phase was estimated by applying second Fick’s Law for free diffusion in the gas phase with respect to the geometry of the migration cell set-up used in the experiments; the simulations were performed with the COMSOL Software.

Table 1 Comparison of the DMSO saturation processes inside pores and in the solid matrix of paper at $T = 296$ K, $P = 1$ atm

As it is shown in Table 1, the saturation concentration in the fibers $q_{sat}$ is about 4,72,000 times larger than that inside of pores. This circumstance can be explained by the fact that the migrant is adsorbed very efficiently by the fibers such that the bounded molecules of the volatile substance, occupying suitable positions within the solid phase, account to significantly larger concentration calculated per unit volume as compared to the gas phase. Moreover, for the experimental set-up used, it took about 2200 times longer to reach $q_{sat}$ inside the fibrous matrix as compared to $c_{sat}$ inside pores.

4.2 Spatial Concentration Profiles

In order to obtain the concentration of DMSO, $c+q$, on paper over time and space, sorption experiments were carried out with a stack of five paper sheets that were individually analyzed after defined time periods. For each time point at least three measurements have been conducted; the sheet-related mean values were used for the subsequent calculations and modeling. Figure 5 depicts the spatial concentration profile (mean value ± standard deviation) for a selection of time points. A continuous nonlinear concentration decline from the 1st paper layer at the bottom of the stack to the 5th layer at the top can be observed with the largest concentration drop between 1st and 2nd layer. The latter indicates that a major amount of DMSO is already retained by the 1st layer.

Fig. 5

Spatial concentration of DMSO in the paper layers for selected time points (mean value ± standard deviation)

4.3 Temporal Concentration Evolution

The phase space (x, t, q) containing the experimentally obtained data points is shown in Fig. 6. The DMSO vapors get transported from the source point on the left at $x=0$ across the paper stack toward the boundary at the right side of x-axis, where the fluxes associated with c and q are kept at zero. The change in the concentration in each paper layer over time can be tracked along the t-axis. The experimental data on concentrations were obtained as average concentration for each paper sheet, and therefore, the position coordinate x for each data point was assigned at the middle-thickness of the respective paper layer.

Fig. 6

Experimentally obtained data for DMSO sorption concentration q in paper vs time and distance

Figure 7 permits a more detailed comparison of the layer-specific time evolution. The amount of DMSO sorbed on the paper sample seems to increase almost in each paper layer during the first few hours. However, the DMSO concentration increases in layer 1 to a distinctly larger extent than in layer 5 with ongoing experimental time. This results in an even more pronounced spatial concentration gradient with its maximum after 28 h.

Afterward, the concentration in the 1st layer seems to approach a maximum as the concentration increment per time unit declines (Fig. 7). In contrast, the concentration in layer 5 does not tend to saturate. Indeed, in this layer the concentration increment toward the end of the experiment is even higher than at the beginning. The concentration drop in the sorption content between 100 and 120 h could be explained by the inhomogeneous nature of paper, production related variations of the used migration cells or uncontrolled environmental influences, for instance humidity.

As a result, the concentrations in the individual layers are converging, which leads to a continuous decline of the concentration gradient. Remarkably, all determined concentrations, even in the 1st layer at the end of the experimental time range are far below the total sorption maximum defined via GC/FID (see Sect. 4.1) as 593 ± 13 mg DMSO/g paper .

Fig. 7

Temporal evolution of the DMSO concentration in all 5 paper layers (mean values)

4.4 Prediction of the Sorption Constant

The sorption constant k was obtained by utilising the PINNs method (Sect. 3.5). The PDEs system (8) was implemented in the framework of the DeepXDE python Package (Lu et al. 2021).

Based on the results for sorption concentrations q of DMSO in paper sheets it was assumed that the saturation process inside the fibrous paper matrix requires a period of 30 days to achieve 90% of maximum concentration $q_{sat}$. The saturation process in the gas phase, $c_{sat}$, is assumed to be completed on a time scale of one hour.

For the inverse problem, the value of characteristic time $\theta$ in the PDEs system (8) was set to 30 days. Further values of the parameters in system (8) used to solve the inverse as well as the forward problem are provided in Table 2.

Table 2 Parameters values in PDE system (8) used for the inverse and the forward problem of DMSO transport through the paper stack

Detailed calculations for $D_p$ for the binary gas system “DMSO—air” can be found in Supporting Information, Section 1, Eq. S1.

The data on the concentration values obtained in Sect. 4.2, shown in Fig. 6, served as anchor points in the PINN framework, i.e., they were assigned the value of the q-function at fixed (x, t) positions.

The PINNs optimization procedure for the sought k-value was initiated in series of simulations with different initial guesses for parameter $k_{0}$. For each $k_{0}$ the calculation was performed in triplicate. Regardless of the initial guess for $k_{0}$, the PINNs solutions converged toward $k * \theta \approx 1.965 \pm 0.02$ once the loss function values dropped below $5\times 10^{-4}$. The best results for the test and train loss were achieved with the multi-objective loss balancing method as described in Lu et al. (2021) and Bischof and Kraus (2021).

Figure 8a, c show the optimization convergence of the k value for the initial guess $k_{0}*\theta = 1.2$ and $k_{0}*\theta = 4$, respectively. Figure 8b, d shows the respective evolution of train losses during the optimization of k.

Fig. 8

Regardless of the initial guess for $k_{0}$, the values of the sorption constant k in the diffusion-sorption system (8) converge to the same value during the PINNs training process. a Initial value $k_{0}*\theta = 1.2$ converges to $k*\theta = 1.951 \pm 0.018$ with an evolution of the train loss shown in b; c Initial value $k_{0}*\theta = 4$ converges to $k*\theta = 1.983 \pm 0.012$ with an evolution of the train loss shown in d. The dashed lines in a and c mark the predicted value $k*\theta$

Finally, the PINNs determined the optimized value of k = 7.65e−07 $s^{-1}$ for DMSO sorbing on the chosen paper type.

4.5 Validation of Mathematical Model. Solutions for Forward Problem

The validation of the mathematical model was performed by solving the PDE system (8) in combination with the results for the sorption constant (Sect. 4.4) and further model parameters as defined in Table 2. The geometry as well as boundary and initial conditions for the simulations were chosen to mimic the experimental set-up for the paper stack experiments from Sects. 4.2 and 4.3. At $x=0$ the stack is offered the saturation concentration $c_{sat}$ and $q_{sat}$, respectively, at all times.

The forward problem simulations were carried out by means of the FEM method and PINNs method. We used an in-built Matlab function ”pdepe” as FEM solver. For PINNs, the same DeepXDE library was used as for the inverse problem.

Fig. 9

PINNs simulation for the DMSO transport through a stack of 5 paper sheets over the duration of 30 days: a gas concentration c(x, t), b sorbed concentration q(x, t)

The calculations were set up for different transport duration periods $\theta$ and varied from 1 minute to 90 days.

Figure 9a, b present the PINNs simulation results obtained for the 30 days of DMSO transport through a stack consisting of 5 sheets of paper with a total thickness of approx. 0.7 mm. In Fig. 9a, the concentration c in the gas phase continuously decreases toward the opposite end of the stack. This spatial gradient gradually vanishes as the time progresses. Although c tends to saturate across the paper sheet to a value of approx. 0.024 mmol/l, there is still a concentration gradient even after 30 days of simulated migration. The sorption concentration q, shown in Fig. 9b, almost reaches its possible maximum of approximately 11,800 mmol/L, even though its growth still continues with a relatively slow rate after 30 days.

Fig. 10

Sorption concentration evolution of DMSO in all layers 1 to 5 of a stack of 5 paper sheets over duration of 30 days. Matlab FEM simulation results (orange dots) in comparison to PINNs (blue triangles) and experimental data (black crosses)

Comparable trends are also obtained with FEM calculated concentrations. Figure 10 compares the evolution of the sorption concentration q predicted by FEM (circles) and PINNs (triangles) with the measured q (crosses) in each of the layers of the 5-sheet paper stack over 30 days.

The predictions of FEM and PINNs are practically identical in all layers apart from the first layer (layer 1). FEM and PINN predicted concentration slightly differ within the first 15 days, as can be seen for layer 2 and 5 in Fig. 10.

Fig. 11

Overview on the Matlab FEM predicted concentrations q and c (orange dots) compared to PINN-predicted concentrations (blue triangles) and experimental data (black crosses) for DMSO migration through a stack of 5 paper sheets over the duration of 30 days. a Sorbed concentration q(x, t) and b gas concentration c(x, t)

To better illustrate how the excellent predictions in layers 2–4 relate to the apparently inferior prediction in layer 1, we provide a three dimensional representation of the concentrations q as function of x and t in Fig. 11a.

This representation reveals that the PINN method tends to overestimate q (triangles) near the left boundary (x = 0), in particular for the first, initial periods of time. This overestimation is a consequence of the PINNs inability to represent the steep, almost step-like concentration gradient between the boundary (at maximum concentration) and the paper interior (practically at zero concentration).

An analogous three dimensional representation in Fig. 11b allows us to critically comment on the predictions of the concentration c, in particular of the values predicted with the FEM method.

The gas concentration c estimated by the FEM solver (orange dots in Fig. 11b) reaches its saturation maximum within the first seconds of the transport process. As a direct consequence of this very rapid approach to saturation, the FEM simulation failed to maintain a nonzero spatial concentration gradient as opposed to the PINN result marked by blue triangles.

A series of simulations for various combinations of mesh-finesse and $\delta t$-steps were carried out in order to investigate the influence of the chosen $\delta x/\delta t$ step sizes on the final results. It was found that the FEM scheme experiences problems to achieve smooth results that comply with the boundary and initial conditions. That problem originated from the very long characteristic time $\theta$ implemented into the model ($\theta$ = 30 days). Therefore, notable deviations from PINNs predictions in q solely occurred at the left boundary ($x=0$) and at the initial stage of the transport process (Fig. 11a).

Nevertheless, for the periods of time on a scale of days and weeks, the model predictions agreed very well to the experimental results obtained in this work. Both FEM-based and PINN-based forward simulations predict that q eventually reaches saturation after 50 days. These results show that the initially proposed mathematical model for DMSO transport through paper is capable to account for migration times on the time scale of months.

5 Conclusion

Transport of polar volatile organic compounds in paper materials was investigated on an example of DMSO vapor sorption in thickness direction of paper sheets subjected to concentration gradients in closed migration cells. We could identify some important features of the DMSO diffusion process. Particularly, the experimental measurements of concentration distributions across the (x, t) domain demonstrated a high affinity of DMSO toward the paper matrix, with the maximum saturation content reaching 660 mg of DMSO per 1 g of paper. It was found that the process of saturation continues for more than 8 weeks.

As the experiment shows, transport of VOCs in paper materials tends to be quite complex and occurs by a number of mechanisms. In the proposed mathematical model we suggest to distinguish between the process of gas diffusion characterized by the changes in concentration c and the process of sorption of the migrant into the fibers associated with the changes in the respective concentration q. Accordingly, the related system of partial differential equations (8) addresses the non-Fickian behavior of the migrant.

The method of PINNs tested in this work proved to be a very useful practical tool in solving the inverse boundary problem for finding material constants relevant for the processes of adsorption of volatile substances in porous media on an example of paper.

Experimental and simulation data show that the process of DMSO diffusion in the gas phase differs greatly in its time characteristics from the process of sorption of the migrant into fibers. This fact significantly complicates the method of choosing an appropriate mesh, as well as $\delta t$ values, for solving a boundary value problem using mesh-based methods such as FEM. In turn, the methods based on PINNs show adequate results also in the areas close to boundary and initial states. The direct numerical solution of the transport model equations for longer periods of ongoing DMSO migration predicts the same concentrations regardless of whether PINNs or FEM are used. These predicted concentrations agree with those obtained experimentally.

The method of PINNs promises different routes of customized model extensions or applications. Readily conceivable are determinations of multiple unknown parameters in inverse problems, consideration of the longitudinal direction rather than through thickness transport, or even to consider advection terms for problems involving pressure gradients. In either case, the method of PINNs calls for experiments that are designed to provide the needed training data and sensible initial and boundary conditions.

Appendix A Nomenclature

c:

Vapor mass concentration of the migrant, mol m$^{-3}$

q:

Amount of the migrant bound to fibers per unit volume of paper, mol m$^{-3}$

$D_{p}$:

Binary diffusion coefficient of a mixture “migrant—air”, m$^2$ s$^{-1}$

$D_q$:

Diffusion coefficient of the bound migrant through the solid matrix m$^2$ s$^{-1}$

t:

Time, s

x:

Coordinate along the sheet thickness, m

L:

Total thickness, m

$\epsilon$:

Pore volume fraction, dimensionless

$\dot{m}$:

Interchange between bound VOC and VOC vapor, mol m$^{-3}$ s$^{-1}$

k:

Internal sorption rate parameter, s$^{-1}$

$q_{sat}$:

Saturation concentration in the fibers, mol m$^{-3}$

$c_{sat}$:

Saturation concentration in the pores, mol m$^{-3}$

$\theta$:

Characteristic time, s

$\alpha$:

$q_{sat}/c_{sat}$, dimensionless

$\gamma$:

$\frac{\theta D_p}{\alpha L^2}$, dimensionless

Dimensionless coordinates:

C:

$c/c_{sat}$

Q:

$q/q_{sat}$

X:

x/L

T:

$t/\theta$