Two level deacidification mathematical model for the description of transport of solid alkaline particles and diffusion of ions in a treated acid paper

Abstract

Industrial progress in papermaking in the early nineteenth century led to the technologies that resulted in more acidic papers, which was caused mainly by the exploitation of alum (KAl(SO₄)₂) and rosin as sizing agents. The papers prepared by such technologies have degraded more quickly. From the 1930s various deacidification and preservation processes with basic agents have been developed. The most widespread deacidification process is with the aerosol (spray system) consisting of microscale particles MgO and perfluoroheptane (PFH) as a carrier (the so-called Bookkeeper process). The shortcomings of this process are the low dissolution of solid MgO particles and the transport to the interior of acidic paper. We have developed a theoretical two-level model of the Bookkeeper process suitable for prediction of deacidification extent. The model involves both the dissolution/reaction of the solid particles and transport of solvated ions and solid particles inside the bulk of paper. The developed model coincides with the results of the performed deacidification experiment. The model is also in good agreement with the Lucas–Washburn equation, which is usually used for the description of the penetration of a deacidifying agent into the paper.

Introduction

Most books printed in the nineteenth and twentieth century (more than 90 and 80%, respectively) were printed on acid-based paper due to technologies with acidic reactants. The industrial progress in papermaking in the early nineteenth century led to technologies using a pulp processed with alum (KAl(SO₄)₂) (which was later replaced by a cheaper Al₂(SO₄)₃), and rosin (Biermann 1996), which increases hydrophobicity and improve conditions for writing and printing. However, introducing of ‘the week basic cation’ Al³⁺ and ‘a strong acid anion’ SO₄²⁻ generates a strong acidic environment (Eq. 1) immediately after the production of the paper. The paper always contains a water; thus, the acid catalyzed degradation has proceeded more rapidly (Jablonský et al. 2020; Jablonský and Šima 2020, 2021).

$$\left[ {{\text{Al}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{\text{x}}} } \right]^{{{3} + }} + {\text{H}}_{{2}} {\text{O}} \rightleftarrows \left[ {{\text{Al}}\left( {{\text{OH}}} \right)\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{{\text{x}} - {1}}} } \right]^{{{2} + }} + {\text{H}}_{{3}} {\text{O}}^{ + }$$

(1)

Hydroxonium cation splits polysaccharide macromolecules into smaller parts, which are virtually immediately oxidized or hydrolyzed and oxidation together with condensation reactions proceed parallelly. Aldehydes, alcohols, acids, and esters are the main degradation products (Area and Cheradame 2011; Clark et al. 2011). A peculiar role is played by formic and acetic acids, and higher organic acids so-called RIA (Reactive Idle Acids). The dissociation of these acids also produces a hydroxonium cation, so these acids have an autocatalytic effect on the hydrolysis. Decomposition reactions reduce the average degree of polymerization of polysaccharide macromolecules, reflected by a decrease in average molecular weight, what is manifested by a decrease in mechanical strength and increasing brittleness of the paper. From the point of view of archives and libraries, acid hydrolysis is classified among the most important and dangerous degradation reaction.

Due to the degradation processes in the acid-based papers, extending their lifespan is of global concern. Several deacidification methods with alkali earth metals (mainly Mg²⁺, Ca²⁺), oxides, carbonates, or organometallic compounds (e.g. Mg(OEt)₂) in polar (mainly water) and non-polar (hydrocarbons, halogenated hydrocarbons, etc.) carriers were developed. In terms of the mass deacidification technologies, the most widespread is the system with microparticles MgO and perfluoroheptane (PFH) as a carrier (the so-called Bookkeeper process) (Buchanan et al. 1994; Kundrot 1985; Polovka et al. 2006; Stadermann and Bischoff 1996; Zumbühl and Wuelfert 2001). Particles are applied by immersion of a treated paper into the suspension or from a spray, while PFH is the most applied carrier. It is assumed that most of the MgO particles remains on the surface and only a small part (the smallest particles; size in tens of nanometers) approaches the macrofibrils. After evaporation of PFH, air humidity begins to act. At first, MgO is transformed to Mg²⁺(aq.) and OH⁻(aq.) and these components are transported by diffusion into the interior of the microfibrils. Acid components are neutralized and after neutralization (pH > 7) an alkaline reserve is created. In spite of many years’ experiences with deacidification processes, there is no available a quantitative model describing processes after applying basic agents, i.e. to have some tools for optimizing the so called after-treatment conditions. In the accessible literature there are only mentions that the process takes very long time (Hubbe et al. 2017; Jablonský et al. 2012) and process has to be accelerated by increasing the humidity (Polovka et al. 2006; Zumbühl and Wuelfert 2001). The only quantitative data is published by Boone et al. (1998). According to this paper the process at ‘normal’ air humidity is not finished after 2 months (no change in color of the used indicator was observed). When the paper is humidified in a warm water passive humidity chamber the process takes approximately 1 day (Boone et al. 1998). These facts and the search for some optimization aids inspired our research.

For description of the penetration of a deacidifying agent into the paper, the Lucas–Washburn equation is used (Lucas 1918; Washburn 1921). The equation describes capillary flow in a bundle of parallel cylindrical tubes; it is extended with some issues to imbibition into porous materials.

$$l={\left(\frac{r\mathrm{ cos}\theta }{2}\right)}^\frac{1}{2}{\left(\frac{\gamma }{\eta }\right)}^\frac{1}{2}{t}^\frac{1}{2}$$

(2)

where l is the penetration depth, r is the capillary radius, θ is the contact angle, γ is the surface tension, η is the dynamic viscosity and t is the time. The important note is that Eq. (2) can describe the penetration of dissolved substances.

The only theoretical model that describes the deacidification process was recently presented by our paper (Danielik et al. 2022). However, the model is rather simple, neglecting several facts: (i) the existence of MgO particles when in contact with air containing CO₂; (ii) neglecting different types of water in the paper structure. Therefore, we have improved the physical reality of the model by incorporating two types of domains presented in the deacidified paper. Of course, if one considers the full hierarchic complexity represented by cellulose fibres, macrofibrils, microfibrils and bundles of cellulose polymer chains (Jablonský et al. 2020; Jablonský and Šima 2020), the model should be even more daedal, i.e. involving separate domains in/around individual parts of a cellulosic object with different diffusivities of acid and deacidifying components. However, parameters (volumes, diffusivities, flows among domains, etc.) of such a model should be very difficult to estimate, and a strong correlation among them decreases a practical physical meaning. Therefore, the two domains type, i.e. the two-level model, has seemed as a good compromise.

When MgO particles are used for the deacidification process, after the evaporation of the organic media, the particles are exposed to the atmosphere containing humidity and carbon dioxide. Several compounds can be present after the reaction; according to Langmuir (1965) and Palache et al. (1951): Periclase (MgO); Brucite (Mg(OH)₂); Magnesite (MgCO₃); Nesquehonite (MgCO₃·3H₂O); Lansfordite (MgCO₃·5H₂O); Artinite (MgCO₃·Mg(OH)₂·3H₂O); Hydromagnesite (3MgCO₃·Mg(OH)₂·3H₂O). Even within the paper, carbonate-containing compounds were found after deacidification (Polovka et al. 2006). The existence of these compounds on the surface of MgO particles can dramatically affect the deacidification process, as their solubility is significantly lower than that of pure MgO (Chang et al. 2021; Pokrovsky and Schott 1998). Based on the papers by Langmuir (1965) and Palache et al. (1951) under normal air conditions (aprox. 400 ppm CO₂), hydromagnesite is one of the stable phases. While in the older literature (Langmuir 1965; Palache et al. 1951), the hydromagnesite is presented as 3MgCO₃·Mg(OH)₂·3H₂O, recently hydromagnesite is assumed as the compound 4MgCO₃·Mg(OH)₂·4H₂O (Berninger et al. 2014; Gautier et al. 2014) and this stoichiometry was used in this paper.

Depending on the humidity, different types of water exist in the paper structure/fibres; so-called unbound water, freezing bound water, and non-freezing bound water (Park et al. 2006, 2007). Water is tightly bound directly to the microfibrils. Subsequently, the water phase between the macrofibrils is the so-called free phase, and depending on its amount, it can have different mobility and continuity (Banik and Brückle 2010, 2011; Brückle 2015; Guhhenheim 1966). The monomolecular layer accumulates between 0 and 20% of relative humidity (RH) at 20 °C and atmospheric pressure, which represents approximately 3 g of water per 100 g of absolutely dry cotton fibres. The first part of the monomolecular layer of water adsorbed on cellulose at RH lower than 1.0% binds so tightly that there is no increase in the volume of cellulose and proportional changes within the structural levels. This kind of water is very close to the bundles of polymer and this portion of water is bound to polymer cellulose chains by strong hydrogen bridges. The water forming the first 0.2% (w/w) of the moisture content of cellulose is referred to as chemically sorbed, bound, mineralization water or ‘constitutional water’ (Brückle 2015). It has a lower freezing temperature and due to deformation by hydrogen bridges it has a higher density than bulk or capillary water. Therefore, this portion of water is also referred as a non-freezing water. The non-freezing water is difficult to remove even under extreme drying conditions and it does not act as a solvent. Therefore, the non-freezing water is not involved in the transport mechanism. In addition to hydrogen bonds with hydroxyl groups of cellulose polymer chains, this type of water can be the, for example, chemically bound by hydration of carbonyl groups or the opening of strained lactones. When more than 0.2% (w/w) of water is absorbed, the additional absorbed water is already bound through weaker bonds, and therefore the volume of the cellulosic structures increases in proportion to the amount absorbed (Brückle 2015; Vajová et al. 2021). It can be assumed that the non-freezing water will not ‘communicate’ with the surrounding water phase and therefore the acid species and the deacidification agent will not diffuse away from it. Moreover, it is likely that ‘direct products’ of the decomposition of cellulose fibres (organic acids) will be found directly in this portion of water. Therefore, the presented model considers two types of water, where the first type will correspond to the mobile water phase containing sulfuric acid and the second type will correspond to the unfreezing water phase containing organic acids and isolated from the surrounding water phase.

In this paper, we will present the theoretical ‘two-level’ model describing the deacidification Bookkeeper process using solid MgO particles. As far as we know, no such mathematical model of this process was presented except for a very simple one (Danielik et al. 2022). Due to necessity to compare the model with experimental data, which are currently not available in the open literature, the quantitative deacidification experiment was realized in this paper, as well.

Theoretical model

The presented model is the two-level cascade model. The direct transport of the deacidification components and the opposite transport of the acid components are considered. The scheme of the model for a substance k is shown in Fig. 1. In this model, cross-sections/layers of paper are considered homogeneous, characterized by a different resistance to the transport of the substance, which is reflected by values of the transport coefficients of the substance and subsequently the flow of the substance between the individual layers (one layer corresponds to one cascade member). The differences in the volumes V_i and the substance transport coefficients k_N,i,k can distinguish the differences in the structure of the paper.

Fig. 1

Schematic illustration of the model for the substance k

We assume that sulfuric acid originating from the hydrolysis of aluminium sulphate is present at the first level, while the organic acids are present in the second level. Dissolved deacidification agents diffuse to both levels, while solid particles can penetrate only to the first level.

Substances assumed in the model and their reactions

The following components are considered in the model:

• (i) Hydromagnesite 4MgCO₃·Mg(OH)₂·4H₂O solid particles (for simplicity, we assume that not only the surface of MgO particles is converted into hydromagnesite, but the whole volume of the MgO particle);

• (ii) Mg(OH)₂ formed by dissolution of hydromagnesite in the water phase;

• (iii) MgCO₃ formed by dissolution of hydromagnesite in the water phase;

• (iv) H₂SO₄ formed by hydrolysis of Al₂(SO₄)₃;

• (v) R¹COOH that represents fast, low molecular weight organic acids such as HCOOH, CH₃COOH;

• (vi) R²COOH that represents slow, higher molecular weight acids, e.g. glycolic acid, so-called RIA.

Components are involved in reactions:

$${\text{4MgCO}}_{{3}} \cdot{\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \cdot{\text{4H}}_{{2}} {\text{O}}\left( {\text{s}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to {\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{4MgCO}}_{{3}} \left( {{\text{aq}}} \right) + {\text{5H}}_{{2}} {\text{O}}\left( {\text{l}} \right)$$

(3)

$${\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{SO}}_{{4}} \left( {{\text{aq}}} \right) \to {\text{MgSO}}_{{4}} \left( {{\text{aq}}} \right) + {\text{2H}}_{{2}} {\text{O}}\left( {\text{l}} \right)$$

(4)

$${\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{2R}}^{{1}} {\text{COOH}}\left( {{\text{aq}}} \right) \to {\text{Mg}}\left( {{\text{R}}^{{1}} {\text{COO}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{2H}}_{{2}} {\text{O}}\left( {\text{l}} \right)$$

(5)

$${\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{2R}}^{{2}} {\text{COOH}}\left( {{\text{aq}}} \right) \to {\text{Mg}}\left( {{\text{R}}^{{2}} {\text{COO}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{2H}}_{{2}} {\text{O}}\left( {\text{l}} \right)$$

(6)

$${\text{MgCO}}_{{3}} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{SO}}_{{4}} \left( {{\text{aq}}} \right) \to {\text{MgSO}}_{{4}} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) + {\text{CO}}_{{2}} \left( {\text{g}} \right)$$

(7)

$${\text{MgCO}}_{{3}} \left( {{\text{aq}}} \right) + {\text{2R}}^{{1}} {\text{COOH}}\left( {{\text{aq}}} \right) \to {\text{Mg}}\left( {{\text{R}}^{{1}} {\text{COO}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) + {\text{CO}}_{{2}} \left( {\text{g}} \right)$$

(8)

$${\text{MgCO}}_{{3}} \left( {{\text{aq}}} \right) + {\text{2R}}^{{2}} {\text{COOH}}\left( {{\text{aq}}} \right) \to {\text{Mg}}\left( {{\text{R}}^{{2}} {\text{COO}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) + {\text{CO}}_{{2}} \left( {\text{g}} \right)$$

(9)

Products of neutralization do not enter further reactions; therefore, their diffusion is not considered in the model; we assume that the influence of their concentrations do not affect the diffusion of other species (reactants).

For the dissolution of hydromagnesite (HyM), the number of particles and their radius are considered (Eq. 3):

$${R}_{\mathrm{i},\mathrm{HyM}}=\frac{{D}_{\mathrm{R},\mathrm{HyM}}}{h}\cdot {n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}\cdot 4\pi {r}_{\mathrm{i},\mathrm{HyM}}^{2}\cdot \left({c}_{\mathrm{sat},\mathrm{HyM}}-{c}_{\mathrm{i},\mathrm{HyM}}\right)$$

(10)

where R_i,HyM is the dissolution rate of hydromagnesite particles in the volume element i (related to the unit volume of the cell; unit: mol m⁻³ s⁻¹); h is the thickness of the diffusion layer on the surface of the solid particle (unit: m); D_R,i,HyM represents the diffusion coefficient in the respective diffusion layer (unit: m² s⁻¹); n_V,i,HyM is the number of solid hydromagnesite particles present in the volume element i (related to the unit volume cell; unit: m⁻³); r_i,HyM is the radius of the hydromagnesite particles in the volume element i (unit: m); c_sat,HyM is the molar concentration of hydromagnesite at saturation (due to the stoichiometry of the dissolution reaction (3) it was assumed to be equal to the molar concentration of Mg(OH)₂ at saturation); c_i,HyM is the molar concentration of hydromagnesite in the volume element i (due to the stoichiometry of the dissolution reaction (3) it was assumed to be equal to the molar concentration of Mg(OH)₂). It should be noted that i = 0 represents the surface of the paper. The thickness of the diffusion layer can be written as h = const × r_HyM (Almeida et al. 1997) and the rate constant of the dissolution reaction k_R,HyM (unit: m² s⁻¹) can be written as the ratio of the diffusion coefficient and const. Thus,

$${R}_{\mathrm{i},\mathrm{HyM}}=\frac{{k}_{\mathrm{R},\mathrm{HyM}}}{{r}_{\mathrm{i},\mathrm{HyM}}}\cdot {n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}\cdot 4\pi {r}_{\mathrm{i},\mathrm{HyM}}^{2}\cdot \left({c}_{\mathrm{sat},\mathrm{HyM}}-{c}_{\mathrm{i},\mathrm{HyM}}\right)$$

(11)

The solubility of hydromagnesite has been published in few papers (Berninger et al. 2014; Gautier et al. 2014). We have taken the solubility from the paper by Berninger et al. (2014) due to the fact that the dissolution rate could be estimated from the data presented in the paper. Thus, the saturation level was assumed to be c_sat,HyM = 5.14 × 10^–4 mol m⁻³; the dissolution rate constant was estimated to be k_R,HyM = 3 × 10^–10 m² s⁻¹ (Berninger et al. 2014).

For the rates of reactions (4)–(9) following expression was used.

$${R}_{j}={k}_{\mathrm{R},\mathrm{j}}\cdot {c}_{\mathrm{A}}\cdot {c}_{\mathrm{B}}$$

(12)

where j denotes the reaction (4)–(9), R_j is the rate of the reaction j and k_R,j is the respective rate constant. A represents Mg(OH)₂ or MgCO₃; B represents H₂SO₄, R¹COOH or R²COOH. The reactions were assumed to be very fast (neutralisation reactions), and the rate constants were supposed to be the same of the value 1000 dm³ mol⁻¹ s⁻¹.

Diffusion of the dissolved substances

The main concept of balancing of substances is based on the presence of the water phase in the paper. From the total area A, the proportional part εA corresponds to a part of the element that is filled with unbound water. Thus, the εA represents the water content in the paper. The width of the balanced element is Δx (considered constant for all the elements for simplicity).

The balanced volume is the volume of the liquid phase:

$$V_{i} = \varepsilon A\;\Delta x$$

(13)

The amount of moles of the substance k transported from the i-1 cell to the cell i (N_i-1,k) can be expressed as

$${N}_{\mathrm{i}-1,\mathrm{k}}={k}_{\mathrm{N},\mathrm{i}-1,\mathrm{k}}\cdot \varepsilon A\cdot \frac{\left({\mathrm{c}}_{\mathrm{i},\mathrm{k}}-{\mathrm{c}}_{\mathrm{i}-1,\mathrm{k}}\right)}{\Delta x}$$

(14)

where k_N,i-1,k is the transport coefficient of the substance k from the i-1 cell to the cell i, c denotes the respective molar concentration of the substance k.

The transports of the substance from cell i to the cell i + 1 and from the cell i to i^S (the superscript S denotes the second level) can be written in a similar way. When we denote the number of moles taking place in the neutralisation reaction as R_k,i, we may write the balance of the substance k:

$$\varepsilon A\cdot \Delta x\cdot \frac{\Delta {\mathrm{c}}_{\mathrm{i},\mathrm{k}}}{\Delta t}={k}_{\mathrm{N},\mathrm{i}-1,\mathrm{k}}\cdot \varepsilon A\cdot \frac{\left({c}_{\mathrm{i},\mathrm{k}}-{c}_{\mathrm{i}-1,\mathrm{k}}\right)}{\Delta x}-{k}_{\mathrm{N},\mathrm{i},\mathrm{k}}\cdot \varepsilon A\cdot \frac{\left({c}_{\mathrm{i}+1,\mathrm{k}}-{c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}-{k}_{\mathrm{N},\mathrm{i},\mathrm{k}}^{s}\cdot \frac{\left(0.002\cdot {c}_{\mathrm{i},\mathrm{k}}^{S*}-\varepsilon A\cdot {c}_{i,k}\right)}{\Delta x}+\varepsilon A\cdot \Delta x\cdot {R}_{\mathrm{k},\mathrm{i}}$$

(15)

where the value 0.002 represents the amount of non-freezing water, which is the amount of water present in the second level of the model and c^S* is the molar concentration in the second level (related to the content of water present in the second level). Treating the third term on the right side of Eq. (15) we get:

$$\frac{\left(0.002\cdot {c}_{\mathrm{i},\mathrm{k}}^{S*}-\varepsilon A\cdot {c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}=\varepsilon A\frac{\left(\frac{0.002}{\varepsilon A}\cdot {c}_{\mathrm{i},\mathrm{k}}^{S*}-{c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}=\varepsilon A\frac{\left({c}_{\mathrm{i},\mathrm{k}}^{S}-{c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}$$

(16)

where c^S $\left(=\frac{0.002}{\varepsilon A}\cdot {c}_{\mathrm{i},\mathrm{k}}^{S*}\right)$ is the molar concentration in the second level related to the total amount of water (εA). Thus, the Eq. (15) can be rewritten:

$$\varepsilon A\cdot \Delta x\cdot \frac{\Delta {c}_{i,k}}{\Delta t}={k}_{\mathrm{N},\mathrm{i}-1,\mathrm{k}}\cdot \varepsilon A\cdot \frac{\left({c}_{\mathrm{i},\mathrm{k}}-{c}_{\mathrm{i}-1,\mathrm{k}}\right)}{\Delta x}-{k}_{\mathrm{N},\mathrm{i},\mathrm{k}}\cdot \varepsilon A\cdot \frac{\left({c}_{\mathrm{i}+1,\mathrm{k}}-{c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}-{k}_{\mathrm{N},\mathrm{i},\mathrm{k}}^{s}\cdot \varepsilon A\cdot \frac{\left({c}_{\mathrm{i},\mathrm{k}}^{S}-{c}_{\mathrm{i},\mathrm{k}}\right)}{\Delta x}+\varepsilon A\cdot \Delta x\cdot {R}_{\mathrm{k},\mathrm{i}}$$

(17)

or (assuming that the transport coefficients are equal at the same level)

$$\frac{{\Delta c}_{\mathrm{i},\mathrm{k}}}{\Delta t}=-{k}_{\mathrm{N},\mathrm{k}}\frac{\left({c}_{\mathrm{i}+1,\mathrm{k}}-2{c}_{\mathrm{i},\mathrm{k}}+{c}_{\mathrm{i}-1,\mathrm{k}}\right)}{{\Delta x}^{2}}-{k}_{\mathrm{N},\mathrm{i},\mathrm{k}}^{s}\cdot \frac{\left({c}_{\mathrm{i},\mathrm{k}}^{S}-{c}_{\mathrm{i},\mathrm{k}}\right)}{{\Delta x}^{2}}+{R}_{\mathrm{k},\mathrm{i}}$$

(18)

It can be seen that the amount of water in the cell does not influence the formula of the material balance of the substance. In limits ∆t → 0; ∆x → 0, the Eq. (18) can be rewritten to the partial differential equation with the corresponding initial and boundary conditions. Thus, with an infinite number of cells, the cascade model leads to a diffusion–reaction relationship. The Eq. (18) can be used to calculate the profiles of all the dissolved components in the system. The transport coefficient k_N,k has the same dimension as the diffusion coefficient, i.e., m² s⁻¹. If only the liquid phase and no cellulose fibres were present in a given cell, the transport coefficient would be equal to the diffusion coefficient in the given liquid phase. However, because there is not only a liquid phase in the cell, the transport coefficient will represent a mixture of diffusion coefficients and transport coefficients through the solid phase.

It should be noted that we assume diffusion of ‘ionic pairs’ due to the preservation of electroneutrality. (We formally write the molecules, Eqs. (3)–(9), but we mean ‘ionic pairs’.)

Transport of solid hydromagnesite particles

For simplicity, let us assume a monodisperse system of spherical particles with radius r_i,HyM where i denotes a cascade cell with volume V_i. Next, consider the number of HyM particles in a given cell n_V,i,HyM, related to the unit volume of cell V_i.

The volume of particles transported is balanced. The driving force for the transport of HyM particles will be the difference in surface activity (per unit volume) in the previous cell of the cascade (or on the surface of the paper) and in the given cell of the cascade, with ‘particle size dependent braking’ (term exp(-k_h,HyM × r_i,HyM)).

$${S}_{\mathrm{V},\mathrm{i},\mathrm{i}+1,\mathrm{HyM}}=\frac{{k}_{\mathrm{N},\mathrm{i},\mathrm{HyM}}^{*}\left({n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}\cdot 4\pi {r}_{\mathrm{i},\mathrm{HyM}}^{2}-{n}_{\mathrm{V},\mathrm{i}+1,\mathrm{HyM}}\cdot 4\pi {r}_{\mathrm{i}+1,\mathrm{HyM}}^{2}\right)}{\Delta x}\cdot {e}^{-{k}_{\mathrm{h},\mathrm{i},\mathrm{HyM}}\cdot {r}_{\mathrm{i},\mathrm{HyM}}}$$

(19)

where S_V,i,i+1,HyM is the transport of the solid particles in terms of their total surface per unit volume of the cell (unit: m² s⁻¹/m³ = m⁻¹ s⁻¹). The ‘braking’ term is not used in the calculation presented in this paper. The term k^*_N,i,HyM (unit: m s⁻¹) is the apparent transport coefficient of the solid particles and can also be expressed by ‘true’ transport coefficient in two ways:

$${k}_{\mathrm{N},\mathrm{i},\mathrm{HyM}}^{*}=\frac{{k}_{\mathrm{N},\mathrm{i},\mathrm{HyM}}}{{r}_{\mathrm{i},\mathrm{HyM}}}\text{ or }{k}_{\mathrm{N},\mathrm{i},\mathrm{HyM}}^{*}=\frac{{k}_{\mathrm{N},\mathrm{i},\mathrm{HyM}}}{\sqrt{\frac{\left({r}_{\mathrm{i},\mathrm{ HyM}}^{2}+{r}_{\mathrm{i}+1,\mathrm{HyM}}^{2}\right)}{2}}}$$

(20)

The latter expression was applied for an apparent transport coefficient.

To express the transport of HyM particles in terms of amount of substance, the following relationship has to be used (recalculation into the volume of the HyM particles per unit volume of the cell and assuming that the solid particles consist of pure HyM):

$${N}_{\mathrm{i},\mathrm{i}+1,\mathrm{HyM}}=\frac{{S}_{\mathrm{V},\mathrm{i},\mathrm{i}+1,\mathrm{HyM}}}{4\pi {r}_{\mathrm{i},\mathrm{HyM}}^{2}}\cdot \frac{4}{3}\pi {r}_{\mathrm{i},\mathrm{HyM}}^{3}\frac{{\rho }_{\mathrm{HyM}}}{{M}_{\mathrm{HyM}}}\cdot \Delta x=\frac{{S}_{\mathrm{V},\mathrm{i},\mathrm{i}+1,\mathrm{HyM}}}{3}\cdot {r}_{\mathrm{i},\mathrm{HyM}}\frac{{\rho }_{\mathrm{HyM}}}{{M}_{\mathrm{HyM}}}\cdot \Delta x$$

(21)

where N_i,i+1,HyM (unit: mol m⁻² s⁻¹) is the transport of solid HyM particles in the term of number of moles from the cascade member i to i + 1. ρ_HyM is the density of HyM particles and M_HyM is the molar weight of hydromagnesite.

Balancing the amount of substance in cell i, the differential equation for the change of number of solid particles in the given cell per unit volume is obtained:

$$\frac{\mathrm{d}{n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}}{\mathrm{d}t}=\left(\frac{{N}_{\mathrm{i}-1,\mathrm{i},\mathrm{HyM}}}{\frac{4}{3}\pi {r}_{\mathrm{i},\mathrm{HyM}}^{3}}-\frac{{N}_{\mathrm{i},\mathrm{i}+1,\mathrm{HyM}}}{\frac{4}{3}\pi {r}_{\mathrm{i},\mathrm{HyM}}^{3}}\right)\frac{{M}_{\mathrm{HyM}}}{{\rho }_{\mathrm{HyM}}}\cdot \frac{1}{\Delta x}$$

(22)

Due to the dissolution reaction of hydromagnesite expressed by Eq. (11), the radius of particles and thus the volume of particles changes

$$\frac{\mathrm{d}{V}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}}{\mathrm{d}t}=\frac{d\left({n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}\cdot \frac{4}{3}\pi {r}_{\mathrm{i},\mathrm{HyM}}^{3}\right)}{dt}={n}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}\cdot 4\pi {r}_{\mathrm{i},\mathrm{HyM}}^{2}\cdot \frac{d{r}_{\mathrm{i},\mathrm{HyM}}}{dt}$$

(23)

It should be noted that the volume of the particles in cell i (V_V,i,HyM) is defined per unit volume of the cell (dimensionless unit: m³/m³). The particle volume change can also be expressed by using the rate of the dissolution reaction (the minus symbol reflects the decrease of the volume due to the dissolution reaction):

$$\frac{\mathrm{d}{V}_{\mathrm{V},\mathrm{i},\mathrm{HyM}}}{\mathrm{d}t}=-{R}_{\mathrm{i},\mathrm{HyM}}\frac{{M}_{\mathrm{HyM}}}{{\rho }_{\mathrm{HyM}}}$$

(24)

Combining of Eqs. (23) and (24) using Eq. (11) we obtain the differential equation for the change of particle radius in cell i:

$$\frac{\mathrm{d}{r}_{\mathrm{i},\mathrm{HyM}}}{\mathrm{d}t}=-\frac{{k}_{\mathrm{R},\mathrm{HyM}}}{{r}_{\mathrm{i},\mathrm{HyM}}}\left({c}_{\mathrm{sat},\mathrm{HyM}}-{c}_{\mathrm{i},\mathrm{HyM}}\right)\frac{{M}_{\mathrm{HyM}}}{{\rho }_{\mathrm{HyM}}}$$

(25)

The overall system of ordinary differential equations (ODE)

The overall system for the solution consists of Eqs. (11), (22) and (25) together with the balances of the dissolved substances (Mg(OH)₂ (MH), MgCO₃ (MC), H₂SO₄ (SA), R¹COOH (R1), R²COOH (R2), respectively). The balance equations have to be distinguished into two types, depending on which level of the model they relate to. For the first level that contains unbound water, the balances are as follows:

$$\frac{{\mathrm{d}c}_{\mathrm{i},\mathrm{MH}}}{\mathrm{d}t}=-{k}_{\mathrm{N},\mathrm{i},\mathrm{MH}}\frac{\left({c}_{\mathrm{i}+1,\mathrm{MH}}-2{c}_{\mathrm{i},\mathrm{MH}}+{c}_{i-1,MH}\right)}{{\Delta x}^{2}}-{k}_{\mathrm{N},\mathrm{i},\mathrm{MH}}^{s}\cdot \frac{\left({c}_{\mathrm{i},\mathrm{MH}}^{S}-{c}_{\mathrm{i},\mathrm{MH}}\right)}{{\Delta x}^{2}}+\frac{{R}_{\mathrm{HyM},\mathrm{i}}}{\varepsilon A}-{R}_{4,\mathrm{i}}$$

(26)

$$\frac{{\mathrm{d}c}_{\mathrm{i},\mathrm{MC}}}{\mathrm{d}t}=-{k}_{\mathrm{N},\mathrm{i},\mathrm{MC}}\frac{\left({c}_{\mathrm{i}+1,\mathrm{MC}}-2{c}_{\mathrm{i},\mathrm{MC}}+{c}_{\mathrm{i}-1,\mathrm{MC}}\right)}{{\Delta x}^{2}}-{k}_{\mathrm{N},\mathrm{i},\mathrm{MC}}^{s}\cdot \frac{\left({c}_{\mathrm{i},\mathrm{MC}}^{S}-{c}_{\mathrm{i},\mathrm{MC}}\right)}{{\Delta x}^{2}}+4\cdot \frac{{R}_{\mathrm{HyM},\mathrm{i}}}{\varepsilon A}-{R}_{7,\mathrm{i}}$$

(27)

$$\frac{{\mathrm{d}c}_{\mathrm{i},\mathrm{SA}}}{\mathrm{d}t}=-{k}_{\mathrm{N},\mathrm{i},\mathrm{SA}}\frac{\left({c}_{\mathrm{i}+1,\mathrm{SA}}-2{c}_{\mathrm{i},\mathrm{SA}}+{c}_{\mathrm{i}-1,\mathrm{SA}}\right)}{{\Delta x}^{2}}-{R}_{4,\mathrm{i}}-{R}_{7,\mathrm{i}}$$

(28)

For the second level, which represents the non-freezing water and contains the organic acids, the balance equations are listed below.

$$\frac{\mathrm{d}{c}_{\mathrm{i},\mathrm{MH}}^{S}}{\mathrm{d}t}={k}_{\mathrm{N},\mathrm{i},\mathrm{MH}}^{s}\cdot \frac{\left({c}_{\mathrm{i},\mathrm{MH}}^{S}-{c}_{\mathrm{i},\mathrm{MH}}\right)}{{\Delta x}^{2}}-\frac{1}{2}{R}_{5,\mathrm{i}}-\frac{1}{2}{R}_{6,\mathrm{i}}$$

(29)

$$\frac{\mathrm{d}{c}_{\mathrm{i},\mathrm{MC}}^{S}}{\mathrm{d}t}={k}_{\mathrm{N},\mathrm{i},\mathrm{MC}}^{s}\cdot \frac{\left({c}_{\mathrm{i},\mathrm{MC}}^{S}-{c}_{\mathrm{i},\mathrm{MC}}\right)}{{\Delta x}^{2}}-\frac{1}{2}{R}_{8,\mathrm{i}}-\frac{1}{2}{R}_{9,\mathrm{i}}$$

(30)

$$\frac{\mathrm{d}{c}_{\mathrm{i},\mathrm{R}1}^{S}}{\mathrm{d}t}=-{R}_{5,\mathrm{i}}-{R}_{8,\mathrm{i}}$$

(31)

$$\frac{\mathrm{d}{c}_{\mathrm{i},\mathrm{R}2}^{S}}{\mathrm{d}t}=-{R}_{6,\mathrm{i}}-{R}_{9,\mathrm{i}}$$

(32)

It should be noted that the reaction rate of reaction (3) is defined per a volume of the element (due to the using of number of particles in the volume of the element), while the reaction rates of the reactions (4)–(9) and the molar concentrations are defined per volume of the liquid phase.

An explicit algorithm according to Ashour and Hanna (1990) was used to solve the ODE system. The algorithm consists of the calculation of the new values using the Euler method and second-order Runge–Kutta method followed by the averaging of the calculated values using the averaging parameter between (0, 1). The advantage of the algorithm is its simplicity, speed, good accuracy, and stability even for medium stiff systems. The simulation proceeded with the time integration step of 0.003 s. It should be noted that after the first 10 min of simulation, the results were recorded each 30 min (because of the simulation of tens of days).

Materials and methods

Paper sample: The acid lignin-containing paper (NOVO test paper) was used from Klug-Conservation. Composition > 55% mechanical wood pulp (CTMP) + bleached paper pulp; lignin 17%, filler (12–15)% kaolin. Sizing Cobb60 OS 19/SS 21 g/m², rosin and alum. pH (4.0–5.0) (adjustment with alum), grammage 90 g/m². No surface sizing, calendaring, no optical brighteners. According to chemical analysis, the treated acid paper contained 0.87 mg of sulphates/1 g of dry paper; 0.164 mg of formic acid/1 g of paper and 0.321 mg of acetic acid/1 g of paper.

The deacidified samples were prepared by immersion in the non-aqua suspension of MgO (Bookkeeper^®) (Preservation Technologies, L.P., supplier Ceiba sro.) for 10 min with constant stirring. After the deacidification, the sample was stored at 75% RH and 25 °C for 30 days. The modifying storage conditions were used to accelerate the neutralization process.

Because XRD or other methods are not suitable to determine element distribution in the cross-section of the paper, elementary distribution SEM WDS was used. The 2 × 1 cm were put to the holder and cut with Mühle Rasor to the same height as the holder. Samples were coated with Au—Sputtercoater SCD 040, BalzersUnionPro. It was measured by the JOEL JMS—7600F, with the detector (Oxford instruments X-Max (50 mm²). Measurement parameters: WD 15.0 mm; Acceleration voltage: 5 kV. Software evaluation by INCA, measurement mode: mapping—SmartMapSetup (frames 500), calibration to magnesium standard. The magnification of the microscope was adjusted to observe the entire cross-section of the paper (from 350 to 500x)—depending on the type of paper. The elementary distribution of magnesium was processed by picture analysis in Matlab, where the cross section of the paper was divided into elementary picture areas whereas the distribution of element was calculated. More details about the used method (SEM WDS analysis) can be found in the Supplementary material.

Results and discussion

Based on the paper by Danielik et al. (2022), 80 members of the cascade were used for the simulation. Three simulation runs were performed. The first ‘basic’ run was meant for the comparison with the experimental data. The radius of the MgO particles (and hydromagnesite) was assumed to be 100 nm based on the SEM figure of the evaporated BookKeeper suspension (Fig. 2).

Fig. 2

MgO particles after the evaporating PFH

The second run tested the penetration of solid hydromagnesite particles in the depth of the paper under the same conditions as run 1. The radius of the hydromagnesite particles was not chosen on the basis of the actual size of particles (Fig. 2), but it was chosen so that the particles could penetrate into the paper. In the third run we tested the influence of the water content on the deacidification. We have been aware that the increase in the water content also increases the transport coefficient of the dissolved substances. However, we wanted to test the correctness of the model whether the increased water content in the model influences the dissolution rate of hydromagnesite particles. Therefore, the values of the transport coefficients were left the same in all the calculations.

In the simulation runs, it was assumed that sulphates originate only from the aluminium sulphate; thus, the experimentally determined content of sulphates was used as the starting content of sulfuric acid in the paper. The contents of formic and acetic acid were treated together as the R¹COOH term in the model. The parameters of the deacidification process were supposed to be (based on the Bookkeeper process) as follows:

• (i) Deacidification by spraying with the cover of both side of the paper;

• (ii) Amount of sprayed MgO 4 mg/1 g of paper;

• (iii) All the MgO particles immediately reacted to hydromagnesite immediately;

• (iv) Radius of solid particles that can penetrate into paper: 50 nm.

The simulation runs are listed in Table 1.

Table 1 Parameters of the simulation runs

The contents of the acids presented in Table 1 were obtained by chemical analysis of the paper used. These all parameters were fixed in the simulation. All the three types of transport coefficients were estimated only by order, and they should be refined in the future. We did not set out to find their exact values, as little experimental data is available. However, the transport coefficients of dissolved substances (k_N,i) were fitted on the experimental data, while the others were fixed assuming them lower by several orders as shown in Table 1. We were only interested in the principled agreement between the experiments and the model. More accurate fitting of transport coefficients is a task for the future, based on more experimental data and their correlation with the properties of paper. The radius of the particles was discussed above and it was used as the input parameter of the simulation. The data on water content and the dissolution rate constant were taken from the literature and served as the input data (see Table 1).

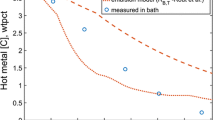
As mentioned above, the simulation run 1 serves as a tool for comparison with the experimental data. As can be seen in Fig. 3, the magnesium distribution in the paper after 30 days of deacidification agrees well with the experimental (in the limits of experimental error). The experimental points represent the average values of 6 measurements. The high uncertainty in the experimental data is caused by the inhomogeneity of the paper rather than of the analytical technique. The comparison for 1 h and 5 days of deacidification is shown in the Supplementary material. It can be concluded that the theoretical model describes the deacidification process. The model results also meet the criterion of the Lucas-Washburn equation (Lucas 1918; Washburn 1921) (Eq. 2). The time dependence in first change of the acid concentration, which corresponds to the depths of the deacidification agent, in different paper depths is shown in Fig. 4. After a very short initial time, the model results agree with the Lucas-Washburn equation, which is demonstrated by the linear correlation of the penetration depth l calculated by our model (values on the vertical axis) and the square root of time (t^1/2) (horizontal axis). At the initial time, the diffusion process is not in a stationary state because the surface concentrations of magnesium hydroxide and magnesium carbonate change. When the stationary state is achieved, i.e. the rate of hydromagnesite dissolution and Mg(OH)₂ and MgCO₃ diffusion into the paper are equal, the model meets the criterion of Lucas–Washburn equation. Another check of the model consistency was the comparison of the hydromagnesite consumption for the deacidification obtained theoretically and from the model results. The difference between these two values was up to 4%, which also reflects a good accuracy of the used algorithm according to Ashour and Hanna (1990).

Fig. 3

Comparison of magnesium distribution in the cross-sections of the paper after 30 days of the deacidification process. Black circle experimental (with the error bars); (red line) calculated

Fig. 4

Time dependence in first change of the acid concentration in different paper depths calculated in run 1

The simulation run 1

The concentration profiles of substances calculated by the model are shown in Figs. 5, 6, 7, and 8. As is known, the deacidification process consists of two phases.

• (i) Deacidification and

• (ii) Creation of the alkaline reserve.

Fig. 5

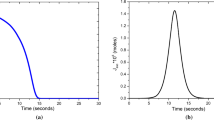
Concentration profiles of magnesium hydroxide in unbound water (the first level of the model) at different depths of paper for the simulation run 1. (red line): surface of the paper (depth of 0 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 6

Concentration profiles of magnesium hydroxide in non-freezing water (second level of the model) in different depths of paper for the simulation run 1. (red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 7

Concentration profiles of sulphuric acid in different depths of paper for the simulation run 1. (red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 8

Concentration profiles of organic R¹COOH acids in different depths of paper for simulation run 1. (red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

These two phases of the process are very well visible in Fig. 5. It can be seen that the deacidification phase lasts a long time; much longer than the creation of the alkaline reserve. The main process in the first part of the deacidification process corresponds to the neutralization of the sulfuric acid in the unbound water (level 1 of the model). During this part, the minimal amount of deacidification agents penetrates into the second level. When the sulfuric acid is almost consumed then the new diffusion stationary state is established. It is visible since the 25^th day of simulation. The establishing of the new stationary state takes ca 2 days and after that the organic acids in the second level are neutralized. Approximately after nearly 55 days, the alkaline reserve begins to create. The process takes around 5 h.

Similar steps are visible in Fig. 6 where the concentration profiles of magnesium hydroxide in non-freezing water (the second level of the model) are shown. It can be nicely visible when the sufficient amount of magnesium hydroxide reaches the microfibrils at the respective depths to establish stationary diffusion. The same results show concentration profiles of magnesium carbonate; they are just 4 times higher due to stoichiometry.

In Figs. 7 and 8, the concentration profiles of sulfuric acid and organic R¹COOH acids are shown. It may seem that the profiles are linear in Fig. 7. However, they are slightly curved; the curvature radius is ca. 850–900 days. It may be also seen that the acid concentrations at different depths of paper are close. It is caused by relatively fast diffusion compared to the total deacidification time. Looking at the details of Figs. 5 and 7, it can be noticed that the time differences for the same concentration at the different depths are decreasing. Usually, when the diffusion of one component is considered, on the contrary, these time differences increase because at a greater depth the driving force is smaller and thus the diffusion is slower. At a cursory glance, it might seem that the Figures show accelerated diffusion, which would be in contradiction the Lucas-Washburn equation (Lucas 1918; Washburn 1921). However, the course of curves in Figs. 5, 6, and 7 is caused not by the accelerated diffusion, but by a back diffusion of acidic components from the depth of the paper to the surface of the paper. This back diffusion is evoked by a decrease of acid components in cells of cascade closer to the surface, from which neutralization components are transported. The decrease in concentration of acids generates a driving force of acid components from the interior cells (closer to the middle of the cross-section). Consequently, in cascade cells closer to the paper surface a higher amount of acids (higher extent of neutralization reactions) is neutralized in comparison with extents of neutralization reaction in cells more distant from the surface. This phenomenon is also reflected by time needed for neutralization, longer for the cells closer to the surface, shorter for the cells more distant from the surface.

Looking at Fig. 8, it can be visible when the deacidification agent reaches the microfibrils (the second level of the model) in the respective depths. A similar phenomenon is also visible in Fig. 6.

On the basis of the simulation results, pH profiles at different depths of the paper were calculated. It was a complex calculation of several reaction equilibria. The unreacted sulfuric acid was recalculated into respective amount of aluminium sulphate. The contents of formic and acetic acid were estimated from the content of R¹COOH using their initial ratio in it. The following ‘acid’ reactions were supposed to occur:

$$0.{\text{5Al}}_{{2}} \left( {{\text{SO}}_{{4}} } \right)_{{3}} \left( {{\text{aq}}} \right) + {\text{6H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to \left[ {{\text{Al}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{6}} } \right]^{{{3} + }} \left( {{\text{aq}}} \right) + {1}.{\text{5SO}}_{{4}}^{{{2} - }} \left( {{\text{aq}}} \right)$$

(33)

$$\left[ {{\text{Al}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{6}} } \right]^{{{3} + }} \left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to \left[ {{\text{Al}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{5}} \left( {{\text{OH}}} \right)} \right]^{{{2} + }} \left( {{\text{aq}}} \right) + {\text{H}}_{{3}} {\text{O}}^{ + } \left( {{\text{aq}}} \right)\quad {\text{pK}}_{{\text{a}}} = {4}.{85}$$

(34)

$${\text{HCOOH}}\left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to {\text{HCOO}}^{ - } \left( {{\text{aq}}} \right) + {\text{H}}_{{3}} {\text{O}}^{ + } \left( {{\text{aq}}} \right)\quad {\text{pK}}_{{\text{a}}} = {3}.{77}$$

(35)

$${\text{CH}}_{{3}} {\text{COOH}}\left( {{\text{aq}}} \right) + {\text{H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to {\text{CH}}_{{3}} {\text{COO}}^{ - } \left( {{\text{aq}}} \right) + {\text{H}}_{{3}} {\text{O}}^{ + } \left( {{\text{aq}}} \right)\quad {\text{pK}}_{{\text{a}}} = {4}.{76}$$

(36)

The pK_a value of the Eq. 34 was taken from Chang and Goldsby 2013, while the pK_a values of the Eqs. 35 and 36 were taken from Evans and Ripin (2022). The dissociation constant of water was also taken into account. The deacidification agents were assumed to be completely dissociated.

$${\text{Mg}}\left( {{\text{OH}}} \right)_{{2}} \left( {{\text{aq}}} \right) + {\text{6H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to \left[ {{\text{Mg}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{6}} } \right]^{{{2} + }} \left( {{\text{aq}}} \right) + {\text{2OH}}^{ - } \left( {{\text{aq}}} \right)$$

(37)

$${\text{MgCO}}_{{3}} \left( {{\text{aq}}} \right) + {\text{7H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \to \left[ {{\text{Mg}}\left( {{\text{H}}_{{2}} {\text{O}}} \right)_{{6}} } \right]^{{{2} + }} \left( {{\text{aq}}} \right) + {\text{2OH}}^{ - } \left( {{\text{aq}}} \right) + {\text{CO}}_{{2}} \left( {\text{g}} \right)$$

(38)

Because the molar concentrations were in the order of mmol dm⁻³, the ‘classic’ Debye-Hückel theory (Debye and Hückel 1923) was used to calculate the mean activity coefficients. The calculated pH profiles are shown in Fig. 9. One can note that the small arc at the top of the rise of the curves is caused by the use of smoothing when drawing the curves. Due to the complex calculation, the pH was calculated in regular time steps, which resulted in that small arc in the drawing. The points in Fig. 9 represent pH calculated from the magnesium distribution measured by SEM WDS. The correlation between pH and magnesium distribution is discussed in the Supplement material. It can be seen that the agreement is reasonable.

Fig. 9

pH profiles at different depths of paper for the simulation run 1. (red line): surface of the paper (depth of 0 µm); (dark red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm). (circles): pH calculated from SEM WDS data—color of circles is defined according to their respective depth

The simulation run 2

This simulation run tested the penetration of solid hydromagnesite particles into the depth of the paper under the same conditions as run 1. As a consequence of the transport of these basic particles, it can be seen that the whole deacidification process is much shorter than in the case of run 1.

The concentration profiles of substances calculated by the model are shown in Figs. 10, 11, 12, and 13 and they may be interpreted similarly as in run 1, except of the part, where solid particles penetrate into the paper. The penetrating starts after ca 2.5 days, and it is seen as a visible break in Figs. 10, 11, 12, and 13. The surface concentration of Mg(OH)₂ decreases significantly at this time as solid hydromagnesite particles began to penetrate the paper (Fig. 10). It is caused by the sudden decrease of the active surface of solid particles, which results in a decrease of the dissolution rate. The sudden decrease of the surface of solid particles is also visible in Fig. 11. The solid particles reach the middle of the paper in ca 30 min, and then new stationary state is achieved. When sulfuric acid in the unbound water is depleted, a new stationary state is achieved again, and the main part of organic acids is neutralized in this step. The achievement of this new stationary state takes ca 5 h. After depleting organic acids, the creation of alkaline reserve starts and it takes approximately 1 h.

Fig. 10

Concentration profiles of magnesium hydroxide in unbound water (the first level of the model) at different depths of paper for the simulation run 2. (red line): surface of the paper (depth of 0 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 11

Surface of the solid hydromagnesite particles at different depths of paper for simulation run 2. (red line): surface of the paper (depth of 0 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 12

Concentration profiles of magnesium hydroxide in non-freezing water (the second level of the model) in different depths of paper for the simulation run 2. (red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

Fig. 13

Concentration profiles of sulfuric acid (left) and organic R¹COOH acids (right) at different depths of paper for the simulation run 2. (red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

When looking at the concentration profiles of magnesium hydroxide in non-freezing water (second level of the model), the same ‘steps’ are visible, except of the penetration of solid particles into the paper (Fig. 12). Solid particles do not reach the microfibrils in the paper. It can be clearly visible when the sufficient amount of magnesium hydroxide reaches the microfibrils at the respective depths to establish the stationary diffusion. The same results show concentration profiles of sulfuric acid and organic acids (Fig. 13). The change in course of the concentration profiles can be visible at the first level of the model (sulfur acid), while in the second level (organic acids), it is not visible. Similarly, to the simulation run 1, the concentration profiles of magnesium carbonate copy the profiles of magnesium hydroxide, they are just 4 times higher due to stoichiometry.

The corresponding calculated pH profiles are shown in Fig. 14. The procedure of pH calculation was the same as described in the section dealing with the simulation run 1.

Fig. 14

pH profiles at different depths of paper for the simulation run 2. (red line): surface of the paper (depth of 0 µm); (dark red line): subsurface of the paper (depth of 1 µm); (blue line): depth of 5 µm; (orange line): depth of 20 µm; (gray line): depth of 40 µm; (yellow line): the middle of paper (depth of 70 µm)

The simulation run 3

In the simulation run 3 the influence of the water content on the deacidification was tested. We wanted to test the correctness of the model to determine whether the increased water content in the model influences the dissolution rate of hydromagnesite particles. Therefore, the values of all the parameters were left the same as in simulation run 1, except for the water content that was increased from 9 to 24% (75 and 100% of relative humidity (Banik and Brückle 2011), respectively). The results were almost the same as in simulation run 1, but the total time of the deacidification process was shortened by approximately 1 day (2%). As expected, the main reason for the faster deacidification process is the increase in transport rates of dissolved species (higher amount of water results in more swelling of cellulose fibres that are more permeable to water and substances dissolved in it).

Conclusions

A two-level model of the deacidification of cellulosic objects using MgO particles was developed. It was assumed that the MgO particles change to hydromagnesite particles due to the CO₂ present in the air. Two levels of the model introduce different types of water that is present in the structure of the paper/cellulose. The first level represents the unbound ‘mobile’ water phase, while the second one represents the non-freezing water tightly bounded to the cellulose microfibrils.

To test the results of the model, quantitative deacidification process was performed experimentally. The model results agree well with the experimental data (in the limits of experimental error). It should be noted that the several conclusions raised in the manuscript are the results of the modelling, e.g. creation of the alkaline reserve After the deacidification step. Due to the lack of experimental data available in the literature, it is not confirmed experimentally. However, due to the reaction rate of the neutralization reactions we may assume that the alkaline components react with the acids and after the depletion of the acids the alkaline reserve starts to create. This demonstrates that the model is sensitive to the setting of the transport coefficients. The values of transport coefficients applied in the model have been imposed from the only available experimental data. Further experiments should be carried out for a more accurate estimate of their values.

After such a précising, the model can be used for the prediction of deacidification process under certain values of temperature and humidity. The model can be used for the deacidification process optimization, and it can explain the stages of the deacidification process. Moreover, pH in the different places of the cellulosic objects (e.g. among the macrofibrils or inside the microfibrils) can be estimated using the model; which cannot be measured. It is sufficient to consider the calculated amounts of acid and basic compounds present in the chosen place, assuming the respective hydrolysis reactions.

The model is also consistent with the Lucas–Washburn equation (Lucas 1918; Washburn 1921), which is commonly used for description of the penetration of a dissolved species into a wet porous material.

Taking into account the complexity of a paper (outer dimensions of a paper sheet, cellulose fibres, macrofibrils, microfibrils, bounds of cellulosic polymer chains), it is evident that the developed model works with simplifications. These simplifications are implied by the uncertainty in the description of all transports and reactions in individual domains of the paper sheet sufficiently quantitatively and in spite of this uncertainty to obtain a useful tool for description of deacidification process. The great advantage of the model is the satisfactory prediction of the neutralization process in a complex material such as paper, where several very complex transport processes of water penetration into the paper take place simultaneously. The model considers the effect of particle size on the penetration into the material, which can account for the porosity itself. In doing so, it also takes into account the fact that the form and localization of water have a decisive influence on neutralization.

As mentioned, the presented model does not set itself the task of fully describing the deacidification process. It only lays the foundations for its description. Transport coefficients also depend on the type of paper, its properties, such as porosity, tortuosity, etc. However, we think that the presented model creates a very good basis for further research on the description of the deacidification process and its modelling. It is a challenge to the future.