1 Introduction

Characterizing flow and solute transport in porous media is essential for numerous applications in earth science, engineering and industry, including \(\hbox {CO}_2\)-storage, drinking water protection, safe disposal of nuclear waste, and enhanced oil recovery. Diffusion-limited transport mechanisms, such as in subsurface gas transport in soils (Jayarathne et al. 2020), preparative chromatography (Schultze-Jena et al. 2020) and heterogeneous catalysis (Ertl et al. 2008), depend on available pore space, i.e., porosity.

While the physics of transport are well understood, the complex geometry of natural materials poses a challenge for determining bulk transport parameters given the spatial heterogeneity of fluxes (Blunt et al. 2013). Even for Fickian diffusion, the impact of the complex heterogeneous pore space on transport behavior is not fully captured in an universal generic mathematical framework. This holds particularly for (observed) irregular pore structures, which cannot be described by simplified models, e.g., packings of spherical particles or bundles (Bear 1972). Or as Bruckler et al. (1989) put it: “It appears that there is not a simple and unique relationship between the gas diffusion coefficient and air-filled porosity. [...] Predicting the gas diffusion coefficient on a large range of soil samples without complete measurements will probably be quite complicated”.

The development of imaging techniques such as micro-computed X-ray tomography (Cnudde and Boone 2013) and electron microscopy (Grunwaldt et al. 2013) offers a novel starting point for studying the scaling behavior of transport in complex pore geometry by providing large data sets. However, calculating petrophysical properties of complex pore geometries requires a sufficient sample number or large sample size to guarantee that results are representative in terms of volume and details captured. Still, detailed statistical analyses of observational data sets on porous media transport in complex pore geometries are rather the exception (de Winter et al. 2016; Jackson et al. 2020; Mehmani et al. 2020; Menke et al. 2021) than the rule. Thus, the predictive capability of geometrical parameters toward transport properties remains a question (Zhang et al. 2021).

Relating transport properties at macroscale, as Darcy or even Field scale, to structural parameters at pore or microscale has a long tradition starting with Hazen (1893); Carman (1937); Kozeny (1953) and many others. Central assumption is the existence of a representative elementary volume (REV) scale (Bear 1972), where fluctuations at microscale cancel out leading to a deterministic value at macro-scale. Innumerable relationships exist in the literature, relating bulk transport parameters such as the diffusion coefficient or permeability to pore structural parameter, where porosity is typically the main determining parameter, complimented by geometrical characteristics, such as tortuosity, constrictivity, formation factor, grain shape factors, etc. (van Brakel and Heertjes 1974; Berson et al. 2011; Ghanbarian and Hunt 2014; Gaiselmann et al. 2014 or Devlin (2015) and references within). A key challenge is determining the contributions of each parameter to transport properties at the Darcy scale, especially for irregular pore geometries. Hence, these parameters are often used as fitting parameters in deterministic functional relationships ignoring the natural scatter in the data due to geometrical heterogeneity of porous material. To our perception, the variety of (semiempirical) relations contradicts the existence of a unique relationship.

We hypothesize that a fundamental reason why researchers have not yet succeeded in finding an universal correlation between the pore structure and transport properties is the misinterpretation of the REV concept and the level at which an REV is reached for transport properties. Transport property variations between volumes having an with similar pore volume do not completely vanish at very large domain sizes, unlike geometrical parameters such as porosity, due their dependency on the complex pore space topology.

We study that hypothesis through an analysis of a large number of microscopy-based 3D domains with irregular sub-REV pore spaces. We refined an upscaling routine of de Winter et al. (2016) allowing the stochastic evaluating of the porosity and the diffusive transport properties as a function of domain size. The key of our work is using a probability distribution function describing the scatter plot of a large number of data points, as opposed to fitting an explicit equation to the scatter plot. Particularly, probability distributions are computed from actual data and not assumed for theoretical expedience.

By showing that the diffusion coefficient in porous media is not a deterministic function of pore structure and porosity but is better represented by a stochastic representation we are able to investigate domain size effects of observed scatter. We make predictions on the REV scale, i.e., the averaging support scale. We further discuss the implications on experimental work, continuum equations and simulations of large-scale processes in the context of the REV concept.

2 Diffusion in Porous Media

Diffusion is the net effect of Brownian motion across a region with a concentration gradient. Diffusion in porous media is classically described by a modified form of Fick’s law, relating diffusive flux \(J_\text {PM}\) to the concentration gradient:

$$\begin{aligned} J_\text {PM} = - D_\text {PM} \frac{\mathrm{d} C(x)}{\mathrm{d}x} \end{aligned}$$
(1)

Equation (1) is valid assuming diluted concentration C of the involved species. Note that we further assume isotropic diffusive transport (based on an isotropic material structure).

The proportionality constant \(D_\text {PM}\) is interpreted as an effective porous media diffusion coefficient being a lumped parameter containing: (1) all the dynamics and interactions of the fluid molecules, e.g., molecular mass, molecular size, electrostatic interactions and thermodynamic properties; (2) the impact of the pore structure; and (3) all interactions between the molecules and the porous material. Consequently, the effective diffusion coefficient \(D_\text {PM}\) is a function of pressure, temperature and molecular diameter. In addition, characteristics of the pore space geometry, such as porosity, tortuosity and constrictivity, are included in the effective diffusion coefficient.

Typically, the effective diffusion coefficient in hydrogeological applications of porous media diffusion at macroscale is defined as \(D_\text {PM} = \frac{\theta D_\text {mol}}{\tau }\). Here, the molecular diffusion constant \(D_\text {mol}\) of the particular fluid phase occupying the pore space covers the fluid effects, while the effective porosity \(\theta\) and tortuosity \(\tau\) represent the impact of pore structure. Note that the \(D_\text {PM}\) given here refers to a particular definition of tortuosity, which is not unified in the literature (Bear 1972; Clennell 1997; Ghanbarian et al. 2013). The use of an effective diffusion coefficients is only valid when the diffusion process has reached the REV scale. Here, the pure characterization through structural components is misleading since their REV scales differ from that of flow and transport properties (Zhang et al. 2000): while porosity as pure volume property converges to REV scale relatively quickly, flow and transport of particles depend on the actual pore space topology having much higher REV scales.

Extracting geometrical parameters, such as porosity \(\theta\) and tortuosity \(\tau\) from microscopy images of the pore space, is not trivial. For example, the total porosity as ratio of pore volume to total sample volume differs from the effective porosity, which does not contain isolated pore space not contributing to flow. Tortuosity \(\tau\) as a measure for the actual length of flow paths is not only ambiguous defined, but also hard to determine experimentally (Ghanbarian et al. 2013; Zhang et al. 2021; Fu et al. 2021). Since it is hardly ever available for porous media samples, empirical values are mostly used for tortuosity, typically in the range of \(\tau = 1.5 - 3\) based on expert knowledge. Also describing tortuosity as explicit function of porosity does not capture the strong scatter of complex pore topologies for identical pore volumes. Thus, the use of a deterministic relationship \(D_\text {eff} = D_\text {mol} \theta /\tau\) based on \(\theta\) measurements has to be critically assessed, since the REV scale is much higher than typically anticipated.

We aim to provide a tool to deal with parameter variations in the diffusion coefficient below REV-scale through a stochastic description. We will make use of a dimensionless parameter representing the effect of the pore structure on diffusive flux: the transport-ability \(\chi\). We define it as the ratio of diffusive flow through the porous volume and the flow through an empty volume (Sect. 3.3.1). At REV scale, it can be interpreted as a mapping of porosity and tortuosity, \(\chi = {\theta }/{\tau }\), and thus \(D_\text {PM} = \chi \cdot D_\text {mol}\).

3 Statistical Description of Observation Data

3.1 Observation Data

We analyze a data set published by de Winter et al. (2016) on fluid catalytic cracking (FCC) particles, which have an average diameter of \(100\,\upmu\)m and pore sizes ranging from 1 nm to roughly \(2\,\upmu\)m. The porosity distribution was determined from scanning electron microscopy (SEM) images. High-resolution segmented images (resolving power after image processing about 10 nm) of cross sections of FCC particles were split in equal sized squares. The porosity of each square was determined as ratio pore pixel over total pixels. The histogram over all squares yielded the porosity distribution. The analysis was performed with grid sizes of \(2\times 2\,\upmu\)m, \(8\times 8\,\upmu\)m and \(32\times 32\,\upmu\)m.

Transport properties were identified on diffusion simulations in 3D pore spaces with their geometries based on the actual FCC particle’s pore space. First, a focused ion beam-scanning electron microscope (FIB-SEM) was employed to analyze the pore space in 3D with voxel size of about \(10\times 10\times 10\) nm. An algorithm tuned toward reproducing the 3D pore space of the FCC particles allowed for generating thousands of small volumes, called ’virtual volumes,’ suitable for diffusion simulations. The simulations obtained the steady-state diffusive flux solving Fick’s equation by an iterative scheme. For each of the complex unstructured pore spaces, it was also determined if they are percolating, i.e., if a connected flow path exists. All technical details can be found in de Winter et al. (2016).

Here, we make use of the porosity distribution functions for various domain sizes, the percolation probability as a function of porosity and a measure for a resistance against diffusive transport as a function of porosity. Details are outlined in the following subsections.

3.2 Porosity

Porosity, the ratio of pore volume to total volume, has been measured for particle sub-samples at domain size r of \(2\,\upmu\)m, \(8\,\upmu\)m, and \(32\,\upmu\)m domain size. Although observations refer to areal investigation, we consider them as representative for the volume property, assuming isotropy in the third dimension. Statistical analysis of measured porosities revealed a normal distribution at all sample scales r. Scale-dependent sample mean \(\mu _r\) and sample standard deviations \(\sigma _r\) are listed in Table 1.

Table 1 Statistical quantities of porosity observations for FCC1 and FCC2 catalytic particles as function of sample domain size \(r = 2, 8, 32\,\upmu\)m
Full size table

The probability of observing a certain porosity \(\theta\) in a sample of domain size r can be described with a truncated normal distribution \(P^{(r)}(\theta )\propto N(\mu _r,\sigma _r,0,1)\), limited to the range of \(\theta \in [0,1]\):

$$\begin{aligned} P_\theta ^{(r)}(\theta = x) = {\left\{ \begin{array}{ll} \frac{1}{ft\cdot \sigma _r\sqrt{2\pi }} \exp {\left( -\frac{(x-\mu _r)^2}{2 \sigma ^2_r}\right) } &{}\quad \text { for } 0<x<1 \\ 0 &{}\quad \text { else } \end{array}\right. } \end{aligned}$$
(2)

to the parameters \(\mu _r\) and \(\sigma ^2_r\). \(ft = \Phi (\mu _r,\sigma _r,1) - \Phi (\mu _r,\sigma _r,0)\) denotes the normalization factor due to truncation which is given by the difference of values of the normal distribution \(\Phi\) at 0 and 1. The truncation formally changes the actual mean and variance of the distribution \(P_\theta ^{(r)}(\theta = x)\). Values differ only slightly from the input parameters \(\mu _r\) and \(\sigma ^2_r\), which is within the uncertainty of the observation values listed in Table 1. Figure 1 shows the truncated normal distributions of porosity’s at all domain size levels for the FCC2 material.

Fig. 1
figure 1

Distribution function of porosity depending on domain size \(r=2, 8, 32 \,\upmu\)m. Solid lines show the truncated Gaussian PDF of the total porosity. The black line shows the connectivity probability \(p_\mathrm {con} (\theta ) \in [0,1]\). The dashed lines indicate the distribution of connected porosity, and the shaded areas between the curves indicate the amount of non-connected porosity’s

Full size image

Porosity statistics show a scale dependency. As expected, mean porosity \(\mu\) remains quasi constant with increasing domain length r (Table 1), whereas the standard deviation \(\sigma\) decreases. For a domain of n units in d dimensions, there are \(n^d\) copies of the porosity. The law of large numbers predicts that the associated variance decreases by a factor of \(1/n^d\) when samples are independent. However, the decrease in the sample standard deviation is slower, with an actual factor of \(1/n^{d/2}\). Thus, samples are not independent indicating the presence of spatial correlations.

The slow decrease in the standard deviation shows that samples are not independent due to spatial correlation given the non-uniform and non-random material structure innate to porous material. The nonzero value of the standard deviation at \(\sigma _{(32)}\) shows another effect: domain size has not yet reached the porosity REV level. The slower convergence of the standard deviation to zero increases the porosity REV scale since deviations of porosity observations can still be present at relatively large samples size. Both aspects, sub-REV scale and spatial correlation of samples need to be accounted for in upscaling processes.

3.3 Transport-Ability

3.3.1 Definition

For investigating the impact of the pore structure on diffusive transport, we define a dimensionless variable transport-ability, mathematically denoted as \(\chi\), as ratio of the flux in the porous medium domain, i.e., a restricted flux \(J_\text {PM}\) (Eq. 1), to the unrestricted flux in a free domain \(J_0 = - D_\text {mol} \frac{d C(x)}{dx}\):

$$\begin{aligned} \chi = \frac{J_\text {PM}}{J_0} = \frac{D_\text{PM} }{D_\text{mol} } \end{aligned}$$
(3)

The definition (3) of \(\chi\) allows extracting the effect of the porous media structure on diffusive fluxes from a fluid specific impact. Thus, \(\chi\) is a sole property of the porous media structure, and we consider it a function of porosity \(\theta\) and the topology of the void space \(\chi = f(\theta , \text {topology})\). Note that \(\chi\) is scale-dependent. As outlined in Sect. 2, at REV scale \(\chi\) can be interpreted as ratio of porosity \(\theta\) to tortuosity \(\tau\), and thus \(D_\text {PM} = \chi \cdot D_\text {mol}\). However, we decided against an explicit functional dependency of \(\chi\) on \(\tau\) given the ambiguous definition and observational limitations of tortuosity. Instead, we reflect the variation of \(D_\text {PM}\) below REV scale by defining \(\chi\) as spatial random variable (Sect. 3.3.3).

\(\chi\) ranges between zero and one. For unrestricted domains, i.e., \(\theta \rightarrow 1\), we have \(\chi \rightarrow \theta /\tau = 1\). However, \(\chi\) is small for strongly restricted domain, related to small porosities \(\theta\) and highly tortuous pore space. \(\chi = 0\) covers the case of a disconnected or non-percolating medium, i.e., no flow path is available through the medium.

\(\chi\) is not a bi-unique property of porosity since various structures with identical porosity show significantly different flux patterns, such as straight flow channels or disconnected void space. The effect of structure is usually lumped into an "effective porosity", while the portion of void space contributing to transport is particularly critical.

3.3.2 Transport-Ability Observations

We use a data set of transport-ability observations from 5128 cubic virtual volumes of \(r=2 \upmu m\) length based on diffusive transport simulations of de Winter et al. (2016) (Sect. 3.1). To derive the probabilistic relation of transport-ability as a function of porosity \(\theta\), each volume i is analyzed with respect to: (i) porosity \(\theta _i\), (ii) connectivity, i.e., if a flow path through the sample exist to allow a diffusive flux, and (iii) transport-ability \(\chi _i\) for the connected samples. We first focus on connected volumes for which the distribution of observed \(\chi _i\) versus porosity \(\theta _i\) is displayed in Fig. 2.

Fig. 2
figure 2

Scatter plot of transport-ability as function of porosity for connected volumes. Dashed line indicates maximal \(\chi\) corresponding to plug flow. Vertical gray lines indicate positions of individual \(\chi (\theta )\) analysis in Fig. 3

Full size image

The data scatter in Fig. 2 shows that the domain scale \(r=2\,\upmu\)m is at sub-REV scale for both \(\chi\) and \(\theta\). Volumes of the same \(\theta\) show large variations in \(\chi\), ruling out a deterministic one-to-one relation between both, certainly at sub-REV level. Consequently, we model \(\chi\) as random function of \(\theta\) with a probability distribution function (PDF) \(P_{\chi }(\theta )\) representing the scatter of \(\chi\) for identical porosities.

3.3.3 Descriptive PDF for Transport-Ability

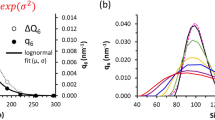
We examine the frequency of \(\chi\) values for small bin ranges of porosity values (e.g., \(0.16< \theta < 0.18\)) as displayed in Fig. 3. Details of the statistical analysis, including normality and log-normality tests are discussed in the Supporting Information.

Fig. 3
figure 3

Statistical analysis of transport-ability \(\chi\) for individual porosity values: normalized frequency distributions of data in normal (top) and log-scale (bottom) compared to normal and log-normal distribution for \(\theta = 0.17\) and \(\theta = 0.31\). n is the number of data samples

Full size image

For each porosity value, the \(\chi\) values follow a log-normal distribution which changes in shape depending on \(\theta\). \(\chi\)-distributions for small \(\theta\)-values show a strong log-normal shape while distributions become less skewed with increasing porosity (Fig. 3). We attribute this tendency to the impact of pore space topology. The scarce pore space at small porosity value is either scattered with several bottlenecks or forms one or few flow channels. In the first domain type, flow is hampered and \(\chi\) will be low, while in the latter we observe quasi plug flow with a relatively high \(\chi\) values. The effect reduces with increasing pore volume.

We calculated expectation values \(a (\theta )\) and standard deviations \(b (\theta )\) for each log-transformed frequency distribution of \(\chi (\theta )\). The log-transformation allows comparing statistics given the logarithmic nature of \(\chi\) values. The log-normal distributions also represents the frequency for higher porosities, as it converges to the normal-distribution for decreasing standard deviations. Results are displayed in Fig. 4.

The \(\log \chi\) mean \(a(\theta )\) shows a linear relationship for porosities smaller than 0.6 and then a flattening toward 0 since \(\chi (\theta =1) = 1\). \(\log \chi\) standard deviation b is high for small porosities and decreases with increasing \(\theta\). For porosities beyond 0.6, the scatter is negligible.

Fig. 4
figure 4

Expectation values (mean) \(a(\theta )\) and standard deviation \(b(\theta )\) of log-transformed transport-ability \(\chi\) as function of porosity \(\theta\)

Full size image

The parameters \(a(\theta )\) and \(b(\theta )\) can be used to encapsulate the dependency of \(\chi\) on porosity \(\theta\) through functional description of the probability distribution \(P_\mathrm {\chi }^\mathrm {con} = LN(a(\theta ),b(\theta ))\):

$$\begin{aligned} P_\mathrm {\chi }^\mathrm {con}(\chi = y,\theta ) = \frac{1}{\sqrt{2\pi }y\cdot b(\theta )} \exp {\left( -\frac{\left( \ln (y) -a(\theta )\right) ^2}{2 b^2(\theta )}\right) } \end{aligned}$$
(4)

\(P_\mathrm {\chi }^\mathrm {con}(\chi = y,\theta )\) describes the probability of \(\chi =y\) given a specific value of porosity \(\theta\) assuming that the domain is connected, i.e., having a flow path through the sample. However, disconnected elements exist and have a \(\chi\) of zero.

3.3.4 Connectivity Statistics

Connectivity is a sub-property of \(\chi\) and depends on porosity: decreasing pore volumes lower the probability of having a void space path through the domain. We model connectivity as probabilistic Bernoulli variable X being either connected (\(\chi \ne 0\)) or not-connected/dead-end (\(\chi =0\)) with the connectivity probability \(p_{\mathrm{con}}(\theta ) \in [0,1]\) as function of porosity \(\theta\): \(P(\chi \ne 1)=p_\mathrm {con}(\theta )\) and \(P(\chi =0)=1-p_\mathrm {con}(\theta )\).

The frequency analysis of the 5128 virtual volumes with regard to connectivity resulted in a function \(p_{\mathrm{con}}(\theta )\) as displayed in Fig. 1. Samples of porosity smaller than 0.07 are never connected \(p_{\mathrm{con}}(\theta <0.07)=0\), whereas samples of \(39\%\) porosity or larger are always connected, \(p_{\mathrm{con}}(\theta \ge 0.39)=1\). For porosities in between, de Winter et al. (2016) determined the functional description:

$$\begin{aligned} p_{\mathrm{con}}(\theta ) = {\left\{ \begin{array}{ll} 0 &{}\quad \text {for } \; \theta \le 0.07\\ \left( c_3\theta ^3+c_2\theta ^2+c_1\theta +c_0\right) ^2 &{}\quad \text {for }\; 0.07< \theta < 0.39 \\ 1 &{}\quad \text {for }\; 0.39 \le \theta \end{array}\right. } \end{aligned}$$
(5)

with \(c_3=27.362\), \(c_2=-27.661\), \(c_1=9.4256\), and \(c_0=-0.0927\).

Relating the porosity distribution and the probability of connectivity in an ensemble allows determining the total number of connected and disconnected samples. The dashed lines in Fig. 1 indicate the distribution of connected porosities. The shaded areas between the curves are the number of dead-end samples with zero \(\chi\): \(1- \int _0^1 P^{(r)}_\theta \cdot p_\mathrm {con} (\theta ) d\theta\). The number decreases with increasing sample size r given the reduction of standard deviation \(\sigma _r\) and thus less samples of small porosity. For the FCC2 material, the predicted total number of disconnected samples is \(14.8\%\) for \(r=2\,\upmu\)m; \(9.7\%\) for \(r=8\,\upmu\)m; and \(6\%\) for \(r=32\,\upmu\)m, respectively. Note that the number of disconnected samples is still significant for the sample size of \(r=32\,\upmu\)m although the standard deviation is small and most samples range around the mean porosity of about 0.3.

Connectivity is closely related to percolation (Berkowitz and Balberg 1993). In the context of percolation theory, the total number of disconnected samples has to be smaller than the percolation threshold to guarantee transport through the network. Given the low values of disconnected samples, and even decreasing with increasing scale r, most of the networks will have at least one connected pathway. The analysis of \(p_\mathrm {con}\) for the data at domain size \(r=2\,\upmu\)m shows that the REV scale is not reached since at REV level, the porosity threshold would separate clearly non-connected to connected samples.

Transport-ability as stochastic function of porosity follows from the statistical descriptions of connectivity (Eq. 5) and connected \(\chi\) (Eq. 4) with

$$\begin{aligned} P_\mathrm {\chi }(\chi = y,\theta ) = {\left\{ \begin{array}{ll} 0 &{}\quad \text { with }\, 1-p_\mathrm {con}(\theta ) \\ y>0 &{}\quad \text { with }\, p_\mathrm {con}(\theta )\cdot P_\mathrm {\chi }^\mathrm{con} (y,\theta ) \end{array}\right. } \end{aligned}$$
(6)

Moments, such as the expectation value and variance of \(\chi\) as function of \(\theta\) can be derived based on the characteristics of the log-normal distribution. Theoretical expressions are listed in the Supporting Information. Regard that moments refer to ergodic conditions, i.e., when the domain size is above REV level for all involved processes.

4 Upscaling

We upscale observations addressing the questions of interest: To what extend is the scatter of transport-ability \(\chi\) and porosity \(\theta\) related to domain size? And at what domain size can we consider the REV to be reached? The evolution of porosity statistics for observations at increasing domain size are outlined in Sect. 3.2. Since observations of transport-ability are not available at domain length beyond \(2\,\upmu\)m, we simulated the scaling behavior of \(\chi\) with increasing domain size deriving statistical relations between \(\chi\) and \(\theta\) as function of the domain size r.

We follow an upscaling procedure exemplified in Fig. 5. We determine \(\chi\) at increasing scales within sub-REV level making use of numerical diffusive flux simulations in a Monte Carlo setting. We study the upscaling behavior in 2D and 3D, since porosity measurements are often taken in a 2D setting, while flow and thus \(\chi\) generally requires observation in 3D volumes. Similar upscaling strategies have been pursued by, e.g., Boschan and Noetinger (2012); Colecchio et al. (2020) who studied the scaling behavior of effective hydraulic conductivity in heterogeneous porous media.

Fig. 5
figure 5

Upscaling scheme: from known porosity distribution at small scale (upper left corner) to desired description of transport-ability \({\bar{\chi }}({{\bar{\theta }}})\) at larger scale (lower right corner). We determine \({\bar{\chi }}({{\bar{\theta }}})\) numerically through flux adapted averaging (lower left corner) and derive a probabilistic relationship from porosities at larger scale \(\bar{\theta }\) (upper right corner)

Full size image

4.1 Numerical Upscaling Procedure

We generate discrete networks each consisting of \(N = n^d\) sub-samples, with d being the dimension. We decided for \(n=16\) elements per direction based on network theory and preliminary tests showing that boundary effects are negligible for \(n>10\) (Supporting Information). For instance, a domain at size \(r=32\,\upmu\)m consists of 16 sub-samples of length \(2\,\upmu\)m within each dimension and a domain of \(2048\,\upmu\)m consists of 16 sub-samples of length \(128\,\upmu\)m. An exception is networks at domain size \(r=8\,\upmu\)m which are upscaled from \(n=4\) elements of length \(2\,\upmu\)m.

We generate ensembles of 10,000 networks with domain sizes between \(r=8\,\upmu\)m and \(r=2048\,\upmu\)m. All networks of an ensemble share the same statistics. Tests on ensemble convergence showed that the ensemble size of 10,000 is sufficient to achieve reproducible results.

The workflow for generating one network within an ensemble comprises:

  • The network is initialized with \(N = n^d\) elements.

  • Porosity of each network element is created by random value sampling from the truncated normal distribution (Eq. 2) with mean \(\mu =0.3\) and \(\sigma _r\) according to the domain size adapted statistics based on the values determined for the FCC2-1 material (Table 1). We account for the spatial correlation of porosity and preserve the statistics observed in the data by reducing the number of samples within the network to \(\sqrt{n}\) instead of n samples per direction. For example, if a network consists of \(n=4\) elements per direction, we randomly draw \(\sqrt{n} = 2\) porosity values and assign one to the first two elements and the second porosity to the third and fourth element. That way the porosity statistics of the entire network scale differently. The variance does not decrease at a rate of \(1/n^d\) but at the actually observed rate of \(1/n^{d/2}\). Assigning identical porosity values to neighboring elements properly reflects the impact of spatial correlation. Although, we only have observations available to domain sizes of \(32\times 32\upmu m\), we assume that the spatial correlation of the material structure and thus of porosity persists at larger scales.

  • Connectivity of each element is randomly specify as either yes(\(=1\)) or no(\(=0\)) based on its porosity \(\theta _i\) and the associated probability of connectivity \(p_\mathrm {con}(\theta _i)\) (Eq. 5), which we considered domain size independent.

  • A transport-ability value \(\chi _i\) of each connected element is drawn from the probability distribution \(P_\mathrm {\chi }^\mathrm {con}(\theta _i)\) (Eq. 4) whose statistics a and b are based on the \(\chi\) value distribution of the domain size r of the elements. Tests using a distribution function based in the histograms of \(\chi _r\) values instead of imposing a log-normal function showed identical results. Note, that we do not explicitly include spatial correlation of \(\chi\) values - only implicitly through their dependency on the elements’ porosity values.

For each generated network, we determine upscaled properties \(\bar{\theta }\) and \({\bar{\chi }}\). The average porosity is the arithmetic mean \({{\bar{\theta }}} = \sum _{i} \theta _i\) of the elements’ porosities. We compute the effective transport-ability \({\bar{\chi }}\) by solving the Laplace equation of steady state diffusion following from (1) in a finite differences scheme on each discrete network. The workflow is outlined in the Supporting Information. The procedure is identical to determining effective hydraulic conductivities by inverting Darcy’s Law (Sánchez-Vila et al. 2006). The workflow is implemented in python and freely available in the GitHub repository https://github.com/AlrauneZ/TransportAbility (Zech 2021).

Fig. 6
figure 6

Results of numerical upscaling for simulated ensembles at different domain sizes r [\(\upmu\)m] in 2D: a Scatter of ensemble transport-ability \({\bar{\chi }}\) vs porosity \({{\bar{\theta }}}\); b, c marginal distributions, i.e., normalized histograms for porosity and transport-ability. Lighter lines slightly visible in (b, c) show the associated theoretical distributions based on ensemble parameters

Full size image

4.2 Numerical Upscaling Results

Figure 6 shows the results of the upscaled transport-ability \({\bar{\chi }}\) and porosity \({{\bar{\theta }}}\) for simulated ensembles at domain sizes \(r=8-2048\,\upmu\)m. Each dot in Fig. 6a represents one of the 10000 networks in the ensemble. Displayed results refer to 2D, while similar results for the 3D setup are accessible in the Supporting Information. Marginal distributions show the normalized frequencies from a histogram analysis of \({{\bar{\theta }}}\) and \({\bar{\chi }}\) data within each ensemble. The marginal distributions confirm that porosity and log-transport-ability follow normal distributions with scale-dependent parameters.

Porosity distributions of each ensemble are normal distributed and are perfectly in line with theoretical upscaling behavior of the FCC particle data (Table 1): constant mean \(\mu\) and decreasing standard deviation \(\sigma _r = 0.15/\root 4 \of {N_r}\) where \(N_r = (r/r_0)^d\) is the total number of elements of size \(r_0=2\,\upmu\)m (the initial value) in each network of total domain size r.

The scaling behavior of transport-ability combines two effects: a decrease in disconnected networks and a decreasing mean in connected transport-ability with increasing domain size. At a level of \(r=512\,\mu\) basically all networks are connected and have \(\chi >0\). However, these values can be rather small and now contribute to the mean of connected transport-ability, which thus decreases. Figure 6c shows that a normal distribution matches well the \(\log \chi\) data, i.e., log-normal for \(\chi\), particularly at increasing domain sizes r. Now, the distribution represents the entire \(\chi\) behavior, since all elements are connected while for small domain sizes the impact of disconnected elements with \(\chi =0\) are not included in the mean a of \(\log \chi\)-values. The standard deviation b of \(\log \chi\) decreases with scale.

Fig. 7
figure 7

Evolution of porosity and transport-ability statistics with increasing domain size r: Diamonds show coefficient of variation of porosity statistics of simulated ensembles \(\mathrm{CV}_{{{\bar{\theta }}}} = \sigma _r/\mu\), circles show geometric coefficient of variation \(\mathrm{GCV}_{{\bar{\chi }}} = \sqrt{\exp {(b^2)} -1}\) for the transport-ability. Lines show theoretical predictions by a scaling proportional to \(1/\root 4 \of {n^d}\). Left scaling according to domain size r, right scaling to number of elements in network \(N_r\)

Full size image

We investigate the scale dependence of the statistics of porosity \({{\bar{\theta }}}\) and transport-ability \({\bar{\chi }}\), in particular that of the standard deviation characterizing the decreasing scatter, making use of the coefficient of variation: \(\mathrm{CV}_{{{\bar{\theta }}}} = \sigma /\mu\) scales the porosity standard deviation by mean. For \(\chi\) we make use of the geometric coefficient of variation \(\mathrm{GCV}_{{\bar{\chi }}} = \sqrt{\exp {(b^2)} -1}\) being more appropriate for a log-normal distribution. We associate a sufficiently low CV with reaching the REV level. For porosity, e.g., a \(\mathrm{CV}<0.025\) corresponds to a standard deviation of \(2.5\%\mu\) and consequently more then \(95\%\) of the porosity values in the PDF lie within a range of \(\mu \pm 2\sigma = [0.95\mu ,1.05\mu ]\).

Figure 7 shows the scaling behavior of the statistics of porosity and transport-ability for both dimensional analyses, 2D and 3D. The display of CV as function of domain size r shows a steeper decrease in 3D due to the larger number of sub-samples with the additional dimension. Differences disappear when displaying the scaling behavior for the total number of elements \(N_r = (r/2)^d\), which is a function of the dimension d.

Parameter scaling of porosity follows the theoretically predicted relation \(\mathrm{CV}_\theta = \sigma _r/\mu =\frac{0.15}{0.3\root 4 \of {N_r}}\), which is \(\mathrm{CV}_\theta ^{(2D)} = 1/2\sqrt{0.5r}\) and \(\mathrm{CV}_\theta ^{(3D)} = 1/2(0.5r)^{3/4}\) in 2D and 3D, respectively. Both relations show a linear fit in log-log display in Fig. 7. The CV is below a level of 0.025 for a domain size of \(n=512\,\mu\). Thus, we consider the REV level for porosity reached at that domain size in a 2D sample analysis.

Parameter scaling of transport-ability, shows a similar trend with decreasing GCV at a rate proportional to \(1/\root 4 \of {N_r}\). However, at large domain sizes the trends flattens out and \(\log \chi\) standard deviation b does not decrease any further. The asymptotic value lies at about \(\alpha = 0.05\). We relate the fact that the spread of \(\log \chi\) does not converge to zero to the dependency of transport-ability on spatial structure. Upscaled values \({{\bar{\chi }}}\) are identify through a process related upscaling procedure not a simple average such as the geometric mean. Thus, networks with identical averages of element-\(\chi\) values can lead to different upscaled values \({{\bar{\chi }}}\) due to the spatial arrangement of elements, including non-connected elements with \(\chi =0\). Consequently, there remains a scatter or nonzero variance in \({{\bar{\chi }}}\) values between networks of the same ensemble.

At the same time, the remaining scatter is small (GCV in Fig. 7 of \(5\%\)) at larger scales. When the remaining fluctuations are not detectable or irrelevant for a process at macro-scale, the value can still be considered as at REV level. We relate the REV of \(\chi\) to the 3D upscaling behavior since flow is best determined in volumes. Assuming REV scale for \(\chi\) at a GCV level of \(\alpha = 5\%\), this is reached at a domain size of \(r=2048\,\upmu\)m which corresponds to a domain volume of about 1e10 \(\upmu m^3\). Figure 7 makes obvious that spatial domain sizes for reaching REV levels differ significantly between porosity and transport-ability.

4.3 Theoretical Upscaling

The statistical descriptions of porosity \(\theta\), connectivity and connected transport-ability \(\chi\) allow for theoretical upscaling of \(\chi\) as stochastic function of \(\theta\). We further make us of the findings of numerical upscaling to derive an expression for the stochastic description of \(\chi\) as function of \(\theta\) and domain size r.

Fig. 8
figure 8

Probability contours for transport-ability \(\chi\) as function of porosity \(\theta\) with various porosity mean \(\mu\) and standard deviation \(\sigma\) values (Eq. 2). Upper row has identical \(\chi\) statistics of \(a_r\) and \(b_r\) of log-normal distribution (Eq. 4) at \(r=2\), while lower row \(\chi\) statistics refer to scales \(r=2\,\upmu\)m, \(r=32\,\upmu\)m and \(r=512\,\upmu\)m which correspond to porosity standard deviations \(\sigma _r\)

Full size image

Starting point is a material at domain size r with a normal porosity distribution \(P_\theta ^{(r)}\) (Eq. 2) of mean \(\mu\) and standard deviation \(\sigma _r\). The distribution \(P_\mathrm {\chi }^{(r)}\) of connected \(\chi\) at r can be assumed as log-normal distributed to parameters \(a_r(\theta )\) and \(b_r(\theta )\) according to (Eq. 4). Non-connected elements distribute with \(p_{\mathrm{con}}(\theta )\) (Eq. 5). The probability distribution of transport-ability versus porosities for an ensemble of networks of domain size r then follows as: \(P^{(r)}(\theta = x,\chi =y) = P_\theta ^{(r)}(x)\cdot p_{\mathrm{con}}(x) \cdot P_\mathrm {\chi }^{(r)}(y)\).

Figure 8 shows the pdf-cloud (as continuous counterpart to Fig. 6a) for various input parameters of porosity statistics \(\mu\) and \(\sigma\) and \(a_r\) and \(b_r\) depending on domain size r. The upper panel shows the isolated impact of the porosity distribution at the small domain size \(r=2\). The range of potential porosity values reduces with decreasing standard deviation \(\sigma\) (Fig. 8c), while transport-ability remains a broad distribution for each porosity value.

The combined effect of increasing scale on the \(\theta -\chi -\)distribution through the reduction in value spreading is displayed in the bottom row of Fig. 8. Here, \(\chi\) statistics decrease similarly to those of \(\sigma _r\) following the scaling behavior identified in the numerical simulations: \(b_r = \max \left( 0.05,b_2/{(r/2)^{d/4}}\right)\).

5 Discussion

The upscaling procedure and CV/GCV graphs (Fig. 7) allow determining a minimum sample size to be considered an REV for the material studied here which is transferable to other observations. In case the experimental equipment or computational resources are insufficient to handle an REV, the alternative is repeating the measurements sufficiently often at similar sub-REV domains. The measurements will reveal a scatter with an unknown standard deviation. An appropriate sample size must be estimated during the process using standard statistical tools.

5.1 REVs of FCC Particles

Figure 7 shows that the investigated FCC particles require a domain size of \(512\,\upmu\)m to guarantee an REV for porosity at a level of \(\alpha = 0.025\). However, FCC particles have an average diameter of \(100\,\upmu\)m being below REV scale. The significant differences in the mean porosity of the 5 particles reported in de Winter et al. (2016) confirm that observations are below REV scale. It takes about 34 individual particles of \(100\,\upmu\)m diameter to cover the same surface area as an REV (\(512\,\upmu\)m \(\times\) \(512\,\upmu\)m). Considering the spatial correlation of porosity and statistical soundness, the minimum number of particles will be much higher than these 34 samples.

Reaching REV level for transport-ability requires even larger surface areas when observing transport in a 2D setting. The domain scale of \(512\,\upmu\)m would provide an acceptable level of deviation when investigating transport in 3D. When limited to particles of \(100\,\upmu\)m diameter, 256 particles are needed to cover the same volume. Even this absolute minimum number of particles is currently beyond the practical capabilities for effective parameter observations in lab studies.

5.2 Implications for Continuum Equations and Experiments

The observation that the GCV of transport-ability does not reach zero at large domain sizes has implications for the use of effective parameters in continuum equations. A certain level of scatter remains in upscaled effective transport parameters. Thus, the application of the REV concept has to be carefully assessed. When parameter fluctuations as result of the pore space complexity impact macro-scale processes, these effects should be accounted for in numerical and analytical solutions of continuum equations. This would require a representation of parameter variation through uncertainty bands and/or stochastic parameter representations which is hardly done.

Diffusion is probably the simplest form of porous media transport. Yet, the scatter in transport-ability does not diminish fast nor completely and remains significant at relatively large length scales. This explains why fitted relations between an effective diffusion coefficient and porosity for porous materials vary among publications. Not even considering experimental errors, a small sample size/number can easily lead to fitting results which do not necessarily be representative for the material under investigation.

Although other materials will reveal different statistical relations and scale-developments as presented here, we conclude that more focus should be given to a sufficient sample scale and sample number in experimental and computational studies aiming to determine effective parameters at Darcy scale. Given a limitation in data points, we strongly advocate the use of probability distributions for upscaling parameters and property relation rather than empirical deterministic fits.

5.3 Perspectives

Suppose we consider more complex processes than diffusion, such as solute transport by advection and dispersion, two-phase flow, evaporation, dissolution-precipitation, coupling of free flow over porous media flow, etc. Each process is influenced by the complexity of the pore space. Crucial open questions for future research remain: Do all processes parameters need their own PDF for a complete description? And how do parameter PDF’s develop during upscaling? What are appropriate REV scales given a certain process and porous material.

6 Summary and Conclusions

Applying the REV concept to transport parameters in porous media relies on the reduction of scatter with increasing observation scale to a negligible level. If significant scatter in observations persists, an effective mean is not a representative parameter for the process of interest. We investigated the scatter in observations of porosity and transport-ability, the latter representing the effect of porous medium structure on pore scale diffusion, with increasing scale from nanometer to micrometer. We made use of FIB-SEM data obtained from FCC materials of de Winter et al. (2016).

The statistical analysis of the large collection of diffusive transport observations in sub-REV porous domains revealed the relationship between porosity and transport-ability at multiple length scales. The assessment included the study of connected and disconnected volumes, where the latter inhibit diffusive flow at all. We observe strong scatter of both, porosity and transport-ability, as expected at sub-REV scale. Consequently, we relate porosity and transport-ability through probability distribution functions (PDFs) instead of attempting to establish an explicit deterministic relation between both, which cannot exist due to the variability of the porous media structure. The PDFs provide a mathematical description of this variability. While porosity follows a normal distribution, transport-ability is best characterized through a log-normal distribution. The statistical descriptions allowed performing numerical and theoretical upscaling.

The scatter in both quantities reduced with increasing scale, but with different convergence behavior. We assess reaching the REV level for porosity by determining the coefficient of variation. The latter reduces linearly with increasing domain size due to a constant mean and the reduction in standard deviation. However, spatial correlation of porosity is observable in the data and reduces the convergence to an REV level.

The scatter of the transport-ability with increasing samples sized does not decrease linearly, but levels off at an asymptotic value \(>0\). Using the geometric coefficient of variation (GCV), the value is in the range of 0.05. Thus, transport-ability measurements will always show a scatter around the mean, regardless of the domain size. This can be easily explained by the natural variability of void space topology of porous media which will be present at all scale leading to a natural scatter in transport characteristics. However, even when considering the scatter to be small enough at GCV\(= 0.05\) and assuming the REV level is reached, the observation scale is in the range of \(2000\,\upmu\)m \(= 2\) mm. Thus, diffusion experiments at microscopic level in heterogeneous porous material must result in scattered observations not leading to representative results unless experiments are repeated for sufficient samples.

The influence of local heterogeneity to the transport behavior has consequences for the application of the REV concept which is key factor for (i) experimental work; (ii) continuum equations; (iii) simulations of large scale processes. Our results lead us to the major conclusions:

  • Although porosity observations converge to an effective value with increasing observation scale and/or number of samples; spatial correlation of samples lead to higher REV levels as typically assumed.

  • The length scale of the REV for (diffusive) transport in porous media is significantly underestimated when based on porosity measurements only.

  • Diffusion parameters for microscopic samples will always show a scatter in measurements for heterogeneous porous material given the tortuous and non-unique pore space topology. In the example of FCC particles, we found a minimum scatter of \(5\%\). However, the level was only reached for large domain sizes leading to an REV level at mm scale.

  • There is no one-to-one deterministic relationship between porosity and transport characterizing parameters, like the diffusion coefficient, in complex porous structures. Instead a probabilistic relation of these parameters to porosity is warranted to capture the effect of the complex pore space, particularly—but not exclusively—below REV level.

Generally, the application of the REV concept in porous media research has to be carefully assessed for each process and process-related quantity. Our results suggest that the REV level is typically underestimated for effective parameters particularly when they are integrating geometrical as well as topological aspects of the porous medium structure. Furthermore, REV scale does not necessarily mean complete absence of scatter in upscaled quantities, but some variation might persists even at large scale given the complexity of porous media structure. However, when these fluctuation are below macroscopic detection level or do not necessarily impact the large scale process behavior, the concept of REV is valid and useful for applications. This should, however, be carefully investigated.