1 Introduction

Flow of emulsion in porous media appears in many practical applications including premix emulsification (Baumann et al. 2012; Nazir et al. 2013, 2014; Mitkowski and Szaferski 2016; Błaszczyk et al. 2017a), remediation (Cortis and Ghezzehei 2007), filtration (Soo and Radke 1984) and enhanced oil-recovery (Thomas and Farouq Ali 1989; Mandal et al. 2010; Guillen et al. 2012a). Much attention has been devoted in the literature to the modeling of the flow of diluted o/w emulsions stabilized by low molecular weight surfactants in porous media (Devereux 1974; Soo and Radke 1984; Romero and Carvalho 2011; Nazir et al. 2013; Moradi et al. 2014; Mandal and Bera 2015; Yu et al. 2017; Błaszczyk et al. 2017a). It has been found that pressure drops and permeability depend on the stability of the emulsion and the droplet size of the dispersed phase relative to the pore size of the medium (Soo and Radke 1984). Cortis and Ghezzehei (2007) have identified three basic classes of emulsion flow in porous media, which need to be considered separately. To the first class were included dilute, relatively unstable emulsions with very small drop-size to pore-size ratio. A second class involves relatively stable emulsions with drop size to pore-size ratio on the order of unity. A third class involves stable emulsions with relatively small drop-size to pore-size ratio (Cortis and Ghezzehei 2007).

In addition to low molecular weight surfactants, emulsions are also stabilized by the addition of polymers. Aqueous polymer solutions are also the most widely used fluids in modeling research on the flow of non-Newtonian fluids in porous media. A number of methods have been proposed for the calculation of pressure drops in semi-rigid chain (mainly the carboxymethylcellulose sodium salt, xanthan gum and guar gum were used) polymer solutions in Darcy flow and non-Darcy flow regimes (González et al. 2005; Amundarain et al. 2009; Kaur et al. 2011).

A critical review of these methods can be found, for example, in the studies by Kaur et al. (2011), Chhabra and Richardson (1999) and Chhabra et al. (2001). A separate problem is the flow of high molecular weight flexible polymer solutions in porous media (HPAM, PEO) (Durst et al. 1981; Haas and Ku1icke 1985; Howe et al. 2015). In this case, a rapid increase in pressure drop is observed above a certain flow rate (apparent flow thickening), which is not attributable to inertia. The causes of apparent flow thickening have not been fully elucidated yet. Most commonly, it has been linked to the high extensional viscosity of polymer solutions (Zhang et al. 2016) or elastic instability (Howe et al. 2015; Kawale et al. 2017).

Currently, there is no information in the literature regarding pressure drops accompanying the flow of polymer-stabilized emulsions in porous media. The continuous phase in emulsions of this type is usually characterized by complex rheological properties (Różańska et al. 2013). Additionally, polymers often cause the flocculation of droplets, which can lead to formation of a gel-like network structure (Dickinson 2009; Krstonošić et al. 2009; Różańska et al. 2013). The aim of the study presented here was to evaluate pressure drops accompanying the flow of diluted o/w emulsions stabilized by the addition of two polymers with a semi-rigid chain (carboxymethylcellulose sodium salt and xanthan gum) and one polymer with a flexible chain (polyethylene oxide) through a medium of spherical glass particles. The ratio of the mean droplet size to the pore size in the emulsions and packed beds used in the study was very small. Also, an analysis was carried out to evaluate the possibilities for using models proposed in the literature for aqueous polymer solutions to calculate pressure drops during the flow of polymer-stabilized emulsions.

2 Experimental Procedures

2.1 Materials

The emulsions used in the study were stabilized following polymers: carboxymethylcellulose sodium salt (NaCMC, Sigma-Aldrich) about two different average molecular weights (Mw = 700,000 g/mol (degree of substitution DS was 0.9) and 250,000 g/mol (degree of substitutions DS was 0.7 and 0.9), xanthan gum (XG, Hortimex, Poland) and poly(ethylene oxide) (PEO, Sigma-Aldrich, Mw = 8,000,000 g/mol). To the emulsion was added a nonionic emulsifier Tween 40 (polyoxyethylenesorbitan monopalmitate, Sigma-Aldrich), whose concentration was 5 vol%. The XG-stabilized emulsion without the addition of Tween 40 was also used in the studies. Polymer concentrations in the continuous phase of the emulsion were, respectively: NaCMC—0.4 wt% for Mw = 700,000 g/mol and 1.5 wt% for 250,000 g/mol, PEO—0.2 wt% and XG—0.2 wt%. The dispersed phase of the emulsion was mineral oil (Institute of Petroleum Technology, Kraków, Poland) with shear viscosity 0.2182 Pa s and density 885 kg/m3 in the temperature 20 °C. Studies were performed in the concentration range of the dispersed phase from 10 to 50 vol%.

2.2 Preparation of Emulsions and Polymer Solutions

First, polymer solutions in deionized water were prepared at a concentration higher than the target concentration in the continuous phase. The solutions of polymers were mixed for 6 h using low-speed impeller and then stored at 4 °C for 24 h to achieve the maximum hydration.

Oil-in-water emulsion was prepared with a homogenizer (IKA, Werke GmbH & Co., KG, Staufen, Germany) equipped with dispersing ending S50N-G45G. The procedure for preparation of emulsion with the addition of NaCMC, XG and PEO was as follows. At first, a specified amount of surfactant (Tween 40) was dissolved in distilled water and it was mixed for 5 min at 6000 rpm by homogenizer. Next, the required amount of oil was added and it was mixed again for 20 min. Finally, aqueous solution of polymer, prepared previously, was added and mixed for 10 min with the same equipment as before. The exceptions were emulsions with added PEO which, in the final stage, were mixed with a slow-speed anchor agitator for 4 h to avoid mechanical degradation of the polymer chain. The XG-stabilized emulsions without Tween 40 were mixed for 10 min at 6000 rpm in a homogenizer.

All emulsions were prepared 1 day prior to the tests. In order to stabilize the temperature for 24 h, the emulsions were stored in an air-conditioned room where the temperature was maintained at 21 °C ± 0.5. During storage the emulsions were continuously mixed with an anchor agitator (11) at a frequency of approximately 0.7 rps, which prevented their creaming.

2.3 Emulsion Droplet Size Analysis

Microstructure of the emulsions was studied using Nikon Eclipse 50i microscope (Tokyo, Japan). The images of the droplets were captured through the CCD camera (OptaTech) mounted on an optical microscopy. A drop of emulsion was placed between a microscope slide and cover slip. The captured images were analysed using the MATLAB programme.

2.4 Experimental Setup

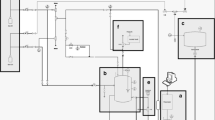
The experimental setup is shown schematically in Fig. 1. A column with an internal diameter D = 0.034 m and length L = 0.338 m was filled with glass beads with a diameter dp = 2.98 ± 0.03 mm. Keller (type PR-35X) pressure sensors with a measuring range of up to 3 bar (accuracy 0.05% full scale) were fitted in the wall of the packed-bed tube. The temperature of the fluid was controlled using a thermocouple sensor (± 0.3 K). The porosity of the packed bed ε in the column determined experimentally

Fig. 1
figure 1

Experimental set up: 1—pipe with a porous bed, 2—computer, 3—pressure transducers, 4—ball valves, 5—tank with fresh fluid, 6—cylinder, 7—piston, 8—ball screw actuator, 9—stepper motor, 10—tank, 11—anchor agitator

Full size image

The flow of the fluid in the system was generated by a syringe pump (1) of our own design. The pump was made from an aluminum cylinder with an internal diameter of 0.032 m (6) and a length of 0.7 m. The piston movement was induced by means of a ball screw actuator (8) driven by a stepper motor (9). The speed of the stepper motor was controlled with the computer program. The design of the pump made it possible to achieve emulsion flow rates in the range from 0.02 × 10−6 to 32 × 10−6 m3/s with an accuracy to 0.25%. The direction of fluid flow in the system was regulated by means of ball valves (4). The tank from which the fluid was sucked via a syringe pump was fitted with an anchor agitator connected to an IKA Eurostar digital laboratory stirrer. The pipe connecting the column filled with the syringe pump had a diameter of 0.034 m. Measurements were taken in an air-conditioned room where the temperature was maintained at 21 ± 0.5 °C.

2.5 Shear and Oscillatory Flow

All the rheological measurements in shear flow were performed on the rotational rheometer Physica MCR 501 produced by Anton Paar (Austria) equipped with concentric cylinder system with shear rate \( \dot{\gamma } \) ranging between 0.1 and 1000 s−1. The measuring device was equipped with a temperature controlling unit (Peltier plate) that provided very good temperature control over an extended period of time. Rheological measurements were conducted at the temperature of the fluid recorded during its flow through the packed bed.

3 Theoretical Background

Results of measurements of pressure drops ΔP during the flow of non-Newtonian fluids in porous media are usually represented in two ways: as a correlation between the modified friction factor and the modified Reynolds number or the so-called apparent viscosity and the apparent shear rate.

The value of the modified friction factor can be calculated from the equation:

$$ f_{\text{BK}} = \frac{\Delta P}{{\rho \cdot v_{0}^{2} }} \cdot \frac{{d_{p} }}{L} \cdot \frac{{\varepsilon^{3} }}{1 - \varepsilon } $$
(1)

where dp is the particle diameter, v0 is the superficial liquid velocity, ρ is the density of liquids, ε is the porosity, and L is the column length. A number of definitions of the modified Reynolds number for the flow of non-Newtonian fluids in porous media have been proposed in the literature. The form of the Reynolds number depends primarily on the rheological model employed to describe the flow curve and the definition of the equivalent diameter used. The most commonly used rheological models include the power law model (Sorbie and Huang 1991), Carreau model (Zamani et al. 2015), Bingham model (Attia et al. 2016; Chen et al. 2005) and Herschel–Bulkley model (Chevalier et al. 2013). It needs to be noted that several different definitions of the modified Reynolds number have been proposed in the literature for the power law model.

The apparent shear viscosity ηapp is defined from Darcy’s law as follows:

$$ \eta_{\text{app}} = \frac{K \cdot A}{Q} \cdot \frac{\Delta P}{L} $$
(2)

where K is the permeability, A is the surface area normal to the flow, and Q is the volumetric flow rate. For packed beds of spheres, permeability may be calculated from Kozeny–Carman equation:

$$ K = \frac{{\varepsilon^{3} \cdot d_{p}^{2} }}{{36\kappa \cdot (1 - \varepsilon )^{2} }} $$
(3)

where κ is the Kozeny–Carman constant, which for beds packed with spherical particles equals 5.

The apparent shear rate \( \dot{\gamma }_{\text{app}} \) can be defined by dividing the superficial velocity v0 by the characteristic microscopic length l of the porous media (Chauveteau 1982; Sorbie et al. 1989; Perrin et al. 2006; Tosco et al. 2013; Rodríguez de Castro et al. 2016). Characteristic microscopic length is very frequently defined as (K × ε)0.5; hence the apparent shear rate is described with the equation:

$$ \dot{\gamma }_{\text{app}} = \alpha \frac{{v_{0} }}{{\sqrt {K \cdot \varepsilon } }} $$
(4)

where α is the shift factor, which is usually found by experiment (Sorbie et al. 1989), but it is also possible to calculate this using pore-scale modeling approaches (Sorbie et al. 1989; Lopez et al. 2003).

In this study, the shift factor was determined for all the emulsions under study using the method described by Rodríguez de Castro and Radilla (2017). The procedure involves selecting a value of α at which there is superimposition of the curves of apparent viscosity calculated from the porous media flow results with the shear viscosity curves. The values of α depend mainly on the pore structure and vary across a wide range from 0.7 to 14.1 (Sorbie et al. 1989).

4 Results and Discussion

4.1 Structure of Emulsions

Research findings published to date show that pressure drops during the flow of aqueous polymer solutions are determined to a significant extent by the rigidity of the polymer chain (González et al. 2005; Haas and Kulicke 1985). Therefore, the polymers used for stabilizing the emulsions were selected in such manner that they differed not only in terms of average molecular mass, but also chain rigidity. NaCMC and XG are anionic polymers with a semi-rigid chain (González et al. 2005; Amundarain et al. 2009; Kaur et al. 2011), whereas PEO is a nonionic polymer with a flexible chain (Durst et al. 1981; Haas and Ku1icke 1985; Howe et al. 2015; McKinley et al. 1996).

The pictures presented in Fig. 2 show the drops of emulsions used in the studies. It can be noted that all emulsions are polydisperse and flocculated. The addition of polymers to the emulsions may result in flocculation by depletion or bridging. Bridging flocculation occurs when polymer molecules adsorb simultaneously on more than one drop (Hogg 2013; Różańska et al. 2013). The polymers used in the study do not adsorb on the surface of oil droplets, so in the emulsions shown in Fig. 2 the fusion of droplets into aggregates is caused by the depletion force (Różańska et al. 2013).

Fig. 2
figure 2

Microscopic pictures of emulsions (ϕ = 20 vol%) with addition of NaCMC250, DS = 0.9 (a), XG (b), XG (Tween 40) (c), PEO (d)

Full size image

In Table 1 are summarized the value of Sauter mean diameter (d32), the De Broucker mean diameter (d43) and polydispersity index (PDI) of the droplets calculated based on the equations (Li et al. 2013; Leal-Castaneda et al. 2018)

$$ d_{32} = \frac{{\sum\nolimits_{i = 1}^{N} {n_{i} d_{i}^{3} } }}{{\sum\nolimits_{i = 1}^{N} {n_{i} d_{i}^{2} } }} $$
(5)
$$ d_{43} = \frac{{\sum\nolimits_{i = 1}^{N} {n_{i} d_{i}^{4} } }}{{\sum\nolimits_{i = 1}^{N} {n_{i} d_{i}^{3} } }} $$
(6)
$$ {\text{PDI}} = \frac{{d_{43} }}{{\frac{{\sum\nolimits_{i = 1}^{N} {d_{i} } }}{N}}} $$
(7)

where di is the droplet diameter, N is the total number of droplets, and ni is the number of droplets having a diameter di. The average number of droplets used to calculations was 20,000 ± 50.

Table 1 Droplets diameter for emulsion used in the study
Full size table

The diameter values (d32, d43 and PDI) listed in Table 1 were determined for the emulsions introduced into the installation, and for the oil volume fraction of 20 vol% also for the emulsions passed through the packed bed (values given in brackets). The fact that the diameters of droplets reaching the packed bed and passed through the packed bed were similar shows that there was no droplet coalescence during the flow.

During preliminary tests, it was found that the droplets of the emulsions stabilized only by the addition of NaCMC and PEO flowing from the packed bed were considerably larger than the droplets of the emulsions introduced into the installation. In order to increase their stability, the emulsions were additionally enriched with Tween 40. There was no droplet coalescence during the flow of the emulsions stabilized with XG only, but the emulsions with added XG and Tween 40 contained smaller droplets. Consequently, the emulsions stabilized with XG and Tween 40 were also included in the tests for comparative purposes.

Since the emulsions used in the tests were flocculated and contained relatively large droplets, their creaming rate was determined. Emulsion stability was analyzed by visual observation of the emulsions placed in glass cylinders with a volume of 1 liter. The emulsions with added XG were stable even 24 h after their preparation. However, a serum layer with a height of 0.5 cm was found to have formed at the bottom of the cylinder after approximately 1.5 h in the emulsion with added NaCMC and after approximately 3 h in the emulsion containing PEO. For this reason, before being introduced into the measuring setup and in the tank feeding the syringe pump, the emulsions were continuously stirred with an anchor agitator at a frequency of approximately 0.9 Hz in order to prevent creaming. The time when the emulsions were inside the installation pipes did not exceed 4 min; hence, it was assumed that the effect of creaming on the measurement of pressure drops was minor.

A factor affecting pressure drops during the flow of emulsions in porous media is the ratio of the droplet size of the dispersed phase to the pore size of the medium (Cortis and Ghezzehei 2007). In the spherical particle packed bed, the hydraulic diameter dh can be calculated from the equation

$$ d_{h} = \frac{2}{3} \cdot \frac{\varepsilon }{1 - \varepsilon } \cdot d_{p} $$
(8)

It follows from the equation in (8) that in the packed bed used dh = 1.252 × 10−3 m and the dh/d43 ratio is in the range from 76 to 347 (Table 1). The majority of studies published to date focus on the flow through a packed bed of emulsions containing droplets with diameters larger than or comparable to the pore diameter (McAuliffe 1973; Guillen et al. 2012b; Błaszczyk et al. 2017b). The results of pressure drop measurements presented in this study apply to the flow of emulsions with a relatively small droplet-size to average pore-size ratio.

4.2 Rheology

All the polymer-stabilized emulsions studied were non-Newtonian fluids. In the case of non-Newtonian fluids, it is necessary to estimate the range of shear rate changes occurring during their flow in porous media. In this study, the range of changes in \( \dot{\gamma } \) was estimated based on Eq. (4), adopting the unique shift factor value c = 1.7 proposed by Meurant (1981) for packs of large spheres having the same diameter. The calculated values of \( \dot{\gamma }_{\text{app}} \) varied from 3 to 1000 s−1.

The microstructure of polymer-stabilized emulsions discussed in the previous section translates into their rheological properties. This is evidenced by the flow and viscosity curves shown in Figs. 3, 4 and 5. A marked increase in the viscosity of emulsions in relation to the viscosity of aqueous solutions of polymers occurs already at the 10 vol% fraction of the oil phase, which is due to the flocculation of droplets.

Fig. 3
figure 3

Flow curves of emulsions stabilized by NaCMC

Full size image
Fig. 4
figure 4

Shear viscosity curves of emulsions stabilized by XG (0.2 wt%)

Full size image
Fig. 5
figure 5

Shear viscosity curves of emulsions stabilized by PEO

Full size image

The flow and viscosity curves shown in Figs. 3, 4 and 5 were obtained for the emulsions introduced into the measuring setup and for the emulsions passed through a packed bed containing 20 vol% of the oil phase. The flow curves generated for the fresh emulsion and for the emulsion which was passed through a packed bed overlap, which shows that no permanent change in the emulsion microstructure occurred during the flow.

The shape of the flow curves obtained for highly flocculated emulsions with the addition of NaCMC is characteristic for yield-stress fluids (Fig. 3). They were described using the Herschel–Bulkley model:

$$ \tau = \tau_{0} + k \cdot \dot{\gamma }^{n} $$
(9)

where τ0 is the yield stress, k is the consistency factor, and n is the power law exponent in Herschel–Bulkley model. The rheological parameters of the Herschel–Bulkley equation are summarized in Table 2. The yield-stress values range from 0.07 to 2.5 Pa and depend on the molecular weight of the polymer, the degree of substitution and the volume fraction of the oil phase.

Table 2 Rheological parameters in Herschel–Bulkley Eq. (9) for emulsions with added NaCMC
Full size table

In the viscosity curves obtained for the emulsions with added XG, a zero shear viscosity range and a shear thinning range can be identified (Fig. 4). They were described with the Carreau model, based on which a number of methods had been proposed in the literature for calculating pressure drops occurring during the flow of polymer solutions in porous media (Zamani et al. 2015). The Carreau model is expressed with the equation:

$$ \eta = \eta_{\infty } + \frac{{\eta_{0} - \eta_{\infty } }}{{\left[ {1 + (\lambda \cdot \dot{\gamma })^{2} } \right]^{{\frac{{1 - n_{C} }}{2}}} }} $$
(10)

where η0 is the zero shear viscosity, η∞ is the infinite shear viscosity, λ is the time constant, and nC is the power law exponent in Carreau model (Table 3).

Table 3 Rheological parameters in Carreau Eq. (10) for emulsions with added XG
Full size table

Figure 5 shows viscosity curves of the emulsions with added PEO and, for comparison, a viscosity curve obtained for propylene glycol (80% solution, Newtonian fluid). The viscosity curves of the aqueous solution of PEO and emulsions containing between 10 and 40 vol% of the dispersed phase show that above a certain shear stress value there is an apparent increase in viscosity, whereas in the non-Newtonian fluid, it remains constant over the entire range of \( \dot{\gamma } \). This indicates that the effect of inertia on the flow is minimal, and the observed apparent flow thickening is caused by elastic instabilities (Groisman and Steinberg 2000; Howe et al. 2015). The presence of elastic flow instabilities is characteristic for solutions of high molecular weight flexible polymers, and it results from the state of non-homogeneous flow field (McKinley et al. 1996).

The slope of the viscosity curves shown in Fig. 5 demonstrates that an increase in the volume fraction of the dispersed phase induces an increase in the shear rate at which the onset of apparent flow thickening occurs (from 132 s−1 for ϕ = 10 vol% to 412.5 s−1 for ϕ = 40 vol%). In addition, at higher shear rates the viscosity of the emulsion at a concentration of 10–40 vol% stabilizes at the same level. An increase in the volume fraction of the oil phase to 50 vol% resulted in the complete loss of apparent flow thickening. These results demonstrate that a rise in emulsion viscosity caused by the flocculation of droplets counteracts elastic flow instability.

5 Flow Through Packed Bed

5.1 Emulsions Stabilized by NaCMC

A study conducted by Sochi (2010) shows that the current flow modeling methodologies cannot cope with the complexity of yield-stress fluids in porous media. In addition, only a few publications have presented the results of experimental studies investigating the flow of this group of fluids in porous media (Al-Fariss and Pinder 1987; Chevalier et al. 2013; Chase and Dachavijit 2005). A method for calculating pressure drops in fluids whose flow behavior can be characterized by the Herschel–Bulkley model has been proposed by Al-Fariss and Pinder (1987), Sochi (2010) and Chevalier et al. (2013). Our calculations indicate that there are significant deviations between the pressure drops measured by us during the flow of the emulsions with added NaCMC and the values of pressure drops determined on the basis of models proposed in the literature (25% and 150%, respectively, in relation to the values calculated using the models by Al-Fariss and Pinder (1987) and Chevalier et al. (2013)).

Pressure drops during the flow of yield-stress fluids through a capillary can be calculated using a method based on the generalized Reynolds number proposed by Metzner and Reed (1955). Originally, the method was employed to calculate pressure drops during the flow of power law fluids and was then generalized to include yield-stress fluids. In the Herschel–Bulkley model, the value of the generalized flow behavior index n′ and generalized flow consistency index K′ can be calculated from the equations (Maleki and Frigaard 2016).

$$ n' = n \cdot (1 - \xi ) \cdot \frac{{(n + 1) \cdot (2n + 1) + 2n(n + 1)\xi + 2n^{2} \xi^{2} }}{{(n + 1) \cdot (2n + 1) + 3n(n + 1)\xi + 6n^{2} \xi^{2} + 6n^{3} \xi^{3} }} $$
(11)
$$ K' = \frac{{\tau_{0} + k\left( {\frac{3n' + 1}{4n'} \cdot \dot{\gamma }_{N,w} } \right)^{n} }}{{(\dot{\gamma }_{N,w} )^{n'} }} $$
(12)

In Eq. (11) ξ is the dimensionless plug size

$$ \xi = \frac{{R_{0} }}{R} = \frac{{\tau_{0} }}{{\tau_{w} }} $$
(13)

where R0 is the radius of constant velocity plastic plug, R is the radius of pipe, τw is the wall shear stress and \( \dot{\gamma }_{N,w} \) is the Newtonian shear rate on the wall.

According to Kembłowski and Michniewicz (1979), the friction factor of power law fluids can be calculated from the equation:

$$ f_{\text{BK}} = \frac{180}{{Re_{\text{BK}}^{*} }} $$
(14)

in cases when the Reynolds number is defined by the relationship:

$$ Re_{\text{BK}}^{*} = \frac{{v_{0}^{2 - n} \cdot d_{p}^{n} \cdot \rho }}{{k(1 - \varepsilon )^{n} }}\left( {\frac{4n}{3n + 1}} \right)^{n} \cdot \left( {\frac{15\sqrt 2 }{{\varepsilon^{2} }}} \right)^{1 - n} $$
(15)

We propose to generalize the Reynolds number proposed by Kembłowski and Michniewicz (1979), to all time independent fluids:

$$ Re_{\text{BK}}^{*} = \frac{{v_{0}^{2 - n'} \cdot d_{p}^{n'} \cdot \rho }}{{K'(1 - \varepsilon )^{n'} }} \cdot \left( {\frac{15\sqrt 2 }{{\varepsilon^{2} }}} \right)^{1 - n'} $$
(16)

The exponent n′ was calculated using the modified dimensionless plug size ξe, introducing the hydraulic radius Rh into Eq. (13):

$$ R_{h} = \frac{{d_{p} }}{6} \cdot \frac{\varepsilon }{1 - \varepsilon } $$
(17)

and the generalized flow consistency index K′ was calculated with the help of the shear rate equation proposed by Kembłowski and Michniewicz (1979), which has the following form for Newtonian fluids:

$$ \dot{\gamma }_{N,w} = 15\sqrt 2 \cdot \frac{1 - \varepsilon }{{\varepsilon^{3} }} \cdot \frac{{v_{0} }}{{d_{p} }} $$
(18)

The relationship between the friction factor fBK and the Reynolds number \( Re_{\text{BK}}^{*} \) in the emulsion with added NaCMC is shown in Fig. 6. With respect to the 10% emulsion, convergence between the experimental points and the line resulting from Eq. (6) (deviation of the experimental points δ < 5%, where δ = (∣fBK(Eq. 6) − fBK(exp.)∣/fBK(Eq. 6)) × 100) is seen across the entire range of Reynolds numbers. The results are not surprising, as the flow curve of the 10 vol% emulsion within the range of shear rates from 3 to 1000 s−1 can be described by the exponential equation. For the emulsions containing 30 vol% and 50 vol% of the oil phase the values of δ are lower than 5% above the \( Re_{\text{BK}}^{*} \) number values equaling 0.012 and 0.0384, respectively. The given values of the number \( Re_{\text{BK}}^{*} \) correspond to similar values of the dimensionless factor R0/Rh amounting to 0.054 and 0.062 for the emulsions containing oil at the concentrations of 30 vol% and 50 vol%, respectively. The results show that Eq. (14) can be used for calculating the friction factor when the plug zone disappears (R0/Rh → 0). Consequently, the proposed method for predicting pressure drops during the flow of yield-stress fluids has limited practical significance.

Fig. 6
figure 6

Dependence of the friction factor on the generalized Reynolds number \( Re_{\text{BK}}^{*} \) for emulsions with the addition of NaCMC (Mw = 250,000 g/mol; DS = 0.9)

Full size image

Figure 7 shows the values of the friction factor fBK multiplied by the product (n/n′)n as a function of the \( Re_{\text{BK}}^{*} \) number. This representation of results of pressure drop measurements in the emulsions with added NaCMC resulted in the experimental points forming a single relationship and, additionally, being aligned along the 180/ \( Re_{\text{BK}}^{*} \) line. The product (n/n′)n has no theoretical justification and arises solely from the observation that its application makes it possible to describe the experimental points by the relationship:

$$ f_{\text{BK}} = \frac{180}{{Re_{\text{BK}}^{*} }} \cdot \left( {\frac{n'}{n}} \right)^{n} $$
(19)

in the range ReBK ∈ 〈0.001; 3〉, R0/Rh < 0.5, dh/d43 > 266 and τ0 ≤ 2.5.

Fig. 7
figure 7

Dependence of the fBK × (n/n′)n on the generalized Reynolds number \( Re_{\text{BK}}^{*} \) for emulsions with the addition of NaCMC

Full size image

The average deviation of experimental points from the line described in Eq. (19) is 2.3% (coefficient of variation).

Equation (19) can be employed to predict pressure drops on the condition that it is possible to calculate the modified dimensionless plug size ξe. Its value depends on the power law exponent n and the Herschel–Bulkley number defined for the flow of fluid in the pipe by the equation (Peixinho et al. 2005):

$$ Hb = \frac{{\tau_{0} \cdot R^{n} }}{{k \cdot v^{n} }} $$
(20)

where R is the inside tube radius and v is the mean flow velocity. For the flow of fluid through the packed bed, the modified Hbe number can be used:

$$ Hb_{e} = \frac{{\tau_{0} \cdot r_{h}^{n} \cdot \varepsilon^{n} }}{{k \cdot v_{0}^{n} }} $$
(21)

The experimental data shown in Fig. 8 indicate that in the emulsions with added NaCMC the effect of the power law exponent n on the value of the modified dimensionless plug size is negligible, and the relationship ξe = f(Hbe) can be described by the correlation equation:

$$ \xi_{e} = 6.36 \times 10^{ - 1} \cdot Hb_{e}^{1.1} + 7.2 \times 10^{ - 4} $$
(22)

and Eq. (22) is correct in the range Hbe ∈ 〈0.0055; 0.73〉 and n ∈ 〈0.634; 0.783〉.

5.2 Emulsions Stabilized by Xanthan Gum

There are several publications describing the results of studies investigating the flow of aqueous XG solutions in porous media (Ghoniem 1985; González et al. 2005; Amundarain et al. 2009; Rodríguez de Castro and Radilla 2017). Rodríguez de Castro and Radilla (2017) attempted to calculate the friction factor during the flow of XG solutions using the Ergun equation:

$$ f_{\text{BK}} = \frac{A}{{Re_{\text{BK}} }} + B $$
(23)

where the Reynolds number was calculated from the modified Blake (1922) equation with the incorporated apparent shear viscosity ηapp

$$ Re_{\text{BK}} = \frac{{v_{0} \cdot d_{p} \cdot \rho }}{{(1 - \varepsilon ) \cdot \eta_{\text{app}} }} $$
(24)

To calculate the apparent shear viscosity ηapp, Rodríguez de Castro and Radilla (2017) used the Carreau equation:

$$ \eta_{\text{app}} = \eta_{\infty } + \frac{{\eta_{0} - \eta_{\infty } }}{{\left[ {1 + (\lambda \cdot \dot{\gamma }_{\text{app}} )^{2} } \right]^{{\frac{{n_{C} - 1}}{2}}} }} $$
(25)

We also used the Carreau model to determine the apparent shear viscosity during the flow of the emulsions with added XG. Table 2 lists the values of the empirical shift factor a determined for the aqueous XG solutions and emulsions with added XG used in the study. These data demonstrate that the values of the shift factor in emulsions depend on the concentration of the dispersed phase and the diameter of droplets. In the aqueous XG solutions and emulsions with added XG with the droplet diameter d43 ≤ 5 μm (dh/d43 ≥ 250 emulsions with the addition of Tween 40), the value of a is equal to 1.3, and for the droplets with the diameter d32 ≥ 6.5 μm the values of a rise from 1.2 to 2.4 along with the increasing volume fractions of oil. These data indicate that pressure drops accompanying the flow of emulsions with larger droplets in porous media cannot be calculated using the shift factor values obtained for the aqueous polymer solutions (Fig. 9).

Fig. 8
figure 8

Dimensionless plug size ξe as a function of modified Herschel–Bulkley number

Full size image

Figure 9 shows the relationship between the friction factor fBK and the number ReBK in the emulsions with 30% volume fraction of the dispersed phase, and varying droplet diameters and XG concentrations. The experimental points obtained for the aqueous XG solutions and emulsions in which the continuous phase contained 0.5% of XG across the entire range of ReBK (from 2.5 × 10−4 to 24.2) are aligned along the line fBK = 180/ReBK (coefficient of variation equal to 4.1%).

Fig. 9
figure 9

Comparison of fBK = f(ReBK) for aqueous solutions of XG and emulsions with addition of XG

Full size image

A different situation occurs during the flow of emulsions containing 0.2% of XG. In this case, over ReBK > 0.15, the deviation from the line described with Eq. (14) begins to rise (exceeding 5%) and reaches 43% at ReBK,1 = 13.7. A similar deviation of the experimental points during the flow of aqueous XG solutions has been observed by González et al. (2005). The authors linked them to an additional pressure drop induced by the extensional component of the flow. The presence of the oil phase leads to a decrease in the extensional viscosity of the XG solutions (Różańska et al. 2013); hence higher values of the friction factor than those calculated from Eq. (14) during emulsion flow may be attributable only to the effect of inertia.

The effect of inertia on the flow at the ReBK value of approximately 0.15 was observed only during the flow of the emulsions, but it was not seen during the flow of the aqueous solution of XG at a concentration of 0.2% even when the value of ReBK was equal to 24.

Figure 10 presents a comparison of the experimental values of fBK with the values calculated from Eq. (23) using A and B constants given by Maconald et al. (1979) (A = 180; B = 1.8). The maximum deviation of the experimental points from the values calculated from Eq. (23) was 28%.

Fig. 10
figure 10

Comparison of experimental values of the friction factor fBK for emulsions stabilized by XG (0.2 wt%) with fBK values calculated from Ergun Eq. (23)

Full size image

5.3 Emulsions Stabilized by PEO

The macroscopic behavior of high molecular weight flexible polymer solutions (HPAM, PEO) when flowed through porous media have been reported a number of times (Haas and Kulicke 1985; Kauser et al. 1999). During the flow of fluids of this type through the packed bed, there is a rapid rise in the apparent viscosity (apparent thickening region) above a certain value of the apparent shear rate \( \dot{\gamma }_{\text{app,onset}} \). Based on the relationship ηapp = f(\( \dot{\gamma }_{\text{app}} \)) shown in Fig. 11a, it can be inferred that the effect also occurs during the flow of emulsions with added PEO. The causes underlying the formation of the apparent thickening region have not been fully clarified (Sochi 2010). In the literature, they are most commonly attributed to the extensional viscosity or elastic instability. Extensional deformation occurring during fluid flow through the packed bed is a result of the presence of a converging–diverging flow path. In the extensional flow, after a certain fluid velocity is exceeded, the polymer chains are stretched, which is taken to explain the increase in pressure drops (Haas and Kulicke 1985; Sáez et al. 1994; Da Rocha et al. 1999; Kauser et al. 1999). Another cause for the sudden increase in pressure drops may be the presence of elastic instability (Howe et al. 2015; Clarke et al. 2015; Kawale et al. 2017). To date, the type of elastic instabilities present in the packed bed still remains to be elucidated. According to Clarke et al. (2015) and Howe et al. (2015) a rapid increase in pressure drops should be attributed to elastic turbulence.

Fig. 11
figure 11

Apparent viscosity ηapp (a) and apparent relative viscosity ηapp/ηapp,2 (b) as a function of shear rate \( \dot{\gamma }_{\text{app}} \) for emulsions stabilized by PEO

Full size image

The presence of elastic instability during the transport of emulsions with added PEO in the shear flow is also associated with the previously discussed viscosity curves (Fig. 5). Markedly higher values of the onset shear rate at which the apparent thickening region starts in the Couette flow than in the porous flow are not surprising because the flow rate value at which the effect of elastic instabilities on the pressure drops is observed depends on the shape of the channel (Shaqfeh 1996; Wang et al. 2011). In addition, there are qualitative differences between the onset shear rate values in the Couette flow and porous flow. In the Couette flow, the onset shear rate rises along with the increasing concentrations of the dispersed phase, and in the porous flow it is approximately independent of its concentration (\( \dot{\gamma }_{\text{app,onset}} \) = 21 s−1 for the aqueous solution of PEO and about 28 s−1 for the emulsion). Also, the apparent thickening region was not present in the Couette flow, but was found in the porous flow, in the emulsion with the dispersed phase concentration of 50%. These results may suggest that a different type of elastic instability may be present in the flow of fluids with added PEO through the packed bed than in the Couette flow. Studies conducted by Kawale et al. (2017) on the flow of aqueous HPAM solutions through a model porous medium identify two distinct elastic instabilities. The former is associated with the formation of apparent stagnation zones (dead zones) around stagnation points, and the latter is linked to the instability of dead zones and their violent disintegration into small eddies. Since there are no stagnation points in the Couette flow, dead zones cannot be formed and hence the mechanism of elastic instability will be different than in the porous flow.

Figure 11b presents additionally relative changes in the apparent viscosity ηapp/ηapp,2 as a function of \( \dot{\gamma }_{\text{app}} \) (where ηapp,2 is the apparent viscosity at \( \dot{\gamma }_{\text{app}} \) = 2 s−1). Over the onset shear rate the values of ηeff/ηeff,2 observed during the flow of the emulsions are lower than during the flow of the aqueous PEO solution. This shows that, similarly to the Couette flow, elastic instability is suppressed by the increase in emulsion viscosity caused by the flocculation of droplets.

6 Conclusions

The study presents the results of measurements of pressure drops during the flow of emulsions stabilized by NaCMC, XG and PEO through a packed bed of glass spheres. The dispersed phase of the emulsion consisted of flocculated droplets with diameters much smaller than the pore size.

Highly flocculated emulsions with the addition of NaCMC were yield-stress fluids whose flow curve can be described by the Herschel–Bulkley Eq. (9). For this non-Newtonian fluid a relationship between the friction factor and the generalized Reynolds number (Eq. (19)) was proposed. Based on Eq. (19), it is possible to determine the friction factor fBK at known rheological parameters of the Herschel–Bulkley model and calculating the modified dimensionless plug size from the empirical correlation [Eq. (22)].

The friction factor of XG-stabilized emulsions can be calculated from Eq. (14) up to the Reynolds number ReBK = 0.15. At a low concentration of XG (0.2%) and with the ReBK values > 0.15, the effect of inertia on pressure drops became manifest. In this flow range the friction factor can be determined from the Ergun equation (A = 180; B = 1.8), if the error level of 25% is acceptable. If the diameter ratio dh/d43 is ≥ 250, and the content of the dispersed phase is ϕ ≤ 30 vol%, calculations of the apparent shear rate can be performed with the shift factor determined during the flow of the aqueous XG solution. If the ratio dh/d43 is ≤ 180 and ϕ ≥ 30 vol%, the values of the shift factor in the emulsions are much higher than the values obtained in the aqueous XG solution, and they increase along with the increasing volume fraction of the oil phase.

During the flow of the emulsion with added PEO through the packed bed, just as during the flow of the aqueous solution of this polymer, an apparent thickening region is noted. Qualitative differences between the viscosity curves obtained in the Couette flow and the apparent viscosity curves in the porous flow show that the mechanism of elastic instability in these flows was different. Furthermore, over the onset shear rate the relative increase in the apparent viscosity of the emulsion with added PEO is lower than the apparent viscosity of the aqueous PEO solution. This shows that elastic instability is suppressed by an increase in emulsion viscosity induced by the flocculation of droplets.