1 Introduction

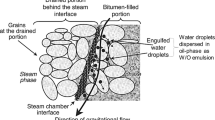
Emulsion flow through porous media is an important phenomenon in oil production operations and is also a topic of special interest in many applications of science and engineering, especially petroleum industries (Soo and Radke 1984; Soma and Papadopoulos 1995; Vidrine et al. 2000; Arhuoma et al. 2009; Cobos et al. 2009). It has been suggested that oil migrates through reservoir sands in the form of a fine, dispersed emulsion of oil in water, and that oil accumulations occur where the stream enters finer-grained rock such as silt or shale. Flow behavior of emulsions in both pipelines and reservoirs can be properly described based on emulsion properties and physical laws controlling their flow through porous media. Emulsions are generally liquid–liquid dispersions, in which the dispersed phase interferes with the flow of the continuous phase through the pore space, as they can partially block the already swept, more permeable paths. Thus, the flow of injected water diverts to unswept regions, leading to more efficient reservoir sweep and higher recovery factor (Thomas and Ali 1989; Seright and Liang 1995; Babadagli 2005). These researchers reported that emulsions would have good displacement properties similar to those of a low-viscosity gel. In petroleum production, heavy crude oils are often produced from natural oil reservoirs in the form of water-in-oil (W/O) or oil-in-water (O/W) emulsion with water (Steinhauff 1962). In enhanced oil recovery (EOR) methods a variety of emulsions are observed (Mandal et al. 2010a). During waterfloods for secondary recovery of oil from reservoirs, there is rapid channeling of water from injection to producing wells through the more permeable portions of reservoirs, resulting in low oil recovery. As water flows through tortuous paths in reservoirs in presence of oil, O/W emulsions are often formed. When the O/W emulsion flows through a heterogeneous reservoir, a great amount of emulsion enters the more permeable zones, so water begins to flow into less permeable zones, resulting in higher sweep efficiency. In this study the flow behavior of O/W emulsions through porous media has been discussed.

Different typical configurations of an emulsion may be categorized as O/W, W/O or a more complex dispersion. In complex dispersion phase a dispersed phase is embedded within each droplet already dispersed in a continuous phase, such as the case of oil-in-water-in-oil emulsions. In porous media, it is of great interest for petroleum engineers to know how the emulsions flow in porous media and the flow rate changes with pressure drop during flowing. Emulsions (O/W and W/O emulsions) are formed in situ under adequate conditions in porous media. A third component often present in an emulsion is an emulsifier or surfactant, which can reduce interfacial tension between liquids and can stabilize emulsions. In oil reservoirs, the added chemicals, or crude oil components such as asphaltenes, waxes, resins, and naphthenic acids act as emulsifying agents. These emulsifiers or stabilizers suppress the emulsion breakdown process (Fingas and Fieldhouse 2004). Many researchers carried out experimental investigation on injection of W/O or O/W emulsion as a selective plugging agent to improve oil recovery in water flooding (McAuliffe 1973a, b; Thomas and Ali 1989). During alkali flooding, alkali can penetrate into heavy oil in porous media by the formation of W/O emulsions in situ. In this connection, rheological properties of emulsions play an important role in efficient oil recovery. Due to high viscosity of W/O emulsions, the resistance to water flow in high water saturation zones can be increased significantly to improve sweep efficiency and thus oil recovery. Most of the cases the power-law model is the simplest representation of the viscosity of non-Newtonian fluids.

The objective of this study is to characterize rheological properties of O/W emulsions and their flow behavior through porous media. For the experiments, emulsions were first prepared by so-called agent-in-water technique (Bennett 1967; Becher 2001; Rastogi 2003, Mandal et al. 2010b). After preparation of emulsions, flow tests were performed in sand packs filled with sand of different sizes at different pressures and the corresponding flow rates were calculated and finally experimental results have been analyzed by a proposed model.

2 Mechanism of oil/water emulsion flow in porous media

Oil and water form an emulsion under favorable conditions in the presence of extraneous materials (Gewers 1968; Rupesh et al. 2008). Emulsions are suspensions of droplets (greater than 0.1 μm) of one immiscible fluid dispersed in another fluid. Their kinetic stability is a consequence of small droplet size and the presence of an interfacial film around oil droplets (Murray et al. 2009). Emulsions may be either oil-in-water or water-in-oil and they are transported in reservoir rocks having permeabilities from very low to several Darcys. Many flow models have been reported in the literature to describe flow mechanisms of emulsions through porous media. McAuliffe (1973a, b) studied mechanisms of oil droplets through porous media, and he described the mechanism of flow of a dispersed oil droplet entering a pore throat smaller than the oil droplet. Al-Faris et al. (1994) reported that during flow of the O/W emulsion the permeability of porous media decreases monotonically with time. Alvarado and Marsden (1979) developed a correlation, which uses both capillary and core flow data for describing flow of non-Newtonian macroemulsions through porous media. Jin and Wojtanowicz (2014) described a model considering mass transfer of the oil phase from the produced water to the rock due to capture effects by dispersion, advection, and adsorption inside the rock. Khambharatana et al. (1998) studied physical mechanisms of stable emulsion flow in Berea sandstones and Ottawa sand packs for systems of comparable droplet and pore sizes. They showed that the change in emulsion rheology in a porous medium has an overall trend similar to that in a viscometer for the shear rates of interest.

The better understanding of flow mechanisms of O/W emulsions through porous rock is of utmost importance during secondary and EOR. Although significant works on mechanism of the O/W emulsion flow through porous media have been reported, the detailed mechanisms are still not well understood. In this study, a mathematical model is developed from basic fluid flow equations, and the model is used to describe the flow behavior of the O/W emulsion through sand packs.

3 Experimental

3.1 Materials used

Gear oil (EPX 90) available in the market with sp. gravity of 0.905 and kinematic viscosity of 197 cSt at 40 °C and 17.3 cSt at 100 °C was used for preparation of emulsion in distilled water. Sodium chloride (NaCl) with 98 % purity, procured from Qualigens Fine Chemicals, India, was used for preparation of a brine solution. Sand used in building was sieved into different particle sizes, 12–30, 30–60, and 60–70 mesh and then was used to prepare sand packs.

3.2 Emulsion preparation

Each emulsion was prepared by mixing gear oil with water using a mixer with a standard three-blade propeller. The quality of lubricating oil is often improved by adding detergent, dispersant, etc. (Atkins et al. 1947; Miller 1956), which enables formation of a milky emulsion when properly mixed with water. For O/W emulsions, distilled water was used as the continuous phase and oil was used as the dispersed phase. The different concentrations of emulsions (5 %, 10 %, and 15 %) were prepared by agitating at 3000 rpm for 6 h, which were found to be the optimum conditions for making emulsions from the brine solution and the gear oil. The emulsion was left to stand in a separation flask for 6 h and the bottom part was separated out as emulsion for the present experiments. The separation flask can easily lead to the separation of two different density fluids based on their density.

3.3 Sand pack preparation and property determination

Sand packs were prepared at the ambient temperature of 27 °C, and fresh sand was used for each test to ensure similar wettability. Three major steps involved in preparing each porous medium included seizing the sand, packing the core holder, and determining properties of the porous medium. First, the sand particles were classified into three categories, namely, A, B and C, each having different mesh: IS 12–30, IS 30–60 and IS 60–70, respectively. The sieving process was undertaken using a sieve shaker with different sieves varying from IS 12 to 70 mesh. Second, the core holder was placed in the bench vice in the vertical position and filled with 1.0 wt% NaCl brine, and then the desired sand was gradually added into the core holder. For sand packs of IS 60–70 mesh sand (sand pack C), 90 mL of brine was used for saturation; for sand packs of IS 30–60 mesh sand (sand pack B), 100 mL brine used; and for sand packs of IS 12–30 mesh sand (sand pack A), 105 mL of brine used for complete saturation. In general a perfect packing was needed for preparation of porous media for experimental purposes. Finally, the porosity was measured by two different methods, namely, the weight and volumetric methods, and the permeability measurement was conducted using Darcy’s law. Table 1 summarizes properties of the three types of porous media used for emulsion flow tests.

Table 1 Properties of three types of porous media used for emulsion flow tests
Full size table

3.4 Determination of flow rate and emulsion viscosity

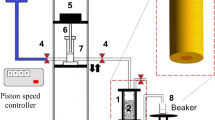
The experimental setup (Fig. 1) for flooding tests in sand packs consisted of four components: a sand pack holder, a displacement pump, cylinders for holding brine and emulsion, and fraction collectors. The detailed procedures for determining the flow rate of emulsions are described as follows:

Fig. 1
figure 1

Schematic diagram of emulsion flow through a sand pack

Full size image

An emulsion flow test was initiated after the properties of the porous medium and emulsions were characterized. First of all the syringe pump is filled with paraffin to maintain the pressure. Once the sand pack was fully saturated with brine, it was placed horizontally. Then, the brine was injected into the sand pack at a pressure of 10 psi. At this point, the flow rate was calculated by measuring the time required to collect 10 mL of brine. Subsequently, the injection pressure of brine was increased to 20 psi and then to 60 psi and the corresponding flow rates were measured. Submitting values of flow rates at different differential pressure (∆P) into the Darcy Equation, the permeability of sand packs was calculated and verified that the permeability is constant at different ∆P. Accordingly, the same procedure was repeated for emulsions (O/W) of different concentrations (5 %, 10 %, and 15 %) and corresponding flow rates were measured at different ∆P.

Rheological properties of emulsions were calculated theoretically from the core flooding data of emulsion flow tests.

The flow of emulsions through porous media has been studied in laboratory by injecting emulsions through sand packs. Let us consider the steady laminar flow of emulsions through porous sand packs with an uniform size of sand and the cross sectional area of the core holder is A. The sand particles are assumed to be largely uniform and spherical. Suppose the average projected area of sand particles is a and the porosity is ϕ. Therefore, the number of sand particles present in the total projected area of flow is given by

$$n_{\text{p}} = \frac{{A\left( {1 - \phi } \right)}}{{{{\pi }}r_{\text{a}}^{2} }}.$$
(1)

Therefore, the wetted perimeter is equal to the number of sand particles, i.e.,

$$2{{\pi }}r_{\text{a}} = \frac{{2A\left( {1 - \phi } \right)}}{{r_{\text{a}} }},$$
(2)

where r a is the average radius of sand particles, cm. Then the hydraulic radius, r H can be expressed as follows:

$$r_{\text{H}} = \frac{{\phi r_{\text{a}} }}{{2\left( {1 - \phi } \right)}},$$
(3)

where r H is the hydraulic radius of sand particles, cm.

Oil/water emulsion is a time-independent non-Newtonian pseudo-plastic fluid and its rheology is described by the Ostwald–Dewaele model or the power-law model as follows:

$$\tau = K \left( {\frac{{\text{d} u}}{{\text{d} y}}} \right)^{n} ,$$
(4)

where \(\tau\) is the shear stress, dynes/cm2; K and n are constants for a particular fluid and the value of n is less than one. The constant K is known as the consistency index of the fluid, Pa sn; the higher the value of K, the more viscous the fluid. The constant n is called the flow index and gives a measure of the degree of departure from Newtonian behavior. The detailed rheological properties have been evaluated for three different emulsions with a standard rheometer and it has been found that the viscosity of emulsions decreases with an increase in the shear rate, showing non-Newtonian behavior. In this study, rheology is described by the Ostwald–Dewaele model or the power-law model as reported in a previous study (Al-Fariss et al. 1994).

In order to develop an expression for the effective viscosity, μ eff for pseudo-plastic flow through a porous media let us consider the general equation (Mandal 2010),

$$- \frac{{\text{d} v}}{{\text{d} r}} = f\left( \tau \right),$$
(5)

where v is the velocity of fluid. For fluid flowing through a porous media, a force balance on a cylindrical fluid element of radius r (imaginary) gives,

$$\tau = \frac{r\Delta P}{2L},$$
(6)

and that at the wall of the core holder and also at the surface of the particle where velocity is zero, \(\tau_{\text{w}}\) can be written as

$$\tau_{\text{w}} = r_{\text{H}} \frac{\Delta P}{2L},$$
(7)

where L is the length of the core holder, cm; \(\tau_{\text{w}}\) is the shear stress at the wall, dynes/cm2.

Therefore,

$$\tau = \tau_{\text{w}} r/r_{\text{H}} .$$
(8)

The volumetric flow rate Q through the porous media is given by

$$Q = \int \limits_{0}^{{r_{\text{H}} }} 2\pi rv\text{d} r,$$
(9)

where v is the average velocity, cm/s; Q is the volumetric flow rate of the emulsion through porous media, cm3/s.

On integration by parts, and applying the condition, at r = r H , v = 0, and substitution of Eq. (9) leads to,

$$\frac{Q}{{\pi r_{\text{H}}^{3} }} = \frac{1}{{\tau_{\text{w}}^{ 3} }} \int \limits_{0}^{{\tau_{\text{w}} }} \tau^{2} f\left( \tau \right)\text{d} \tau .$$
(10)

Since for pseudo-plastic fluids,

$$f\left( \tau \right) = \left( {\tau /K} \right)^{\frac{1}{n}} ,$$
(11)

therefore,

$$\frac{Q}{{\pi r_{\text{H}}^{3} }} = \frac{v}{{r_{\text{H}} }} = \frac{1}{{\tau_{\text{w}}^{3} }}\mathop{\displaystyle \int \limits_{0}^{{\tau_{\text{w}} }} \tau^{2}} \left( {\frac{\tau }{K}} \right)^{\frac{1}{n}} \text{d} \tau ,$$
(12)

which on integration gives,

$$\frac{v}{{r_{\text{H}} }} = \frac{n}{{\left( {3n + 1} \right)}}\left( {\frac{{\tau_{\text{w}} }}{K}} \right)^{\frac{1}{n}} .$$
(13)

Rearranging one gets,

$$\tau_{\text{w}} = K\left( {2v/D_{\text{H}} } \right)^{n} \left( {\frac{3n + 1}{n}} \right)^{n} ,$$
(14)

or,

$$\tau_{\text{w}} = K\left( {8v/D_{\text{H}} } \right)^{n} \left( {\frac{3n + 1}{4n}} \right)^{n} ,$$
(15)

where D H is the hydraulic diameter of the sand particles, cm.

From the definition of μ eff,

$$\mu_{\text{eff}} = \frac{{\tau_{\text{w}} }}{8V/D} = K\left( {8v/D_{\text{H}} } \right)^{n - 1} \left( {\frac{3n + 1}{4n}} \right)^{n} ,$$
(16)
$$\mu_{\text{eff}} = 8^{n - 1} v^{n - 1} D_{\text{H}}^{1 - n} K^{\prime },$$
(17)

with

$$K^{\prime } = K\left( {\frac{3n + 1}{4n}} \right)^{n}.$$

Therefore, the value of μ eff can be evaluated if K and n are known. It is clear from Eq. (15) that if a logarithmic plot is made between \(\tau_{\text{w}}\) and 8v/D H, a linear relationship will obtained and the slope of the line should give the value of n and the intercept \(K\left( {\dfrac{3n + 1}{4n}} \right)^{n}\) i.e., K′.

4 Results and discussion

4.1 Characterization of emulsions

Emulsions are characterized by analyzing their stability, rheological properties, temperature effects on rheological properties, etc. Figure 2 shows the variation of viscosity with shear rate at different temperatures. Viscosity of emulsions decreases with an increase in the shear rate at lower shear rates, showing non-Newtonian behavior of emulsions. On the other hand, at higher shear rates emulsions show Newtonian behavior. It is also observed from figure that with an increase in temperature the viscosity of the O/W emulsion decreases. This is due to the fact that with an increase in temperature the average speed of the molecules in a liquid increases and the amount of time they spend “in contact” with their nearest neighbors decreases. Thus, as the temperature increases, the average intermolecular forces decrease and hence the viscosity decreases. The variation of viscosity of emulsions of different concentrations is presented in Fig. 3. It may be found that at low shear rates the viscosity of emulsions with higher oil concentration is higher though the variation is only marginal.

Fig. 2
figure 2

Viscosity (cP) versus shear rate (s) for 15 % O/W emulsion at different temperatures

Full size image
Fig. 3
figure 3

Viscosity versus shear rate at 30 °C for different O/W emulsion concentrations

Full size image

Microscopic images of O/W emulsions were taken with a polarizing microscope. A typical microscopic image of 10 % O/W emulsion is shown in Fig. 4. The particle size distribution (PSD) of oil in the emulsion was studied using a particle size analyzer. The PSD curve of 10 % O/W emulsion is shown in Fig. 5 and it shows maximum intensity at 466.1 nm.

Fig. 4
figure 4

Microscopic image of the 10 % O/W emulsion

Full size image
Fig. 5
figure 5

Particle size distribution of 10 % O/W emulsion

Full size image

4.2 Pressure drop of emulsion through a porous media

The emulsion concentration significantly affects the flow rate of emulsions through porous media. In Figs. 6, 7, 8, pressure drop versus flow rate curves are depicted for sand packs A, B and C at different emulsions of varying concentrations. In addition, the rate of brine flow was also measured. In all cases, the flow rate decreases with increasing emulsion concentration. This is due to the differences in viscosity between the different concentrations of injected emulsions. Brine has a higher flow rate compared to emulsions. For a particular pressure gradient, the flow rate decreases with an increase in emulsion concentration. In all cases the relationship between pressure drop and flow rate is linear.

Fig. 6
figure 6

Plot of pressure drop versus flow rate for O/W emulsions and brine for sand pack A

Full size image
Fig. 7
figure 7

Plot of pressure drop versus flow rate for O/W emulsions and brine for sand pack B

Full size image
Fig. 8
figure 8

Plot of pressure drop versus flow rate for O/W emulsions and brine for sand pack C

Full size image

The effect of sand particle size on the flow rate versus pressure drop traces for 10 % O/W emulsion is shown Fig. 9. With an increase in the sand particle size the effective flow area decreases and hence for the same flow rate the higher pressure drop is observed with an increase in the particle size.

Fig. 9
figure 9

Plot of pressure versus flow rate for 10 % O/W emulsions with different mesh sizes

Full size image

4.3 Rheological behavior of emulsions through porous media

The rheological properties of emulsions are explained on the basis of shear stress versus shear rate relationship. The curves of shear stress versus shear rate of 5 %, 10 %, and 15 % emulsions in different sand packs are shown in Figs. 10, 11, 12, respectively. The flow behavior index (n) and consistency constant (K) have been calculated from log–log plots of shear stress versus shear rate. The relationship between “n” and “K” with different emulsion concentrations is shown in Fig. 13. From Fig. 13, it is clear that with an increase in the emulsion concentration “n” decreases and in all cases the value is less than unity. This indicates that the emulsion is a non-Newtonian fluid in behavior (Uzoigwe and Marsden 1970; Masalova et al. 2011; Saiki et al. 2007). It was also found that “K” increases with an increase in the emulsion concentration. Therefore, the fluid with higher “K” value has a higher viscosity. So 15 % O/W emulsion has the highest viscosity at different shear rates. The effective viscosity has been calculated from the derived model and shown in Fig. 14 as function of shear rate. It has been found that the effective viscosity of emulsions increases with an increase in oil concentration in the O/W emulsion when flowing through porous media at a specified shear rate.

Fig. 10
figure 10

Rheological behavior of emulsions in sand pack A

Full size image
Fig. 11
figure 11

Rheological behavior of emulsions in sand pack B

Full size image
Fig. 12
figure 12

Rheological behavior of emulsions in sand pack C

Full size image
Fig. 13
figure 13

Rheological parameters (flow index, n and consistency constant, K) as a function of emulsion concentration

Full size image
Fig. 14
figure 14

Effective viscosity of emulsions calculated from the derived model at different shear rates (sand pack B)

Full size image

5 Conclusions

Oil-in-water emulsions are characterized in terms of their rheological behavior and sizes of the dispersed oil globules in water. It has been found that the viscosity of emulsions decreases with an increase in shear rate at lower shear rates, showing non-Newtonian behavior. At low shear rates, the emulsions of higher oil concentration show higher viscosity though the viscosity variation is only marginal. The flow characteristics of different emulsions through porous media have been studied. The pressure drop for emulsions flowing through porous media depends significantly on the oil concentration in the O/W emulsion and the average particle size of the medium. A mathematical model has been developed to analyze the experimental data of flow of emulsions through porous media. The shear stress–shear rate behavior of different emulsions through porous media shows non-Newtonian behavior and follows the power-law model. The variation of rheological parameters (flow index and consistency constant) as a function of emulsion concentration has also been presented. The effective viscosity of the emulsion calculated from the derived model equation has been presented as a function of shear rate for different sand packs.