1 Introduction

Bargaining involves, sometimes implicitly and sometimes explicitly, utilitarian and egalitarian considerations. From a normative point of view, an impartial arbitrator may invoke such considerations in his attempt to produce fair compromises. From a strategic perspective, such considerations may be phrased as arguments by self-interested bargainers. For instance, a bargainer may complain that “it is not fair that I will gain only this much when you gain that much,” thereby resorting to egalitarian reasoning; his opponent may counter this argument with “do me a favor, it will only cost you a little but will help me a lot,” thereby invoking a utilitarian principle.

The relevance of utilitarianism and egalitarianism to game theoretic bargaining dates back to Shapley (1969), who showed that the Nash bargaining solution (Nash, 1950) is the unique scale covariant solution that satisfies simultaneously the utilitarian and egalitarian objectives for some scaling of the individual utilities. This implies that, for any bargaining problem, the “Nash point” lies on the Pareto frontier in between the utilitarian point and the egalitarian one.Footnote 1\(^,\)Footnote 2

In a previous paper, Rachmilevitch (2015), I provided an alternative proof of the aforementioned betweenness. In that paper, as well as in Rachmilevitch (2016), I showed that the Nash solution, in several senses, is closer to utilitarianism than it is to egalitarianism. In particular, I showed how the portion of the Pareto frontier that ranges from the utilitarian point to the egalitarian point can be meaningfully divided into two parts, and the Nash point lies in the part closer to the utilitarian choice.

A different view was expressed by Brock (1979), according to which the Nash solution is egalitarian, because it equates the ratio of utilities to that of marginal utilities. More specifically, suppose that bargaining is over the division of a pie, and that the bargainers’ utility functions from consumption are u and v. The forgoing condition can be written as:

$$\begin{aligned} \frac{u'}{u}=\frac{v'}{v}. \end{aligned}$$
(1)

Namely, egalitarianism is expressed in the equalization of functions of the players’ utilities, where each player would like the expression that pertains to him to be as small as possible.

Therefore, there are (at least) two competing views regarding whether the Nash solution is “more utilitarian or more egalitarian.” On the one hand, it expresses egalitarianism in the sense of (1). On the other hand, it is closer—in a certain geometric sense—to the utilitarian point. In the present paper I unify these approaches, and combine them into a single criterion of proximity to utilitarianism and/or egalitarianism. This criterion is as follows.

Let \(\rho =\rho (u,v)\), hereafter the Nash ratio, be the number to which either side of (1) is equal to. For each \(\alpha \in [0,1]\), let \(m=m(\alpha )\) be the number that satisfies:

$$\begin{aligned} \alpha u(m)-(1-\alpha )\cdot u'(m)=\alpha v(1-m)-(1-\alpha )\cdot v'(1-m). \end{aligned}$$

It is easy to see that m(0) describes utilitarianism and m(1)—egalitarianism. Therefore, I take \(m(\frac{1}{2})\) to represent a “midpoint” between these two extremes. The main result of this paper, which pertains to bargaining problems in which the egalitarian and utilitarian points are distinct, is this: if the Nash ratio \(\rho\) is smaller than one, then player 1’s Nash payoff is between his utilitarian payoff and the midpoint \(m(\frac{1}{2})\); but if \(\rho\) is greater than one, then player 1’s Nash payoff is between the midpoint and his egalitarian payoff.

The result is a consequence of a general (yet simple) mathematical theorem. This theorem is in Sect. 2, and its application to bargaining is in Sect. 3.

2 A theorem about monotone functions

Theorem 1

Let \(\{A,B,a,b\}\) be four continuous functions from (0, 1] to \({\mathbb {R}}_{++}\), such that:

  • A and B are strictly increasing, and there exists a unique \(x\in (0,1)\) such that \(A(x)=B(1-x)\);

  • a and b are strictly decreasing, and there exists a unique \(y\in (0,1)\) such that \(a(y)=b(1-y)\).

Then:

  1. 1.

    there exists a unique z such that:

    $$\begin{aligned} \frac{a(z)}{A(z)}=\frac{b(1-z)}{B(1-z)}. \end{aligned}$$
  2. 2.

    there exists a unique w such that \(A(w)-a(w)=B(1-w)-b(1-w)\).

  3. 3.

    \(z,w\in [\text {min}\{x,y\},\text {max}\{x,y\}]\).

Proof

Suppose, w.l.o.g, that \(x\ge y\). The number z: On the one hand, at \(z\in (x,1)\) it holds that:

$$\begin{aligned} \frac{a(z)}{A(z)}<\frac{a(x)}{A(x)}\le \frac{a(y)}{B(1-x)}=\frac{b(1-y)}{B(1-x)}<\frac{b(1-z)}{B(1-z)}. \end{aligned}$$
(2)

The first strict inequality is due to the monotonicity of a and A; the second inequality is due to the facts that \(A(x)=B(1-x)\) by assumption and \(a(y)\ge a(x)\); the equality is due to the fact that \(a(y)=b(1-y)\); and the last strict inequality is again by monotonicity.

On the other hand, at \(z\in (0,y)\) it holds that:

$$\begin{aligned} \frac{a(z)}{A(z)}>\frac{a(y)}{A(y)}\ge \frac{b(1-y)}{A(x)}=\frac{b(1-y)}{B(1-x)}>\frac{b(1-z)}{B(1-z)}, \end{aligned}$$

where the inequalities and equality have analogous justifications to the ones given for (2). Therefore, if there exists a z such that \(\frac{a(z)}{A(z)}=\frac{b(1-z)}{B(1-z)}\) then it necessarily satisfies \(z\in [y,x]\). Existence of this z follows from the continuity of the four functions involved, and its uniqueness is implied by their monotonicity.

The number w: At \(w>x\) it holds that:

$$\begin{aligned} A(w)-a(w)>A(x)-a(y)=B(1-x)-b(1-y)>B(1-w)-b(1-w), \end{aligned}$$

and at \(w<y\) the opposite holds. Therefore, if there exists a w such that \(A(w)-a(w)=B(1-w)-b(1-w)\) then it necessarily satisfies \(w\in [y,x]\). Existence and uniqueness of w follow from the continuity and monotonicity of \(\{A,B,a,b\}\). \(\square\)

3 Application to bargaining

Here is a simple version of Nash’s bargaining model. There are two players who need to divide a size-1 pie. Player 1’s utility function is u, that of player 2 is v, both are strictly increasing, differentiable and strictly concave, and satisfy \(u(0)=v(0)=0\). I refer to the utilities \(\{u,v\}\) as a bargaining problem. In this context, the Nash bargaining solution assigns to player 1 the unique \(x\in [0,1]\) that maximizes \(u(x)\cdot v(1-x)\), the egalitarian bargaining solution (Kalai, 1977) assigns player 1 the \(x\in [0,1]\) that satisfies \(u(x)=v(1-x)\), and the utilitarian bargaining solution assigns player 1 the \(x\in [0,1]\) that maximizes \(u(x)+v(1-x)\). The utilitarian point is unique, due to the strictly concavity of the utility functions. I will further assume that it is an interior point, namely in (0, 1); this is guaranteed, for example, if both players have sufficiently large marginal utility at zero. Thus, the point selected by the utilitarian solution, denoted by \(x^\star\), is characterized by the first-order condition \(u'(x^\star )=v'(1-x^\star )\). It is well-known (and easy to check) that the point selected by the Nash solution, denoted hereafter by n, is characterized by the first-order condition \(\frac{u'(n)}{u(n)}=\frac{v'(1-n)}{v(1-n)}\equiv \rho (u,v)\). Finally, I denote the point selected by the egalitarian solution by e.

As mentioned in the Introduction, the Nash solution is “sandwiched” between utilitarianism and egalitarianism. As the following corollary shows, in the present model this betweenness property is an immediate consequence of Theorem 1.

Corollary 1

\(\text {min}\{e,x^\star \}\le n\le \text {max}\{e,x^\star \}\).

Proof

Follows from the first-order condition of the Nash solution and parts 1 and 3 of Theorem 1, when one sets \(A=u\), \(a=u'\), \(B=v\), and \(b=v'\).Footnote 3\(\square\)

Given \(\alpha \in [0,1]\), consider the number \(m=m(\alpha )\in [0,1]\) that satisfies:

$$\begin{aligned} \alpha u(m)-(1-\alpha )\cdot u'(m)=\alpha v(1-m)-(1-\alpha )\cdot v'(1-m). \end{aligned}$$
(3)

Clearly, \(m(0)=x^\star\) and \(m(1)=e\). The following result speaks of the remaining \(m(\alpha )\)’s.

Corollary 2

For every \(\alpha \in (0,1)\), there exists a unique \(m(\alpha )\) that satisfies (3). Moreover, \(\text {min}\{e,x^\star \}\le m(\alpha )\le \text {max}\{e,x^\star \}\).

Proof

Follows from parts 2 and 3 of Theorem 1, when one sets \(A=\alpha u\), \(a=(1-\alpha )u'\), \(B=\alpha v\), and \(b=(1-\alpha )v'\). \(\square\)

Let \(a\equiv m(\frac{1}{2})\). This number a can be viewed as a midpoint (or average, hence “a”) between utilitarianism and egalitarianism.

Say that the Nash solution is closer to utilitarianism in the problem \(\{u,v\}\) if \(\text {min}\{a,x^\star \}\le n\le \text {max}\{a,x^\star \}\), and is closer to egalitarianism in the problem \(\{u,v\}\) if \(\text {min}\{a,e\}\le n\le \text {max}\{a,e\}\).

The question is which case obtains, and when. The following result provides an answer; in its proof, it will be convenient to refer to the equation that defines a, which can be written as:

$$\begin{aligned} u(a)-u'(a)=v(1-a)-v'(1-a). \end{aligned}$$
(4)

Theorem 2

Let \(\{u,v\}\) be a bargaining problem such that \(x^\star \ne e\). Then the Nash solution is closer to utilitarianism in this problem if the Nash ratio satisfies \(\rho (u,v)<1\), and it is closer to egalitarianism in this problem if that ratio satisfies \(\rho (u,v)>1\).

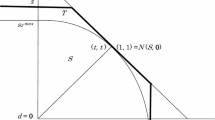
Figure 1 illustrates, in the utility space, Theorem 2 for the case \(x^\star <e\) and \(\rho (u,v)<1\). In this case, player 1’s pie-share according to the Nash solution, n, satisfies \(x^\star<n<e\), and so player 1’s utility is ranked in the same fashion: \(u(x^\star )<u(n)<u(e)\). As seen in the figure, the “Nash utility” u(n) is closer to the utilitarian one, in the sense that it lies between \(u(x^\star )\) and the midpoint utility u(a).

Proof of Theorem 2: Assume, w.l.o.g, that \(x^\star < e\).

Case 1: \(\rho (u,v)<1\). Here, what needs to be proved is that \(x^\star \le n\le a\). The left inequality follows from Corollary 1, so all that needs to be proved is \(n\le a\). Assume by contradiction that \(n>a\). Therefore,

$$\begin{aligned} u(n)-u'(n)>u(a)-u'(a). \end{aligned}$$
Fig. 1
figure 1

Ordering of the solutions when \(x^\star <e\) and \(\rho (u,v)<1\)

Full size image

By the definition of a, the RHS of the above inequality equals \(v(1-a)-v'(1-a)\), which is greater than \(v(1-n)-v'(1-n)\). Therefore,

$$\begin{aligned} u(n)-u'(n)>v(1-n)-v'(1-n). \end{aligned}$$
(5)

By the first-order condition of the Nash solution, \(u'(n)=u(n)\cdot \frac{v'(1-n)}{v(1-n)}\). Plugging this into (5) gives:

$$\begin{aligned} u(n)\cdot \left[1-\frac{v'(1-n)}{v(1-n)}\right]>v(1-n)-v'(1-n), \end{aligned}$$

or, multiplying both sides by \(v(1-n)\),

$$\begin{aligned} u(n)\cdot [v(1-n)-v'(1-n)]>v(1-n)\cdot [v(1-n)-v'(1-n)]. \end{aligned}$$

Since \(\rho (u,v)<1\) the bracketed term on either side is positive; canceling it yields \(u(n)>v(1-n)\), which means that the Nash point is to the right of the egalitarian one. That is, \(n>e\). However, this contradicts the fact that \(x^\star \le n\le e\).

Case 2: \(\rho (u,v)>1\). Here, what needs to be proved is that \(a\le n\le e\). The right inequality follows from Corollary 1, so all that needs to be proved is \(a\le n\). Assume by contradiction that \(n<a\). Therefore,

$$\begin{aligned} u(n)-u'(n)<u(a)-u'(a). \end{aligned}$$

By the definition of a, the RHS of the above inequality equals \(v(1-a)-v'(1-a)\), which is smaller than \(v(1-n)-v'(1-n)\). Therefore,

$$\begin{aligned} u(n)-u'(n)<v(1-n)-v'(1-n). \end{aligned}$$
(6)

By the first-order condition of the Nash solution, \(u'(n)=u(n)\cdot \frac{v'(1-n)}{v(1-n)}\). Plugging this into (6) gives:

$$\begin{aligned} u(n)\cdot \left[1-\frac{v'(1-n)}{v(1-n)}\right]<v(1-n)-v'(1-n), \end{aligned}$$

or, multiplying both sides by \(v(1-n)\),

$$\begin{aligned} u(n)\cdot [v(1-n)-v'(1-n)]<v(1-n)\cdot [v(1-n)-v'(1-n)]. \end{aligned}$$

Since \(\rho (u,v)>1\) the bracketed term on either side is negative; canceling it and reversing the inequality sign yields \(u(n)>v(1-n)\), which means that the Nash point is to the right of the egalitarian one. That is, \(n>e\). However, this contradicts the fact that \(x^\star \le n\le e\). \(\square\)

Three remarks regarding Theorem 2 are in order. First, it only speaks of problems in which \(x^\star \ne e\). When \(x^\star =e\) it holds that \(n=x^\star =e\), regardless of \(\rho\)’s value (in particular, regardless of whether it is smaller or greater than one).

Second, for concrete utility functions, the theorem can be applied to verify whether the Nash solution is closer to egalitarianism or egalitarianism. For example, it is easy to check that if \(u(x)\equiv x^\alpha\) and \(v(x)\equiv x^\beta\), where \(\alpha ,\beta \in (0,1)\) and \(\alpha \ne \beta\), the Nash solution is closer to utilitarianism if \(\alpha +\beta <1\) and closer to egalitarianism if the reverse strict inequality holds.Footnote 4

Third, the analysis does not extend to the case of \(N\ge 3\) players, since in this case the point selected by the Nash solution need not lie, coordinate-wise, between the utilitarian and egalitarian points. Here is an example. Consider three players with utility functions \(u_i(x)=k_ix^{1-\epsilon }\), where \((k_1,k_2,k_3)=(\alpha , \beta ,\gamma )\in {\mathbb {R}}_{++}^3\) and \(\epsilon >0\) is a small positive number. If what follows, I will show that betweenness fails when \(\epsilon =0\), and by continuity it would follow that it fails when \(\epsilon >0\). The positive \(\epsilon >0\) guarantees that the utility functions are strictly concave, so all the assumptions made throughout the paper are maintained. If \(\alpha >\beta ,\gamma\), then the utilitarian point is \((\alpha ,0,0)\). The points selected by the Nash and the egalitarian solutions are \((\frac{\alpha }{3},\frac{\beta }{3},\frac{\gamma }{3})\) and \((\frac{\alpha \beta \gamma }{\alpha \beta +\alpha \gamma +\beta \gamma },\frac{\alpha \beta \gamma }{\alpha \beta +\alpha \gamma +\beta \gamma },\frac{\alpha \beta \gamma }{\alpha \beta +\alpha \gamma +\beta \gamma })\), respectively.Footnote 5 Therefore, to show that player 2’s Nash payoff exceeds both his utilitarian and egalitarian payoffs it is enough to establish \(\frac{\beta }{3}>\frac{\alpha \beta \gamma }{\alpha \beta +\alpha \gamma +\beta \gamma }\), which clearly holds for a sufficiently small \(\gamma\). This example shows the role of there being at least (in this case: exactly) three players—it is the presence of player 1 that makes player 2’s Nash payoff exceed his utilitarian payoff, and the presence of player 3 makes player 2’s Nash payoff exceed his egalitarian payoff.

Finally, it is worth mentioning that, while the above analysis of the “more utilitarian or more egalitarian” concept revolves around the midpoint a, equation (3), on the basis of which a was defined, can be used to formulate an alternative relation between n, e, and \(x^\star\), as follows.

If n is such that \(n\notin \{x^\star ,e\}\), then there exists a unique \(\alpha ^*\in (0,1)\) such that:

$$\begin{aligned} \alpha ^* u(n)-(1-\alpha ^*)\cdot u'(n)=\alpha ^* v(1-n)-(1-\alpha ^*)\cdot v'(1-n). \end{aligned}$$

Plugging the first-order condition of the Nash solution into this equation, one can easily verify that \(\rho <1\) (proximity to utilitarianism in the sense of Theorem 2) is equivalent to \(\alpha ^*<\frac{1}{2}\), and \(\rho >1\) (proximity to egalitarianism) is equivalent to \(\alpha ^*>\frac{1}{2}\).