1 Introduction

Nash (1950) formulated the bargaining problem and characterized a bargaining solution satisfying the axioms of scale invariance, symmetry, contraction independence, and weak Pareto optimality. This solution is called the Nash solution. Since then, many researchers have investigated the properties of this solution and provided other characterizations of it.

In the real world, people sometimes reach inefficient agreements. Even when the resulting outcome is physically efficient, they often spend considerable time resolving conflicts. When the timing of agreements affects their utility levels, conflicts may be resolved at inefficient points in the utility space. Thus, it is important to investigate what class of solutions can be obtained if we do not impose weak Pareto optimality a priori.

In this paper, we propose a very mild condition of individual rationality called possibility of utility gain. This requires that there exists at least one bargaining problem in which at least one player improves his or her utility at the agreement. Were it violated, in any bargaining problems, no player could achieve a utility gain over the disagreement point.

Several researchers have characterized the Nash solution without weak Pareto optimality. Roth (1977) showed that weak Pareto optimality can be replaced by strong individual rationality. Anbarci and Sun (2011, 2013), Rachmilevitch (2015b), and Mori (2018) also provided efficiency-free characterizations of the Nash solution using scale invariance, symmetry and contraction independence. Under the assumption that for each player, all feasible agreements are weakly better than the disagreement point, Rachmilevitch (2021) provided efficiency-free characterizations of it using other sets of axioms. Lensberg and Thomson (1988) and Driesen (2016) examined the role of weak Pareto optimality in a model with a variable number of players. Vartiainen (2007) discussed the limited significance of weak Pareto optimality in bargaining problems without disagreement points. For a survey of the literature about efficiency-free characterizations, see Thomson (2022).

This paper provides two novel characterizations of the Nash solution with almost no individual or collective rationality. First, we show that the Nash solution is the only solution satisfying possibility of utility gain and feasible set continuity in conjunction with Nash’s axioms except for weak Pareto optimality. Our new axiom is weaker than the rationality axioms examined in Anbarci and Sun (2011, 2013), Rachmilevitch (2015b), and Mori (2018). The first result provides an axiomatic foundation of the Nash solution based on the weakest rationality requirement in the literature.

Second, we show that in Nash’s theorem, weak Pareto optimality can be replaced by conflict-freeness introduced in Rachmilevitch (2015b). This requires that if there is a feasible agreement that is most preferred by all players in the feasible set, then this agreement should be chosen. As a corollary of the theorem in Rachmilevitch (2015b), we obtain that the Nash solution is the unique solution satisfying scale invariance, symmetry, contraction independence, conflict-freeness, and feasible set continuity. Compared with this result, our new characterization implies that feasible set continuity is redundant. These new results mean that the Nash solution can be obtained even when we require very mild efficiency or individual rationality.

Furthermore, we provide unified proofs of other efficiency-free characterizations by using several lemmas that we show to prove our first result. We clarify the role of each axiom introduced in the related literature. The second novel characterization is provided in line with this discussion.

This paper is organized as follows. Section 2 introduces the bargaining problem. Section 3 defines several axioms, including our novel axiom, possibility of utility gain. Section 4 characterizes the Nash solution by using this new axiom. Section 5 provides unified proofs of related results, and also presents another new axiomatization of the Nash solution. Finally, Sect. 6 has some concluding comments.

2 The bargaining problem

This paper considers n-person bargaining problems. Let \(I = \{1,2, \ldots , n \} \) be the set of players. Let \(S \subset {\mathbb {R}}^n\) be a set of utility vectors that they can achieve by a unanimous agreement.Footnote 1 They stay at the disagreement point, denoted by \(d \in S,\) if they do not agree. A (bargaining) problem is a pair (S, d). We assume that S is a compact and convex set and that there exists \(s \in S\) such that \(s \gg d.\)Footnote 2 These assumptions are standard in the literature. The set of all problems is denoted by \({\mathcal {B}}.\)

A (bargaining) solution is a function \(f: {\mathcal {B}} \rightarrow {\mathbb {R}}^n\) such that \(f(S, d) \in S\) for all \((S, d) \in {\mathcal {B}}.\) For each \((S, d) \in {\mathcal {B}}\) and each \(i \in I ,\) \(f_i (S, d)\) is player i’s utility level. Nash (1950) characterized the following solution N. For all \((S, d) \in {\mathcal {B}},\)

$$\begin{aligned} N (S, d) = \mathop {{\text {arg max}}}\limits _{d \le s \in S} \prod _{i \in I} (s_i - d_i). \end{aligned}$$

This solution is called the Nash solution. The disagreement solution D is defined as \(D (S, d) = d\) for all \((S, d) \in {\mathcal {B}}.\)

We introduce the following notation. For all \(A \subset {\mathbb {R}}^n,\) \(\text {ch} (A)\) is the convex hull of A. Let \({\textbf{0}} = (0,0, \ldots , 0)\) and \({\textbf{1}} = (1,1, \ldots , 1).\) For all \(s, \alpha , \beta \in {\mathbb {R}}^n,\) let \(\alpha s = (\alpha _1 s_1, \alpha _2 s_2, \ldots , \alpha _n s_n)\) and \(\alpha s + \beta = (\alpha _1 s_1 + \beta _1, \alpha _2 s_2 + \beta _2, \ldots , \alpha _n s_n + \beta _n).\) Also, let \(\alpha S = \{ \alpha s \in {\mathbb {R}}^n ~ | ~ s \in S\}\) and \(\alpha S + \beta = \{ \alpha s + \beta \in {\mathbb {R}}^n ~ | ~ s \in S\}\) for all \(\alpha \in {\mathbb {R}}^n_{++}\) and \(\beta \in {\mathbb {R}}^n.\)

3 Axioms for solutions

Natural or reasonable properties of solutions, which we call axioms, have been considered in the literature. Nash (1950) introduced the following four axioms to characterize the Nash solution.

Scale invariance.:

For all \((S, d) \in {\mathcal {B}}\) and all \(\alpha \in {\mathbb {R}}^n_{++},\) \(\beta \in {\mathbb {R}}^n,\) \(f(\alpha S + \beta , \alpha d + \beta ) = \alpha f(S, d) + \beta .\)

Weak Pareto optimality.:

For all \((S, d) \in {\mathcal {B}},\) if there exists \(y\in S\) such that \(y \gg x,\) then \(f(S, d) \ne x.\)

We say that a problem (S, d) is symmetric if for all one-to-one functions \(\pi : I \rightarrow I,\) \(S = \{ (s_{\pi (1)}, s_{\pi (2)}, \ldots , s_{\pi (n)}) ~ | ~ s \in S\}\) and for all \(i, j \in I,\) \(d_i = d_j.\)

Symmetry.:

If \((S, d) \in {\mathcal {B}}\) is symmetric, then \(f_i (S, d) = f_j(S, d)\) for all \(i, j \in I.\)

Contraction independence.:

For all \((S, d), (T, d) \in {\mathcal {B}},\) if \(S \subset T\) and \(f(T, d) \in S,\) then \(f(S, d) = f(T, d).\)

In real-life bargaining, people do not always reach Pareto optimal agreements. Therefore, it is important to explore bargaining solutions without imposing weak Pareto optimality a priori. In fact, Roth (1977) showed that in Nash’s theorem, weak Pareto optimality can be replaced by the axiom which requires that all players receive utility levels strictly higher than the disagreement point. Formally, this requirement is defined as follows:

Strong individual rationality.:

For all \((S, d) \in {\mathcal {B}},\) \(f(S, d) \gg d.\)

Anbarci and Sun (2011), Rachmilevitch (2015b) and Mori (2018) also introduced weak axioms of rationality and provide efficiency-free characterizations of the Nash solution using scale invariance, symmetry and contraction independence.

We now introduce a new axiom. It requires that there exists at least one problem such that at least one player can gain more utility than the disagreement point. This axiom is logically weaker than strong individual rationality and the axioms introduced by Anbarci and Sun (2011), Rachmilevitch (2015b) or Mori (2018).

Possibility of utility gain.:

There exists \((S, d) \in {\mathcal {B}}\) such that \(f_i (S, d) > d_i\) for some \(i \in I.\)

We also introduce an axiom of continuity. This requires that small changes in the bargaining situation do not lead to large changes in the chosen outcome.Footnote 3

Feasible set continuity.:

If a sequence \(\{ S^k \}_{k = 1}^{\infty }\) converges to S in the Hausdorff topology as \(k\rightarrow \infty \) and \(\{ (S^k, d) \}_{k = 1}^{\infty }\cup \{ (S, d) \} \subset {\mathcal {B}},\) then

$$\begin{aligned} \lim _{k \rightarrow \infty } f(S^k , d) = f(S, d). \end{aligned}$$

Note that under appropriate assumptions, this requirement is satisfied by almost all bargaining solutions examined in the literature, such as the Nash solution, the Kalai–Smorodinsky solution (Kalai and Smorodinsky 1975), the Raiffa solution (Raiffa 1953), the equal-loss solution (Chun 1988), and others.

4 Main results

Our main result is the following: the Nash solution is the unique solution satisfying possibility of utility gain and feasible set continuity together with Nash’s axioms except for weak Pareto optimality.

Theorem 1

A solution satisfies scale invariance,  symmetry,  contraction independence,  feasible set continuity,  and possibility of utility gain if and only if it is the Nash solution.

In this section, we prove this theorem and check the independence of each axiom. Furthermore, we discuss whether we can weaken possibility of utility gain or not.

4.1 Preliminary lemmas

We start by proving three lemmas elucidating the implications of scale invariance, symmetry and contraction independence together. We use these lemmas again in Sect. 5 to prove other characterizations in a unified way.

Lemma 1

Let f be a solution satisfying scale invariance and contraction independence. If there exists a problem \((S, d) \in {\mathcal {B}}\) such that d is an interior point of S and \(f(S, d) = d,\) then \(f=D.\)

Proof

Let (S, d) be a problem satisfying the hypothesis of the lemma. Let \((S' , d' ) \in {\mathcal {B}}.\) By scale invariance, we can assume that \(d = {\textbf{0}}\) and \(d' = {\textbf{0}}.\) We show that \(f(S', {\textbf{0}}) = {\textbf{0}}.\)

Let \(\alpha \in {\mathbb {R}}^n_{++}\) such that \(S' \subset \alpha S.\) (Note that there exists such an \(\alpha \) since d is an interior point of S.) By scale invariance, \(f(\alpha S, {\textbf{0}}) = {\textbf{0}}.\) Since \(S' \subset \alpha S\) and \(f(\alpha S, {\textbf{0}}) = {\textbf{0}}\in S',\) contraction independence implies \(f(S', {\textbf{0}}) = {\textbf{0}}.\) \(\square \)

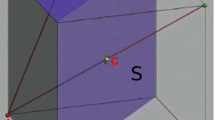
For all \(c \le 0,\) let \(\triangle (c) = \{ s \in {\mathbb {R}}^n ~ | ~ s \ge c {\textbf{1}} \ \text {and}\ s_1 + s_2+ \cdots + s_n \le n \} .\) (Figure 1 illustrates \(\triangle (c)\) in the two-person case.)

For all symmetric problems (S, d),  let \(\overline{l} (S) = x {\textbf{1}}\) where \(x = \max _{(y,y, \ldots , y) \in S} y\) and \(\underline{l} (S) = x' {\textbf{1}}\) where \(x' = \min _{(y,y, \ldots , y)\in S} y.\)

Fig. 1
figure 1

\(\triangle (c)\) in the case where \(n = 2\)

Full size image

Lemma 2

Suppose that a solution f satisfies scale invariance,  symmetry and contraction independence. Then,  for all symmetric problems (S, d),  f(S, d) is either \(\underline{l} (S),\) d or \(\overline{l} (S).\) In particular,  \(f(\triangle (c), {\textbf{0}})\) is either \(c {\textbf{1}},\) \({\textbf{0}}\) or \({\textbf{1}}\) for each \(c \le 0.\)

Proof

Let (S, d) be a symmetric problem. By scale invariance, we can assume that \(d = {\textbf{0}}.\) By symmetry, there exists \(x \in [\underline{l}_1 (S), \overline{l}_1 (S)]\) with \(f(S, {\textbf{0}}) = x {\textbf{1}}.\) Suppose to the contrary that \(x \in (\underline{l}_1 (S), 0) \cup (0, \overline{l}_1 (S)).\) Fix \(\varepsilon > 0\) small enough such that \(x {\textbf{1}} \in \alpha S\) where \(\alpha = (1- \varepsilon ) {\textbf{1}} \in {\mathbb {R}}^n.\) By scale invariance, \(f(\alpha S ,{\textbf{0}}) = \alpha x {\textbf{1}}.\) Since \(\alpha S \subset S\) and \(f(S, {\textbf{0}}) =x {\textbf{1}} \in \alpha S.\) By contraction independence, \(f(\alpha S ,{\textbf{0}}) = x {\textbf{1}},\) a contradiction. \(\square \)

Lemma 3

Let f be a solution satisfying scale invariance and contraction independence. If \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}\) for all \(c \le 0,\) then \(f = N.\)

Proof

When \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}\) for all \(c \le 0,\) we prove \(f = N.\) Let (S, d) be an arbitrary problem. By scale invariance, we can assume that \(d = {\textbf{0}}\) and \(N (S, d) = {\textbf{1}}.\) There exists \(c < 0\) such that \(S \subset \triangle (c).\) Since \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}} \in S,\) contraction independence implies \(f(S, d) = {\textbf{1}} = N (S, d).\) \(\square \)

4.2 Characterization of the Nash solution

Using the lemmas in the previous section, we prove Theorem 1.

Lemma 4

Let f be a solution satisfying scale invariance,  symmetry,  and contraction independence. If \(f(\triangle (c) , {\textbf{0}}) = c {\textbf{1}}\) for all \(c \le 0,\) then \(f(S , d) \le d\) for all \((S, d) \in {\mathcal {B}},\) i.e.,  it violates possibility of utility gain.

Proof

Step 1. Let (S, d) be a problem such that d is in the interior of S. By scale invariance, we can assume that

$$\begin{aligned} \mathop {{\text {arg max}}}\limits _{d \ge s \in S} \prod _{i \in I} |s_i - d_i| = - {\textbf{1}} \end{aligned}$$

and \(d = {\textbf{0}}.\) There exists a symmetric problem \((T^1, {\textbf{0}})\) satisfying the following conditions:

  • \(S \subset T^1 \subset \{ s \in {\mathbb {R}}^n ~ | ~ s_1 + s_2 + \cdots + s_n \ge -n \}.\)

  • \(T^1 \cap {\mathbb {R}}^n_{+} = x {\textbf{1}} \triangle (0)\) for some \(x \in {\mathbb {R}}_{++}.\)

(See Fig. 2 for \((T^1 , {\textbf{0}})\) in the two-person case.) By Lemmas 1 and 2, \(f(T^1, {\textbf{0}})\) is either \(- {\textbf{1}}\) or \(x {\textbf{1}}.\) If \(f(T^1, {\textbf{0}}) = x {\textbf{1}},\) then scale invariance and contraction independence imply that \(f(\triangle (0), {\textbf{0}}) = {\textbf{1}},\) a contradiction. Thus, \(f(T^1, {\textbf{0}}) = - {\textbf{1}}.\) By contraction independence, \(f(S, {\textbf{0}}) =- {\textbf{1}} \le {\textbf{0}} (= d).\)

Fig. 2
figure 2

\((T^1,0)\) in the case where \(n = 2\)

Full size image

Step 2. Let (S, d) be a problem such that d is on the boundary of S and that there is no \(s \in S \backslash \{ d \}\) satisfying \(s \le d.\)

By scale invariance, we can assume that \(d = {\textbf{0}}\) and \(S \subset \{ s \in {\mathbb {R}}^n ~ | ~ s_1 + s_2 + \cdots + s_n \ge 0 \}.\) (We show the existence of such a positive affine transformation \(\tau .\) Since f satisfies scale invariance, we can set \(d = {\textbf{0}}.\) By the supporting hyperplane theorem, there exists \(k = (k_1, k_2, \ldots , k_n) \in {\mathbb {R}}^{n}_{++}\) such that \(k_1 s_1 + k_2 s_2 + \cdots + k_n s_n \ge 0\) for all \(s \in S.\) Let \(\tau : {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) be a function such that for all \(s' \in {\mathbb {R}}^n,\) \(\tau (s') = k s'.\) We have \(\tau ({\textbf{0}}) = {\textbf{0}}\) and for all \(s \in S,\) \(\tau _1 (s) + \tau _2 (s) + \cdots + \tau _n (s)= k_1 s_1 + k_2 s_2 + \cdots + k_n s_n \ge 0,\) as required.)

Let \((T^2 , {\textbf{0}})\) be a symmetric problem satisfying the following conditions:

  • \(S \subset T^2 \subset \{ s \in {\mathbb {R}}^n ~ | ~ s_1 + s_2 + \cdots + s_n \ge 0 \}.\)

  • \(T^2 \cap {\mathbb {R}}_{+}^n = x {\textbf{1}} \triangle (0)\) for some \(x \in {\mathbb {R}}_{++}.\)

(See Fig. 3 for the two-person case.) By Lemma 2, \(f(T^2, {\textbf{0}})\) is either \({\textbf{0}}\) or \(x {\textbf{1}}.\) If \(f(T^2, {\textbf{0}}) = x {\textbf{1}},\) scale invariance and contraction independence imply that \(f (\triangle (0), {\textbf{0}} ) = {\textbf{1}},\) a contradiction to \(f(\triangle (0), {\textbf{0}}) = {\textbf{0}}.\) Thus, \(f(T^2, {\textbf{0}}) = {\textbf{0}}.\) By contraction independence, it follows that

$$\begin{aligned} f(S, {\textbf{0}}) = {\textbf{0}}. \end{aligned}$$
Fig. 3
figure 3

\((T^2, {\textbf{0}})\) in the case where \(n = 2\)

Full size image

Step 3. Let (S, d) be a problem such that d is on the boundary of S and there is \(s \in S \backslash \{ d \}\) satisfying \(s \le d.\) By scale invariance, we can set \(d = {\textbf{0}}.\) Suppose to the contrary that \(f(S, {\textbf{0}}) \le {\textbf{0}}\) does not hold. Let \(T^3 = \text {ch} ((S \cap {\mathbb {R}}^n_{+}) \cup \{ f(S, {\textbf{0}})\}).\) By contraction independence, \(f(T^3, {\textbf{0}}) = f(S, {\textbf{0}}).\) Since \((T^3 , {\textbf{0}})\) is in the class of problems examined in Step 2, we have \(f(T^3, {\textbf{0}}) = {\textbf{0}} \ne f(S, d),\) a contradiction. Hence, \(f(S, d) \le d.\) \(\square \)

Lemma 5

Let f be a solution satisfying scale invariance,  symmetry,  contraction independence and feasible set continuity. Then,  one of the following statements holds : 

(L5-1):

\(f(\triangle (c), {\textbf{0}}) = {\textbf{0}}\) for all \(c\le 0.\)

(L5-2):

\(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}\) for all \(c \le 0.\)

(L5-3):

\(f(\triangle (c), {\textbf{0}}) = c {\textbf{1}}\) for all \(c \le 0.\)

Proof

By Lemma 1, if there exists \(c < 0\) such that \(f(\triangle (c) , {\textbf{0}}) = {\textbf{0}},\) then \(f(\triangle (c') , {\textbf{0}}) = {\textbf{0}}\) for all \(c' \le 0,\) i.e., (L5-1) holds.

Consider the case when there is no \(c < 0\) such that \(f(\triangle (c) , {\textbf{0}}) = {\textbf{0}}.\) By Lemma 2, for all \(c' \le 0,\)

$$\begin{aligned} f(\triangle (c') , {\textbf{0}})\in \{{\textbf{1}}, c' {\textbf{1}} \}. \end{aligned}$$
(1)

To prove (L5-2) and (L5-3), suppose to the contrary that for some \(c^1 \le 0\) and \(c^- \le 0,\) \(f(\triangle (c^1), {\textbf{0}} ) = {\textbf{1}}\) and \(f(\triangle (c^-), {\textbf{0}} ) = c^- {\textbf{1}}.\) Let \(C^1 = \{ e \le 0 ~ | ~ f(\triangle (e), {\textbf{1}}) = {\textbf{1}} \}\) and \(C^- = \{ e \le 0 ~ | ~ f(\triangle (e), {\textbf{1}}) = e {\textbf{1}} \}.\) By (1), \(C^1 \cup C^- = (- \infty , 0].\) Since f satisfies feasible set continuity, both sets are closed. By \(c^1 \in C^1\) and \(c^- \in C^-,\) they are nonempty. Since \((- \infty , 0]\) is connected, \(C^1 \cap C^- \ne \emptyset ,\) a contradiction.Footnote 4\(\square \)

Proof of Theorem 1

It is clear that the Nash solution satisfies the five axioms of the theorem. Let f be a solution satisfying these axioms. By Lemma 5, either (L5-1), (L5-2), or (L5-3) holds. By Lemma 1 and Lemma 4, (L5-2) and (L5-3) violate possibility of utility gain. By Lemma 3, \(f=N.\) \(\square \)

4.3 The independence of axioms in Theorem 1

In the following, we show the independence of the axioms in Theorem 1.

Example 1

Let NU be the solution defined as follows: for all \((S, d) \in {\mathcal {B}},\)

$$\begin{aligned} NU (S, d) = \mathop {{\text {arg max}}}\limits _{d \le s \in S} \Bigg ( \prod _{i \in N} (s_i - d_i) + \sum _{i \in N} (s_i - d_i) \Bigg ). \end{aligned}$$

This solution satisfies all of the axioms except for scale invariance.Footnote 5

We briefly verify that NU does not satisfy scale invariance in the two-person case. Let \(S = \text {ch} ( \{ (2,0), (0,1), {\textbf{0}} \}).\) If NU satisfies scale invariance, then \(NU (S , {\textbf{0}} ) =( 2 NU_1 (\triangle (0), {\textbf{0}}) , NU_2 (\triangle (0), {\textbf{0}})).\) However, by the Lagrangian method, we obtain \(NU (\triangle (0), {\textbf{0}}) = (1/2, 1/2)\) and \(NU (S , {\textbf{0}}) = (3/2, 1/4).\)

Example 2

Let \(\theta \in {\mathbb {R}}_{++}^n \backslash \{ (1/n, 1/n, \ldots , 1/n)\}\) with \(\sum _{i \in I}\theta _i = 1.\) The weighted Nash solution \(N^\theta \) is the maximizer of the product \( \prod _{i \in I} (s_1 - d_1)^{\theta _i}\) in \(s \in \{ s' \in S ~ | ~ s' \ge d \}\) for each \((S, d )\in {\mathcal {B}}.\) (See Kalai 1977a.) This solution does not satisfy symmetry, but satisfies the other axioms.

Example 3

Given \(\lambda \in (0,1),\) let f be a solution defined as follows: for all \((S, d) \in {\mathcal {B}},\)

$$\begin{aligned} f (S, d) = \lambda \Bigg ( \mathop {{\text {arg max}}}\limits _{d \le s \in S} \prod _{i \in I} (s_i - d_i) \Bigg ) + (1- \lambda ) d. \end{aligned}$$

This solution satisfies all of the axioms in Theorem 1 other than contraction independence.Footnote 6

Example 4

Let \(NP^+ (S, d) = \max _{d \le s \in S} \prod _{i \in I} (s_i - d_i)\) and \(NP^- (S, d) = \max _{d \ge s \in S} \prod _{i \in I} |s_i - d_i|.\) Let f be a solution defined as follows: for all \((S, d)\in {\mathcal {B}},\)

$$\begin{aligned} f (S, d)= \left\{ \begin{array}{ll} N (S, d) &{}\quad ( NP^+ (S, d) \ge NP^- (S, d))\\ \mathop {{\text {arg max}}}\limits _{d \ge s \in S} \prod _{i \in I} |s_i - d_i| &{}\quad ( NP^+ (S, d) < NP^- (S, d)). \end{array} \right. \end{aligned}$$

This solution does not satisfy feasible set continuity, but satisfies the other axioms.

Example 5

The disagreement solution D satisfies all of the axioms except for possibility of utility gain.

4.4 Weakening possibility of utility gain

We examine whether it is possible to weaken possibility of utility gain in Theorem 1. Consider the following weaker axiom:Footnote 7

Non-triviality.:

\(f\ne D.\)

Mathematically, possibility of utility gain can be replaced by this axiom.

Proposition 1

A solution satisfies scale invariance,  symmetry,  contraction independence,  feasible set continuity,  and non-triviality if and only if it is the Nash solution.

Proof

It is clear that the Nash solution satisfies the five axioms of the theorem. Let f be a solution satisfying these axioms. In the proof of Theorem 1, possibility of utility gain is only used to exclude the cases (i) \(f(\triangle (c) , {\textbf{0}} ) = {\textbf{0}}\) for all \(c\le 0\) and (ii) \(f(\triangle (c) , {\textbf{0}} ) = c {\textbf{1}}\) for all \(c\le 0.\) Since the case (i) can be excluded by non-triviality, it is sufficient to show that the case (ii) does not hold. Suppose to the contrary that \(f(\triangle (c), {\textbf{0}}) = c {\textbf{1}}\) for all \(c \le 0.\)

Step 1. Let (S, d) be a problem such that d is on the boundary of S and there is no point \(s \in S \backslash \{ d\}\) with \(s \le d.\) As in Step 2 of the proof of Lemma 4, we can show \(f (S, d) = d.\)

Step 2. For all \(a \in {\mathbb {R}}_{-}^n,\) let \(\text {tr} (a) = \{ s \in {\mathbb {R}}^n ~ | ~ s \ge a ~ \text {and} ~ s_1 + s_2+ \cdots + s_n \le n \}.\) Note that for all \(c \le 0,\) \(\triangle (c) = \text {tr} (c {\textbf{1}}).\) We show that for all \(a \in {\mathbb {R}}^n_{-},\) \(f(\text {tr} (a) , {\textbf{0}}) = a.\)

For each \(a \in {\mathbb {R}}^n_{--},\) scale invariance and contraction independence imply \(f(\text {tr} (a), {\textbf{0}}) = a.\)Footnote 8 For each \(b\in {\mathbb {R}}^n_{-},\) consider a sequence \(\{ b^k \}_{k= 1}^{\infty } \subset {\mathbb {R}}^n_{--}\) such that \(\{ b^k \}_{k= 1}^{\infty }\) converges to b. Since f satisfies feasible set continuity, it follows that \(f(\text {tr} (b), {\textbf{0}}) = \lim _{k \rightarrow \infty } f(\text {tr} (b^k), {\textbf{0}}) = \lim _{k \rightarrow \infty } b^k = b.\)

Step 3. Consider the sequence \(\{ a^k \}_{k = 1}^{\infty } \subset {\mathbb {R}}^n\) defined by \(a^k= (1/k, -1, -1, \ldots , -1)\) for all \(k\in {\mathbb {N}}.\) Let \(a^*= (0,-1, -1, \ldots , -1) (= \lim _{k \rightarrow \infty } a^k).\) Let \(S^k = \text {ch} (\triangle (0) \cup \{ a^k \} ) \) for each \(k \in {\mathbb {N}}.\) The sequence \(\{ S^k \}_{k\in {\mathbb {N}}}\) converges to \(S^*=\text {ch} (\triangle (0) \cup \{ a^*\} ) .\)

Since \(S^*\subset \text {tr} (a^*),\) the result of Step 2 and contraction independence imply \(f(S^*, {\textbf{0}}) = a^*.\) Since \((S^k, {\textbf{0}})\) is in the class of problems considered in Step 1, \(f(S^k , {\textbf{0}}) = {\textbf{0}}\) holds for each \(k \in {\mathbb {N}}.\) Feasible set continuity implies \(f(S^*, {\textbf{0}}) = {\textbf{0}},\) a contradiction. Thus, there is no f such that \(f(\triangle (c), {\textbf{0}}) = c {\textbf{1}}\) for all \(c \le 0.\) \(\square \)

However, Proposition 1 highly depends on the domain assumption. To see this, consider the slightly different domain of problems. Let \({\mathcal {B}}^0\) be the subset of \({\mathcal {B}}\) such that for all \((S, d) \in {\mathcal {B}}^0,\) d is an interior point of S. Solutions and axioms on \({\mathcal {B}}^0\) are defined in the same way as \({\mathcal {B}}.\) When considering this domain \({\mathcal {B}}^0,\) the counterpart of Proposition 1 does not hold. Indeed, then the following solution \(N^-\) on \({\mathcal {B}}^0\) also satisfies all the axioms in Proposition 1: for all \((S, d)\in {\mathcal {B}}^0,\)

$$\begin{aligned} N^-(S, d) = \mathop {{\text {arg max}}}\limits _{d \ge s \in S} \prod _{i \in I} |s_i - d_i|. \end{aligned}$$

5 Unified proofs of other characterizations

In this section, we use the lemmas in Sect. 4.1 to provide unified proofs of other efficiency-free characterizations. This clarifies the technical role of each axiom introduced in the literature. We also provide one new characterization of the Nash solution.

5.1 Rachmilevitch (2015b)

Rachmilevitch (2015b) proposed the requirement that if there is a feasible outcome which is most preferred by each player, then this outcome should be chosen. To introduce this formally, let \(\text {id}_i (S) = \max _{s \in S} s_i\) and \(\text {id}(S) = (\text {id}_1 (S), \text {id}_2(S), \ldots ,\text {id}_n (S) ).\) His axiom is defined as follows.

Conflict-freeness.:

For all \((S, d ) \in {\mathcal {B}},\) if \(\text {id} (S) \in S,\) then \(f(S, d) = \text {id} (S).\)

This axiom is stronger than possibility of utility gain. In Rachmilevitch (2015b), the class of weighted Nash solutions is characterized by scale invariance, contraction independence, feasible set continuity, and conflict-freeness. As a corollary, if we impose symmetry in addition to these axioms, then the Nash solution is obtained.

Using the lemmas in Sect. 4.1, we can easily derive this corollary. Moreover, even if we do not impose feasible set continuity, the Nash solution is the only solution satisfying all the axioms. The following result is also a new efficiency-free characterization of the Nash solution.

Theorem 2

A solution satisfies scale invariance,  symmetry,  contraction independence,  and conflict-freeness if and only if it is the Nash solution.

Proof

Let f be a solution satisfying the axioms of the theorem. For all \(c \le 0,\) let \(T_c = \{ s \in {\mathbb {R}}^n ~ | ~c {\textbf{1}} \le s \le {\textbf{1}} \}.\) If \(f(\triangle (c),{\textbf{0}}) = {\textbf{0}}\) or \(c {\textbf{1}},\) then by contraction independence, \(f(T_c, {\textbf{0}}) \) is either \({\textbf{0}}\) or \(c {\textbf{1}}.\) This violates conflict-freeness. By Lemma 2, \(f(\triangle (c),{\textbf{0}}) = {\textbf{1}}\) for all \(c \le 0.\) Lemma 3 implies \(f = N.\) \(\square \)

5.2 Two characterizations by Roth (1977, 1979a)

Now, we derive two characterizations shown by Roth (1977, 1979a).

Proposition 2

(Roth 1977) A solution satisfies scale invariance,  symmetry,  contraction independence,  and strong individual rationality if and only if it is the Nash solution.

Proof

Let f be a solution satisfying the axioms of the proposition. By Lemma 2 and strong individual rationality, \(f(\triangle (c) , {\textbf{0}}) = {\textbf{1}}\) for each \(c \le 0.\) By Lemma 3, \(f = N\) holds. \(\square \)

Roth (1979a) used a weaker version of individual rationality.

Weak individual rationality.:

For all \((S, d) \in {\mathcal {B}},\) \(f(S, d) \ge d.\)

If we impose weak individual rationality on a solution along with Nash’s axioms other than weak Pareto optimality, then the solution is either the Nash solution or the disagreement solution.

Proposition 3

(Roth 1979a) A solution satisfies scale invariance,  symmetry,  contraction independence,  and weak individual rationality if and only if it is the Nash solution or the disagreement solution.

Proof

Let f be a solution satisfying all axioms. By Lemma 2 and weak individual rationality, \(f(\triangle (c), {\textbf{0}})\) is either \({\textbf{0}}\) or \({\textbf{1}}\) for each \(c \le 0.\) By Lemma 1, if there exists \(c < 0\) such that \(f(\triangle (c), {\textbf{0}}) = {\textbf{0}},\) then \(f=D.\) If \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}\) for all \(c < 0,\) then contraction independence implies \(f(\triangle (0), {\textbf{0}}) = {\textbf{1}}.\) By Lemma 3, \(f = N.\) \(\square \)

5.3 Anbarci and Sun (2011)

Anbarci and Sun (2011) used the following axiom to characterize the Nash solution.

Weakest collective rationality.:

For all \((S, d) \in {\mathcal {B}}\) and for all \(s \in S,\) if there is no \(t \in S \backslash \{ s\}\) such that \(s \ge t,\) then \(f(S, d) \ne s.\)Footnote 9

Proposition 4

(Anbarci and Sun 2011) A solution satisfies scale invariance,  symmetry,  contraction independence,  and weakest collective rationality if and only if it is the Nash solution.

Proof

Let f be a solution satisfying the axioms of the proposition. By Lemma 3, it is sufficient to show that for all \(c \le 0,\) \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}.\) By Lemma 2, \(f(\triangle (c), {\textbf{0}})\) is \(c {\textbf{1}},\) \({\textbf{0}}\) or \({\textbf{1}}\) for each \(c \le 0.\) If there exists \(c < 0\) such that \(f(\triangle (c'), {\textbf{0}}) = {\textbf{0}},\) then by Lemma 1, \(f(\triangle (0), {\textbf{0}}) = {\textbf{0}}.\) This violates weakest collective rationality. Also, by weakest collective rationality, there is no \(c'' \le 0 \) satisfying \(f(\triangle (c''), {\textbf{0}}) = c'' {\textbf{1}}.\) Therefore, for all \(c \le 0,\) \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}.\) \(\square \)

5.4 Mori (2018)

Mori (2018) also characterized the Nash solution. He used an axiom that requires that the solution outcome should not be weakly dominated by the disagreement point. He argued that this axiom is more natural and intuitive than weakest collective rationality.

Strong undominatedness.:

For all \((S, d) \in {\mathcal {B}},\) \(f(S, d) \le d\) does not hold.

His result is as follow:

Proposition 5

(Mori 2018) A solution f satisfies scale invariance,  symmetry,  contraction independence,  and strong undominatedness if and only if it is the Nash solution.

Proof

Let f be a solution satisfying the axioms of the proposition. By Lemma 2, \(f(\triangle (c), {\textbf{0}})\) is \(c {\textbf{1}},\) \({\textbf{0}}\) or \({\textbf{1}}\) for each \(c < 0.\) By strong undominatedness, \(f(\triangle (c), {\textbf{0}}) = {\textbf{1}}\) for all \(c \le 0.\) Lemma 3 implies that \(f = N.\) \(\square \)

6 Conclusion

This paper has provided novel characterizations of the Nash solution without weak Pareto optimality. Our new axiom, possibility of utility gain, requires less rationality than the axioms imposed to characterize the Nash solution in the literature. Also, we characterized this solution using conflict-freeness, which is a mild axiom of efficiency. Furthermore, we have provided unified proofs of other efficiency-free characterizations of the Nash solution. These proofs clarify the role of each axiom in the literature.

Motivated by the fact that people do not always reach efficient agreements, we have provided new axiomatic foundations of the Nash solution without depending on efficiency a priori. Our results are important in the sense that the Nash solution can be obtained even when we require very weak individual or collective rationality instead of weak Pareto optimality. It is also interesting to examine not weakly Pareto optimal solutions. To the best of our knowledge, only Roth (1979b) and Mariotti (1996) have examined such solutions in the standard setting of bargaining problems. We leave the investigation of this issue for future work.