Abstract
In this paper, we analyse higher-order risky choices by the representative cumulative prospect theory (CPT) decision maker from three alternative reference points. These are the status quo, average payout and maxmin. The choice tasks we consider in our analysis include binary risks, and are the ones employed in the experimental literature on higher order risk preferences. We demonstrate that the choices made by the representative subject depend on the reference point. If the reference point is the status quo and the lottery choices exhibit symmetric risk, we demonstrate that there is no third order reflection effect of lottery choices but there is a fourth order reflection effect. When the average payout is the reference point, we demonstrate that any third or fourth order lottery choice is possible dependent upon the lottery payoffs. However, under the assumption of maxmin reference point, the risky choices are prudent and temperate. In addition to these results, our analysis reveals that the representative CPT subject can choose combinations of second with third and fourth order risky options that differ from those in other major models of decision under risk. We contrast our theoretical predictions with the empirical results reported in the literature on higher order risk preferences and are able to reconcile some conflicting experimental evidence.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last three decades, theoretical research has demonstrated the important role that higher order risk preferences, particularly prudence and temperance, play in economic models of risky choice such as savings, auctions, asset pricing, prevention and several other (see Trautmann & van de Kuilen, 2018 for a review of this literature).Footnote 1 Experimental evidence of the ‘pure’ effect of those higher order risk attitudes was facilitated by the introduction of choice-based definitions of risk preferences of any order by Eeckhoudt and Schlesinger (2006). This major contribution set out the method for revealing higher order risk preferences employing experimental methods. They demonstrated how the choices between particular lottery pairs could be employed to elicit higher order preferences within a model-free framework. Subsequently, a number of experimental studies have employed choices between lotteries to reveal the higher order risk preferences of experimental subjects (a few prominent examples within the framework of risk include Deck & Schlesinger, 2010; 2014; Maier & Rüger, 2012; Noussair et al., 2014; Ebert & Wiesen, 2011; 2014; Heinrich & Mayrhofer, 2018, Bleichrodt & van Bruggen, 2022, and within the framework of ambiguity, Baillon et al. 2018).
In this paper, we will examine the decision maker’s choice in risk-apportionment tasks within the framework of, arguably, the most common reference-dependent model in behavioural economics, cumulative prospect theory (CPT). Our analysis will employ choice tasks with binary risks, which are the ones used in the experimental literature on the elicitation of higher order risk preferences. Reference-dependent models in general, and CPT in particular, have become the main modeling device to describe decisions under risk in experimental settings. In reference-dependent models, the decision maker (DM) evaluates outcomes as gains and losses from a reference point. However, an unresolved issue with these models is how to determine such a point. The reference point depends both on how a subject selects the reference point and on the experimental stimuli. Regarding the latter, a key feature of the experimental research reported to date on lottery choices to elicit higher order risk attitudes is that researchers have endeavoured to implement their appropriate reference point by experimental procedure and lottery design. This reference point is then assumed in the analysis of the responses of the experimental subjects. For instance, the experimental design in Maier and Rüger (2012) was set up to try to ensure that the status quo was the reference point. They write: “We carefully designed our experiment to implement the status quo prior to the second date as the reference point .”Footnote 2 Brunette and Jacob (2019) endowed subjects with an amount that appeared on the screen of the experiments. Their lottery choices included lotteries in the loss domain. Bleichrodt and van Bruggen (2022) gave experimental subjects an endowment equal to the expected value of participating and assumed this was the reference point which was also considered to be consistent with the status quo.Footnote 3 Alternatively, Deck and Schlesinger (2010) and Ebert and Wiesen (2014) assumed that the reference point was the average payout. The average payout reference point implies in those cases that the lotteries fall within the mixed domain.
In our theoretical analysis, we will consider both the status quo and the average reference point given their use in salient experimental research, but also a third one, the maxmin (the maximum outcome subjects can obtain for sure). The rationale for inclusion of the maxmin reference point is that Baillon et al. (2020) designed a novel experimental approach to identify which reference point DMs use in the context of CPT. They reported that the maxmin and status quo reference points were the two most frequently employed reference points.
From a given reference point, it is well known that the flexibility of a multiplicative model such as CPT is able to generate different second order risk preferences, namely, risk aversion or risk seeking, over gains and losses, such as the so-called four-fold pattern over outcome probabilities. It is, however, less known the type of higher order risk preferences the CPT model is able to generate over either gains or losses, and if any discernable pattern emerges as a consequence. Deck and Schlesinger (2010, p. 1414; 2012, pp. 28–29) conjecture that any higher order lottery choices are in principle consistent with CPT due to the interplay of cumulative weighting of probabilities, the value function’s properties over gains and losses, and loss aversion.
In this paper, we examine this conjecture in a model setup that allows to identify the role played by, on the one hand, the curvature of the utility for money, and, on the other hand, the probability weighting. To study the effect of the latter, we will assume linear utility for money and therefore outcomes are not transformed, while probabilities are. To make the analysis both tractable and relevant for the experimental literature at hand, we will consider a range of parameter values for the inverse-S-shaped probability weighting function reported in prominent research on CPT. Likewise for the parameters of the value function when its curvature is also taken into consideration in our analysis.
Our analysis reveals that third and fourth order risky choices are not invariant to the specified reference point or to whether binary risks are specified as symmetric or non-symmetric. With the average payout as the reference point, we find, as conjectured by Deck and Schlesinger, that any higher order lottery choices are consistent with CPT. This is also the case from the status quo reference point for fourth order choices with non-symmetric risk or for lotteries in the mixed domain. However, we do find unambiguous predictions. In particular, from the status quo reference point with symmetric risk, we find that a CPT DM exhibits prudent and temperate choices in the domain of gains but prudent and intemperate choices in the domain of losses. Consequently, we derive the new result that there is no reflection effect of third order choices but a reflection effect for fourth order. Similarly, from the maxmin reference point, we also find that third and fourth order risky choices are not ambiguous, and the representative CPT DM makes prudent and temperate choices.
These findings have a number of implications for experimental research. First, insights about lottery choices of CPT DMs can inform the design of experiments aimed at identifying alternative models of decision under risk. For instance, by including lotteries whose choice imply a different behaviour under CPT than under other models such as the combining good with bad paradigm (see Crainich et al., 2013; Deck & Schlesinger, 2014). Second, we provide an explanation of how experimental findings in the literature on higher order risk preferences can or cannot be reconciled with CPT. This will be the case for studies that assume either the status quo (e.g. Maier & Rüger, 2012; Brunette & Jacob, 2019) or the average payout (e.g. Deck & Schlesinger, 2010, Ebert & Wiesen, 2014).
The rest of the paper is organised as follows. In Sect. 2, we set out the method to elicit prudent and temperate choices as well as the parametric model of CPT employed in our analysis. Sections 3, 4, and 5 each present the predictions of CPT for risky choices of order 3 and 4 assuming a different reference point, namely, status quo, average payoff, and maxmin, respectively. The final section provides concluding remarks.
2 The CPT model and higher order risk apportionment tasks
Our analysis follows the methodology developed by Deck and Schlesinger (2014) (DS14 hereafter) based on the elicitation of preferences through binary choices. Their method derives from Eeckhoudt et al. (2009) and generalises the approach of Eeckhoudt and Schlesinger (2006). An individual’s endowment is denoted as W, \(W>0.\) We will write [x, y] to denote a lottery of equally likely payoffs x and y. Consider the following two pairs of random variables \(\{ \widetilde{X}_{1},\widetilde{Y} _{1}\}\) and \(\{ \widetilde{X}_{2},\widetilde{Y}_{2}\},\) and assume that \( \widetilde{Y}_{1}\) has more nth-degree risk than \(\widetilde{X}_{1},\) and that \(\widetilde{Y}_{2}\) has more mth-degree risk than \(\widetilde{X}_{2}.\)Footnote 4 Eeckhoudt et al. (2009) prove that lottery \( A_{s}=[W+\widetilde{X}_{1}+\widetilde{X}_{2},W+\widetilde{Y}_{1}+\widetilde{Y }_{2}]\) has more sth-degree risk than lottery \(B_{s}=[W+\widetilde{X}_{1}+ \widetilde{Y}_{2},W+\widetilde{Y}_{1}+\widetilde{X}_{2}]\) where \( s=(m+n),m\ge 1,n\ge 1.\) The individual’s preference is denoted with \( \succeq \). A DM who is “risk apportionate of order s” will always have a preference for lottery \(B_{s},\) that is, \(B_{s}\succeq A_{s},\) and therefore is someone who dislikes the lotteries with more sth degree risk and has a preference for combining the relatively “good” random variable \( \widetilde{X}_{i}\) with the relatively “bad” random variable \(\widetilde{Y}_{i}\). “Anti-risk apportionate of order s” is the reverse preference, \(A_{s}\succeq B_{s}\). We will only examine risk attitudes up to order four, hence \(s=2,3,\) and 4. We note that stochastic dominance preferences imply both a preference for combining the “good” with the “bad” lottery, and risk apportionment preferences (see Eeckhoudt et al., 2009).
Let us consider monetary payoffs \(k_{1},k_{2},\) such that \(k_{1}>0,k_{2}>0,\) and zero-mean random variables \(\widetilde{\varepsilon }_{1}\) and \( \widetilde{\varepsilon }_{2}\) whose distributions are assumed to be statistically independent of one another. To simplify the analysis, we consider the random variables \(\widetilde{X}_{1},\widetilde{X}_{2}\) are fixed monetary outcomes which can be denoted as \(\widetilde{X}_{1}=X_{1}, \widetilde{X}_{2}=X_{2},\) and that \(X_{1}+X_{2}=X.\) We now describe the lottery pair structure for each risk attitude and provide an example using tasks from DS14 to make notation easier to understand.
Risk aversion: \(s=m+n=2,\) with \(m=1,n=1.\) Variable \(\widetilde{Y} _{1}=X_{1}-k_{1}\) and variable \(\widetilde{Y}_{2}=X_{2}-k_{2}\). The lottery pair to elicit risk aversion is \(A_{2}=[W+X,W+X-k_{1}-k_{2}]\) and \( B_{2}=[W+X-k_{2},W+X-k_{1}].\) Lottery \(A_{2}\) is therefore a mean-preserving spread of lottery \(B_{2}.\) For example, for task 4 in DS14, \( X_{1}=X_{2}=7.5,k_{1}=k_{2}=5,\) and therefore \(A_{2}=[15,5]\) and \( B_{2}=[10,10].\)
Prudence: \(s=m+n=3,\) with \(m=1,n=2.\) In this case, \(\widetilde{Y} _{2}=X_{2}-k_{2}\) and \(\widetilde{Y}_{1}=X_{1}+\widetilde{\varepsilon }_{1}.\) The lottery pair to elicit prudence is \(A_{3}=[W+X,W+X-k_{2}+\widetilde{ \varepsilon }_{1}]\) and \(B_{3}=[W+X-k_{2},W+X+\widetilde{\varepsilon }_{1}].\) A DM who is prudent has a preference to combine the relatively “good” outcome (payment X without the loss of \(k_{2}\)) with the “bad” outcome (zero-mean risk \(\widetilde{\varepsilon }_{1}\)), as in lottery \(B_{3}\), instead of combining the two relatively “bad” outcomes together (wealth reduction of \(k_{2}\) and the zero-mean risk \(\widetilde{\varepsilon }_{1}\)), as it is the case in lottery \(A_{3}\), for all \(k_{2}>0,\) and zero-mean risk \(\widetilde{ \varepsilon }_{1}\). Lottery \(A_{3}\) can also be interpreted as a downside risk increase of lottery \(B_{3}\) (see Menezes et al., 1980). For example, for task 11 in DS14, \(X_{1}=0,X_{2}=10,k_{2}=5,\widetilde{\varepsilon } _{1}=[-2,2],\) and therefore \(A_{3}=[10,5+[-2,2]]\) and \(B_{3}=[5,10+[-2,2]].\)
Temperance: \(s=m+n=4,\) with \(m=2,n=2.\)Footnote 5 In this case, \(\widetilde{Y}_{2}=X_{2}+ \widetilde{\varepsilon }_{2}\) and \(\widetilde{Y}_{1}=X_{1}+\widetilde{ \varepsilon }_{1}.\) The lottery pair to elicit temperance is therefore \( A_{4}=[W+X,W+X+\widetilde{\varepsilon }_{1}+\widetilde{\varepsilon }_{2}]\) and \(B_{4}=[W+X+\widetilde{\varepsilon }_{2},W+X+\widetilde{\varepsilon } _{1}]\). A DM is temperate if she prefers to combine the relatively “good” and “bad” outcomes (\(B_{4}\)) instead of combining the two “bad” outcomes together (zero-mean risks \(\widetilde{\varepsilon }_{1}\) and \(\widetilde{\varepsilon }_{2}\)) as it is the case in \(A_{4},\) for all zero-mean \(\widetilde{\varepsilon }_{1}\) and \( \widetilde{\varepsilon }_{2}\). Lottery \(A_{4}\) is an outer risk increase of lottery \(B_{4}\). For example, for task 18 in DS14, \(X_{1}=X_{2}=17, \widetilde{\varepsilon }_{1}=[-10,10],\widetilde{\varepsilon }_{2}=[-4,4],\) and therefore \(A_{4}=[34,34+[-10,10]+[-4,4]]\) and \( B_{4}=[34+[-4,4],34+[-10,10]].\)
We now turn to the specification of the CPT model. We assume the representative DM is defined by the most common parameterization of CPT that includes power value function, v(.), with reference point r, parameter \(\alpha \in [0,1],\) and a loss aversion parameter \(\lambda ,\) in conjunction with an inverse-S-shaped probability weighting function, w(p).Footnote 6\(w^{+}(p)\) and \(w^{-}(p)\) are the probability weighting functions for gains and losses, respectively. We illustrate our framework with the function in Tversky and Kahneman (1992) since it is employed in many of the prominent studies in this area. However, our results apply in general to any probability weighting function that overweights small probabilities and underweights large probabilities, i.e., any typically employed inverse-S-shaped function.
There is a wide range of parameter values for (1) and (2) one can in principle consider in the study of risk preferences under CPT. However, to make the analysis both tractable and meaningful with respect to the extant literature, we restrict the range of parameter values to those typically found in the literature (see Fox and Poldrack, 2014 table A.3). In particular, we will consider \(\alpha \in \left[ 0,1\right] ,\lambda \in \left[ 1.31,2.65\right] ,\gamma \in \left[ 0.43,0.91\right] ,\delta \in \left[ 0.43,0.91\right] .\) Furthermore, we will illustrate our findings in the following sections with examples using the parameter estimates reported in the prominent research of Tversky and Kahneman (1992), Deck and Schlesinger (2010), Ebert and Wiesen (2014), and Baillon et al. (2020), which we will refer to from here onwards as TK, DS, EW, and BBS, respectively.Footnote 7 Table 1 lists these four model specifications.
The next three sections present the analyses corresponding to the elicitation of prudent and temperate choices each based on one of the three different reference points assumed in the CPT model.
3 Reference point 1: status quo
3.1 Third order risky choice
3.1.1 Domain of gains
Within the DS14 framework described in the previous section, the status quo corresponds to the level of initial wealth or endowment, W, and therefore \( r=W\) in (1). We note that, in experimental research, this mirrors the notion of the proceeds from the first stage in a two-stage experiment, or of a show-up fee being the status quo (e.g. Maier & Rüger, 2012; Bleichrodt & van Bruggen, 2022). The domain of gains implies that \(X_{1},X_{2}>0,X_{2}>k_{2},\) and \(X_{1}\) is larger than the absolute value of the lower bound of the support of risk \(\widetilde{ \varepsilon }_{1}.\)
We will initially assume that the zero-mean risk is binary and symmetric and therefore defined as \(\widetilde{\varepsilon }_{1}=[-e_{1},e_{1}]\). This is the form of risk most typically employed in the experimental literature (see Appendix A for an analysis with asymmetric risk). All experimental studies on higher order risk preferences cited in this paper employ binary symmetric zero-mean risk except Ebert and Wiesen (2011, 2014) and Heinrich and Mayrhofer (2018) that employ binary asymmetric risk of the type examined in Appendix A. Bleichrodt and van Bruggen (2022) also employ symmetric zero-mean risks in their experiments. However, they differ in that the lottery pair is asymmetric because of the introduction of small probabilities through a linear combination of the lotteries and a fixed payout. Although in our analysis below we cover the types of risks used in experimental studies on higher order risk preferences, there are other types of zero-mean risks. Predictions may not extend to the general case with arbitrary non-binary zero-mean risks. We therefore characterise the predictions in this paper in terms of risky choice rather than risk attitude.
Because the lottery pairs examined now also involve probabilities different from 50–50, we extend the definitions above. Let L denote a lottery with payoffs \(x_{1},x_{2}, \ldots x_{j}\) and corresponding probabilities \( p_{x_{1}},p_{x_{2}}, \ldots p_{x_{j}},\) where \(\sum \nolimits _{i=1}^{j}p_{x_{i}}=1,\) and we represent it by \(L:\left[ p_{x_{1}},x_{1};p_{x_{2}},x_{2}; \ldots ;p_{x_{j}},x_{j}\right] .\) We denote the value of the lottery L as V(L) (see Tversky and Kahneman (1992) for a formal definition of the value function that combines the utility function and the decision weights that depend upon the probability weighting function).
The lottery pair that elicits third order risky choice is given by
We recall that, in CPT, the probability weighting function does not apply to the probability density function but to the cumulative probability distribution. In the domain of gains, the cumulative weighting is applied from the largest to smallest gain. This implies there are two cases depending on the relative magnitudes of \(k_{2}\) and \(e_{1}.\) However, the conclusions drawn from our analysis are the same, and we therefore only show the analytical derivations for one of those cases. Let us consider \( k_{2}>e_{1}.\) Given this lottery payoff structure, the value of the prospects, \(V(B_{3})\) and \(V(A_{3}),\) from the status quo reference point, are given by the following expressions
We will initially assume a linear value function, i.e. \(\alpha =1\). Assuming linearity of the value function implies that the representation of different choices is done exclusively through subjective cumulative probability weighting transformations.Footnote 8 This assumption enables us to gain intuition about the effect of decision weights on the determination of higher order choices. In this case, the prudent choice requires \( V(B_{3})>V(A_{3}),\) and this condition is met if
This condition is consistent with the empirical literature on CPT that finds inverse-S-shaped probability weighting functions (concave for low probability and convex for high probability, i.e., increments near the end points of the probability scale loom larger than increments near the middle of the scale). Expression (4) can also be written in terms of probability distortion as \(\widetilde{w}^{+}(0.25)>\widetilde{w}^{+}(0.75),\) where \(\widetilde{w}^{+}(p)=w^{+}(p)-p.\) This condition holds for the representative CPT DM because she overweights probabilities of 0.25 \(( \widetilde{w}^{+}(0.25)>0)\) and underweights probabilities of 0.75 \(( \widetilde{w}^{+}(0.75)<0)\). Adding 0.25 probability mass has more effect near zero. Tversky and Wakker (1995) refer to this as lower subadditivity. The probability weighting function assumed for the representative CPT DM therefore implies that, with linear value function, lottery \(B_{3}\) will be chosen.Footnote 9
Relaxing the linearity assumption of the utility function does not change the lottery choice by the DM. Power utility (with exponent less than unity) is sufficient for prudence. This result is intuitive since convexity of marginal utility, \(v^{\prime \prime \prime }(.)>0\) over gains, in the absence of probability distortion, implies a prudent choice.
3.1.2 Domain of losses
In this case, we note that both \(X_{1}\) and \(X_{2}\) are negative, \( X_{1},X_{2}<0,\) and that \(\left| X_{1}+X_{2}\right| =\left| X\right| \) is larger than the upper bound of risk \(\widetilde{ \varepsilon }_{1}\). We recall that for the domain of losses, the weighting of cumulative probability of payoffs is from largest loss to smallest loss. Like in the case of gains, there are two cases depending on the relative magnitudes of \(k_{2}\) and \(\left| e_{1}\right| .\) The predictions are the same in both cases and we therefore only illustrate one of them. Let us consider \(k_{2}>\left| e_{1}\right| .\) For the case of symmetric risk, \(\widetilde{\varepsilon }_{1}=[-e_{1},e_{1}],\) we obtain the value of the lottery pair \(B_{3}\) and \(A_{3}\)
Since we are dealing with losses, the prudent lottery choice requires the absolute value of \(V(B_{3})\) to be less than the absolute value of \(V(A_{3})\) .Footnote 10 The value of lottery \(B_{3}\) is greater than lottery \(A_{3}\) with a linear value function when \(\alpha =1\) given the condition that \( 2w^{-}(0.75)<1+2w^{-}(0.25)\). This is the same condition for the prudent choice in the domain of gains as in (4). Consequently, the cumulative weighting of probabilities implies that a CPT DM with a linear value function will make the prudent lottery choice both over gains and over losses.
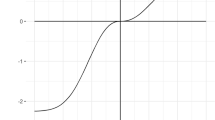
In this case, convexity in the value function over losses reinforces the effect of probability weighting given the standard assumption that the third derivative of the value function in CPT is positive over gains and negative over losses. Given this point, it follows that lottery \(B_{3}\) is preferred to lottery \(A_{3}\). We illustrate this in Fig. 1 employing the parameterisations of DS and EW described above. We observe that across all values of \(\alpha \) \((0<\alpha \le 1)\) the absolute value of \(V(B_{3})\) is below that of \(V(A_{3})\) and that they only intersect at \(\alpha =0.\)Footnote 11
3.2 Fourth order risky choice
3.2.1 Domain of gains
We proceed as in the previous subsection and first consider the case where all payoffs are in the gains domain. This implies that \(X_{1},X_{2}>0,\) and \( \left| X_{1}+X_{2}\right| =\left| X\right| \) is larger than the sum of the lower bounds of the two independent risks, \(\widetilde{ \varepsilon _{1}}\) and \(\widetilde{\varepsilon _{2}}.\) We first consider the case of symmetric risks, i.e., \(\widetilde{\varepsilon }_{1}=[-e_{1},e_{1}], \widetilde{\varepsilon }_{2}=[-e_{2},e_{2}]\) with non-equal payoffs such that \(e_{2}>e_{1}.\)Footnote 12 The lottery pair to elicit fourth order risky choices is
The value of the prospects from the status quo is calculated as follows
In the case of a linear value function, \(\alpha =1,\) the condition for the temperate lottery choice, \(V(B_{4})>V(A_{4})\), is given by
This condition can also be written in terms of probability distortion as \( \widetilde{w}^{+}(0.5)>\widetilde{w}^{+}(0.125)+\widetilde{w}^{+}(0.875)\). For the inverse-S-shaped probability weighting function in CPT modelling as specified in Sect. 2, including the ones reported in Table 1, this condition holds. Since all lottery payoffs are gains, introducing the power function (\(\alpha <1\)) into the value function reinforces the effect of the probability weighting (power utility in its own implies temperate behaviour) so that the representative CPT DM makes the temperate lottery choice when the status quo is the reference point.
3.2.2 Domain of losses
In the case of losses, payments \(X_{1}\) and \(X_{2}\) are both negative, \( X_{1},X_{2}<0,\) and their overall amount in absolute value, \(\left| X\right| \), has to be larger than the sum of the upper bounds of risks \( \widetilde{\varepsilon }_{1}\) and \(\widetilde{\varepsilon }_{2}\). We recall that for the domain of losses, the weighting of cumulative probability of payoffs is from largest loss to smallest loss. Let us first consider the case of symmetric risks \(\widetilde{\varepsilon }_{1}=[-e_{1},e_{1}], \widetilde{\varepsilon }_{2}=[-e_{2},e_{2}]\) with non-equal payoffs such that \(e_{2}>e_{1}.\) In this case, the values of the lottery pair from the status quo are given by
It is easily verifiable given the calculations above for the domain of gains that, under the assumption of linear value function, \(\alpha =1,\) the value of the lottery that combines both “harms” into the same state, \(A_{4}\), has a higher value (or smaller absolute value given they are negative) within the lottery pair. Consequently, with linear value functions, the representative CPT DM makes the intemperate choice. Introducing convexity, \(\alpha <1\), favours the choice of lottery \( A_{4}\) as discussed above. The representative CPT DM therefore makes the intemperate lottery choice. Consequently, there is a reflection effect in fourth order choices when the status quo is the reference point.
3.3 Mixed domain
In the case where lottery payoffs involve both gains and losses, the DM does not exhibit an unambiguous risky choice. We note that there are many possible lottery structures in this case dependent on the precise values of the payoffs (\(X,k_{2},\widetilde{\varepsilon _{1}}\)). We found, after analysing these different lottery structures, that the representative CPT DM can make either prudent or imprudent, temperate or intemperate lottery choices. The conclusion is that, within the mixed domain, heterogeneity about risky choices of order 3 and 4 across- as well as within-subjects is possible. This heterogeneity can be illustrated with examples using the parametric specifications presented in Table 1 which we make available upon request.
3.4 Predictions and empirical evidence
Our findings so far have uncovered a defined pattern of risky choices in risk apportionment tasks of order 3 and 4 over gains and losses for the representative CPT DM under the assumption that the status quo is the reference point. The pattern is no reflection effect for order 3 (prudent choice in both domains) and a reflection effect for order 4 (temperate choice over gains and intemperate over losses).Footnote 13 We now put this result into the context of existing experimental research that assume the status quo. Table 2 presents both the predicted behaviour following the results obtained in this section and the experimental findings of some prominent studies in this literature. We note that while some studies find that the majority of risky choices do not contradict the prediction of commonly used CPT models, others find results that are at odds with those predictions. For instance, Maier and Rüger (2012) find that the majority of choices are temperate in both domains. Brunette and Jacob (2019) find, based on the average number of choices, a reflection effect for third order lottery choices but not for fourth order. Finally, Bleichrodt and van Bruggen (2022) find a reflection effect of both order three and order four risky choices, with the latter being intemperate over gains and temperate over losses. In any case, we point out that in those studies the proportion of choices consistent with a particular risk attitude varies substantially across subjects.
4 Reference point 2: average payout
Deck and Schlesinger (2010) and Ebert and Wiesen (2014) are notable papers that analyse higher order risk preferences assuming the reference point is average payoff from the lottery. The average pay-out for the lottery pairs to elicit third and fourth order risky choices are \(r=W+X-0.5k_{2}\) and \( r=W+X\), respectively. We make two remarks regarding this reference point. First, given that \(W+X\) is present in all the branches of lottery pairs \( A_{i}\) and \(B_{i}\) \(\left( i=3,4\right) \) implies that the lotteries now exhibit both gains and losses and therefore fall within the mixed domain. Second, this also implies that both the endowment, W, and payment \(X\left( =X_{1}+X_{2}\right) ,\) play no role in determining risky choices of order 3 and 4 because they will both cancel out when computing the values of the lottery pairs \(V(A_{i}),V(B_{i})\). In this section, we determine the implications if binary risk is symmetric, and in Appendix A, the implications of asymmetric risk.
4.1 Third order risky choice
The relative sizes of \(k_{2}\) and \(e_{1}\) imply there are three formulations of the values of the lottery pairs defined by (3). However, we find the same qualitative implications in terms of choice made by the DM, and we therefore only report here the implications when \(e_{1}\ge k_{2}>0.5k_{2}.\) The values of the two lotteries are given by
We first consider the case where outcomes are not transformed but probabilities are, i.e., \(\alpha =1\). We find that the prudent lottery choice \(B_{3}\) will be made if
It is easy to verify that this condition holds for all representative CPT parameter values because small probabilities are overweighted while large probabilities are underweighted. Conversely, if we consider the limiting case as \(\alpha \rightarrow 0,\) the prudent choice will be made if
Consequently, the representative DM will choose \(A_{3}\) for a small enough value of the exponent \(\alpha \).Footnote 14 Since the representative CPT DM will make the prudent lottery choice with linear value functions but the imprudent choice if a power utility function is sufficiently concave over gains or convex over losses assuming representative values of loss aversion, this implies that there can be prudent or imprudent lottery choices dependent upon the parameter values. This can explain heterogeneity of third order choices across subjects in experimental research when the average payout was the reference point. For example, in the case of lottery payoffs \( e_{1}=9,k_{2}=1,\) in three out of the four CPT parameterisations in Table 1, namely TK, EW, and DS, the DM would choose \(B_{3}\), whilst in the fourth parameterisation, BBS, the CPT DM would choose \(A_{3}\).
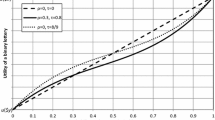
In addition to across-subjects heterogeneity, the CPT model assuming the expected payout as reference point, also implies that heterogeneity within subjects is possible. The following example illustrates how payoff magnitudes can impact the cross over point for \(\alpha \) that determines different choices of order 3 employing parameter values reported by TK and BBS. Let us consider two different lottery pairs, one with \(e_{1}=9,k_{2}=1,\) and another one with \(\varepsilon _{1}=25,k_{2}=25.\) Figure 2 plots the value of the prospects in each of those two cases. We observe that the level of concavity at which agents switch behaviour differs across the two parameterisations and lottery payoff structure giving rise to the heterogeneity indicated above.
4.2 Fourth order risky choice
There is currently no consensus in the literature about the relative prevalence of temperate or intemperate risky choices in experimental research employing the average pay-out reference point. For example, EW report that temperate choices are the majority, whilst DS report intemperate choices are the majority. To examine whether those findings could be accommodated within the CPT framework assuming the average pay-out as the reference point, we consider the case of symmetric zero-mean risk with different pay-offs, \(e_{2}>e_{1}\). The value of the lottery pair (5) for our representative CPT DM from the average payout reference point (\(W+X\)) are given by
To determine whether the valuation of the lottery pair by the DM is unambiguous or not, we consider the lottery choices of two limiting cases regarding the curvature of the value function. Let us first consider the choice of lottery when the DM transforms probabilities but not outcomes, i.e., \(\alpha =1.\) We find that, in this case, \(V(B_{4})>V(A_{4})\), if the following condition holds
Therefore, the probability weighting and loss aversion parameters play a crucial role in determining the fourth order lottery choice when the value functions are linear. For the EW and BBS parameterisations, we find their representative DM will make the temperate choice, whilst the representative subjects of TK and DS would make an intemperate choice. When we set \( \alpha \rightarrow 0,\) \(V(B_{4})>V(A_{4})\) if
In this case, we find with the representative set of parameters an unambiguous prediction of intemperate choice.
Consequently, our analysis can explain the conflicting experimental results. With linear value function assumed, temperate or intemperate risky choices occur dependent upon the precise probability weighting and loss aversion parameters reported in influential studies reported in different studies. As concavity over gains and convexity over losses is increased, the temperate choice will become dominant. Our analysis explains why the experimental results reported on four order risky choice can differ in influential studies. The precise values of the risky choice parameters play a crucial role in determining whether, from the average pay-out reference point, a temperate or intemperate lottery choice will be made. This analysis provides a rationale for the seemingly conflicting experimental results.
To provide further diagrammatical evidence of this analysis, we illustrate the point in Fig. 3. We employ lottery payoffs \(e_{1}=3.5,e_{2}=7\) (as in Ebert & Wiesen, 2014), and parameter values from the four CPT specifications outlined in Table 1. In two of the cases, TK and DS, the lines for \(V(B_{4})\) and \(V(A_{4})\) never cross each other, implying the DM would always prefer \(A_{4}\). In the other two cases, EW and BBS, the two lines cross each other, meaning the curvature of the value function will determine whether the DM makes the temperate or intemperate lottery choice. For example, for the values of \(\alpha \) reported in their papers, 0.97 in EW and 0.48 in BBS, the DM would choose \(B_{4}\) and \(A_{4}\), respectively. Hence, within this framework, we show that experimental research could well find heterogeneity both across as well as within subjects.
Combinations of second with third or fourth order risk. We now demonstrate that the representative CPT DM can exhibit combinations of second and third or fourth order risky choices not readily available within the EUT framework such as the combination of risk averse and imprudent, or risk averse and intemperate choices. The possibility of such combinations is interesting since for all utility functions that are commonly used in the literature under EUT, DMs must make a prudent choice regardless of whether they make risk averse or risk seeking second order choices, and that they make risk averse choices in combination with temperate choices. This includes the combining good with bad and good with good paradigm discussed in Crainich et al. (2013) and DS14. In Appendix B, we provide the derivation of second order lottery choices for a CPT specification under the average payout reference point, and we illustrate different combinations of second with third or fourth order lottery choices. This implies, within this setting, a potential weak correlation between risky choices of different orders across experimental subjects.
4.3 Predictions and empirical evidence
We again refer to Table 2 where the predicted behaviour obtained in this section and the results of a selected number of studies are displayed. Our new result that, from the average payout reference point, the CPT DM can exhibit any third or fourth order choice, enables us to help reconcile the experimental findings reported by, for instance, DS and EW. In these two studies the average reference point was assumed. Whilst both studies reported a majority third order preference of prudence, they differed in the majority fourth order preference. The parameter values of the CPT model reported in DS imply an intemperate majority choice employing their lottery payoffs and would also imply an intemperate majority choice employing the lottery payoffs employed in EW. Conversely, the model parameter values reported in EW imply a majority temperate choice employing their lottery payoffs and would also imply a majority temperate choice employing the lottery payoffs employed in DS. It is also worth noting that both sets of parameters reported in these two studies imply majority prudent choices for the lottery payoffs employed by them.
In addition, we note that the case of asymmetric risk, as analysed in Appendix A, implies that the DM is more willing to combine ‘bad’ with ‘bad’ in third order risky choices the more rightly skewed the risk is. This would be consistent with the experimental evidence in EW of stronger prudence the more left-skewed risk \(\widetilde{\varepsilon }\) is, and also with other studies such as Ebert’s (2015) that find that the precautionary motive is lower for right skewed background risk.
More broadly, we note that Trautmann and van de Kuilen (2018) in their review paper report the range of the average proportions of risk averse, prudent and temperate choices observed in experimental research which span the proportions 46–84, 45–96, and 38–87, respectively.Footnote 15 Overall, the experimental results reveal that there is a non-negligible proportion of imprudent and intemperate lottery choices which are inconsistent with commonly used EUT models. We have shown that heterogeneity across- and within-subjects can be accommodated within a CPT framework.
5 Reference point 3: MaxMin
Baillon et al. (2020) report that the maxmin criterion, defined as the maximum outcome that a subject can reach for sure, is, together with the status quo, the most common reference point used in decision under risk. The results in their study of second order risky choices show that maxmin is employed by \(30\%\) of experimental subjects as the reference point.
Employing the same framework used above for the other two reference points, we find, from the maxmin reference point, the representative CPT DM will always choose the prudent and the temperate lotteries.Footnote 16 Consequently, the representative CPT DM from the maxmin reference point makes the same third and fourth order lottery choices than the DM under the status quo reference point in the domain of gains.
6 Conclusions
In this paper, we have investigated the choice in risk apportionment tasks of order three and four made by a representative DM within a CPT framework. In our analysis, we employ risky choice elicitation tasks with binary risks, which are the ones used in the experimental literature on higher order risk preferences. CPT does not specify the way the reference point is formed. We therefore examine three alternative reference points that have been found to be the most commonly used in experimental studies or have been used in prominent studies on higher order risk preferences. Our results highlight the importance of specifying the reference point since the implied behaviour depends on it. An important finding is that a CPT DM will, in common with an EUT subject, always make prudent and temperate lottery choices in the gains domain from the status quo reference point. The DM will, on the other hand, choose the prudent and intemperate lottery in the domain of losses. As a consequence, there is no reflection effect for third order lottery choices but there is for fourth order lottery choices from the status quo reference point. We also find that this pattern would prevail under symmetric risk as it is most typically assumed in experimental research, but not under asymmetric risk because, in this case, the DM exhibits ambiguous choice of order 4.
From the average payout reference point, we demonstrate that all possible third and fourth order risky choices can be made by the representative CPT DM defined by the range of parameter values for probability weighting, power value functions and loss aversion reported in prominent studies. We show that heterogeneity of preferences across- as well as within-subjects can be a feature of an experimental study on higher order risk preferences, and we point to how results in the literature can be reconciled within our framework. Our analysis also reveals that from the average payout reference point there are combinations of second and third or fourth order risky choices not available for any of the utility functions typically used in the literature under EUT.
Our results have further implications for experimental research that considers alternative models to describe risk preferences. For instance, our findings shed light on whether the design of an experiment would be informative enough to discriminate between CPT and alternative risky-choice models. This could be achieved by endeavouring to ensure that the lottery structure and payoffs domain are the most appropriate to elicit risky choices for a range of representative CPT parameters and therefore more likely to reject alternative models.
Notes
Note that higher order choices which involved lotteries in the domain of gains, losses and mixed were made in an experiment taking place a few weeks after the experimental subjects all made gains in a non-higher-order experimental task.
In particular, they write: “To induce a strong reference point, subjects face both gains and losses relative to their initial endowment....subjects were given a 15-euro endowment at the start of the experiment. They were told that this endowment was their payment for participating in the experiment, that they could gain additional money or lose part of it, and that it was equal to the expected value of participating. Throughout our analysis we assume that subjects take the initial endowment as their reference point.”
\(\widetilde{Y}\) has more nth-degree than \(\widetilde{X}\) if \( \widetilde{X}\) dominates \(\widetilde{Y}\) via nth-order stochastic dominance. For \(n>1\), these two random variables have the same first \(n-1\) moments. See Ekern (1980).
The lottery structure to elicit temperance could also be constructed with a combination of \(n=1,m=3\). To simplify notation and the analysis below, we only consider the case of \(n=2,m=2.\)
The value function v(x) can be generalised if parameter \(\alpha \) differs over gains and over losses. It is common in the experimental literature that even when researchers are assuming different values, that the estimated coefficients are not significantly different (Fox and Poldrack, 2014). In addition, we keep this simpler form for the following reasons: (i) it provides a more intuitive understanding of the role played by the degree of risk seeking/risk aversion in the determination of higher order risky choices; (ii) generalising the results would be relatively straightforward.
The parameters of DS and EW are based on studies on third and fourth order risk preferences and that of TK and BBS on second order. BBS report a one parameter Prelec weighting function \(w(p)={\text {e}}^{-(-\ln p)^{0.43}}\) with the same parameter over gains and losses. When \(\gamma =\delta =0.53\) the weighting function described in this section is employed to proxy the Prelec function since it makes no important difference to our reported results in our setting.
In experimental research on second order risk preferences over small lottery payoffs numerous researchers report that linear value functions are a good approximation to the value function (e.g. Fehr-duda et al., 2006; Abdellaoui et al., 2008; Ring et al., 2018; L’Haridon & Vieider, 2019). It is also of interest to note that, in the only paper that has estimated a CPT model in the context of higher order preferences, Ebert and Wiesen (2014) report a value of the power exponent \(\alpha \) of 0.97, presumably not statistically different from unity. Although Yaari’s (1987) model lacks reference dependence, dual theory can be considered to arise if the status quo is the reference point, we are in the gains domain, and the value function is the identity (\(\alpha =1\)).
Under the dual theory (DT), the CPT DT DM exhibits dual prudence if \(\left( w^{+}\right) ^{\prime \prime \prime }\) \(>0\) (see Eeckhoudt et al., 2020). For instance, this condition holds for the case that \(w^{+}\) is represented by (2), and given that (4) also holds for any \( \gamma \in \left( 0.1\right) ,\) the CPT DM would be dual prudent and make the prudent lottery choice.
To clarify the argument about lottery pair choices in the domain of losses, we provide the following numerical example. For simplicity, let us consider a linear value function, \(\alpha =1\), and assume that \(X=-8,\) \(k_{2}=5,\) \( \widetilde{\varepsilon }_{1}=[-2,2],\)
$$\begin{aligned} V(B_{3})= & {} -\lambda \left\{ w^{-}(0.5)(13)+\left( w^{-}(0.75)-w^{-}(0.5)\right) (10)+\left( 1-w^{-}(0.75)\right) (6)\right\} \\= & {} -\lambda \left\{ 3w^{-}\left( 0.5\right) +4w^{-}\left( 0.75\right) +6\right\} \\ V(A_{3})= & {} -\lambda \left\{ w^{-}(0.25)(15)+\left( w^{-}(0.5)-w^{-}(0.25)\right) (11)+\left( 1-w^{-}(0.5)\right) (8)\right\} \\= & {} -\lambda \left\{ 4w^{-}\left( 0.25\right) +3w^{-}\left( 0.5\right) +8\right\} \end{aligned}$$so that \(V(B_{3})>V(A_{3})\) if \(4w^{-}\left( 0.75\right) <4w^{-}\left( 0.25\right) +2,\) which is equivalent to the expression \(2w^{-}(0.75)<\left( 1+2w^{-}(0.25)\right) .\)
Note that \(\alpha <1\) is a necessary condition for risk seeking over losses with a power value function. Ceteris paribus, a smaller \(\alpha \) implies a higher degree of risk seeking.
It is obviously innocuous whether we set \(e_{1}>e_{2}\) or \(e_{1}<e_{2}\). When \(e_{2}=e_{1},\) the conclusions of our analysis are not changed but the mathematics is, and they are available upon request.
This pattern was already stated, although no formal analysis or derivation provided, in Bleichrodt and van Bruggen (2022).
The imprudent choice would imply a lack of skewness preference, a result not consistent with the other two reference points. This is an interesting counter example to the general observation of skewness preference observed in experiments with binary lotteries.
Those figures are based on table A.1 in Trautmann and van de Kuilen (2018). The figures in the text correspond to averages in the studies reported in Trautmann and van de Kuilen (2018), but if the range within each of those studies were to be employed instead, the overall range of values would be significantly wider.
This result applies to the case of symmetric zero-mean risks. In this section, we have omitted the formal derivations to preserve some space, but they are all available upon request. It is possible to find cases where a CPT DM makes the intemperate choice. An example of this is to consider \( \alpha =0.93\), and parameters \(\lambda =1.3,\) \(\gamma =\delta <0.52\), and lottery design \(e_{2}=9,e_{1}=1.\) However, we do not consider this parameterisation as a representative CPT DM because the loss aversion parameter \(\lambda \) is too low. We note that only two out of the 14 studies reviewed in Fox and Poldrack (2014) report an estimate of loss aversion as low as \(\lambda \le 1.3.\)
This format of the lottery pair allows probabilities other than 50–50, and it easily relates to the form described in Sect. 2 by considering \( p=0.5,x=W+X,\) \(y=W+X-k_{1}-k_{2},\) and \(k_{1}=k_{2}.\)
References
Abdellaoui, M., Bleichrodt, H., & L’Haridon, O. (2008). A tractable method to measure utility and loss aversion under prospect theory. Journal of Risk and Uncertainty, 36, 245–266. https://doi.org/10.1007/s11166-008-9039-8.
Baillon, A., Bleichrodt, H., & Spinu, V. (2020). Searching for the reference point. Management Science, 66, 93–112. https://doi.org/10.1287/mnsc.2018.3224.
Baillon, A., Schlesinger, H., & van de Kuilen, G. (2018). Measuring higher order ambiguity attitudes. Experimental Economics, 21, 233–256. https://doi.org/10.1111/ecoj.12358.
Bleichrodt, Han, & van Bruggen, Paul. (2022). Reflection for higher order risk preferences. Review of Economics and Statistics, 104, 705–717. https://doi.org/10.1162/rest_a_00980.
Brunette, Marielle, & Jacob, Julien. (2019). Risk aversion, prudence and temperance: An experiment in gain and loss. Research in Economics, 73, 174–189. https://doi.org/10.1016/j.rie.2019.04.004.
Crainich, D., Eeckhoudt, L., & Trannoy, A. (2013). Even (mixed) risk lovers are prudent. American Economic Review, 103, 1529–1535. https://doi.org/10.1257/aer.103.4.1529.
Deck, C., & Schlesinger, H. (2010). Exploring higher-order risk effects. Review of Economic Studies, 77, 1403–1420. https://doi.org/10.1111/j.1467-937X.2010.00605.x.
Deck, C., & Schlesinger, H. (2012). Consistency of higher order risk preferences. CESifo Working Paper No 4047.
Deck, C., & Schlesinger, H. (2014). Consistency of higher order risk preferences. Econometrica, 82, 1913–1943. https://doi.org/10.3982/ECTA11396.
Ebert, S. (2015). On skewed risks in economic models and experiments. Journal of Economic Behavior and Organization, 112, 85–97. https://doi.org/10.1016/j.jebo.2015.01.003.
Ebert, S., & Wiesen, D. (2011). Testing for prudence and skewness seeking. Management Science, 57, 133–1349. https://doi.org/10.1287/mnsc.1110.1354.
Ebert, S., & Wiesen, D. (2014). Joint measurement of risk aversion, prudence, and temperance: A case for prospect theory. Journal Risk and Uncertainty, 48, 231–252. https://doi.org/10.1007/s11166-014-9193-0.
Eeckhoudt, L., Laeven, R. J. A., & Schlesinger, H. (2020). Risk apportionment: The dual story. Journal of Economic Theory, 185, 1–27. https://doi.org/10.1016/j.jet.2019.104971.
Eeckhoudt, L., & Schlesinger, H. (2006). Putting risk in its proper place. American Economic Review, 96, 280–289. https://doi.org/10.1257/000282806776157777.
Eeckhoudt, L., Schlesinger, H., & Tsetlin, I. (2009). Apportioning of Risks via Stochastic Dominance. Journal of Economic Theory, 144, 994–1003. https://doi.org/10.1016/j.jet.2008.11.005.
Ekern, S. (1980). Increasing Nth degree risk. Economics Letters, 6, 329–333. https://doi.org/10.1016/0165-1765(80)90005-1.
Fehr-Duda, H., de Gennaro, M., & Schubert, R. (2006). Gender, financial risk, and probability weights. Theory and Decision, 60, 283–313. https://doi.org/10.1007/s11238-005-4590-0.
Fox, C. R., & Poldrack, R. A. (2014). Chapter 11—Prospect theory and the brain. In P. W. Glimcher, C. F. Camerer, E. Fehr, & R. A. Poldrack (Eds.), Neuroeconomics (pp. 145–173). London: Academic Press.
Heinrich, T., & Mayrhofer, T. (2018). Higher-order risk preferences in social settings: An experimental analysis. Experimental Economics, 21, 434–456. https://doi.org/10.1007/s10683-017-9541-4.
Kimball, M. S. (1990). Precautionary savings in the small and in the large. Econometrica, 58, 53–73. https://doi.org/10.2307/2938334.
Kimball, M. S. (1992). Precautionary motives for holding assets. In P. Newman, M. Milgate, & J. Falwell (Eds.), The New palgrave dictionary of money and finance. London: MacMillan.
L’Haridon, O., & Vieider, F. M. (2019). All over the map: A worldwide comparison of risk preferences. Quantitative Economics, 10, 185–215. https://doi.org/10.3982/QE898.
Maier, J., & Rüger, M. (2012). Experimental evidence on higher-order risk preferences with real monetary losses. University of Munich Working Paper
Menezes, C., Geiss, C., & Tressler, J. (1980). Increasing downside risk. American Economic Review, 70(5), 921–32.
Noussair, C. N., Trautmann, S. T., & van de Kuilen, G. (2014). Higher order risk attitudes, demographics, and saving. Review of Economic Studies, 81, 325–355. https://doi.org/10.1093/restud/rdt032.
Ring, P., Probst, C. C., Neyse, L., Wolff, S., Kaernbach, C., van Eimeren, T., et al. (2018). It’s all about gains: Risk preferences in problem gambling. Journal of Experimental Psychology: General, 147, 1241–1255. https://doi.org/10.1037/xge0000418.
Trautmann, S. T., & van de Kuilen, G. (2018). Higher order risk attitudes: A review of experimental evidence. European Economic Review, 103, 108–124. https://doi.org/10.1016/j.euroecorev.2018.01.007.
Tversky, A., & Kahneman, D. (1992). Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty, 5, 297–324. https://doi.org/10.1007/BF00122574.
Tversky, A., & Wakker, P. (1995). Risk attitudes and decision weights. Econometrica, 63, 1255–1280. https://doi.org/10.2307/2171769.
Yaari, M. E. (1987). The dual theory of choice under risk. Econometrica, 55, 95–115. https://doi.org/10.2307/1911158.
Acknowledgements
Ivan Paya acknowledges financial support from Consellería de Innovación, Universidades, Ciencia y Sociedad Digital de la Generalitat Valenciana (CIPROM/2021/060), from MCIN/AEI/10.13039/501100011033, and from FEDER through grant PID2021-124860NB-I00
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: asymmetric risk
Although the majority of experimental studies on higher order risk preferences employ binary zero-mean risks that are symmetric, binary risk can also be asymmetric. Zero-mean asymmetric risk can be represented by \( \widetilde{\varepsilon }=\left[ q,e;\left( 1-q\right) ,\frac{-eq}{\left( 1-q\right) }\right] \) (see Ebert & Wiesen, 2014; Heinrich & Mayrhofer, 2018).
Reference point 1: status quo
Third order risky choice. In this case, our analysis shows that there will be two conditions for \(V(B_{3})>V(A_{3})\), depending on the relative values of \(k_{2}\) and e. We obtain that both over gains and over losses, the condition holds and the DM exhibits a prudent choice. Given the results are qualitatively similar to the case of symmetric risk presented above, we do not show here the analytical derivations to conserve space, but they are available upon request.
Fourth order risky choice. In this case, unlike in the case of third order choice, asymmetric risk modifies the relative valuation of the lottery pair, \(B_{4},A_{4}\). We represent the zero-mean asymmetric risks by \( \widetilde{\varepsilon _{1}}=\left[ q,e_{1};\left( 1-q\right) ,\frac{-e_{1}q }{\left( 1-q\right) }\right] ,\) \(\widetilde{\varepsilon _{2}}=\left[ q,e_{2};\left( 1-q\right) ,\frac{-e_{2}q}{\left( 1-q\right) }\right] \) with non-equal payoffs such that \(e_{2}>e_{1}\) and \(q>0.5\) (see Ebert & Wiesen, 2014). In this case, the lottery pair is the following:
The value of the lottery pair under the status quo reference point is obtained by
Whether \(V(B_{4})\) is larger or smaller than \(V(A_{4})\) depends on the precise parameter values of the representative CPT model and the lottery payoffs. This is the case even under the restricted version of the asymmetric risks such as \(\widetilde{\varepsilon _{1}}=\left[ q,e_{1};\left( 1-q\right) ,\frac{-e_{1}q}{\left( 1-q\right) }\right] ,\) \(\widetilde{ \varepsilon _{2}}=\left[ q,-e_{1};\left( 1-q\right) ,\frac{e_{1}q}{\left( 1-q\right) }\right] \), which is the form used by Ebert and Wiesen (2014). Hence, the lack of symmetry in the binary risk may imply heterogeneity of fourth order choice. We note that this would also be the case for the domain of losses, and we will therefore omit the analysis here.
Reference point 2: average payout
Third order choice. To illustrate the effect of an asymmetric risk under the expected payout reference point, we employ the same form of asymmetric risk as described in the previous section, i.e., \(\widetilde{ \varepsilon }=\left[ q,e;\left( 1-q\right) ,\frac{-eq}{\left( 1-q\right) } \right] \). We note that, in this case, the lottery pair is the following
To obtain the value of each lottery, we first need to specify the relative values of \(k_{2}\) and e. For the case that \(e>0.5k_{2},\) we obtain under the average payout reference point (note that \(0.5q\in \left( 0.5,0\right) \))
Numerical analysis suggests that there is not an unambiguous prediction in this case. As a matter of fact, we find that, not only the prudent choice depends on specific model parameters which suggests across-subjects heterogeneity, but that it also depends on lottery payoffs which suggests within-subject heterogeneity. We also find that the more rightly skewed the risk is (i.e. the lower q or the higher e are) the more likely the DM is to choose \(A_{3}\). This implies that the DM is more willing to combine the two ‘bads’, zero-mean risk and loss of wealth, the more rightly skewed the risk is.
Fourth order choice. The implications of assuming asymmetric risk will be the same as the ones for symmetric risk presented in Sect. 4, and we have therefore omitted the analysis here.
Appendix B: Average payout reference point: combinations of second with third or fourth order risky choices
We consider model specification (1) assuming the average payout (\(\mu \)) as the reference point, that is, \(r=\mu \). To illustrate combinations of second with higher order risky choices, the second order risk elicitation task is characterised by the lottery pair \(B_{2}=\left[ 1-p,\mu ;p,\mu \right] \) and \(A_{2}=\left[ 1-p,y;p,x\right] ,\) with \(y<x.\)Footnote 17 The average payout of each lottery is \(\mu =px+\left( 1-p\right) y.\) The value of the lottery pair is the following
A risk averse choice requires \(V(B_{2})>V(A_{2}),\) which yields the following condition: \(\lambda >\frac{w^{+}\left( p\right) }{w^{-}\left( 1-p\right) } \frac{\left( 1-p\right) ^{\alpha }}{p^{\alpha }}.\) Consequently, the second order risky choice depends on the CPT model parameters, and they can imply a risk averse or a risk seeking choice.
To illustrate this feature as well as the combinations of second with higher order risky choices, we provide the following examples. We initially simplify the model specification by assuming linear utility \(\alpha =1,\) and \( w^{+}\left( p\right) =w^{-}\left( p\right) =w(p).\) In this case, the condition for risk averse choice derived above simplifies to \(\lambda >\frac{ w\left( p\right) }{w\left( 1-p\right) }\frac{\left( 1-p\right) }{p}.\) Under these assumptions, for probabilities that are overweighted, \(w(p)>p,\) which is typically found in experimental research for the case of small probabilities (p) of larger outcomes (x), the DM would not make a risk averse choice unless she is loss averse (\(\lambda >1\)). For example, assuming \(\gamma =\delta =0.65\), and a binary lottery with \(p=0.25,\) the condition above is equal to \(\frac{w\left( 0.25\right) }{w\left( 0.75\right) }\frac{0.75}{0.25}=1.47.\) Therefore, if \(\lambda >1.47\) the DM makes the risk averse lottery choice, and if \(\lambda <1.47\) she would make the risk seeking choice. Regarding combinations with higher order choices, looking at conditions (6) and (7) derived in Sect. 4 under linear utility, we note that the DM with any degree of loss aversion (\( \lambda >1\)) would make the prudent and intemperate lottery choices. Consequently, depending on the loss aversion parameter, the choices would be prudent, intemperate and either risk averse or risk seeking.
A further example, departing now from linear utility, \(0<\alpha <1\), illustrates that the CPT DM under the average payout reference point can make a different combination of second with third and fourth order choices. For instance, assuming \(\alpha =0.8,\lambda =1.5,\gamma =\delta =0.65,\) and the lottery pairs to elicit second, third and fourth order risky choices determined by \(x=2,y=0,p=0.05,\) \(e_{1}=9,k_{2}=1,e_{2}=12\), the DM makes the risk seeking, imprudent, and intemperate lottery choices.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Paya, I., Peel, D.A. & Georgalos, K. On the predictions of cumulative prospect theory for third and fourth order risk preferences. Theory Decis 95, 337–359 (2023). https://doi.org/10.1007/s11238-022-09920-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-022-09920-w