Higher order risk attitudes: new model insights and heterogeneity of preferences

Abstract

It is now well established that higher-order risk preferences play a crucial role in determining the risky choices of decision makers in a wide range of important areas such as economics, finance and health. While influential theories of risky choice in those fields can explain attitudes to second order risk, the implications of these models for higher order risk preferences is still to be developed. This paper addresses that gap for the Markowitz (J Political Econ, 60:151–58, 1952) (M) model of utility which embodies reference-dependent utility, loss aversion and was seemingly the first model to explain the fourfold attitude to risk. In this paper, we set out new properties of the M model for higher order preferences, such as higher-order risky choice reversals, that can help explain experimental evidence not readily reconcilable with other models of risky choice. A second contribution of the paper is to empirically examine the heterogeneity of preference functionals describing second as well as higher order risky choices using hierarchical Bayesian estimation methods. Our analysis of the risky choices revealed in three prominent studies provides support for the M model as a useful complement to other leading models of risky choice such as cumulative prospect theory (CPT). In addition, we set up a new experiment whose design is shown to have satisfactory discriminatory power between the M and CPT specifications, and our results based on the Bayes factor confirm the heterogeneity of preference functionals across decision makers, and that the CPT specification is more prevalent.

1 Introduction

It is now well established that many decisions in the fields of economics, finance and health are dependent not only on second order risk preferences but also upon higher order risk attitudes such as prudence and temperance (e.g. Bleichrodt et al., 2003; Deck & Schlesinger, 2014; Eeckhoudt & Schlesinger, 2013; Noussair et al., 2014; Trautmann & van de Kuilen, 2018; White, 2008). Models of Expected Utility Theory (EUT) that have been employed in the literature of higher order risk attitudes, such as mixed-risk aversion and mixed-risk loving, predict that a risk averse decision maker (DM) would exhibit prudence and temperance, while a risk lover DM would exhibit prudence and intemperance (see Deck and Schlesinger (2014), Eeckhoudt and Schlesinger (2006), Noussair et al. (2014)].

While there is some empirical evidence consistent with EUT models of mixed-risk aversion and mixed-risk loving, other experimental literature has provided evidence on higher order risk attitudes that are difficult to reconcile with EUT. For instance, many experimental studies reveal that imprudent choices, which are not consistent with the EUT models mentioned above, constitute a non-negligible share of total choices. The proportion of imprudent choices reported is sometimes close to forty percent, as illustrated in Table 1 of the review paper by Trautmann and van de Kuilen (2018). Other experimental findings reported are also inconsistent with models of EUT. Some examples are the lack of correlation between risk aversion and temperance (Bleichrodt & van Bruggen, 2022), a stronger correlation between third and fourth order risk preferences than between second and fourth order (Maier & Rüger, 2012; Ebert & Wiesen, 2014), strong correlation between odd and even moments of risk attitudes (Maier & Rüger, 2012; Noussair et al., 2014), and evidence of a “stakes effect” on higher order risk attitudes exhibited by the DM (Deck & Schlesinger, 2010).

Reference-dependent models are more flexible and, in principle, capable of providing a framework able to accommodate this body of experimental evidence, as they have successfully accomplished with many other aspects of behavioural decision making. It is therefore surprising that, despite the relevance of reference dependence in explaining behaviour under risk and uncertainty, little is known about the predictions of those models regarding higher order risk preferences. Furthermore, taking into consideration that reference-dependent models lack clarity about the way the reference point is formed and that a variety of reference points ought to be considered when eliciting risk preferences [see Baillon et al. (2020)], our understanding of those models in relation to higher order risk attitudes under alternative reference points is even more limited. The norm in experimental research reported to date on lottery choices eliciting risk apportionment is that researchers have endeavoured to implement their appropriate reference point by experimental procedure and lottery design. This reference point is then assumed in the analysis of the responses of the experimental subjects. For example, Maier and Rüger (2012), Brunette and Jacob (2019), and Bleichrodt and van Bruggen (2022) report results where the status quo reference point is assumed. Alternatively, Deck and Schlesinger (2010) and Ebert and Wiesen (2014) assumed that the reference point was the expected value of the lottery. One of the early attempts to address the gap in the literature about reference dependence and higher order risk preferences can be found in Paya et al. (2022). They examine the behaviour with regard to third and fourth order risky choices of a DM using a cumulative prospect theory (CPT) specification under three alternative reference points. However, there are still empirical regularities and findings in experimental studies on higher order risk preferences that are not consistent with the predictions of the mainstream models of decision making under risk such as CPT and EUT. Our paper provides new insights within this literature and includes two contributions.

First, we provide a comprehensive analysis about the implications for higher order risk preferences of a reference-dependent model consistent with Markowitz’s (1952) hypotheses, which we will refer to as the M model. These hypotheses include loss aversion, reference dependence, and the fourfold attitude to risk over binary lottery choices. Empirical and experimental evidence on second order lottery choices of decision making under risk is consistent with those hypotheses (e.g. Hershey & Shoemaker, 1980; Pennings & Smidts, 2000; 2003; Post & Levy, 2005; Scholten & Read, 2014).¹ Furthermore, the analysis by Georgalos et al. (2021) suggests that the M model can be a valuable complement to other reference-dependent and EUT models to explain risky binary lottery choices. The complementarity of the M model is also manifested by the fact that it can parsimoniously explain certain regularities observed in experimental studies that are difficult to reconcile with other models, such as violations of the separability principle underlying prospect theory² [especially over gains, see Bouchouicha and Vieider (2017), Chark et al. (2020), Hogarth and Einhorn (1990)], or a reported high proportion of risk-seeking in lottery choices between a risky positive payoff(s) with a 0.5 probability(ies) and the safe alternative which has the same expected value (e.g. Battalio et al., 1990; Hershey & Shoemaker, 1980; 1985; Maier & Rüger, 2012; Vieider et al., 2015; Weber & Chapman, 2005). Given this potential for complementarity, Scholten and Read (2014) explore whether it is possible for a weighted-value model such as CPT exhibiting the fourfold attitude to risk over outcome probabilities, to also encompass the fourfold attitude to risk over outcome magnitude, as predicted by the M model. They present the condition needed for this to happen and suggest the use of a multiplicative model that includes a decreasingly elastic value function in conjunction with a probability weighting function. The applicability of such specification is, however, very limited because the condition is met for a very reduced range of parameter values (see Appendix A).

Our analysis of the M model extends previous analyses in the literature since we examine for the first time its predictions over higher order risky choices from a number of alterative reference points. As noted by Baillon et al. (2020), when Markowitz (1952) introduced the reference-dependent utility theory, he was not explicit about the reference point to be used in his modeling framework, as was also the case for subsequent reference dependence models developed in the literature. We therefore examine the predictions of the M model assuming three reference points, namely, status quo, MaxMin, and expected value. All those three reference points are examined by Baillon et al. (2020), and two of those are identified as the most frequently employed when eliciting risk aversion under CPT, namely, status quo and MaxMin. The other reference point, the average payout, is incorporated in our analysis because it has previously been used in prominent studies on higher order risk preferences (Deck & Schlesinger, 2010; Ebert & Wiesen, 2014).

We employ recently developed elicitation methods of risk preferences and show that the M model can explain high order risky choices as well as combinations of second with higher order choices not readily available from other reference-dependent models. This finding is particularly interesting from the status quo reference point. From this reference point, we are able to demonstrate a different prediction of the M model to that of the representative CPT, rank dependent utility (RDU) or EUT DMs. In particular, the representative CPT or RDU subject will, in common with the mixed-risk averse model of EUT, always make a prudent or temperate lottery choice whithin the gains domain. In contrast, a decision maker with M preferences can make choices consistent with any third and fourth order risk attitude from the status quo reference point dependent upon the precise magnitude of the lottery payoffs. Furthermore, the M model can accommodate a reflection effect on third order choices, a feature that is absent in other models [see Bleichrodt and van Bruggen (2022)]. Finally, the M model also enjoys the unique property of ‘higher-order reversals ’, implying that a given set of parameters predicts that the DM will exhibit a risk attitude for specific risks, and the reverse preference for others.³

The second contribution is that this is the first paper we are aware of that uses an empirical approach that allows for more than one preference functional to fit experimental data on risk apportionment tasks eliciting higher order risk preferences. This is particularly relevant in this literature given there is no consensus about a single parametric specification that can accommodate the accumulated experimental evidence on higher order preferences [see Trautmann and van de Kuilen (2018)]. We employ the datasets from three of the most prominent studies on higher order risk attitudes, namely, Deck and Schlesinger (2010, 2014), and Nousssair et al. (2014) (DS10, DS14 and NTK, respectively, hereafter). The preference functionals include both an M specification and a CPT specification, each under three alternative reference points (and where EUT can be nested). Our results based on hierarchical Bayesian estimation methods show that both preference functionals are useful to describe the experimental evidence as there is not a single model that dominates the others across the three datasets. We point out that the higher the proportion and variety of (anti) risk apportionment choices of different orders, the more helpful the M model is to explain risky choices, and it therefore becomes a valuable complement to rank dependent preference functionals to account for high order risk attitudes. We assess the econometric method employed here through a set of simulations, and show that it can satisfactorily identify an assumed model specification, and discriminate among alternative ones.

In addition to this empirical analysis, we set up a new experiment to further investigate heterogeneity of risky choices of different orders across subjects, and to discriminate between M and CPT specifications. The new insights about the M model we provide in this paper, together with existing analysis about higher order risk preferences in the CPT model (Bleichrodt & van Bruggen, 2022; Paya et al., 2022), reveal different predictions between the two models under the status quo reference point that are exploited in the design and analysis of the experiment to discriminate between the two models. A comprehensive simulation exercise shows that the experimental design has satisfactory discriminatory power between M and CPT specifications that can be considered as ‘representative’ of those models. The results of the experiment confirm the presence of heterogeneity of preference functionals and that, based on the Bayes factor, around a third of DMs are classified as consistent with the M specification and two thirds consistent with the CPT one.

The rest of the paper is structured as follows. In Sect. 2, we set out the properties of a parametric M model of utility. In Sect. 3, we employ the framework developed by DS14 to illustrate the key properties of the M model for third and fourth order risky choices. In Sect. 4, we discuss the econometric method and the estimation results employing the experimental datasets from DS10, DS14 and NTK. Section 5 presents a new experiment on higher order risk preferences, and Sect. 6 provides a brief conclusion.

2 Properties of the M model of utility

Markowitz (1952) proposed a new model of non-expected utility to resolve some of the counterfactual implications of the Friedman and Savage (1948) model of expected utility. For example, Markowitz pointed out that the Friedman-Savage model of expected utility implies individuals of middle income would engage in large symmetric bets or extend insurance even at an expected loss to themselves. From a reference point, Markowitz assumed that a DM exhibits a fourfold attitude to risk: risk seeking (risk averse) over small gains (losses) and risk averse (risk seeking) over large gains (losses), and that the value functions are bounded from above and below. This modeling framework, which we refer to as the M model, offers an explanation of local-risk-seeking behaviour within a money value function without the counterfactual implications of assuming everywhere risk-seeking preferences. This is relevant in the context of, e.g., Deck and Schlesinger (2014, p.1914) who have drawn attention to the need to explain risk-loving behaviour. Everywhere risk-seeking preferences, such as the ones defined by mixed-risk loving EUT models, also imply that the individual would wager all their wealth at actuarially unfair odds. Consequently, whist theoretically attractive, it is not clear it can characterise individual outcomes in experimental research.

Markowitz assumed objective and subjective probabilities were equal and also that the representative agent exhibited loss aversion.⁴ Our parametric specification of the M model is the same as the one in Georgalos et al. (2021) and we therefore closely follow their setup. The value functions over gains (G) and over losses (L) are the following

$$\begin{aligned} \begin{array}{cc} U(G)=1-e^{-\alpha G^{\eta }} &{} \\ U(L)=-\lambda (1-e^{-\beta L^{\eta }}), &{} \end{array} \end{aligned}$$

(1)

where $\alpha ,\beta ,\lambda$ and $\eta$ are all positive constants, $\beta \le \alpha ,$ and parameter $\eta$ above unity ($\eta >1$) captures the hypotheses of the Markowitz model.⁵ The mathematics of the expo-power value function (1) reveal that for gains and losses of the same amount the decision maker is, when risk seeking over gains, risk averse over losses. However, when risk averse over gains, they can be either risk averse or risk seeking over losses of the same amount. As a consequence, the M model may or may not exhibit a reflection effect of second order preferences for lottery choices which have the same payoff structure and absolute expected return.

To gain intuition about the role played by $\eta$ in the determination of risk attitudes, it is worth noting that, with $\eta >1$, the derivatives change sign as outcome magnitudes change. Furthermore, parameter $\alpha >0$ implies the function exhibits, over gains, increasing relative risk aversion (IRRA), and that the smaller the value of $\alpha$, the wider the range of values of G the DM exhibits risk seeking behaviour. An additional interesting property of the expo-power function is that, in this case, if $\eta <1,$ the function accommodates both decreasing absolute risk aversion (DARA) and IRRA, which are two behavioural traits commonly found in the empirical literature of decision under risk [see Wakker (2010)]. Finally, within a gains domain framework, the M model nests an EUT maximiser with exponential utility when $\eta =1$ , and it approximates the (CRRA) power value function $G^{\eta }$ when $\alpha$ $\rightarrow 0$.

The definition of loss aversion, LA, introduced by Markowitz (1952), is the ratio of the absolute magnitude of the utility of losses to the utility of gains for symmetric losses (L) and gains (G):

$$\begin{aligned} LA=\frac{\lambda (1-e^{-\beta L^{\eta }})}{(1-e^{-\rho \beta G^{\eta }})}. \end{aligned}$$

(2)

In expression (2), we have expressed the constant parameter $\alpha =\rho *\beta$ , $\rho \ge 1,$, to note that when gains and losses of the same absolute magnitude tend to zero, the lower bound of loss aversion is given by $\frac{\lambda }{\rho }$ and when gains and losses of the same absolute magnitude are large, LA is given by $\lambda$.⁶ Figure 1 depicts an example of the M model employing the expo-power function with parameter values that will be used later in this paper, $\eta =2.4,\rho =1.1,$ $\beta =0.0018,\lambda =2.25.$ A crucial property of the Markowitz model, not shared by other models of risky choice, is that the third and fourth order derivatives of the value function over either gains or losses can change sign at least once and sometimes twice as lottery payoffs are increased, while the second derivative can remain either positive or negative. This seemingly unique property is illustrated in

Fig. 1

Expo-power function (1) with parameter values $\eta =2.4, \alpha =0.002,\beta =0.0018,\lambda =2.25$

Figure 2 that plots the second, third and fourth derivatives for parameter values employed in Fig. 1. A consequence of this property for an M DM is that the revealed correlation between second and higher order preferences exhibited in experimental research can be positive, negative or zero. Correlations between risk attitudes are therefore not predetermined like in other models of decision under risk. We will discuss this issue in detail in the next section.

Fig. 2

Plots of the second (top), third (middle), and fourth (bottom) derivatives over gains of value function (1) with parameter values $\eta =2.4, \alpha =0.002$

3 Risky choices in the M model of utility

We employ the model-free framework developed by DS14 to elicit risk attitudes of different orders. Their framework is based on Eeckhoudt et al. (2009) and generalises the method developed by Eeckhoudt and Schlesinger (2006) which was a major contribution in the elicitation of higher order preferences. Let us denote an individual’s endowment as W,  $W>0.$ We will write ${\mathcal {L}}\equiv [x,y]$ to denote a lottery of equally likely payoffs x and y,  where both x and/or y might themselves be lotteries. The two pairs of random variables $\{{\widetilde{X}}_{1},{\widetilde{Y}}_{1}\}$ and $\{{\widetilde{X}}_{2},{\widetilde{Y}}_{2}\}$ are such that ${\widetilde{Y}}_{1}$ has more nth-degree risk than ${\widetilde{X}}_{1},$ and ${\widetilde{Y}}_{2}$ has more mth-degree risk than ${\widetilde{X}}_{2}.$⁷ Under these assumptions, lottery $A_{s}=[W+{\widetilde{X}}_{1}+{\widetilde{X}}_{2},W+ {\widetilde{Y}}_{1}+{\widetilde{Y}}_{2}]$ has more sth-degree risk than lottery $B_{s}=[W+{\widetilde{X}}_{1}+{\widetilde{Y}}_{2},W+{\widetilde{Y}}_{1}+ {\widetilde{X}}_{2}]$ where $s=(m+n),m\ge 1,n\ge 1$ [see Eeckhoudt et al. (2009)], in our case $s=2,3,$ and 4. The individual’s preference is denoted with $\succeq$. “Risk apportionment of order s ” implies a preference of lottery $B_{s}$ over $A_{s},$ that is, $B_{s}\succeq A_{s}.$ A DM with this preference dislikes the lotteries with more sth degree risk, $A_{s},$ and exhibits a preference for combining the relatively “good” random variable ${\widetilde{X}}_{i}$ with the relatively “bad” random variable ${\widetilde{Y}}_{i},$ as it happens in $B_{s}$. “Anti-risk apportionate of order s ” is the reverse preference, $A_{s}\succeq B_{s}$.

We now specify the elements of the random variables included in the lottery pairs to elicit risk preferences. First, we consider that the random variables ${\widetilde{X}}_{1},{\widetilde{X}}_{2},$ are fixed monetary outcomes denoted as ${\widetilde{X}}_{1}=X_{1},{\widetilde{X}}_{2}=X_{2},$ and that $X_{1}+X_{2}=X.$ $k_{1}$ and $k_{2}$ are monetary payoffs such that $k_{1}>0,k_{2}>0.$ ${\widetilde{\varepsilon }}_{1}$ and ${\widetilde{\varepsilon }}_{2}$ are zero-mean random variables that are independent of each other and of any other random variable. We will initially assume that the zero-mean risk is binary and symmetric, as typically used in the experimental literature on higher order preferences, and therefore defined as ${\widetilde{\varepsilon }} _{1}=[-e_{1},e_{1}]$ and ${\widetilde{\varepsilon }}_{2}=[-e_{2},e_{2}]$.

We describe below the lottery pair structure for $s=2,3,$ and 4,  together with an example from Table II of DS14.

Risk aversion: $s=m+n=2,$ with $m=1,n=1.$ Variable ${\widetilde{Y}} _{1}=X_{1}-k_{1}$ and variable ${\widetilde{Y}}_{2}=X_{2}-k_{2}$. The lottery pair to elicit risk aversion is $A_{2}=[W+X,W+X-k_{1}-k_{2}]$ and $B_{2}=[W+X-k_{2},W+X-k_{1}].$ Lottery $A_{2}$ is a mean-preserving spread of lottery $B_{2}.$ For example, $X_{1}=X_{2}=10,k_{1}=k_{2}=5,$ and therefore $A_{2}=[20,10]$ and $B_{2}=[15,15].$

Prudence: $s=m+n=3,$ with $m=1,n=2.$ In this case, ${\widetilde{Y}} _{2}=X_{2}-k_{2}$ and ${\widetilde{Y}}_{1}=X_{1}+{\widetilde{\varepsilon }}_{1}.$ Therefore $A_{3}=[W+X,W+X-k_{2}+{\widetilde{\varepsilon }}_{1}]$ where the two relatively “bad” outcomes are combined together (wealth reduction of $k_{2}$ and zero-mean risk ${\widetilde{\varepsilon }}_{1}$), and $B_{3}=[W+X-k_{2},W+X+{\widetilde{\varepsilon }} _{1}]$ where the relatively “good” outcome (payment X without the loss of $k_{2}$) is combined with the “bad” outcome (zero-mean risk ${\widetilde{\varepsilon }}_{1}$). For example, $X_{1}=0,X_{2}=10,k_{2}=5, {\widetilde{\varepsilon }}_{1}=[-4,4],$ and therefore $A_{3}=[10,5+[-4,4]]$ and $B_{3}=[5,10+[-4,4]].$

Temperance: $s=m+n=4,$ with $m=2,n=2.$ ${\widetilde{Y}}_{2}=X_{2}+{\widetilde{\varepsilon }}_{2}$ and ${\widetilde{Y}}_{1}=X_{1}+{\widetilde{\varepsilon }} _{1}.$ Therefore $A_{4}=[W+X,W+X+{\widetilde{\varepsilon }}_{1}+\widetilde{ \varepsilon }_{2}]$ combines the two “bad” outcomes together (zero-mean risks ${\widetilde{\varepsilon }}_{1}$ and ${\widetilde{\varepsilon }}_{2}$), while $B_{4}=[W+X+{\widetilde{\varepsilon }} _{2},W+X+\widetilde{\varepsilon }_{1}]$ disaggregates those two risks. Lottery $A_{4}$ is, in this case, an outer risk increase of lottery $B_{4}$. For example, $X_{1}=X_{2}=8.5,{\widetilde{\varepsilon }}_{1}=[-5,5],\widetilde{ \varepsilon }_{2}=[-2,2],$ and therefore $A_{4}=[17,17+[-5,5]+[-2,2]]$ and $B_{4}=[17+[-2,2],17+[-5,5]].$

Given that elicitation of risk attitudes in reference-dependent models depends upon the specific reference point used by the DM,we consider in the analysis below three different reference points, namely, status quo, average payout, and MaxMin. In addition to the reference point, lottery choices made by the DM in the analysis of risk apportionment of order three and four depend upon model parameter values, stake size and lottery design. Given this complexity, the theoretical analysis below will use numerical analysis to examine whether lottery preferences and their associated behavioural traits are exhibited within a range of feasible parameter values, and will also make use of examples and counterexamples to illustrate cases where certain risk attitudes are attainable for a risky choice model but not for an alternative one.

3.1 Reference point 1: Status Quo

Within the DS14 framework described above, the status quo reference point corresponds to the level of initial wealth or endowment, W. The probabilities and outcomes of the lottery pair to elicit risk apportionment of order 3 are the following⁸

$$\begin{aligned} B_{3}&:&0.5,W+X-k_{2};\,0.25,W+X+e_{1};\,0.25,W+X-e_{1} \\ A_{3}&:&0.5,W+X;\,0.25,W+X-k_{2}+e_{1};\,0.25,W+X-k_{2}-e_{1}. \end{aligned}$$

Over gains, the expected utility of the two lotteries are evaluated from the status quo reference point and given by these two expressions:

$$\begin{aligned} U(B_{3})= & \, 0.5\left( 1-e^{-\rho \beta (X-k_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X+e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X-e_{1})^{\eta }}\right) \nonumber \\ U(A_{3})= & \, 0.5\left( 1-e^{-\rho \beta (X)^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X-k_{2}+e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X-k_{2}-e_{1})^{\eta }}\right) . \end{aligned}$$

(3)

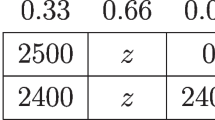
We illustrate in Table 1 the risky choices of an M decision maker with parameter values similar to the ones reported by Georgalos et al. (2021) for the dataset from Scholten and Read (2014), namely, $\alpha =\rho *\beta =0.002,\eta =2.4,\rho =1.1$. This particular parameterisation is helpful because it allows us to demonstrate the unique property that the decision maker can, in principle, make lottery choices consistent with all possible combinations of second, third and fourth order risk attitudes depending on the precise lottery payoffs. We start with the lotteries designed to elicit risk aversion. Those lotteries denoted as RA1, RA2, RA3 and RA4 are described in Table 1 Panel A. For those four lotteries, the decision maker with the parameter values described above would make two risk seeking choices ($A\succeq B$), and two risk averse choices ( $B\succeq A$). For example, lottery pair RA1 implies a choice between a certain 5 and a 50-50 chance of receiving either 7 or 3 and the DM chooses the latter.

Table 1 Second-, third-, and fourth-order risky choices over gains for the SQ reference point

We now turn to the lottery pairs revealing choices of order three (lottery structure P1, P2, P3 and P4 described in Table 1 Panel B). With these lottery payoffs, the DM with the parameters assumed above would make two imprudent choices ($A_{3}\succeq B_{3}$) for lottery payoffs P2 and P3. In these two lotteries, the DM prefers to receive the zero-mean risk ${\widetilde{\varepsilon }}_{1}=[2,-2]$ when payoffs 10 and 15 are experiencing the loss of $k_{2}=3$. In contrast, she prefers $B_3$ for lottery structures P1 and P4 ($B_{3}\succeq A_{3}$). In these two lotteries, the zero-mean risk ${\widetilde{\varepsilon }} _{1}=[2,-2]$ is preferred when payoffs 5.5 and 25 are not experiencing the loss of $k_{2}=3$, i.e., a preference for combining ‘good with bad’.

The fact that utility function (1) has inflection points implies there is not a one-to-one mapping between second and higher order risk attitudes. Therefore, to determine the second order preferences consistent with the third order lottery choices described above, we uncover the certainty equivalent (CE) of the lottery choice, $B_{3}$ or $A_{3},$ and compare it with its expected value ($\mu$). By applying this method, one of the lotteries for which the decision maker’s choice was $A_{3}\succeq B_{3}$, in this case lottery P2, the CE for lottery $A_{3}$ is higher than the expected value of the lottery ($\mu =8.5$) and she therefore is locally risk loving. However, for the lottery choice in P3, the opposite is true, and the decision maker chooses lottery $A_{3}$ but she is locally risk averse ( CE of the preferred lottery is lower than its expected value $\mu =13.5$). The same analysis is applied to the two lottery structures where the individual exhibits prudent choices, P1 and P4. We find that, for P1, the CE of $B_{3}$ is higher than the expected value $\mu =4$ and therefore locally risk loving, while for P4, the CE is lower than 23.5 and the risky choice is risk averse. For large enough payoffs, the DM always makes risk averse and prudent lottery choices.

Figure 2 presented above helps to provide an intuition about the relationship between second and third order risky choices. The second order derivative (top graph) switches sign at gains equal to 10.6,  and the third derivative (middle graph) displays both positive and negative values within the range [0, 10.6]. We would therefore expect that, for lottery pairs designed to elicit prudence, with an expected value less than 10.6 such as P1 and P2, the agent would exhibit risk-seeking choices combined with either prudent or imprudent choices. On the other hand, we would expect risk aversion for lottery pairs with an expected value larger than 10.6 as it is indeed the case for P3 and P4. Given that the third derivative switches sign for values of gains that are higher than 10.6,  we would again expect that the second order preference of risk aversion can be combined with either imprudent or prudent choices, as it is the case with P3 and P4, respectively.

We now turn to risk apportionment of order 4, where the payoffs of the two zero-mean independent risks can be different, $e_{2}\ge e_{1}$. In this case, the probabilities and outcomes of the two lotteries are the following

$$\begin{aligned} B_{4}&:&0.25,W+X+e_{2};\,0.25,W+X+e_{1};\,0.25,W+X-e_{1};\,0.25,W+X-e_{2} \\ A_{4}&:&0.5,W+X;\,0.125,W+X+e_{2}+e_{1};\,0.125,W+X+e_{2}-e_{1};\,0.125,W+X-e_{2}+e_{1};\,0.125,W+X-e_{2}-e_{1}. \end{aligned}$$

The corresponding value functions for these two lotteries evaluated from the status quo reference point are

$$\begin{aligned} U(B_{4})= & \, 0.25\left( 1-e^{-\rho \beta (X+e_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X+e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X-e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (X-e_{2})^{\eta }}\right) \nonumber \\ U(A_{4})= & \, 0.5\left( 1-e^{-\rho \beta (X)^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (X+e_{2}+e_{1})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (X+e_{2}-e_{1})^{\eta }}\right) \nonumber \\{} & {} +0.125\left( 1-e^{-\rho \beta (X-e_{2}+e_{1})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (X-e_{2}-e_{1})^{\eta }}\right) . \end{aligned}$$

(4)

The choices that the M decision maker characterised in Table 1 Panel C (and Figs. 1 and 2) would make in the four lotteries of order 4 (T1, T2, T3 and T4 in Table 1 Panel C) also illustrate that temperate as well as intemperate choice can be consistent with both risk loving and risk averse preferences, although for large enough payoffs, she always makes risk averse and temperate lottery choices.

These combinations of risky choices can be intuitively understood by looking at the top and bottom graphs of Fig. 2. Tasks designed to elicit fourth order choices with an expected value less than 10.6 such as T1 and T2 will combine local risk loving behaviour with either risk or anti-risk apportionment of order 4. This is illustrated by the fact that the fourth derivative changes sign prior to 10.6. Interestingly enough, the fourth derivative changes sign again for values that are higher than 10.6 and therefore this parameterisation permits that a DM that makes risk averse choices can also make temperate or intemperate choices depending on the lottery payoffs.

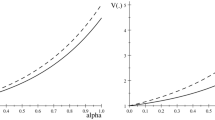
The examples in Table 1 illustrate that a DM described by the M model can make combinations of second with third and fourth order choices not seemingly feasible in EUT or CPT. To illustrate that our parameters chosen above are not special, we illustrate in Figs. 3 and 4 that very different parameterisations of the M model specification can also exhibit a rich set of risk preferences. In Fig. 3, the vertical axis represents the differences in utility between lotteries B and $A,U(B_{3})-U(A_{3}),$ for lottery P3 defined above in Table 1. We set parameter $\alpha$ at value 0.002, and the horizontal axis represents values of the other parameter of the expo-power value function, $\eta$. Positive values in Fig. 3 imply that the decision maker’s choice is the prudent one, $B\succeq A$, while she exhibits the imprudent one for the cases of negative values.

Fig. 3

Plot of $U(B_3)-U(A_3)$ in prudence task $P_3$ defined in Table 1. Parameter $\alpha =0.002$

Figure 4 illustrates that decision makers characterised by different combinations of the two parameters of the value function, $\alpha$ and $\eta$, can exhibit different combinations of second and third order when making lottery choices in P3. In the diagram, individuals defined by values of $\alpha$ and $\eta$ above the solid line exhibit risk averse and prudent choices. Alternatively, for parameter values between the solid and the dash line, the lottery choices are risk averse and imprudent. Finally, parameter values below the dash line imply the decision maker exhibits risk loving and imprudent choices.

Fig. 4

Regions of risk aversion/loving (RA/RL) and prudence/imprudence (PR/IMP). Solid line: combinations of $\alpha$ and $\eta$ that yield prudent neutral lottery choice in task $P_3$ defined in Table 1. Dashed line: combinations of $\alpha$ and $\eta$ that yield risk neutral lottery choice in task $P_3$

We conclude the discussion about the status quo reference point by noting that the fact that a DM characterised by the M model can make choices consistent with any third and fourth order risk is an important result since, in the three papers we are aware of that assume the status quo reference point, the reported proportion of imprudent or intemperate choices is substantial.⁹ Furthermore, the M DM also exhibits any third or fourth order risky choices in the domain of losses, although we do not report the analytical work here to save spece. Therefore, the M model is in principle able to accommodate the reflection effect in higher order risk such as the one reported in Bleichrodt and van Bruggen (2022).¹⁰ This is an important property in discriminating between different models of risky choice.

3.2 Reference point 2: average payout

The average payout of the lotteries has been assumed as the reference point in prominent experimental studies on higher order preferences (e.g. DS10; and Ebert & Wiesen, 2014). The expected value of the lottery pair to elicit risk apportionment of order 3, $A_{3}$ and $B_{3}$, is $W+X-\frac{ k_{2}}{2}.$ With this reference point, there are two valuations of the lottery pair to elicit third order choices which depend on the relative magnitudes of $\frac{k_{2}}{2}$ and $e_{1}.$ When $e_{1}\ge \frac{k_{2}}{2}$ the utilities of $B_{3}$ and $A_{3}$ are given by

$$\begin{aligned} U(B_{3})= & \, 0.25\left( 1-e^{-\rho \beta (e_{1}+\frac{k_{2}}{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1}-\frac{k_{2}}{2})^{\eta }}\right) -\lambda 0.5\left( 1-e^{-\beta (\frac{k_{2}}{2})^{\eta }}\right) \\ U(A_{3})= & \, 0.5\left( 1-e^{-\rho \beta (\frac{k_{2}}{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{1}-\frac{k_{2}}{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1}+\frac{k_{2}}{2})^{\eta }}\right) . \end{aligned}$$

On the other hand, when $e_{1}<\frac{k_{2}}{2},$ the utilities of the lotteries are given by

$$\begin{aligned} U(B_{3})= &\, 0.25\left( 1-e^{-\rho \beta (e_{1}+\frac{k_{2}}{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (\frac{k_{2}}{2}-e_{1})^{\eta }}\right) -\lambda 0.5\left( 1-e^{-\beta (\frac{k_{2}}{2})^{\eta }}\right) \\ U(A_{3})= & \, 0.5\left( 1-e^{-\rho \beta (\frac{k_{2}}{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (\frac{k_{2}}{2}-e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (\frac{k_{2}}{2}+e_{1})^{\eta }}\right) . \end{aligned}$$

We determined the lottery choices in these two pairs of lotteries employing numerous combinations of parameter values (including gain-seeking as well as loss-averse preferences) and payoff magnitudes. We found that the behavioral trait exhibited by the DM depends on the payoff structure. In particular, when payoffs were relatively small, the M decision maker would always make the prudent choice.¹¹ However, for lotteries where $\frac{k_{2}}{2}$ is large relative to $e_{1},$ or $e_{1}$ is large relative to $\frac{k_{2}}{2 },$ she can make the imprudent choice.

Regarding risky choices of order 4, the utilities of the lottery pair from the average payout reference point, which in this case is $W+X,$ are given by

$$\begin{aligned} U(B_{4})= &\, 0.25\left( 1-e^{-\rho \beta (e_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1})^{\eta }}\right) \\ U(A_{4})= &\, 0.125\left( 1-e^{-\rho \beta (e_{2}+e_{1})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (e_{2}-e_{1})^{\eta }}\right) -\lambda 0.125\left( 1-e^{-\beta (e_{2}+e_{1})^{\eta }}\right) \\{} & {} -\lambda 0.125\left( 1-e^{-\beta (e_{2}-e_{1})^{\eta }}\right) . \end{aligned}$$

As with third order risky choices, we determined the preferred lottery employing numerous combinations of parameter values and payoff magnitudes. We found that temperate or intemperate lottery choices were possible depending on the precise lottery payoffs and parameter values. For example, employing the four lottery choices to determine risk apportionment of order 4 in DS10, who assumed expected value as the reference point, we found that we only had one temperate choice which occurred when payoffs were small and $\eta >2.4.$ This result is noteworthy given that DS10 found that, for their experimental subjects, the lottery choices consistent with intemperate behaviour were greater than the ones consistent with temperate behaviour.

From the average payout reference point, it is necessary to compare the certainty equivalent of the untransformed lottery choice to the expected value of the higher order lottery choice, in order to determine the subject’s risk attitude. Since, as shown above, the endowment W and payoff X play no role in the lottery choice from the expected value reference point, the preferred lottery choice is consistent with any value of them. Experimental evidence showing ambiguous patterns of correlation among risk attitudes would therefore not be at odds with the M model. In this regard, Ebert and Wiesen (2014) report the strongest correlation between lottery choices occurs for risk apportionment tasks of third and fourth order, whilst DS10 find no significant correlation among them.

3.3 Reference point 3: MaxMin

Baillon et al. (2020) estimate that MaxMin is, together with the status quo, the most common reference point employed in their study of second order lottery choices. MaxMin is determined as the maximum outcome subjects can reach for sure, and it is therefore considered a security-based rule. There are two possible MaxMin reference points for the lottery pairs employed to elicit third order choices. First, when $k_{2}\ge e_{1},$ the reference point is $W+X-k_{2},$ and the expected utility of the lottery pairs are

$$\begin{aligned} U(B_{3})= & \, 0.25\left( 1-e^{-\rho \beta (k_{2}+e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (k_{2}-e_{1})^{\eta }}\right) \\ U(A_{3})= & \, 0.5\left( 1-e^{-\rho \beta (k_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1})^{\eta }}\right) . \end{aligned}$$

Second, when $e_{1}>k_{2},$ the reference point becomes $W+X-e_{1},$ and the expected utilities are the following

$$\begin{aligned} U(B_{3})= & \, 0.5\left( 1-e^{-\rho \beta (e_{1}-k_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (2e_{1})^{\eta }}\right) \\ U(A_{3})= & \, 0.5\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (2e_{1}-k_{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (k_{2})^{\eta }}\right) . \end{aligned}$$

We determined the lottery choices in these two pairs of lotteries employing numerous combinations of parameter values and different payoff magnitudes. As it was the case with the average payout reference point, the DM, with given parameters, can make prudent or imprudent choices and can also switch between the prudent or imprudent choices as lottery payoffs are varied. We find that the possibility to switch can be easily demonstrated by increasing the magnitude of either $k_{2}$ relative to $e_{1}$, or $e_{1}$ relative to $k_{2},$ for given parameters of the value function.

To examine lottery choices of order four, the reference point under MaxMin is $W+X-e_{2}$ (assuming $e_{2}\ge e_{1}$). This is without loss of generality given that it is innocuous to define the payoffs of either of the two zero-mean risks, $e_{2}$ and $e_{1}$, as the larger one. The expected utility values of the lottery pair are given by

$$\begin{aligned} U(B_{4})= &\, 0.25\left( 1-e^{-\rho \beta (2e_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{2}+e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{2}-e_{1})^{\eta }}\right) \\ U(A_{4})= &\, 0.5\left( 1-e^{-\rho \beta (e_{2})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (2e_{2}+e_{1})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (2e_{2}-e_{1})^{\eta }}\right) \\{} & {} +0.125\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.125\left( 1-e^{-\beta (e_{1})^{\eta }}\right) . \end{aligned}$$

Our analysis reveals that, as it happened for third order preferences, the M DM with given parameters can make temperate or intemperate lottery choices and switch choices dependent upon the precise lottery payoffs. This result implies that, as it was the case for the previous two reference points, the property of higher-order reversal is still present.

3.4 Effect of different reference points

The decision maker with given parameters of the M model can exhibit different fourth order risk preferences for the same lottery payoffs as the reference point is changed from average payout to MaxMin. To illustrate this point, we employ payoffs ${\widetilde{\varepsilon }}_{2}=[7,-7],{\widetilde{\varepsilon }} _{1}=[3.5,-3.5]$, and parameter values $\rho =2,\beta =\frac{0.002}{\rho } ,\lambda =4.5$ (hence, LA ranges from 2.25 to 4.5). Figure 5 plots the difference in utility, $U(B_{4})-U(A_{4})$, against the expo-power exponent $\eta$. From the MaxMin reference point, for $\eta <3.1$ the lottery choice is temperate, while intemperate for $\eta \ge 3.1.$ However, from the average-payoff reference point, the lottery choice is temperate for $\eta \in [2,3.37]$ and intemperate for parameter values of the expo-power exponent outside that interval. Paya et al. (2022) find that the representative CPT subject will choose the prudent and temperate lottery choices from the MaxMin reference point. That result contrasts with the one for the M model and could be used to discriminate alternative preference functionals in future experimental research which can, by experimental design, implement the MaxMin reference point.

Fig. 5

$U(B_4)-U(A_4)$ is plotted against parameter $\eta$ under reference point average payout (solid line) and Maxmin (dashed line)

Table 2 presents a summary of the predictions about higher order risk choices of order 3 and 4 derived in this section for the M model of utility. We also include in this table the predictions for some of the main models of decision under risk and uncertainty, namely, EUT-mixed risk averse, EUT-mixed risk loving, and CPT under three alternative references points (status quo, expected value, and MaxMin). There are other reference points that could in principle be also considered. For instance, Baillon et al. (2020) include in their analysis two additional deterministic reference points, namely, MinMax and X at Max P. However, they found they are barely used by DMs. We have examined risky choice behaviour assuming those two reference points and found they did not provide differential predictions across alternative model specifications/reference points (see Appendix B). Therefore, we decided to leave them out of the main analysis.

Table 2 Second-, third-, and fourth-order risk choices for commonly used decision theory models under risk and uncertainty

4 Econometric analysis

The paper has so far shed light on the predicted risky choice of up to order four for the Markowitz model of utility under three alternative reference points. This section contains another contribution, namely, the first paper about higher order risk preferences that (i) presents estimates within a framework of heterogeneity of preference functionals; and (ii) it includes model estimates at the subject and group level. The estimation of models include M and CPT parameterisations (that can nest EUT) for three of the most relevant studies done on higher order preferences, namely, DS10, DS14 and NTK. The use of mixture models addresses the issue previously raised in the literature about the difficulty of finding one single preference functional that fits any data exactly [see Conte et al. (2011), Fehr-Duda et al. (2010), Georgalos et al. (2021)].

There are various ways to estimate structural decision making models ranging from individually estimating preference functional for each subject, to fully pooling the data together and estimating a representative agent model. Both approaches suffer from a series of drawbacks such as over-fitting in the case of individual level estimates, or failures to capture heterogeneity in preferences, in the case of pooled estimations. [see Conte et al. (2011), Fehr-Duda et al. (2010), Georgalos et al. (2021), Harrison and Ruström (2009)]. To mitigate these drawbacks, we adopt hierarchical Bayesian estimation techniques [see Balcombe and Fraser, (2015), Ferecatu and Öncüler (2016)] for some recent applications of hierarchical Bayesian models for choice models under risk, or Wright and Leyton-Brown (2017) for some applications in games). The key aspect of hierarchical modelling is that even though it recognises individual variation, it also assumes that there is a distribution governing this variation (individual parameter estimates originate from a group-level distribution). A hierarchical Bayesian model simultaneously estimates the individual level parameters, along with the hyper-parameters of the group level distributions. In typical hierarchical models, the estimates of the low level parameters are pulled closer together than they would in the absence of a higher-level distribution, leading to the so called shrinkage of the estimates.

We are assuming three reference points, the status quo, where all the outcomes are regarded as gains, the average payout of the lottery, and the MaxMin reference point. In the two latter cases, there are mixed gambles including both gains and losses. For each of the datasets, and for each of the three reference points we estimate both the M and the CPT models (6 parametric specifications per dataset) using Bayesian modelling.

We reproduce here the utility function for the M choice model given above by the expo-power specifications (1):

$$\begin{aligned} u(x)=\left\{ \begin{array}{ll} (1-\exp (-\alpha (x-r)^{\eta }))/\alpha &{} \hbox {if } x\ge \hbox { r} \\ -\lambda (1-\exp (-\beta (r-x)^{\eta }))/\beta &{} \hbox {if } x< \hbox { r} \end{array} \right. \end{aligned}$$

(5)

The CRRA utility function for the CPT model is given by:

$$\begin{aligned} u(x)=\left\{ \begin{array}{ll} (x-r)^{\alpha }/\alpha &{} \hbox {if } x\ge \hbox { r} \\ -\lambda (r-x)^{\alpha }/\alpha &{} \hbox {if } x< \hbox { r} \end{array} \right. \end{aligned}$$

(6)

with $\alpha$ being the curvature of the utility function and $\lambda$ the loss aversion parameter. Following Nilsson et al. (2011) and Baillon et al. (2020), we assume the same curvature parameter for gains and losses. The Tversky and Kahneman (1992) weighting function is assumed for the decision weights, with the following specification:¹²

$$\begin{aligned} w(p)=\frac{p^{\gamma }}{(p^{\gamma }+(1-p)^{\gamma })^{1/\gamma }}. \end{aligned}$$

(7)

The parameter $\gamma$ is assumed to be common for both gains and losses.

To account for the stochastic nature of the choices, and given that all the datasets include binary choices between two alternatives A and B, we assume a logistic choice rule of the form Luce (1959):

$$\begin{aligned} P(A,B)=\frac{1}{1+\exp (\varphi [EU(B)-EU(A)])}, \end{aligned}$$

where P(A, B) is the probability of choosing prospect A over B, EU(A) and EU(B) are the expected utilities for prospects A and B, for a given set of behavioural parameters (similarly for the CPT model) and $\varphi \ge 0$ is a precision parameter. $\varphi$ measures the sensitivity of choices on the size of the difference between the value of the two prospects. $\varphi =0$ implies random choice between the two prospects, larger values of $\varphi$ imply higher precision in choices, while $\varphi \rightarrow \infty$ implies deterministic choice.

Each subject i makes a series of N binary choices in a given dataset and the observed choices vector is denoted by $D_{i}=(D_{i1}\cdots D_{iN})$. Every subject is characterised by its own parameter vector $\theta _{i}=(\alpha _{i},\gamma _{i},\lambda _{i},\varphi _{i})$ ($\theta _{i}=(\alpha _{i},\beta _{i},\eta _{i},\lambda _{i},\varphi _{i})$ for the M model) and following Nilsson et al. (2011) we assume that all the individual parameters are normally distributed $(\theta _{i}\sim N(\mu _{b},\sigma _{b}))$, while for the hyper-parameters we assume normal priors for the mean $\mu _{b}$ and uninformative priors (uniform) for $\sigma _{b}$. We also follow the standard procedure and transform all the parameters to their exponential form to ensure that they lie within the appropriate bounds.

The likelihood of subject’s i choices is given by:

$$\begin{aligned} P(D_{i}|\theta _{i})=\prod _{n=1}^{N}P(D_{i,n}|\theta _{i}), \end{aligned}$$

where $P(D_{i,n}|\theta _{i})$ is given by Luce’s rule, for each lottery pair n, as presented above. Combining the likelihood of the observed choices and the probability distribution of all the behavioural parameters, the posterior distribution of the parameters is given by:

$$\begin{aligned} P(\theta |D)\propto P(D|\theta )\times P(\theta ), \end{aligned}$$

with $P(D|\theta )$ being the likelihood of observed choices over all the subjects and $P(\theta )$ the priors for all parameters in the set $\theta$.

Monte Carlo Markov Chains (MCMC) were used to estimate all the specifications. The estimation was implemented in JAGS (Plummer, 2017). The posterior distribution of the parameters is based on draws from two independent chains, with 100,000 MCMC draws each, for all the specifications. Due to the high level of non-linearity of the models, there was a burn-in period of 50,000 draws, while to reduce autocorrelation on the parameters, the samples were thinned by 10 (every tenth draw was recorded). Convergence of the chains was confirmed by computing the ${\hat{R}}$ statistic (Gelman & Rubin, 1992). All the inference and the subsequent comparison of the models is based on the log Bayes Factor measure (Kass & Raftery, 1995). This measure is the difference between the log-marginal likelihoods of the two models. Bayes factors penalize models with a large number of parameters, prevent over-fitting, and are a good measure of the predictive capacity of each model. The estimation Tables report the point estimates for all model parameters which are obtained from the posterior distribution (posterior mode).

DS10 include a battery of 10 sets of lotteries, 6 designed to elicit third order choices and 4 to elicit fourth order. DS14 include 38 pairs of lotteries to elicit higher order preferences up to the 6th degree. NTK include 15 lotteries to elicit 2nd, 3rd and 4th order preferences, 5 for each order. In our analysis, we use the lotteries intended to elicit risky choices of order 3 and 4 because it was not possible to use the lotteries for the 2nd order when the average payout or the MaxMin were assumed as reference points. Appendix C presents the stimuli of the three datasets.

4.1 Empirical results

The first result worth noting is that there is strong evidence that decision makers’ risky choices are best described by more than one preference functional. Both the classification of subjects based on the Bayes Factor reported in Table 3 and the individual estimates reported in Tables 4, 5 and 6 imply that there is not a reference-dependent model that dominates the other from the three reference points considered in this paper.

Table 3 reports the number and proportion of subjects that have been classified as either M or CPT, employing the reference points status quo, average payout and MaxMin, in each of the three datasets we consider in this section (DS10, DS14, and NTK). The classifications of the reference points based on the Bayes factor estimates imply that the status quo reference point is employed by around 30% across all subjects in each of the three data sets, a similar proportion to that estimated by Baillon et al. (2020) for second order preferences. Since from this reference point, the M model also nests EUT, the significance of the Markowitz model is particularly noteworthy.

Table 3 Classification of subjects

Tables 4, 5 and 6 present parameter estimates of the models that include both M and CPT preference functionals for each of the three datasets separately. The estimates of the parameters of the CPT model displayed in Tables 4, 5 and 6 are similar to the ones obtained in the literature of risky choice. For instance, the review paper of Fox and Poldrack (2014) report estimates from many papers and the parameter values fall within the following ranges, $\alpha \in$ (0.19, 1.19), $\lambda \in$ (1, 2.63), $\gamma \in$ (0.56, 0.96).¹³ These estimates imply under-weighting of the 0.5 probability as do Tversky and Kahneman (1992). We consider evidence about overweighting 0.5 probabilities at odds with CPT assuming the representative DM is defined by the parametric model and range of parameter values typically reported or employed in the literature and because it implies a violation of subcertainty (Kahneman & Tversky, 1979). The parameter values of the expo-power function ($\alpha ,\beta ,\eta$) obtained in the econometric analysis are within the range of the ones found in the literature on risky choices [e.g. Abdellaoui et al. (2021), Bouchouicha & Vieider (2017), Georgalos et al. (2021)].

Overall, the empirical results differ markedly between the two data sets of DS10 and DS14 and the one of NTK. In DS10 and DS14, expected value is found to be the reference point employed by around half of the subjects and MaxMin by around a fifth of them. However, in NTK, MaxMin is the most popular reference point. Estimates from the three studies also reveal that the M model of utility is consistent with the majority higher order choices from the average payout in the DS10 and DS14 data sets, whilst for the NTK dataset, the CPT specification under MaxMin is the preferred model. The M model does not parsimoniously fit the data from the MaxMin reference point since, in Tables 4, 5 and 6, the estimated exponent in the expo-power value function ($\eta$) is not greater than unity. Those estimates are consistent with a model which exhibits decreasing absolute risk aversion (DARA), and, since $\alpha >0$, increasing relative risk aversion (IRRA).

There are two characteristics that may explain the differences in the agents. First, the proportion of prudent and temperate choices, i.e. preferences for combining ‘good with bad’, is lower in DS10 and DS14. In particular, 61% and 76% of prudent choices, and 38% and 58% of temperate choices, respectively. These numbers contrast with the higher proportions found by NTK, 89% of prudent and 62% of temperate choices. Second, the correlation coefficients between prudent and temperate choices in the Deck and Schlesinger studies are low ($-0.06$, and 0.067, respectively) and not statistically significant, while in the study by NTK the positive correlation coefficient is higher (0.18) and significant, albeit only at 10% level.

Table 4 Estimates for the DS10 dataset

Table 5 Estimates for the DS14 dataset

Table 6 Estimates for the NTK dataset

These features of the experimental results suggest that a parsimonious estimation of the data in DS10 and DS14 probably requires a model that can more readily accommodate preferences for combining both ‘good with bad’ and ‘good with good’ and ‘bad with bad’ outcomes, i.e., prudent and imprudent, temperate and intemperate choices. Furthermore, some of the findings in DS14 are at odds with the mixed-risk averse/mixed-risk loving models of EUT. For instance, they report (see Table A.III) a higher proportion of subjects classified as risk loving and imprudent than as risk loving and prudent, and a higher proportion of subjects classified as risk-loving and temperate than as risk loving and intemperate. Moreover, the proportion of experimental subjects classified as temperate and prudent or intemperate and prudent are less than half. The M model of utility can accommodate those possibilities under any of the three reference points employed in the estimations as shown in the previous section. In that regard, the CPT model is more limited given that, for instance, under either status quo or MaxMin reference points, decision makers only exhibit prudent and temperate choices in the gains domain [see Paya et al. (2022)]. It is therefore probably not surprising that the CPT specification more successfully explains the experimental results in NTK relative to those in DS10 and DS14.

4.2 Method assessment

The empirical analysis in this section aims to identify and discriminate subjects’ risky choices among six different specifications, that is, two decision models, with a third one, EUT, nested within them, and three reference points for each model. Given the number of alternative specifications, it is important to assess whether the econometric method can satisfactorily achieve its goal. We have run a series of simulation exercises with two purposes. First, to show whether any given specification could be satisfactorily identified and discriminated from the different possible alternatives from a statistical point of view. Second, to check whether the parameters of an assumed model specification could be recovered once that model is estimated, and also to check the parameter estimates obtained if other alternative models are estimated instead. The results of the simulations confirmed that the statistical method implemented in the paper is able to identify an assumed model, discriminate between that model and alternative model specifications, and largely recover the ‘true’ parameter values. This exercise is described in detail in Appendix D.1.

5 New experiment

The extant literature on higher order risk attitudes has been mainly developed with the objective to classify subjects as prudent and temperate, predominantly based on the raw count of lottery choices on risk apportionment tasks. The analyses and interpretation of the results in this literature face two challenges. First, the need to take into account the stochastic nature of decision making. Second, as it has been revealed in this paper, the lack of a one-to-one mapping between a given behavioural trait and a risky choice model. To address these issues, we design and conduct a novel laboratory experiment to discriminate between the M and the CPT model specifications.

The new insights we provide in this paper about the M model, together with existing analyses about higher order risk preferences in the CPT model (Paya et al., 2022; Bleichrodt & van Bruggen, 2022), suggest the status quo is an appropriate candidate for a reference point to be applied in the experiment due to the different predictions on risky choices between the two models. Furthermore, this reference point is in principle possible to be implemented using similar procedures other researchers have previously employed in the literature [e.g. Maier and Rüger (2012), Bleichrodt and van Bruggen (2022).

To facilitate the structural estimation of the models under investigation, our design differs from the previous literature on higher order risk preferences in various ways. First, to discriminate between second order risk attitudes towards outcome magnitudes and outcome probabilities, we include tasks that have either the same probability but different payoff sizes, or the same stake size but different probabilities. The purpose of this is to exploit the different predictions across the two models, where the M model predicts the four-fold attitude to outcome magnitude, while CPT predicts the four-fold attitude to outcome probabilities. Furthermore, since we are interested in estimating latent risk parameters (utility curvature and probability weighting) the latter kind of tasks allowed us to further vary the range of probabilities of the lotteries, while keeping the set of prizes fixed, in an effort to increase the robustness of the estimates. Second, since we are interested in estimating the coefficients of both the utility curvature and the probability weighting, we have complemented the typically employed 50-50 lotteries à la Eeckhoudt and Schlesinger (2006), with other binary lotteries that have the same first and second but different third central moment across several probability values. Finally, we examined, ex-ante, the payoff magnitudes and probability values employed in the experiment by means of a simulation exercise.

The tasks in our experiment are presented in reduced form. This differentiates our experiment from the three studies examined in the previous section. Presenting the tasks in reduced or compound form should not have an impact on the lottery choices made if DMs do not violate the reduction of compound lottery (ROCL) axiom, while it would, if that was the case [for violations of the axiom see Harrison et al. (2015), Fan et al. (2019)]. This way, if an overall conclusion from both this and the previous section were to be drawn, it could not be attributed to a violation of ROCL.

5.1 Experimental design

A total of 49 participants were recruited from the Lancaster Experimental Economics Lab (LExEL) subject pool. The sessions lasted 30 minutes, and the average earnings were £19.4, including a show-up fee of £5 (the minimum payment was £6 and the maximum £55). Payments to subjects were made by automatic bank transfer. The experiment was computerised. Upon entering the lab, participants were randomly allocated to one of the terminals and were visually isolated from other participants. They proceeded to read the instructions of the experiment and they had the chance to ask clarification questions. Then, subjects were presented with a total of 29 lottery pairs.

The status quo was implemented following a similar method to that employed by other researchers [e.g. Bleichrodt and van Bruggen (2022), Brunette and Jacob (2019), Maier and Ruger (2012)].

The 29 tasks were grouped in to four blocks. The first block comprised 9 tasks which were designed to elicit second order risk preferences. Four out of these nine tasks were choices between a sure payoff and a 50-50 risky lottery with the same expected value, while the remaining five tasks were a modified version of the Holt and Laury (2002) risk elicitation task. The second block included seven tasks designed to elicit third order risk preferences over a range of probability values that can help the estimation of a probability weighting function. The third and fourth blocks of tasks comprised standard lotteries of the form proposed by Eeckhoudt and Schlesinger (2006) to elicit third and the fourth order risk preferences, respectively. There were 6 tasks for third order and 7 tasks for fourth order. All the tasks are listed in Table 7.¹⁴

The selection of the lottery pairs included in the tasks was not arbitrary. We run a series of simulations to select the lotteries according to the following criteria. First, there was a distinct lottery choice across the two decision models for the majority of the tasks considering a wide range of parameter values as representative for each choice model. Second, the tasks contained significant probabilistic information content, in the sense that they would predict choice probability in favour of a lottery with at least 60% (see Appendix D). Third, the tasks selected allowed the estimates to largely recover ‘true’ model parameters, and, finally, the tasks selected had good discriminatory power between the two models based on the value of the pairwise Bayes Factor. We detail the simulation exercise in Appendix D.2.

The lotteries in the experiment were presented as a pie chart that displays the probability of each outcome as a slice of the pie (a screenshot of the experimental interface is shown in Appendix E). In the instructions, the subjects were informed that one of their choices in the experiment would be played out for real. In an effort to minimise potential order effects, the tasks were presented to the participants in a random order, different for each participant. The location, left or right, of the option that satisfies lottery A or B was randomised for each subject and for each task. After answering all questions in the experiment, the software would randomly choose one of the tasks. After recovering the actual choice of the subject, in that particular task, the software would generate a random number to determine the winning probability, and therefore the payoff of the subject.

5.2 Results

Table 7 presents the description of the tasks as well as the proportion of DMs that chose the A lottery. This proportion varies substantially within tasks of the same order, with differences of around 20%. Although it is typically assumed that a stochastic element in the DMs’ underlying preferences may drive choices of opposite risk attitude, it is also possible that it is actually the DMs’ preferences that imply such choices. This ‘higher-order reversal’ can be accommodated by the M model of utility, as shown above in Sect. 3, but not by alternative model specifications such as CPT or EUT under the status quo reference point.

Table 7 List of choice tasks

We follow Deck & Schlesinger (2014, 2018) and test whether the data are generated from random behaviour. Table 8 reports the observed mean and median of A choices, the mean and median if choice is generated by a random process, and the p-values of the Wilcoxon and the t-test of random choice. The results suggest that behaviour is statistically different from random behaviour for all the three orders of risky preferences.

Table 8 Statistical significance against random choice

We now proceed to the classification of experimental subjects as averse, neutral or seeker to risks of order 2, 3 and 4, based on the number of A lottery choices made.¹⁵ Table 9 presents the results. Following the classification system of DS14, a subject with 3 or more A choices on second-order tasks is considered risk loving, while those with 1 or 0 A choices, are considered to be risk averse. Similarly a subject is classified as prudent (temperate) when she makes 4 (2) or less A choices, and imprudent (intemperate) when she makes 8 (5) or more A choices. This exercise is to contrast our results within the EUT mixed risk averse/mixed risk loving paradigm given that this way of classifying subjects as either averse or seeker to risk of different orders does not conform with the M model, or with the CPT model for risks of order two, given the DM could switch her preference depending on the task at hand.

Some results are at odds with the EUT paradigm. First, subjects classified as risk averse and temperate are less than half than the total number of temperate subjects. Second, the number of subjects classified as prudent is around half than those classified as both risk averse and risk seeking, when, according to the mixed risk averse/risk loving model, all of them should be prudent. Third, we find more risk seekers that are classified as temperate than as intemperate, when according to this theory, risk seekers are intemperate. Fourth, out of the subjects classified as intemperate, the number of either prudent neutral or imprudent is larger than those that are prudent. Finally, the number of risk averse subjects that are prudent is less than those that are either neutral or imprudent. Overall, we find several results that are at odds with the predictions of the combining good with bad or good with good model. In this regard, our results are in line with those found in Bleichrodt and van Bruggen (2022).

Table 9 Frequency table of higher order preferences

The model estimation procedure is the same as the one implemented in Sect. 4. Table 10 presents the median individual M and CPT model parameter estimates and their standard deviation. The CPT parameter values of $\gamma$ and $\alpha$ do not differ much from those estimated in the previous section for the other three studies, and are within the range of values found in the literature [see Fox and Poldrack (2014)].¹⁶ To further understand the rich heterogeneity of preferences generated by the M model, it is worth noting that the number of A lottery choices varies depending on the parameter value. For instance, out of the 29 tasks, the number of A lotteries chosen by the DM would increase from 8 to 17 when, relative to the median values, $\alpha$ is one standard deviation below the median and $\eta$ is one standard deviation above the median. However, the number of A lottery choices under the CPT specification would not vary. In terms of classifying the subjects to one of the two decision models, we find that, based on the value of the Bayes Factor, 16 out of 49 (32.7%) subjects are classified as Markowitz, and 33 out of 49 (67.3%) are classified as CPT with a CRRA utility function. The statistical validity of the method applied here is examined in Appendix D.2, and the results provide reassurance about the properties of the method to identify, discriminate and estimate the two different model specifications.

Table 10 Parameter estimates

6 Conclusions

It is now widely accepted that higher order preferences play a significant role in the analysis of issues such as health, precautionary savings, asset pricing, bargaining, contests and auctions. However, although there is abundant evidence within the behavioural literature suggesting that preferences are reference dependent, little is known about the predictions of reference-dependent theories on higher order risk attitudes. The knowledge gap is even wider if the specification of the reference point within a given reference-dependent model is also to be considered. We provide two contributions that attempt to address that gap.

First, we employ recently developed elicitation methods of higher order risk attitudes to determine the higher order lottery choices of a decision maker consistent with Markowitz’s (1952) hypotheses, which we refer to as the M model. This model of utility embodied the concepts of reference-dependent utility, loss aversion and the fourfold attitude to risk over outcome magnitude. Previous studies show that the implications of the M model of utility for second order risky choices imply that the model can be a proper complement to better known models of risky choice such as CPT, RDU or EUT. Our analysis about higher order risky choices provides further support to that argument. We demonstrate that decision makers characterised by the M model can exhibit either prudent or imprudent, temperate or intemperate lottery choices dependent upon the chosen reference point (status quo, expected payout or MaxMin) and the different magnitudes of lottery payoffs. A seemingly unique characteristic of the M model is that of ‘higher order reversal.’ In discriminating between different models of risky choice, an important finding is that, from the status quo reference point, the M decision maker can make imprudent or intemperate lottery choices in the gains domain. This property differs from the representative CPT, RDU or the standard mixed-risk averse EUT, subject who will only make prudent or temperate lottery choices. This is relevant given the high proportion of imprudent and intemperate lottery choices reported in experimental research employing the status quo reference point. This is also the case when the MaxMin is the reference point. Furthermore, we also demonstrate that the M decision maker can exhibit combinations of risky choices not seemingly possible in other behavioural models.

The second contribution includes the estimation of parametric models that allow for heterogeneity of preference functionals and reference points to fit experimental data designed to elicit higher order risk preferences. In a first analysis, we employ datasets from three of the most prominent studies in this field, and estimate two choice models, the M and the CPT model (where EUT is also nested), and three alternative reference points for each of them. Our results based on hierarchical Bayesian estimation methods favoured heterogeneity of preference functionals and reference points. An extensive simulation exercise shows that this method can satisfactorily identify an assumed model specification, and discriminate among alternative ones. In a second analysis, we set out a new experiment to discriminate between M, CPT and EUT preference functionals. We implement the experiment under the status quo reference point because, following from the insights in this paper, is the reference point that provides the cleanest test among competing models. Furthermore, the tasks used in the experiment have been selected following a series of simulation exercises that confirm the discriminatory power among alternative model specifications. The results of this new experiment confirm that both models are helpful to describe risky choices across the subject pool. Overall, these two empirical analyses suggest, first, that the M model is not a replacement, but a complement to alternative, more typically employed, model specifications of decision under risk; and, second, that a one-model-fits-all approach might prove insufficient to accommodate heterogeneity of risky choices.

Appendices

Appendix A: The fourfold pattern to risk over outcome magnitude and probabilities

Cumulative prospect theory accommodates the fourfold pattern to risk over outcome probabilities, that is, as the probability increases from low to high, risk preferences change from risk seeking to risk aversion over gains, while those preferences change from risk aversion to risk seeking over losses. This is because, as Scholten and Read (2014) point out, prospect theory retained some of the notions introduced by Markowitz (1952) such as reference dependence and loss aversion, but introduced new ones such as probability weighting and a singly inflected value function. Scholten and Read provide an insightful account about the possible reasons the fourfold pattern to risk over outcome magnitude was not addressed by Kahnemann and Tversky. Furthermore, Scholten and Read (2014) contribute to this literature by showing that it is in principle possible for a CPT specification to account for both fourfold patterns. This is the case for a value function v(.) and a weighting probability function w(.) that meet the following condition for the case of a lottery that pays x with probability p and nothing otherwise ($m>1$):

$$\begin{aligned} \frac{v\left( mx\right) }{v\left( \frac{1}{p}mx\right) }>w\left( p\right) > \frac{v\left( x\right) }{v\left( \frac{1}{p}x\right) }. \end{aligned}$$

(a1)

Therefore, a necessary condition is that the value function has to be decreasingly elastic. Although this theoretical insight is certainly appealing, it faces practical limitations. The reason is that, even within decreasingly elastic value functions, inequalities (a1) are only met for a limited number of cases. We illustrate this point in Fig. 6. Following Scholten and Read, we use a normalised logarithmic value function, $v(x)= \frac{1}{a}\left( \log \left( 1+ax\right) \right) ,$ and the Tversky and Kahnemann probability weighting functions $w(p)=\frac{p^{\gamma }}{ (p^{\gamma }+(1-p)^{\gamma })^{1/\gamma }}$. We use the following range of parameter values consistent with the literature: $\alpha \in [0.01,0.1],$ $\gamma \in [0.50,0.95]$. We use a payoff value $x=25$ and $p\in [0.01,0.35]$, such that lowest expected payout is 0.25 as in Scholten and Read experimental data. The red shaded areas are the ones for which (a1) is met. Similar result is obtained for different values of m. As payoff value x is increased, the number of instances for which conditions (a1) are met decreases substantially. Actually, the largest value of x where (a1) holds is $x=40$ (shown in blue in Fig. 6).

Fig. 6

Combination of parameters for which the inequality holds $\frac{v\left( mx\right) }{v\left( \frac{1}{p}mx\right) }>w\left( p\right) > \frac{v\left( x\right) }{v\left( \frac{1}{p}x\right) }$

Appendix B: Two additional reference points: MinMax and X at Max P

In addition to the reference points considered in Sect. 3 of this paper, Baillon et al. (2020) examined two additional deterministic reference points: MinMax and X at Max P. The use of these two reference points in the literature is scarce. We are not aware of any study on higher order risk preferences, either theoretical or empirical, that employ these two reference points. Nevertheless, we present below the analytical derivations of the valuation of lottery pairs to elicit third and fourth order risky choices assuming these two reference points under two different model specifications, the M model and a CPT model.

1.1 B.1 MinMax

1.1.1 B.1.1 Third order risky choice

We recall the probabilities and outcomes of the lottery pair of order 3 are the following

$$\begin{aligned} & B_{3}:\,0.5,W+X-k_{2};\,0.25,W+X+e_{1};\,0.25,W+X-e_{1} \\ &A_{3}:\,0.5,W+X;\,0.25,W+X-k_{2}+e_{1};\,0.25,W+X-k_{2}-e_{1}. \end{aligned}$$

There are two possible reference points for this lottery pair. First, when $k_{2}\ge e_{1},$ the MinMax reference point is $W+X.$

For the M model of utility defined in (1), the expected utility of the lottery pair is

$$\begin{aligned} U(B_{3})= & {} -\lambda 0.5\left( 1-e^{-\beta (k_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1})^{\eta }}\right) \\ U(A_{3})= & {} -\lambda 0.25\left( 1-e^{-\beta (k_{2}-e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (k_{2}+e_{1})^{\eta }}\right) . \end{aligned}$$

For the CPT model, we assume a specification with a power value function, parameter $\alpha \in [0,1],$ loss aversion parameter $\lambda ,$ and an inverse-S-shaped probability weighting function, w(p), where $w^{+}(p)$ and $w^{-}(p)$ are the probability weighting functions for gains and losses, respectively. In this case, the subjective expected values, $V(\bullet )$, are the following

$$\begin{aligned} V(B_{3})= & {} w^{+}(0.25)\left( e_{1}\right) ^{\alpha }-\lambda w^{-}(0.5)\left( k_{2}\right) ^{\alpha }-\lambda \left( w^{-}(0.75)-w^{-}(0.5)\right) (e_{1})^{\alpha } \\ V(A_{3})= & {} -\lambda w^{-}(0.25)\left( k_{2}-e_{1}\right) ^{\alpha }-\lambda \left( w^{-}(0.5)-w^{-}(0.25)\right) (k_{2}+e_{1})^{\alpha }. \end{aligned}$$

Second, when $e_{1}>k_{2},$ the MinMax reference point becomes $W+X-k_{2}+e_{1}.$

For the M model, the expected utility of the lottery pair is

$$\begin{aligned} U(B_{3})= & {} -\lambda 0.5\left( 1-e^{-\beta (e_{1})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (k_{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (2e_{1}-k_{2})^{\eta }}\right) \\ U(A_{3})= & {} -\lambda 0.5\left( 1-e^{-\beta (e_{1}-k_{2})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (2e_{1})^{\eta }}\right) . \end{aligned}$$

For the CPT model, the subjective expected values are the following

$$\begin{aligned} V(B_{3})= & {} w^{+}(0.25)\left( k_{2}\right) ^{\alpha }-\lambda w^{-}(0.25)\left( 2e_{1}-k_{2}\right) ^{\alpha }-\lambda \left( w^{-}(0.75)-w^{-}(0.25)\right) (e_{1})^{\alpha } \\ V(A_{3})= & {} -\lambda w^{-}(0.25)\left( 2e_{1}\right) ^{\alpha }-\lambda \left( w^{-}(0.75)-w^{-}(0.25)\right) (e_{1}-k_{2})^{\alpha }. \end{aligned}$$

Our analysis reveals that the M DM can exhibit in both cases either prudent or imprudent choices, depending on the value of the model parameters and payoff sizes, although the imprudent choice is present for a wider range of parameter values. However, we find that the CPT DM chooses $B_3$, except if the loss aversion parameter $\lambda$ exceeds extreme values such as 6.

1.1.2 B.1.2 Fourth order risky choice

The payoffs of the two zero-mean independent risks can be different, $e_{2}>e_{1}.$ In this case, we recall the probabilities and outcomes of the two lotteries are the following

$$\begin{aligned} B_{4}&:&\,0.25,W+X+e_{2};\,0.25,W+X+e_{1};\,0.25,W+X-e_{1};\,0.25,W+X-e_{2} \\ A_{4}&:&\,0.5,W+X;\,0.125,W+X+e_{2}+e_{1};\,0.125,W+X+e_{2}-e_{1}; \\{} & {} 0.125,W+X-e_{2}+e_{1};\,0.125,W+X-e_{2}-e_{1}. \end{aligned}$$

The MinMax reference point is $W+X+e_{2}.$

For the M model, the expected utility values of the lottery pair are given by

$$\begin{aligned} U(B_{4})= & {} -\lambda 0.25\left( 1-e^{-\beta (e_{2}-e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{2}+e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (2e_{2})^{\eta }}\right) \\ U(A_{4})= & {} -\lambda 0.5\left( 1-e^{-\beta (e_{2})^{\eta }}\right) +0.125\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.125\left( 1-e^{-\beta (e_{1})^{\eta }}\right) \\{} & {} -\lambda 0.125\left( 1-e^{-\beta (2e_{2}-e_{1})^{\eta }}\right) -\lambda 0.125\left( 1-e^{-\beta (2e_{2}+e_{1})^{\eta }}\right) . \end{aligned}$$

For the CPT model, the value of the prospects are given by

$$\begin{aligned} V(B_{4})= & {} -\lambda w^{-}(0.25)(2e_{2})^{\alpha }-\lambda \left( w^{-}(0.5)-w^{-}(0.25)\right) (e_{1}+e_{2})^{\alpha }-\lambda \left( w^{-}(0.75)-w^{-}(0.5)\right) (e_{2}-e_{1})^{\alpha } \\ V(A_{4})= & {} w^{+}(0.125)\left( e_{1}\right) ^{\alpha }-\lambda w^{-}(0.125)\left( 2e_{2}+e_{1}\right) ^{\alpha }-\lambda \left( w^{-}(0.25)-w^{-}(0.125)\right) \left( 2e_{2}-e_{1}\right) ^{\alpha } \\{} & {} -\lambda \left( w^{-}(0.75)-w^{-}(0.25)\right) \left( e_{2}\right) ^{\alpha }-\lambda \left( w^{-}(0.875)-w^{-}(0.75)\right) \left( e_{1}\right) ^{\alpha }. \end{aligned}$$

Our analysis reveals that the M DM can exhibit either temperate or intemperate choices, depending on the value of the model parameters and payoff sizes, although the intemperate choice is present for a wider range of parameter values. However, we find that the CPT DM makes the temperate choice.

Overall, taking into consideration both third and fourth order risky choices, we find that the predictions of the two models under this reference point are similar to the case of MaxMin.

1.2 B.2 X at Max P

1.2.1 B.2.1 Third order risky choice

In the third order lottery pairs, there is one payoff in each lottery with equal probability of 0.5. Following Baillon et al. (2020), we take as the reference point the payoff of the A lottery. Therefore, the reference point is $W+X.$

There are two cases. First, when $k_{2}\ge e_{1},$ the value of the lottery pair is the same as in the case under MinMax examine above.

Second, when $e_{1}>k_{2},$ for the M model, the expected utility of the lottery pair is

$$\begin{aligned} U(B_{3})= & {} -\lambda 0.5\left( 1-e^{-\beta (k_{2})^{\eta }}\right) +0.25\left( 1-e^{-\rho \beta (e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (e_{1})^{\eta }}\right) \\ U(A_{3})= & {} 0.25\left( 1-e^{-\rho \beta (-k_{2}+e_{1})^{\eta }}\right) -\lambda 0.25\left( 1-e^{-\beta (k_{2}+e_{1})^{\eta }}\right) . \end{aligned}$$

For the CPT model, the subjective expected values are the following

$$\begin{aligned} V(B_{3})= & {} w^{+}(0.25)\left( e_{1}\right) ^{\alpha }-\lambda w^{-}(0.25)\left( e_{1}\right) ^{\alpha }-\lambda \left( w^{-}(0.75)-w^{-}(0.25)\right) (k_{2})^{\alpha } \\ V(A_{3})= & {} w^{+}(0.25)\left( e_{1}-k_{2}\right) ^{\alpha }-\lambda w^{-}(0.25)\left( k_{2}+e_{1}\right) ^{\alpha }. \end{aligned}$$

1.2.2 B.2.2 Fourth order risky choice

The reference point under X at max P is $W+X.$ Therefore, the implications for both models are the same as under the reference point average payout described in Section 3.2.

Appendix C: Stimuli

Table 11 List of choice tasks from Deck and Schlesinger (2010)

Table 12 List of choice tasks from Deck and Schlesinger (2014)

Table 13 List of choice tasks from Noussair et al. (2014)

Appendix D: Simulations

In this appendix, we describe two extensive Monte Carlo simulation exercises and report their results. The scope of the simulations is two-fold. First, we want to confirm that the statistical method employed in the paper is able to identify the different model specifications as well as to discriminate among them. Second, we want to confirm that the tasks selected in the new experiment are useful to empirically estimate and classify subjects across the alternative choice models.

1.1 D.1 Simulation 1: Assessment of the econometric method

The objective of the first simulation exercise is to explore whether the statistical method employed here can successfully identify and discriminate among the different model specifications using the experimental designs analysed in this paper, and the model selection method we are using to classify subjects, i,e, calculation of the Bayes Factor based on the Marginal Log-Likelihood. The Bayes factor is known to balance the quality of the fit versus the model complexity, and it therefore, rewards highly predictive models and penalises models with “wasted” parameter space.

We define a specification as the combination of a decision model and a reference point. We have 2 decision models (M and CPT) and three reference points (SQ, AP and MaxMin), giving a total of 6 specifications. Depending on the value of the parameters of some of those specifications, EUT is nested within them. The simulation follows a number of steps. For each of the six specifications, and for a given set of choice tasks, we assume a set of behavioural parameters and we generate an artificial dataset consisting of the choices of 100 subjects. We subsequently run a cross-estimation exercise where all the specifications are used to estimate that dataset. For each iteration, we check whether it is possible to identify the data generating specification and recover the behavioural parameters that generated the simulated dataset. We repeat this process 100 times. For the set of behavioural parameters, we used values that fall within a range that can be considered as representative for the utility curvature, the probability weighting and the precision (noise) (see Abdellaoui et al. (2021), Noussair et al. (2014), Scholten and Read (2014)]. We have repeated the simulation exercise for various levels of noise and the results reported below remain qualitatively identical. Here we report the results of a medium value of the parameter $\phi$ that is usually observed empirically (Tables 11, 12 and 13).

The values of the parameters for all the specifications are listed in Table 14. Following the assumptions of the Hierarchical Bayesian modeling, for each iteration of the simulation, the parameters of the individual subjects are drawn from a Normal distribution centered around the true parameter values. Finally, for the set of choice tasks we are using the lotteries from DS10. The reason behind this choice is that, from all the experimental data we analyse and report in this study, the experimental design of DS10 is the less informative one as far as our objective to estimate parametric models is concerned. In particular, DS10 includes only 10 pairwise choices (6 tasks for third order and 4 tasks for fourth order risk preferences) and therefore, it is expected to be the most challenging dataset in terms of identification and estimation of the models.

Table 15 reports the mean aggregate absolute value of the Log-Marginal Likelihood for all the 36 cross-specification combinations. The specifications across the rows represent the true DGP, while the specifications across the columns represent the estimated ones. For instance, in the first row, the DGP is M/SQ and the entry in each cell of that row is the average value of the marginal likelihood when the corresponding column model is the estimated one. Across the diagonal is when the true and the estimated models coincide. Hence, if identification is feasible, one would expect the entry on the diagonal to be the smallest number for each of the rows (here a lower value of the likelihood indicates a better fit of the model). This pattern is confirmed in Table 15. In every row, the diagonal element is always the minimum, confirming that, on average, the true DGP is identified. This evidence suggests that the different specifications are not observationally indistinguishable.

Table 16 reports the pairwise comparison of specifications based on the value of the Bayes Factor. Again, the specification in the rows represent the true DGP, and the ones in the columns the estimated one. For example, in the first row, where M/SQ is the the DGP, the number of times the M/SQ was classified as the best model when each of the other specifications was assumed, is reported. As expected, the diagonal element is always 0 as the Bayes Factor is 1. Then, for instance, when M/SQ is compared to M/AP, the former was identified as the best model for each of the simulations, while when M/SQ was compared to CTP/SQ, the model was classified best in 93% of the simulations. Overall, it appears that, on average, the true DGP can be identified with confidence.

Finally, we examine whether the value of the parameters can be successfully recovered. Tables 17, 18, 19, 20, 21 and 22 report the median estimates from this cross-estimation exercise. Following the standard practice, we have constrained the upper bounds of the parameters. For the M model, we have set the upper bound of $\alpha$ to 0.1, of $\eta$ to 2 and $\lambda$ to 5. For the CPT model, we have set the upper bound of $\alpha$ and $\gamma$ to 2, and $\lambda$ to 5. For example, Table 17 reports the estimates when the true DGP is M/SQ and each of the six model specifications has been employed to estimate the dataset. The results of this table show that the recovered values are quite close to the true ones (0.041 for parameter $\alpha$ compared to the true value of 0.05, and 1.193 for the $\eta$ parameter compared to the true value of 1.200). However, when a different model specification is estimated, we obtain parameter estimates that differ substantially from the true ones. For example, $\alpha =0.000$ and $\eta =1.945$ in the case of M/AP, and $\alpha =0.098$, almost twice the true value, and $\eta =1.507$ in the case of M/MaxMin. Similarly, when CPT is estimated, we obtain large estimates for both the probability weighting function and the utility curvature, with $\gamma >1$ implying over-weighting of all probabilities, or $\alpha >1$ implying risk seeking behaviour. A similar pattern is observed for the remaining 5 cases.

Table 14 Simulation parameters

Table 15 Log-Marginal likelihoods

Table 16 Classification based on Bayes Factor

Table 17 Estimates when M/SQ is the true DGP

Table 18 Estimates when M/AP is the true DGP

Table 19 Estimates when M/MAXMIN is the true DGP

Table 20 Estimates when CPT/SQ is the true DGP

Table 21 Estimates when CPT/AP is the true DGP

Table 22 Estimates when CPT/MAXMIN is the true DGP

1.2 D.2 Simulation 2: Tasks in the new experiment

The objective of the second simulation is to assist with the selection of choice tasks to use in our experiment. The selection of the experimental tasks is based on four criteria. First, we selected lottery pairs that generated different choices across the two decision models for the majority of a wide range of model parameter values. Second, we include in the experiment choice tasks with a significant probabilistic information content. That is, for increased levels of noise in the stochastic component of choice, and for a given set of parameters, we kept those tasks that would predict choice probability in favour of a lottery of at least 60%. Third, the lottery pairs selected need to provide enough information to satisfactorily recover the parameters of the DGP. Fourth, the choice tasks selected should have discriminatory power between the two models based on the value of the pairwise Bayes Factor.

This simulation is focused on the SQ reference point because is the one we endeavoured to implement through experimental procedure as described in Sect. 5. Like we did in simulation 1, we simulate data from an either M or CPT specification, and estimate those datasets with the two possible specifications. Table 23 reports the mean aggregate absolute value of the Log-Marginal Likelihood for all the 4 cross-specification combinations. The specifications across the rows represent the true data generating specification, while the specifications across the columns represent the estimated ones. If the method correctly identifies the model, the diagonal element should be the lowest in each row, which is the case in our simulation. In addition, we find that the true DGP specification is identified 100% of the times based on the value of the Bayes Factor. Finally, Tables 24 and 25 report the parameters that have been recovered in the estimations of the simulations. The estimates are close to the true values when the DGP coincides with the assumed specification. When the true DGP is M/SQ, the parameter in the CPT value function is close to unity, suggesting linear utility and probability distortion. When the true DGP is CPT/SQ, parameter $\eta$ in the expo-power function is unity which would suggest an EUT model with exponential utility rather than the M model of utility.

Table 23 Log-Marginal likelihood

Table 24 Estimates when M/SQ is the true DGP

Table 25 Estimates when CPT/SQ is the true DGP

Appendix E Screenshot

See Fig. 7.

Fig. 7

Screenshot of the experimental interface