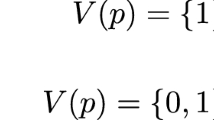Realizing impossibilities

Abstract

It is common in epistemic modal logic to model the epistemic states of agents via box operators in the normal logic S5. However, this approach treats agents as logically omniscient by requiring their knowledge to be closed under classical logical consequence. A promising way of avoiding logical omniscience consists in extending epistemic models with impossible states, that is states, where complex formulas are not evaluated recursively. However, this approach faces the dual problem of logical ignorance by modeling agents as not even minimally logically competent. In this paper I will outline an epistemic logic that combines impossible states with dynamic realization modalities akin to the dynamic announcement operators from public announcement logic (PAL). I will show that this epistemic logic avoids both the problem of logical omniscience and the problem of logical ignorance. Furthermore, I prove that so-called successful updates in my logic can be characterized in the same way as in PAL and that a similar logic due to Johan van Benthem can be simulated in my logic. Finally, I will compare my epistemic logic with a similar one, which has recently been advanced by JC Bjerring and Mattias Skipper.

1 Logical omniscience and open worlds

It is common in epistemic modal logic to model the epistemic states of agents via box operators in the normal logic $\textsf {S5}$. We quickly go through the syntax and semantics of the single agent version of $\textsf {S5}$ which will also fix notation.

For a finite or countably infinite set of propositional variables (or atoms) $\Phi$ the language of basic epistemic logic for one agent is generated by the following BNF:

$$\begin{aligned} \varphi {:}{:}{=} ~ p ~| ~\lnot \varphi ~ | ~(\varphi _1 \wedge \varphi _2)~ |~ K \varphi ~~~ ~(p \in \Phi ) \end{aligned}$$

The intended reading of $K \phi$ is that the agent knows that $\varphi$. We let an epistemic model be a tuple $M = (S, R, V)$, where $S \not = \varnothing$ is the set of epistemic states of the agent, $R \subseteq S \times S$ models the relation of epistemic accessibility and $V: \Phi \rightarrow \wp (S)$. We let an $\textsf {S5}$ epistemic model be an epistemic model, whose accessibility relation is an equivalence relation. The satisfaction relation between states and formulas in an $\textsf {S5}$ model is defined in the usual way with the clause for the K-operator being

• $M, s \models K \varphi ~ :\Leftrightarrow ~ M, t \models \varphi$, for all $t \in S$ with sRt.

Let $\varphi$ be valid in an epistemic model $M =(S, R, V)$ ($M \models \varphi$), if $M, s \models \varphi$, for all $s \in S$. Finally, we call a formula $\varphi$ valid in a class $\textsf {M}$ of epistemic models ($\textsf {M} \models \varphi$), if $M \models \varphi$, for all $M \in \textsf {M}$; in case $\textsf {M}$ is the class of all epistemic models we write $\models \varphi$, instead of $\textsf {M} \models \varphi$.

It is well known that epistemic $\textsf {S5}$ is highly unsuited for formalizing the epistemic states of agents that are resourcebounded, that is, who have limited time and memory for computing what they know.¹ The reason for this representational mismatch is that according to $\textsf {S5}$ the knowledge of agents is subject to closure conditions which require inter alia that agents know everything that logically follows from what they know. Even worse, these closure conditions already hold for the smallest normal epistemic logic $\textsf {K}$, which is characterized by the class of all epistemic models. The collection of these closure conditions can be addressed as the problem of logical omnscience. Here are some of the most salient closure conditions, which we represent as closure conditions on the set of $\textsf {K}$-validities.

• $\models K (\varphi \rightarrow \psi ) \rightarrow (K \varphi \rightarrow K \psi )~$ (Distribution)

• $\models \varphi ~ \Rightarrow ~ \models K \varphi ~$ (Knowledge of validities)

• $\models \varphi \rightarrow \psi ~\Rightarrow ~ \models K\varphi \rightarrow K \psi ~$ (Closure under valid implications)

• $\models \varphi \leftrightarrow \psi ~ \Rightarrow ~ \models K \varphi \leftrightarrow K\psi$ (Closure under valid equivalences)

• $\models (K \varphi \wedge K \psi ) \rightarrow K(\varphi \wedge \psi )~$ (Closure under adjunction)

• $\models K \varphi \rightarrow K(\varphi \vee \psi )~$ (Closure under weakening)

There are many different proposals of how best to solve the problem of logical omniscience (for a survey see Fagin (1995a), Sim (1997)). On the impossible worlds approach epistemic possibilities are not logically transparent to agents: Among the epistemic alternatives there may be some that, unbeknownst to the agent, are logically impossible in the sense of not respecting classical consequence. In particular, agents may consider states epistemically possible that verify contradictions. Technically, this approach is implemented by extending the set of states with non-standard states that do not represent models from classical propositional logic and by restricting the definition of logical notions to standard states. As non-standard states lie beyond the reach of (classical) logic it is common to call them (logically) impossible worlds (Hintikka, 1975).²

There are two main versions of the impossible worlds approach. According to the open world approach, impossible worlds are not closed under any non-trivial consequence relation.³ Consequently, impossible worlds can be taken to be arbitrary functions from formulas to (classical) truth-values (Cresswell, 1970, 1972; Rantala, 1982a, 1982; Wansing, 1989; Jago, 2014; Priest, 2016). The relevantist approach, on the other hand, holds that impossible worlds are closed under the consequence relation of some relevant logic, $\textsf {FDE}$ being the first choice among proponents of the approach. Thus, after relevantism, impossible worlds can be equated with models from the various model-theories for $\textsf {FDE}$ in existence (Levesque, 1984; Priest, 1992; Fagin, 1995b; Levesque & Lakemeyer, 2000).

Relevantist approaches are troubled by the fact that they treat agents as perfect reasoners in a relevant logic. If one is interested in representing the epistemic states of a knowledge based agent, that is a system whose knowledge is the deductive closure of a knowledge base (a finite set of purely propositional formulas), closure under relevant consequence may be acceptable. However, it is evident that the epistemic states of human agents are not closed under classical consequence nor under relevant consequence. Thus, the relevantist approach simply reproduces the problem of logical omniscience, but now with a logic weaker than classical logic (Fagin & Halpern, 1988).

Open world approaches are more promising, since they allow epistemic states to resist any non-trivial deductive closure. However, a dual problem arises here: Open world approaches seem to deprive agents of even the most basic logical competence. Let’s call  impossible worlds that are not closed under any non-trivial consequence relation open worlds. Any minimally logically competent reasoner a who knows that $\varphi \wedge \psi$, should be in a position to know $\varphi$. But not so on the open world approach, or so it appears: Suppose that open world s is an epistemic possibility of a that does not verify $\varphi$ and suppose further that every epistemic alternative of a makes $\varphi \wedge \psi$ true. On the open world approach this implies that a knows that $\varphi \wedge \psi$ and that a does not know $\varphi$. It seems to follow that open world approaches model agents that are logically ignorant, that is agents, which are not even minimally logically competent. We call this apparent consequence the problem of logical ignorance for open world approaches (Lewis, 2004), (Jago, 2014). In the next section we will propose a solution to this problem. This proposal augments the open world approach with techniques from dynamic epistemic logic.

2 DEL meets the impossible

Every adequate solution to the problem of logical ignorance must answer the question which properties of the open world approach lead to the problem and how these properties can be eliminated. My claim is that the problem arises on account of the fact that open world approaches lack the means to represent informational or epistemic actions such as observation, communication or inference. More precisely, resource bounded agents such as humans have the cognitive resources to update their epistemic states in such a way that, after the update, they can realize that worlds they took to be epistemically possible before the update are in fact logically impossible and so do not count as epistemic alternatives any more.

I call the kind of epistemic action that induces the elimination of impossible worlds realizations. Intuitively, realizations consist in recognizing that certain formulas should be true in every world, given that certain other formulas are true in all the possible worlds. Realizations may be connected to acts of inference, but I will not discuss this issue here. Realizations of formulas $\varphi$ can be formalized as dynamic modalities $[\varphi ]$ in a logic that takes a basic epistemic logic with open worlds as its static base and adds machinery from dynamic epistemic logic (DEL) on top. In particular, the dynamic component is a slight modification of the simplest dynamic epistemic logic, namely public announcement logic or $\textsf {PAL}$ (Plaza, 2008; Gerbrandy & Groeneveld, 1997; van Ditmarsch, 2008). The resulting logic will deliver validities that tell us that agents are not logically ignorant. In this way we can solve the problem of logical ignorance while at the same time avoiding logical omniscience. Here are the formal details.

We extend the language of basic epistemic logic with a clause for realization modalities. So, for a set of atoms $\Phi$ the realization language for one agent, denoted by ${\mathcal {L}}$, is given by the BNF:

$$\begin{aligned} \varphi {:}{:}{=} ~ p ~| ~\lnot \varphi ~ | ~(\varphi _1 \wedge \varphi _2)~ |~ K \varphi ~|~[\varphi _1]\varphi _2~~~ ~(p \in \Phi ) \end{aligned}$$

The intended interpretation of $[\varphi ] \psi$ is that after every realization of $\varphi$, $\psi$ holds. Let’s turn to the structures on which the realization language will be interpreted.

Definition 1

• (i) An open world frame is a tuple $F = (W, W^*, R)$ such that $W, W^*$ are sets with $W \not = \varnothing , W \cap W^* =\varnothing$ and $R \subseteq (W \cup W^*)^2$.

• (ii) A valuation on an open world frame $F=(W, W^*, R)$ is a pair $(V, V^*)$ such that $V: W \rightarrow 2^{\Phi }$ and $V^*: W^* \rightarrow 2 ^{{\mathcal {L}}}$.

• (iii) An open world model is a tupel $M =(F, (V, V^*))$, where F is an open world frame and $(V, V^*)$ is a valuation on F.

Points from the set $W \cup W^*$ are called states or worlds; points from W are addressed as possible states and the points from $W^*$ are called impossible states.

Satisfaction in states from open world models can then be defined as follows.

Definition 2

Let $M = (W, W^*, R, V, V^*)$ be an open world model.

• (i) For every $w \in W$ we set:

  • $M, w \models p ~ :\Leftrightarrow ~ V(w)(p) = 1$;

  • $M, w \models \lnot \varphi ~ :\Leftrightarrow ~ M, w \not \models \varphi$;

  • $M, w \models (\varphi \wedge \psi ) ~ :\Leftrightarrow ~ M, w \models \varphi ~ \text {and}~ M, w \models \psi$;

  • $M, w \models K \varphi ~ :\Leftrightarrow ~ M, v \models \varphi$, for all $v \in W \cup W^*$ with wRv;

  • $M, w \models [\varphi ] \psi ~ :\Leftrightarrow ~ M, w \not \models \varphi$ or $M\restriction _ {\varphi }, w \models \psi$.

• (ii) For every $w^* \in W^*$ and every $\varphi \in {\mathcal {L}}$ we let

  • $M, w^* \models \varphi ~ :\Leftrightarrow ~ V^*(w^*)(\varphi ) = 1$.

In the last clause of (i) $M\restriction _ {\varphi }$ is the submodel of M generated by the set of impossible states where $\varphi$ is true. More precisely $M\restriction _ {\varphi } =(W, W^*_{\varphi }, R_{\varphi }, V, V^*_{\varphi })$, where

• $W^*_{\varphi } = \{ w^* \in W^*: M, w^* \models \varphi \}$;

• $R_{\varphi } = R~ \cap ~(W \cup W^*_{\varphi })^2$;

• $V^*_{\varphi } = V^*\restriction W^*_{\varphi }$.

As usual, validity in models is restricted to possible states. We let $\varphi$ be valid in open world model M ($M \models \varphi$), if $M, w \models \varphi$, for every $w \in W$. $\varphi$ is valid in an open world frame F ($F \models \varphi$), if $\varphi$ is valid in every model M based on F, that is every $M =(F, (V, V^*))$ for some $(V,V^*)$ on F. $\varphi$ is valid  in a class $\textsf {F}$ of frames, if $F \models \varphi$, for every $F \in \textsf {F}$. In case $\textsf {F}$ is the class of all open world frames we write $\models \varphi$ instead of $\textsf {F} \models \varphi .$ Let’s call the resulting logic realization logic.

It is obvious that realization logic avoids the problem of logical omniscience by invalidating the epistemic closure conditions mentioned in section  1. But it also avoids the problem of logical ignorance for open world approaches. To show this, we need the following simple lemma. Let a factual formula be any formula containnig no occurrences of K or of $[\varphi ]$, for any formula $\varphi$.

Lemma 3

Let $M =(W, W^*, R, V, V^*)$ be an open world model, $v \in W \cup W^*$ and $\psi$ be factual. Then it holds that

$$\begin{aligned} M, v \models \psi \Leftrightarrow M \restriction _{\psi }, v \models \psi . \end{aligned}$$

Proof

If $v \in W$ the result follows by a straightforward induction on the structure of formulas. If $v \in W^*$ the result is immediate by the definition of $V^*$. $\square$

Now, consider the argument concerning conjunction from section  1. The argument aimed to show that on open world approaches agents may know conjunctions without being in an position to know one of the conjuncts. Realization logic, however, yields validities, which tell us that agents knowing some conjunction with factual conjuncts know either conjunct after realizing that the respective conjunct is true. This, I take it, amounts to an agent being in a position to know the conjunct: After performing a certain epistemic action, the agent knows the conjunct. So agents are not logically ignorant when it comes to conjunction reduction, at least when restricted to factual formulas. The validities showing this are the formulas

• $K(\varphi \wedge \psi ) \rightarrow [\varphi ] K \varphi$, where $\varphi$ is factual;

• $K(\varphi \wedge \psi ) \rightarrow [\psi ] K \psi$, where $\psi$ is factual.

That the first of these formuals is valid in every open world model can be shown as follows. Suppose $M, w \models K(\varphi \wedge \psi )$ and $v \in W \cup W^*_{\varphi }$ with $w R_{\varphi } v$. If $v \in W$ we have $M, v \models \varphi$ and so by Lemma 3, $M \restriction _{\varphi }, v \models \varphi$. The same follows, if $v\in W^*_{\varphi }$. So, $M, w \models [\varphi ] K \varphi$. The validity of the second formula is shown analogously.

More generally, realization logic validates the following relativized versions of the $\textsf {K}$-validities characterizing logical omniscience (again with partial restrictions to factual formulas).

Proposition 4

For every $\varphi , \psi \in {\mathcal {L}}$ it holds that:

• (a) $\models K(\varphi \rightarrow \psi ) \rightarrow (K \varphi \rightarrow [\psi ] K \psi )$, if $\psi$ is factual.

• (b) $\models \varphi ~ \Rightarrow ~ \models [\varphi ] K \varphi$, if $\varphi$ is factual.

• (c) $\models \varphi \rightarrow \psi ~ \Rightarrow ~ \models K \varphi \rightarrow [\psi ] K \psi$, if $\psi$ is factual.

• (d) $\models \varphi \leftrightarrow \psi ~\Rightarrow ~ \models [\varphi ] K \varphi \leftrightarrow [\psi ] K \psi$, if $\varphi$ and $\psi$ are factual.

• (e) $\models (K\varphi \wedge K\psi ) \rightarrow [\varphi \wedge \psi ] K (\varphi \wedge \psi )$, if $\varphi$ and $\psi$ are factual.

• (f) $\models K\varphi \rightarrow [\varphi \vee \psi ] K (\varphi \vee \psi )$, if $\varphi$ and $\psi$ are factual.

Proof

The only non-trivial case is (d). We prove its left-to-right direction. Let M be any model based on a frame F and let $M, w \models [\varphi ] K\varphi , \psi$. Furthermore, consider any $v \in W \cup W^*_{\psi }$ with $w R_{\psi } v$. We show that $M\restriction _{\psi } , v \models \psi$. If $v \in W^*_{\psi }$ the result is immediate by Lemma 3. Suppose $v \in W$. Then we have that $w R_{\varphi } v$. Since $M, w \models \psi$, it holds that $M \restriction _{\varphi }, w \models \varphi$. Two applications of Lemma 3 then yield $M\restriction _{\psi }, v \models \psi$. $\square$

Each of these relativized validities of realization logic says that agents can update their epistemic state in such a way that after the update they know the respective $\textsf {K}$-validity. In other words, although agents’ epistemic states are not subject to the closure conditions constituting logical omniscience, agents are in a position to know the validities characterizing these conditions. Thus, on our approach agents are not logically ignorant, nor are they logically omniscient.

3 Successful updates

In the present section and the next we look more closely at some of the properties of realization logic. Here we discuss successful updates, which is a standard theme in $\textsf {PAL}$ (Gerbrandy, 1998; van Ditmarsch, 2008). It is tempting to assume that after the realization of any formula, the formula holds. However, in general this is not the case. First let’s fix some terminology.

Definition 5

Let $\varphi \in {\mathcal {L}}$.

• (i) An open world model $M_1 =(W_1, W^*_1, R_1, V_1, V^*_1)$ is a submodel of open world model $M_2=(W_2, W^*_2, R_2, V_2, V^*_2)$ if the following conditions hold:

  • $W_1 \subseteq W_2$ and $W^*_1 \subseteq W^*_2$;

  • $R_1 = R_2~\cap ~(W_1 \cup W^*_1)^2$;

  • $V_1 = V_2 \restriction W_1$ and $V^*_1 = V^*_2 \restriction W^*_1$.

• (ii) $\varphi$ is closed under submodels, if for all open world models $M_1$ and all $w \in W_1 \cup W^*_1$ it holds that: If $M_1, w \models \varphi$ and $M_2$ is a submodel of $M_1$ with $w \in W_2 \cup W^*_2$, then $M_2, w \models \varphi$.

• (iii) $\varphi$ is a successful update, if  $\models ~[\varphi ] \varphi$.

Not all formulas are successful updates. For a start, note that the satisfaction of a formula that contains the K-operator can change due to the elimination of impossible worlds, where the formula in question does not hold. A simple example is the model $M =(\{w\}, \{w^*\}, \{(w, w^*)\}, V, V^*)$ with $V^*(w^*)(p) = V^*(w^*)(\lnot K p) =0$ and V arbitrary. It is evident that $M, w \models \lnot Kp$, but $M \restriction _{\lnot Kp}, w \not \models \lnot Kp$. So, $M, w \not \models [\lnot K p] \lnot Kp$.

What are conditions for a formula to be a successful update? We can give a necessary syntactic condition, which coincides with that which holds for $\textsf {PAL}$. We start with another simple lemma.

Lemma 6

Every formula closed under submodels is a successful update.

Proof

Let M be any model based on an open world frame F and let $w \in W$ with $M, w \models \varphi$. Since $M \restriction _{\varphi }$ is a submodel of M and $w \in W \cup W^*_{\varphi }$ we have that $M\restriction _{\varphi }, w \models \varphi$. $\square$

Next we define the set of formulas which will turn out to contain only formulas whose satisfaction is preserved under submodels.

Definition 7

The set of stable formulas is the least subset of ${\mathcal {L}}$ generated by the BNF

$$\begin{aligned} \varphi {:}{:}{=} p~|~ \lnot p ~|~(\varphi _1 \wedge \varphi _2)~|~K\varphi ~|~[\lnot \varphi _1] \varphi _2 ~~~~(p\in \Phi ) \end{aligned}$$

Now, we can prove the main result concerning successful updates for realization logic.

Proposition 8

Every stable formula is closed under submodels.

Proof

A straightforward induction on the structure of stable formulas. We show the case involving realization modalities. Assume towards a contradiction that $M, w \models [\lnot \psi ] \chi$ and $N, w \not \models [\lnot \psi ] \chi$, where N is a submodel of M that contains w. Since $N, w \models \lnot \psi$, the induction hypothesis implies that $M, w \models \lnot \psi$ and so $M\restriction _{\lnot \psi }, w \models \chi$. Because $N\restriction_{\lnot \psi }$ is a submodel of $M \restriction _{\lnot \psi }$ and w is contained in $N\restriction _{\lnot \psi }$, we have that $N \restriction _{\lnot \psi }, w \models \chi$. Contradiction, since $N \restriction_{\lnot \psi }, w \not \models \chi$. $\square$

Corollary 9

Every stable formula is a successful update.

4 Van Benthem’s access logic

Johan van Benthem has formulated a dynamic epistemic logic that is meant to model realizations in our sense. Indeed, our logic follows some suggestions van Benthem makes in passing as to how to reformulate his own logic more along the lines of $\textsf {PAL}$ by using impossible worlds (van Benthem, 2008, 2011). Van Benthem conjectures that the resulting logic should be equivalent with his own. In this section we show that van Benthem is wrong and that his logic can be simulated in ours. First let’s briefly outline the syntax and semantics of van Benthem’s logic, which I will call (for reasons that will become clear shortly) access logic.

The language ${\mathcal {L}}^a$ of access logic extends the language of realization logic by adding a unary sentential operator I with the syntactic clause that $I \varphi$ is a formula, for any factual formula $\varphi$. Sets that contain only factual formulas are themselves called factual. Models for the access language are tuples $M =(W, W^a, \sim \pi ,)$, where

• $W \not = \varnothing$ is set of possible states;

• $W^a \subseteq W \times \wp ({\mathcal {L}}^a)$ is the graph of a total function from states to factual sets;

• $\sim ~ \subseteq ~W \times W$ is an equivalence relation modelling epistemic indistinguishability;

• $\pi$ is a valuation sending atoms to subsets of W.

If $(w, X) \in W^a$, (w, X) is termed an access state and X its access set. Models in addition obey the restriction that epistemically indistinguishable states have the same access set: If $w \sim v$ and $(w, X), (v, Y) \in W^a$, then $X = Y$.

The recursive definition of the satisfaction relation between models, access states and formulas has the following main clauses:

• $M, (w, X) \models p~ :\Leftrightarrow ~ w \in \pi (p)$;

• $M, (w, X) \models K \varphi ~ :\Leftrightarrow ~M, (v, X) \models \varphi$, for all $v \in W$ with $w \sim v$;

• $M, (w,X) \models I\varphi ~ :\Leftrightarrow ~ \varphi \in X$ and $M, (w, X) \models \varphi$;

• $M, (w, X) \models [\varphi ] \psi ~ :\Leftrightarrow ~ M, (w, X) \not \models K \varphi$ or $M \restriction ^a_{\varphi }, (w, X \cup \{\varphi \}) \models \psi$.

Here, for an access model $M =(W, W^a, \sim , \pi )$, let

$$\begin{aligned} M \restriction ^a_{\varphi } :=(W, \{(v, Y \cup \{\varphi \}): (v, Y) \in W^a \}, \sim , \pi ). \end{aligned}$$

Additionally, the satisfaction relation is subject to the requirement that $M, (w, X) \models \psi$, for all $\psi \in X$, which we call the access requirement. Validity of formulas in an access model is defined as satisfaction in every access state of the model.

Some remarks may be in order: First $I \varphi$ has as its intended interpretation that the agent is explicitly informed that $\varphi$, while $K\varphi$ is to be understood as saying that the agent is implicitly informed that $\varphi$. Secondly, access states are ways in which the agent cognitively accesses epistemic states, the access consisting in factual formulas that represent aspects of the state for the agent. Finally, note that under the access requirement the satisfaction conditions of formulas of the form $I \varphi$ can be simplified to $M, (w, X) \models I\varphi$ iff $\varphi \in X$.

Obviously, implicit information is subject to logical omniscience. Explicit information, on the other hand, can easily avoid any of the omniscience closure conditions simply by syntactically filtering out unwanted formulas. In addition, access logic can solve the problem of logical ignorance by providing validities that tell us that agents can extend their access to states in such ways as to know the omniscience formulas in question. For instance, the following restriction of the distribution axiom is valid in all access models.

$$\begin{aligned} K(\varphi \rightarrow \psi ) \rightarrow (K \varphi \rightarrow [\psi ] I\psi ), \end{aligned}$$

where $\psi$ is factual.

So, access logic appears to be similar to realization logic. However, these logics are not equivalent, contrary to what van Benthem conjectured. To see this note that the following recursion axiom is valid in every access model.

$$\begin{aligned} {[}\varphi ] K\psi \leftrightarrow (K \varphi \rightarrow K[\varphi ] \psi ) \end{aligned}$$

While the left-to-right direction is valid in every open world model, this is not the case for the right-to-left direction. Here is a counter model: Let $M =(\{w\}, \{w', w'', w'''\}, R, V , V^*)$ with $wRw', wRw'', wRw'''$ and $V^*(x)([p]q) = V^*(x)(p) =1$, for $x = w', w'', w'''$ and $V^*(w')(q) =0$.

Even though realization logic and access logic are not equivalent in the sense of having exactly the same validities in the intersection of their languages, we may ask whether the logics can simulate each other.More precisely: Does every access model induce an open world model such that both have exactly the same validities from the access language? And conversely, does every open world model induce an access model such that both models validate the same formulas from the realization language? We can answer the first question in the affirmative; the second is still open.

The proof that follows will proceed by induction on a complexity measure that is standardly used in completeness proofs for $\textsf {PAL}$ (van Ditmarsch, 2008).

Definition 10

Let $c: {\mathcal {L}}^a \rightarrow {\mathbb {N}}$ be defined by recursion as follows:

• $c(p) = 1$;

• $c(\lnot \varphi ) = 1 + c(\varphi )$;

• $c(\varphi \wedge \psi ) = max\{ c(\varphi ), c(\psi )\}$;

• $c(K \varphi ) = 1 + c(\varphi )$;

• $c( I\varphi ) = 1 + c(\varphi )$;

• $c([\varphi ] \psi ) = (4+c(\varphi )) \cdot c (\psi )$.

It is easy to show that the ordering of ${\mathcal {L}}^a$ induced by this complexity measure preserves the subformula ordering of this language.

Now, we can turn to the embedding result.

Proposition 11

Every access model M induces an open world model $M'$ such that for all $\varphi \in {\mathcal {L}}^a$ we have:

$$\begin{aligned} M \models \varphi ~\Leftrightarrow ~ M' \models \varphi . \end{aligned}$$

Proof

For any access model $M =(W, W^a, \sim , \pi )$ let $M' =(W, W^*, R, V, V^*)$ with

• $W^* ~=~ W^a$;

• $R ~= ~\sim \cup ~ \{ (w, (v, X)): (v, X) \in W^a~ \text {and}~ w \sim v\}$;

• $V(p)(w)~ = ~1 ~ :\Leftrightarrow ~ w \in \pi (p)$, for every $w \in W$;

• $V^*(\varphi )(w, X) ~= ~1~:\Leftrightarrow ~ M, (w, X) \models \varphi$, for every $(w, X) \in W^*$.

We can then define satisfaction in states from $M'$ as follows. Let $M', (w, X) \models \varphi ~:\Leftrightarrow ~ V^*(\varphi )(w, X) = 1$. For every $w \in W$:

• $M', w \models p ~:\Leftrightarrow ~ V(w)(p) =1$;

• $M', w \models \lnot \varphi ~ :\Leftrightarrow ~ M', w, \not \models \varphi$

• $M', w \models (\varphi \wedge \psi ) ~ : \Leftrightarrow ~ M', w \models \varphi , \psi$;

• $M', w \models K \varphi ~ : \Leftrightarrow ~ M', v \models \varphi$, for all $v \in W \cup W^*$ with wRv;

• $M', w \models I \varphi ~:\Leftrightarrow ~ M', w \models \varphi$ and $\varphi \in X$, for the unique X with $(w, X) \in W^*$.

• $M', w \models [\varphi ] \psi ~ : \Leftrightarrow ~ M', w \not \models K \varphi$ or $M'^a\restriction _{\varphi }, w \models \psi$.

Here, $M'^a \restriction _{\varphi } = (W, \{ (w, X \cup \{ \varphi \}): (w, X) \in W^*\}, R_{\varphi }, V, V^*_{\varphi })$, where $R_{\varphi }$, $V^*_{\varphi }$ are the obvious restrictions.

By induction on the complexity of access formulas $\varphi$ we show that for all $w \in W$:

$$\begin{aligned} M, (w,X) \models \varphi ~ \Leftrightarrow ~ M', w \models \varphi . \end{aligned}$$

The base case $c(\varphi ) = 1$ is trivial. Suppose that $c(\varphi ) = n +1$ and that the result holds for all formulas $\psi$ with $c(\psi ) \le n$. If $\varphi$ is a negation, a conjunction or has the form $I\psi$, the result follows straightforwardly from the induction hypothesis. Let $\varphi$ have the form $K \psi$ and assume that $M, (w,X) \models K \psi$ and that $v\in W \cup W^*$ with wRv. If $v \in W$, we have $w \sim v$ and so by the induction hypothesis it follows that $M', v \models \psi$. If $v \in W^*$, we have $v =(v', Y) \in W^a$ and $w \sim v'$. By the induction hypothesis this implies that $M', v \models \psi$. The other direction is shown similarly. Finally assume that $\varphi$ has the form $[\psi ] \chi$. Let $M, (w,X) \models [\psi ] \chi$ and $M', w \models K \psi$. Since $c(K \psi ) < c([\psi ]\chi )$ the induction hypothesis implies that $M, (w, X) \models K \psi$. So, $M^a\restriction _{\psi }, (w, X \cup \{ \psi \}) \models \chi$. Since $c(\chi ) < c([\psi ] \chi )$ the induction hypothesis implies that $M'^a \restriction _{\psi }, w \models \chi$. So, $M', w \models [\psi ] \chi$. The other direction is shown analogously. $\square$

It may be conjectured that realization logic can be simulated in access logic as well. The reason for this conjecture lies in two facts: Firstly, as van Benthem himself points out (van Benthem, 2011), access logic is a dynamization of the general awareness logic of Fagin and Halpern (1988). Realization logic itself is a dynamization of the open world approach. Secondly, it is an established result that the general awareness approach and the open world approach can simulate each other (Wansing, 1990; Thijsse, 1993). Future work has to show whether the conjecture concerning access logic and realization logic is correct.⁴

5 Bjerring and Skipper’s logic

The idea that non-omniscient yet non-ignorant agents are best modeled via epistemic logics that combine impossible worlds with techniques from dynamic epistemic logic is not entirely new. Although a relative newcomer to the scene of epistemic logic, the idea has already been spelled out in a variety of different logical systems (Rasmussen, 2015; Bjerring & Skipper, 2018; Solaki, 2019, 2022).⁵ In this section I situate realization logic with respect to this research. However, since these logics involve a certain amount of mathematical complexity and space limitations should not be overextended, it is not possible to compare realization logic with all of these in a way that would do each of them justice. Instead, I will contrast realization logic with one of the most influential systems among those mentioned, namely the logic advanced by Bjerring and Skipper in Bjerring and Skipper (2018).⁶

Bjerring and Skipper’s logic (in what follows abbreviated by ‘BS logic’) combines an open world approach with machinery from dynamic epistemic logic in order to model non-omniscient agents that are logically competent. Logical competence is intuitively spelled out via a notion of trivial consequence that is relative to deductive resources. The deductive resource of an agent is determined by a pair consisting of a set of inference rules R and a natural number n, where n is the greatest natural number m, such that the agent can easily perform m inference steps by applying rules from R. A formula $\varphi$ is then defined to be a trivial logical consequence from a formula set $\Sigma$ relative to a resource (R, n), if $\varphi$ can be deduced from $\Sigma$ by at most n applications of inference rules from R. Finally, an agent a with associated resource (R, n) is defined to be logically competent, if a can deduce $\psi$, where $\psi$ is any formula that is a trivial consequence of a’s belief set relative to (R, n).

To formalize this intuitive notion of logical competence the language of basic epistemic logic is extended by countably infinitely many deduction operators to the language ${\mathcal {L}}^{BS}$ of BS logic:

$$\begin{aligned} \varphi {:}{:}{=} ~ p ~| ~\lnot \varphi ~ | ~(\varphi _1 \wedge \varphi _2)~ |~ B \varphi ~|~\langle n \rangle \varphi ~|~~[n] \varphi ~~~~ ~(p \in \Phi , n \in {\mathbb {N}}) \end{aligned}$$

Here, B is a belief operator and the intended reading of $\langle n \rangle \varphi$ ($[n] \varphi$) is that after some (every) sequence of n inference steps, $\varphi$ holds.

Turning to semantic matters, let a doxastic model for one agent be a tupel $M =(W^p, W^i, f, V)$, where

• $W^p, W^i$ are non-empty sets of possible and impossible worlds, respectively, and $W := W^p \cup W^i$;

• $f: W \rightarrow {\wp}(W)$ is an accessibility function sending every world to the set of worlds that are doxastic alternatives for the agent;

• $V: W\rightarrow {\wp}({\mathcal {L}}^{BS} )$ is a valuation function.

${\wp}(W)$ To define the semantic clauses for the deduction modalities, we need some definitions. Let $\Sigma \cup \Gamma \cup \{\psi \} \subseteq {\mathcal {L}}^{BS}$. Say that $\Sigma \vdash ^n_R \psi$, if the agent can deduce $\psi$ from $\Sigma$ in at most n steps via rules from R (where (R, n) is the resource of the agent). Let $\Sigma \vdash ^n_R \Gamma$, if $\Sigma \vdash ^n_R \psi$, for all $\psi \in \Gamma$. For a doxastic model M, any $w \in W$ and $n \in {\mathbb {N}}$ define the n-radius of w by

$$\begin{aligned} w^n := {\left\{ \begin{array}{ll} \{w\}, &{}\text {if}~ w \ W^p; \\ \{w' \in W^i: V(w) \subseteq V(w') \wedge V(w) \vdash ^n_R V(w')\}, &{} \text {if}~ w \in W^i. \end{array}\right. } \end{aligned}$$

The elements of $w^n$ are the n-expansions of w. Note that impossible worlds can have more than one n-expansion.

For a doxastic model M let $C: {\wp}({\wp}(W)) \rightarrow {\wp}({\wp}(W))$ be a function, called a choice function, such that, for all $X \subseteq {\wp}(W)$ we have: C(X) is the set of all choice sets for X, if X is a set of non-empty and pairwise disjoint sets; otherwise, let $C(X) = \varnothing$.⁷ Deduction modalities $\langle n \rangle , [n]$ are interpreted via relations $\sim ^n$ between pointed doxastic models, that is, pairs (M, w) consisting of doxastic models M and worlds $w \in W$. The idea is that pointed models characterize doxastic states of an agent and that $(M, w) \sim ^n (M', w')$, if $(M', w')$ is a doxastic state that the agent can reach from the state (M, w) by performing at most n inferential steps. This idea is captured formally by letting $(M, w) \sim ^n (M', w')$, if the set of doxastic alternatives of w in M is replaced by a choice set of the n-expansions of these alternatives. If $M=(W^p, W^i, f, V)$ and $w \in W$, let $g: W \rightarrow {\wp}(W)$ be an (w, n)-variation of f, if for every $v \in W$ we have:

$$\begin{aligned} g(v) := {\left\{ \begin{array}{ll} c, &{}\text {if}~v=w; \\ f(v), &{} \text {else}, \end{array}\right. } \end{aligned}$$

where $c \in C(\{ u^n: u \in f(w)\})$. ${\mathcal {F}}^n(M, w)$ denotes the set of all (w, n)-variations of f. Finally, let $M =(W^p, W^i, f, V)$, $M'=(W'^p, W'^i, f', V' )$, $w \in W$ and $w'\in W'$. Then define $(M, w) \sim ^n (M',w')$ iff $w = w'$, $W = W'$, $V=V'$ and $f' \in {\mathcal {F}}^n(M, w)$. In the definition of the satisfaction relation between worlds and formulas the belief operator and the boolean connectives are treated analogously to the case of realization logic. As regards deduction modalities, a pointed model (M, w) satisfies $\langle n \rangle \varphi$ ($[n] \varphi$) iff $\varphi$ is satisfied in some (every) $\sim ^n$-successor of (M, w). Logical consequence is defined as preservation of satisfaction in every possible world from every doxastic model.⁸

For BS logic we can prove the following result:

• If $\{ \varphi _1, \ldots , \varphi _n \} \vdash ^n_ R \varphi$, then $\{B\varphi _1, \ldots , B\varphi _n\} \models \langle n \rangle B \varphi$,

where $\models$ denotes logical consequence as defined above. It is evident that BS logic can model non-omniscient agents. The result above is supposed to show that BS logic also captures logical competence. Assume that (R, n) is the resource of the agent, (M, w) satisfies $B \varphi$, for some $w \in W^p$, and $\varphi \vdash ^n_R \psi$. By the result it then follows that (M, w) satisfies $\langle n \rangle B \psi$. Thus, according to BS logic, agents have the ability to believe formulas ‘immediately’ (that is, after performing some easy inference steps) which trivially follow from their beliefs.

Let’s turn to a comparison between BS logic and realization logic, which will also highlight some shortcomings of the former. Firstly, the semantics for the deduction modalities of BS logic involves what in the AI literature is sometimes called a syntactic approach (Levesque, 1984): The satisfaction conditions of deduction formulas essentially refer to syntactic objects like formulas and inference rules. That’s because the $\sim ^n$-successors of pointed models (M, w) are determined by the set of n-radii of the doxastic alternatives to w and every such n-radius is in turn determined by the resource (R, n) of the agent. In contrast, realization logic appeals only to non-syntactic objects when it comes to the satisfaction conditions of realization formulas. After all, the submodels where the operand formulas of realization modalities are evaluated are just tupels of sets.

Sometimes it is objected to syntactic approaches that they make ad hoc assumptions about what syntactic objects are assigned to what agents as their deductive resources or as their objects of belief (Levesque, 1984). However, every serious logic that tries to avoid logical omniscience uses a semantics for epistemic or doxastic operators that involves syntactic objects to a more or less apparent degree: Awareness logics use awareness functions, which output sets of formulas, impossible world approaches use impossible states that may be formally equated with sets of formulas⁹ and syntactic approaches use syntactic entities as deductive resources or as objects of knowledge or belief.

Secondly, in BS logic the semantics of the deduction modalities is evidently much more complex than the semantic treatment of realization modalities in realization logic. This property of BS logic is potentially problematic as it may complicate the study of its metalogical features such as expressiveness, succinctness or computational complexity. The same aspect of BS logic could also limit its use as an applied logic to describe resource bounded reasoning. For the relative complexity of the semantics makes model building much more difficult than in the case of realization logic.

Thirdly and relatedly, the usual formalisms of dynamic epistemic logic use model transformations that are familiar from classical model theory and that therefore are well understood mathematically. Realization logic sticks to this way of formalizing dynamics by using a simple mechanism of submodel construction. BS logic, on the other hand, employs model transformations whose model theoretic underpinnings are not entirely clear (at least to me). This has to do with the liberal use of choice functions in BS logic. Bjerring and Skipper seem to presuppose that in their semantics choice functions never output the empty set. But this is the case only if, for every world w, the set containing exactly the n-radii of successors of w is a set of non-empty and pairwise disjoint sets. It is clear that every n-radius of any world is non-empty. However, it is not straightforward to see that a situation never occurs, where the set of n-radii of successors has the form $\{ \{w \} , \{w, v\}, \{v \}\}$, for some worlds w, v with $w \ne v$. Such a set does not admit a choice set.

The conceptual idea behind BS logic, namely that logically competent agents can update their doxastic states via deduction actions, is a very promising one. Nonetheless, I think that the formalism Bjerring and Skipper use to implement the idea is not optimal. It is worth pointing out that there are regular dynamic logics used in AI, such as descriptive dynamic logic (Sierra et al., 2002), that are specifically designed to model deduction actions via program modalities and that are easily adaptable to an open world approach. Indeed, I have recently worked out an epistemic logic that combines open worlds with machinery from descriptive dynamic logic that allows a simple proof of Bjerring and Skipper’s central result mentioned above. This logic has a comparatively simple semantics and is based on well understood mathematical formalisms (Mai, 2022).

6 Coda on hyperintensionality

What is the hyperintensional picture that emerges from the current approach? I take propositions to be entities that play certain roles, like being the meanings of declarative sentences and being the primary truth bearers. Let’s call a proposition hyperintensional, if its identity is not determined by its truth-conditions. Now, there has been a lot of philosophical debate on whether propositions are hyperintensional and what hyperintensionality precisely consists in. I think that the intuitive notion of proposition is a quite messy one with different conceptual desiderata pulling in different directions. It is questionable that we can single out one precisely defined kind of objects comprising all and only the propositions (Lewis, 1986).

My take is that we may choose to model propositions in different ways, depending on the context and our interests. In the case of propositions expressed by attitude reports there are many contexts where we are interested in the linguistic ways speakers express their attitudes. In these contexts we should regard the propositions expressed by the attitude reports in question as hyperintensional propositions. My favourite way of modeling hyperintensional propositions that are attitude contents is to treat them as sets of possible or impossible worlds and that may well be the best modeling we have at present.

However, there are also contexts, where the choice of words speakers use to give voice to their attitudes is immaterial to our interests. In these cases we may model the attitude contents expressed as coarse-grained objects such as sets of possible worlds. Different types of propositions are suited for different purposes and I do not see why we should favour one type over all the others. So, according to the present approach attitude reports at least sometimes report attitude relations to hyperintensional propositions, which are sets of possible or impossible worlds. Realization logic is meant to model the reasoning of resource bounded agents regarding some of these attitude relations.