On the heuristic power of mathematical representations

Abstract

I argue that mathematical representations can have heuristic power since their construction can be ampliative. To this end, I examine how a representation (a) introduces elements and properties into the represented object that it does not contain at the beginning of its construction, and (b) how it guides the manipulations of the represented object in ways that restructure its components by gradually adding new pieces of information to produce a hypothesis in order to solve a problem.

In addition, I defend an ‘inferential’ approach to the heuristic power of representations by arguing that these representations draw on ampliative inferences such as analogies and inductions. In effect, in order to construct a representation, we have to ‘assimilate’ diverse things, and this requires identifying similarities between them. These similarities form the basis for ampliative inferences that gradually build hypotheses to solve a problem.

To support my thesis, I analyse two examples. The first one is intra-field (intra-mathematical), that is, the construction of an algebraic representation of 3-manifolds; the second is inter-fields, that is, the construction of a topological representation of DNA supercoiling.

1 Introduction

Mathematical representations and their role in scientific understanding have been increasingly investigated in the last few decades. These investigations examine several kinds of representations, such as visualizations¹, diagrams², icons³, notations⁴, and modes of representation in general⁵. Moreover, these investigations shed light on crucial properties of mathematical representations such as their faithfulness and partiality⁶, the manipulations⁷ that they involve, and the kind of epistemic gain that they enable⁸.

This paper focuses on three crucial questions underlying these investigations. The first one is the heuristic power of representations. I show how the construction of a representation can be ampliative since a representation introduces elements and properties into the represented object that it does not contain at the beginning of this construction, enabling the production of hypotheses to solve a problem. I focus on the kind of epistemic gain that mathematical representations enable. Most of the literature cited here characterises this gain in ‘economic’ terms: using representations provides us with a more efficient way (e.g., a smaller number of actions) of acquiring pieces of knowledge that could have been achieved less efficiently (e.g. a greater number of actions). In this paper I set out to show that we can characterize such an epistemic gain in terms of novelty⁹: there are cases where specific representations enable us to discover genuinely new pieces of knowledge that could have not been achieved without employing those specific representations. Two case studies are provided to support this claim (§2).

The second question is about the nature of the manipulations involved in a representation. Here, I focus on a less explored subject. Most of the literature cited above focusses on the manipulations that are performed on the representation in order to achieve knowledge about the represented object. In this paper I set out to shed light on those manipulations of the represented object using the features of the adopted representation. Those manipulations enable us to attribute new elements and relations to the represented object and are essential to drawing up hypotheses to solve a problem.

Thirdly, I argue that this process is inferential in nature: those manipulations involve ampliative inferences that guide the tentative construction of a mathematical representation designed to solve a determined problem.

Thus, in this paper I argue that mathematical representations can have ampliative power by examining at a fine-grained level their ampliative way of working both intra-field and inter-fields (Darden-Muall, 1977).¹⁰ In addition, I argue that the construction of a representation is inferential as it employs ampliative inferences (e.g. Cellucci, 2013), that is, non-deductive inferences such as analogies, inductions, and combinations thereof.¹¹

1.1 Repraesentans, repraesentatum, and mathematics

The two parts involved in a representation, the repraesentans (the representation) and the repraesentatum (the represented object), can be very different and, in a sense, they must be. As already theorized by Plato with the argument of the ‘imperfect resemblance’ and the paradox of the ‘two Cratyluses’ (Cratylus, 431c-433b, see also Sedley, 2003), a perfect isomorphism is not possible because it implies the ‘paradox of the duplicate’, that is, we will produce not a representation of a given thing, but rather a perfect duplicate.¹² Since the repraesentans and the repraesentatum are necessarily different, Plato maintains that an omission or addition does not prevent a representation from being a representation of a given object (see e.g. Ademollo, 2011). That is, representations can work not only in a subtractive, but also in an additive way.¹³

This implies that a representation is always selective: it requires a choice, a trade-off, between the features to show or disregard. The selection depends on the aim of a representation, and therefore a representation is never neutral or passive: while something is lost in representation, something else can be gained since we can add new features to the repraesentatum by means of a suitably chosen repraesentans. There is always an intention behind a representation.

It is useful to make a distinction here. On the one hand there is the selection of which known properties of the repraesentatum to show in the representation; on the other, there is the construction of new elements in the repraesentatum that might allow new actions or manipulations and consequently new inferences about the represented object. Not only are representations always partial and selective but they can involve the manipulations of certain features of the repraesentatum in order to regard it as equivalent, isomorphic, or equal to the repraesentans under a given viewpoint.¹⁴

1.1.1 Representations and assimilations

In order to construct a mathematical representation and to consider objects that can be very different in nature as equivalent, isomorphic, or equal under a given viewpoint, we have to assimilate them (see Thomas, 2011). Thomas stresses that even if an assimilation fails or is misleading, it permeates and regulates mathematical practice¹⁵: “we can assimilate anything we want to anything else we want; it just means ignoring the differences” (Ibid., 365) and “the result of our doing this, which we do with all of our concepts, is to create what I call assimilation classes” (Ibid.). In more detail, Thomas notes that:

• (i) Mathematics operates on the basis of a ‘principle of assimilation’, which is a sort of methodological principle that allows us to safely ignore the differences between the objects we assimilate.

• (ii) Assimilation is useful since it meets a basic principle of economy in scientific inquiry. From a human point of view, most objects have an infinite number of characteristics, most of which are irrelevant to the goal of a particular inquiry. And so objects that do not differ in ways that are pertinent to the goal can be assimilated. But this depends on a carefully judged combination of salience and relevance.

• (iii) This is highly context-sensitive since it is obviously relative to one’s goals.

Now, I argue that the very first step of an assimilation requires identifying, typically at an informal level, similarities between elements and properties of different objects in order to consider them as equivalent, isomorphic or equal under a certain viewpoint.¹⁶

More precisely:

• a. An assimilation draws on similarity¹⁷: assimilating diverse objects requires finding similarities between them, which depends on the way we connect and represent them.

• b. This implies the adoption of a viewpoint, which is obtained from the problem to solve and its subproblems.

A finer-grained characterization of assimilation requires taking the role of representations into account. This means that we also must consider the role of the repraesentatum and not only that of the repraesentans in the analysis of the process aiming to treat them as equivalent in some way when solving a problem. To develop an assimilation, we could also perform certain manipulations and inferences on the repraesentatum in order to construct elements that can reproduce properties or relations in the repraesentatum that are analogous to those of the repraesentans. This gives mathematical representations a great heuristic power, since in this way they introduce new features into the repraesentatum and do not only select certain known features to express and make visible in the repraesentans. In this case, the adopted repraesentans is crucial to suggesting what features can be added to the repraesentatum and how to do it.

For instance, when we use algebra to solve a problem in topology, we aim at assimilating elements belonging to these two distinct domains. To this end, we can design and add new elements in topology, like simple points, sets of paths, or loops, because they enable us to reproduce certain algebraic structures and their relations into a topological space like a 3-manifold (see e.g. §2.1). Thus, the algebraic representation suggests how to adapt a topological space in a way that makes its elements and relations treatable analogously to how an algebraic structure treats its own elements and relations. Of course, this does not tell us exactly how and what elements to design or draw in a repraesentatum, a topological space X, but it does suggest and delimit what they should be like in order to achieve this goal. Therefore, once we have added certain elements to a topological space, like a basepoint and sets of loops, we can build over them other functions (e.g. an orientation for loops or their composition on a basepoint), making it possible to build more articulated structures that are the analogue of the algebraic ones (e.g. a semi-group or a group). We can use them to approach a solution to a problem to solve in topology, for example to find invariants to tell 3-manifolds apart. That is, we produce similarities that can be the basis for ampliative inferences (e.g. analogies or inductions) that gradually structure a hypothesis to solve the problem.

1.1.2 Representations’ faithfulness

Especially in science, these characteristics of a representation raise the question of the faithfulness of a representation and how to choose one specific representation over another (see e.g. Frigg and Nguyen, 2016). One way of dealing with this issue in science and mathematics is to employ the notion of relevance (e.g. Bueno, 2016). In effect, a specific representation like a diagram does not need to convey faithfully every aspect of the relations between the relevant mathematical objects, but it is crucial that the central, relevant relations are properly displayed in the diagram; instead, the non-relevant relations need not be properly represented at all, and diagrams often knowingly misrepresent many unimportant features of the objects under consideration.

Here, of course, the problem is how to identify these relevant relations—and do it in a rational way. The adequacy of this selection varies according to its purpose and in science the relevance depends, in the first place, on the goal of our inquiry, which is given by the problem we are trying to solve.¹⁸ To mention a simple example, to represent planets as points on a Cartesian coordinate system can be convenient for calculating the trajectory of an interplanetary trip, but not for calculating how to land on a specific point on one of those planets.

It is worth noting that we have an additional issue here. Since a mathematical representation contains a partial interpretation (explicit or not) of the elements involved in a problem to solve, the selection of relevant properties can be opportunistic. This means that we could consider certain properties as relevant or salient because they can be approached and expressed by known mathematical formalisms and not because we think that they are the most relevant for solving a problem.¹⁹ In other words, a selection of variables for a given problem identifies certain features as pertinent or prominent for solving a problem because they can be approached by means of the available mathematical apparatus.

A more detailed characterization of ‘faithfulness’ is advanced by Carter (2018, 2019), who defines it in terms of heuristic power and manipulations.²⁰ She maintains that when certain objects “are manipulated so that new relations become visible, [it] gives rise to a faithful representation” (Carter, 2019, 4013). In more detail, a faithful representation is one that:

• “represents as either an image (resembling what it stands for) or as a metaphor (sharing some underlying structure) […] certain relevant relations” (Ibid.) and,

• “manipulations on the representations respect manipulations on the objects they represent, so that new relations may be found” (Ibid.).²¹

Carter argues that representations produce an epistemic gain in this way, and she offers diagrams as a paradigmatic example in virtue of their two unique features:

• i) they exhibit the type of relation, that is, they show that a relation exists rather than simply stating in words that it exists.

• ii) they present multiple relations in a single diagram.

For instance, in the case of C*-algebras (Carter, 2018), representations based on graphs can be produced and manipulated so as to reveal relations on the represented object: “the representations of graphs become concrete objects that can be manipulated, or experimented on, in order to obtain knowledge about C*-algebras” (Ibid., 185). In particular, Carter argues that they present relevant information in a more tractable way than other representations: a diagram can require a smaller number of actions than a formal presentation in accomplishing a specific task.²² Thus, the epistemic gain provided by diagrammatic representations is ‘economic’ in nature, and hence a representation has heuristic power in the sense that it allows us to solve problems in a more efficient way. We can define it as a ‘weak’ form of heuristic power as compared to a ‘strong’ form. As a matter of fact, the construction of a repraesentans can be characterized in a strong heuristic way, that is, in terms of novelty and not only in terms of efficiency, for there are cases where it enables us to discover genuinely new pieces of knowledge that are not accessible otherwise. In these cases, a specific representation can bring new features and constraints into the repraesentatum that are essential to solving a problem, and that enable the construction of new elements in the repraesentatum that allow new actions or manipulations and consequently new inferences about it.

1.1.3 Manipulations of the repraesentatum

These actions and inferences are proposed in the first place using the information content embedded in the adopted repraesentans, that is its specific set of elements, properties, and functions. Since different representations do not convey the same information content and handle the repraesentatum in different fashions, they can change the repraesentatum suggesting different operations and inferences for it. This step is typically informal, material and goal oriented. For example, determining specific points on a 3-manifold and connecting them with simple paths or determining a single point and using it as a base for loops (see §2.1) serves the goal of providing an increasingly better basis for taking the information content contained in the formal algebraic structures and making it applicable to 3-manifolds.

These actions are preliminaries to certain structures and inferences whose aim is bringing the information content of the repraesentans and its formal apparatus (e.g. algebra) into the repraesentatum (e.g. 3-manifolds). Naturally, the proposed actions and inferences can turn out to be inadequate to achieve the desired goal, so we must abandon or refine them.

It is in this sense that representations are heuristic and ampliative. They are heuristic because they provide the means to solve a problem in the form of a hypothesis with specific information content that is gradually regulated by the adopted repraesentans. They are ampliative because they bring new knowledge and information into the represented object by (re)structuring its elements and adding new pieces of information. So, this characteristic way of working of representations, that is, not only by subtraction, but also by addition, gives them great heuristic power. This also implies a form of sensitivity to representation, in the sense that what we can discover about the repraesentatum depends on the adopted mathematical repraesentans: a new representation does not simply make certain elements visible (Carter, 2018), but it can gradually build new ones in the repraesentatum so as to lead us to discover something new about it.

In more detail, the repraesentans has specific information content that can be used to adapt the elements of the repraesentatum in ways that enable us to develop a new approach to a problem. When we introduce something like a specific point into a topological space and we stipulate that it acts as a base for loops (§2.1), we are literally adding new elements to the topological space by reasoning by analogy with a specific repraesentans (algebra). We are adapting a topological space to introduce a few properties into it that are equivalent to those of an algebraic structure in order to achieve a certain purpose or advantage. In this case, the purpose is to develop a calculation that can assign unique values to different 3-manifolds. Of course, this analogy is not purely formal but is based on features that are material and content in kind.

Moreover, not all the similarities between two given objects may be evident at the very beginning, and a manipulation of one object may be necessary in order to find them, while the other object involved in the assimilation suggests how to manipulate it so as to express these similarities.

Now, as we have noted, we can advance different mathematical representations for a given object, each generating different interpretations of it²³, that is, they suggest different actions and inferences to perform on it. Indeed, solving a problem in science and mathematics, as Grosholz (2007) also notes, is typically carried out by employing multiple representations, both formal and informal, that contribute to constructing a hypothesis to solve a problem. These representations can interact at different stages of problem-solving and in different forms—such as juxtaposition (Grosholz, 2007), composition (Carter, 2019, Ippoliti 2018), and concatenation (Spiro et al., 1989)—and they connect several parts of a field (intra-domain) or different fields (inter-domains). Therefore, the choice of the repraesentans is crucial to solving a problem, since each different repraesentans will bring in new and diverse elements, properties, and relations in various combinations.

The presence of multiple representations raises an important issue, that is, how to select one specific representation over another. The answer advanced in this paper is that, especially at intra-field level²⁴, they are evaluated and selected in the first place on the basis of their efficacy in tracking certain properties of the repraesentatum that are crucial to solving a problem.²⁵ Of course, this does not guarantee a solution to the problem, but offers a rational albeit not mechanical way of improving our representations and favouring (abandoning or adjusting) one or more of them.

In the next section, I will consider two different examples to substantiate and ground this analysis in detail, namely the classification of 3-manifolds and DNA supercoiling.

1.2 Main points of the paper

Before discussing the two examples, I will provide a brief outline of the main points of the paper to make it easier to follow how the case studies instantiate the heuristic treatment of mathematical representation presented here.

In brief:

• 1. A representation (repraesentans) is not the same as what it seeks to represent, its object (repraesentatum). It is not a copy; a map is not a landscape, a planetary system is not an atom.

• 2. A representation is by its nature partial and selective, and the selection is tentatively regulated by the problem and subproblems we are trying to solve.

• 3. The repraesentans must be ‘faithful’ in that it must express selected relations of the repraesentatum so that manipulations of the repraesentans reproduce manipulations on the repraesentatum. For example, a change in position of a planet in a planetary representation of atoms should reflect an equivalent change in the position of an electron around a proton-nucleus.

• 4. A representation assimilates its object, that is, it treats the object as equivalent, isomorphic, or equal to itself under a certain viewpoint.

• 5. In some scientific or mathematical cases, a representation requires a manipulation of the represented object. For example, the introduction of a planetary representation to describe an atom imposes new elements, like the elliptic orbits in a fixed plane for electrons moving around a fixed proton-nucleus. Electrons do not have orbits like this, but representing them as such allows us to perform certain actions on them, for example by moving them on a fixed plane, we can calculate their fixed energy. I will describe this mechanism in detail in the paper.

• 6. The specific information content of a repraesentans, i.e. its specific set of elements and properties, suggests manipulations, i.e. actions that can be performed on the repraesentatum. This content permits new elements and properties to be attributed to the repraesentatum and (i) helps us to identify which elements and relations of a hypothesis are needed to solve a particular problem, and (ii) puts constraints on the many possible ways of designing those elements and relations.

• 7. Since a representation can add new elements to the represented object, its construction has ampliative power, that is, it brings pieces of information into the repraesentatum that were not present at the beginning of this construction. This is not a purely formal process but is content-sensitive.

  • a. This construction of a representation is provisional and employs ampliative inference like analogies and induction drawn on the basis of certain similarities that become more evident during the construction, and a manipulation of the represented object may be necessary in order to help those similarities emerge.

  • b. To this end, several repraesentans are proposed, and their efficacy is evaluated on the basis of the goal we are trying to achieve. Again, it is context dependent.²⁶

• 8. When it works in this ampliative way, a new mathematical representation brings out new relations and properties, which can in turn be employed to produce new theorems for the represented object. Since these relations and properties may depend on the chosen repraesentans, the same goes for the theorem derived from it. Thus, a problem of sensitivity to representation may arise.

2 Inter-field and intra-field heuristic powers of representations: two examples

The analysis of two case studies of the classification of 3-manifolds and of DNA supercoiling enables us to bring out a few salient features of the heuristic power of mathematical representations in the case of both intra-field (algebra-topology) and inter-fields (topology-molecular biology).

First, they show that a representation can act in an ampliative way, and not only as an ‘economic’ device (revealing more easily or efficiently something that could be found otherwise).

Secondly, they show that a representation allows us to identify actions and operations to perform on the repraesentatum in a rational way by suggesting what the element and relations contained in the hypothesis should be like, and putting constraints that reduce the several ways of designing these new elements and that regulate how to favour one set of actions and operations over another. Moreover, they show that the construction of a representation is inferential in kind: these representations draw on ampliative inferences to build elements and relations that can be transformed into formal results.

Thirdly, they show that the heuristic procedure is representation-sensitive, as the specific information content that a particular repraesentans embeds is crucial to giving content to a candidate hypothesis. Different representations can attribute different set of elements, properties, and functions to the represented object, which can be employed to produce new theorems for the represented object. I will explain it in detail in the next paragraphs.

2.1 Intra-field heuristic representations: the case of the first homotopy group

The search for a solution to a problem in topology provides us with a remarkable example of the heuristic power of mathematical representation in the advancement of intra-field knowledge, that is intra-mathematical. One of the initial aims of topology was to classify manifolds²⁷ of all dimensions completely, for example by finding topologically invariant numbers. A very interesting case is the class of 3d-manifolds. Here the construction of a new representation of a topological structure is the key to solving the long-standing mathematical problem of classifying them. It requires establishing when two given 3d-manifolds are equivalent or not, that is, if one can be transformed into the other by a set of specific operations and constraints. This can then be used to classify them. The search for this solution ends up with the production of the first homotopy group (or ‘fundamental group’).

2.1.1 Development of solutions using mathematical representation

The first attempts to solve the problem of the classification of 3-manifolds were based on geometrical notions such as genus, orientability, or boundary components, which worked for 2-manifolds (see for example Stillwell, 2012). The goal was to determine certain characteristic numbers for closed three-dimensional spaces to show the possibility of their one-to-one geometrical correspondence. Those attempts all failed since they did not produce a characterization of 3-manifolds that was rich enough to produce a hypothesis to tell apart even very simple instances. Therefore, another attempt was put forward using invariants, that is ‘structures’ that remain unchanged under a given class of transformations. Again, these invariants were sought within geometry—e.g. using the Euler characteristic χ. These geometrical representations put forward certain actions and inferences on a topological space, like keeping track of bent regions, which seemed more promising. Unfortunately, also these invariants based on geometrical representations turned out to be useless because their values became zero for 3-manifolds, and therefore they were not able to distinguish them.

So, in order to find good invariants for 3-manifolds, a new attempt was put forward using not a geometric representation of the elements, but an algebraic one. The choice of algebra was suggested not only by its previous successful application to geometry, but also by the fact that algebra provides us with several examples of invariants (see Cayley, 1845, 1849). The core of this approach to classifying 3-manifolds is to find a way of associating algebraic structures to topological entities, that is, building a bridge to assimilate them and employing the calculation of algebraic formal apparatus to assign a different value to each 3-manifold. In effect, if we can design a topological entity that reproduces certain features of an algebraic structure, and if this algebraic structure can be uniquely associated to the topological entity and is preserved under certain transformations, then we could employ it to tell 3-manifolds apart and classify them. In effect, algebra offers a better way of constructing a (partial) solution to this problem by proposing actions like the introduction of points connected by a set of paths, then basepoints for loops, and later for oriented loops.

The first step towards building such an algebraic representation is to show how and which basic algebraic elements, if any, can be uniquely associated to basic topological elements. That is, we try to mimic certain features of the repraesentans in the represented object. Poincarè (1895) developed this approach ending up with the construction of the first homotopy group. Of course, there are several possible ways of associating algebraic structures to topological spaces using entities like rings, semi-groups, groups, and modules. So, we face a typical under-determination problem here, that is, the data of the problem do not uniquely determine the most appropriate algebraic representation. The choice of one representation over another, as we will see, is guided by the features of the problem we are trying to solve, that is, by the way the candidate representations capture and track certain features that are relevant to solving that problem.

The search for such a representation requires looking for similarities and then drawing ampliative inferences for the repraesentatum, a 3-manifold. The first homotopy group is the outcome of such a step-by-step construction and ends up associating a group to a 3-manifold: this group comprises a set of elements with a composition map and three properties—associativity, identity element, inverse element. Essentially, the first homotopy group provides an algebraic way of telling topological spaces apart by assigning them different numerical values using algebraic calculations.

I argue that the first homotopy group (or ‘fundamental group’, see Poincaré 1904), the endpoint of the search for a solution to this problem, is the outcome of the construction of a new representation that assimilates two diverse mathematical structures, i.e., topological and algebraic structures, and that construction transforms the problem so as to introduce new information into topology. This information (which takes the form of new functions, relations, elements) is not contained in it at the beginning of the assimilation that makes the construction of the new representation possible. The search for a solution to the classification of 3-manifolds is paradigmatic in this sense as it shows us that the assimilation of diverse entities is the first step of the construction of a representation.

In more detail, in order to build this bridge between algebra and topology, it is also necessary to manipulate a topological space and its elements in the light of algebraic properties so as to construct:

• A topological counterpart of the set of elements of an algebraic structure.

• A topological counterpart of operations over algebraic structures.

• A topological equivalence (a homeomorphism) that reproduces algebraic invariance so that we can tell when certain entities are equivalent or not.

It is worth noting that homotopy is a legitimate candidate to help reach this goal as it is a kind of homeomorphism that allows a continuous deformation that compresses a geometrical element, as well as pulling and stretching it. The point here is to establish if homotopy can be adapted to serve as a discriminant for telling topological spaces apart, and to what extent it can do this. Tellingly, the employment of homotopy introduces a new topological feature (i.e. ‘contractibility’) to approaching the problem, which implies that it is possible to change dimension: something that is not possible with other forms of homeomorphism. For instance, under homotopy, a solid disk can be reduced to a single point, that is, to a one-dimensional object: you can deform the disk continuously to a single point. They are equivalent in homotopy. By contrast, they are not homeomorphically equivalent because there is no bijection function between them since one is an infinite set, while the other—the single point—is of course finite.

The first and critical step of this construction is to identify actions and operations to perform on a topological space X in order to give content to a hypothesis to solve the problem. In effect, we can design and define new elements (a point, a segment, a curve, etc.), connect or compose them, define operations for them, and we can so in many ways. The problem is how to limit and regulate this process. The use of a representation, an algebraic one in this case, allows us to shape part of this process in a rational way by putting constraints that cut back several ways of designing these new elements, and that regulate how to favour one set of actions and operations over another. These constraints are of course provisional and revisable, but they structure this set of actions and operations by trying to match them with the specific information content of the repraesentans. In this case, the actions and operations on a topological space X should (a) express certain features of X that are relevant to solving the problem, and (b) do so in a way that matches algebraic structures and calculations. That is, we draw specific elements on a topological space and operate on them on the basis of their ability both to reproduce desired algebraic properties and relations and to keep track of features that are relevant for solving the problem of differentiating 3-manifolds.

Different algebraic structures can suggest different sets of actions and operations to perform on a topological space, different elements to add to it, and different ways to structure them. I will examine three ways of using homotopy to construct different algebraic representations of topological entities, ways that describe the most plausible inferential path that Poincaré followed in approaching the problem of classifying 3-manifolds, and that finally produced the first homotopy group.²⁸

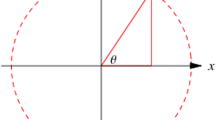
The first attempt employs the set of all paths a_i of a topological space X between two given points, say p₀ and p₁, and then defines a composition for them—their product (Fig.1).

Fig. 1

Set of paths a_1,a_2,…,a_i expressing and keeping track of features of a topological space X

This way of manipulating X offers certain advantages: the paths capture and keep track in a proper way of certain information about the shape of the space, e.g. degrees of curvature, and their product regulates the behaviour of these paths under homotopy in a way that can be expressed algebraically. But even if they can reproduce some algebraic structures in X, unfortunately, they do not provide even a partial solution to the problem as they cannot distinguish even simple and distinct topological spaces. So, this way of keeping track of topological features does not produce a hypothesis to solve the problem. Of course, we can give up on this specific representation without abandoning the analogy with algebra, that is, we can adjust it.

In effect, a second attempt can be put forward by manipulating the topological elements of X in a way that mimics the behaviour of algebraic elements better. One way is to use loops as basic elements instead of simple paths—that is, paths beginning and ending at the same base point x₀ in X (Fig.2).

Fig. 2

Loops expressing and keeping track of features of a topological space X

The use of loops (α, β, γ in Fig.2) instead of simple paths is rational because it provides us with a representational advantage: we can now express and keep track of more salient features of X that are relevant to solving the problem of classifying 3-manifolds, features like a hole h, angles, or axes. These features cannot be expressed fully by simple paths. This way of manipulating X is suggested by an analogy with a more complex algebraic structure, i.e. a semi-group. It is better than the previous one because using loops rather than paths provides at least three important advantages.

First, loops can be deformed into another one under homotopy so they can be considered as a single ‘element’. Consequently, a loop that cannot be continuously deformed into another, such as α, β, γ in Fig.2, identifies and keeps track of the substantially distinct properties of a 3-manifold. In this way, loops provide a better way of distinguishing specific regions of a 3-manifold, introducing a finer-grained classification for it and, at the same time, expressing properties that can be approached in algebraic terms. Secondly, loops keep track of fundamental topological properties of a manifold, such as holes in it, that cannot be tracked properly by means of simple paths. Thirdly, loops enable us to define the equivalent of an algebraic composition: since loops start and end at the same place (the base point x₀), their composition is certainly defined at x₀.

This algebraic representation provides us with a better tool than the previous one (sets of paths), but it is still limited as we must adjust it further to account for more properties of a 3-manifold that reproduce algebraic properties concurrently. In fact, the base point can be thought of as acting as the topological counterpart of the identity element e in algebra²⁹ and the identity path e is also a multiplicative identity. In this way, we have constructed a semi-group with identity for X—the topological counterpart of a ‘monoid’—which is given by the set of all x₀-based loops in X.

But our manipulation of a topological space regulated by an algebraic representation can be pushed forward and improved. We can also define the equivalent of the inverse element in algebra—the inverse of a loop—thus strengthening the assimilation between an algebraic and a topological structure. To obtain this, we introduce a new property, the orientation of paths, by simply allowing a loop to be followed in the reverse direction (see arrows in Fig.2) and denoting it as a^− 1. In this way we have gradually introduced new information into a topological space thanks to deeper analogies with algebraic structures. This new information takes the form of:

• New elements—like a basic point or the identity element.

• New properties—like orientation.

• New notations—like ‘e’ or ‘a^− 1’.

Thus, these analogies have suggested actions to perform in order to obtain a good candidate to solve a problem that (a) expresses substantial features of a 3-manifold, and (b) can approach them using the formal apparatus of algebraic groups.

The last step of this process is to take into account the set of all paths and ‘equivalent paths’, that is, to consider a broader basic set whose elements are the equivalence classes of paths: the first homotopy group is obtained combining this idea and the idea of loops (Crowell and Fox, 1963, 17). By doing so, we obtain a more refined algebraic structure, namely a group, which can be associated to a topological space and thus generates the first homotopy group. Such a group is given by the set of equivalence classes of loops at basepoint p under the equivalence relation of homotopy.

2.1.2 Assessing the role of mathematical representation

This process shows that the construction of a specific representation is provisional, tentative, and revisable. It is continually evaluated and tested on the basis of its efficacy in tracking certain properties of the repraesentatum (a topological space X) that can be crucial to solving the problem—e.g. holes or axes. The construction of a suitable algebraic representation is made step-by-step, and several algebraic representations are tried, evaluated, and then abandoned or refined. For instance, the algebraic representation based on simple paths proposes certain actions and inference to perform on a topological space X (the repraesentatum). The first actions proposed are identifying points in the surface and connecting them with simple paths in order to (a) keep track of certain basic properties of the topological space, and (b) provide the basis for mimicking an algebraic structure—that is, to define at least a set of basic elements and a composition function for them. At this stage, the proposed actions and operations allow us to perform a sort of experiment in the repraesentatum (see also Carter, 2019 on this point): by means of these actions we build new elements and inferences for a topological space, we see their consequences and then we check if they are satisfactory, i.e. if and to what extent they meet our goal by providing us with a hypothesis that is a sufficient condition to solve the problem or part of it. Since the actions and inferences proposed by the simple paths cannot be developed into structures rich enough to enable the algebraic calculations that would permit us to distinguish between different 3-manifolds, we must abandon them and look for a new set of basic elements and a composition function that will still satisfy (a) and (b). Then, a more refined version based on loops is introduced and tested.

New representations are put forward and adjusted on the basis of the failures or the weaknesses of the previous ones, so benefiting from them: the first homotopy group is built on the notion of invariant, which takes advantage of the failures of previous approaches based on pure geometrical representations. This construction, when successful, creates new pieces of information in the repraesentatum that can generate the hypothesis to solve the problem. This example also shows, as noted also by Grosholz (2007), that a representation is not simply a passive, static transfer of properties: it does not leave the repraesentatum unaltered but requires a dynamic, active construction that gradually changes it. In this sense, we have a way of improving our representations and we can favour one representation over another on the basis of it—the sets of equivalence classes of loops are preferable to sets of loops, which are in turn preferable to sets of paths.

Moreover, this construction shows how a gradual assimilation of a topological space into algebraic structure takes place. It exhibits the steps necessary to adjust a topological space in order to treat it as isomorphic to an algebraic structure under a certain point of view, and how new information that is not there at the beginning is introduced, providing us with a way of approaching the problem that would not be possible otherwise. The employment of algebraic representation guides the construction of new elements into a 3-manifold, like the identity element, or the inverse element, which are literally added to the topological space and are not there at the beginning of the process. The example also shows how this construction is regulated by the goal of the problem that we are trying to solve—in this case, to find a structure (i.e. classes of equivalence) that keeps track of features of 3-manifolds thus enabling us to distinguish between them.

In addition, this construction is inferential in kind, as it employs ampliative inference in order to propose and refine a hypothesis to solve the problem. The first step for constructing the representation is to find similar features in topological and algebraic entities. Similarity is defined with respect to a given viewpoint, i.e., a specific property or a set of properties—in the case of the first homotopy group, invariance under a form of homeomorphism. Again, the features of the problem to solve regulate the choice of these properties. The search for these similarities, as we have seen, requires an adaptation of the elements of a 3-manifold. These similarities are the basis of analogies, which can be transformed into (partial) isomorphisms or reductions that are eventually formalized in a theorem. For example, first we construct an analogical counterpart in topology of algebraic elements and functions—the identity elements, the inverse element, the class of elements, and their composition—in the form of base-points, orientation for loops, classes of loops, and homotopy, and then we can advance an analogical inference in order to obtain a hypothesis to solve (at least a part of) the problem of classifying 3-manifolds. More formally, if g stands for a group, t for a 3-manifold, P for the properties of having a unique numerical value, ≈ for being similar, the following analogical inference regulates the search for a solution to the problem of classifying 3-manifolds:

(m≈ t ∧ P(g)) → P(t) (A1).

A1 formalises the ampliative reasoning stating that on the basis of certain known similarities between a 3-manifold, m, and an algebraic group, g, (here, similarity means equivalence under a given viewpoint), we can conjecture that m has a unique value on the basis that g has the same property. A1 regulates the construction of the problem space (Simon et al., 1987) as it (i) sets the goal, (ii) puts a few constraints on this space thanks to the specific information content of algebraic structures, and (iii) suggests the elements and relations of the hypothesis to solve the problem.

After the algebraic representation of a topological entity has been constructed, we can use algebraic operations and results as a means for investigating topological properties and entities, and we can conduct ‘experiments’ on it. The first homotopy serves this purpose as it can tell several surfaces (sphere, torus, annulus) apart, and it advances mathematical problem-solving by enabling us both to solve previously unsolved problems³⁰ and to find new problems³¹.

This case study also shows why the search for a proof of a representation theorem is so important and intensely sought in mathematics. A new representation theorem establishes and formalizes an intra-field bridge between distinct mathematical structures that boosts problem solving by enabling us to handle certain entities in terms of others that do not have the same information content and which can be fruitfully employed to add new pieces of knowledge to those entities.

Nevertheless, since the assimilation of diverse mathematical entities and the representation that it produces are partial and selective, a problem of sensitivity to representation can arise. In effect, some results deriving from a specific representation might hold only for that specific representation and thus impossible to extend to the original elements. Topology, namely knot theory, provides us with a remarkable example in this respect.

In knot theory the use of projections onto a plane, that is, a 2-D representation, requires that several 3-D features of knots are lost, while others are added. An example of a feature that is added is overcrossings, which are literally defined only in a 2-D representation. Now, we cannot be sure that results obtained for the 2-D representation will hold also for the 3-D original knot. The use of a specific representation (a 2-D projection) might produce results that are valid only for this representation and cannot be extended to the original 3-D mathematical knot.³²

Tellingly, the choice of this specific representation, a 2-D projection, enables the use of other representations and tools that would be impossible to employ otherwise. An example is colouring in knot theory, which needs a 2-D projection.³³ In fact, an interesting feature of the application of colouring to knot theory is the fact that in principle there are no components for knots. In this sense, a 2-D representation literally introduces new information into the problem: a knot is a single strand in 3-D space, and as such it has no crossings. Accordingly, it cannot be discretized as required by colouring: no labels for items can be identified for colouring, for there is only one item—the single string in 3D. On the other hand, a 2-D entity, like a knot diagram, can be discretized and hence coloured. So even if colourability cannot be defined for 3D knots, it does reveal interesting new properties for them and not simply for their diagrams.

Moreover, this shows that the search for a solution to this problem requires the interplay of multiple representations, that in this case a ‘concatenation’³⁴, that is, a precise order of inferences and representations.

Such a role of mathematical representations highlights an important historical dimension of mathematical research and growth of knowledge. In effect, the construction of a new representation draws on the corpus of available knowledge, which is a historical body. As this body expands or changes, new representations can be built or old ones modified, so that new assimilations of objects and fields become possible. A new representation of a certain object that was previously impracticable becomes available, and our toolbox for approaching that problem expands and opens the road to new possible solutions to it.

2.2 Inter-fields heuristic representations: the case of DNA supercoiling

Topology also provides us with an interesting example that illustrates the heuristic power of mathematical representations at an inter-fields level (mathematics and molecular biology): the topological representations of DNA (see e.g. Benham at al., 2000).³⁵ In what follows, I will focus on the problem of DNA supercoiling.³⁶

DNA supercoiling describes a higher-order DNA structure, that is, the interwinding of two complementary strands going around one another or around a common helical axis (see Fig.3).

Fig. 3

Pictures of DNA and DNA supercoiling and their topological representation

Supercoiling is important because it gives structural and energetic properties to DNA that affect its biological functions up to eventually inhibiting the ability of DNA or RNA polymerases to continue the DNA strand. Thus, supercoiling is important in several biological phenomena and strongly impacts DNA metabolism and gene expression (see e.g. White, 1995 for more detail). Supercoiling can emerge in two ways:

• 1. When DNA winds around proteins.

• 2. When the axis of the DNA assumes an interwound (or plectonemic) form.

Supercoiling has been conceptualized geometrically in two ways(see e.g.Fogg et al., 2009): over-winding (also called ‘positive’ or ‘left-handed’) or under-winding (also called ‘negative’ or ‘right-handed’) of a DNA strand (see Fig.4).

Fig. 4

The two geometrical conceptualizations of supercoiling (under-winding over-winding

These different geometrical structures play salient biological roles: underwinding facilitates strand separation, while overwinding inhibits it. Moreover, because of the right-handed nature of the DNA helix, the positive and negative supercoils are not equivalent. For instance, negatively supercoiled DNAs are transcribed more efficiently than relaxed DNA, “most likely because torsional stress helps to separate DNA strands and facilitates open complex formation within promoter/RNA polymerase complexes” (Hsieh, 2013,154). The study of the biological function of DNA requires a detailed understanding of these geometrical and spatial properties, which can be observed by means of several biological experiments—e.g. those based on sedimentation, X-ray diffraction, electron microscopy, nuclease digestion, footprinting, and gel electrophoresis (see Fig.5).

Fig. 5

Images of DNA obtained by different techniques ((a) DNA electron microscopy (b) DNA gel electrophoresis (c) DNA X-ray diffraction)

These experiments enable us to visualise several properties of DNA in 2D representations. These DNA images are empirical data that need to be interpreted and fully understood. Mathematics, and topology in particular, can provide us with such an understanding: as noted by White (1995), a mathematical representation and a mathematical interpretation are necessary “for describing and understanding closed circular DNA […] and to explain and classify the data obtained from these experiments” (White, 1995, 154).

2.2.1 Development of solutions by mathematical representation

The construction of suitable mathematical representations enables us to approach the problem of DNA supercoiling in new ways and to advance several solutions to interesting questions. For example, a major factor in supercoiling dynamics is the action of the main types of cutting enzymes, namely topoisomerases.

Topoisomerases can decatenate, unknot, relax, and supercoil DNA. They are classified into two types—Type I and Type II (see Fig.6). Type I introduces transient single-strand breaks in DNA to permit adjustments in helical winding. Type II enables the passage of one portion of duplex DNA into the same or a different molecule by means of a provisional double-strand break.

Fig. 6

Types of topoisomerases (Type I Type II)

Since supercoiling requires measuring the interwinding of the backbone strands and the compacting of the DNA into a relatively small space, it can be approached as a geometrical problem, in particular a topological one. The construction of such a topological approach outlines the heuristic power of mathematical representations and their way of working at a fine-grained level.

A mathematical representation of supercoiling in DNA has been put forward by introducing three mathematical (geometric) descriptors: linking (L), twisting (T), and writhing (W) number (Fuller, 1971, 1978).³⁷ These descriptors are the basis for creating a topological representation of DNA sequences (Vinograd et al., 1965), and they were at least in part developed formally before being applied to this specific problem (see Listing, 1847; Tait, 1877). For instance, the Writhing number (W) was developed to account for knots and was then adjusted to provide a suitable representation of some properties of DNA that are conjectured to be relevant to solving the problem, that is, overcrossing and undercrossing of two strands (see. Figure7). They are denoted by two numbers (+ 1, -1).

Fig. 7

Writhing number for the overcrossing (+ 1) and undercrossing (-1) of two strands

Moreover, L, T and W, are connected by an important relationship that has been proved formally. The three quantities are interrelated by a theorem stating that, for a closed curve on a surface, the linking number is given by the sum of the surface writhe number and the twist number, namely L = W + T (White, 1969). This implies that for a closed DNA strand of constant linking number, a change in W implies that there must be an equal but opposite change in sign in T. Moreover, “the biological importance of this relationship is that all three of these quantities are experimentally measurable. Thus, having determined any two of them, one can calculate the other and then compare with the experimental value” (White, 1995, 174).

Essentially, these topological descriptors aim at representing salient features of the action of the major types of cutting enzymes, topoisomerases of Type I and Type II, and at developing “the differential topological invariants necessary to describe the structural changes that occur in the DNA” (White-Bauer, 1989, 334). In effect, L, T and W turn out to be good devices for representing and measuring the interwinding of the backbone strands and the compacting of the DNA into a relatively small volume. In more detail, the linking number is a measure of the crossings “seen” in any view and these crossings can be divided into two categories:

• distant crossings, occurring when the DNA axis is “seen” to cross itself (the backbone curve of one crossing segment is seen to cross the axis of the other segment)—represented and measured by W (writhe).

• local crossings, occurring when the helical winding of the backbone curves around the axis—represented and measured by T (twist).

So, the linking number associated with two closed oriented curves remains unchanged when the two curves are distorted but not broken.

Just as for the algebraic representation of the classification of 3-manifolds, there are several possible ways of treating DNA supercoiling by means of a mathematical representation, such as elastic rod theory, isotropic elastic polymer, or freely-jointed chain model (Stump et al., 2000). They represent the DNA sequence and some of its geometrical properties in different fashions and suggest different ways of acting on it: for example, in the freely-jointed chain model the molecule is represented as broken down into disjointed sections (i.e. discretized), which can be labelled, while in the others the molecule is represented as a continuous curve for which folding and twisting is distributed uniformly throughout.

2.2.2 Assessing the role of mathematical representation

This case study shows again that the construction of a suitable representation is partial, selective, and ampliative as it picks out which aspects to show or add, and which to neglect in a mathematical representation of DNA supercoiling. Regarding the neglected features, we note that in the construction of the linking number the feature of bond polarity is explicitly neglected, as the two strands are represented as oriented in a parallel fashion even if this is “not consistent with the bond polarity”, and the reason for this is that it “greatly facilitates the mathematics necessary for the description of supercoiling” (White, 1995, 155).

On the other hand, this representation is ampliative because it adds new elements to the biological problem that can turn out to be crucial to solving the problem. Specifically, a topological representation introduces new elements and new ways of organizing and decomposing DNA. In effect, linking, writhe and twist do not exist in 3D space stricto sensu, and they are added to DNA as a result of its interpretation by means of a 2D representation. Thus, the attempt to apply a topological representation of DNA supercoiling suggests how to manipulate DNA and how to introduce elements and information (notations, elements, properties) that can be used in order to advance a hypothesis to solve the problem. In more detail, topology suggests how to introduce suitable start-points and endpoints into the DNA so as to divide it into segments, which are literally not there before the employment of this representation. These segments are obtained on the basis of the specific information content of the adopted topological representation. In principle, DNA is a double strand in 3-D space, and as such it has no crossings and no contacts between the strands: accordingly, it is not a discrete object and no segments for it can be identified, for there is just one item—a continuous curve in 3D space. This is true, even when we introduce overcrossings, because we consider DNA as a 2D object in order to enable a geometrical and topological approach to it. We represent DNA and some of its properties in this specific mathematical fashion to assimilate DNA and topological elements, that is, to ignore many differences between them, and we do this because of the heuristic and ampliative power of such a representation: a 2-D representation (like a knot diagram or a Writhe), which can be discretized, adds new information to the elements involved in the problem, so as to make it possible to define new components and investigate their properties at a mathematical level and compared them with existing data and knowledge about DNA sequences.

Naturally, unlike in the case of 3-manifods classification, the set of actions and operations to perform on a DNA sequence is limited by constraints that come not only from topology, but also from empirical data. Nonetheless, the use of a topological representation enables us to shape part of this process in a rational way by imposing constraints that reduce the number of ways of designing these new elements and that regulate how to favour one set of possible actions and operations over another.

It is worth noting that in order to represent supercoiling and the winding problem of DNA in mathematical terms, we need to make certain assumptions about it that are dictated by the adopted mathematical representations and not necessarily by the empirical data (i.e., DNA images). In effect, when mathematical representations are inter-fields, the properties or relations suggested by a specific repraesentans might go beyond the empirical data. A representation may project properties that are contained explicitly only in the adopted mathematical representation but not in the data. A paradigmatic example is the mathematical representation of time as a real number line in classical Newtonian mechanics,³⁸ where properties such as linearity or continuity, rather than a discrete representation of time (see e.g. Ardourel and Barberousse 2017), are ascribed to the data by an adopted mathematical representation but are not necessarily required by the data.

In this respect, also a few properties contained in the assumptions about DNA might go beyond the data, in the sense that the data do not necessarily require these properties: using Hesse’s terminology (Hesse, 1966), these properties are neutral analogies, as we do not already know if they are shared by the target system (DNA) even if they are present in the adopted mathematical representation of it. Nonetheless, these properties structure the content of the hypotheses and their predictions, and they suggest how to manipulate the elements of the represented object under inquiry. Thus, certain properties might be tentatively ascribed to elements of DNA sequence in order to apply certain mathematical representations, but they do not derive from the data. This makes a proposed representation fallible, but it is also what gives it heuristic power. In effect, as noted by Fogg: “predicting the extension of a supercoiled molecule is non-trivial and requires numerous model-dependent assumptions (Strick et al., 1998). Consequently, the conclusions from the single-molecule data are only as reliable as the model used to interpret them. Nevertheless, these single-molecule experiments have provided an unprecedented insight into the properties of DNA” (Fogg et al., 2000, 83).

This shows, again, that a problem of sensitivity to representation may arise. In this inter-fields case, the problem can be solved partially by means of empirical data and experiments that are suggested by the adopted mathematical representation alone.

Moreover, also the understanding of DNA supercoiling requires the interplay of multiple representations. This pluralism explicitly characterizes the study of this problem: “in order to quantify and interpret the effects of various topoisomerases on the DNA, biologists rely on a combination of experimental techniques, theoretical mathematical models, and computational visualization” (Robic and Jungck 2011, 115). These representations generate an epistemic gain because they allow us to pose and solve problems. First, they put us in a position to pose and, when possible, to answer “what if questions, and carefully investigate the utility of the assumptions” (Sumners, 2011, 350). Secondly, they enable predictions about DNA or suggest how to set up an experiment. For instance, it is possible to use crossing-number information to qualify and predict the geometry of the packing of viral DNA in organisms like phage capsids (see White, 1995, 177). Once we know the crossing number of the DNA products, we can write down tangle equations and solve them. This task requires us to plug in all the possible knot (link) products of a given crossing number for the right-hand sides of each tangle equation. It can be performed by computer programs that also visualize the answer.

To further illustrate the heuristic power of a topological treatment of DNA supercoiling, it is worth mentioning here that it makes it possible to answer an important question in the study of minichromosomes, that is, small circles of DNA carrying the normal origin of replication. The question is the following:

(Q) does the helical repeat of relaxed DNA (i.e., the number of base pairs per turn) remain unchanged (10.5) when the DNA is wrapped around the nucleosome?

A theorem in differential topology can give us the answer. But to use this theorem, we must adjust our mathematical representation once again. In the case of geometric and topological analyses of DNA lying on a surface, a better representational approach (see White, 1995, 166-7) is provided by dividing the linking number not into twist and writhe, which relate only to spatial properties of the DNA, but into components that relate directly to the surface and surface-related experiments. The linking number of a closed section of DNA made to lie on a surface can be divided into two integral quantities, the surface linking number, which measures the wrapping of the DNA around the surface, and the winding number, which is a measure of the number of times that the backbone contacts or rises away from the surface. We have now two new descriptors—surface linking number (SL) and winding number (T) for a closed section of DNA on a protein surface—and in addition, we can measure the first quantity experimentally using X-ray diffraction, and the second by digestion or footprinting. At this point, we can use the apparatus of topology to answer the question Q. A topological theorem tells us that SL = L + T, that is, for a closed section of DNA on a surface, the linking number (L) is the sum of the surface linking number (SL) and the winding number T (White and Bauer, 1988). So, since in this case L = 475 and SL = -45, T must be 520. However, we also know that for relaxed SV40, T is equal to L = − 500. Because T = 520, the average helical repeat for minichromosomal SV40 equals 5,250/520 = 10.10. It follows that the answer to the question Q is negative. Now, even if of course “in this analysis, we have made a great many simplifications it is noteworthy that this number is in remarkably good agreement with the number 10.17 that is obtained by nuclease digestion experiments” (White, 1995, 177).

Thanks to the construction and adjustment of a mathematical representation of DNA sequences, we can find a fundamental relationship L = SL + T for three quantities that are directly accessible to experiment: L by electrophoresis, SL by X-ray diffraction, and T by digestion. Once two of these three quantities are known, we can use this relationship both to predict and to verify the experimental evidence for finding the third. This gives differential topology a strong role in molecular biology, which is a consequence of the heuristic power of mathematical representation.

3 Conclusion

I have shown that a mathematical representation can work in a genuinely ampliative, ‘strong’ heuristic way. When it works that way, it can change the repraesentatum to make some new elements, relations and properties emerge in it, and it can also employ them to produce new theorems or formal pieces of knowledge. Those new elements, relations and properties are literally built and added to the repraesentatum on the basis of the adopted repraesentans and its specific information content.

Different repraesentans can propose different actions and inferences to perform on the represented object. Since the relations and properties that we find at the end of this construction may depend on the adopted repraesentans, the same holds for the results following from it (e.g. a theorem). Thus, a serious problem of sensitivity to representation may arise. Moreover, a representation draws on the corpus of available knowledge, which is a historical body. As the corpus of our knowledge grows and changes, new representations can be built or old ones modified, so that new assimilations of diverse objects and fields become possible. As we have shown, for instance, abstract algebra provides us with a large number of possible structures (e.g. rings, lattices, etc.) that could be used to create new representations of a geometrical object. So, this process is highly context sensitive.

Sensitivity to representation is typically addressed by proving that this dependence from a specific representation does or does not hold. For example, we have seen (§2.1.) that knot theory is approached by several two-dimensional representations of a mathematical object, i.e. a knot, which is tri-dimensional in nature. The use of these two-dimensional representations might produce results that are valid only for this specific 2d representation and thus cannot be extended to the original 3-D mathematical knot. It is not by chance that it took Reidemeister’s theorem (1927) to show when results for certain 2-D projections are valid also for original 3-D knots. Of course, it is not always possible to produce these results and to exclude kinds of sensitivity to representation in the body of our knowledge.