Vertex transitivity, distance metric, and hierarchical structure of the dual-cube

Abstract

The dual-cube, derivable from the hypercube, admits a number of good properties that render it as a good network topology, especially when the node size exceeds several million. This paper presents several other welcome characteristics of the graph. Prominent among them are: (1) vertex transitivity that facilitates the working of an algorithm meant for a “local” context in the global context as well, (2) an exact formula for the distance between two nodes, which leads to a precise result on the distance-wise node distribution of the graph and an exact formula for the average node distance, and (3) a hypercube-like hierarchical structure of the graph that is amenable to an inductive treatment.

1 Introduction

The dual-cube is a special kind of a more general network topology, called the metacube (introduced by Li et al. [14]) that itself is derivable from the hypercube. The idea has been to mitigate the problem of the rapid increase in the degree of the hypercube when the node size exceeds several million.

With the same node degree n, the dual-cube contains $2^{n+1}$ as many nodes as the hypercube $Q_n$, and with the same number of nodes, it has about 50% fewer edges [22]. Remarkably, it retains most good characteristics of the latter, notably, high connectivity, high fault tolerance, low diameter, and easy routing [14].

1.1 Objectives of the paper

The central objective of this paper is to present certain key results that significantly enhance the importance of the dual-cube from both theoretical point of view and the engineering point of view. Here are the salient points.

• 1. The first major objective is to prove that that the graph is vertex-transitive.

  A vertex-transitive graph offers a huge advantage, viz. “local” algorithms on it would work globally as well, since all vertices hold equivalent roles in the global context. Furthermore, vertex-transitive graphs are more strongly connected than other regular graphs. Not surprisingly, most network topologies in use today (notably the hypercube, the torus, and the circulants) are vertex-transitive and, to a lesser extent, edge-transitive. (Definitions of the technical terms appear in Sect. 1.2.)

• 2. The second objective is to present an algorithm that traces a shortest path between two nodes in the dual-cube.

  The distance metric plays an important role in the efficiency of routing algorithms and leads to the average node distance that is an important quality measure of a network.

• 3. The third objective is to present a scheme that generates a sequence of graphs $\langle G_0,\ldots ,G_{2m}\rangle$, where $G_0$ is the two-node graph $0 - 1$ and $G_{i+1}$ is obtainable by introducing a matching between two copies of $G_i$, and where $G_{2m}$ is isomorphic to ${\text {DQ}}_m$. (The situation is somewhat similar to the recursive structure of the hypercube.)

1.2 Definitions and preliminaries

A graph connotes a finite, simple, undirected and connected graph. Let G be a graph, and let dist(u, v) denote the (shortest) distance between vertices u and v in G [21]. Further, let $\hbox {dia}(G)$ denote the diameter of G [21].

For n-bit strings x and y, let H(x, y) denote the Hamming distance between the two. The n-dimensional hypercube $Q_n$ (also called the n-cube) is the graph on the vertex set $\{0, 1\}^n$, where nodes x and y are adjacent iff $\hbox {H}(x, y) = 1$.

Let $x\cdot y$ (or xy) denote the concatenation of the binary strings x and y, and let $\overline{a} := 1-a$, where $a\in \{0, 1\}$. Next, let $x\,\veebar \,y$ denote the n-bit string obtainable by the bitwise XOR operation between two n-bit strings x and y. It is easy to see that $\, \veebar \,$ is both commutative and associative.

Definition 1.1

For an n-bit string $x=b_{n-1}\ldots b_0$ (so $0\le x\le 2^n-1$ in decimal), let $x^{(i)}$ be the n-bit string obtainable from x by replacing $b_i$ by $\overline{b}_i$, where $0\le i\le n-1$.

Definition 1.2

For $m\ge 1$, the dual-cube ${\text {DQ}}_m$ is a spanning subgraph of the hypercube $Q_{2m+1}$. Its edge set is given by $E_0\cup E_1\cup E_2$, where

• 1. $E_0 = \{\{uv0, uv^{(0)}0\}, \ldots , \{uv0, uv^{(m-1)}0\}\;|\; |u|=|v| = m\}$

• 2. $E_1 = \{\{uv1,u^{(0)}v1\}, \ldots , \{uv1,u^{(m-1)}v1\}\;|\;|u|=|v|=m\}$, and

• 3. $E_2 = \{\{x0, x1\}\;|\; |x|=2m\}$.

Definition 1.3

The nodes of ${\text {DQ}}_m$ are distinguishable into two types, as follows:

• Type 0: those that are of the form x0 (binary) or 2i (decimal), and

• Type 1: those that are of the form x1 (binary) or $2i+1$ (decimal).

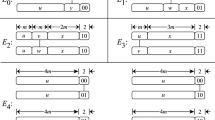
Let $e\in E({\text {DQ}}_m)$. Call e an edge of Type i if $e\in E_i$, $0\le i\le 1$, and call e a cross edge if $e\in E_2$. See Fig. 1 for a depiction of the three edge types. Meanwhile, a node of the hypercube/dual-cube is viewable both as a binary string, say, x and as the corresponding nonnegative integer N(x), a formula for which appears in Equation (1).

$$\begin{aligned} N(x) = {\left\{ \begin{array}{ll} 0 &{} \text{ if } x = 0 \\ 1 &{} \text{ if } x = 1 \\ 2^{|v|}N(u)+N(v) &{} \text{ if } x = uv, \text{ where } |u|, \; |v|\ge 1. \end{array}\right. } \end{aligned}$$

(1)

Fig. 1

The three edge types of ${\text {DQ}}_m$, vide Definition 1.2

It is easy to see that ${\text {DQ}}_m$ is a regular graph of degree $m+1$. Figure 2 presents four different drawings of ${\text {DQ}}_2$. Among other things, they show that the graph admits (1) an embedding on the torus without any edge crossing, (2) an edge decomposition into a Hamiltonian cycle and a perfect matching, (3) a vertex partition into four copies of ${\text {DQ}}_1$, i.e., $C_8$, and a vertex partition into eight copies of the four-cycle.

Fig. 2

Four drawings of ${\text {DQ}}_2$

Definition 1.4

• 1. A graph is said to be vertex-transitive if for every pair of vertices u and v, it admits an automorphism that sends u to v.

• 2. A graph is said to be edge-transitive if for every pair of edges $\{u,v\}$ and $\{x,y\}$, it admits an automorphism f such that $f(\{u,v\})=\{x,y\}$.

The concepts of vertex transitivity and edge transitivity are distinct. In particular, a vertex-transitive graph is necessarily regular, whereas an edge-transitive graph need not be regular. If a graph is both vertex-transitive and edge-transitive (called a symmetric graph), then its vertex connectivity as well as its edge connectivity is optimally equal to its degree.

For a set S of integers and an integer j, let $S+j$ denote the set $\{i+j\,|\,i\in S\}$, and let C(n, i) denote the binomial coefficient $\left( {\begin{array}{c}n\\ i\end{array}}\right)$, where $n\ge i\ge 0$. For any undefined term, see West [21].

1.3 Hypercubes and related networks

The hypercube possesses an extremely rich structure [6, 20]. For example, it is symmetric, distance-regular, and Hamiltonian decomposable. Further, its diameter is logarithmic relative to its order, and it is amenable to emulating a wide variety of other frequently used networks. Not surprisingly, it has been one of the most popular interconnection networks. For example, the architectures of Intel iPSC, the nCUBE, the Connection Machine CM-2, and SGI Origin 2000 are based on the hypercube [14].

Despite its attractive features, the hypercube suffers from certain practical problems. In particular, its scalability is an issue. (A scalable network is one whose size may be increased in such a way that changes to the existing configuration are minor, and performance degradation, if at all, is negligible.) In response, size-scalable network topologies such as mesh/torus, ring, and the tree have been used in practice, despite their inherently limited topological characteristics such as low connectivity, large diameters, large average node distances, and lack of fault tolerance.

At the other end of the spectrum, when the number of nodes in a network exceeds several million (which is a reality in the ever-expanding digital world today), increase in the degree of the hypercube becomes an issue. To mitigate this problem, Loh et al. [16] presented the exchanged hypercube. See [3, 5, 7, 9, 10, 25] for certain related studies. Working along this line of research, Li et al. [14] introduced a regular network (also derivable from the hypercube), called the metacube, of which the dual-cube is a special case. Interestingly, the dual-cube is a special kind of the exchanged hypercube as well.

A number of other hypercube-related networks are discussed by Li et al. [14] and Pai and Chang [18].

1.4 Studies specific to the dual-cube

Here are some of the prominent results that appeared on various aspects of the dual-cube during the past two decades.

• 1. Jha [8] presented a 1-perfect code in ${\text {DQ}}_m$, where $m=2^k-2$.

• 2. Lai and Tsai [11] showed that every node of ${\text {DQ}}_m$ lies on a cycle of every possible even length and that the graph maintains this property even if it has up to $m-1$ edge faults. (The result is optimal with respect to the number of edge faults.)

• 3. Li et al. [12] established that collective communications may be carried out in the dual-cube almost as efficiently as in the hypercube.

• 4. Shih et al. [19] proved that ${\text {DQ}}_m$ admits $m+1$ mutually independent Hamiltonian cycles. (The result is optimal since each vertex of this graph has exactly $m+1$ neighbors.)

• 5. Wu and Wu [22] showed that ${\text {DQ}}_m$ admits $\lfloor (m-1)/2\rfloor$ edge-disjoint Hamiltonian cycles.

• 6. Chen and Tsai [2], Li et al. [13], and Zhang et al. [24] presented certain results on fault tolerance and fault diagnosability of the dual-cube.

Interestingly, the dual-cube itself admits certain variants. See Angjeli et al. [1] and Chen and Kao [4].

1.5 Comparison of interconnection networks

Comparing interconnection networks is tricky, since there is no single network that is the best for all applications and all operating environments, still some comparisons are in order. Here are pointers to certain relevant studies on this topic.

• 1. Loh et al. compare the following networks on the basis of their diameter, cost-effectiveness, and the ability to emulate other networks: n-cube, Gaussian cube, reduced hypercube, and exchanged hypercube.

• 2. Li et al. [14] present a comparison table that details the degree, diameter, average distance, and bisection width of the following: hypercube, dual-cube, quad-cube, and the more general metacube.

• 3. Li et al. [15] present a comparison table that details the number of nodes, degree, diameter, and cost ratio of the following: p-ary three-cube, n-cube, cube-connected cycle, dual-cube, WK-recursive network, and recursive dual-net.

1.6 A brief commentary on certain claims by other authors

• 1. Some authors [10, 14] stated without a proof that the dual-cube is vertex-transitive. This paper fills up the gap.

• 2. Loh et al. (resp. Klavžar and Ma [10]) discuss the shortest distance between two nodes in the exchanged hypercube (resp. average node distance of the exchanged hypercube), from which the corresponding measures in the dual-cube follow. However, the proofs in this paper are more constructive and intuitive.

• 3. Contrary to another claim [14], the dual-cube is not edge-transitive. See Fact 2.1.

1.7 What follows

Section 2 establishes vertex transitivity of the dual-cube, while Sect. 3 derives a formula for the (shortest) distance between Node 0 and a given node z of the graph. (Vertex transitivity ensures an easy generalization of the formula.) Section 3.2 presents a description of the distance-wise node distribution of the graph that leads to an exact formula for the average node distance. Later, Sect. 4 shows that ${\text {DQ}}_m$ admits an elegant hierarchical structure. The paper ends with certain concluding remarks in Sect. 5.

2 Vertex transitivity

Lemma 2.1

${\text {DQ}}_m$ admits an automorphism that carries a given node of Type 0 to Node 0.

Proof

Let $z=uv0$ (binary), where $|u|=|v|=m$, and consider the mapping $\phi _z: V({\text {DQ}}_m)\rightarrow V({\text {DQ}}_m)$ given by $pqa\mapsto (p\veebar u)(q\veebar v)a$, where $|p|=|q|=m$ and $a\in \{0,1\}$. It is easy to see that $\phi _z$ is well defined and $\phi _z(z)=0$ (decimal). Further, $\phi _z(x)=y$ iff $\phi _z(y)=x$, so the mapping is total and invertible, hence a bijection.

To prove that the adjacency (resp. non-adjacency) is preserved under the mapping, first consider a node of Type 0, say pq0, where $|p|=|q|=m$. Whereas one of its neighbors is pq1, the others are $p\,q^{(0)}\,0,\; p\,q^{(1)}\,0,\,\ldots ,\,p\,q^{(m-1)}\,0$. Note that $\phi _z(pq0)=(p\veebar u)(q\veebar v)0$, and further observe that

• (a) $\phi _z(pq1)=(p\veebar u)(q\veebar v)1$ that is adjacent to $\phi _z(pq0)$ via a cross edge, and

• (b) $\phi _z\big (p\,q^{(j)}\,0\big )=(p\veebar u)(q^{(j)}\veebar v)0$ that is adjacent to $\phi _z(pq0)$ via an edge of Type 0, whre $0\le j\le m-1$.

By a similar argument, an analogous conclusion is reachable with respect to a node of Type 1.

Finally, let x and y be nonadjacent. If $\phi _z(x)$ and $\phi _z(y)$ were adjacent, then so must be $\phi _z(\phi _z(x))$ and $\phi _z(\phi _z(y))$. However, $\phi _z(\phi _z(x))=x$ and $\phi _z(\phi _z(y))=y$, a contradiction. $\square$

Figure 3 illustrates the proof of Lemma 2.1, where $m=2$ and $z=4$. (The i-th node in a particular row to the left maps to the respective node on the same row to the right.

Fig. 3

An automorphism on ${\text {DQ}}_2$, ($4\leftrightarrow 0$), vide Lemma 2.1

Lemma 2.2

${\text {DQ}}_m$ admits an automorphism that carries a given node of Type 1 to Node 1.

Proof

Similar to that of Lemma 2.1. $\square$

Lemma 2.3

${\text {DQ}}_m$ admits an automorphism that carries Node 1 to Node 0.

Proof

Let $\phi : V({\text {DQ}}_m)\rightarrow V({\text {DQ}}_m)$ be given by $uva\mapsto vu\overline{a}$, where $|u|=|v|=m$ and $a\in \{0,1\}$. It is clear that the mapping is well-defined. Further, $\phi (y)=z$ iff $\phi (z)=y$, which means that it is a bijection. Notice that $\phi (1)=0$ (decimal).

Let $z_1,z_2\in V({\text {DQ}}_m)$, and let $z_1=u_1v_1a_1$ and $z_2=u_2v_2a_2$, where $|u_1|=|v_1|=|u_2|=|v_2|=m$, and $|a_1|=|a_2|=1$, so $\phi (z_1)=v_1u_1\overline{a}_1$ and $\phi (z_2)=v_2u_2\overline{a}_2$.

• 1. First suppose that $z_1$ and $z_2$ are adjacent.

  • (a) Let $z_1$ and $z_2$ be adjacent via a cross edge, so $u_1=u_2$, $v_1=v_2$ and $a_2=\overline{a}_1$. In this case, $\phi (z_1)=v_1u_1\overline{a}_1$ and $\phi (z_2)=v_1u_1a_1$ that are clearly adjacent via a cross edge.

  • (b) Let $z_1$ and $z_2$ be both of Type 0 and adjacent, so $z_1=u_1v_10$ and $z_2=u_1\,v_1^{(j)}\,0$, where $0\le j\le m-1$. In this case, $\phi (z_1)=v_1u_11$ and $\phi (z_2)=v_1^{(j)}\,u_1\,1$. It is clear that $\phi (z_1)$ and $\phi (z_2)$ are adjacent. Similarly, if $z_1$ and $z_2$ be both of Type 1 and adjacent, then $\phi (z_1)$ and $\phi (z_2)$ are adjacent.

• 2. Next suppose that $z_1$ and $z_2$ are non-adjacent. If $\phi (z_1)$ and $\phi (z_2)$ were adjacent, then so must be $\phi (\phi (z_1))$ and $\phi (\phi (z_2))$. However, $\phi (\phi (z_1))=z_1$ and $\phi (\phi (z_2))=z_2$, a contradiction. $\square$

Remark

It is easy to compute the inverses of the foregoing automorphisms.

Theorem 2.4

${\text {DQ}}_m$ is a vertex-transitive graph.

Proof

Let $y,z\in V({\text {DQ}}_m)$, where $y\ne z$. An automorphism that takes y to z is obtainable by using the constructions in Lemmas 2.1, 2.2, and 2.3, as follows.

• 1. If y and z are the same type, say t, then compose the automorphism that takes y to t with the one that takes t to z.

• 2. If y and z are of different types, then build an automorphism that takes y to z as per the schematic that appears in Fig. 4. $\square$

Fig. 4

Automorphisms that take a node of one type to one of another

Fact 2.1

${\text {DQ}}_m$ is not edge-transitive. For example, observe from Fig. 3i that the edge $\{0,2\}$ of ${\text {DQ}}_2$ lies on a four-cycle, whereas the edge $\{0,1\}$ does not lie on any four-cycle.

3 Distance metric

Theorem 3.1

Table 1 presents the distance between Node 0 and a givn node z in ${\text {DQ}}_m$.

Table 1 Distance between Node 0 and a given node z in ${\text {DQ}}_m$

Proof

See Algorithm 1 that traces a shortest path between two nodes in ${\text {DQ}}_m$. Check to see that, in each case, any other path is at least as long. $\square$

Corollary 3.2

$\hbox {dia}({\text {DQ}}_m)=2m+2$.

Proof

By Table 1, there is exactly one node, viz., $1^m1^m0$ arising out of Case 1(b) that is at the distance of $2m+2$ from Node 0. Indeed, $2m+2$ is the largest such integer. This fact and the vertex transitivity of the graph together ensure that $\hbox {dia}({\text {DQ}}_m)=2m+2$. $\square$

Note that ${\text {DQ}}_m$ is a spanning subgraph of $Q_{2m+1}$, having about 50% fewer edges, yet its diameter is practically equal to that of the latter.

3.1 Distance-wise node distribution

For $1\le d\le 2m+2$, let $n_d$ denote the number of nodes at a distance of d from Node 0 in ${\text {DQ}}_m$, and let $q_d$ denote the number of nodes at a distance of $d-1$ from Node 0 in $Q_{2m+1}$. It is well known that $q_d=C(2m+1,d-1)$.

Theorem 3.3

If $m\ge 1$, then $n_d=C(2m+1,d-1)+C(m,d)-C(m,d-2)$.

Proof

Refer to Table 1. Whereas Case 1(a) contributes C(m, d) nodes, Case 1(b) contributes $C(2m,d-2)-C(m,d-2)$ nodes, where $C(m,d-2)$ denotes the number of nodes of the form $0^mv0$, already covered in Case 1(a). Finally, Case 2 contributes $C(2m,d-1)$ nodes. The claim is immediate. $\square$

Table 2 exemplifies Theorem 3.3 for $m=10$, whereas Fig. 5 depicts it. Not surprisingly, $n_d$ achieves its maximum at $d=m+2$. Meanwhile, let diff $=n_d-q_d=C(m,d)-C(m,d-2)$.

Table 2 ${\text {DQ}}_m$ vs. $Q_{2m+1}$, $m=10$

Fig. 5

Distance-wise node distribution of ${\text {DQ}}_{10}$

3.2 Average node distance of ${\text {DQ}}_m$

Table 3 computes the average node distance of ${\text {DQ}}_m$, i.e., $\frac{1}{2^{2m+1}}\sum _{d\,=\,0}^{2m+2}d\cdot n_d$ $=\frac{1}{2^{2m+1}}\sum _{d\,=\,0}^{2m+2} \Big (d\cdot C(2m+1,d-1)+d\cdot C(m,d)-d\cdot C(m,d-2)\Big )$.

Table 3 Computing the average node distance

Notice that the average node distance of ${\text {DQ}}_m$ is practically equal to that of $Q_{2m+1}$, viz., $m+\frac{1}{2}$.

3.3 ${\text {DQ}}_m$ versus $Q_{2m+1}$

It turns out that the distance-wise node distribution of ${\text {DQ}}_m$ closely parallels that of $Q_{2m+1}$. To that end, recall that diff $=n_d-q_d=C(m,d)-C(m,d-2)$.

The following points are relevant.

• 1. If $2m+2\ge d\ge m+3$, then diff = 0..

• 2. If $m+2\ge d\ge \frac{1}{2}(m+2)$, then diff is negative.

• 3. If $\frac{1}{2}(m+2)\ge d\ge 1$, then diff is positive.

• 4. For $m+2\ge d\ge 1$, diff is symmetric about the point $d=\frac{1}{2}(m+2)$, and its absolute value is a very small percentage of $C(2m+1,d-1)$.

Figure 6 presents the trace of diff vs. d for $m=10$.

Fig. 6

diff vs. d for $m=10$, $0\le d\le 2m + 2 = 22$, vide Table 2

4 Hierarchical structure of ${\text {DQ}}_m$

It turns out that ${\text {DQ}}_m$ admits an interesting hierarchical structure. In particular, there exists a sequence of graphs $\langle G_0,\ldots ,G_{2m}\rangle$ such that (1) $G_0=K_2$, (2) $G_{i+1}$ is obtainable from $G_i$ by introducing (not a perfect) matching between two copies of $G_i$, $0\le i\le 2m-1$, and (3) $G_{2m}$ is isomorphic to ${\text {DQ}}_m$. See Algorithm 2.

It is easy to see that each statement of the algorithm is well-defined. See Fig. 7 for an illustration, where $m=2$.

Fig. 7

Hierarchical structure of ${\text {DQ}}_2$

Lemma 4.1

For $m\ge 1$, let $G_1,\ldots ,G_{2m}$ be the sequence of graphs returned by Algorithm 2, and let $1\le i\le 2m$. Then

• 1. $G_i$ is a bipartite graph, where each partite set is of the same cardinality

• 2. Each partite set of $G_i$ has as many nodes of Tyoe 0 as those of Type 1

• 3. $V(G_i)=\{0,\ldots ,2^{i+1}-1\}$

• 4. Each edge of $G_i$ is valid relative to ${\text {DQ}}_m$

• 5. $|E(G_i)|=(i+2)2^{i-1}$.

Proof

Use induction on i. To that end, first check to see that the claim holds with respect to $G_1$ that is the graph $1-0-2-3$. The induction step follows.

• 1. Let $V_0$ and $V_1$ be the two partite sets of $G_i$, so $V_0+2^{i+1}$ and $V_1+2^{i+1}$ are the two partite sets of of the second copy of $G_i$ immediately after the execution of Step 4 (resp. Step 13) of the algorithm.

  Every edge introduced during execution of each of the two “inner for” loops runs between $V_0$ and $V_0+2^{i+1}$, or between $V_1$ and $V_1+2^{i+1}$. In that light, $G_{i+1}$ is a bipartite graph with $V_0\cup (V_1+2^{i+1})$ and $V_1\cup (V_0+2^{i+1})$ as the two partite sets. Further, the hypothesis that nodes of the two types are equinumerous in each of $V_0$ and $V_1$ ensures that this is the case with respect to each of $V_0\cup (V_1+2^{i+1})$ and $V_1\cup (V_0+2^{i+1})$ as well. Simultaneously, $|V_0|=|V_1|$ ensures that $|V_0\cup (V_1+2^{i+1})|=|V_1\cup (V_0+2^{i+1})|=2^{i+1}$.

  The foregoing argument also shows that $V(G_{i+1})=\{0,\ldots ,2^{i+2}-1\}$.

• 2.

  • (a) Let $\{x,y\}\in E(G_i)$. By induction hypothesis, $|x|=|y|=i+1$, where x and y are in binary. (In decimal, $0\le x,y\le 2^{i+1}-1$.) Also by induction hypothesis, $\{x,y\}$ is a valid edge relative to ${\text {DQ}}_m$. In that light, the edge $\{1x,1y\}$, which appears in the second copy of $G_i$, is valid relative to ${\text {DQ}}_m$. Indeed, if $\{x,y\}$ is a cross edge (resp. an edge of Type 0, or an edge of Type 1), then so is $\{1x,1y\}$. (In decimal, $1x=2^{i+1}+x$ and $1y=2^{i+1}+y$.)

  • (b) If $1\le i\le m-1$, then each edge introduced during execution of the “first inner for” loop runs between two nodes of the form $0^mx0$ and $0^my0$ (binary) that are of Type 0, where $|x|=|y|=m$ and H$(x,y)=1$. Analogously, if $m\le i\le 2m-1$, then each edge introduced during execution of the “second inner for” loop runs between nodes of the form ux1 and vx1 that are of Type 1, where $|u|=|v|=|x|=m$ and H$(u,v)=1$. In either case, all such edges are valid relative to ${\text {DQ}}_m$.

  It follows that the edges that appear in $G_{i+1}$ are valid relative to ${\text {DQ}}_m$.

• 3. Note that $|E(G_1)| = 3$, and $|E(G_{i+1})|=2|E(G_i)| +2^i$, where $i\ge 1$. (Each partite set of $G_{i+1}$ has $2^i$ nodes of each type.) Here is a solution to the recurrence: $|E(G_{i+1})| = (i+3)2^i$.

This concludes the induction. $\square$

Note: It is easy to see that the running time of Algorithm 2 is proportional to the sum of the sizes of the graphs $G_0,\ldots , G_{2m}$.

Theorem 4.2

The graph $G_{2m}$ returned by Algorithm 2 is isomorphic to ${\text {DQ}}_m$.

Proof

By Lemma 4.1, (1) $V(G_{2m})= \{0,\ldots ,2^{2m+1}-1\}$ that coincides with $V({\text {DQ}}_m)$, (2) each edge of $G_{2m}$ is valid relative to ${\text {DQ}}_m$, and (3) $|E(G_{2m})| = (m+1)2^{2m}$ that coincides with $|E({\text {DQ}}_m)|$. Hence the result. $\square$

Remark

The result of this section is likely to be useful in the future in deriving other results with respect to the dual-cube and probably the exchanged hypercubes. This is because the sequence of graphs returned by Algorithm 2 is amenable to an inductive treatment.

Interestingly, it is easy to construct an algorithm that takes $G_{2m}$ as the input and performs a sequence of “inverse” operations, as follows: At the i-th step, partition $G_{2m-i}$ into two subgraphs, each isomorphic to $G_{2m-i-1}$, $0\le i\le 2m-1$, where $G_0,\ldots ,G_{2m}$ are as in Algorithm 2.

5 Concluding remarks

The dual-cube ${\text {DQ}}_m$ is a regular, connected spanning subgraph of the hypercube $Q_{2m+1}$ [14]. It admits a number of welcome properties that make it amenable to an application as a network topology, especially for systems with large node sizes [8, 11, 12, 19, 22]. Results in this paper significantly enhance the importance of the network. Further, the techniques employed are likely to pave the way for similar studies on the quad-cube and the oct-cube that belong to the greater family of such graphs, called the metacube [14].

It is conceivable that there exists a closer relationship between the exchanged hypercubes and the dual-cube. Algorithm 2 is likely to be extended for that purpose. Another relevant question is to determine the smallest n such that ${\text {DQ}}_m$ is a vertex-induced subgraph of $Q_n$.