Vertex transitivity and distance metric of the quad-cube

Abstract

The quad-cube is a special case of the metacube that itself is derivable from the hypercube. It is amenable to an application as a network topology, especially when the node size exceeds several million. This paper presents the following welcome properties of the graph, relating to its structure: (1) vertex transitivity that facilitates the working of an algorithm meant for a “local” context in the global context as well, and (2) an exact formula for the distance metric, which leads to a precise result on the distance-wise vertex distribution of the graph and an exact formula for the average vertex distance. Remarkably, the vertex distribution of the quad-cube resembles, to a large extent, the vertex distribution of the twin copies of a hypercube. In a parallel study, the author recently reported similar results with respect to the dual-cube (Jha in J Supercomput 78:17758–17775, 2022)

1 Introduction

The quad-cube is a network topology that is a special case of the metacube [9] that itself is obtainable from the hypercube. The objective behind its introduction has been to mitigate the problem of the rapid increase in the degree of the hypercube when the node size exceeds several million. With the same node degree n, the quad-cube has $2^{3n-6}$ as many nodes as the hypercube, where $n\ge 3$, and with the same number of nodes, the quad-cube has about 75% fewer edges than the hypercube, yet its diameter is practically equal to that of the latter.

This paper presents results relating to the vertex transitivity, distance metric and distance-wise node distribution of the quad-cube that significantly enhance its importance from both theoretical point of view and the engineering point of view. Interestingly, the node distribution of $CQ_m$ parallels, to a large extent, the node distribution of $2Q_{4m+1}$, i.e., a set of twin copies of $Q_{4m+1}$. Meanwhile, $CQ_m$ admits a 1-perfect code under a certain condition [5]. (The formal definitions appear below.)

In a parallel study, the author [6] recently presented analogous results relating to the dual-cube that is another (relatively simpler) derivative of the hypercube.

1.1 Definitions and preliminaries

A graph connotes a finite, simple, undirected and connected graph. Let G be a graph, and let dist(u, v) denote the (shortest) distance between vertices u and v in G [12]. Further, let dia(G) denote the diameter of G.

For n-bit binary strings x and y, let H(x, y) denote the Hamming distance between the two. The n-dimensional hypercube $Q_n$ (also called the n-cube) is the graph on the vertex set $\{0, 1\}^n$, where nodes x and y are adjacent iff H$(x, y) = 1$.

Let xy denote the concatenation of the strings x and y, and let ${\overline{a}}:= 1-a$, where $a\in \{0, 1\}$.

Definition 1.1

For an n-bit integer $x=b_{n-1}\ldots b_0$ (so $0\le x\le 2^n-1$ in decimal), let $x^{(a)}$ be the n-bit integer obtainable from x by replacing $b_a$ by ${\overline{b}}_a$, where $0\le a\le n-1$. $\square$

It is easy to see that $x^{(a)}=x\veebar 2^a$, where $\veebar$ is the XOR operation. (See Definition 1.4.)

Definition 1.2

For $m\ge 1$, the quad-cube $CQ_m$ is a spanning subgraph of $Q_{4m+2}$. Its edge set is given by $E_0\cup E_1\cup E_2\cup E_3\cup E_4$, where

• 1. $E_0 = \{\{ux00, ux^{(0)}00\}, \ldots , \{ux00, ux^{(m-1)}00\}\,|\, u\in \{0,1\}^{3\,m}$ and $x\in \{0,1\}^m\}$

• 2. $E_1 = \{\{uvx01,uv^{(0)}x01\}, \ldots , \{uvx01,uv^{(m-1)}x01\}\,|\,u\in \{0,1\}^{2\,m}$ and $v,x\in \{0,1\}^m\}$

• 3. $E_2 = \{\{uvx10,uv^{(0)}x10\}, \ldots , \{uvx10,uv^{(m-1)}x10\}\,|\,u,v\in \{0,1\}^m$ and $x\in \{0,1\}^{2m}\}$

• 4. $E_3 = \{\{ux11, u^{(0)}x11\}, \ldots , \{ux11, u^{(m-1)}x11\}\,|\, u\in \{0,1\}^m$ and $x\in \{0,1\}^{3\,m}\}$, and

• 5. $E_4 = \{\{u00, u01\},\, \{u00, u10\}, \, \{u01, u11\}, \, \{u10, u11\}\, |\, u\in \{0,1\}^{4\,m}\}$. $\square$

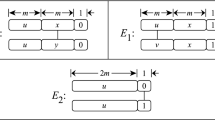
Let $e\in E(CQ_m)$. Call e an edge of Type i if $e\in E_i$, $0\le i\le 3$, and call e a cross edge if $e\in E_4$. See Fig. 1 for a depiction of the five edge types. Meanwhile, a node of the hypercube/quad-cube is viewable both as a binary string, say, x and as the corresponding nonnegative integer denoted by x.

It is easy to see that $CQ_m$ is a regular graph of degree $m+2$. Accordingly, $|V(CQ_m)|=2^{4\,m+2}$ and $|E(CQ_m)|=(m+2)2^{4\,m+1}$.

Definition 1.3

The nodes of $CQ_m$ are distinguishable into four types, as follows:

• Type 0: those that are of the form u00 (binary) or $4i+0$ (decimal)

• Type 1: those that are of the form u01 (binary) or $4i+1$ (decimal)

• Type 2: those that are of the form u10 (binary) or $4i+2$ (decimal) and

• Type 3: those that are of the form u11 (binary) or $4i+3$ (decimal). $\square$

A node z of $CQ_m$ (in binary) is of the form

, where $|u|=|v|=|w|=|x|=m$, and $a,b\in \{0,1\}$.

Fig. 1

Five edge types of $CQ_m$, vide Definition 1.2

Fig. 2

Three drawings of $CQ_1$

See Fig. 2 that presents three drawings of $CQ_1$. Among other things, it shows that the graph admits (a) a vertex partition into sixteen copies of the four cycles, (b) an embedding on the torus without any edge crossing and (c) an edge decomposition into a Hamiltonian cycle and a perfect matching. Meanwhile, Brouwer et al. ([1], p. 27) present the drawing in Fig. 2a to depict the graph as a vertex-transitive induced subgraph of $Q_8$.

Definition 1.4

For n-bit strings x and y, let $x\,\veebar \,y$ denote the n-bit string obtainable by the bitwise XOR operation between x and y. $\square$

It is easy to see that $\, \veebar \,$ is both commutative and associative.

Definition 1.5

A graph is said to be vertex-transitive if for every pair of vertices u and v, it admits an automorphism that sends u to v.

Let $k\ge 0$. For a set S of integers, let $(S+k)$ denote the set $\{i+k\,|\,i\in S\}$, and for a graph G, let $(G+k)$ be the graph on the vertex set $\{x+k\,|\,x\in V(G)\}$, where $\{x+k,y+k\}\in E(G+k)$ iff $\{x,y\}\in E(G)$. Further, let

$$\begin{aligned} C(n,k)= \left\{ \begin{array}{cl} \left( {\begin{array}{c}n\\ k\end{array}}\right) &{} \hbox { if}\;\ n\ge k\ge 0\\ 0 &{} \;\hbox {if}\;\; k>n \hbox {or} k<0 \end{array} \right. \end{aligned}$$

(1)

where $\left( {\begin{array}{c}n\\ k\end{array}}\right)$ denotes the binomial coefficient. For any undefined term, see West [12].

1.2 Literature review

The concepts of vertex transitivity and distance metric are of prime importance in the design and working of a viable network topology.

Informally, a graph is vertex-transitive if every vertex in it has the same local environment, so no vertex is distinguishable from any other based on the vertices and edges surrounding it. In that light, a vertex-transitive graph (that is necessarily regular) offers a huge advantage, viz., “local” algorithms on it work globally as well, since all vertices hold equivalent roles in the global context. Another plus is that a vertex-transitive graph is more strongly connected than other regular graphs ([2], p. 33). Not surprisingly, most network topologies in use today (notably the hypercube, the torus and the circulants) are vertex-transitive. See Heydemann [4] and the references therein for applications of these graphs in interconnection networks.

The importance of the distance metric in a graph is well-understood and well documented in the literature [12]. In particular, given two nodes, say, u and v, a shortest $u-v$ path has the least total cost among all $u-v$ paths. Not surprisingly, several routing protocols base their decisions on a shortest path to a given destination. Examples include (i) RIP (Routing Information Protocol) that is widely used for routing traffic in the global internet and (ii) IGRP (Interior Gateway Routing Protocol) that is a Cisco standard routing protocol. In that light, the results of this paper are directly relevant to the construction of smart routing algorithms around the quad-cube.

See Saad and Schultz [11], and Hayes and Mudge [3] for certain similar results relating to the hypercube, and see Loh et al. [10] for those relating to the exchanged hypercube.

1.3 Quad-cube vis-à-vis dual-cube

Although the quad-cube and the dual-cube have the same lineage, the former is qualitatively more complex than the latter [9]. Therefore, results relating to the dual-cube do not automatically carry over to those relating to the quad-cube. In particular, the author [6] recently studied vertex transitivity and distance metric of the dual-cube. In each category, there are far fewer cases than those in the present study. Indeed, the issues addressed here are lot more challenging.

Probably because of its relative simplicity, the dual-cube has been an object of study by many. See the references in [6]. The results in the present paper are likely to stimulate deeper studies around the quad-cube. Possible areas of investigation include collective communications [8], effective fault tolerance, Hamiltonian decomposability and the design of efficient routing algorithms.

1.4 What follows

Section 2 establishes vertex transitivity of the quad-cube, while Sect. 3 derives a formula for the (shortest) distance between Node 0 and a given node z in the graph. (Vertex transitivity ensures an easy generalization of the formula.) Section 4 makes an effective use of the distance formula to develop the distance-wise node distribution of the graph that, in turn, leads to an exact formula for the average node distance of the graph. The paper ends with certain concluding remarks in Sect. 5.

2 Vertex transitivity

Lemma 2.1

$CQ_m$ admits an automorphism that carries a given node of Type 0 to Node 0.

Proof

Let $z=uvwx00$ (binary) be an arbitrary but fixed node of Type 0, where $|u|=|v|=|w|=|x|=m$, and consider the mapping $\phi _z: V(CQ_m)\rightarrow V(CQ_m)$ given by $pqrsab\mapsto (p\veebar u)(q\veebar v)(r\veebar w)(s\veebar x)ab$, where $|p|=|q|=|r|=|s|=m$ and $a,b\in \{0,1\}$. It is easy to see that $\phi _z$ is well defined. Further, it maps a node of a particular type to one of the same types, and $\phi _z(z)=0$ (decimal). Note next that $\phi _z(y_1)=y_2$ iff $\phi _z(y_2)=y_1$, so the mapping is total and invertible, hence a bijection.

Consider a node pqrsab, and first assume that it is of Type 0, so $a=b=0$. Two of its neighbors are pqrs01 and pqrs10, while the remaining are $pqr(s\veebar 2^0)00,\,\ldots ,\,pqr(s\veebar 2^{m-1})00$. It is easy to see that $\phi _z(pqrs00)$ is adjacent to each of $\phi _z(pqrs01)$ and $\phi _z(pqrs10)$. Consider next $pqr(s\veebar 2^j)00$, $0\le j\le m-1$. By virtue of the fact that H$(p_1,p_2)=1$ iff H$(p_1\veebar t,p_2\veebar t)=1$ (where $p_1,p_2$ and t are m-bit strings), it is easy to see that $\phi _z(pqrs00)$ is adjacent to $\phi _z(pqr(s\veebar 2^j)00)$, $0\le j\le m-1$.

By an analogous argument, the foregoing conclusion is reachable with respect to nodes of Type 1 (resp. Type 2 and Type 3) as well. Finally, there exists a one-to-one correspondence between the $m+2$ neighbors of pqrsab and those of $\phi _z(pqrsab)$. $\square$

Figure 3 illustrates the proof of Lemma 2.1 where $m=1$ and $z=4$ and where the i-th node in a particular row to the left maps to the i-th node on the same row to the right. (See the dotted arcs.)

Fig. 3

An automorphism on $CQ_1$, ($4\leftrightarrow 0$), vide Lemma 2.1

Corollary 2.2

The following holds with respect to the mapping $\phi _z$ in the proof of Lemma 2.1:

• Every quadrilateral tab – $ta{\overline{b}}$ – $t{\overline{a}}{\overline{b}}$ – $t{\overline{a}}b$ – tab maps to a (not necessarily distinct) quadrilateral induced by the corresponding nodes $\phi _z(tab)$, $\phi _z(ta{\overline{b}})$, $\phi _z(t{\overline{a}}{\overline{b}})$ and $\phi _z(t{\overline{a}}b)$, where $t\in \{0,1\}^{4\,m}$ and $a,b\in \{0,1\}$. $\square$

Lemma 2.3

There exists an automorphism $\phi _z$ on $CQ_m$ that carries a given node z of Type t to the Node t, where $t\in \{1,2,3\}$. $\square$

Proof

Similar to that of Lemma 2.1. $\square$

Lemma 2.4

There exists an automorphism on $CQ_m$ that carries Node i to Node 0, where $i=1,2,3$.

Proof

Let $\phi _1$, $\phi _2$ and $\phi _3$ be the mappings, each from $V(CQ_m)$ to $V(CQ_m)$, whose definitions appear in Table 1. Figure 4 depicts the mappings themselves. It is easy to see that $\phi _i(y_1)=y_2$ iff $\phi _i(y_2)=y_1$, $i=1,2,3$; hence, each is a well-defined bijection.

Table 1 Mappings $\phi _1$, $\phi _2$ and $\phi _3$, vide Lemma 2.4

Consider $\phi _1$ first, and let $z_1=u_1v_1w_1x_1a_1b_1$ and $z_2=u_2v_2w_2x_2a_2b_2$, so $\phi _1(z_1)= v_1u_1x_1w_1a_1{\overline{b}}_1$ and $\phi _1(z_2)= v_2u_2x_2w_2a_2{\overline{b}}_2$.

• 1. Let $z_1$ and $z_2$ be adjacent via a cross edge, so $u_1=u_2$, $v_1=v_2$, $w_1=w_2$, $x_1=x_2$ and H$(a_1b_1,a_2b_2)=1$. That H$(a_1b_1,a_2b_2)=1$ ensures that H$(a_1{\overline{b}}_1,a_2{\overline{b}}_2)=1$; hence, $\phi _1(z_1)$ and $\phi _1(z_2)$ are adjacent via a cross edge. Further, the converse is equally true.

• 2. Let $z_1$ and $z_2$ be both of Type 0 and adjacent, so $z_1=u_1v_1w_1x_100$ and $z_2=u_1v_1w_1(x_1\,\veebar \, 2^j)00$, where $0\le j\le m-1$. In this case, $\phi _1(z_1)=v_1u_1x_1w_101$ and $\phi _1(z_2)=v_1u_1(x_1\veebar 2^j)w_101$. It is clear that $\phi _1(z_1)$ and $\phi _1(z_2)$ are both of Type 1, and they are adjacent by virtue of H$(x_1,\,(x_1\,\veebar \, 2^j))$ being equal to one. Further, the converse is equally true.

The other cases, where $z_1$ and $z_2$ are adjacent, both of Type 1 (resp. Type 2 and Type 3), are similar. Finally, it is not difficult to check that the mappings $\phi _2$ and $\phi _3$ admit characteristics that are analogous to those of $\phi _1$. $\square$

Fig. 4

Mappings $\phi _1$, $\phi _2$ and $\phi _3$, vide Lemma 2.4

Remark

It is easy to compute the inverses of the automorphisms that appear in Lemmas 2.1, 2.3 and 2.4.

Theorem 2.5

$CQ_m$ is a vertex-transitive graph.

Proof

Recall that automorphisms are closed under composition and that the inverse of an automorphism is again such. In that light, let $y,z\in V(CQ_m)$, where $y\ne z$. An automorphism that takes y to z is obtainable by using the constructions in Lemmas 2.1, 2.3 and 2.4, as follows.

• 1. If y and z are both of the same type, say i, then use the construction in the proof of Lemma 2.1/2.3, and compose the automorphism that takes y to i with the one that takes i to z.

• 2. If y and z are of types i and j, respectively, where $i\ne j$, then build an automorphism that takes y to z as per the schematic that appears in Fig. 5. $\square$

Fig. 5

Automorphisms that take a node of one type to one of another

Remark

$CQ_m$ is not edge-transitive. For example, observe from Fig. 3(i) that the edge $\{0,1\}$ of $CQ_1$ lies on a four-cycle, whereas the edge $\{0,4\}$ does not lie on any four-cycle.

3 Distance metric

Theorem 3.1

Table 2 presents the distance between Node 0 and Node z in $CQ_m$.

Table 2 Distance between Node 0 and Node z in $CQ_m$

Proof

A (shortest) path between the respective nodes appears below. Check to see that, in each case, any other path is at least as long. (As stated earlier, $|u|_1$ stands for the number of 1’s in the binary string u.)

The remaining cases are similar. $\square$

Evidently, the parity of the distance between two nodes in the quad-cube is equal to that of the Hamming distance between the two. Meanwhile, it is easy to see from Table 2 that $|z|_1\le$ dist$(0,z)\le |z|_1+4$. In that light, there are three possibilities: (i) dist$(0,z)=|z|_1$, (ii) dist$(0,z)=|z|_1+2$ and (iii) dist$(0,z)=|z|_1+4$. Interestingly, it is possible to enumerate the nodes in each category. See Lemmas 3.2, 3.3 and 3.4.

Lemma 3.2

There are a total of $2^{3m+1}+2^{2m}+2^m$ nodes z for which dist$(0,z)=|z|_1$.

Proof

Refer to Table 3, and first note that Cases 1(a), 2(a) and 3(a) are easy. For Cases 4(a) and 4(b) together, there are $2^{4m}$ nodes of the form uvwx11, out of which $2^m(2^m-1)(2^m-1)2^m$ are such that $|v|_1\cdot |w|_1>0$, so there are $2^{4m}-2^m(2^m-1)(2^m-1)2^m=2^{3m+1}-2^{2m}$ nodes of that form. Finally, the four cases are mutually exclusive, hence the result. $\square$

Table 3 Various cases relating to the proof of Lemma 3.2 ($|u|=|v|=|w|=|x|=m$)

Lemma 3.3

There are a total of $3\times 2^{4m} - 2^{3m+1}+2^{2m}-2^{m+1}$ nodes z for which dist$(0,z)=|z|_1+2$.

Proof

See Table 4. $\square$

Table 4 Various cases relating to the proof of Lemma 3.3 ($|u|=|v|=|w|=|x|=m$)

Lemma 3.4

There are a total of $2^{4m} - 2^{2m+1}+2^m$ nodes z for which dist$(0,z)=|z|_1+4$.

Proof

See Table 5. $\square$

Table 5 Various cases relating to the proof of Lemma 3.4 ($|u|=|v|=|w|=|x|=m$)

Remark

All nodes z for which dist$(0,z)=|z|_1+4$ are of Type 0.

4 Distance-wise node distribution

Let $n_d$ denote the number of nodes at a distance of d from Node 0 in $CQ_m$. As stated earlier, C(n, k) denotes the binomial coefficient $\left( {\begin{array}{c}n\\ k\end{array}}\right)$, if $n\ge k\ge 0$, and $C(n,k)=0$, if $k>n$ or $k<0$.

Lemma 4.1

If $m\ge 2$ and $0\le d\le 4\,m+4$, then $n_d$ is equal to

$2C(4m+1,d-3)$

$+$ $\big (2C(3m,d-2)\,-\,2C(3m,d-4)\big )$

$+$ $\big (C(2m+1,d-1)-\,C(2m+1,d-3)\,+\,C(2m,d-1)\,-\,C(2m,d-3)\big )$

$+$ $\big (C(m,d)\,-\,2C(m,d-2)\,+\,C(m,d-4)\big )$.

Proof

Refer to Table 2. $\square$

• 1.

  • (a) Case 1(a) contributes C(m, d) nodes.

  • (b) Case 1(b) contributes $C(2m,d-2)-C(m,d-2)$ nodes, where $C(m,d-2$ denotes the number of nodes of the form $0^m0^mwx00$ with $|w|_1=0$.

  • (c) Case 1(c) is identical to Case 1(b), so the answer in this case, too, is $C(2m,d-2)-C(m,d-2)$.

  • (d) Case 1(d) contributes $C(3m,d-4)\,-2\,C(2m,d-4)+C(m,d-4)$ nodes, where $C(2m,d-4)$ denotes the number of nodes of the form $0^mvwx00$ in which $|v|_1=0$ (resp. $|w|_1=0$), and $C(m,d-4)$ denotes the number of nodes of that form in which $|v|_1$ and $|w|_1$ are both zero.

  • (e) Case 1(e) contributes $C(4m,d-4)\,-\,C(3m,d-4)$ nodes, where $C(3m,d-4)$ denotes the number of nodes of the form uvwx00 in which $|u|_1=0$.

  It is easy to see that the foregoing cases are mutually exclusive.

• 2.

  • (a) Relative to Case 2(a), $|w|_1+|x|_1=d-1$, so this case contributes $C(2m,d-1)$ nodes.

  • (b) Relative to Case 2(b), $|v|_1+|w|_1+|x|_1=d-3$, where $|v|_1>0$, so the answer in this case is $C(3m,d-3)\,-\,C(2m,d-3)$.

  • (c) Check to see that Case 2(c) contributes $C(4m,d-3)-\,C(3m,d-3)$ nodes.

• 3.

  • (a) Case 3(a) is similar to Case 2(a), so the answer is $C(2m,d-1)$.

  • (b) Case 3(b) is similar to Case 2(b), so the answer is $C(3m,d-3)\,-\,C(2m,d-3)$.

  • (c) Case 3(c) is similar to Case 2(c), so the answer is $C(4m,d-3)-\,C(3m,d-3)$.

• 4.

  • (a) Case 4(a) and Case 4(b) are not entirely exclusive, since strings of the form $u0^m0^mx$ belong to each. Accordingly, these two together contribute $2C(3m,d-2)-C(2m,d-2)$ nodes.

  • (b) Relative to Case 4(c), $|u|_1+|v|_1+|w|_1+|x|_1=d-4$, where $|v|_1\cdot |w|_1>0$, so the answer in this case is $C(4m,d-4)-\,2C(3m,d-4)+C(2m,d-4)$, where $C(3m,d-4)$ denotes the number of nodes in which $|v|_1=0$ (resp. $|w|_1=0$), and $C(2m,d-4)$ denotes the number of nodes in which $|v|_1$ and $|w|_1$ are both zero.

See Table 6 that summarizes the foregoing, and establishes the claim. $\square$

Table 6 Computing $n_d$, $0\le d\le 4m+4$, vide Lemma 4.1, where $m\ge 2$

Corollary 4.2

Every vertex in $CQ_m$ admits exactly two diametrical vertices, and the radius as well as the diameter of the graph is equal to $4m+4$.

Proof

By Table 2, there are exactly two nodes, viz., $1^{4m}00$ and $1^{4m+2}$ (binary), arising out of Cases 1(e) and 4(c), that are at the distance of $4m+4$ from Node 0. Indeed, $4m+4$ is the largest such integer. This fact and the vertex transitivity of the graph together lead to the claim. $\square$

Corollary 4.3

Let $m\ge 2$.

• 1. If $3m+5\le d\le 4m+4$, then $n_d=2\,C(4m+1,d-3)$.

• 2. If $m\ge 3$ and $2\,m+5\le d\le 3\,m+4$, then $n_d=2C(4m+1,d-3)-2C(3m,d-4)+2C(3m,d-2)$.

• 3. If $m\ge 3$ and $m+5\le d\le 2\,m+4$, then $n_d=2C(4m+1,d-3)-2C(3m,d-4)+2C(3m,d-2)$ $+\,C(2\,m+1,d-1)-C(2\,m+1,d-3)+C(2\,m,d-1)-C(2\,m,d-3)$. $\square$

4.1 $CQ_m$ versus twin copies of $Q_{4m+1}$

Let $2Q_n$ denote a set of disjoint twin copies of $Q_n$, and assume that the two copies are laid out in the plane in parallel in such a way that Node 0 of each appears at the zeroth level, and the nodes at the distance of d from Node 0 appear at the d-th level, where $0\le d\le n$. It is easy to see that there are $2\,C(n,d)$ nodes at the d-th level of the graph. See Fig. 6 that depicts $2Q_3$.

Fig. 6

Twin copies of $Q_3$

Interestingly enough, the distance-wise node distribution of $CQ_m$ closely parallels that of $2Q_{4m+1}$. To that end, let diff denote the difference between the number of nodes at the d-th level of $CQ_m$ and the number of nodes at the $(d-3)$-rd level of $2Q_{4m+1}$, where $3\le d\le 4m+4$. See Table 7, Fig. 7 and Fig. 8.

Table 7 $CQ_m$ versus $2Q_{4m+1}$, $m=5$

Fig. 7

Distance-wise node distribution of $CQ_5$

Fig. 8

Diff versus d for $m=5$, $3\le d\le 4m+4$, vide Table 7

Here are important observations on diff.

• 1. If $4m+4\ge d\ge 3m+5$, then diff = 0, vide Corollary 4.3.

• 2. If $3m+4\ge d\ge 2m+5$, then diff is equal to $-2C(3m,d-4)+2C(3m,d-2)$ that is negative in this range.

• 3. If $2m+4\ge d\ge m+5$, then diff is equal to $-2C(3m,d-4)\,+\,2C(3m,d-2)$ − $C(2m+1,d-3)\,+\,C(2m+1,d-1)$ − $C(2m,d-3)\,+\,C(2m,d-1)$. Notice that $-2C(3m,d-4)\,+\,2C(3m,d-2):=D$ (say) constitutes the dominant term in the foregoing expression.

  • (a) If m is even, and $d=\frac{3m}{2}+3$, then $D=0$.

  • (b) If m is even, then D is positive at $d=\frac{3m}{2}+3-i$, and it is negative at $d=\frac{3m}{2}+3+i$, yet the absolute value is the same at each, where $1\le i\le \frac{m}{2}+1$.

  • (c) If m is odd, then D is positive at $d=\frac{3m+1}{2}+2-i$, and it is negative at $d=\frac{3m+1}{2}+3+i$, yet the absolute value is the same at each, where $0\le i\le \frac{m+1}{2}$.

  For $2m+4\ge d\ge m+2$, therefore, D is symmetric about the point $d=\frac{3m}{2}+3$, and diff is practically equal to $-2C(3m,d-4)\,+\,2C(3m,d-2)$ whose absolute value is a small percentage of $2C(4m+1,d-3)$ in this range.

• 4. For $m+1\ge d\ge 3$, diff remains positive, and its value progressively declines. At the same time, the value relative to $2C(4m+1,d-3)$ is no longer negligible, particularly for small values of m.

Table 8 presents $n_d$ for certain small values of d and certain large values of d. It relies on the results in Table 6.

Table 8 Computing $n_d$ for $1\le d\le 4$ and $4\,m\le d\le 4\,m+4$, where $m\ge 2$

4.2 Average node distance of $CQ_{m}$

Table 9 computes the average distance of $CQ_m$. It relies on the expression for $n_d$ developed in Table 6. The identities used are: $\sum _{i=0}^nC(n,i)=2^n$ and $\sum _{i=0}^ni\,C(n,i)=n2^{n-1}$.

Table 9 Computing the average distance

5 Concluding remarks

The quad-cube is a special case of a network topology called the metacube [9] that belongs to the family of networks derivable from the hypercube. It has emerged as a viable topology for a system in which the number of nodes exceeds several million. Among other things, it admits a 1-perfect code under a certain condition [5]. This paper presents results relating to its vertex transitivity, distance metric and distance-wise node distribution that significantly enhance its importance from both theoretical point of view and the engineering point of view. Interestingly, the node distribution of $CQ_m$ closely parallels that of $2Q_{4m+1}$, i.e., a set of twin copies of $Q_{4m+1}$.

Graph invariants like Wiener index and surface area [7] of the quad-cube are easily obtainable from the distance-wise node distribution of the graph that appears in Sect. 4.