Introduction

The phenomenon of prototropic tautomerism is common amongst biologically active molecules containing heteroatoms. It has been estimated that about 26% of 1791 marketed drugs can exist as three possible tautomers [1]. To properly determine the mechanism of action of a drug, it is important to know the composition of the tautomeric mixture [2, 3]. However, it is not always the dominant form which interacts with the enzyme or receptor active site. Therefore, all possible tautomeric forms and their relative stabilities should be determined. The Gibbs-free energy is the proper measure of the relative ratio of the tautomers, because it relates directly to the equilibrium constant of the tautomerization reaction. If the energy gap between the dominant form and other form is small enough, roughly about several kcal/mol, there may exist other tautomeric forms in certain amount. If the energy gap is large, roughly more than 10 kcal/mol, it may be assumed that the high-energy forms are not present in the tautomeric mixture. Most often, the prototropic tautomers easily interconvert, especially in water solution, by proton transfer (most often water-assisted) and the determination of relative Gibbs-free energies, giving reliable information on the tautomeric mixture composition. While it is possible to experimentally determine the position of hydrogen atoms in a medicine-ligand complex [4], it is most convenient to model all possible tautomeric forms by means of quantum-chemical calculations. Regarding the computational power of modern computers, it is quite easy to calculate the thermochemical parameters including Gibbs-free energy at the accurate-enough level of theory, often with the so-called chemical accuracy of 1 kcal/mol.

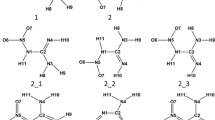
In this study, we focus on the sildenafil molecule, a selective cGMP phosphodiesterase inhibitor, used in male erectile dysfunction treatment [5]. Three distinct tautomeric forms are possible for this molecule (Scheme 1), and we will enumerate them according to Katritzky et al. [3].

Scheme 1
scheme 1

Schematic representation of three possible sildenafil molecule tautomers

Full size image

Tautomers A and B are lactams, and tautomer C is a lactim. Therefore, this is a case of lactam-lactim tautomerism, although for convenience, we use often the terms keto for lactam tautomer and enol for lactim tautomer. The literature data on relative stabilities of these tautomers is very scarce, in fact, we found only one paper which describes the semiempirical AM1 study [6], and its conclusion is that the pyrimidinone tautomers A and B are more stable than 4-hydroxypyrimidine tautomer C. Thus, there is a need to perform a computational study on much more sophisticated level to determine the relative stabilities of these tautomers.

Tautomerism of 2-hydroxypyridine/2-pyridone

In order to find a valid model chemistry to accurately determine tautomer energy differences, we first focus on a very simple and well-studied parent tautomeric system, namely the 2-hydroxypyridine/2-pyridone. We will use the same convention for naming tautomers as for the sildenafil molecule in Scheme 1. We will name the tautomers from 2-hydroxypyridine; thus, there is 2HP_C which is 2-hydroxypyridine itself and the second tautomer is 2-pyridone: 2HP_B (Scheme 2).

Scheme 2
scheme 2

Schematic representation of three possible tautomers of 2-pyrimidone/2-hydroxypyridine

Full size image

The relative stability of these two tautomeric forms in the gas phase presents a challenge to determine, because their stabilities are quite similar. The 2-pyridone form is stabilized by strong carbonyl bond, but the 2-hydroxypyridine form benefits from higher aromaticity of the phenolic ring. Therefore, as these two factors compensate, the relative stability is similar. Some early studies in the gas phase postulated that the 2-hydroxypyridine tautomer is dominant [7, 8]; others found that both tautomers exist in similar amounts [9] and yet another that the 2-pyridone tautomer is slightly dominant [10]. A recent study seems to confirm the last result with an experimental enthalpy difference of 0.46 kcal/mol [11].

As the sildenafil molecule is a medicine acting in vivo in water solution, we are especially interested in modelling the tautomeric equilibria in this environment. In apolar solvents, the 2-hydroxypyridine tautomer seems to dominate, and in polar solvents, the 2-pyridone is dominant regardless of the solvent being protic or aprotic [12, 13] which can be rationalized by higher dipole moment of the 2-pyridone tautomer. Cook estimated the enthalpy gap in polar non-aqueous media to be 3.4 kcal/mol [14]. Recent theoretical estimation by Fu et al. of the Gibbs-free energy at the B3LYP/6–311 +  + G(2d,2p) level including water environment by means of PCM model yielded 3.7 kcal/mol [15].

Tautomerism of 4-hydroxypyrimidine/pyrimidinones

The actual proton transfer in the sildenafil molecule occurs within the 4-pyrimidone/4-hydroksypyrimidine ring; the tautomeric proton can be attached to one of the nitrogen atoms or to the oxygen atom. We will use the same convention for naming tautomer as for sildenafil molecule in Scheme 1. We will name the tautomer from the 4-hydroxypyrimidine, so in case of an enol form of 4-hydroxypyrimidine, we have the 4HP_C and the two pyrimidinone forms: 4HP_A and 4HP_B (Scheme 3).

Scheme 3
scheme 3

Schematic representation of three possible tautomers of pyrimidinone/4-hydroksypyrimidine

Full size image

According to early studies, the 4-hydroksypyrimidine (4HP_C) tautomer is predominant in the gas phase [16]. However, a recent microwave experimental study shows the dominance of the pyrimidinone 4HP_B tautomer [17] which is more stable by 0.48 kcal/mol than 4-hydroxypyrimidine tautomer 4HP_C. The other pyrimidinone tautomer 4HP_A was not detected in the tautomeric mixture. In the same paper, the theoretical estimation at the B3LYP/6-31G(d,p) level yielded 1.0 kcal/mol which is in reasonable agreement with the experimental result. However, the MP2/6–311 +  + G(d,p) calculation gave the reversed stability order and the energy difference of − 1.24 kcal/mol. The fact that MP2 calculation overestimates the enol form stability has been already recognized [18]. The difficulty in studying tautomeric equilibria of these systems is confirmed by another study by Giuliano et al. [19]. The authors performed the B3LYP/6–311 +  + G(d,p) calculation which gave a value of 2.1 kcal/mol, thus overestimating the stability of the keto 4HP_B tautomer. On the other hand, the MP2/6–311 +  + G(d,p) calculations gave − 0.55 kcal/mol favouring the enol 4HP_C tautomer as more stable. Another recent theoretical paper points out that the SCS-MP2 variant of the MP2 method gives proper tautomer order [20]. However, the SCS-MP2 variant, because of introduction of empirical parameters, loses unfortunately its ab initio flavour and belongs rather to first-principles methods, like DFT. According to this study, the keto 4HP_B tautomer is more stable than 4HP_C enol by 0.29 kcal/mol at the SCS-MP2/cc-pVTZ level, which is close to experimental value.

The influence of the other parts of the molecule on sildenafil tautomerism

The fusion with the pyrazole ring in sildenafil molecule ring does not introduce more tautomeric forms because the pyrrole-type nitrogen atom of the pyrazole is methylated. However, this fusion may severely alter the relative values of tautomer, which will be investigated in the course of this study. The other parts of the sildenafil molecule also may influence the tautomeric equilibrium, mainly by the possibility of formation of intramolecular hydrogen bonds.

The aims of the study

In the course of this article, we will try to (1) determine the proper theoretical model chemistry to reliably evaluate the Gibbs-free energy of the sildenafil molecule, (2) calculate the Gibbs-free energy of the three sildenafil tautomers at chosen theoretical level/levels to determine their relative stability and (3) understand the reasons behind the differences of tautomer stability order of sildenafil compared to 4-pyrimidinone/4-hydroxypiridine system by building several in-between model molecules and evaluating the relative tautomer stability for each of them.

Computational details

Main density functional theory (DFT) and ab initio calculations were performed by using the Gaussian 16 suite of programs [21]. The geometric parameters of all molecules were fully optimized and followed by the IR frequency calculations to ensure that the obtained stationary points are true minima on the potential energy surface. For the 2-hydroxypyridine/2-pyridone system, the DFT methods B3LYP [22, 23] and M06-2X [24], ab initio methods: MP2 [25] and CCSD(T) [26, 27] (single-point energy) and compound method CBS-QB3 [28, 29] were employed in connection with basis sets of Pople: 6-31G(d,p) [30], 6–311 +  + G(d,p) [31, 32] and Dunning: aug-cc-pVXZ where X = D,T,Q [33]. The modelling in solution was done by employing the polarizable continuum model [34] (PCM) built in the Gaussian program. The conformational analysis of the sildenafil molecule was done by using the free Avogadro [35] software using the MMFF molecular mechanics force field. The lowest energy conformers were optimized first at the B3LYP/6-31G(d,p) level and finally at the B3LYP/aug-cc-pVDZ and M06-2X/aug-cc-pVDZ levels of theory. Aromaticity of the 6-membered and 5-membered rings was estimated by using the free AromaTcl [36] software. Two aromaticity indices were calculated: geometric — HOMA [37, 38] and electronic — pEDA [39, 40].

Results and discussion

First, we need to choose an appropriate model chemistry which gives tautomer energies of a parent molecule as close as possible to the experimental results. The method should not be very computationally expensive because our main subject — the sildenafil molecule — contains 63 atoms; thus, the number of atomic orbital basis functions will be quite large, and the computations can be very time-expensive.

Choosing the model chemistry

We begin by evaluating the 2-hydroxypyridine/2-pyridone relative tautomer stability at various levels of theory and comparing them to the experimental results. First, the tautomers were optimized at the B3LYP/6-31G(d,p) level. We decided to use the 6-31G(d,p) basis set instead of standard 6-31G(d) because of the presence of additional polarization p-function for hydrogen atoms in the former, which is better suited for modelling the proton-transfer and prototropic tautomerism. The obtained enthalpy and Gibbs-free energy are presented in Table 1.

Table 1 The enthalpy and Gibbs-free energy of the 2-hydroxypyridine (2HP_C) and 2-pyridone tautomers (2HP_B) optimized at the B3LYP/6-31G(d,p) level of theory
Full size table

It follows from Table 1 that this simple theoretical level agrees well with the experimental results, especially in the water solution. In the gas phase, the order of tautomers is reversed, but the enthalpy difference is very small. This can be of course because of a fortuitous cancellation of errors, so we followed with B3LYP calculations using more extended orbital basis sets. The results are gathered in Table 2 where we give only the enthalpy as the focus is on comparison with the experiment, and the experimental data is enthalpy. We will follow the convention of subtracting the pyridone tautomer energy from the hydroxypyridine tautomer energy in the following tables as the pyridone tautomers most often have lower energy, and operating the positive values is more convenient.

Table 2 The relative enthalpy of the 2-hydroxypyridine/2-pyridone tautomers optimized at the B3LYP level of theory with various basis sets (ACCX = aug-cc-pVXZ)
Full size table

It follows from Table 2 that larger basis sets give the proper tautomer order in the gas phase. In the water solution modelled by the PCM method, the theoretical methods seem to overestimate the pyridone tautomer stability in comparison to the experimental result. The results of calculations using the correlation-consistent basis sets behave as expected with ACCT and ACCQ basis sets giving almost the same result. However, even the simpler ACCD basis set gives a result within 0.2–0.3 kcal/mol from larger bases; thus, for sildenafil molecule, the ACCD basis set should be of appropriate size. Therefore, we decided that our method of choice for evaluation of sildenafil molecule tautomer stability will be B3LYP/aug-cc-pVDZ.

We also tested the other DFT method, namely M06-2X, a compound method: CBS-QB3 and two ab initio methods: MP2, CCSD(T) (single-point energy). The results are compared in Table 3.

Table 3 The relative enthalpy of the 2-hydroxypyridine/2-pyridone tautomers optimized at the various levels of theory and aug-cc-pVDZ (ACCD) basis set
Full size table

Using the MP2, M06-2X and CBS-QB3 calculations, the tautomers were fully optimized, but in the case of the CCSD(T) method, the single-point energy calculation was performed on B3LYP and MP2 optimized geometries, and the proper thermal corrections to enthalpy were added.

It follows that ab initio methods seem to overestimate the stability of enol (2-hydroxypyridine) tautomer in gas phase, a fact that is well known for the MP2 method and was mentioned in the “Introduction”. A similar problem is present with the CBS-QB3 compound method and also with the M06-2X DFT method. It is interesting to note that the M06-2X functional results are close to the MP2 results. In the water solution, the order of tautomers is at least proper; however, we observe the same bias — the enol tautomer stability is overestimated by other methods comparing to B3LYP and the experimental results.

The MP2, CCSD(T) and CBS-QB3 methods are too time expensive to employ them for such a large molecule as sildenafil. As the M06-2X method gives similar results to them, but at a substantially lower computational cost, we decided to use it as a second method of choice and to compare its results to the B3LYP results. Thus, the second theoretical method used for the sildenafil molecule will be M06-2X/aug-cc-pVDZ.

Tautomerism of sildenafil molecule

The initial structure of sildenafil molecule was downloaded from the PubChem database [41]. This is the B type of pyrimidinone tautomer. The two other possible tautomeric forms A and C were built on the basis of the PubChem structure by proper shifts of the proton. Next, these three tautomers were optimized at the B3LYP/6-31G(d,p) level of theory in gas phase and water solution using the PCM model. The Gibbs-free energy and relative energies of these structures are gathered in Table 4.

Table 4 The Gibbs-free energy/relative energy of the sildenafil tautomers optimized at the B3LYP/6-31G(d,p) level of theory in the gas phase and in water environment modelled by the PCM method
Full size table

From these initial results, we see that the keto B tautomer is most stable in both environments. The most striking feature is that the energy difference between it and the enol C tautomer is very large (13.83 kcal/mol) comparing to the 4-hydroxypyrimidine/4-pyrimidinone (0.48 kcal/mol) mentioned in the “Introduction”. In water environment, this energy gap stays at a very similar level. In the gas phase, the energy of the A form is slightly lower than C so both A and C are not detectable in the tautomeric mixture. However, in water solution, the energy gap to A pyrimidinone form is lowered.

As the sildenafil molecule contains some rotatable single bonds, it is necessary to perform a conformational analysis to obtain the lowest energy conformations of all tautomers. This should not have a large impact on the result, but is necessary to perform, if our aim is to obtain the real lowest energy tautomers. All three tautomers were thus subjected to systematic rotor search procedure; all single bonds were rotated and all possible conformers generated using the Molecular Mechanics MMFF force field. The resulting conformers were ordered by increasing energy, and the 5 lowest energy conformers for each tautomer were chosen for optimization at the B3LYP/6-31G(d,p) level in the gas phase. The Gibbs-free energies of the optimized conformers are presented in Table 5.

Table 5 The Gibbs-free relative energy of the lowest energy conformers of sildenafil tautomers A, B, C reoptimized at the B3LYP/6-31G(d,p) level of theory in the gas phase. The “starting structure” is the original structure before the conformational search. Lowest energy conformers are in bold
Full size table

Note that the order of conformers in the Table 5 is by the MMFF energy, and it follows that according to B3LYP/6-31G(d,p), the order of stability is a little bit different. In each column in the last row, the starting structure which was optimized before the conformational search is shown. It follows that for all three tautomers, thanks to conformational analysis, we obtained the lower energy conformers. The energy lowering is at a level of fraction of kcal/mol but it nevertheless exists. In Table 6, we gathered the lowest energy conformers of our 3 sildenafil tautomers.

Table 6 The Gibbs-free energy/relative energy of the sildenafil tautomers optimized at the B3LYP/6-31G(d,p) level of theory in the gas phase
Full size table

Comparing to Table 4, the absolute values of Gibbs-free energy are lower, but relative values are similar because the energy lowering were quite similar, and thus, they did not influence the relative energies much. Next, we reoptimized these best conformers at the B3LYP/aug-cc-pVDZ level of theory. The results are gathered in Table 7.

Table 7 The Gibbs-free energy/relative energy of the sildenafil tautomers optimized at the B3LYP/aug-cc-pVDZ level of theory in the gas phase and in water environment modelled by the PCM method
Full size table

It follows from Table 7 that at this level of theory, the B tautomer is still dominant; however, the energy gap to A and C is slightly lowered. For the water solution, the similar trend is observed, the B tautomer is dominant but the gap to A is lowered by about 2 kcal/mol (compare Tables 7 and 4).

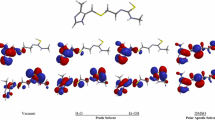
The 3d models of optimized sildenafil tautomers are shown in Fig. 1.

Fig. 1
figure 1

The 3d models of tautomers of sildenafil molecule optimized at the B3LYP/aug-cc-pVDZ level of theory

Full size image

One striking structural feature is that in both A and B tautomers, there exists an intramolecular hydrogen bond between the N–H of the pyrimidinone ring and O from the ethoxy group of the second phenyl ring. A second, much weaker hydrogen bond is formed by C–H of the phenole ring and the pyrimidine-type nitrogen atom of the pyrimidinone. The whole fragment of the sildenafil molecule is appropriately rotated to facilitate the hydrogen bonds, and thus, the three rings lie approximately in one plane. The case of C tautomer is different. Only the weak C–H …. N hydrogen bond is possible, but there is an unfavourable steric interaction of oxygen and nitrogen atoms from both 6-membered rings, which causes the rotation of the C–C bond connecting the rings, and thus, the two rings do not lie in one plane. It is a factor which certainly destabilizes the C tautomer comparing to A and B tautomers.

As a second method of choice, we performed the M06-2X/aug-cc-pVDZ calculations for the lowest conformers of the sildenafil molecule. The results are gathered in Table 8.

Table 8 The Gibbs-free energy/relative energy of the sildenafil tautomers optimized at the M06-2X/aug-cc-pVDZ level of theory in the gas phase and in the water environment modelled by the PCM method
Full size table

Comparing Tables 8 and 7, we see the trend previously observed for 2-hydroxypyridine tautomers that the M06-2X method slightly favours the enol tautomers both in gas phase and in water solution. Therefore, the energy difference between enol tautomer and keto tautomers is lowered by about 2 kcal/mol. Also, the energy difference between two keto tautomers is lowered by about 1 kcal/mol.

Tautomerism of the model in-between molecules

To look more deeply into the reasons behind the relative energy differences of A, B and C tautomers, we decided to build and optimize model molecules which are in-between 4-hydroxypyrimidine/4-pyrimidinone and sildenafil and to compare the relative tautomer energies at each step. As we need only the qualitative explanation, the simple B3LYP/6-31G(d,p) model was chosen for these calculations. We decided to use the following model molecules.

Thus, first, we observe how the fusion of the pyrazole ring influences the tautomeric equilibrium of 4-hydroxypyrimidine; second, we observe how the addition of the ethoxy-phenyl ring affects the equilibrium, and at the end, we observe the effect of addition of the rest of the sildenafil molecule. The results obtained are gathered in Table 9.

Table 9 The Gibbs-free energy (kcal/mol) of the model in-between and sildenafil tautomers optimized at the B3LYP/6-31G(d,p) level of theory in the gas phase
Full size table

The results are shown also in Fig. 3 to better illustrate the trends in the energy change.

The difference of energy between A and B tautomers is changing not very much. It basically oscillates within 10 kcal/mol for all the studied molecules. A very different picture emerges for C and B relative energy. For the starting 4-hydroxypyrimidine/4-pyrimidinone system, this energy gap is very small. Experimentally, it is determined as 0.48 kcal/mol and theoretically estimated by us at 1.29 kcal/mol. Thus, these two forms coexist in equilibrium. However, even the first step – fusion with pyrazole ring — dramatically influences this equilibrium by strongly disfavouring the C form. For the 4HP-pz system, the energy gap is 7.55 kcal/mol, and the C tautomer is already almost not present in the tautomeric mixture. The reason for this behaviour can be associated with changes of aromaticity. The 6-membered ring of the C form is highly aromatic comparing to the B form. A very rough and approximate measure of this aromaticity can be drawn from the picture of the “aromatic” bonds in which the order is between 1 and 2. This is nicely illustrated in Fig. 2: almost all the ring bonds of 4HP_C are aromatic but only two of them in 4HP_B. Now, let us compare the 4HP-pz molecules (after the fusion with pyrazole): the 4HP-pz_C tautomer lost one aromatic bond and the 4HP-pz_B tautomer got two additional aromatic bonds. Thus, we may expect increase of aromaticity of the B tautomer (stabilization) and decrease of C (destabilization).

Fig. 2
figure 2

Model in-between molecules optimized at the B3LYP/6-31G(d,p) level of theory

Full size image

The next step, addition of the phenyl ring with the etoxy group, enlarges the energy gap between C and B tautomers up to 13.6 kcal/mol. This time, the reason is a strong intramolecular hydrogen bond present in B (and also in A) but not present in C. Additionally, in the C tautomer, there exists an unfavourable steric repulsion between O (ethoxy group) and N (6-membered ring) atoms.

In order to understand deeper the trends presented in Table 9 and Fig. 3, we performed the aromaticity estimation using two indices: geometric HOMA and electronic pEDA. The results are presented in Tables 10 and 11.

Fig. 3
figure 3

The differences in Gibbs-free energy between tautomers at the B3LYP/6-31G(d,p) level of theory: A and B in blue, B and C in orange

Full size image
Table 10 HOMA index of various parent molecules of sildenafil
Full size table
Table 11 pEDA index of various parent molecules of sildenafil
Full size table

The value for 5-membered ring for 4HP is absent because there is no 5-membered ring in this molecule. In order to get reference for the indices of a free 5-membered ring, we optimized the N-methylated 3-Me-pyrazole — see Fig. 4. The aromaticity indices for this molecule are as follows: HOMA = 0.8906 and pEDA =  − 0.01782.

Fig. 4
figure 4

The N-Me 3-Me-pyrazole molecule

Full size image

The geometric HOMA index is based on the length of the bonds. Basically, HOMA index tends to unite when the bond lengths of the ring are all close to the aromatic bond length similar to that in benzene. On the contrary, if the bonds are purely single and double, the HOMA tends to 0. As we see in Table 10 for 4HP molecule, the HOMA for C tautomer is quite close to 1, thus is highly aromatic. The B tautomer is much less aromatic, and the A tautomer is even less aromatic. If we take a look at Fig. 2, we see that in case of B tautomer, the two aromatic bonds are separated by a double bond, and in the A tautomer, both are connected to the same pyrrole-type nitrogen atom. Apparently, the latter is regarded by HOMA algorithm as less aromatic. Fusion with pyrazole ring is reflected by de-aromatization of the C ring (from 0.99 to 0.94) and aromatization of the A (from 0.42 to 0.59) and B (0.63 to 0.68) rings. The aromaticity of A and B rings are now much more similar; however, still, the B tautomer is more aromatic. Addition of ethoxy-phenyl ring still increases the aromaticity of A and B tautomers but do not lower that of C tautomer, and the final addition of the rest of the sildenafil molecule does not alter the situation much.

As far as the 5-membered (pyrazole) ring is concerned, we see that for the 4HP-pz molecule, it loses its aromaticity for B tautomer and especially for C, but slightly increases for A. The aromaticity of the 5-membered ring does not change much for the consecutive, more complex molecules.

Regarding the pEDA index, it is defined here as the electron excess/deficiency from the ideal Huckel sextet (6 pi electrons). Thus, we see that for the 4HP molecule, we observe a slight excess for highly aromatic C tautomer (only 0.15e) and much larger excess for A and B molecules (more than 0.5e). Such large pi-electron excess means lower aromaticity, and this picture is in accordance to HOMA — the B tautomer is more aromatic than A. After fusion with pyrazole, the pi-electron excess of C tautomer is increased, and this is in accordance with the decrease of HOMA. However, for A and B tautomers, pEDA indicates similar increase of pi-electron excess; therefore, we see that the fusion with pyrazole increases the pi-electron excess for all tautomers. As it follows from Table 11, for the rest of the molecules, there is no great change in pi-electron excess of the 6-membered ring.

Regarding the 5-membered ring, it becomes more pi-deficient which can be especially seen for B and C (the largest change) tautomers.

Conclusions

  • The ab initio MP2, single-point CCSD(T), composite CBS-QB3 method and also the DFT methods B3LYP and M06-2X were tested at 2-hydroxypyridine/2-pyridinone system and compared to the experimental results

  • The B3LYP/aug-cc-pVDZ (B3LYP/ACCD) seems to be a reasonable model chemistry for studying the sildenafil molecule’s thermodynamic aspects of tautomeric equilibrium composition.

  • The ab initio MP2, single-point CCSD(T), composite CBS-QB3 method and the M06-2X method in connection with ACCD basis set gave the reversed tautomer order for the gas phase and weaker dominance of the keto form than the experiment for the PCM modelled water solution.

  • According to the B3LYP/ACCD method in the gas phase, the most stable tautomer is the B keto form in which the tautomeric proton is connected to the nitrogen atom closest to the carbonyl bond. The Gibbs-free relative energy to the next stable A keto form is 10 kcal/mol. Thus, the keto B tautomer dominates in the gas phase

  • For the water solution modelled by the PCM method at the B3LYP/ACCD level, the most stable is the same B tautomer; the only difference is that the energy gap to the next stable A keto tautomer is only 5.5 kcal/mol. In the water solution (e.g. in vivo), the B tautomer dominates, but there is some small amount of the A tautomer.

  • The C enol tautomer is the least stable both in gas phase and water solution with the difference in Gibbs-free energy to B keto tautomer close to 12 kcal/mol. It may be safe to assume that regardless of the conditions, this tautomer is not present in the tautomeric mixture.

  • The M06-2X/ACCD results were similar, and the differences were quantitative. For the gas phase the A keto form was less stable by 9 kcal/mol and for water solution by 4.3 kcal/mol. The C form was less stable by about 10 kcal/mol in both environments.

  • The calculations at the B3LYP/6-31G(d,p) level of theory for series of parent molecules shed some light on the reasons behind the differences of sildenafil tautomerism and parent 4-hydroxypyrimidine tautomerism.

  • The fusion with pyrazole ring results in large destabilization of C tautomer mainly by causing electron excess in the 6-memberd ring and thus decreasing its aromaticity. This is documented by the changes in HOMA and pEDA aromaticity indices. Further destabilization of this tautomer is caused by unfavourable steric interactions of oxygen and nitrogen atoms of two 6-membered rings and the lack of strong intramolecular hydrogen bond present in A and B tautomers.

  • The relative energy between the A and B tautomers does not change much for the consecutive model molecules and is only about 1 kcal/mol larger than in the smallest parent molecule.