Abstract
In the present account, we investigate electronic properties of diphenylfulvene and its derivatives substituted in phenyl rings. The results were compared with the analogous properties of fulvene and its derivatives with the same substituents at the exocyclic carbon atom. All properties were evaluated and compared in the ground electronic S0 state and in the first excited T1 triplet state. These properties are dipole moments, charges, number of π electrons, and aromaticity of the fulvenic, five-membered ring in the two sets of compounds. The latter property was estimated by the harmonic oscillator model for aromaticity (HOMA) index and, for the fulvenes group, by the calculation of aromatic stabilization energy in both electronic states. It was also investigated whether Baird’s rule alone can account for the aromaticity differences in the two electronic states.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
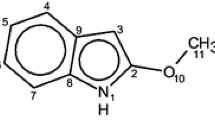
Diphenylfulvene is a derivative of fulvene, a nonalternant hydrocarbon, which is an isomer of benzene. Diphenylfulvenes, substituted at the para position in benzene ring, are shown in Scheme 1. The structures presently considered were as follows: diphenylfulvenes substituted at phenyl rings and, for comparison, fulvenes with exocyclic substituents. Fulvene has been shown by spectroscopic methods to be a planar, non-aromatic molecule of C2v symmetry with C-C bonds that alternate in length, consistent with localized single and double bonds [1, 2]. The fulvene properties, as well as properties of its derivatives (fulvenes), have been the subject of numerous experimental [2,3,4,5] and theoretical investigations [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Further, the methods for generation of fulvenes and their rich cycloaddition chemistry have been recently reviewed [3]. The properties of fulvenes studied by theoretical methods have included the aromaticity and electronic structures [5, 7,8,9,10, 12,13,14,15,16,17,18,19]. It has been found that electron-donating substituents attached to the exocyclic carbon in fulvenes significantly increase their aromatic character [5, 7, 13, 14]. However, we have found only one investigation devoted to the computational studies of diphenylfulvene (its geometry and spectroscopic properties [4]). Apart from the focusing on the electronic and geometric structure of fulvenes in the ground electronic states S0, papers have also focused on these properties in the lowest excited triplet state, T1. For comparison, the aromaticity of fulvenes in the S0, S1, and T1 state, a bond order of Jug [22] was used [1]. More recently, other indices, based on geometric, magnetic, electronic, and energetic properties of several substituted fulvenes, were regressed against ΔS−T, the energy difference between the two states [18]. Interest in the aromaticity of fulvenes in excited states stems from Baird’s rule on excited-state modification of aromaticity and antiaromaticity of molecules on transition from the S0 to the excited S1 and T1 states [23], which is elicited from the deduction that benzene in the T1 state is antiaromatic [24]. Arguments based on the simple perturbation theory indicate that the rules for ground state aromaticity are reversed in the 3ππ* state (4n rings display “aromatic” character, whereas 4n + 2 systems display antiaromaticity). The conclusion is based on the Dewar resonance energy [25] values of the lowest ππ* triplet state of a cyclic hydrocarbon defined relative to the open-chain polyene which contains the same numbers of carbon atoms. This view has been shared in a few papers but none have estimated either the resonance energy for fulvenes or other indices usually applied for characterizing aromatic properties.
Molecule of diphenylfulvene substituted in phenyl rings. In fulvenes, numbering of the atoms from C1 to C10 is the same
One of the proposed models explained that the differences in the S0 and T1 states are attributed to the adaptation of their electron densities [6] to conform to the different aromaticity rules in the two states (Hückel rule in S0 and Baird’s rule in the T1 state). The model also explained calculated dipole moment changes between the two states that differ in the distribution of electron density (negative charge) between fulvenic ring and the exocyclic carbon atoms bearing substituents [18].
It appeared that, in both states, the sign of dipole moment depends strongly on the electronegativity of the substituents. The difference between C5H4-C(NO2)2 and C5H4-(N(CH3)2)2 amounts to 11 D; in the first compound, it is directed from the CR2 group to the ring, and in the second compound, the reverse sign of the dipole moment was found. Similar difference in dipole moments in the T1 state is 1.5–4.7 D. In ref. 12, a comparison of the dipole moments of fulvenes, fulvalenes, and azulene in the S0 and T1 revealed that owing to the reversal of Hückel’s aromaticity rule in T1, the dipoles should be in the opposite direction compared to the molecules in the S0 state (but the dipole moments should be of comparable magnitude).
The aim of the present study was to calculate the charge distribution and aromatic properties in the molecules of a group of diphenylfulvenes and compare them with those of a group of substituted fulvenes bearing the same substituents. Diphenylfulvenes are supposed to display multiple cycloaddition profiles, as has been thoroughly examined for fulvenes. We aimed to evaluate the effects of the two additional phenyl rings on the electronic properties of the reactive five-membered rings [3]. For the investigation of the aromaticity, two measures were applied: first, HOMA, based on the bond lengths of π electron cyclic system, which is the most frequently used index for evaluating the aromatic character of a plethora of compounds [26, 27]. For fulvenes, the second measure involved the calculation of the aromatic stabilization energy, ASE, for S0 and T1 states in order to determine whether the two measures generate compatible conclusions. The HOMA and ASE values are correlated with evaluated properties such as the dipole moments, charges of the five-membered rings, and number of π electrons in the rings. The properties and their correlations are compared in the two electronic states. The sites of the greatest spin density in the triplet state are to be identified.
Theoretical methods
Molecular geometries were optimized at the B3LYP/6-311++G(d,p) level as well as the NBO charges. The QTAIM properties were obtained with Keith’s AIMAll software [T.A. Keith, AIMALL, version 11.12.19, www.aim.tkghristmill.com 2011]. All other calculations were carried out with Gaussian 09, Revision D.01, implemented with the NBO 3.1 method [28].
The Hammett σ p constants were taken from the compilation of Hansch et al. [29].
Results
Dipole moments
The starting point for our investigations was the calculation of dipole moments of eight diphenylfulvenes in the S0 and T1 states and their comparison with the analogous properties of fulvenes bearing the same substituents. The results are shown in Table 1.
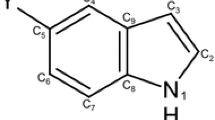
The dipole moments are directed along the z-axis from C10 through C9 and the center of the C2-C3 bond. The positive value of dipole moment (for R=NO2, CN, NC, Cl) indicates that the electron density in the region of space surrounding the C10=R2 or C10-(C6H4-R)2 group is larger than that in the region surrounding C5H4 five-membered ring. Therefore, the electric charge of the latter is positive, while that of the first region is negative. In fulvenes and diphenylfulvenes with the negative dipole moments (R=H, OH, NH2, N(CH3)2), the charges of both moieties are reversed. Such behavior is expected based on the electronic properties of the substituents, i.e., their electronegativity, and mirrored by good correlations of the calculated dipole moments with Hammett σ p constants. Correlation coefficients for the plots of the dipole moments against σ p are 0.990 (S0) and 0.957 (T1) for fulvenes, and 0.962 (S0) and 0.947 (T1) for diphenylfulvenes. Therefore, it is convenient to organize these and the other properties by similar correlations with the Hammett constants.
It is worth noting that for both groups of compounds, the dipole moment in T1 state is more positive (or less negative) than in the S0 state (the difference being 2.6–3.8 D for diphenylfulvenes, 1.4–4.7 D for fulvenes). This is equivalent to a flow of the electron density from the ring to the exocyclic C10=R2 group.
Figure 1 illustrates the impact of the substituent type on the values and directions of dipole moments of diphenylfulvenes.
Dipole moments of diphenylfulvenes bearing three substituents, calculated at the B3LYP/6-311++G** level, in the S0 and T1 states
The conclusion provided by dipole moments can be supplemented by the results of calculation of the total charges of the five-membered ring in both groups.
Electron density
The results of the calculated sums of atomic charges in the five-membered rings are shown in Table 2. It can be seen that in both electronic states, the charge of the five-membered ring is more positive (or less negative), as the substituent R is more electron-accepting.
Sum of charges in the fulvene ring correlated very well with the Hammett constants. The correlation is shown in Fig. 2a (for fulvenes) and 2b (for diphenylfulvenes).
Comparison of summed atomic charges of atoms in the five-membered fulvenic ring in substituted diphenylfulvenes (b) and fulvenes (a). Similar comparison of π electron numbers in diphenylfulvenes (d) and fulvenes (c)
Regardless of whether R had the donor or acceptor properties, in the T1 state, the five-membered ring in diphenylfulvene behaved as an electron donor to the rest of the molecule. The value of the charge transferred between the five-membered ring and the rest of the molecule was equivalent to providing to the molecule an additional dipole moment directed from C10=R2 or C10-(C6H4R)2 to the ring.
To complete the electronic characteristics of fulvenes and diphenylfulvenes, we also determined numbers of π electrons in the five-membered rings (Table 3). Previously, the correlation of the number of π electrons in the monosubstituted fulvenes with σ p + Hammett constants and aromaticity index NICS were investigated [13], in addition to the correlations of a few magnetic indices of aromaticity with ASE and HOMA for disubstituted fulvenes [14]. However, the correlations had been studied only for the molecules in the ground electronic state.
Data from Table 3 are plotted in Fig. 2c and 2d using the same graduation every 0.2 e on all vertical axes for comparison of the total charges of the fulvenic rings with the number of π electrons.
The lower slopes of all four lines for diphenylfulvenes compared to those for fulvenes indicate the attenuation of the substituent effects in the first group of compounds.
Both N π (S0) as N π(T1) correlate well with the σ p Hammett constants (Fig. 2c, d). In all compounds, there are more π electrons in S0 than in the T1 state. Therefore, the five-membered rings are more negative in S0 than in T1 both for fulvenes and diphenylfulvenes (Fig. 2a, b). Data in Table 3 prove that the substituents in both electronic states have similar impact on the number of π electrons in the ring.
For more negative substituents, the number of the π electrons is lower in both states. It can be seen that, in the T1 state, the total electron density as well as the π electron density leaks from the five-membered ring. The decreasing number of π electrons in T1 is in accordance with the tendency indicated by Baird’s rule. One can expect that in the range 4.67–5.12 electrons (Table 3, fulvenes in the T1 state) and in the range 4.96–5.06 electrons (Table 3, diphenylfulvenes in the T1 state), the lesser (electrons), the better (for aromatic properties). However, the question is how much lesser is better? We would like to take note of one point: the differences of π electrons number in the T1 and S0 states for all compounds are not as large as one might expect. The highest difference between N π(T1) and N π(S0) is −0.4 e in fulvenes and −0.2 e in diphenylfulvenes (both for R=NH2, columns 4 and 7 in Table 3). Differences in N π calculated for one state (S0 and T1) and different substituents are 0.6 and 0.4 e for fulvenes and 0.2 and 0.1 e for diphenylfulvenes (columns 2, 3, 5, and 6 of Table 3).
Aromaticity
In view of the previously reported findings that anti- or non-aromatic fulvenes become aromatic after excitation to the first triplet state, we would like to investigate the impact of the insertion of two benzene rings between the fulvene ring and the substituents on the aromatic properties of the diphenylfulvene molecules with respect to fulvenes, in the S0 and T1 states.
For this purpose, the commonly used aromaticity index, HOMA, was used. The results are shown in Table 4. The most interesting fact is that, for fulvenes in the ground state, the HOMA index is negative for the substituents extracting electrons from the ring (and for R=H) and positive for the electron-donating ones.
For fulvenes with the first six substituents, index HOMA in T1 is larger than that in S0. However, for fulvenes with R=NH2 and R=N(CH3)2, which in S0 may be regarded as moderately aromatic, index HOMA is significantly lower in the T1 state. The fulvenes bearing those substituents possess the greatest number of electrons and π electrons in both states (Tables 2 and 3). This finding is in agreement with the 4n + 2 rule for the S0 state: the more π electrons in the ring, the more aromatic it turns out, while for T1, the analogous 4n rule does not favor the rings possessing significantly more π electrons than 4, as is in the two fulvenes with the electron-donating substituents (N π = 5.1). This is in accordance with the crossing plots of the HOMA index vs. σ p in both states, shown in Fig. 3a. For fulvenes in T1 state, the increase in N π by 0.4 e brought about decrease in HOMA of 0.3. In diphenylfulvenes, a slight increase in N π electrons in T1, equal 0.1 e, also brought about a slight decrease in HOMA (Fig. 3b). Evidently, the effect of attenuation of impact of electron-donating substituents comes into play. The data in Table 4 also show that, in the T1 state of diphenylfulvenes, we observe an increase in the HOMA index, as compared to that in S0 and hence aromaticity, for the all substituents in the table. Thus, the two lines in Fig. 3b do not cross. This is probably the first observation that the 4n Baird’s rule for aromaticity can be controlled by substituents in the triplet state. Owing to these different indications for aromaticity in both states, the slopes for the plots of HOMA (S0 state) and HOMA (T1 state) against the Hammett constants are of the opposite sign (−0.995 and +0.976). In other words, in the S0/T1 states, the more/less electrons, the better (for the aromatic properties).
Dependence of HOMA index on the electronegativity of substituents for fulvenes (a) and for diphenylfulvenes (b)
The latter properties of molecules in excited states which should be aromatic according to Bairds’ rule were generally investigated for molecules with 4n π electrons [30,31,32,33,34,35,36] (for instance, annulenes [36] or cationic fulvene [31, 32]). The compounds studied here show amplified aromatic properties in T1 state in spite of having π electrons’ number appreciably different than the nearest 4n value.
The changes in aromatic properties when they are compared in both electronic states are routinely explained by Baird’s rule which also rationalizes the present results. Therefore, the effects of the not quite so large differences in the N π (0.6 electrons) generated large leaps of HOMA in fulvenes in the S0 state; from −0.55 (for R=NO2) to 0.42 (for R=NH2), larger than we could expect. Corresponding values were lower for diphenylfulvenes owing to the attenuation of the substituent effect by phenyl rings, inserted between substituents and the fulvenic ring (0.2 e, difference in HOMA from −0.22 to 0.04).
However, what about differences in the number of π electrons between the two electronic states? The largest values were −0.4 e (for fulvenes) and −0.2 e (for diphenylfulvenes). For some molecules (e.g., C6H4-(CN)2), the difference is as small as −0.1 e (Table 3). However, for this compound, the differences in HOMA are very significant: −0.38 in S0 and 0.44 in T1. Therefore, we suspect that the number of π electrons is not the only reason for the larger values of the aromaticity indices in the T1 state. Other contributions to the larger values of aromaticity indices in the T1 state will be discussed in a forthcoming paper.
Figure 3 displays not only the opposed effects of the electron density within the ring (dependent on substituent) on HOMA in both electronic states but also degree of attenuation of the impact of substituents in diphenylfulvenes (compared to the substituents impact in fulvenes), owing to a larger separation of substituents from the ring.
In order to investigate the relation of the π electrons number with aromaticity, the latter was additionally investigated by the calculation of the aromatic stabilization energy, ASE. The reaction scheme used was the same that was found to be the best (out of six investigated) for the ASE evaluation in 105 five-membered π electron system [37]. It has been stated that the homodesmotic Scheme 2 was the most reliable and performed best as the ASE evaluation standard. Other schemes, especially those containing acyclic reference compounds did not yield satisfactory results. The reaction scheme has been previously used only for the evaluation of aromaticity in the ground electronic state [37].
Homodesmotic reaction, used for the calculation of the aromatic stabilization energies of fulvenes
ASE was calculated as a sum of energies of the molecules on right side minus a sum of energies of reagents (on the left side). The more negative ASE, the more aromatic one (or more) of the products. The systems with strongly positive ASE are antiaromatic. In order to use the scheme for molecules in the T1 state, the energy of one molecule for each side of the scheme was calculated in its T1 state. The molecules were forth on the left side and first on the right side (the latter being the molecule whose ASE is to be calculated). The values of ASE for fulvenes are shown in Table 5.
It can be seen that the stabilization energy in the S0 state is, for the most substituents, positive; fulvenes with such substituents can be considered as antiaromatic. For two electron-donating substituents, the negative stabilization energy indicates that the augmented number of the π electrons in the ring is linked to some aromatic character. In contrast, in the T1 state, the ASE values are all negative and lower than those in the S0 state up to −35 kcal/mol. The smallest decrease in the stabilization energy is found for the fulvenes substituted with NH2 and N(CH3)2, which exhibited some aromatic characteristics also in the ground state. The largest T1-S0 values (−35 and −34 kcal/mol) characterize molecules for which the difference in N π is very small (−0.2 and −0.1 e). This comparison validates our suggestion that Baird’s rule is not the only reason for the larger aromaticity in T1.
A comparison of the two measures of the aromaticity augmentation in the triplet state of fulvene is relevant. Therefore, the difference in the ASE value in the T1 state vs. that in the S0 state is plotted against the similar differences of the HOMA index. The correlation between the two measures is shown in Fig. 4. We may think that the two measures of aromaticity are equivalent for comparison of the aromatic properties in the two electronic states.
Comparison of two gauges of difference in aromaticity of the fulvene ring in substituted fulvenes (Estab, based on the aromatic stabilization energy and HOMA, based on the geometric criteria)
Some remarks on the diphenylfulvene/fulvene geometry
It has previously been found that the result of phenyl torsion angle calculation for diphenylfulvene is 46°, at the B3LYP/6-311+G)(d,p) level [4]. Here, we noticed that this angle, in the S0 state, varied significantly for different substituents, being the largest for the ones with the most electron-accepting properties. The regression coefficient of the torsion angle with the Hammett sigma constant is 0.950. We cannot find any reason for such correlation.
Another property, which to our knowledge has not been previously described, was the transformation from a diene-like five-membered fulvenic ring in the two groups of compounds, which they possess in the S0 state, into the ene-like one (only one double bond out of five) in the T1 state. The C-C bond lengths in diphenylfulvene, starting from C9, are 1.47, 1.36, 1.46, 1.36, and 1.47 in the S0 state and 1.42, 1.46, 1.36, 1.46, and 1.42 in the T1 state.
Spin densities
We investigated the free spins in the T1 state by using the AIM method. It was found that in fulvenes, the most part of the two spins (about 1.3–1.4) is located in the ring, and two atoms, C1 and C4, carry about 0.5 of the free spin each. The rest of spin density is dispersed on C10=R2. In diphenylfulvenes, for all substituents, about 1.2 of free spin is located in the five-membered ring. Most of the spin density is found at the three carbon atoms: two at the same position as in fulvenes’ molecules and the third at the carbon C10 that is a shackle between the three rings.
Conclusions
The five-membered ring charges in both groups of compounds strongly depend on the electronic properties of substituents, both in the S0 and T1 states. They range from 0.13 to −0.46 e (fulvenes, S0) and from 0.29 to −0.12 e (fulvenes, T1). For diphenylfulvenes, the corresponding values are from −0.05 to −0.22 e (S0) and from 0.13 to 0.01 e (T1). The electronic properties of the both groups of compounds in S0 appeared more susceptible to the influence of substituents, when compared to the case of T1. At the moment, we cannot propose any reason for this greater impact of substituents on the electronic properties in the ground state than in the T1 state. It would be interesting to determine whether a similar effect can be observed in other systems. It can also be seen that in fulvenes the increments of the five-membered ring charges (0.59 and 0.41) were larger than those in diphenylfulvenes (0.17 and 0.12).
The ASE has been, to our knowledge, evaluated for the first time in the T1 state by a homodesmotic reaction, characterized by the same number of bonds between the given atoms in each state of hybridization both in products and reactants, and the same number of hydrogen atoms. In addition, the reaction scheme was modified by taking into consideration molecules possessing the cyclopentadiene ring in the T1 state. As a result, the number of reagent and product molecules in the S0 and T1 states matched. It appeared that the two measures of aromaticity based on different premises generated a coherent description of the aromaticity differences for fulvenes in the T1 and S0 states, with the correlation of the differences of HOMA with those of ASE being high (R = -0.975, Fig. 4).
It was found that increment of dipole moments in diphenylfulvenes from S0 to T1 showed similar trend as in fulvenes. The dipole values, charges of five-membered rings, and number of π electrons as well as aromaticity indices correlated well with the electronegativity of substituents gauged by the Hammett σ p constant, in spite of different environment than that used for determining the substituents electronic properties [29]. Therefore, the σ p constants helped us in sequencing the properties, for diphenylfulvenes and fulvenes.
The calculated number of π electrons in the triplet state was 4.7–5.1 for fulvenes and 5.0–5.1 for diphenylfulvenes (Table 3). The values are significantly higher than those given by Baird’s rule for the triplet state, 4n (the nearest value being 4). Nevertheless, the investigated molecules are characterized by moderate aromatic properties, expressed as HOMA indices 0.46 and 0.38 for fulvene and diphenylfulvene substituted by 2NO2 (Table 4). The ASE values, calculated only for fulvenes, also indicate significant aromatic properties of the molecules in the T1 state. It was found that even very small differences in the number of π electrons (0.1 e, Table 3, for C6H4-(CN)2 in the S0 and T1 states) are accompanied by a significant differences in the aromaticity measures: the HOMA increases from −0.38 to 0.44 and the ASE values changed from 14.5 to −19.7 kcal/mol. This finding is not in line with the model that the tendency to adapt the electron density distribution to those given by Baird’s rule in the T1 state can be the only factor responsible for the augmented aromaticity in the triplet state. Our results indicate that the aromaticity increase in T1, as compared to that in S0, cannot be thoroughly accounted for by the difference in the number of calculated π electrons. Further, perhaps other factors, despite the lack of satisfactory identification at present, are operative here.
It is perhaps worth mentioning that the triplet state aromaticity, with reference to Baird’s rule, was previously considered generally for the 4π electron systems, such as cationic fulvene [16, 32].
Some structural variability of the five-membered ring in the S0 and T1 states was noticed but not fully explained, in addition to a putative vibronic coupling resulting in the dependence of the phenyl torsion angle on substituents in diphenylfulvenes in the S0 state.
When diphenylfulvenes are used as reagents in the cycloaddition reaction elaborated for fulvenes [3], we could expect generation of a number of interesting new compounds.
References
Padma Malar EJ, Neumann F, Jug K (1995) Investigation of aromaticity in the excited state of fulvene J Mol Struct (THEOCHEM) 336:81–84
Baron PA, Brown RD, Burden FR, Domaille PJ, Kent JE (1972) The microwave spectrum and structure of fulvene J Mol Spectrosc 43:401–410
Preethalayam P, Krishnan KS, Thulasi S, Chand SS, Joseph J, Nair V, Jaroschik F, Radhakrishnan KV (2017) Recent advances in the chemistry of pentafulvenes Chem Rev 117:3930–3989
Connors RE, Lacroix M, Chen B (2009) Spectroscopic and computational studies of fulvenic molecules J Mol Struct 935:13–18
Neuenschwander M (2015) Substituent effects on π-bond delocalization of fulvenes and fulvalenes. Are fulvenes aromatic? Helv Chim Acta 98:763–784
Ottosson H, Kilså K, Chajara K, Piqueras MC, Crespo R, Kato H, Muthas D (2007) Scope and limitations of Baird’s theory on triplet state aromaticity: application to the tuning of singlet-triplet energy gaps in fulvenes Chem Eur J 13:6998–7005
Krygowski TM, Ciesielski A, Cyrański M (1995) Aromatic character and energy of the five- and seven-membered rings in derivatives of penta- and heptafulvene substituted in exocyclic position Chem Pap 49:128–132
Tokatli A, Ucun F (2014) CTED: the new aromaticity index based on corrected total electron density at bond critical point J Phys Org Chem 27:380–386
Kleinpeter E, Fettke A (2008) Quantification of the (anti)aromaticity of fulvenes subject to ring size Tetrahedron Lett 49:2776–2781
Krygowski TM, Ozimiński WP, Palusiak M, Fowler PW, McKenzie AD (2010) Aromaticity of substituted fulvene derivatives: substituent-dependent ring currents Phys Chem Chem Phys 12:10740–10745
Dreyer J, Klessinger M (1994) Excited states and photochemical reactivity of fulvene. A theoretical study J Chem Phys 101:10655–10665
Möllerstedt H, Piqueras MC, Crespo R, Ottosson H (2004) Fulvenes, fulvalenes, and azulene: are they aromatic chameleons? J Am Chem Soc 126:13938–13939
Ozimiński WP, Krygowski TM (2011) Natural bond orbital approach to the transmission of substituent effect through the fulvene and benzene ring systems. J Mol Model 17:565–572
Stępień BT, Krygowski TM, Cyrański MK (2002) Extent of cyclic π-electron delocalization modification in exocyclically substituted fulvenes J Org Chem 67:5987–5992
Rosenberg M, Ottosson H, Kilså K (2011) Influence of excited state aromaticity in the lowest excited singlet states of fulvene derivatives Phys Chem Chem Phys 13:12912–12919
Najafian K, Schleyer PR, Tidwell TT (2003) Aromaticity and antiaromaticity in fulvenes, ketocyclopolyenes, fulvenones, and diazocyclopolyenes Org Biomol Chem 1:3410–3417
Rosenberg M, Dahlstrand C, Kilså K, Ottosson H (2014) Excited state aromaticity and antiaromaticity: opportunities for photophysical and photochemical rationalizations Chem Rev 114:5379–5425
Jorner K, Emanuelsson R, Dahlstrand C, Tong H, Denisova AV, Ottosson H (2014) Impact of ground- and excited-state aromaticity on cyclopentadiene and silole excitation energies and excited-state polarities Chem Eur J 20:9295–9303
Ozimiński WP, Krygowski TM, Fowler PW, Soncini A (2010) Aromatization of fulvene by complexation with lithium Org Lett 12:4880–4883
Ozimiński WP, Krygowski TM, Noorizadeh S (2012) Aromaticity of pentafulvene’s complexes with alkaline metal atoms Struct Chem 23:931–938
Finke AD, Jahn BO, Saithalavi A, Dahlstrand C, Nauroozi D, Haberland S, Gisselbrecht J-P, Boudon C, Mijangos E, Schweizer WB, Ott S, Ottosson H, Diederich F (2015) The 6,6-dicyanopentafulvalene core: a template for the design of electron-acceptor compounds Chem Eur J 21:8168–8176
Jug K (1983) A bond order approach to ring current and aromaticity J Org Chem 48:1344–1348
Baird NC (1972) Quantum organic photochemistry: II. Resonance and aromaticity in the lowest *ππ state of cyclic hydrocarbons J Am Chem Soc 94:4941–4948
Papadakis R, Ottosson H (2015) The excited state antiaromatic benzene ring: a molecular Mr Hyde? Chem Soc Rev 44:6472–6493
Baird NC (1971) Dewar resonance energy J Chem Edu 48:509–514
Kruszewski J, Krygowski TM (1972) Definition of aromaticity basing on the harmonic oscillation model Tetrahedron Lett 13:3839–3842
Krygowski TM (1993) Crystallographic studies on inter- and intramolecular interactions reflected in aromatic character of π-electron systems J Chem Inf Comput Sci 33:70–78
Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery Jr JA, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Keith T, Kobayashi R, Normand J, Raghavachari K, Rendell A, Kurant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salwador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2013) Gaussian 09, Revision D.01. Gaussian, Inc., Wallingford,
Hansch C, Leo A, Taft RW (1991) A survey of Hammett substituent constants and resonance and field parameters Chem Rev 91:165–195
Feixas F, Vandenbussche J, Bultinck P, Matito E, Solà M (2011) Electron delocalization and aromaticity in low-lying excited states of archetypal organic compounds Phys Chem Chem Phys 13:20690–20703
Ke An, Zhu J (2014) Evaluation of triplet aromaticity by the indene-isoindene isomerization stabilization energy method Eur J Org Chem 2014:2764–2769
Villaume S, Fogarty HA, Ottosson HA (2008) Triplet-state aromaticity of 4nπ-electron monocycles: analysis of bifurcation in the π contribution to the electron delocalization function ChemPhysChem 9:257–264
Wu JI, Dobrowolski MA, Cyrański MK, Merner BL, Bodwell GJ, Mo Y, Schleyer PR (2009) On the aromatic stabilization energy of the 4N π electron pyrene Mol Phys 107:1177–1186
Karadakov PB (2008) Ground- and excited state aromaticity in benzene and cyclobutadiene J Phys Chem A 112:7303–7309
Fowler PW, Steiner E, Jenneskens LW (2003) Ring-current aromaticity in triplet states of 4np electron monocycles Chem Phys Lett 371:719–723
Gogonea V, Schleyer PR, Schreiner PR (1998) Consequences of triplet aromaticity in 4nπ-electron annulenes: calculation of magnetic shieldings for open-shell species Angew Chem Int Ed 37:1945–1948
Cyrański MK, Schleyer PR, Krygowski TM, Jiao H, Hohlneicher G (2003) Facts and artifacts about aromatic stability estimation Tetrahedron 59:1657–1665
Acknowledgments
The computing grant G44-18 from the Interdisciplinary Center for Mathematical and Computer Modeling (ICM) of Warsaw University and the financial support from the Polish Ministry of Science and Higher Education are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sadlej-Sosnowska, N. Electronic properties and aromaticity of substituted diphenylfulvenes in the ground (S0) and excited (T1) states. Struct Chem 29, 23–31 (2018). https://doi.org/10.1007/s11224-017-0995-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11224-017-0995-y