Abstract
In this study, the influence of the size on the electronic properties (e.g. electronic energy) of three nanometal oxides: ZnO, TiO2, and Al2O3 were investigated. The wurtzite, rutile and corundum type of clusters were selected to represent ZnO, TiO2, and Al2O3, respectively. To study the effect of the size on the property, we have build several molecular cluster models with different number of atoms and performed for those clusters quantum–mechanical calculations. For small clusters, up to 40 atoms, the calculations at different levels of theory, including: density functional theory (DFT), Hartree–Fock method, and the semi-empirical PM6 method were carried out. The results from ab initio and DFT calculations were utilized to validate the less time-consuming PM6 approach. The PM6 method was then employed for larger clusters. Linear regression models were developed to describe the relationships between size (number of atoms in cluster) and the electronic properties. The developed and validated methodology is transferable and could be applied for other type of nanosized clusters to calculate properties that are considered as potential nanodescriptors for nano-QSAR modelling.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
During the last 15 years, the number of studies devoting to the investigation of the influence of size of nanoparticles (NPs) on the biological response and their physical/chemical properties has been significantly increased [1–4]. The main conclusion from those studies is that size of the NPs is an important factor that determines both biological effects of nanoparticles and their properties [5, 6]. Other parameters that have been proved to influence the activity and properties of NPs include: shape, composition, surface structure, and the ratio of the surface area to volume [6]. Properties, for which the size influence was investigated, mostly included the physical characteristic of NPs, such as: their magnetism [7], photodegradation efficiency [8], and optical properties [1]. However, since various computational approaches (e.g. quantitative structure–activity relationships and read-across approach) that utilized the electronic properties, such as: the HOMO–LUMO gap energy, the heat of formation, and the total energy are currently more often applied to nanomaterials [9–12], there is an urgent investigate the impact of their size also on those properties. There are few papers considering this subject [5, 13–16]. Authors of those studies noticed that electronic properties can change with size according to two main schemes: (1) increase/decrease linearly or (2) increase/decrease nonlinearly up to the saturation points [5]. Since there is a relationship between size and the property at least for some characteristics, the question is raised if there is possibility to describe this relationship by means of chemometrics methods. Consequently, assuming that there would be the possibility to develop the linear relationships model applying the results computed for series of small molecular clusters one could by means of these models estimate the property of a given, larger size nanoparticle. In this way the computing resources employed and the time required for performing theoretical studies for large clusters be significantly reduced.
The goal of our study is twofold: (1) first to provide a methodology on how the size-dependent electronic properties for nanoclusters should be efficiently calculated and (2) to develop and describe proper linear regression models (LRs) allowing to predict electronic property for particular size of the nanoparticle. We have selected three nanosized metal oxides that received significant interest, particularly by their wide and still growing range of applications. The selected oxides include: ZnO, TiO2, and Al2O3 [17, 18]. Moreover, this selection allowed us to make the comparison between size-dependent electronic properties obtained for metal oxides that differ in stoichiometry (different metal oxidation numbers: Zn2+, Al3+, Ti4+) and symmetry. The calculated properties could be utilized in nano-QSAR models as a new class of nanodescriptors.
Methodology
Cluster construction
Based on the experimental crystal lattice parameters taken from the literature, we have generated a series of molecular clusters for three nanometre-sized metal oxides, ZnO, TiO2, and Al2O3 [19–21]. Appropriate size of clusters was obtained by subsequently increasing the lattice parameters in three dimensions. Consequently, supercells differing in size, ranging from 12 to 99 atoms, from 30 to 39 atoms, and from 10 to 40 for ZnO, TiO2, and Al2O3, respectively, were constructed. This procedure was described and applied in our previous studies [5]. Molecular clusters were generated by means of Mercury software packages [22].
Quantum–mechanical calculations
The coordinates of the experimental crystal lattice parameters propagated in three dimensions were utilized as inputs for quantum–mechanical calculations. For small clusters, up to 40 atoms, single point-type calculations were performed by employing several theory levels including: (1) semi-empirical Parameterized Model 6 (PM6) method [23]; (2) density functional theory (DFT) using B3LYP—Becke, three-parameter Lee–Yang–Parr functional [24] and M06—the hybrid Meta Density functional [25] with the following basis sets: 3-21++G** [26] and aug-cc-pVDZ [27] and (3) Hartree–Fock method followed by Moller–Plesset perturbation theory (MP2) [28] in order to account for electron correlation effects. Calculations of various electronic properties for larger clusters were conducted with single point-type semi-empirical PM6 method. We calculated properties that are proved to have application in QSAR studies as descriptors [29–31]. All calculated properties are summarized in Table 1. Calculations were performed by employing the MOPAC 2012 [32] and Gaussian [33] software packages.
Relationships between size and properties (chemometrics analysis)
We have used electronic properties calculated for various sizes of molecular clusters to investigate the influence of size (expressed in total number of atoms per cluster) on the properties of nanosized metal oxides: ZnO, TiO2, and Al2O3.
Validation of PM6 methods: analysis of small clusters data
Results obtained for small clusters (up to 40 atoms) were applied to validate the less time-consuming method of calculation: the semi-empirical PM6 method. In this case, for each data set (data calculated at different theory levels: PM6; DFT; HF), we developed a linear regression model (LR model), according to the formula:
where Y X_P electronic property predicted at X level of theory (X meaning PM6; DFT; HF; etc.); nAt size expressed by total number of atoms per cluster; A X regression coefficient; B X intercept. To estimate the values of A X and B X, we utilized the approach that minimizes the sum of squared residuals [35]. The goodness-of-fit of each model was evaluated by calculating the determination coefficient (R 2) [36]. To estimate errors of the models, we calculated for each cluster the relative errors, according to Eq. 2:
where Y X property calculated at X level of theory; Y X_P property predicted at X level of theory.
The model developed for data calculated with the PM6 method was further applied to predict property at different levels of theory, e.g. at DFT level, according to formula:
where Y Xvs.PM6 re-calculated electronic property from PM6 method using X method; nAt size expressed in total number of atoms per cluster; A PM6 regression coefficient of model developed for data calculated using PM6 method; B PM6 intercept for model developed for data calculated using PM6 method; αXvs.PM6 and β Xvs.PM6 correction coefficient that are the ratios of equations’ coefficients obtained in LR models (Eq. 1).
To statistically compare the calculated properties with those predicted according to two strategies (Eqs. 1 and 3), we have applied the pairwise Student’s t test (defined pairwise are as follow: Y X/Y X_P; Y X/Y Xvs.PM6, where Y X property calculated at X level of theory; Y X_P property predicted at X level of theory; Y Xvs.PM6 property re-calculated from PM6 to X level of theory).
Relationships between size of wurtzite-type clusters of ZnO and the selected properties: the key study
The validated PM6 method was then utilized to investigate the influence of size on the properties for clusters containing more then 40 atoms. We applied this for wurtzite-type clusters of ZnO. The relationships between size and each particular property were investigated. In the case of linear type of changes the LR models were developed and evaluated according to the same protocol described for small clusters.
The diagram that illustrates methodology applied is presented in Fig. 1.
Results and discussion
Cluster construction
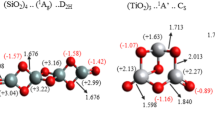
We studied the influence of size on the electronic properties of three nanometre-sized metal oxides, ZnO, TiO2, and Al2O3. Molecular clusters various in size were constructed for each oxide. In the case of zinc oxide, there are several existing crystal structures: (1) wurtzite; (2) zinc blend and (3) rocksalt [37]. Rutile and anatase are two most common and widely used polymorphs of TiO2 [38, 39]. Taking into account the thermodynamic stability, we considered wurtzite-type, rutile-type, and corundum-type clusters for ZnO, TiO2, and Al2O3 [20, 37, 39], respectively. Clusters ranging from 12 to 99 atoms, from 30 to 39 atoms, and from 10 to 40 atoms for ZnO, TiO2, and Al2O3, respectively, were constructed. In order to obtain hexagonal-ZnO structures, tetragonal-TiO2, and trigonal-Al2O3 structures of appropriate size, the crystal lattice parameters were increased in all three dimensions. Examples of generated clusters are shown in Fig. 2.
Quantum–mechanical calculations
The coordinates of the experimental crystal lattice parameters propagated in three dimensions were used as the inputs for quantum–mechanical calculations. For small clusters (up to 40 atoms), we performed calculations at several theory levels: (1) semi-empirical, i.e. PM6 method; (2) DFT method using B3LYP and M06 functionals; and (3) ab initio methods.
Comparison of the results obtained for small-size clusters (SI: Table S.1; Table S.2 and Table S.3) indicated that there are no significant differences in DFT-based outcomes produced with different functionals applied. More significant differences are observed between results obtained from PM6 method and calculations performed by means of other methods, which is reasonable according to the differences in each of the methods [40]. However, comparison of the Hartree–Fock method relying on the single-electron approximation with the DFT technique that includes electron correlation suggests that DFT produces better estimates of molecule structural parameters [40].
One can notice that results obtained at PM6 level differ from DFT ones by approximately constant values, e.g. \({\text{TE}}_{{{\text{PM6}}\_{\text{TiO}}_{2} }} /{\text{TE}}_{{{\text{B3LYP}}/3 {-} 21 + + {\text{G}}**\_{\text{TiO}}_{2} }} = 0.025,\)regardless of total number of atoms included in rutile-type clusters of TiO2. It could suggest that calculations at PM6 level corrected by this constant value could be comparable with those obtained by more sophisticated and computationally more expensive methods (at least with DFT ones).
Relationships between size and properties (chemometrics analysis)
Validation of PM6 methods: analysis for small clusters
In the main text, we presented figures and tables related to one property per metal oxide; other detail information could be found in the supplementary materials.
Results obtained for small-size clusters, Table S.1, Table S.2 and Table S.3 in SI, indicated that in this range of sizes, total energy (TE) and electronic energy (EE) changed linearly, regardless of method of calculations. This is in agreement with our previous studies [5]. In case of HOMO and LUMO energy, the changes with increasing number of atoms included in cluster are not linearly size-dependent. Considering that, these properties will not be analysed and further used in order to validate the PM6 computations. Consequently, linear regression models were developed only for size changes of TE and EE, according to Eq. 1; results are summarized in Table 2. Determination coefficient (R 2) of each model that is close or even equal to 1 (see Table 2) indicates that there is good fit of models to calculated data. Moreover, we have also investigated the relative errors for each prediction performed, calculated according to Eq. 2. Relative low values of errors that in most cases do not exceed 10 % confirm the good quality of the models (See Table S.4 in SI).
However, it needs to be pointed out that electronic properties for small-size clusters might be computed with the approximate high error. It is related to their high reactivity. Decreasing size of nanomaterials causes increase in surface-to-edge ratio, which, in other words means that atoms at the surface (which are scaled with n 2/3, where n is the number of atoms) are in close neighbourhood with the smaller number of atoms compared to macro scale materials [41, 42]. Thus, the small clusters of nanoparticles have higher bond energy per atom that could result in lower accuracy of calculations performed for them. In this contribution, we took into account small clusters, for which fraction of atoms included at the surface is equal to about 30 % of all atoms, regardless of studied cluster. This means that these small-sized clusters can be scaled up to larger clusters, for which this ratio is more or less similar (~30 %).
We applied here a model developed for data computed at PM6 level of theory to predict properties for more sophisticated methods, according to Eq. 3 (model developed for data computed with PM6 method corrected by means of corrections coefficients). In order to validate PM6 method, we statistically compared the properties calculated at DFT level (applying the following functional and basis: B3LYP/3-21++G** and M06/3-21++G** for ZnO and Al2O3 and B3LYP/aug-cc-pVDZ and M06/aug-cc-pVDZ for TiO2) with those predicted by means of the PM6-corrected model (property calculated by means of Eq. 1 and property calculated by means of Eq. 3). To do so, we applied the pairwise Student’s t test. The calculated values of p > 0.05 indicate that the results from each of the compared models do not differ significantly, Table 3. Therefore, PM6-corrected model might be applied to predict total energy and electronic energy with good approximation to those calculated at higher level of theory.
This conclusion was confirmed in relative residual investigation performed for developed models, Fig. 3 and Fig. 4. There are not significant differences between residuals obtained with strategy 1 (%|Error|X, where X means the method of calculation) and strategy 2 (%|Error|Xvs.PM6). Moreover, residuals obtained by employing PM6-corrected method to re-calculate properties at higher levels of theory are in many cases lower than residuals obtained by employing model developed for particular method of calculations, e.g. relative errors obtain for total energy computed for ZnO cluster containing 36 atoms are as follows: %|Error|B3LYP/3-21++G** = 3.8 in comparison to %|Error|B3LYP/3-21++G**vs.PM6 = 2.9 ( Fig. 3 upper, left panel). Thus, based on the computed results and considering the time and resources employed to perform calculations, PM6 method can be used for the qualitative calculation of the selected electronic properties of the studied metal oxides. Therefore, this method was applied to calculate properties of larger clusters including more than 40 atoms, for which fraction of atoms at the surface do not exceed 30 % of all atoms.
Relationships between size of wurtzite-type clusters of ZnO and the selected properties: the key study
The validated PM6 method was applied in order to study the influence of size on the total energy and electronic energy of wurtzite-type clusters of ZnO (Table S.5 in SI). We have noticed that these properties of ZnO decreasing linearly with increasing size of cluster, which is in agreement with our previous studied [5].
Additionally, we developed linear regression models for the total energy, Fig. 5a, and the electronic property, Fig. 5b, that allow predicting these properties based on the size of the cluster, at least in the investigated range of size. Developed models, see Fig. 5 and Table S.5 in SI, are characterized by high determination coefficient and relatively low errors.
Conclusions
A novel methodology that facilitates predictions of size-dependent electronic properties of nanometre-sized metal oxides was developed. The application of this methodology was tested and confirmed for metal oxides containing metals at different oxidation states (Zn2+, Al3+, Ti4+), which means that they differ in stoichiometry and symmetry. This allows one to assume that it could be employed for other oxides.
For wurtzite-type clusters of ZnO, the influence of size on their electronic property has also been investigated. The LR models allowing predicting selected properties of ZnO, based just only on the size of cluster, were developed. Predicted characteristics could be considered as potential nanodescriptors, vital for nano-QSAR studies. In further way, it would be reasonable to expand these studies for other metal oxides as well as for metal oxides differ in shape.
References
Kelly KL, Coronado E, Zhao LL, Schatz GC (2003) The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. J Phys Chem B 107(3):668–677. doi:10.1021/jp026731y
Ma NN, Ma C, Li CY, Wang T, Tang YJ, Wang HY, Mou XB, Chen Z, He NY (2013) Influence of nanoparticle shape, size, and surface functionalization on cellular uptake. J Nanosci Nanotechnol 13(10):6485–6498. doi:10.1166/jnn.2013.7525
Xiong SJ, George SJ, Ji ZX, Lin SJ, Yu HY, Damoiseaux R, France B, Ng KW, Loo SCJ (2013) Size of TiO2 nanoparticles influences their phototoxicity: an in vitro investigation. Arch Toxicol 87(1):99–109. doi:10.1007/s00204-012-0912-5
Niikura K, Matsunaga T, Suzuki T, Kobayashi S, Yamaguchi H, Orba Y, Kawaguchi A, Hasegawa H, Kajino K, Ninomiya T, Ijiro K, Sawa H (2013) Gold nanoparticles as a vaccine platform: influence of size and shape on immunological responses in vitro and in vivo. ACS Nano 7(5):3926–3938. doi:10.1021/nn3057005
Gajewicz A, Puzyn T, Rasulev B, Leszcxynska D, Leszczynksi J (2011) Metal oxide nanoparticles: size-dependence of quantum-mechanical properties. Nanosci Nanotechnol Asia 1:53–58
Puzyn T, Gajewicz A, Leszczynska D, Leszczynski J (2010) Nanomaterials—the next great challenge fo QSAR modelers. In: Puzyn T, Lesczynski J, Cronin MTD (eds) Recent advanced in QSAR studies. Springer, New York
Wei XH, Skomski R, Balamurugan B, Sun ZG, Ducharme S, Sellmyer DJ (2009) Magnetism of TiO and TiO2 nanoclusters. J Appl Phys. doi:10.1063/1.3074509
Wang HH, Xie CS, Zhang W, Cai SZ, Yang ZH, Gui YH (2007) Comparison of dye degradation efficiency using ZnO powders with various size scales. J Hazard Mater 141(3):645–652. doi:10.1016/j.jhazmat.2006.07.021
Gajewicz A, Rasulev B, Dinadayalane TC, Urbaszek P, Puzyn T, Leszczynska D, Leszczynski J (2012) Advancing risk assessment of engineered nanomaterials: application of computational approaches. Adv Drug Deliv Rev 64(15):1663–1693. doi:10.1016/j.addr.2012.05.014
Gajewicz A, Cronin MT, Rasulev B, Leszczynski J, Puzyn T (2015) Novel approach for efficient predictions properties of large pool of nanomaterials based on limited set of species: nano-read-across. Nanotechnology 26(1):015701. doi:10.1088/0957-4484/26/1/015701
Puzyn T, Rasulev B, Gajewicz A, Hu XK, Dasari TP, Michalkova A, Hwang HM, Toropov A, Leszczynska D, Leszczynski J (2011) Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat Nanotechnol 6(3):175–178. doi:10.1038/NNANO.2011.10
Rasulev B, Gajewicz A, Puzyn T, Leszczynska D, Leszczynski J (2013) Nano-QSAR: advances and challenges. RSC Nanosci Nanotechnol 25:220–256. doi:10.1039/9781849735476-00220
Albaret T, Finocchi F, Noguera C (1999) Ab initio simulation of titanium dioxide clusters. Appl Surf Sci 144–45:672–676. doi:10.1016/S0169-4332(98)00896-4
Albaret T, Finocchi F, Noguera C (1999) First principles simulations of titanium oxide clusters and surfaces. Faraday Discuss 114:285–304. doi:10.1039/A903066b
Jeong KS, Chang C, Sedlmayr E, Sulzle D (2000) Electronic structure investigation of neutral titanium oxide molecules TixOy. J Phys B At Mol Opt 33(17):3417–3430. doi:10.1088/0953-4075/33/17/319
Rana TH, Kumar P, Solanki AK, Skomski R, Kashyap A (2013) Ab-initio study of free standing TiO2 clusters: stability and magnetism. J Appl Phys. doi:10.1063/1.4799616
Gupta S, Tripathi M (2011) A review of TiO2 nanoparticles. Chin Sci Bull 56(16):1639–1657. doi:10.1007/s11434-011-4476-1
Vassem M, Umar A, Hahn Y-B (2010) Zno nanoparticles: growth, properties and applications. In: Umar A (ed) Metal oxides nanostructures and their applications. American Scientific Publishers, New York
Kim YI, Page K, Seshadri R (2007) Synchrotron x-ray study of polycrystalline wurtzite Zn1–xMgxO (0 ≤ x ≤ 0.15): evolution of crystal structure and polarization. Appl Phys Lett 90(10):1019. doi:10.1063/1.2711289
Kondo S, Tateishi K, Ishizawa N (2008) Structural evolution of corundum at high temperatures. Jpn J Appl Phys 47(1):616–619. doi:10.1143/JJAP.47.616
Qu ZW, Kroes GJ (2007) Theoretical study of stable, defect-free (TiO2)(n) nanoparticles with n = 10-16. J Phys Chem C 111(45):16808–16817. doi:10.1021/jp073988t
Stewart JJP (2004) Optimization of parameters for semiempirical methods IV: extension of MNDO, AM1, and PM3 to more main group elements. J Mol Model 10(2):155–164. doi:10.1007/s00894-004-0183-z
Zhao Y, Truhlar DG (2008) Density functionals with broad applicability in chemistry. Acc Chem Res 41(2):157–167. doi:10.1021/ar700111a
Zhao Y, Truhlar DG (2008) The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor Chem Acc 120(1–3):215–241. doi:10.1007/s00214-007-0310-x
Binkley JS, Pople JA, Hehre WJ (1980) Self-consistent molecular-orbital methods. 21. Small split-valence basis-sets for 1st-row elements. J Am Chem Soc 102(3):939–947. doi:10.1021/Ja00523a008
Papajak E, Zheng JJ, Xu XF, Leverentz HR, Truhlar DG (2011) Perspectives on basis sets beautiful: seasonal plantings of diffuse basis functions. J Chem Theory Comput 7(10):3027–3034. doi:10.1021/ct200106ac
Head-Gordon M, Pople JA, Frisch MJ (1988) MP2 energy evaluation by direct methods. Chem Phys Lett 153(6):503–506
Gajewicz A, Haranczyk M, Puzyn T (2010) Predicting logarithmic values of the subcooled liquid vapor pressure of halogenated persistent organic pollutants with QSPR: how different are chlorinated and brominated congeners? Atmos Environ 44(11):1428–1436. doi:10.1016/j.atmosenv.2010.01.041
Puzyn T, Gajewicz A, Rybacka A, Haranczyk M (2011) Global versus local QSPR models for persistent organic pollutants: balancing between predictivity and economy. Struct Chem 22(4):873–884. doi:10.1007/s11224-011-9764-5
Sosnowska A, Barycki M, Jagiello K, Haranczyk M, Gajewicz A, Kawai T, Suzuki N, Puzyn T (2014) Predicting enthalpy of vaporization for Persistent Organic Pollutants with Quantitative Structure–Property Relationship (QSPR) incorporating the influence of temperature on volatility. Atmos Environ 87:10–18. doi:10.1016/j.atmosenv.2013.12.036
Stewart JJP (2009) MOPAC 2009. Stewart Computational Chemistry. http://openmopac.net/MOPAC2009.html
Nowack B, Bucheli TD (2007) Occurrence, behavior and effects of nanoparticles in the environment. Environ Pollut 150(1):5–22. doi:10.1016/j.envpol.2007.06.006
Gramatica P, Giani E, Papa E (2007) Statistical external validation and consensus modeling: a QSPR case study for Koc prediction. J Mol Graph Model 25(6):755–766. doi:10.1016/j.jmgm.2006.06.005
Gramatica P (2007) Principles of QSAR models validation: internal and external. QSAR Comb Sci 26(5):694–701. doi:10.1002/qsar.200610151
Ozgur U, Alivov YI, Liu C, Teke A, Reshchikov MA, Dogan S, Avrutin V, Cho SJ, Morkoc H (2005) A comprehensive review of ZnO materials and devices. J Appl Phys. doi:10.1063/1.1992666
Lazzeri M, Vittadini A, Selloni A (2002) Structure and energetics of stoichiometric TiO2 anatase surfaces (vol 63, art no 155409, 2001). Phys Rev B. doi:10.1103/Physrevb.65.119901
Lazzeri M, Vittadini A, Selloni A (2001) Structure and energetics of stoichiometric TiO2 anatase surfaces. Phys Rev B. doi:10.1103/Physrevb.63.155409
Young DC (2010) Computational chemistry. A practical guide for applying techniques to real-world problems. Willey, New York
Baletto F, Ferrando R (2005) Structural properties of nanoclusters: energetic, thermodynamic, and kinetic effects. Rev Mod Phys 77(1):371–423. doi:10.1103/Revmodphys.77.371
Sizochenko N, Rasulev B, Gajewicz A, Kuz’min V, Puzyn T, Leszczynski J (2014) From basic physics to mechanisms of toxicity: the “liquid drop” approach applied to develop predictive classification models for toxicity of metal oxide nanoparticles. Nanoscale 6(22):13986–13993. doi:10.1039/c4nr03487b
Acknowledgments
The authors are grateful for the financial support of the European Commission through Marie Curie IRSES program: NanoBRIDGES Project (FP7-PEOPLE-2011-IRSES, Grant Agreement No. 295128) and NanoPUZZLES Project (Grant Agreement No. 309837). Calculations were carried out at the Academic Computer Center in Gdansk.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jagiello, K., Chomicz, B., Avramopoulos, A. et al. Size-dependent electronic properties of nanomaterials: How this novel class of nanodescriptors supposed to be calculated?. Struct Chem 28, 635–643 (2017). https://doi.org/10.1007/s11224-016-0838-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11224-016-0838-2