Outlier detection in non-elliptical data by kernel MRCD

Abstract

The minimum regularized covariance determinant method (MRCD) is a robust estimator for multivariate location and scatter, which detects outliers by fitting a robust covariance matrix to the data. Its regularization ensures that the covariance matrix is well-conditioned in any dimension. The MRCD assumes that the non-outlying observations are roughly elliptically distributed, but many datasets are not of that form. Moreover, the computation time of MRCD increases substantially when the number of variables goes up, and nowadays datasets with many variables are common. The proposed kernel minimum regularized covariance determinant (KMRCD) estimator addresses both issues. It is not restricted to elliptical data because it implicitly computes the MRCD estimates in a kernel-induced feature space. A fast algorithm is constructed that starts from kernel-based initial estimates and exploits the kernel trick to speed up the subsequent computations. Based on the KMRCD estimates, a rule is proposed to flag outliers. The KMRCD algorithm performs well in simulations, and is illustrated on real-life data.

1 Introduction

The minimum covariance determinant (MCD) estimator introduced in Rousseeuw (1984, 1985) is a robust estimator of multivariate location and covariance. It forms the basis of robust versions of multivariate techniques such as discriminant analysis, principal component analysis, factor analysis and multivariate regression, see e.g. Hubert et al. (2008, 2018) for an overview. The basic MCD method is quite intuitive. Given a data matrix of n rows with p columns, the objective is to find $h < n$ observations whose sample covariance matrix has the lowest determinant. The MCD estimate of location is then the average of those h points, whereas the scatter estimate is a multiple of their covariance matrix. The MCD has good robustness properties. It has a high breakdown value, that is, it can withstand a substantial number of outliers. The effect of a small number of potentially far outliers is measured by its influence function, which is bounded (Croux and Haesbroeck 1999).

Computing the MCD was difficult at first but became faster with the algorithm of Rousseeuw and Van Driessen (1999) and the deterministic algorithm DetMCD (Hubert et al. 2012). An algorithm for n in the millions was recently constructed (De Ketelaere et al. 2020). But all algorithms for the original MCD require that the dimension p be lower than h in order to obtain an invertible covariance matrix. In fact it is recommended that $n>5p$ in practice (Rousseeuw and Van Driessen 1999). This restriction implies that the original MCD cannot be applied to datasets with more variables than cases, that are commonly found in spectroscopy and areas where sample acquisition is difficult or costly, e.g. in the field of omics data.

A solution to this problem was recently proposed in Boudt et al. (2020), which introduced the minimum regularized covariance determinant (MRCD) estimator. The scatter matrix of a subset of h observations is now a convex combination of its sample covariance matrix and a target matrix. This makes it possible to use the MRCD estimator when the dimension exceeds the subset size. But the computational complexity of MRCD still contains a term $O(p^3)$ from the covariance matrix inversion, which limits its use for high-dimensional data. Another restriction is the assumption that the non-outlying observations roughly follow an elliptical distribution.

To address both issues we propose a generalization of the MRCD which is defined in a kernel-induced feature space ${\mathcal {F}}$, where the proposed estimator exploits the kernel trick: the $p \times p$ covariance matrix is not calculated explicitly but replaced by the calculation of a $n \times n$ centered kernel matrix, resulting in a computational speed-up in case $n \ll p$. Similar ideas can be found in the literature, see e.g. Dolia et al. (2006, 2007) which kernelized the minimum volume ellipsoid (Rousseeuw 1984, 1985). The results of the KMRCD algorithm with the linear kernel $k(x,y) = x^\top y$ and radial basis function (RBF) kernel $k(x,y) = e^{-\Vert x-y\Vert ^2/(2\sigma ^2)}$ are shown in Fig. 1. This example will be described in detail in Sect. 6.

The paper is organized as follows. Section 2 describes the MCD and MRCD estimators. Section 3 proposes the kernel MRCD method. Section 4 describes the kernel-based initial estimators used as well as a kernelized refinement procedure, and proves that the optimization in feature space is equivalent to an optimization in terms of kernel matrices. The simulation study in Sect. 5 confirms the robustness of the method as well as the improved computation speed when using a linear kernel. Section 6 illustrates KMRCD on three datasets, and Sect. 7 concludes.

Fig. 1

Illustration of kernel MRCD on two datasets of which the non-outlying part is elliptical (left) and non-elliptical (right). Both datasets contain $20\%$ of outlying observations. The generated regular observations are shown in black and the outliers in red. In the panel on the left a linear kernel was used, and in the panel on the right a nonlinear kernel. The curves on the left are contours of the robust Mahalanobis distance in the original bivariate space. The contours on the right are based on the robust distance in the kernel-induced feature space

2 The MCD and MRCD methods

2.1 The minimum covariance determinant estimator

Assume that we have a p-variate dataset X containing n data points, where the ith observation $x_i = (x_{i1}, x_{i2}, \dots , x_{ip})^\top$ is a p-dimensional column vector. We do not know in advance which of these points are outliers, and they can be located anywhere. The objective of the MCD method is to find a set H containing the indices of $|H|=h$ points whose sample covariance matrix has the lowest possible determinant. The user may specify any value of h with $n/2 \leqslant h < n$. The remaining $n-h$ observations could potentially be outliers. For each h-subset H the location estimate $c^H$ is the average of these h points:

$$\begin{aligned} c^H = \frac{1}{h} \sum _{i \in H}x_i \end{aligned}$$

whereas the scatter estimate is a multiple of their covariance matrix, namely

$$\begin{aligned} c_{\alpha }\hat{\Sigma }^H = \frac{c_{\alpha }}{h-1} \sum _{i \in H} \left( x_i - c^H\right) \left( x_i - c^H\right) ^\top \end{aligned}$$

where $c_{\alpha }$ is a consistency factor (Croux and Haesbroeck 1999) that depends on the ratio $\alpha = h/n$. The MCD aims to minimize the determinant of ${\hat{\Sigma }}^H$ among all $H \in {\mathcal {H}}$, where the latter denotes the collection of all possible sets H with $|H| = h$:

$$\begin{aligned} {\hat{\Sigma }}_{\mathrm {MCD}} = \underset{H \in {\mathcal {H}}}{\text {argmin}}\; \det \Big (\hat{\Sigma }^H\Big )\;. \end{aligned}$$

(1)

Computing the exact MCD has combinatorial complexity, so it is infeasible for all but tiny datasets. However, the approximate algorithm FastMCD constructed in Rousseeuw and Van Driessen (1999) is feasible. FastMCD uses so-called concentration steps (C-steps) to minimize (1). Starting from any given ${\hat{\Sigma }}^H$, the C-step constructs a more concentrated approximation by calculating the Mahalanobis distance of every observation based on the location and scatter of the current subset H:

$$\begin{aligned} \text{ MD }\Big (x,c^H,\hat{\Sigma }^H\Big ) = \sqrt{\Big (x - c^H\Big )^\top \Big ({\hat{\Sigma }}^H\Big )^{-1} \Big (x - c^H\Big )}\;. \end{aligned}$$

These distances are sorted and the h observations with the lowest $\text{ MD }(x_i,c^H,{\hat{\Sigma }}^H)$ form the new h-subset, which is guaranteed to have an equal or lower determinant (Rousseeuw and Van Driessen 1999). The C-step can be iterated until convergence.

2.2 The minimum regularized covariance determinant estimator

The minimum regularized covariance determinant estimator (MRCD) is a generalization of the MCD estimator to high dimensional data (Boudt et al. 2020). The MRCD subset H is defined by minimizing the determinant of the regularized covariance matrix ${\hat{\Sigma }}^H_{\mathrm {reg}}$:

$$\begin{aligned} \hat{\Sigma }_{\mathrm {MRCD}} = \underset{H \in {\mathcal {H}}}{\text {argmin}}\left( \det \Big (\hat{\Sigma }^H_{\mathrm {reg}}\Big )\right) , \end{aligned}$$

where the regularized covariance matrix is given by

$$\begin{aligned} \hat{\Sigma }^H_{\mathrm {reg}} =\rho T + (1-\rho ) c_{\alpha } {\hat{\Sigma }}^H \end{aligned}$$

with $0< \rho < 1$ and T a predetermined and well-conditioned symmetric and positive definite target matrix. The determination of $\rho$ is done in a data-driven way such that ${\hat{\Sigma }}_{\mathrm {MRCD}}$ has a condition number at most $\kappa$, for which Boudt et al. (2020) proposes $\kappa = 50$. The MRCD algorithm starts from six robust, well-conditioned initial estimates of location and scatter, taken from the DetMCD algorithm (Hubert et al. 2012). Each initial estimate is followed by concentration steps, and at the end the subset H with the lowest determinant is kept. Note that approximate algorithms like FastMCD and MRCD are much faster than exhaustive enumeration, but one can no longer formally prove a breakdown value. Fortunately, simulations confirm the high robustness of these methods. Also note that such approximate algorithms are guaranteed to converge, because they iterate C-steps starting from a finite number of initial fits. The algorithm may converge to a local minimum of the objective rather than its global minimum, but simulations have confirmed the accuracy of the result.

3 The kernel MRCD estimator

We now turn our attention to kernel transformations (Schölkopf et al. 2002), formally defined as follows.

Definition 1

A function $k:{\mathcal {X}} \times {\mathcal {X}} \rightarrow {\mathbb {R}}$ is called a kernel on ${\mathcal {X}}$ iff there exists a real Hilbert space $\mathcal {F}$ and a map $\phi : {\mathcal {X}} \rightarrow \mathcal {F}$ such that for all x, y in ${\mathcal {X}}$:

$$\begin{aligned} k(x, y)=\langle \phi (x),\phi (y)\rangle , \end{aligned}$$

where $\phi$ is called a feature map and ${\mathcal {F}}$ is called a feature space.

We restrict ourselves to positive semidefinite (PSD) kernels. A symmetric function $k:{\mathcal {X}} \times {\mathcal {X}} \rightarrow {\mathbb {R}}$ is called PSD iff $\sum _{i=1}^n \sum _{j=1}^n c_i c_j k(x_i, x_j) \geqslant 0$ for any $x_1, \dots , x_n$ in ${\mathcal {X}}$ and any $c_1, \dots , c_n$ in ${\mathbb {R}}$. Given an $n \times p$ dataset X, its kernel matrix is defined as $K = \Phi \Phi ^\top$ with $\Phi = [\phi (x_1),...,\phi (x_n)]^\top$. The use of kernels makes it possible to operate in a high-dimensional, implicit feature space without computing the coordinates of the data in that space, but rather by replacing inner products by kernel matrix entries. A well known example is given by kernel PCA (Schölkopf et al. 1998), where linear PCA is performed in a kernel-induced feature space ${\mathcal {F}}$ instead of the original space ${\mathcal {X}}$. Working with kernel functions has the advantage that non-linear kernels enable the construction of non-linear models. Note that the size of the kernel matrix is $n \times n$, whereas the covariance matrix is $p \times p$. The latter is an advantage when dealing with datasets for which $n \ll p$, for then the memory and computational requirements are considerably lower.

Given an $n \times p$ dataset $X = \{x_1, \ldots , x_n\}$ we thus get its image $\{\phi (x_1),\ldots \phi (x_n)\}$ in feature space, where it has the average

$$\begin{aligned} c_{\mathcal {F}} = \frac{1}{n} \sum _{i=1}^{n} \phi (x_i)\;. \end{aligned}$$

Note that the dimension of the feature space ${\mathcal {F}}$ may be infinite. However, we will restrict ourselves to the subspace $\tilde{{\mathcal {F}}}$ spanned by $\{\phi (x_1) - c_{\mathcal {F}},\dots , \phi (x_n) - c_{\mathcal {F}}\}$ so that $m{:}{=}\mathrm {dim}(\tilde{{\mathcal {F}}}) \leqslant n-1$. In this subspace the points $\phi (x_i) - c_{\mathcal {F}}$ thus have at most $n-1$ coordinates. The covariance matrix in the feature space given by

$$\begin{aligned} \hat{\Sigma }_{\mathcal {F}} = \frac{1}{n-1} \sum _{i =1}^n (\phi (x_i) - c_{\mathcal {F}}) (\phi (x_i) - c_{\mathcal {F}})^\top \end{aligned}$$

is thus a matrix of size at most $(n-1) \times (n-1)$. Note that the covariance matrix is centered but the original kernel matrix is not. Therefore we construct the centered kernel matrix ${\tilde{K}}$ by

$$\begin{aligned} {\tilde{K}}_{ij}&= \Big (\phi (x_i) - \frac{1}{n}\sum _{\ell = 1}^n \phi (x_\ell )\Big )^\top \Big (\phi (x_j) - \frac{1}{n}\sum _{\ell '=1}^n \phi (x_{\ell '})\Big ) \nonumber \\&= K_{ij} - \frac{1}{n} \sum _{\ell = 1}^n K_{\ell j} - \frac{1}{n} \sum _{\ell ' = 1}^n K_{i\ell '} + \frac{1}{n^2}\sum _{\ell = 1}^n \sum _{\ell ' = 1}^n K_{\ell \ell '} \nonumber \\&= \Big (K - 1_{nn} K - K 1_{nn} + 1_{nn} K 1_{nn}\Big )_{ij} \end{aligned}$$

(2)

where $1_{nn}$ is the $n\times n$ matrix with all entries set to 1/n. Note that the centered kernel matrix is equal to ${\tilde{K}} = {\tilde{\Phi }} {\tilde{\Phi }}^\top$ with ${\tilde{\Phi }} = [\phi (x_1) - c_{\mathcal {F}}, \ldots ,\phi (x_n) - c_{\mathcal {F}}]^\top$ and is PSD by construction. The following result is due to Schölkopf et al. (1998).

Theorem 1

Given an $n \times p$ dataset X, the sorted eigenvalues of the covariance matrix ${\hat{\Sigma }}_\mathcal {F}$ and those of the centered kernel matrix ${\tilde{K}}$ satisfy

$$\begin{aligned} \lambda _j^{{\hat{\Sigma }}_\mathcal {F}} = \frac{\lambda _j^{{\tilde{K}}}}{n-1} \end{aligned}$$

for all $j=1, \ldots , m$ where $m=\mathrm {rank}(\hat{\Sigma }_{\mathcal {F}})$.

Proof of Theorem 1

The eigendecomposition of the centered kernel matrix ${\tilde{K}}$ is

$$\begin{aligned} {\tilde{K}} = {\tilde{\Phi }} {\tilde{\Phi }}^\top = V \Lambda V^\top \end{aligned}$$

where $\Lambda = \mathrm {diag}(\lambda _1, \ldots ,\lambda _n)$ with $\lambda _1 \geqslant \cdots \geqslant \lambda _n$ . The eigenvalue $\lambda _j$ and eigenvector $v_j$ satisfy

$$\begin{aligned} {\tilde{\Phi }} {\tilde{\Phi }}^\top v_j = \lambda _j v_j \end{aligned}$$

for all $j=1, \ldots , m$. Multiplying both sides by ${\tilde{\Phi }}^\top /(n-1)$ gives

$$\begin{aligned} \left( \frac{1}{n-1} {\tilde{\Phi }}^\top {\tilde{\Phi }}\right) \Big ({\tilde{\Phi }}^\top v_j\Big ) = \frac{\lambda _j}{n-1} \Big ({\tilde{\Phi }}^\top v_j\Big ). \end{aligned}$$

Combining the above equations results in

$$\begin{aligned} {\hat{\Sigma }}_{\mathcal {F}} v^{{\hat{\Sigma }}_{\mathcal {F}}}_j = \frac{\lambda _j}{n-1} v^{{\hat{\Sigma }}_{\mathcal {F}}}_j \end{aligned}$$

for all $j=1, \ldots , m$ where $v^{{\hat{\Sigma }}_{\mathcal {F}}}_j = ({\tilde{\Phi }}^\top v_j)$ is the jth eigenvector of ${\hat{\Sigma }}_{\mathcal {F}}$. The remaining eigenvalues of the covariance matrix, if any, are equal to zero. $\square$

The above result can be related to a representer theorem for kernel PCA (Alzate and Suykens 2008). It shows that the nonzero eigenvalues of the covariance matrix are proportional to the nonzero eigenvalues of the centered kernel matrix, thus proving that ${\hat{\Sigma }}_{\mathcal {F}}$ and ${\tilde{K}}$ have the same rank.

What would a kernelized MCD estimator look like? It would have to be equivalent to applying the original MCD in the feature space, so that in case of the linear kernel the original MCD is obtained. The MCD estimate for location in the subspace $\tilde{\mathcal {F}}$ is

$$\begin{aligned} c_\mathcal {F}^H = \frac{1}{h} \sum _{i \in H} \phi (x_i) \end{aligned}$$

whereas the covariance matrix now equals

$$\begin{aligned} \hat{\Sigma }_\mathcal {F}^H = \frac{1}{h-1}\sum _{i \in H} \Big (\phi (x_i) - c_\mathcal {F}^H\Big ) \Big (\phi (x_i) - c_\mathcal {F}^H\Big )^\top . \end{aligned}$$

Likewise, the robust distance becomes

$$\begin{aligned} \text{ MD }\Big (\phi (x),c_\mathcal {F}^H,\hat{\Sigma }_\mathcal {F}^H\Big ) = \Big (\phi (x) - c_\mathcal {F}^H\Big )^\top \Big (\hat{\Sigma }^{H}_\mathcal {F}\Big )^{-1} \Big (\phi (x) - c_{\mathcal {F}}^H\Big )\;. \end{aligned}$$

In these formulas the mapping function $\phi$ may not be known, but that is not necessary since we can apply the kernel trick. More importantly, the covariance matrix may not be invertible as the $\phi (x_i) - c_\mathcal {F}^H$ lie in a possibly high-dimensional space $\tilde{\mathcal {F}}$. We therefore propose to apply MRCD in $\tilde{\mathcal {F}}$ in order to make the covariance matrix invertible. Let ${\tilde{\Phi }}_H$ be the row-wise stacked matrix

$$\begin{aligned} {\tilde{\Phi }}_H = \left[ \phi (x_{i(1)}) - c_\mathcal {F}^H,\ldots , \phi (x_{i(h)}) - c_\mathcal {F}^H\right] ^\top \end{aligned}$$

where $i(1),\ldots ,i(h)$ are the indices in H. For any $0< \rho < 1$ the regularized covariance matrix is defined as

$$\begin{aligned} \hat{\Sigma }^H_{\mathrm {reg}} = (1-\rho )\hat{\Sigma }^H_\mathcal {F}+ \rho I_m = \frac{1-\rho }{h-1} {\tilde{\Phi }}_H^\top {\tilde{\Phi }}_H + \rho I_m \end{aligned}$$

where $I_m$ is the identity matrix in $\tilde{\mathcal {F}}$. The KMRCD method is then defined as

$$\begin{aligned} \hat{\Sigma }_{\mathrm {KMRCD}} = \underset{H \in {\mathcal {H}}}{\text {argmin}}\det \Big (\hat{\Sigma }_{\mathrm {reg}}^H\Big ) \end{aligned}$$

(3)

where ${\mathcal {H}}$ is the collection of subsets H of $\{1,\ldots ,n \}$ such that $|H| = h$ and ${\hat{\Sigma }}^H$ is of maximal rank, i.e. $\mathrm {rank}({\hat{\Sigma }}^H) = \mathrm {dim}(\mathrm {span} (\phi (x_{i(1)}) - c_\mathcal {F}^H, \ldots , \phi (x_{i(h)}) - c_\mathcal {F}^H)) = q$ with $q{:}{=} \min (m,h-1)$. We can equivalently say that the h-subset H is in general position. The corresponding regularized kernel matrix is

$$\begin{aligned} \tilde{K}_{\mathrm {reg}}^H = (1-\rho )\tilde{K}^H + (h-1) \rho I_h \end{aligned}$$

(4)

where ${\tilde{K}}^H = {\tilde{\Phi }}_H {\tilde{\Phi }}_H^{{\text {T}}}$ denotes the centered kernel matrix of h rows, that is, (2) with n replaced by h. The MRCD method in feature space $\tilde{\mathcal {F}}$ minimizes the determinant in (3) in $\tilde{\mathcal {F}}$. But we would like to carry out an optimization on kernel matrices instead. The following theorem shows that this is possible.

Theorem 2

Minimizing $\det (\hat{\Sigma }^H_\mathrm {reg})$ over all subsets H in ${\mathcal {H}}$ is equivalent to minimizing $\det (\tilde{K}^H_\mathrm {reg})$ over all h-subsets H with $\mathrm {rank}(\tilde{K}^H) = q.$

Proof of Theorem 2

From Theorem 1 it follows that the nonzero eigenvalues of ${\hat{\Sigma }}^H_{\mathcal {F}}$ and ${\tilde{K}}^H$ are related by $\lambda _j^{{\hat{\Sigma }}_{\mathcal {F}}^H} = \frac{1}{h-1}\lambda _j^{{\tilde{K}}^H}$. If H belongs to ${\mathcal {H}}$, ${\hat{\Sigma }}_{\mathcal {F}}^H$ has exactly q nonzero eigenvalues so ${\tilde{K}}^H$ also has rank q, and vice versa. The remaining $m-q$ eigenvalues of ${\hat{\Sigma }}^H$ are zero, as well as the remaining $h-q$ eigenvalues of ${\tilde{K}}^H$. Now consider the regularized matrices

$$\begin{aligned} \hat{\Sigma }^H_\mathrm {reg} = (1-\rho ) \hat{\Sigma }_\mathcal {F}^H + \rho I_m \end{aligned}$$

and

$$\begin{aligned} \tilde{K}^H_\mathrm {reg} = (1-\rho ) \tilde{K}^H + (h-1)\rho I_h\;. \end{aligned}$$

Computing the determinant of both matrices as a product of their eigenvalues yields:

$$\begin{aligned} \det \Big (\hat{\Sigma }^H_\mathrm {reg}\Big ) = \rho ^{m-q} \prod _{j=1}^q \Big ((1-\rho ) \lambda _j^{{\hat{\Sigma }}^H_{\mathcal {F}}} + \rho \Big ) \end{aligned}$$

and

$$\begin{aligned} \det \Big (\tilde{K}^H_\mathrm {reg}\Big )&= \rho ^{h-q} \prod _{j=1}^q \Big ((1-\rho ) \lambda _j^{\tilde{K}^H} + (h-1)\rho \Big ) \\&= \rho ^{h-q} \prod _{j=1}^q (h-1)\Big ((1-\rho ) \lambda _j^{\hat{\Sigma }_\mathcal {F}^H} + \rho \Big )\\&= \frac{\rho ^{h-q}}{\rho ^{m-q}} (h-1)^q \det \Big (\hat{\Sigma }^H_\mathrm {reg}\Big )\;. \end{aligned}$$

Therefore $\mathrm {det}({\tilde{K}}^H_\mathrm {reg}) = \rho ^{h-m} (h-1)^q \det ({\hat{\Sigma }}^H_\mathrm {reg})$ in which the proportionality factor is constant, so the optimizations are equivalent. $\square$

Following Haasdonk and Pekalska (2009) we can also express the robust Mahalanobis distance in terms of the regularized kernel matrix, by

$$\begin{aligned}&\text{ MD }\left( \phi (x),c_\mathcal {F}^H, \hat{\Sigma }_{\mathrm {reg}}^H\right) \nonumber \\&= \sqrt{\left( \phi (x) - c_\mathcal {F}^H\right) ^\top \left( \hat{\Sigma }_{\mathrm {reg}}^H\right) ^{-1} \left( \phi (x) - c_\mathcal {F}^H\right) } \nonumber \\&= \sqrt{\frac{1}{\rho }\left( {\tilde{k}}(x,x)-(1-\rho ){\tilde{k}}(H,x)^\top \left( {\tilde{K}}_{\mathrm {reg}}^H\right) ^{-1} {\tilde{k}}(H,x)\right) } \end{aligned}$$

(5)

where ${\tilde{k}}(x,x) = (\phi (x) - c_\mathcal {F}^H)^\top (\phi (x) - c_\mathcal {F}^H)$ is a special case of the formula ${\tilde{k}}(x,y) = k(x,y) - \sum _{i \in H} k(x_i,x) - \sum _{i \in H} k(x_i,y) - \sum _{i \in H} \sum _{j \in H} k(x_i,x_j)$ for $x=y$. The notation ${\tilde{k}}(H,x)$ stands for the column vector ${\tilde{\Phi }}_H (\phi (x) - c_\mathcal {F}^H) = ({\tilde{k}}(x_{i(1)},x), \ldots , {\tilde{k}}(x_{i(h)},x))^\top$ in which $i(1), \ldots , i(h)$ are the members of H. This allows us to calculate the Mahalanobis distance in feature space from the kernel matrix, and consequently to perform the C-step procedure on it. Note that (5) requires inverting the matrix ${\tilde{K}}_{\mathrm {reg}}^H$ instead of the matrix $\hat{\Sigma }_{\mathrm {reg}}^H$.

The C-step theorem of the MRCD in Boudt et al. (2020) shows that when you select a new h-subset as those i for which the Mahalanobis distance relative to the old h-subset is smallest, the regularized covariance determinant of the new h-subset is lower than or equal to that of the old one. In other words, C-steps lower the objective function of MRCD. Using Theorem 2, this C-step theorem thus also extends to the kernel MRCD estimator.

4 The kernel MRCD algorithm

This section introduces the elements of the kernel MRCD algorithm. If the original data comes in the form of an $n \times p$ dataset X, we start by robustly standardizing it. For this we first compute the univariate reweighted MCD estimator of Rousseeuw and Leroy (1987) with coverage $h = [n/2] + 1$ to obtain estimates of the location and scatter of each variable, which are then used to transform X to z-scores. The kernel matrix K is then computed from these z-scores. Note, however, that the data can come in the form of a kernel matrix that was not derived from data points with coordinates. For instance, a so-called string kernel can compute similarities between texts, such as emails, without any variables or measurements. Such a kernel basically compares the occurrence of strings of consecutive letters in each text. Since the KMRCD method does all its computations on the kernel matrix, it can also be applied to such data.

4.1 Initial estimates

The MRCD estimator needs initial h-subsets to start C-steps from. In the original FastMCD algorithm of Rousseeuw and Van Driessen (1999) the initial h-subsets were obtained by drawing random $(p + 1)$-subsets out of the n data points. For each its empirical mean and covariance matrix were computed as well as the resulting Mahalanobis distances of all points, after which the subset with the h smallest distances was obtained. However, this procedure would not be possible in situations where $p > n$ because Mahalanobis distances require the covariance matrix to be invertible. The MRCD method instead starts from a small number of other initial estimators, inherited from the DetMCD algorithm in Hubert et al. (2012).

For the initial h-subsets in KMRCD we need methods that can be kernelized. We propose to use four such initial estimators, the combination of which has a good chance of being robust against different contamination types. Since initial estimators can be inaccurate, a kernelized refinement step will be applied to each. We will describe these methods in turn.

The first initial method is based on the concept of spatial median. For data with coordinates, the spatial median is defined as the point m that has the lowest total Euclidean distance $\sum _i ||x_i-m||$ to the data points. This notion also makes sense in the kernel context, since Euclidean distances in the feature space can be written in terms of the inner products that make up the kernel matrix. The spatial median in coordinate space is often computed by the Weiszfeld algorithm and its extensions, see e.g. Vardi and Zhang (2000). A kernel algorithm for the spatial median was provided in Debruyne et al. (2010). It writes the spatial median $m_{\mathcal {F}}$ in feature space as a convex combination of the $\phi (x_i)$:

$$\begin{aligned} m_\mathcal {F}= \sum _{i=1}^{n} \gamma _i \phi (x_i) \end{aligned}$$

in which the coefficients $\gamma _1, \dots , \gamma _n$ are unknown. The Euclidean distance of each observation to $m_\mathcal {F}$ is computed as the square root of

$$\begin{aligned}&||\phi (x_i) - m_\mathcal {F}||^2 \nonumber \\&\quad = || \phi (x_i) - \sum _{j=1}^n \gamma _j \phi (x_j)||^2 \nonumber \\&\quad = || \phi (x_i)||^2 + || \sum _{j=1}^n \gamma _j \phi (x_j)||^2 - 2 \langle \phi (x_i), \sum _{j=1}^n \gamma _j \phi (x_j)\rangle \nonumber \\&\quad = k(x_i,x_i) + \sum _{j=1}^n \sum _{\ell =1}^n \gamma _j \gamma _\ell k(x_j,x_\ell ) - 2 \sum _{j=1}^n\gamma _j k(x_i,x_j) \end{aligned}$$

(6)

and the coefficients $\gamma _1,\dots ,\gamma _n$ that minimize $\sum _i ||\phi (x_i)-m_\mathcal {F}||$ are obtained by an iterative procedure described in Algorithm 2 in Sect. A.1 of the Supplementary Material. The first initial h-subset H is then given by the objects with the h lowest values of (6). Alternatively, H is described by a weight vector $w = (w_1,\ldots ,w_n)$ of length n, where

$$\begin{aligned} w_i {:}{=} {\left\{ \begin{array}{ll} 1 \quad &{} \text {if } i\in H \\ 0 \quad &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(7)

The initial location estimate $c_\mathcal {F}$ in feature space is then the weighted mean

$$\begin{aligned} c_{\mathcal {F}} = \frac{\sum _{i=1}^n w_i\phi (x_i)}{\sum _{i=1}^n\! w_i} \;. \end{aligned}$$

(8)

The initial covariance estimate $\hat{\Sigma }_\mathcal {F}$ is the weighted covariance matrix

$$\begin{aligned} \hat{\Sigma }_\mathcal {F}= \frac{1}{\sum _{i=1}^n\! u_i} \, {\tilde{\Phi }}^\top \mathrm {diag}(u_1,\ldots ,u_n)\,{\tilde{\Phi }} \end{aligned}$$

(9)

given by covariance weights $(u_1,\ldots ,u_n)$ that in general may differ from the location weights $(w_1,\ldots ,w_n)$. But for the spatial median initial estimator one simply takes $u_i {:}{=} w_i$ for all i.

The second initial estimator is based on the Stahel-Donoho outlyingness (SDO) of Stahel (1981), Donoho (1982). In a space with coordinates it involves projecting the data points on many unit length vectors (directions). We compute the kernelized SDO (Debruyne and Verdonck 2010) of all observations and determine an h-subset as the indices of the h points with lowest outlyingness. This is then converted to weights $w_i$ as in (7), and we put $u_i {:}{=} w_i$ again. The entire procedure is listed as Algorithm 3 in the Supplementary Material.

The third initial h-subset is based on spatial ranks (Debruyne et al. 2009). The spatial rank of $\phi (x_i)$ with respect to the other feature vectors is defined as:

$$\begin{aligned} R_i&= \frac{1}{n}\left\| \sum _{j \ne i} \frac{\phi \left( x_{i}\right) - \phi \left( x_{j}\right) }{\left\| \phi \left( x_{i}\right) - \phi \left( x_{j}\right) \right\| }\right\| \nonumber \\&= \frac{1}{n}\left[ \left( \sum _{j\ne i} \frac{\phi \left( x_{i}\right) - \phi \left( x_{j}\right) }{\left\| \phi \left( x_{i}\right) - \phi \left( x_{j}\right) \right\| }\right) ^\top \left( \sum _{\ell \ne i} \frac{\phi \left( x_{i}\right) - \phi \left( x_\ell \right) }{\left\| \phi \left( x_{i}\right) - \phi \left( x_\ell \right) \right\| }\right) \right] ^{\frac{1}{2}} \nonumber \\&= \frac{1}{n}\left[ \sum _{j \ne i} \sum _{\ell \ne i} \frac{k(x_{i}, x_{i})-k(x_{i}, x_{j})- k(x_{i}, x_\ell ) + k(x_{j}, x_\ell )}{\alpha (x_i,x_j) \alpha (x_i,x_\ell )} \right] ^{\frac{1}{2}} \end{aligned}$$

(10)

where $\alpha (x_i,x_j) = [k(x_{i}, x_{i})+ k(x_{j}, x_{j})- 2 k(x_{i}, x_{j})]^{\frac{1}{2}}$. If $R_i$ is large, this indicates that $\phi (x_i)$ lies further away from the bulk of the data than most other feature vectors. In this sense, the values $R_i$ represent a different measure of the outlyingness of $\phi (x_i)$ in the feature space. We then consider the h lowest spatial ranks, yielding the location weights $w_i$ by (7), and put $u_i {:}{=} w_i$. The complete procedure is Algorithm 4 in the Supplementary Material. Note that this algorithm is closely related to the depth computation in Chen et al. (2009) which appeared in the same year as Debruyne et al. (2009).

The last initial estimator is a generalization of the spatial sign covariance matrix (Visuri et al. 2000) (SSCM) to the feature space $\mathcal {F}$. For data with coordinates, one first computes the spatial median m described above. The SSCM then carries out a radial transform which moves all data points to a sphere around m, followed by computing the classical product moment of the transformed data:

$$\begin{aligned} {\hat{\Sigma }}^{\mathrm {SSCM}} = \frac{1}{n-1} \sum _{i=1}^{n} \frac{\left( x_i-m\right) }{||x_i-m||} \frac{\left( x_i-m\right) ^\top }{||x_i-m||}. \end{aligned}$$

The kernel spatial sign covariance matrix (Debruyne et al. 2010) is defined in the same way, by replacing $x_i$ by $\phi (x_i)$ and m by $m_\mathcal {F}= \sum _{i=1}^{n} \gamma _i \phi (x_i)$. We now have two sets of weights. For location we use the weights $w_i = \gamma _i$ of the spatial median and apply (8). But for the covariance matrix we compute the weights $u_i = 1/||\phi (x_i) - m_\mathcal {F}||$ with the denominator given by (6). Next, we apply (9) with these $u_i$. The entire kernel SSCM procedure is listed as Algorithm 5 in the Supplementary Material. Note that kernel SSCM uses continuous weights instead of zero-one weights.

4.2 The refinement step

It happens that the eigenvalues of initial covariance estimators are inaccurate. In Maronna and Zamar (2002) this was addressed by re-estimating the eigenvalues, and Hubert et al. (2012) carried out this refinement step for all initial estimates used in that paper. In order to employ a refinement step in KMRCD we need to be able to kernelize it. We will derive the equations for the general case of a location estimator given by a weighted sum (8) and a scatter matrix estimate given by a weighted covariance matrix (9) so it can be applied to all four initial estimates. We proceed in four steps.

• 1. The first step consists of projecting the uncentered data on the eigenvectors $V_\mathcal {F}$ of the initial scatter estimate $\hat{\Sigma }_\mathcal {F}$:

  $$\begin{aligned} B = \Phi V_\mathcal {F}= \Phi {\tilde{\Phi }}^\top D^{\frac{1}{2}}V = \Big (K - K w 1_n^\top \Big )D^{\frac{1}{2}}V, \end{aligned}$$

  (11)

  where $D{=}\mathrm {diag}(u_1,\ldots ,u_n)/ (\sum _{i=1}^n\! u_i)$, $1_{n}{=}(1,\ldots ,1)^\top$, and $V_\mathcal {F}= {\tilde{\Phi }}^\top D^{\frac{1}{2}}V$ with V the normalized eigenvectors of the weighted centered kernel matrix ${\hat{K}} = (D^{\frac{1}{2}}{\tilde{\Phi }}) (D^{\frac{1}{2}}{\tilde{\Phi }})^\top = D^{\frac{1}{2}}{\tilde{K}}D^{\frac{1}{2}}$.

• 2. Next, the covariance matrix is re-estimated by

  $$\begin{aligned}\Sigma ^{*}_\mathcal {F}= V_\mathcal {F}L V_\mathcal {F}^\top = {\tilde{\Phi }}^\top D^{\frac{1}{2}}V L V^\top D^{\frac{1}{2}}{\tilde{\Phi }}\;, \end{aligned}$$

  where $L=\mathrm {diag}(Q_{n}^{2}\left( B_{.1}\right) , \ldots , Q_{n}^{2}\left( B_{.n}\right) )$ in which $Q_{n}$ is the scale estimator of Rousseeuw and Croux (1993) and $B_{.j}$ is the jth column of B.

• 3. The center is also re-estimated, by

  $$\begin{aligned} c^*_\mathcal {F}= (\Sigma _\mathcal {F}^*)^{\frac{1}{2}} \text{ median }\Big (\Phi (\Sigma _\mathcal {F}^*)^{-\frac{1}{2}}\Big ) \end{aligned}$$

  where $\text{ median }$ stands for the spatial median. This corresponds to using a modified feature map $\phi ^{*}(x) = \phi (x)(\Sigma _\mathcal {F}^*)^{-\frac{1}{2}}$ for the spatial median or running Algorithm 2 with the modified kernel matrix

  $$\begin{aligned} K^*&= \Phi {\tilde{\Phi }}^\top D^{\frac{1}{2}}V L^{-1} V^\top D^{\frac{1}{2}}{\tilde{\Phi }} \Phi ^\top \nonumber \\&= \Big (K - K w 1_n^\top \Big ) D^{\frac{1}{2}} V L^{-1}D^{\frac{1}{2}} \Big (K - K w 1_n^\top \Big )^\top . \end{aligned}$$

  (12)

  Transforming the spatial median gives us the desired center:

  $$\begin{aligned} c^*_\mathcal {F}= (\Sigma ^*_\mathcal {F})^{\frac{1}{2}} \sum _{i=1}^n (\Sigma ^*_\mathcal {F})^{-\frac{1}{2}} \gamma ^*_i \phi (x_i) = \sum _{i=1}^n \gamma ^*_i \phi (x_i), \end{aligned}$$

  where $\gamma ^*_i$ are the weights of the spatial median for the modified kernel matrix.

• 4. The kernel Mahalanobis distance is calculated as

  $$\begin{aligned} d^{*}_\mathcal {F}(x)&= \Big (\phi (x) - c^*_\mathcal {F}\Big )^\top \, (\Sigma ^{*}_\mathcal {F})^{-1} \, \Big (\phi (x) - c^*_\mathcal {F}\Big ) \nonumber \\&= \Big (\phi (x) - c^*_\mathcal {F}\Big )^\top \, {\tilde{\Phi }}^\top D^{\frac{1}{2}}V L^{-1} V^\top D^{\frac{1}{2}} {\tilde{\Phi }} \, \Big (\phi (x) - c^*_\mathcal {F}\Big ) \nonumber \\&= k^*(x,X) D^{\frac{1}{2}} V L^{-1} V^\top D^{\frac{1}{2}}{k^*(x,X)}^\top \end{aligned}$$

  (13)

  with,

  $$\begin{aligned} k^*(x,X)&= k(x,X) - \sum _{i=1}^{n} w_i k(x,x_i) 1_n^\top \\&\quad - \sum _{j=1}^{n} \gamma _j^* k(x_j,X) - \sum _{i=1}^{n} \sum _{j=1}^{n} w_i \gamma _j^* k(x_i,x_j) 1_n^\top \end{aligned}$$

  where $k(x,X) = (k(x,x_1),\ldots ,k(x,x_n))$.

The h points with the smallest $d^{*}_\mathcal {F}(x)$ form the refined h-subset. The entire procedure is Algorithm 6 in the Supplementary Material.

4.3 Kernel MRCD algorithm

We now have all the elements to compute the kernel MRCD by Algorithm 1. Given any PSD kernel matrix and subset size h, the algorithm starts by computing the four initial estimators described in Sect. 4.1. Each initial estimate is then refined according to Sect. 4.2. Next, kernel MRCD computes the regularization parameter $\rho$. This is done with a kernelized version of the procedure in Boudt et al. (2020). For each initial estimate we choose $\rho$ such that the regularized kernel matrix ${\tilde{K}}^H_\mathrm {reg}$ of (4) is well-conditioned. If we denote by $\lambda$ the vector containing the eigenvalues of the centered kernel matrix ${\tilde{K}}^H$, the condition number of ${\tilde{K}}^H_\mathrm {reg}$ is

$$\begin{aligned} \kappa (\rho ) = \frac{(h-1)\rho + (1-\rho )\max (\lambda )}{(h-1)\rho + (1-\rho )\min (\lambda )} \end{aligned}$$

(14)

and we choose $\rho$ such that $\kappa (\rho ) \leqslant 50$. (Sect. A.3 in the supplementary material contains a simulation study supporting this choice.) Finally, kernel C-steps are applied until convergence, where we monitor the objective function of Sect. 3.

In the special case where the linear kernel is used, the centered kernel matrix ${\tilde{K}}^H$ immediately yields the regularized covariance matrix $\hat{\Sigma }_\mathrm {reg}^H$ through

$$\begin{aligned} \hat{\Sigma }_\mathrm {reg}^H = \frac{1-\rho }{h-1}\Big ({\tilde{X}}^H\Big )^\top {\tilde{V}} \Lambda {\tilde{V}}^\top {\tilde{X}}^H + \rho I_h \end{aligned}$$

where ${\tilde{X}}^H = X^H - \frac{1}{h} \sum _{i \in H} x_i$ is the centered matrix of the observations in H and $\Lambda$ and ${\tilde{V}}$ contain the eigenvalues and normalized eigenvectors of ${\tilde{K}}^H$. (The derivation is given in Sect. A.2.) So instead of applying MRCD to coordinate data we can also run KMRCD with a linear kernel and transform ${\tilde{K}}^H$ to $\hat{\Sigma }_\mathrm {reg}^H$ afterward. This computation is faster when the data has more dimensions than cases.

4.4 Anomaly detection by KMRCD

Mahalanobis distances (MD) relative to robust estimates of location and scatter are very useful to flag outliers, because outlying points i tend to have higher $\text{ MD}_i$ values. The standard way to detect outliers by means of the MCD in low dimensional data is to compare the robust distances to a cutoff that is the square root of a quantile of the chi-squared distribution with degrees of freedom equal to the data dimension (Rousseeuw and Van Driessen 1999). However, in high dimensions the distribution of the squared robust distances is no longer approximately chi-squared, which makes it harder to determine a suitable cutoff value. Faced with a similar problem (Rousseeuw et al. 2018) introduced a different approach, based on the empirical observation that robust distances of the non-outliers in higher dimensional data tend to have a distribution that is roughly similar to a lognormal. They first transform the distances $\text{ MD}_i$ to $\text{ LD}_i = \log (0.1 + \text{ MD}_i)$, where the term 0.1 prevents numerical problems should a (near-)zero $\text{ MD}_i$ occur. The location and spread of the non-outlying $\text{ LD}_i$ are then estimated by $\hat{\mu }_\mathrm {MCD}$ and $\hat{\sigma }_\mathrm {MCD}$, the results of applying the univariate MCD to all $\text{ LD}_i$ using the same h as in the KMCRD method itself. Data point i is then flagged iff

$$\begin{aligned} \frac{\text{ LD}_{i}-\hat{\mu }_\mathrm {MCD}(\text{ LD})}{\hat{\sigma }_\mathrm {MCD}(\text{ LD})} > z(0.995) \end{aligned}$$

where z(0.995) is the 0.995 quantile of the standard normal distribution. The cutoff value for the untransformed robust distances is thus

$$\begin{aligned} c=\exp \left( \hat{\mu }_\mathrm {MCD}(\text{ LD})+ z(0.995)\hat{\sigma }_\mathrm {MCD}(\text{ LD}) \right) -0.1. \end{aligned}$$

(15)

The user may want to try different values of h to be used in both the KMRCD method itself as well as in the $\hat{\mu }_\mathrm {MCD}$ and $\hat{\sigma }_\mathrm {MCD}$ in (15). One typically starts with a rather low value of h, say $h=0.5n$ when the linear kernel is used and there are up to 10 dimensions, and $h=0.75n$ in all other situations. This will provide an idea about the number of outliers in the data, after which it is recommended to choose h as high as possible provided $n-h$ exceeds the number of outliers. This will improve the accuracy of the estimates.

4.5 Choice of bandwidth

A commonly used kernel function is the radial basis function (RBF) $k(x,y) = e^{-\Vert x-y\Vert ^2/(2\sigma ^2)}$ which contains a tuning constant $\sigma$ that needs to be chosen. When the downstream learning task is classification $\sigma$ is commonly selected by cross validation, where it is assumed that the data has no outliers or they have already been removed. However, in our unsupervised outlier detection context there is nothing to cross validate. Therefore, we will use the so-called median heuristic (Gretton et al. 2012) given by

$$\begin{aligned} \sigma ^2 = \text{ median }\big \{ \Vert x_{i}-x_{j}\Vert ^2 ; 1 \leqslant i<j \leqslant n\big \} \end{aligned}$$

(16)

in which the $x_i$ are the standardized data in the original space. We will use this $\sigma$ in all our examples.

4.6 Illustration on toy examples

We illustrate the proposed KMRCD method on the two toy examples in Fig. 1. Both datasets consist of $n=1000$ bivariate observations. The elliptical dataset in the left panel was generated from a bivariate Gaussian distribution, plus 20% of outliers. The non-elliptical dataset in the panel on the right is frequently used to demonstrate kernel methods (Suykens et al. 2002). This dataset also contains $20\%$ of outliers, which are shown in red and form the outer curved shape. We first apply the non-kernel MCD method, which does not transform the data, with $h=\lfloor 0.75n \rfloor$. (Not using a kernel is equivalent to using the linear kernel.) The results are in Fig. 2. In the panel on the left this works well because the MCD method was developed for data of which the majority has a roughly elliptical shape. For the same reason it does not work well on the non-elliptical data in the right hand panel.

Fig. 2

Results of the non-kernel MCD method on the toy datasets of Fig. 1. The contour lines are level curves of the MCD-based Mahalanobis distance

We now apply the kernel MRCD method to the same datasets. For the elliptical dataset we use the linear kernel, and for the non-elliptical dataset we use the RBF kernel with tuning constant $\sigma$ given by formula (16). This yields Fig. 3. We first focus on the left hand column. The figure shows three stages of the KMRCD runs. At the top, in Fig. 3a, we see the result for the selected h-subset, after the C-steps have converged. The members of that h-subset are the green points, whereas the points generated as outliers are colored red. Since h is lower than the true number of inlying points, some inliers (shown in black) are not included in the h-subset. In the next step, Fig. 3b shows the robust Mahalanobis distances, with the horizontal line at the cutoff value given by formula (15). The final output of KMRCD shown in Fig. 3c has the flagged outliers in orange and the points considered inliers in blue. As expected, this result is similar to that of the non-kernel MCD in the left panel of Fig. 2.

The right hand column of Fig. 3 shows the stages of the KMRCD run on the non-elliptical data. The results for the selected h-subset in Fig. 3a look much better than in the right hand panel of Fig. 2, because the level curves of the robust distance now follow the shape of the data. In stage (b) we see that the distances of the inliers and the outliers are fairly well separated by the cutoff (15), with a few borderline cases, and stage (c) is the final result. This illustrates that using a nonlinear kernel allows us to fit non-elliptical data.

Fig. 3

Kernel MRCD results on the toy datasets of Fig. 1. In the left column the linear kernel was used, and in the right column the RBF kernel. The three stages a, b and c are explained in the text

5 Simulation study

5.1 Simulation study with linear kernel

In this section we compare the KMRCD method proposed in the current paper, run with the linear kernel, to the MRCD estimator of Boudt et al. (2020). Recall that using the linear kernel $k(x,y) = x^\top y$ means that the feature space can be taken identical to the coordinate space, so using the linear kernel is equivalent to not using a kernel at all. Our purpose is twofold. First, we want to verify whether KMRCD performs well in terms of robustness and accuracy, and that its results are consistent with those of MRCD. And secondly, we wish to measure the computational speedup obtained by KMRCD in high dimensions. In order to obtain a fair comparison we run MRCD with the identity matrix as target, which corresponds to the target of KMRCD. All computations are done in MATLAB on a machine with Intel Core i7-8700K and 16 GB of 3.70GHz RAM.

For the uncontaminated data, that is, for contamination fraction $\varepsilon = 0$, we generate n cases from a p-variate normal distribution with true covariance matrix $\Sigma$. Since the methods under consideration are equivariant under translations and rescaling variables, we can assume without loss of generality that the center $\mu$ of the distribution is 0 and that the diagonal elements of $\Sigma$ are all 1. We denote the distribution of the clean data by ${\mathcal {N}}(0,\Sigma )$. Since the methods are not equivariant to arbitrary nonsingular affine transformations we cannot set $\Sigma$ equal to the identity matrix. Instead we consider $\Sigma$ of the ALYZ type, generated as in Sect. 4 of Agostinelli et al. (2015), which yields a different $\Sigma$ in each replication, but always with condition number 100. The main steps of the construction of $\Sigma$ in Agostinelli et al. (2015) are the generation of a random orthogonal matrix to provide eigenvectors, and the generation of p eigenvalues such that the ratio between the largest and the smallest is 100, followed by iterations to turn the resulting covariance matrix into a correlation matrix while preserving the condition number. (In Sect. A.3 of the supplementary material also $\Sigma$ matrices with higher condition numbers were generated, with similar results.)

For a contamination fraction $\varepsilon > 0$ we replace a random subset of $\lfloor \varepsilon n \rfloor$ observations by outliers of different types. Shift contamination is generated from ${\mathcal {N}}(\mu _C, \Sigma )$ where $\mu _C$ lies in the direction where the outliers are hardest to detect, which is that of the last eigenvector v of the true covariance matrix $\Sigma$. We rescale v by making $v^T \Sigma ^{-1} v = E[Y^2] = p$ where $Y^2 \sim \chi ^2_p$. The center is taken as $\mu _C = k v$ where we set $k=200$. Next, cluster contamination stems from ${\mathcal {N}}(\mu _C, 0.05^2\,I_p)$ where $I_p$ is the identity matrix. Finally, point contamination places all outliers in the point $\mu _C$ so they behave like a tight cluster. These settings make the simulation consistent with those in Boudt et al. (2020), Hubert et al. (2012) and De Ketelaere et al. (2020). The deviation of an estimated scatter matrix $\hat{\Sigma }$ relative to the true covariance matrix $\Sigma$ is measured by the Kullback–Leibler (KL) divergence $\text{ KL }(\hat{\Sigma },\Sigma ) = \mathrm {trace}( \hat{\Sigma }\Sigma ^{-1}) - \log (\det ( \hat{\Sigma }\Sigma ^{-1})) - p$. The speedup factor is measured as $\text{ speedup }=\text{ time }(\text{ MRCD})/ \text{ time }(\text{ KMRCD})$. Different combinations of n and p are generated, ranging from $p = n/2$ to $p = 2n$.

Table 1 presents the Kullback–Leibler deviation results. The top panel is for $\varepsilon =0$, the middle panel for $\varepsilon =0.1$ and the bottom panel for $\varepsilon =0.3$ . All table entries are averages over 50 replications. First look at the results without contamination. By comparing the three choices for h, namely $\lfloor 0.5n \rfloor$, $\lfloor 0.75n \rfloor$ and $\lfloor 0.9n \rfloor$, we see that lowering h in this setting leads to increasingly inaccurate estimates $\hat{\Sigma }$. This is the price we pay for being more robust to outliers, since $n-h$ is an upper bound on the number of outliers the methods can handle. When we look at the panels for higher $\varepsilon$ we see a similar pattern. When $\varepsilon = 0.1$ the choice $\lfloor 0.9n \rfloor$ is sufficiently robust, and the lower choices of h have higher KL deviation. But when $\varepsilon = 0.3$ only the choice $h = \lfloor 0.5n \rfloor$ can detect the outliers, the other choices cause the estimates to break down. These patterns are confirmed by the averaged $\text{ MSE }=\sum _{i=1}^{p}\sum _{j=1}^{p} (\hat{\Sigma }- \Sigma )^2_{ij}/p^2$ shown in Table 7 in the Supplementary Material.

From these results we conclude that it is important that h be chosen lower than n minus the number of outliers, but not much lower since that would make the estimates less accurate. A good strategy is to first run with a low h, which reveals the number of outliers, and then to choose a higher h that can still handle the outliers and yields more accurate results as well.

As expected the KMRCD results are similar to those of MRCD, but not identical because there are differences in the selection of initial estimators, also leading to differences in the resulting regularization parameter $\rho$ shown in Table 8 in the Supplementary Material.

Table 1 Kullback–Leibler deviations of $\hat{\Sigma }$ from $\Sigma$

Table 2 Speedup factors of KMRCD relative to MRCD

We now turn our attention to the computational speedup factors in Table 2, that were derived from the same simulation runs as Table 1. Overall KMRCD ran substantially faster than MRCD, with the factor becoming larger when n decreases and/or the dimension p increases. There are two reasons for the speedup. First of all, the MRCD algorithm computes six initial scatter estimates, of which the last one is the most computationally demanding since it computes a robust bivariate correlation of every pair of variables, requiring $p(p-1)/2$ computations whose total time increases fast with p. Part of the speedup stems from the fact that KMRCD does not use this initial estimator, whereas its own four kernelized initial estimates gave equally robust results. This explains most of the speedup in Table 2.

For $p>n$ there is a second reason for the speedup, the use of the kernel trick. In particular, each C-step requires the computation of the Mahalanobis distances of all cases. MRCD does this by inverting the $p \times p$ covariance matrix $\hat{\Sigma }^H_\mathrm {reg}$ , whereas KMRCD uses equation (5) which implies that it suffices to invert the $n \times n$ kernel matrix ${\tilde{K}}_{\mathrm {reg}}^H$ , which takes time complexity $O(n^3)$ instead of $O(p^3)$.

5.2 Simulation with nonlinear kernel

In this section we compare the proposed KMRCD estimator to the MRCD estimator of Boudt et al. (2020) on two types of non-elliptical datasets. The first type is generated by a copula. The black points in the left panel of Fig. 4 were generated from the t copula (Nelsen 2007) with Pearson correlation 0.1 and $\nu = 1$ degrees of freedom. We then added 20% of outliers shown in red, generated from the uniform distribution on the unit square but restricted to points that are far from the black points. In Fig. 9 of Sect. A.6 we show similar figures with the Frank, Clayton, and Gumbel copulas.

Fig. 4

The left panel shows black data points generated from the t copula, plus 20% of outliers in red. The middle panel shows the contour curves of the Mahalanobis distance from the MRCD estimator, and the right panel those of the KMRCD estimator. Both estimators were computed for $h=0.75n$ . The points in the h-subset are shown in green, the other points with the 80% lowest Mahalanobis distance in grey, and the remainder in red. (colour figure online)

Figure 5 illustrates a second setting, where the regular observations in black are generated near the unit circle, and inside the circle are red outliers generated from the Gaussian distribution with center 0 and covariance matrix equal to 0.04 times the identity matrix. This is a simple example where the clean data lie near a manifold.

Fig. 5

The left panel shows data generated near the unit circle in black, plus 20% of outliers in red. The other panels are analogous to Fig. 4. (colour figure online)

In the simulation we generated 100 datasets of each type, with $n=500$ and the outlier fraction $\varepsilon$ equal to 0.1 or 0.2, so the number of regular observations is $n(1-\varepsilon )$. With all four copulas the KMRCD estimator used the radial basis function with bandwidth (16). For the circle-based data the polynomial kernel $k(x,y) = (x^\top y + 1)^2$ of degree 2 was used.

We measure the performance by counting the number of outliers in the h-subset, and among the $n(1-\varepsilon )$ points with the lowest (kernel) Mahalanobis distance. The averaged counts over the 100 replications are shown in Table 3. By comparing the rows of KMRCD and MRCD with the same $\varepsilon$, we see that MRCD has more true outliers in its h-subset and its $n(1-\varepsilon )$ set. In the table, KMRCD outperforms MRCD for both choices of $\varepsilon$ and for all three choices of h. The good performance of KMRCD is also seen in the right panel of Fig. 4, where the contours of the kernel Mahalanobis distance nicely follow the distribution. The difference between MRCD and KMRCD is most apparent on the circle-based data: in Fig. 5 the KMRCD fits the regular data on the circle, whereas the original MRCD method, by its nature, considers the outliers in the center as regular data.

Table 3 Average number of outliers in the h-subset H, and among the $n(1-\varepsilon )$ points with lowest (kernel) Mahalanobis distance

We conclude that in this nonlinear setting, KMRCD has successfully extended the MRCD to non-elliptical distributions. We want to add two remarks about this. First, as in all kernel-based methods the choice of the kernel is important, and choosing a different kernel can lead to worse results. And second, just as in the linear setting h should be lower than n minus the number of outliers, so in practice it is recommended to first run with a low h, look at the results in order to find out how many outliers there are, and possibly run again with a higher h.

Section A.4 of the supplementary material contains additional simulation results about the computation time of the four initial estimators in KMRCD and their subsequent C-steps, in different settings with linear and nonlinear kernels.

6 Experiments

6.1 Food industry example

We now turn our attention to a real dataset from the food industry. In that setting datasets frequently contain outliers, because samples originate from natural products which are often contaminated by insect damage, local discolorations and foreign material. It also happens that the image acquisition signals yield non-elliptical data, and in that case a kernel transform can help.

Fig. 6

Food industry example: KMRCD results with the linear kernel (left column) and the RBF kernel (right column). The top row contains the training data, and the resulting fits were applied to the test data in the bottom row

Fig. 7

MNIST denoising results based on the classical covariance matrix (top panel) and on the KMRCD estimate (bottom panel). The first and second rows of each panel show the same original and noise-added test set images. The remaining rows contain the results of projecting on the first 5, 15, and 30 eigenvectors

The dataset is bivariate and contains two color signals measured on organic sultana raisin samples. The goal is to classify these into inliers and outliers, so that during production outliers can be physically removed from the product in real time. There are training data and test data, but the class label ‘outlier’ is not known beforehand. The scatter plot of the training data in Fig. 6a reveals the non-elliptical (and to some extent triangular) structure of the inliers. Three types of outliers are visible. Those with high values of $\lambda _1$ and low $\lambda _2$ at the bottom right correspond to foreign, cap-stem related material like wood, whereas points with high values of $\lambda _2$ represent discolorations. There are also a few points with high values of both $\lambda _1$ and $\lambda _2$ which correspond to either discolored raisins or objects with clear attachment points of cap-stems. Outliers of any of these three types need to be flagged and removed from the product. From manually analyzing data of this product it is known beforehand that the fraction of outliers is rather low, at most around $2\%$.

We first run KMRCD on the training data. In its preprocessing step it standardizes both variables. For comparison purposes we use two kernels. In the left hand column of Fig. 6 we apply the linear kernel, and in the right hand column we use the RBF kernel with tuning constant $\sigma$ given by (16). Since we know the fraction of outliers is low we can put $h = \lfloor 0.95n \rfloor$. Each figure shows the flagged points in orange and the remaining points in blue, and the contour lines are level curves of the robust distance.

The fit with linear kernel in Fig. 6a has contour lines that do not follow the shape of the data very well, and as a consequence it fails to flag some of the outliers, such as those with high $\lambda _2$ and some with relatively high values of both $\lambda _1$ and $\lambda _2$. The KMRCD fit with nonlinear kernel in Fig. 6b has contour lines that model the data more realistically. This fit does flag all three types of outliers correctly. Both trained models were then used to classify the previously unseen test set. The results are similar to those on the training data. The anomaly detection with linear kernel in Fig. 6c again misses the raisin discolorations, which would keep these impurities in the final consumer product. Fortunately, the method with the nonlinear kernel in panel (d) does flag them.

6.2 MNIST digits data

Our last example is high dimensional. The MNIST dataset contains images of handwritten digits from 0 to 9, at the resolution of $28 \times 28$ grayscale pixels (so there are 784 dimensions), and was downloaded from http://yann.lecun.com/exdb/mnist. There is a training set and a test set. Both were subsampled to 1000 images. To the training data we added noise distributed as ${\mathcal {N}}(0,(0.5)^2)$ to $20\%$ of the images, and in the test set we added noise with the same distribution to all images. We then applied KMRCD with RBF kernel with tuning constant $\sigma$ given by (16) and $h=\lfloor 0.75n \rfloor$ to the 1000 training images. Next, we computed the eigenvectors of the robustly estimated covariance matrix.

Our goal is to denoise the images in the test set by projecting them onto the main eigenvectors found in the training data. As we are interested in a reconstruction of the data in the original space rather than in the feature space, we transform the scores back to the original input space by the iterative optimization method of Mika et al. (1999).

The top panel of Fig. 7 illustrates what happens when applying this computation to the classical covariance matrix in feature space, which corresponds to classical kernel PCA (Schölkopf et al. 1998). The bottom panel is based on KMRCD. The first row of each panel displays original test set images, and the second row shows the test images after the noise was added. The first and second rows do not depend on the estimation method, but the remaining rows do. There we see the results of projecting on the first 5, 15, and 30 eigenvectors of each method. In the top panel those images are rather diffuse, which indicates that the classical approach was affected by the training images with added noise and considers the added noise as part of its model. This implies that increasing the number of eigenvectors used will not improve the overall image quality much. The lower panel contains sharper images, because the robust fit of the training data was less affected by the images with added noise that acted as outliers.

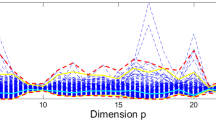
We can also compute the mean absolute error $\sum _{i=1}^n\sum _{j=1}^{p}s |x_{i,j} - {\hat{x}}_{i,j}|/(np)$ between the original test images (with $p=784$ dimensions) and the projected versions of the test images with added noise. Figure 8 shows this deviation as a function of the number of eigenvectors used in the projection. The deviations of the robust method are systematically lower than those of the classical method, confirming the visual impression from Fig. 7.

Fig. 8

The mean absolute error of the denoised images to the original test images in function of the number of eigenvectors used in the projection. The top curve is for the classical covariance matrix in feature space, the lower curve for KMRCD

7 Conclusions

The kernel MRCD method introduced in this paper is a robust method that allows to analyze non-elliptical data when used with a nonlinear kernel. Another advantage is that even when using the linear kernel the computation becomes much faster when there are more dimensions than cases, a situation that is quite common nowadays. Due to the built-in regularization the result is always well-conditioned.

The algorithm starts from four kernelized initial estimators, and to each it applies a new kernelized refinement step. The remainder of the algorithm is based on a theorem showing that C-steps in feature space are equivalent to a new type of C-steps on centered kernel matrices, so the latter reduce the objective function. The performance of KMRCD in terms of robustness, accuracy and speed is studied in a simulation, and the method is applied to several examples. Potential future applications of the KMRCD method are as a building block for other multivariate techniques such as robust classification.

Research-level MATLAB code and an example script are freely available from the webpage http://wis.kuleuven.be/statdatascience/robust/software.