Recent Developments in Particle Acceleration at Shocks: Theory and Observations

Perri, Silvia; Bykov, Andrei; Fahr, Hans; Fichtner, Horst; Giacalone, Joe

doi:10.1007/s11214-022-00892-5

Open Access
Published: 05 May 2022

Recent Developments in Particle Acceleration at Shocks: Theory and Observations

Silvia Perri ORCID: orcid.org/0000-0002-8399-3268¹,
Andrei Bykov²,
Hans Fahr³,
Horst Fichtner⁴ &
Joe Giacalone⁵

Space Science Reviews volume 218, Article number: 26 (2022) Cite this article

480 Accesses
1 Citations
Metrics details

Abstract

Energetic particles represent an important component of the plasma in the heliosphere. They range from particles accelerated at impulsive events in the solar corona and at large scale structures in the interplanetary medium, to anomalous cosmic rays accelerated at the boundaries of the heliosphere. In-situ satellite observations, numerical simulations and theoretical models have advanced, often in a cooperative way, our knowledge on the acceleration processes involved. In this paper we review recent developments on particle acceleration, with major emphasis on shock acceleration, giving an overview of recent observations at interplanetary shocks and at the termination shock of the solar wind. We discuss their interpretation in terms of analytical models and numerical simulations. The influence of the particle transport properties on the acceleration mechanism will also be addressed.

Introduction

Energetic particles are ubiquitous in space and astrophysical environments. In the interplanetary space, energetic particles populating the suprathermail tail of the low-energy cosmic ray spectrum range from solar energetic particles (SEPs) (Lin 1974, 2005) to pick-up ions, to corotating interaction region particles, energetic storm particles, impulsive-solar-flare-related particles, to anomalous cosmic rays observed close to the termination shock (TS) of the solar wind (Giacalone et al. 2012) (see Lee et al. (2012), Mewaldt (2000) for a general overview), and to galactic cosmic rays (Potgieter 1998). Understanding the different acceleration mechanisms represents an open challenge for modern astrophysics. It has recently been discovered that the presence of coherent structures, such as current sheets, flux tubes, or multiple reconnecting islands, represents an efficient stochastic acceleration mechanism for charged particles accounting for the generation of power law tails of suprathermal particles (Drake et al. 2006; Hoshino 2012; Vlahos et al. 2004, 2016). Actually, the presence of vortical structures and reconnecting magnetic islands can also play a fundamental role during particle shock acceleration, as pointed out by Zank et al. (2015a,b) and, e.g., le Roux and Zank (2021). Indeed, considering that the plasma downstream of a shock wave is highly compressed and turbulent, it is natural to consider that a sea of fluctuations, flux ropes, and magnetic islands emerge causing an efficient pitch-angle scattering of particles and a local acceleration in response to island contraction and electric fields from merging structures. Including such effects in the particle transport equation (Zank et al. 2014; le Roux et al. 2015), Zank et al. (2015b) found that the peak of the energetic particle intensity is located downstream behind the shock front; this was observed to be in qualitative agreement with Voyager 2 observations of energetic particle fluxes at the TS of the solar wind (Decker et al. 2008).

Major sources of suprathermal particles in the heliosphere are interplanetary shocks, i.e., driven by coronal-mass-ejections while expanding into the interplanetary medium (Vourlidas et al. 2003; Cliver and Ling 2009; Grechnev et al. 2015), corotating interaction region shocks (Crooker et al. 1999; Allen et al. 2021), and the heliospheric TS (Decker et al. 2005, 2008). However, these mechanisms are also invoked in astrophysical systems to account for galactic (Aharonian et al. 2004; Helder et al. 2012; Reynolds et al. 2012) and extra galactic (Van Weeren et al. 2016; Kang et al. 2012) cosmic rays. The acceleration process is based on the first order Fermi mechanism, where turbulent magnetic field fluctuations in the upstream and in the downstream regions scatter particles back and forth across the shock front several times, thus increasing the efficiency of the acceleration. Particles can also gain energy by drifting along the shock front, due to the effect of the gradient in the magnetic field magnitude, in the same direction as the motional ($\mathbf{V}\times \mathbf{B}$) electric field. In the limit of no pitch-angle scattering, this process is known as shock drift acceleration. Both shock-drift acceleration and first-order Fermi acceleration are subsets of the general process known as diffusive shock acceleration (DSA) (Bell 1978; Lee and Fisk 1982; Jokipii 1987; Liu and Jokipii 2021). It leads to a power law energy distribution $dN/dE\sim E^{-\gamma}$ where

$$ \gamma =\frac{r+2}{r-1}, $$

(1)

and $r=V_{u}/V_{d}$ is the compression ratio of the shock. $V_{u}$ is the unshocked plasma and $V_{d}$ is the shocked plasma speed measured in the shock frame. In the strong shock regime $r=4$, the spectral index $\gamma =2$. Furthermore, starting from a test particle approach, assuming a planar shock, stationary conditions, and a spatially independent diffusion coefficient, the solution of the transport equation is given by (Drury 1983)

$$ f(x,p)= \bigg\{ \textstyle\begin{array}{l@{\quad}l} f_{u}(p)+g_{u}(p)\exp (\frac{V_{u} x}{D_{x}}) & x< 0 \\ f_{d}(p) & x\ge 0 \end{array} $$

(2)

where $x<0$ indicates the upstream region and $x\ge 0$ the downstream region. $g_{u}(p)=f_{d}(p)-f_{u}(p)$ depends on the particle momentum and ensures that the particle distribution is continuous across the shock, $D_{x}\equiv D_{x}(p)$ is the spatial diffusion coefficient component along the shock normal, and $f_{d}(p)$ is the finite value reached downstream for the particle distribution function. Thus, the “standard” DSA prediction implies that the energetic particle flux falls off exponentially with increasing distance from the shock front far upstream and remains constant in the downstream side. Another important aspect that needs to be considered is the influence of the turbulent properties of the magnetic field fluctuations on their interaction with energetic particles; for example, it has been shown that at perpendicular shocks a strong correlation exists between the maximum energy reached by accelerated particles and the slope of the power spectral density of the magnetic field, i.e., a steeper power spectrum leads to higher maximum energies (Dosch and Shalchi 2010). It is also well known that magnetic turbulence has a great impact on the properties of the energetic particle transport, since transport regimes can be different in the directions parallel and perpendicular to the average magnetic field (Jokipii 1966; Matthaeus et al. 2003; Webb et al. 2006; Shalchi and Kourakis 2007; Dosch and Shalchi 2010; Shalchi 2011; Zimbardo et al. 2012; Ferrand et al. 2014). At the same time the cosmic ray driven instabilities are able to amplify the background plasma magnetic fluctuations (see e.g. Bell 2004; Bykov et al. 2013a; Schure et al. 2012; Marcowith et al. 2016) to produce strong magnetic turbulence. The effect is widely discussed to operate in DSA of cosmic rays in supernova remnants. Recent direct, multi-spacecraft THEMIS/ARTEMIS observations revealed the effect of a pool of energetic non-thermal ions on the very strong super-adiabatic magnetic field amplification during a passage of a rotational discontinuity through the Earth bow shock in accordance with the results of the hybrid-code simulations (Kropotina et al. 2021).

Numerical simulations of energetic particle transport in synthetic magnetic turbulence have shown that in quasi-slab turbulence the transport along the direction parallel to the mean field can be faster than normal, i.e., superdiffusive, while along the perpendicular direction it can be slower than normal, namely subdiffusive (Zimbardo et al. 2006; Pommois et al. 2007; Shalchi and Kourakis 2007). Further, using a combined slab/2D turbulence model, Hussein and Shalchi (2016) have observed normal diffusion for energetic particles, with mean free paths in excellent agreement with the Palmer consensus (Palmer 1982). The key role of magnetohydrodynamic (MHD) turbulence on the cosmic ray propagation has been investigated in depth by Lazarian and Yan (2014), where perpendicular superdiffusion at scales smaller than the turbulence injection scale has been found. Such a behavior has been ascribed to the turbulent wandering of the magnetic field lines and has effects on the acceleration efficiency at shocks. Thus, the interaction of suprathermal particles with magnetic field turbulence and the related transport properties can affect the shock acceleration process (Perri and Zimbardo 2012a; Giacalone 2013; Zimbardo and Perri 2013; Perri and Zimbardo 2015b). Since the discovery of the DSA mechanism (Axford et al. 1977; Krymskii 1977; Bell 1978; Blandford and Ostriker 1978) many interesting results were obtained in the application of DSA to astrophysical objects of different scale sizes (see for a review e.g. Blandford and Eichler 1987; Berezhko and Krymskiĭ 1988; Jones and Ellison 1991; Malkov and Drury 2001; Ptuskin et al. 2013; Sironi et al. 2015; Marcowith et al. 2016; Blasi 2019). In this review we will primarily focus on the shock acceleration mechanism, giving emphasis to the broad number of observations of shock waves in the interplanetary space, as a place to infer acceleration properties for shocks in the outer heliosphere with potential applications for astrophysics. We review current theoretical interpretations of the observations and highlight the remaining unanswered questions.

The manuscript is organized as follows: in Sect. 2 we review observations of supra-thermal particle fluxes during spacecraft shock crossings and we detail recent interpretations in terms of anomalous transport; we focus on energy spectra, acceleration times, and magnetic field amplification. In Sect. 3 the role of magnetic turbulence in the shock acceleration process is discussed. Section 4 is dedicated to recent observations of flat energy spectra of energetic particles at interplanetary shock waves that challenge standard theory predictions. In Sect. 5 we review a mechanism for electron acceleration at the TS, addressing the role of plasma instabilities that eventually give rise to preferential electron heating. In Sect. 6 we discuss a multiple shock acceleration process as a mechanism connected to the acceleration of cosmic rays at multiple corotating interaction regions in the heliosphere. In Sect. 7 we summarize the content and address unanswered questions.

Observations of Suprathermal Particle Fluxes Upstream of Interplanetary Shock Waves and the Role of Anomalous Transport

Although DSA can be considered one of the fundamental processes that can account for cosmic ray acceleration, there are some observational evidences that question its validity. Indeed, Voyager 2 LECP observations of energetic ions accelerated at the solar wind TS indicate that the measured spectral index is consistent with a compression ratio of $r=3$ according to Eq. (1), while the observed compression ratio is $r=2$ (Decker et al. 2008). Furthermore, the PAMELA experiment has found evidence of different spectral indices for hydrogen and helium ions (within the 30–1000 GV rigidity range) (Adriani et al. 2011), which is not consistent with the DSA prediction of a spectral index that depends on the compression ratio only. Caprioli et al. (2017), by means of 2D hybrid simulations, have shown that the time-dependent acceleration process of ions at non-relativistic shocks has a dependence on the ratio between the ion atomic mass ($A$) and the charge ($Z$). At fixed $Z$ the thermal peak in the energy spectra is shifted towards high energies as $A$ increases (mass dependence), while the non-thermal tail in the spectra rolls of at the same $E_{max}/Z$, since DSA is a rigidity dependent process. Also the efficiency of injection into DSA depends on $A/Z$. At late times all the species tend to show the same universal DSA spectrum. However, cosmic ray spectral differences still remain an open question (Aguilar et al. 2021). Observations of suprathermal particle fluxes from $\sim 100$ keV to MeV energies accelerated at interplanetary shock waves do not always show an exponential time decrease from upstream of the shock and a constant profile downstream, as predicted by Eq. (2) (Perri and Zimbardo 2008; Sugiyama and Shiota 2011; Giacalone 2012; Perrone et al. 2013; Tessein et al. 2015). In this Section we review recent works that have included anomalous transport of particles in the shock acceleration process to explain some observations in the heliosphere.

Superdiffusive Transport as Inferred from Energetic Particle Fluxes Far Upstream of Shocks

In a series of papers Perri and Zimbardo (2007, 2008, 2009) have found evidence of energetic ion and electron fluxes, accelerated at interplanetary shocks, decaying as power laws far upstream. In the events analyzed, the magnetic field fluctuations in the upstream region, computed at the time scale in resonance with energetic particles, are independent of the shock distance, so that the observed power law time profile cannot be ascribed to a spatial dependent parallel diffusion coefficient (Perri and Zimbardo 2012b). One example of the event investigated is displayed in Fig. 1, which reports a corotating interaction region (CIR) (indicated in the figure by the vertical dashed line) crossed by the Ulysses spacecraft on 1992 October 11. From top to bottom: the hourly resolution radial solar wind bulk speed and the proton temperature from SWOOPS (Bame et al. 1992), the electron and the proton fluxes in some energy channels (see legend) as measured by LEFS 60/HI-SCALE, both plotted in log-lin axis, and the magnetic field normalized variance computed as $\sigma ^{2}_{|B|}/|B|^{2}=\sum _{i=1}^{3} \sigma _{i}^{2}/|B|^{2}$ over a time scale $T=10$ s (where $\sigma _{i}^{2}=\langle (B_{i}-\langle B_{i} \rangle )^{2} \rangle _{T}$ is calculated over the $i$-th component of the magnetic field). Such a time scale corresponds to the Larmor radius $\rho _{e}$ of electrons of $\sim 200$ keV propagating in the upstream magnetic field of the event reported in Fig. 1, since $f=1/T=V_{SW}/(2\pi \rho _{e})$. A closer look at the electron fluxes as a function of the distance from the front in log-log axis is reported in Fig. 2 (Perri et al. 2009), where the far upstream decay can be fitted by a power law $J(t)\propto t^{-\beta}$. The slopes of the power law found in Perri et al. (2009) for the electron fluxes are $\beta \in [0.30-0.56]$. Notice that the normalized magnetic field variance in Fig. 1 from about 10 to 100 hr (delimited by the thin red vertical lines) from the shock crossing, i.e., the time range over which the best fits of the electron fluxes have been performed, does not show a significant trend with time in the upstream. Energetic particle power law time profiles have also been detected during the TS crossing by the Voyager 2 spacecraft on August 2007 (Perri and Zimbardo 2009). The spacecraft crossed a supercritical quasi-perpendicular shock (Richardson et al. 2008) and the fluxes of energetic ions from about 540 keV to 3500 keV were observed to decay far upstream of the shock with slope $\beta \in [0.68-0.71]$, as shown in Fig. 3. All those evidences of power law energetic particle time profiles upstream of shock waves have been ascribed to the possibility of parallel anomalous transport for particles during the shock acceleration process. In particular, a transport faster than normal diffusive, i.e., superdiffusive, can explain those observations. It is worth recalling that superdiffusion can be described by a mean square displacement $\langle \Delta r^{2} \rangle $ growing with time $t$ as

$$ \langle \Delta r^{2} \rangle = 2 {\mathcal{D}}_{\alpha} \ t^{\alpha} $$

(3)

where ${\mathcal{D}}_{\alpha}$ is the anomalous diffusion coefficient and ${\alpha}$ is the anomalous diffusion exponent, which is $>1$ for superdiffusion. The anomalous diffusion coefficient ${\mathcal{D}}_{\alpha}$ has dimensions $[L^{2}/t^{\alpha}]$ different from the standard (i.e., normal) diffusion coefficient. Recently, superdiffusion has been found in several physical systems (Sokolov and Klafter 2005; Zimbardo et al. 2015; Sioulas et al. 2020). For example, numerical simulations have shown that particle transport in presence of magnetic turbulence can be superdiffusive along the mean magnetic field direction (Zimbardo et al. 2006; Pommois et al. 2007; Shalchi and Kourakis 2007). However, when the level of fluctuations is very low, superdiffusion can also characterize the particle transport along the perpendicular direction (Pommois et al. 2007). Further, it has been highlighted how superdiffusive transport has a great influence on shock acceleration (Ragot and Kirk 1997; Perri and Zimbardo 2012a; Zimbardo and Perri 2013; Bykov et al. 2017), leading to a reformulation of the energetic particle spectral index and of the acceleration time (Perri and Zimbardo 2012a; Zimbardo and Perri 2013; Perri and Zimbardo 2015a,b), as it will be discussed in Sect. 2.4.

There are several observations that indicate anomalous transport in astrophysical systems: the transport of non-relativistic electrons accelerated in solar events (Lin 1974), the analysis of transport properties from X-ray synchrotron emission from relativistic electrons accelerated at supernova remnants (Perri et al. 2016; Perri 2018), as well as the analysis of diffuse emission from electrons in the Coma cluster, which claims for nearly ballistic motion of energetic electrons (Ragot and Kirk 1997).

Therefore, both observations and numerical studies have pointed out how particle transport largely influences the efficiency of shock acceleration. Indeed, energetic particles can be scattered by the magnetic field fluctuations in resonance. The efficiency of such a scattering strongly depends on the fluctuation amplitude at the resonant scales. In case of very low $(\delta B/B)^{2}$ at the resonant scales, the particle scattering can be reduced, leading to an almost scatter-free propagation, i.e., non diffusive transport (Bieber et al. 1994; Zimbardo et al. 2012).

The analysis method adopted by Perri and Zimbardo (2007, 2008) and Zimbardo and Perri (2013) for deriving the energetic particle fluxes under the assumption of superdiffusive transport is based on the propagator formalism (Zumofen and Klafter 1993). A propagator $P(x-x', t-t')$ gives the probability of observing a particle at $(x, t)$ if injected at $(x', t')$. Its mathematical form does depend on the particle transport regime: normal diffusion is properly described by a Gaussian propagator with a width proportional to the diffusion coefficient and to $t-t'$ (Metzler and Klafter 2000); superdiffusion is modeled by a power-law propagator (Zumofen and Klafter 1993):

$$ P(x-x',t-t')\propto \frac{t-t'}{(x-x')^{\mu}} $$

(4)

with $2 <\mu < 3$. A “macroscopic” description of the anomalous transport by means of fractional Fokker-Planck equations in space and time is described in Engelbrecht et al. (2022) in this volume.

Under the hypothesis of a planar 1D shock moving at constant speed $V_{\mathrm{sh}}$ with respect to the observer into a statistically homogeneous medium characterized by an almost constant level of magnetic field turbulence (Lee 2005), and injecting the energetic particles at the shock, the particle density with energy $E$ can be calculated via

$$ n(x,E,t)=\int P(x-x',t-t')S(x',E,t')dx'dt', $$

(5)

where $S(x',E,t')=\varPhi _{0}(E) \delta (x'-V_{\mathrm{sh}}t')$ is the source term that depends on the flux of particles of energy $E$ injected at the shock front. Further, assuming a shock that comes from $x<0$ for $t< 0$, the profile in equation (5) can be easily calculated by inserting the form of the propagator that describes the process. In case of normal diffusion, i.e., for a Gaussian propagator, we recover equation (2). So that for an observer at $x=0$ and a shock coming from far upstream (i.e., $t<0$) we end up with $n(0,E,t)\sim \exp{(V_{\mathrm{sh}}^{2}t/D})$. In case of superdiffusion, i.e., for the power-law propagator, a power-law decay is derived as (Perri and Zimbardo 2008)

$$ n(0,E,t)\propto \frac{1}{(-t)^{\beta}}, $$

(6)

where the exponent $\beta = \mu -2$ ranges between $0 <\beta < 1$, being $2 <\mu < 3$. Notice that the exponent $\beta $ is directly related to the exponent of the mean square displacements in superdiffusive transport (see equation (3)), namely $\alpha = 2-\beta $ (Perri and Zimbardo 2007, 2008).

Kappa Distributions and Non-thermal Particle Populations

In the context of the acceleration of suprathermal particle populations an analytical description of their velocity or momentum or energy spectra is of interest. Particular useful tools are so-called kappa distributions, which have been employed for solar energetic particles (Oka et al. 2013; Effenberger et al. 2017), for the suprathermal solar wind components (Lazar 2017; Yoon et al. 2018), for pick-up ions (Fahr et al. 2016; Heerikhuisen et al. 2019), for cosmic rays (Treumann and Baumjohann 2018) as well as for studies of various wave modes in the corresponding plasma milieus (e.g., Husidic et al. 2020, and references therein).

In all of these studies kappa distributions of the form

$$\begin{aligned} F_{\kappa ,Olbertian}(v) = A_{\kappa}\left (1 + \frac{v^{2}}{\kappa \theta _{M}^{2}}\right )^{-\kappa -1} \end{aligned}$$

(7)

or variants thereof have been employed. Therein $v$ is the particle speed, $\theta _{M}$ is a reference speed corresponding to the thermal speed of the associated Maxwellian, and $A_{\kappa}$ is a normalisation constant.

The above representation can be referred to as an (isotropic, non-relativistic) Olbertian (see the left panel of Fig. 4) since it dates back to Olbert (1968, see also Vasyliunas (1968)) for a detailed overview see Lazar and Fichtner (2021) and for relativistic kappa distributions see Han-Thanh et al. (2022). In the following, we discuss a few topics that may, so far, not be as well known as they deserve to be. This will comprise a brief review of different versions of kappa distribution, their application-related limitations, and their connection to nonlinear and anomalous diffusion.

Different Versions of Kappa Distributions

While it is straightforward to generalize any given isotropic kappa distribution to its anisotropic counterpart (Scherer et al. 2019; Lazar and Fichtner 2021), for simplicity we consider only the former here. Closer inspection of the above Olbertian reveals that it describes suprathermal distributions characterized (i) by the same constant reference speed $\theta = \theta _{M}$ and (ii) by temperatures that are increasing with decreasing kappa parameter according to

$$\begin{aligned} T_{\kappa}= \frac{m}{k_{B}}\frac{\kappa}{2\kappa -3}\,\theta ^{2} \geq T_{M} \end{aligned}$$

(8)

with $m$ being the particle mass, $k_{B}$ the Boltzmann constant, and $T_{M}$ the temperature of the associated Maxwellian. This kappa dependence of the temperature is a feature that was desired by Olbert (1968) to quantify the deviations of observed energetic (in his case magnetospheric) electrons from thermal equilibrium and has, more recently, been shown to hold in the solar wind as well (Lazar et al. 2017). Note that, of course, the velocity dependence can straightforwardly translated in to one on momentum or on kinetic energy, so that in the following we continue to use the velocity formulation.

The first variant of the Olbertian was originally introduced by Matsumoto (1972) and consists in an interchange of the kappa-dependence of the reference speed and the temperature, so that the latter becomes independent of kappa:

$$\begin{aligned} F_{\kappa ,modified}(v) = \tilde{A}_{\kappa}\left (1+ \frac{m}{k_{B} (2\kappa -3)}\frac{v^{2}}{T_{M}} \right )^{-\kappa -1}. \end{aligned}$$

(9)

This modified kappa distribution (see the right panel in Fig. 4), which has been favoured in recent years by Livadiotis (2015), is, however, only applicable to specific physical systems as discussed in Lazar et al. (2016). One of the features of this particular distribution to be explained is the enhancement of particles in the core region compared to the associated Maxwellian, which is, thus, not approximating the core, as in the case of the Olbertian (see Fig. 4).

Beyond these principal differences between these two so-called standard kappa distributions (SKDs), which have significant implications, e.g. for the properties of waves maintained in a suprathermal plasma (Lazar et al. 2015), both alternatives face common problems. First, the velocity moments, which are necessary for the derivation of a macroscopic fluid description from kinetic theory, are diverging for $l \geq 2\kappa -1$ with $l$ denoting the order of the moment. Second, all moments are diverging for $\kappa \leq 3/2$. On the one hand, this prevents the formulation of a consistent hydrodynamical treatment of a given physical system and, on the other hand, power laws with $\kappa \lesssim 2$ cannot justifiably represented with a SKD. Third, it has been demonstrated that a SKD implies a non-extensive entropy (Tsallis 1988), which is a questionable property (Nauenberg 2003).

In order to remove these conceptual difficulties, Scherer et al. (2017) introduced the regularized kappa distribution (RKD, see Fig. 5), which equips the SKDs with an exponential, Maxwellian-like cut-off:

$$\begin{aligned} F_{RKD}(v) = A_{RKD} \left (1 + \frac{v^{2}}{\kappa \theta ^{2}} \right )^{-\kappa -1} \exp \left (-\alpha ^{2} \frac{v^{2}}{\theta ^{2}}\right ) \end{aligned}$$

(10)

Again, $A_{RKD}$ is a normalisation factor. The cut-off is controlled with the parameter $\alpha $. Such a cut-off can be motivated theoretically by the finiteness of scales: in a given physical system an acceleration process takes place within a maximum spatial scale and within a finite period of time. These constraints limit any acceleration process correspondingly, so that a resulting spectrum of accelerated particles cannot extend to arbitrarily high velocity (momentum, energy) but rather must be cut off. Given that a consistency of kinetic and fluid theory requires the existence of all velocity moments, such cut-off must be exponential.

The RKD has not only the advantage of having finite velocity moments at arbitrary order, but it also avoids all divergences for $\kappa \leq 3/2$ so that it is defined for all positive kappa values. The latter property makes it possible to treat significantly harder power laws than a SKD would allow. Furthermore, almost surprisingly but very satisfactorily, it is consistent with an extensive entropy (Fichtner et al. 2018) and, thus, with the fundamental laws of thermodynamics. Consequently, the entropy of a RKD can then be compared to that of a Maxwellian and, as to be expected, it is always lower for a given system.

While the RKD can, as outlined above, be constructed on purely theoretical grounds, it can also be motivated by observations. Scherer et al. (2017) pointed out that both pick-up ion and anomalous cosmic ray spectra have previously been described by RKD-like distributions, see, e.g., Fisk and Gloeckler (2012) and Steenberg and Moraal (1999), respectively. Further information and various recent applications of the concept of kappa distributions to suprathermal particle populations can be found in Lazar and Fichtner (2021). We note that the acceleration mechanism of anomalous cosmic rays was the subject of the review by Giacalone et al. (2012). It is briefly been summarized again in the review of Giacalone et al. (2022) (this volume), which includes some recent insights.

Kappa Distributions and Generalized Diffusive Transport

It is also interesting to note that kappa distributions appear to be related to both nonlinear and anomalous diffusion. Tsallis and Bukman (1996) have considered a nonlinear Fokker-Planck (i.e. diffusion) equation and, by using the SKD-related concept of non-extensive entropy, have demonstrated that this way anomalous transport, i.e. sub- and superdiffusion, can be described. They refer to this type of anomalous diffusion, that was also found by Litvinenko et al. (2017), as ‘driven’ or ‘correlated’ and distinguish it from ‘Levy-like’ anomalous diffusion described by linear but fractional Fokker-Planck/diffusion equations, see, e.g., Stern et al. (2014), Perri et al. (2015), Zimbardo et al. (2015, 2017). The significance of RKDs in this context still needs to be explored.

Combining the observations of power-law energetic particle time profiles described above with the findings about nonlinear Fokker-Planck equations, one can indeed, in a first approach, attempt to fit the time profiles on the basis of a simple one-dimensional nonlinear diffusion equation of the form

$$\begin{aligned} \frac{\partial f}{\partial t} = \frac{\partial}{\partial x} \left (D \left \vert \frac{\partial f}{\partial x}\right \vert ^{-\mu} \frac{\partial f}{\partial x} + V f \right ) + S \delta (x) H(t). \end{aligned}$$

(11)

Doing so for shock-accelerated electrons observed by the Ulysses spacecraft gives the results shown in Fig. 6. While such studies are still in their infancy, it is, nonetheless, obvious that solutions of a nonlinear diffusion equation allow to fit the data reasonably well. Thus, the exploration of such equation in application to energetic particle populations looks promising and is presently ongoing (e.g., Litvinenko et al. 2019; Walter et al. 2020).

The Possibility of a Non-markovian Pitch-Angle Scattering

Now, it is important to address at least one of the physical arguments that are at the basis of the anomalous diffusion. A relation between pitch-angle scattering and parallel spatial diffusion in non-diffusive regimes has been discussed in Shalchi et al. (2012). Here we start from some evidence that emerged in both numerical studies and natural environments. Recently, simulating the transport of energetic particles in static 3D isotropic turbulence, Pucci et al. (2016) have highlighted how particles that diffuse normally in the direction parallel to the mean magnetic field, exhibit a power-law distribution of the pitch-angle scattering times with no characteristic values close to the quasi-linear prediction (Kennel and Petschek 1966; Amato 2014). Such a distribution tend to broaden over a larger range of values of the scattering times for high level of magnetic turbulence intermittency (i.e., when the degree of spatial non-homogeneity of the turbulence increases) and for $\delta B/B_{0}\ll 1$ (Pucci et al. 2016; Perri et al. 2019). A power-law distribution of the particle scattering times have also been found for energetic particles upstream of interplanetary shock waves (Perri and Zimbardo 2012b; Perri et al. 2021), where the scattering times have been evaluated via the power of the magnetic field fluctuations at the particle resonant scale (Crooker et al. 1999). A theoretical explanation has been formally given in Zimbardo and Perri (2020), where the power-law distribution of the particle scattering times has been shown to be the basis of anomalous pitch-angle scattering. This eventually gives rise to spatial superdiffusion in the direction parallel to the mean magnetic field.

In another numerical study that simulates the collisionless plasma close to a shock region, Riordan and Pe’er (2019) found a distribution of the particle scattering time that extends over several decades, depending on the magnetic turbulence level $\delta B/B_{0}$ (spanning from weak to strong turbulence).

Thus, pitch-angle scattering of energetic particles in presence of magnetic turbulence can be modeled as a non-Markovian process with a power-law distribution of the particle scattering times. Indeed, the distribution of the particle free path lengths can be described in the framework of the Lévy random walks, i.e.,

$$ \psi (\ell ,\tau )=C |\ell |^{-\mu}\delta (\ell -v_{||}\tau ), \quad |\ell |>\ell _{0}, \quad \tau >0 $$

(12)

with $C$ being a normalization constant, $\ell $ is the particle jump length, $v_{||}$ is the particle’s parallel speed, and $\tau $ represents the scattering time. Equation (12) is valid for large $\ell $ (Metzler and Klafter 2004). Integrating over the path lengths, it is possible to get $\psi (\tau )= C |v_{||}|^{-\mu} \tau ^{-\mu}$. For $2<\mu <3$ superdiffusive transport is obtained. Thus, Zimbardo and Perri (2020) has shown that assuming a distribution of the particle scattering times $\psi (\tau ) \propto \tau ^{-(1+\beta )}$, with $0<\beta <1$, it is possible to formally derive a non-Markovian Fokker-Planck equation, where the time derivative is replaced by a fractional time derivative (Caputo 1967). By solving the fractional Fokker-Planck equation for two different forms of the pitch-angle scattering coefficient, the parallel velocity autocorrelation function has been found to decay as a power-law in time (long range correlations) and the spatial transport along the mean field direction to be superdiffusive.

The Influence of Superdiffusive Transport on the Shock Acceleration Process

Starting from a first order Fermi process, where test particles of velocity $v$ can cross the shock front several times, gaining a relative energy at each crossing $\Delta E/E=(4/3) (V_{u}-V_{d})/v$, where $V_{u}$ and $V_{d}$ are the fluid speeds in the upstream and downstream regions, respectively, it is possible to include the effect of superdiffusive motion in the shock acceleration process. Perri and Zimbardo (2012a), Zimbardo and Perri (2013) have generalized the DSA mechanism including anomalous, faster, transport. Assuming a shock coming from $(x,t)=(-\infty ,-\infty )$ that is moving to the observer according to $x'=V_{\mathrm{sh}}t'$, where the shock speed $V_{\mathrm{sh}}$ is kept fixed to a constant value in the downstream frame, Perri and Zimbardo (2012a) have derived the probability of escape for particles from the acceleration region. Such a probability is directly related to the spectral index and is given by the ratio of the fluxes upstream and downstream, namely $P_{\mathrm{esc}}=\varPhi _{d}/\varPhi _{u}=n_{d}V_{d}/(n_{0}v/4)$. Notice that the flux upstream is derived under the usual isotropic conditions (Drury 1983; Gaisser 1990), and $n_{0}$ is the density of particles coming from upstream with speed $v$ at the shock front. Further, following Kirk et al. (1996) and assuming stationary conditions, far downstream the particle density is proportional to the flux of particles at injection, i.e., $n_{d}=\varPhi _{0}(E)/V_{\mathrm{sh}}$. The crucial point is to derive the particle density at the shock $n_{0}$ assuming a superdiffusive motion. This has been computed by using equation (5) with the correct form of the propagator (i.e., see equation (4)). Setting $\int _{-\infty}^{\infty}P(x,t)dx=1$, Perri and Zimbardo (2012a), Zimbardo and Perri (2013) end up with

$$ \frac{n_{d}}{n_{0}}=2\frac{\mu -2}{\mu -1}=2\frac{2-\alpha}{3-\alpha}, $$

(13)

where the relation that links $\mu $ to the exponent of superdiffusion $\alpha $ in equation (3), namely $\mu =4-\alpha $, has been used. Equation (13) basically relates the density at the shock to the density far downstream. It is worth addressing that Equation (13) tends to its diffusive limit $n_{d}/n_{0}=1$ for $\alpha \rightarrow 1$. This directly leads to an escape probability $P_{\mathrm{esc}}=(n_{d} V_{d})/(n_{0} v/4)=8 (\mu -2)/(\mu -1)V_{d}/v=8 (2- \alpha )/(3-\alpha )V_{d}/v$.

Particle Energy Spectra

From equation (13), it is straightforward to derive the exponent of the integral energy spectrum (i.e., $N(\ge E)\propto (E/E_{0})^{-\tilde{\gamma}}$) of relativistic particles,

$$ \tilde{\gamma}=\frac{P_{\mathrm{esc}}}{\Delta E/E}= 6\quad \frac{\mu -2}{\mu -1}\frac{1}{r-1} = 6\;\;\frac{2-\alpha}{3-\alpha} \frac{1}{r-1}. $$

(14)

Again, for $\alpha \rightarrow 1$ (diffusive transport) equation (14) tends towards $\tilde{\gamma}=3/(r-1)$ (Fisk and Lee 1980), and then the exponent of the differential energy spectrum towards $\gamma =\tilde{\gamma}+1=(2+r)/(r-1)$. Perri and Zimbardo (2012a), Zimbardo and Perri (2013) also derived the spectral indices for non relativistic particles. Considering a relative gain in momentum during the acceleration process $\Delta p/p=(4/3) (V_{u}-V_{d})/v$, they get

$$ \tilde{\gamma}=\frac{1}{2}\biggr[6\;\;\frac{\mu -2}{\mu -1} \frac{1}{r-1}+1\biggl]=\frac{1}{2}\biggr[6\quad \frac{2-\alpha}{3-\alpha}\frac{1}{r-1}+1\biggl]. $$

(15)

The exponent of the differential energy spectrum is found to be $\gamma =3/(r-1)(2-\alpha )/(3-\alpha )+1$ (Zimbardo and Perri 2013). Basically, the superdiffusive correction in equations (14) and (15) is due to the ratio between the density far downstream and the density at the shock as in equation (13). Examples of the spectral indices as a function of the compression ratio of the shock are reported in Fig. 7.

Superdiffusion leads to smaller spectral indices and thus harder energy spectra than DSA. This has been interpreted as due to the fact that downstream of the shock two physical effects are at play, namely advection ($\Delta x\sim V_{d} t$) and random superdiffusive motion $\langle \Delta x^{2}\rangle \sim t^{\alpha}$, with $\alpha >1$. In the limit of long times even in the presence of advective motion, energetic particles can propagate upwind more easily than in the DSA framework, so that they have a higher probability to return to the shock. This will also lead to shorter acceleration times, as it will be discussed in Sect. 2.4.2. Notice that we have not considered here the effect of adiabatic cooling, which can have influence on the acceleration process when the particle mean free-path is large upstream (Ruffolo 1995).

An example of particle differential energy spectrum calculated averaging the ion fluxes within a time window of about 80 min downstream is displayed in Fig. 8 for an interplanetary shock crossing of the Advanced Composition Explorer (ACE) spacecraft at 1 AU that occurred on 2010 August 3. Both the DSA prediction (black line) and the spectra derived within the superdiffusive framework are shown (red lines). In these events upstream fluxes have been found to follow a power-law similar to the ones displayed in Fig. 2. Notice that the two red lines are calculated by considering the lowest and the highest $\alpha $ values obtained by fitting the upstream energetic particle fluxes in different energy channels (see Sect. 2.1). A better agreement is found with the energy spectrum predicted assuming superdiffusive motion of energetic particles.

Acceleration Times

The occurrence of superdiffusive transport for energetic particles during the shock acceleration process affects also the acceleration time. In the framework of DSA the acceleration time is given by

$$ t^{D}_{\mathrm{acc}} = {\frac{3}{V_{u} - V_{d}}} \left ({ \frac{D_{ux} }{V_{u}}} + {\frac{D_{dx} }{V_{d}}}, \right ) $$

(16)

where $D_{ux}$ ($D_{dx}$) is the upstream (downstream) diffusion coefficient perpendicular to the shock front (e.g., Drury 1983). They are related to both the parallel and the perpendicular diffusion coefficient, although in case of a dominant parallel transport it is possible to get $D_{x}\sim D_{||}\cos ^{2}{\theta _{Bn}}$, where $\theta _{Bn}$ is the angle between the normal to the shock front and the upstream magnetic field. Perri and Zimbardo (2012a) have derived a similar relation for the acceleration time in presence of superdiffusion, by equating the macroscopic plasma advective motion, $\Delta x=V \Delta t$, with the microscopic particle superdiffusive motion $\langle \Delta x^{2}\rangle \sim {\mathcal{D}}_{\alpha x}\Delta t^{\alpha}$ along the direction of propagation of the shock. The residence time within the acceleration region can be considered equal to the ratio between the number of particle present in a region of length $\Delta x$ and the incident energetic particle flux coming from upstream (e.g., Drury 1983), i.e., $t_{res}=n\Delta x/(nv/4)$. Substituting $\Delta x$ obtained from the balance of advective and superdiffusive motions and resolving for the acceleration time $t_{\mathrm{acc}}^{S}=t_{res}/(\Delta p/p)$ it is easy to obtain (Perri and Zimbardo 2012a)

$$ t_{\mathrm{acc}}^{S}= \frac{3}{V_{1}-V_{2}}\biggl[\biggl( \frac{{\mathcal{D}}_{1\alpha x}}{V_{1}^{\alpha}}\biggr)^{1/(2-\alpha )}+ \biggl(\frac{{\mathcal{D}}_{2\alpha x}}{V_{2}^{\alpha}}\biggr)^{1/(2- \alpha )}\biggr]. $$

(17)

The key point in such an expression is the derivation of the anomalous diffusion coefficient $D_{\alpha}$. Indeed, as shown in Zimbardo and Perri (2013), it is related to the exponent of superdiffusion $\alpha $, to the particle speed, and also to a length $\ell _{0}$ that comes from the probability $\psi (\ell , t)$ of making for a particle a jump of length $\ell $ in a time $t$ (Klafter et al. 1987; Zumofen and Klafter 1993) shown in equation (12), namely

$$ {\mathcal{D}}_{\alpha}=\frac{2(2-\alpha )}{(3-\alpha )(4-\alpha )}\varGamma ( \alpha -1) \ell _{0}^{2-\alpha} v^{\alpha}, $$

(18)

which is the parallel anomalous diffusion coefficient (${\mathcal{D}}_{ \alpha}={\mathcal{D}}_{\alpha x}/\cos ^{2}{\theta _{Bn}}$). It is worth noting that for $\ell \rightarrow 0$ $\psi (\ell ,t)$ is bell-shaped, so that we have no divergence in equation (12). Thus, $\ell _{0}$ represents the minimum length at which the power-law probability for the jump lengths holds in the particle random walk. As shown in Perri and Zimbardo (2015b), it is possible to derive $\ell _{0}$ directly from spacecraft in-situ observations. Moreover, coming back to the propagator formalism, it has been shown that in case of superdiffusion the propagator in equation (4) holds far from the source of energetic particles, while close to it the form of the propagator changes towards a modified Gaussian distribution (Zumofen and Klafter 1993). Zumofen and Klafter (1993), Zimbardo and Perri (2013), Perri and Zimbardo (2015b) have defined a scaling variable $\xi =(x/\ell _{0})/(t/t_{0})^{1/\mu}$ (where $t_{0}=\ell _{0}/v$) such that for $\xi \ll 1$ particles are close to the shock and for $\xi \gg 1$ particles are far upstream from the source. Perri and Zimbardo (2015b) have suggested that the change in the functional form of the propagator corresponds in terms of spacecraft observations to a change in the energetic particle fluxes in the entire upstream region (from close upstream towards far upstream). This happens when the spacecraft detects a power-law decay in the particle flux at a certain distance/time from the shock, i.e., $t_{\mathrm{break}}^{\mathrm{s/c}}=x_{\mathrm{break}}/V_{\mathrm{sh}}^{\mathrm{s/c}}$, where $V_{\mathrm{sh}}^{\mathrm{s/c}}$ is the relative speed between the shock front and the satellite.

In Fig. 9 it is reported an example of identification of $t_{\mathrm{break}}$ directly from observations. Figure 9 is relevant to a CIR crossing by Ulysses on 1993 May 10. Thus, if at $\xi =1$ the two forms of the propagator match, Perri and Zimbardo (2015b) have derived

$$ \ell _{0}\sim x_{\mathrm{break}}\biggr(\frac{V_{1}^{\mathrm{sh}}}{v}\biggl)^{1/(2- \alpha )}. $$

(19)

Using equation (19) an estimation of equation (18) from satellite data can be obtained. By applying such an analysis to a series of interplanetary shock waves and to the TS of the solar wind, Perri and Zimbardo (2015b) have found that the acceleration times for energetic protons in the presence of superdiffusive transport are largely reduced with respect to the ones derived from equation (16). They are also shorter than the typical shock lifetimes. This has been ascribed to the scale-free nature of the particle jump lengths (see equation (12)), since the probability $\psi $ of very long displacements is non-negligible with respect to a Gaussian distribution. Further, also very short jumps are highly probable increasing both the probability to return to the shock for particles travelling far upstream, and the probability for particles close to the front to cross the shock several times. For interplanetary shocks at 1 AU, superdiffusion reduces the acceleration time to a fraction of day, while for corotating interaction regions in the outer heliosphere and for the TS the acceleration time has been estimated to be ∼ few days.

Magnetic Field Amplification in Superdiffusive Shock Acceleration in Supernova Remnants

Microscopic plasma modeling of cosmic ray (CR) acceleration by collisionless shocks (both PiC and hybrid) demonstrated an efficient formation of non-thermal particle population simultaneously with the accompanied spectra of magnetic fluctuations (for a review see Marcowith et al. 2016). To model cosmic ray acceleration in supernova shocks computer simulations with a wide dynamical range are needed and instead of computationally expensive PiC simulations one can use simplified kinetic equations or Monte Carlo models. The models use some more or less justified recipes to connect the CR transport to magnetic fluctuation spectra. A nonlinear Monte Carlo model of collisionless shock flow structure with super-diffusive propagation of high-energy particles coupled to particle acceleration and magnetic field amplification was presented by Bykov et al. (2017). The cosmic ray anisotropy provided strong non-adiabatic amplification of magnetic fluctuations due to the resonant and non-resonant instabilities in the model that allows the Lévy-walk type propagation of CRs in the shock flow. The model uses a semi-phenomenological equation to calculate the local spectral energy densities of magnetic fluctuations assuming a balance between the magnetic field growth and the spectral cascading. Contrary to the widely used advection-diffusion equations, the Monte Carlo technique includes the full angular anisotropy of the particle distribution at all spatial positions. A distinctive feature of the non-linear Monte Carlo model of super-diffusive shock acceleration is the relatively strong quadruple anisotropy in the precursor CR distribution, which produces a nonresonant mirror-type instability that amplifies compressible wave modes with wavelengths longer than the gyroradii of the high-energy protons produced by the shock. In Fig. 10 taken from Bykov et al. (2017) we illustrated the magnetic field amplification by CR-driven instabilities in shocks with super-diffusive transport. The strong super-adiabatic amplification of the magnetic field is apparent both in the case of the turbulence cascading to the short scales and with suppression of the cascade along the mean large scale magnetic field.

The Role of Pre-Existing Turbulence Upstream of Shock Waves in the Acceleration Process

A pivotal role in the evolution of the shock waves is played by their interaction with magnetic turbulence of the ambient medium. Indeed, it is well known that the magnetic field turbulent cascade spontaneously generate coherent structures and wave modes over a broad number of spatial scales (Bale et al. 2005; Greco et al. 2010; Gary et al. 2012; Karimabadi et al. 2013). Shock waves that propagate through such a complex medium will be highly distorted with amplification of the upstream turbulent fluctuations at the shock (Zank et al. 2002), a spatial (and time) change in the compression ratio of the shock (Giacalone and Neugebauer 2008), and in the geometry along the shock surface (Giacalone 2017; Kajdič et al. 2019). Such effects are worth being investigated since they can have a large affect on the process of particle acceleration at the shocks. Using multi-spacecraft data techniques, distorted fronts were observed in the near-Earth environment as non-planar rippled surface with a radius of curvature consistent with the interplanetary magnetic field correlation length and characterized by different energetic particle fluxes at different spacecraft locations (Neugebauer and Giacalone 2005).

Recently, Kajdič et al. (2019), taking advantage of the multispacecraft Cluster mission, reported four observations of irregular shock surfaces in the near-Earth environment. During the four encounters, the inter-spacecraft distance were varying, ranging from few ion inertial lengths to about $100 d_{i}$ ($d_{i}=c/\omega _{pi}$, where $c$ is the speed of light and $\omega _{pi}$ is the ion plasma frequency). In terms of distances they correspond to tens km up to $10^{4}$ km. This was a unique opportunity to explore the spatial variations of the shocks at different spatial scales. Further, the shocks analyzed exhibit a geometry that varies from quasi-parallel to quasi-perpendicular. Kajdič et al. (2019) computed the normal to the shock front using a minimum variance analysis technique (Sonnerup and Cahill 1968) and consequently estimated the $\theta _{bn}$ angle, with an uncertainty of about $5^{\circ}$. In addition, thanks to the multispacecraft measurements, they were able to compute the angle between two shock normals for pairs of satellite: such an angle was found to be small for small interspacecraft separation and up to $30^{\circ}$ for largely separated satellites. Thus, the angle $\theta _{bn}$ tends to vary from probe to probe, especially for large spacecraft separations. These evidences imply that the shock geometry changes locally at the different satellite positions, probably caused by an irregular shock surface. Data were also supported by a 2D hybrid simulation of a shock with an Alfvénic Mach number $M_{A}\sim [4,6.6]$. Pre-existing compressive structures in the upstream, once convected toward the shock front, tend to rise in amplitude and merge with the front causing a local shock reformation. Such a process makes the shock surface highly corrugated and irregular, with a local change in the shock geometry. Thus, the presence of upstream structures can cause strong deformation of the shock front when interacting with them. Giacalone and Jokipii (2007) investigated a similar effect induced by turbulent density fluctuations upstream of a hydrodynamic shock, the interaction between the shock wave and these turbulent fluctuations also caused the formation of a turbulent postshock region and magnetic field amplification.

A more realistic situation has been explored by Trotta et al. (2021) using a 2D hybrid code, where a turbulent jet generated by a 2.5D compressible MHD simulation can interact with an oblique supercritical shock wave. This aims at reproducing the shock dynamics when expanding in a highly turbulent medium. The level of turbulence is controlled by the values of $\delta B/B_{0}$ and the upstream condition is passed to the hybrid code when the MHD turbulence is already fully developed and coherent structures are formed. For typical heliospheric conditions, i.e., $\delta B/B_{0}\sim 0.8$, the interaction between upstream turbulent structures/waves and the shock causes a high distortion of the propagating front. In such a scenario, energy spectra of particles are characterized by a high energy field aligned beam that moves towards higher energy and spread as the $\delta B/B_{0}$ increases and by a formation of a very low energy population of particles that is probably emerging due to trapping mechanisms between particles and coherent turbulent structures. The effect of turbulence on the particle spatial and velocity diffusion has deeply been explored by using a coarse-graining of the Vlasov equation, in order to get an equation for the reduced particle density. The terms in the equation corresponding to spatial and velocity diffusion were computed within the simulation domain finding a large enhancement in both space transport and velocity transport upstream as $\delta B/B_{0}$ increases. This implies that the acceleration process is not only limited to the shock front but can involve the turbulent fluctuations in the box. The velocity diffusion was also found to be correlated with the electric field parallel to the mean field direction, which is a source of particle energization upstream. Interestingly, it was discussed that the fast particle reflection at the shock can lead to superdiffusion upstream (as already pointed out in a 2D hybrid simulation by Trotta et al. (2020), where superdiffusive transport was found for energetic particles in the upstream region), while the emergence of coherent structures can act as particle traps and accelerators.

Exploring years of ACE measurements, Tessein et al. (2013, 2015) found a good correlation between the presence of energetic particle enhancements and magnetic field discontinuities, as computed from the Partial Variance of Increments (PVI) technique (Greco et al. 2008, 2018). PVI basically measures the local magnetic energy over a given time scale with respect to the average magnetic energy of the data-set. Beside particle flux enhancements close to shock crossings, discontinuities characterized by high values of PVI (strong variations in the magnetic field) have associated high energetic particle fluxes. Such coherent structures are also detected in the vicinity of shocks, thus probably contributing to the particle acceleration process. Tessein et al. (2015) also pointed out how energetic particle flux decays can be observed near magnetic discontinuities that act as a magnetic barrier. In either case it is an important open question how structures emerging from a turbulent background can influence the processes of particle acceleration and energization.

These studies point out the fundamental role of magnetic turbulence in the shock acceleration process from the thermal pool towards supra-thermal energies (Giacalone 2005a,b).

Observations of Flat Spectra of Energetic Particles Accelerated at Interplanetary Shocks

Energetic particle observations that question standard theory results were investigated by Lario et al. (2018). They found several large CME-shock related SEP events which revealed a common, but previously unreported characteristic that the SEP energy spectra upstream of the shock were independent of energy over a fairly broad range of energy. An example is shown in Fig. 11. The SEP event in this figure was included in the analysis of Lario et al. (2018), but we present a re-formatted version for this paper in order to highlight a few key points. The figure shows data from the MAG and EPAM instruments onboard ACE. Panel (a) shows the fluxes of energetic ions with the energies shown in the legend. This data comes from the LEMS120 detector on EPAM. Panels (b) and (c) show the magnetic field magnitude and components, respectively. The vertical dashed lines and numbers are used to indicate some key time periods. The shock arrives at the end of period 2, and period 3 is associated with the CME sheath region, between the shock and CME flux rope, which crosses the spacecraft at the dashed line between periods 3 and 4. Period 4 is the CME flux rope. Consider time period 1 in Fig. 11. This is a ∼ 17-hr period, over which the flux of 68-keV - 1.9-MeV ions have very nearly the same flux at all energies. Thus, in terms of flux, this is a flat energy spectrum. During period 2, the fluxes increase rapidly to where they peak at the shock, and do so in a manner which is dependent on energy since just downstream of the shock, the fluxes clearly depend on energy, despite that they are nearly constant in time.

Since the differential flux, $J$ (flux per energy) is related to the distribution function, $f$ according to $f=p^{2}J$, where $p$ is the momentum, we note that an energy-independent differential flux spectrum corresponds to $f\propto p^{-2}$. Note also that the fluxes all rise at the same rate from the background level near the start of the time period, to the end of the time period, increasing by a factor of about ten. Thus, it seems that not only is the energy spectrum independent of energy, the diffusion coefficient associated with the transport of these particles must also be independent of energy. This is an important constraint on particle-transport theory. For example, the prediction from quasi-linear theory (e.g. Jokipii 1966; Hasselmann and Wibberenz 1970; Giacalone and Jokipii 1999) for the parallel diffusion coefficient of charged particles moving in a turbulent magnetic field having a Kolmogorov-like power spectrum gives $\kappa _{\parallel}\propto p^{4/3}$ (for non-relativistic energies). This is clearly inconsistent with the observations. It is also important to note that the start of this period is so far in advance of the shock that it is reasonable to expect that the magnetic turbulence during this period is likely quite similar to the ambient turbulence in the solar wind. Thus, the observations of flat-energy spectra upstream of shocks provide important clues into the nature of energetic particle transport in the ambient solar wind. It is noteworthy that there is a significant discrepancy between the estimates of the diffusion coefficient (or mean-free path of scattering) from quasi-linear theory and observations (e.g Palmer 1982; Bieber et al. 1994).

Previous numerical modeling of SEP events reveal some results which show a flat energy spectrum upstream of the shock (c.f. Fig. 18 of Prinsloo et al. 2019). These authors suggest that the cause of this in their simulations is the competing effects of shock acceleration and adiabatic cooling of the particles, with cooling being the dominant factor for shocks that are farther from the Sun (close to 1 AU). The model of Ng et al. (2003) also reveals spectra that have some similarities to the observations; however, there is no long-lasting period where the spectrum is flat in these results (see Figs. 1 and 8 of Ng et al. 2003). In this model, energetic particles excite magnetic fluctuations upstream of the shock, leading to a spatial variation in the turbulent magnetic power spectrum upstream. The source at the shock is assumed, based on standard shock acceleration theory. In each of these models, there are notable differences between the behavior of the time intensity profile in these simulations and the observations shown in Fig. 11. Thus, the cause of the flat-spectra period upstream of the shock remains a poorly understood phenomenon.

The transition from period 1 to period 2 in Fig. 11 also provides an important constraint on acceleration and transport theory. The fact that the intensities rise dramatically over a short (∼ 10-30 minute) period before the shock crossing is not unusual (c.f. Giacalone 2012, and references therein), and is thought to be due to reduced transport in increased magnetic fluctuations near the shock, possibly due to the energetic particles themselves (e.g. Lee 1983; Kennel et al. 1986). However, this particular observation, and several authors as reported by Lario et al. (2018), suggest that not only is there a reduction in the transport coefficient near the shock, but there is also a change in its dependence on energy. These observations, therefore, present important challenges to theory, and to our general understanding of how charged-particles scatter in interplanetary magnetic fields.

Electron Acceleration at the Heliospheric Termination Shock

For many years now the solar wind TS has been treated as a multifluid phenomenon. The fluids, not separately but jointly, have to fulfil the Rankine-Hugoniot conservation laws (e.g., Fahr and Siewert 2013, 2015, and references therein). It turned out more recently that pick-up ions play a fairly important role for the entropy mediation at the TS, since they absorb, in form of their downstream temperature, a substantial part of the upstream ion kinetic energy. Hence these ions need to be considered as an independent entropy-transporting fluid (e.g., Decker et al. 2008; Fahr and Siewert 2015). Kinetic features of this multifluid ion shock have been studied by, e.g., Zank et al. (2010) and Fahr and Siewert (2013): they found quantitative relations between upstream and downstream ion distribution functions that are substantially different for solar wind protons and pick-up protons.

Surprisingly these refinements did not lead to a completely satisfying representation of the most relevant properties of the downstream plasma as observed by Voyager 2 (Richardson et al. 2008). As demonstrated by Chalov and Fahr (2013) these data can be explained when allowing also the solar wind electrons to thermodynamically behave as a separate, independent fluid. In a simple parameter study, allowing electrons to be heated at the passage over the shock more effectively than protons by a factor $\xi \gg 1$, they obtained best-fitting results to the relevant Voyager 2 data for $\xi \geq 10$. Such a specific heating of electrons at fast mode MHD shocks had already earlier been pointed out as a rather likely process by Leroy and Mangeney (1984), Tokar et al. (1986), and Schwartz et al. (1988). Furthermore, a preferential shock-heating of electrons has become manifest in plasma shock simulations in which electrons are treated kinetically (Lembège et al. 2003, 2004). Due to strongly acting two-stream and viscous interactions, they become de-magnetized and do not get Lorentz-wound by the frozen-in, convected magnetic fields, but instead attain downstream temperatures increased by factors of $\xi \geq 50$ compared to protons.

To achieve a similar level of consistency Fahr et al. (2012) have described the conditions of the upstream and downstream plasma in the bulk frame systems with frozen-in magnetic fields. Describing via the Liouville-Vlasov theorem the shock transition as an instantaneous conversion of the velocity distribution functions, they could determine all relevant downstream plasma quantities. The excessive heating of electrons at the solar wind TS as described by these authors (see also Fahr and Siewert 2013) was obtained with a semi-kinetic theory of the multi-fluid shock with electrons and protons reacting in mass- and charge-specific forms to the electric shock ramp. Again these studies show that electrons do enter the downstream side as a strongly energized, mass-less plasma fluid that even dominates the downstream plasma pressure (for latest results see Fahr and Heyl 2020). These results are also supported by Zieger et al. (2015) through a multi-fluid approach to the solar wind TS in which the plasma electrons are admitted as a separate third fluid. This study gives full support for claims raised by Chalov and Fahr (2013), Fahr and Siewert (2015), and Fahr et al. (2015), namely that electrons are preferentially heated when converting their overshoot velocities into thermal energies, and, w.r.t. their pressure, then play an important role for the downstream plasma flow. Fahr and Verscharen (2016) found that the self-consistent transition structure at the shock in a stationary flow can be described by three consecutive regions, region I with strongly upflashing charge-induced electric fields, region-II with Lorentz reactions of the electrons to the co-convected frozen-in magnetic fields, and region III with a relaxation towards isotropic thermal distributions characterizing the joined downstream plasma flow (see Fig. 12). In the following we explain more carefully, why electrons not only can, but must be expected and respected as a preferentially heated fluid at the passage over the shock describing them by their adequate distribution functions.

The Liouville Theorem and the Electron Distribution Function in Shock-Region I

For arbitrarily, but isotropically distributed particles of a medium, if only co-moving with the plasma bulk velocity $U$, in absence of particle sources or sinks, the Liouville theorem requires the following form of a conservation of the phase space current (e.g., Goedbloed and Lifschitz 1997; Fahr and Lay 2000)

$$ f_{1}(z_{1},v)d^{3}v_{1}U_{1}=f_{2}(z_{2},v)d^{3}v_{2}U_{2}. $$

(20)

Here $f_{1}$ and $f_{2}$ denote the distribution functions of the species at coordinates $z_{1},v$ and $z_{2},v$. Considering now infinitesimally neighbored places on the $z$-axis, i.e. with $z_{2}=z_{1}+dz$, the above relation expresses itself in the more evolved differential form

$$ f_{1}(z_{1},v)d^{3}v_{1}U_{1}=f_{1}(z_{1},v)d^{3}v_{1}U_{1}+dz \frac{d}{dz}[f_{1}(z_{1},v)d^{3}v_{1}U_{1}] $$

(21)

simply requiring that

$$ \frac{d}{dz}[f_{1}(z_{1},v)d^{3}v_{1}U_{1}]=0. $$

(22)

The latter requirement can be expressed in a more evolved form by

$$ \frac{d}{dz}[f_{1}(z_{1},v)]d^{3}v_{1}U_{1}+f_{1}(z_{1},v)U_{1} \frac{d}{dz}[d^{3}v_{1}]+f_{1}(z_{1},v)d^{3}v_{1}\frac{d}{dz}U_{1}=0. $$

(23)

Now we assume that - while doing a space step $dz$ - particles in this shock region I exclusively experience the action of the mono-directional shock-electric field $E=E_{z}$ along the flow direction and find

$$ \frac{d}{dz}[\ln f_{1}(z_{1},v)]=-\frac{1}{d^{3}v_{1}}\frac{d}{dz}d^{3}v_{1}-\frac{1}{U_{1}}\frac{d}{dz}U_{1}. $$

(24)

If applied to electrons co-moving with their genuine bulk velocity $U_{e}>U_{p}$, one obtains

$$ \frac{d}{dz}U_{e}=\frac{dU_{e}}{dt}\left \langle \frac{dt}{dz}\right \rangle =\frac{eE}{m}\frac{1}{U_{e}} $$

(25)

and analogously for each individual electron with the velocity $v_{z}$ in the co-moving electron frame. Hence deriving in $z$ the given velocity space volume $d^{3}v_{1}=dv_{x}dv_{y}dv_{z}$ one can express

$$ \frac{d}{dz}dv_{z}=\frac{dv_{z}}{dt}\frac{dt}{dz}-\frac{dv_{z}'}{dt} \frac{dt}{dz^{\prime }} = \frac{eE}{m}\left (\frac{dt}{dz}- \frac{dt}{dz^{\prime }}\right ). $$

(26)

If we now make use of the fact that all electrons co-move with $U_{e}$, then $dz/dt=dz^{\prime }/dt=U_{e}$, one can conclude that the velocity space volume $d^{3}v_{1}$, transported with the bulk flow, appears as an invariant along the $z$-axis. The differential equation further simplifies to

$$ \frac{d}{dz}[\ln f_{1}(z_{1},v)]=-\frac{1}{U_{1}}\frac{dt}{dz} \frac{d}{dt}U_{1}=-\frac{eE}{mU_{e}^{2}}. $$

(27)

Now we use the result of Fahr and Verscharen (2016) that the electric field for the deceleration of the protons (or vice-versa acceleration of the electrons) is given by

$$ E=\frac{M}{2e}\frac{dU^{2}}{dz}, $$

(28)

we find the following solution of the differential equation in the co-moving electron frame

$$ f(z,v)=f_{1}(z_{1},v)\cdot \exp \left (-\frac{M}{2m}\int _{z_{1}}^{z} \frac{dU^{2}}{dz}\frac{1}{U_{e}^{2}}dz\right ). $$

(29)

Adopting upstream conditions with identical bulk velocities of electrons and protons, i.e. $U_{p1}= U_{e1}=U_{1}$, integrating by parts, and since the deceleration of protons and acceleration of electrons are simply complimentary effects in energy, being related by

$$ \frac{dU^{2}}{dz}=-\frac{m}{M}\frac{dU_{e}^{2}}{dz} $$

(30)

the above solution reduces to

$$ f(z,v)=f_{1}(z_{1},v)\exp \left (-\frac{1}{2}\int _{z_{1}}^{z} \frac{d\ln U_{e}^{2}}{dz}dz\right )=f_{1}(z_{1},v)\left (U_{1}/U_{e}\right ). $$

(31)

Here the function $f_{1}(z_{1},v)$ is the initial electron distribution in the co-moving upstream frame and may simply be expected to be a Maxwellian $f_{1}(z_{1},v)=Max(n_{1},U_{1},T_{e1})$, with $n_{1},U_{1},T_{e1}$ denoting the first three Maxwellian velocity moments, i.e. number density $n_{e1}=n_{1}$, bulk velocity $U_{e1}=U_{1}$ and temperature $T_{e1}$. In case good physical reasons exist to assume upstream electrons as non-Maxwellian, one can simply replace $f_{1}(z_{1},v)$ by the expression favoured.

The above expression reveals that the temperature of the electron population in region I of the shock due to $(4\pi /3)m\int f_{1}(z_{1},v)v^{2}dv=n_{e}K$ $T_{e1}$ is conserved, while the number density of the population changes inversely proportional to $U_{e}$, and the kinetic electron bulk energy changing with $z$. The same is valid for the shocked protons along analogous arguments, but of course with their genuine bulk velocity, i.e. $U=U_{p}\ll U_{e}$.

Electric Currents and Excited Instabilities

As mentioned, the shock transition region can be divided into three different regions I,II,III amongst which the region I is responsible for a basic proper oscillation. As soon as the shock-electric field has self-installed in this region, protons are slowed down and electrons are accelerated, meaning that the local bulk velocities of protons and electrons $U_{p}\ll U_{e}$ are becoming very different in magnitudes whereby also the quasi-neutrality of the upstream plasma is locally violated, however leading in a time average to a stationary (w.r.t. shock standing) charge structure. Let us assume a linear extent $\varLambda $ of this electric field structure, then upstream the electron density is $n_{e1}$, but downstream it only is $n_{e1}(U_{1}/U_{e})$. In a linear approach this resembles an electric capacitor with a surface charge of $C=e(n_{e1}- n_{e1}(U_{1}/U_{e})) \simeq en_{e1}$ and a constant electric field $E$ between the capacitor plates. The linear dimension $\varLambda $ is related to the restoring polarisation forces with $eE\varLambda =(1/2)m_{e}U_{e}^{2}$ and can be expressed through its 1D-Debye analogue:

$$\begin{aligned} \varLambda =& \sqrt{\frac{4\pi }{e^{2}n_{e1}}(\frac{1}{2}m_{e}U_{e2}^{2})} =\sqrt{\frac{4\pi }{e^{2}n_{e1}}(\frac{1}{2}m_{p}(U_{1}^{2}-U_{2}^{2})} \\ =& 4\pi \sqrt{\frac{KT_{1}}{4\pi e^{2}n_{e1}}M_{1}^{2}(1- \frac{1}{s^{2}})} =4\pi \lambda _{D1}M_{1}\sqrt{(1-\frac{1}{s^{2}})} \end{aligned}$$

(32)

where $\lambda _{D1}$ as the upstream Debye length, $M_{1}\simeq 10$ as the upstream sonic Mach number, and the shock compression ratio $s\simeq 3$. Reminding that the upstream Debye length is calculated by $\lambda _{D1}= \sqrt{\frac{KT_{1}}{4\pi e^{2}n_{e1}}}\simeq 3000$ cm, then one finds $\varLambda = 12$ km.

Now one can calculate the typical time period $\tau _{\varLambda }$ during which an electron is passing over this transition length to change the capacitor charge:

$$ \tau _{\varLambda }=\frac{\varLambda }{U_{e}}= \frac{\varLambda }{(m_{p}/m_{e})U_{1}} $$

(33)

Connected with this period also is a proper oscillation frequency for the transition region which is given by

$$\begin{aligned} \omega _{\varLambda } =&2\pi \frac{(m_{p}/m_{e})U_{1}}{\varLambda }= \frac{2\pi (m_{p}/m_{e})U_{1}}{4\pi \lambda _{D1}M_{1}\sqrt{1-\frac{1}{s^{2}}}} \\ =& \frac{(m_{p}/m_{e})}{\sqrt{\frac{m_{p}}{2\pi e^{2}n_{e1}}}\sqrt{1-\frac{1}{s^{2}}}}=\omega _{e1} \frac{\sqrt{\frac{m_{p}}{m_{e}}}}{\sqrt{1-\frac{1}{s^{2}}}}\simeq 45\omega _{e1} \end{aligned}$$

(34)

where $\omega _{e1}$ is the upstream electron plasma frequency. This hence means that the jet of overshooting electrons is oscillating with typical frequencies of the order $\omega _{\varLambda }\simeq 45\omega _{e1}$ and hence excites turbulence for shock region II.

The Electron Distribution Function in Shock Region II

Now we start with the distribution function of the electrons derived for shock region I. In region II this distribution function due to the upcoming dominance of Lorentz forces has to adapt to the magnetic field, frozen-in to the downstream bulk solar wind proton flow, moving there with the plasma bulk velocity $U_{2}$. Hence the bulk of the overshooting electrons moves with a velocity $\Delta U=U_{e}-U_{2}$ relative to the bulk of the protons and consequently has velocity components $\Delta U_{\perp }= \sin \alpha _{2}\cdot \Delta U$ and $\Delta U_{\parallel }= \cos \alpha _{2}\cdot \Delta U$ perpendicular and parallel to the downstream magnetic field $\mathbf {B}_{2}$. Here $\alpha _{2}$ denotes the angle between the downstream frozen-in field $\mathbf {B}_{2}$ and the velocity $\Delta \mathbf {U}$. Due to the acting Lorentz forces electrons are forced to first produce a torus distribution with an average velocity $\Delta U_{\perp }$ and a thermal spread around with a velocity of $\delta v=\sqrt{3KT_{1}/m_{e}}$. If this toroidal distribution is subject to a fast and effective pitch-angle scattering process ((e.g., Wykes et al. 2001), then an isotropic shell distribution evolves from the initially occurring toroidal distribution given by

$$ f_{2e}(v)=n_{e2} \exp \left (- \frac{m_{e}(v-\Delta U_{\perp })^{2}}{KT_{1}}\right ). $$

(35)

This intermediate shell electron distribution function, which is again unstable as shown for the case of pick-up protons by Fahr and Fichtner (2011), will be subject to strong velocity diffusion due to whistler wave turbulence driven by the fluctuating jet of overshooting electrons. The original non-equilibrium shell distribution will asymptotically deform into a quasi-equilibrium distribution, which we assume to be a kappa shell distribution:

$$ f_{2e}^{\infty }(v)=A \left [1+ \frac{(v-\Delta U_{\perp })^{2}}{\kappa \varTheta ^{2}}\right ]^{-( \kappa +1)}, $$

(36)

which may be considered as the solution of the following kinetic transport equation for the intermediate semi-stationary state arising as the first quasi-stationary case 〈 $\partial f_{2e}(v)/\partial t\rangle _{t=\tau _{1}}=0$

$$ \frac{1}{v^{2}}\frac{\partial }{\partial v}\left (v^{2}D_{vv} \frac{\partial f}{\partial v}\right )=-\frac{1}{\tau _{vv}}[f_{2e}(v)-f_{2e}^{\infty }(v)] $$

(37)

Instabilities Excited in Region II

After the passage through the layer of strong electric field (i.e. region I) the following physical situation is established. The electron bulk velocity, achieved at the end of region I, is higher than both the electron and the proton thermal velocity at its upstream border, i.e. $U_{e}>c_{e,1} \gg c_{p,1}$ (see also Fig. 12). Hence at a first glance one is confronted with plasma conditions similar to a strong electron current flowing into a background magnetic field and a slow proton bulk flow. This, as is well known, can trigger the Buneman instability (e.g., Alexandrov et al. 2013; Chen 2016), possibly in competition with the modified two-stream instability, (e.g., Matsukiyo and Scholer 2003; Vasko et al. 2018; Egedal et al. 2021) both exciting whistler turbulence.

In view of the above statement, the assumption of a cold plasma is applicable, and the dispersion relation describing the Buneman instability in the reference frame of the proton bulk motion $U_{p2}\ll U_{e}$ reads (Chashei and Fahr 2013):

$$\begin{aligned} \omega _{pe}^{2}\cos ^{2}\theta \lbrack \frac{1}{(\omega -\mathbf{k}\cdot \boldsymbol{\Delta} \mathbf{U})^{2}}+ \frac{m_{e}}{m_{p}\omega ^{2}}] +&\omega _{pe}^{2}\sin ^{2}\theta \lbrack \frac{1}{(\omega -\mathbf{k}\cdot \boldsymbol{\Delta} \mathbf{U})^{2}-\omega _{Be}^{2}} \\ +&\frac{m_{e}}{m_{p}}\frac{1}{\omega ^{2}-\omega _{Bp}^{2}}]=1. \end{aligned}$$

(38)

Here $k$ and $\omega $ denote wave vector and frequency of the excited wave, and $\theta $ is the inclination between the downstream magnetic field and the velocity $\boldsymbol{\Delta} \mathbf {U}$. At the entrance to region II we furthermore can assume $\mathbf{k}\cdot \boldsymbol{\Delta} \mathbf{U}=\mathbf{k}\cdot (\mathbf{U}_{e}-\mathbf{U}_{p})=k_{z}(U_{e}-U_{p})$. Looking now for maximum wave growth at $\omega \ll k_{z}(U_{e}-U_{p}) \simeq \omega _{p_{e}}$ and keeping in mind that close to the TS one has the following relation between the electron plasma frequency and the gyro frequencies: $\omega _{pe}\gg \omega _{Be}\gg \omega _{Bp}$, the above relation leads to the constraint

$$ \cos ^{2}\theta \frac{\omega _{pe}^{2}}{(k\Delta U\mathbf{)}^{2}}+ \sin ^{2}\theta \lbrack \frac{\omega _{pe}^{2}}{(k\Delta U\mathbf{)}^{2}}+ \frac{m_{e}}{m_{p}}\frac{\omega _{pe}^{2}}{\omega ^{2}-\omega _{Bp}^{2}}]=1. $$

(39)

For $\omega ^{2}\gg \omega _{Bp}^{2}$, one simply obtains

$$ \omega ^{2}=-\frac{m_{e}}{m_{p}}\sin ^{2}\theta \frac{\omega _{pe}^{2}(k\Delta U\mathbf{)}^{2}}{\omega _{pe}^{2}-(k\Delta U\mathbf{)}^{2}}. $$

(40)

Now one can see that for wavelengths corresponding to $\omega _{pe}^{2}\geq (k\Delta U\mathbf{)}^{2}$ there exists a wavepower growth (generation of whistler wave turbulence) according to a growth rate

$$ \gamma (k)=\sqrt{\frac{m_{e}}{m_{p}}\sin ^{2}\theta \frac{\omega _{pe}^{2}(k\Delta U\mathbf{)}^{2}}{\omega _{pe}^{2}-(k\Delta U\mathbf{)}^{2}}}=\omega _{pe}\sin \theta \cdot \sqrt{\frac{m_{e}}{m_{p}} \frac{(k\Delta U\mathbf{)}^{2}}{\omega _{pe}^{2}-(k\Delta U\mathbf{)}^{2}}} $$

(41)

This for $\sin \theta \simeq 1$ clearly indicates that within typical growth periods $(1/\gamma (k))$ smaller than electron gyroperiods $\tau _{ge}$

$$ \gamma ^{-1}=\sqrt{M/m}/\omega _{pe}=\sqrt{M/m}/10^{2}\omega _{ge}=0.4 \tau _{ge} $$

(42)

the accumulated excess kinetic energy of the electrons, gained in form of overshoot velocities in region I, is then very rapidly redistributed, presumably equally branched into turbulent whistler wave energies and thermal energies of the electrons, respectively. This would, however, then mean that the action of the Buneman instability is so strong, that the Lorentz-induced winding of overshooting electrons practically does not occur, but instead the electrons are strongly decelerated by the instability down to the proton bulk velocity $U_{p}$ (i.e. to $\Delta U\simeq 0$), and most probably the electron kinetic energy of the overshoot $E_{over}=(1/2)m_{e}(U_{e}^{2}-U_{p}^{2})$ is redistributed in equal shares both to the whistler wave power and to the thermal energy of electrons, i.e. electron pressure.

What can be concluded from the above? The aforegoing investigation did show that the two-stream ion-proton distribution, which had developed in region I, as reaction to the strong electric fields of the shock, dissolves in region II, where Lorentz forces in connection with the frozen-in magnetic fields start controlling the ongoing physical motions. However, instead of a Lorentz winding of the motion, the Buneman instability within a period of only a few electron gyroperiods $\tau _{ge}$ must be expected to remove the kinetic excess energy of the electrons, to take care of a bulk velocity adaptation of protons and electrons, i.e. $U^{II}=U_{p}^{II}\simeq U_{e}^{II}$, and to arrange a thermalization or heating of the electrons to an energy equivalent of about one half of the original overshoot kinetic energy (i.e. a branching ratio of 0.5 between electron thermal and whistler turbulent energies, respectively). This nevertheless would mean that, after the Buneman instability has stopped operating, an electron temperature $T_{e}^{II}$ of the order of $T_{e}^{II}\simeq 0.5(1/4k)MU_{1}^{2}=2.5\cdot 10^{5}~\mbox{K}$ can be expected to prevail, meaning that (comparing this result with the proton temperatures of the order of $T_{1}^{II}\simeq 1\cdot 10^{5}~\mbox{K}$ measured by Voyager-2), electrons, even after the occurrence of this relaxation process in shock region II, still reflect an effective thermal excess heating w.r.t. protons by at least a factor 2.5. That appears to clearly point out the fact that further downstream of the TS electrons have to be considered as the hotter, more pressurized plasma population compared to the shocked solar wind protons.

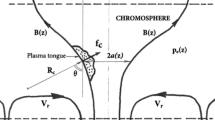
Multiple Shock Acceleration

As we have shown in previous sections, particle acceleration at MHD shocks is directly observed in the heliosphere. Fast and efficient acceleration of ions at the Earth bow shock detected with Magnetospheric Multiscale mission (MMS) was reported recently in Turner et al. (2018), which is consistent with the models of first-order Fermi acceleration. Turner et al. (2018) identified an efficient form of Fermi acceleration that involves two large-scale converging shocks in some intermittent hot flow anomalies. Electron acceleration by non-resonant compressible fluctuations (magnetic pumping) in the Earth bow shock ripples is shown to be consistent with MMS observations (Lichko and Egedal 2020).

At larger scales in the heliospheric hierarchy the pile-up twin-shock collision scenario (Wang et al. 2019) is successful in modeling observed ground-level enhancements, which were associated with some of the fast coronal mass ejections produced by gradual solar events. Dynamic Monte Carlo simulations were used in Wang et al. (2019) to model the MeV regime ion enhancements in CME events. In the larger scale astrophysical events, like a collision of a supernova shock with stellar wind, the non-linear back-reaction effects may affect CR spectra evolution at colliding shock flows (Bykov et al. 2013b; Vieu et al. 2020). The colliding shock flow models are applied to studies of CR acceleration in the interaction between the strong stellar winds in the colliding-wind binaries (Grimaldo et al. 2019) and in the bow shock pulsar wind nebulae (Bykov et al. 2019a).

Re-acceleration of the fast solar flare electrons by shocks associated with CME events was suggested to explain the observed electron spectral hardening (Petrosian 2016). The combined effect of shocks and turbulent (resonant and non-resonant) acceleration (e.g. (Petrosian and Bykov 2008)) is widely used in solar events.

Particle acceleration at multiple shocks (both identical and with different strengths) and its effect on particle spectral index has been investigated in Pope and Melrose (1994). Recent particle-in-cell simulations of collisionless shock formation and non-thermal particle acceleration are very successful in modeling many astrophysical phenomena (Marcowith et al. 2016). They provided the microscopic description of particle acceleration in the magnetic field reconnection processes (Comisso and Sironi 2019). On the other hand, the limited computational resources do not allow at present to model non-thermal particle distributions with a wide dynamical range in complicated astrophysical multi-scale MHD flows with multiple shocks and the accompanied rarefaction plasma motions. In the extended astrophysical objects, like the clusters of galaxies, the energy containing scale of magnetic turbulence may exceed 10 kpc while the gyroradius of radio-emitting GeV regime electrons is below 10¹⁴ cm. In the case of supernova remnants and in the co-rotation interaction regions of the stellar winds the dynamical range is very wide as well to be covered by the exact PiC models.

Particle acceleration by a strong magnetic turbulence with coherent structures and plasma velocity gradients may need kinetic description outside the quasi-linear theory (e.g. Bykov and Toptygin 1993; Lemoine 2021). In many cases the intensive energy release in active regions is accompanied with formation of shocks of different strengths due to supersonic flow collisions or just non-linear breaking of Riemann type waves. The MHD flow where fast particles are interacting with large amplitude magnetic fluctuations in the presence of the flow discontinuities will produce the intermittent distributions of particles in phase space (Lemoine 2021).

The presence of intermittency requires special description even in statistically homogeneous strong compressible MHD turbulence with shocks comparing to that in the case of the weak turbulence. Apart from the pair correlation functions of the plasma bulk velocity some extra correlation functions describing the shock ensemble are needed to construct the kinetic equations (Bykov and Toptygin 1993). In the test particle case the intermittent distribution function of CRs have strong localized peaks in the vicinity of shock front surfaces. One can use local plain solutions in the vicinity of a shock of a given strength like that given by Eq. (2) to obtain the kinetic equation for $F(\boldsymbol{r},p,t)$, the average phase space distribution function in between the shocks that is a smooth function in the phase space. The distribution function in Eq. (2) in the vicinity of each of $i$-th shock is parameterized by the local diffusion coefficient $D_{x}^{i}$ and the index $\gamma _{i}$ which is determined by the shock compression ratio $r_{i}$. It should be noted here that $F\cdot p^{2}$ corresponds to $f_{u}(p)$ in Eq. (2).

The distribution function averaged over an ensemble of turbulent motions and shocks satisfies the kinetic equation

$$ \frac{\partial F}{\partial t} - \frac{\partial}{\partial r_{\alpha}} \: D_{\alpha \beta} \: \frac{\partial F}{\partial r_{\beta}} - \frac{1}{p^{2}} \: \frac{\partial}{\partial p} \: p^{4} D^{pp} \: \frac{\partial F}{\partial p} = \hat{L}\big[ G F + A \hat{L} F + 2B \hat{P} F \big]+ Q(p), $$

(43)

where the source term $Q(p)$ is determined by injection of the nuclei at some momentum range. The operators $\hat{L}$ and $\hat{P}$ for the ensemble of strong shocks (providing the close values of the index $\gamma $) are given by

$$ \hat{L}= \frac{1}{3p^{2}} \: \frac{\partial}{\partial p} \: p^{3- \gamma} \: \int _{0}^{p} {\mathrm{d}}p' \: {p'}^{\gamma}\frac{\partial}{\partial p'} \;;~~~~~ \hat{P}= \frac{p }{3} \: \frac{\partial}{\partial p} \, . $$

(44)

The kinetic coefficients of test particles $D_{\alpha \beta}$, $D^{pp}$, $A,B$ and $G$ in the case of the strong intermittent shock turbulence satisfy the renormalization equations (Bykov and Toptygin 1993; Bykov et al. 2019b, 2020). The spatial diffusion coefficient $D_{\alpha \beta}$ describes the particle transport by strong long-wavelength MHD fluctuations in the presence of short scale resonant fluctuations. At low CR energies the transport is dominated by turbulent CR advection with $D_{\alpha \beta}$ which does not depend on the CR energy. At high energies the CR energy dependent diffusion is determined by the spectrum of MHD turbulence (see e.g. Jokipii 1966; Bykov and Toptygin 1987; Bieber et al. 1994; Casse et al. 2001). The momentum diffusion coefficient $D^{pp}$ is dominated here by the long-wavelength compressible fluctuations. The terms with $\hat{L}$ are describing the CR spectra transformations at individual shocks, while the kinetic coefficients $A,B$ described the cross-correlations of shocks with the MHD compressible turbulence.

Cosmic ray acceleration by large scale plasma motions with the ensemble of MHD shocks are expected to occur in a number of astrophysical objects including clusters of galaxies (Bykov et al. 2019b), clusters of massive stars with energetic stellar winds and supernovae shocks (Bykov et al. 2020), fast radiation-driven stellar winds (White and Chen 1994) and many others. The time dependent solutions of Eq. (43) for CR distribution started from a narrow range of particle momenta injected into the large scale compressible turbulence discussed in Bykov et al. (2019b) to model CRs in clusters of galaxies are approaching the asymptotic power law of the form $F(p) \propto p^{-5}$. This is rather a soft CR spectrum which may explain the results of the recent analysis of the GeV regime gamma ray data from Fermi LAT on the Coma cluster (Adam et al. 2021). The direct measurements of the characteristics of the magnetic turbulence and cosmic rays are available in the heliosphere where detailed analysis of CR spectra in the quiet periods (i.e. in between of the events accompanied with shocks) revealed the spectra $F(v) \propto v^{-5}$ (Fisk and Gloeckler 2006, 2014, 2017) which is consistent with that discussed above.

The time dependent particle acceleration model solutions for the averaged distribution function of CRs in between the shocks approached the time asymptotic behaviour $F(p) \propto p^{-a}$. In Fig. 13 we illustrate the temporal evolution of the spectra of CRs accelerated by multiple shocks. The power-law exponent $a$ depends on the effective adiabatic index of the system. The index $a = 5$ for the systems with injection of non-relativistic particles as shown in Fig. 13. However, if the pressure of the accelerated relativistic CR component is comparable to the background plasma pressure as it is the case in the active regions of the ISM such as the superbubbles the power-law exponent is approaching $a = 4$. This power-law distribution extends up to some characteristic momentum $p_{c}$ which depends on the small scale MHD turbulence in the system (see Bykov et al. (2020) for details). Such a model can be applied to interpret the existing gamma-ray observations of both large scale superbubbles and compact clusters of young massive stars (Ackermann et al. 2011; Bykov 2014; Aharonian et al. 2019; Bykov et al. 2020).

Concluding Remarks

In this review we focus on recent developments in the shock acceleration mechanism, also in relation with particle transport. The results reported comes mainly from investigations of particle acceleration in the heliosphere but have strong implications also in distant astrophysical environments. We included evidences of anomalous transport as deduced from the analysis of in-situ data upstream of interplanetary shocks and in numerical simulations. In particular, superdiffusion has been found to give rise to power-law energetic particle fluxes far upstream of the shock when the level of magnetic field fluctuations, at the scales in resonance with the energetic particle Larmor radius, does not depend on the distance from the shock (which suggest a spatially independent diffusion coefficient) (Perri and Zimbardo 2012b). It also reduces the acceleration times and flattens the particle energy spectra with respect to the standard DSA prediction. Further, Monte Carlo models of collisionless shocks with superdiffusive energetic particle transport have addressed how superdiffusion plays an important role in magnetic field amplification in astrophysical shocks. Indeed, superdiffusion upstream of shocks gives rise to a strong particle anisotropy, which resultant pressure generates instabilities in the plasma that amplify the magnetic field. This is a point that is worth investigating using in-situ data in the heliospheric environment, as a natural laboratory for investigation, with the joint analysis of magnetic field, plasma, and energetic particles data. New space missions, such as MMS, Parker Solar Probe and Solar Orbiter will surely advance such a point thanks to the unprecedented high time cadence in plasma and energetic particle data. Also particle anisotropy is a key point that needs to be taken into account when including superdiffusion in shock acceleration.

Since superdiffusion is due to a stochastic process (Lévy walk) that is characterized by a power-law distribution of the free path lengths, the probability of occurrence for long displacements is higher than the one associated to a Gaussian process; very short displacements have an associated high probability, too. Such a scale-free nature of the walk allows particles to make both very long and very short jumps, reducing the time of the particle acceleration process (Perri and Zimbardo 2012a). Further, Zimbardo and Perri (2020) have shown that assuming a power-law distribution for the scattering times, it is possible to derive a fractional Fokker-Planck equation that yields to a superdiffusive spatial transport; anomalous transport can also emerge as solution of a non-linear Fokker-Planck equation in presence of an external force (Tsallis and Bukman 1996).

An efficient process for accelerating CR at high energies is the acceleration at pairs or multiple shocks. Such a mechanism is reported in this review and the governing kinetic equation is discussed, since it finds applicability within a broad range of astrophysical systems. Colliding supersonic flows occur in colliding wind binaries (e.g. Pittard et al. 2021) and can be realized in different astrophysical environments including relativistic pulsar winds or jets produced by black holes in gamma-ray binaries (Bykov et al. 2021). A very efficient first order Fermi-type acceleration can be expected in such of the flows which may form a hard spectral component at the highest energies of CRs accelerated in this sources (Bykov et al. 2013b; Grimaldo et al. 2019; Vieu et al. 2020; Bykov et al. 2021). This type of CR accelerators can produce the high energy CRs component beyond the knee of the galactic CRs spectrum.

One aspect that is fundamental in shock physics is the interaction of propagating shocks with upstream turbulence, since it can play a key role in the evolution of particle energy spectra. As we described in Sect. 3, numerical simulations have shown that the interaction between a propagating shock and turbulence upstream causes a high distortion of the shock front and high spatial and velocity particle diffusion when the amplitude of magnetic field fluctuations upstream is large. Fast particle reflection at the shock can probably be source of superdiffusion. However, further study is required especially from the observational side. Indeed, a possible relation between turbulence properties upstream and particle transport regimes is still poorly understood. Also how shock geometry influences energetic particle transport needs a deeper investigation.

Another observational evidence presented in this review that challenges the standard shock acceleration theory is the presence of flat energy spectra at some interplanetary shock waves. Whether the explanation has to be ascribed to changes in the connection with the satellite and the shock front, or to the interaction between energetic particles and pre-existing turbulent fluctuations that lead to a diffusion coefficient independent of energy remains an open question. Additional insights can of course come from the joint study of observations, analytical and numerical modellings.

Recent studies on particle acceleration at the TS address the importance of the energetic electron population as a major source of plasma heating (Chalov and Fahr 2013). Electrons are found to represent the preferentially heated fluid at MHD shocks, are hotter than shocked protons, and dominate the plasma pressure downstream of the TS. This has been taken into account when interpreting Voyager 2 observations during the TS crossings.

References

M. Ackermann, M. Ajello, A. Allafort, L. Baldini, J. Ballet, G. Barbiellini, D. Bastieri, A. Belfiore, R. Bellazzini, B. Berenji, R.D. Blandford, E.D. Bloom, E. Bonamente, A.W. Borgland, E. Bottacini, M. Brigida, P. Bruel, R. Buehler, S. Buson, G.A. Caliandro, R.A. Cameron, P.A. Caraveo, J.M. Casandjian, C. Cecchi, A. Chekhtman, C.C. Cheung, J. Chiang, S. Ciprini, R. Claus, J. Cohen-Tanugi, A. de Angelis, F. de Palma, C.D. Dermer, E. do Couto e Silva, P.S. Drell, D. Dumora, C. Favuzzi, S.J. Fegan, W.B. Focke, P. Fortin, Y. Fukazawa, P. Fusco, F. Gargano, S. Germani, N. Giglietto, F. Giordano, M. Giroletti, T. Glanzman, G. Godfrey, I.A. Grenier, L. Guillemot, S. Guiriec, D. Hadasch, Y. Hanabata, A.K. Harding, M. Hayashida, K. Hayashi, E. Hays, G. Jóhannesson, A.S. Johnson, T. Kamae, H. Katagiri, J. Kataoka, M. Kerr, J. Knödlseder, M. Kuss, J. Lande, L. Latronico, S.H. Lee, F. Longo, F. Loparco, B. Lott, M.N. Lovellette, P. Lubrano, P. Martin, M.N. Mazziotta, J.E. McEnery, J. Mehault, P.F. Michelson, W. Mitthumsiri, T. Mizuno, C. Monte, M.E. Monzani, A. Morselli, I.V. Moskalenko, S. Murgia, M. Naumann-Godo, P.L. Nolan, J.P. Norris, E. Nuss, T. Ohsugi, A. Okumura, E. Orlando, J.F. Ormes, M. Ozaki, D. Paneque, D. Parent, M. Pesce-Rollins, M. Pierbattista, F. Piron, M. Pohl, D. Prokhorov, S. Rainò, R. Rando, M. Razzano, T. Reposeur, S. Ritz, P.M.S. Parkinson, C. Sgrò, E.J. Siskind, P.D. Smith, P. Spinelli, A.W. Strong, H. Takahashi, T. Tanaka, J.G. Thayer, J.B. Thayer, D.J. Thompson, L. Tibaldo, D.F. Torres, G. Tosti, A. Tramacere, E. Troja, Y. Uchiyama, J. Vandenbroucke, V. Vasileiou, G. Vianello, V. Vitale, A.P. Waite, P. Wang, B.L. Winer, K.S. Wood, Z. Yang, S. Zimmer, S. Bontemps, A cocoon of freshly accelerated cosmic rays detected by Fermi in the Cygnus Superbubble. Science 334(6059), 1103 (2011). https://doi.org/10.1126/science.1210311
ADS Article Google Scholar
R. Adam, H. Goksu, S. Brown, L. Rudnick, C. Ferrari, $\gamma$-ray detection toward the Coma cluster with Fermi-LAT: implications for the cosmic ray content in the hadronic scenario. Astron. Astrophys. 648, A60 (2021). https://doi.org/10.1051/0004-6361/202039660. 2102.02251
ADS Article Google Scholar
O. Adriani, G.C. Barbarino, G.A. Bazilevskaya, R. Bellotti, M. Boezio, E.A. Bogomolov, L. Bonechi, M. Bongi, V. Bonvicini, S. Borisov, S. Bottai, A. Bruno, F. Cafagna, D. Campana, R. Carbone, P. Carlson, M. Casolino, G. Castellini, L. Consiglio, M.P. De Pascale, C. De Santis, N. De Simone, V. Di Felice, A.M. Galper, W. Gillard, L. Grishantseva, G. Jerse, A.V. Karelin, S.V. Koldashov, S.Y. Krutkov, A.N. Kvashnin, A. Leonov, V. Malakhov, V. Malvezzi, L. Marcelli, A.G. Mayorov, W. Menn, V.V. Mikhailov, E. Mocchiutti, A. Monaco, N. Mori, N. Nikonov, G. Osteria, F. Palma, P. Papini, M. Pearce, P. Picozza, C. Pizzolotto, M. Ricci, S.B. Ricciarini, L. Rossetto, R. Sarkar, M. Simon, R. Sparvoli, P. Spillantini, Y.I. Stozhkov, A. Vacchi, E. Vannuccini, G. Vasilyev, S.A. Voronov, Y.T. Yurkin, J. Wu, G. Zampa, N. Zampa, V.G. Zverev, PAMELA measurements of cosmic-ray proton and helium spectra. Science 332(6025), 69 (2011)
ADS Google Scholar
M. Aguilar, L. Ali Cavasonza, G. Ambrosi, L. Arruda, N. Attig, F. Barao, L. Barrin, A. Bartoloni, S. Başeğmez-du Pree, J. Bates, R. Battiston, M. Behlmann, B. Beischer, J. Berdugo, B. Bertucci, V. Bindi, W. de Boer, K. Bollweg, B. Borgia, M.J. Boschini, M. Bourquin, E.F. Bueno, J. Burger, W.J. Burger, S. Burmeister, X.D. Cai, M. Capell, J. Casaus, G. Castellini, F. Cervelli, Y.H. Chang, G.M. Chen, H.S. Chen, Y. Chen, L. Cheng, H.Y. Chou, S. Chouridou, V. Choutko, C.H. Chung, C. Clark, G. Coignet, C. Consolandi, A. Contin, C. Corti, Z. Cui, K. Dadzie, Y.M. Dai, C. Delgado, S. Della Torre, M.B. Demirköz, L. Derome, S. Di Falco, V. Di Felice, C. Díaz, F. Dimiccoli, P. von Doetinchem, F. Dong, F. Donnini, M. Duranti, A. Egorov, A. Eline, J. Feng, E. Fiandrini, P. Fisher, V. Formato, C. Freeman, Y. Galaktionov, C. Gámez, R.J. García-López, C. Gargiulo, H. Gast, I. Gebauer, M. Gervasi, F. Giovacchini, D.M. Gómez-Coral, J. Gong, C. Goy, V. Grabski, D. Grandi, M. Graziani, K.H. Guo, S. Haino, K.C. Han, R.K. Hashmani, Z.H. He, B. Heber, T.H. Hsieh, J.Y. Hu, Z.C. Huang, W. Hungerford, M. Incagli, W.Y. Jang, Y. Jia, H. Jinchi, K. Kanishev, B. Khiali, G.N. Kim, T. Kirn, M. Konyushikhin, O. Kounina, A. Kounine, V. Koutsenko, A. Kuhlman, A. Kulemzin, G. La Vacca, E. Laudi, G. Laurenti, I. Lazzizzera, A. Lebedev, H.T. Lee, S.C. Lee, C. Leluc, J.Q. Li, M. Li, Q. Li, S. Li, T.X. Li, Z.H. Li, C. Light, C.H. Lin, T. Lippert, Z. Liu, S.Q. Lu, Y.S. Lu, K. Luebelsmeyer, J.Z. Luo, S.S. Lyu, F. Machate, C. Mañá, J. Marín, J. Marquardt, T. Martin, G. Martínez, N. Masi, D. Maurin, A. Menchaca-Rocha, Q. Meng, D.C. Mo, M. Molero, P. Mott, L. Mussolin, J.Q. Ni, N. Nikonov, F. Nozzoli, A. Oliva, M. Orcinha, M. Palermo, F. Palmonari, M. Paniccia, A. Pashnin, M. Pauluzzi, S. Pensotti, H.D. Phan, V. Plyaskin, M. Pohl, S. Porter, X.M. Qi, X. Qin, Z.Y. Qu, L. Quadrani, P.G. Rancoita, D. Rapin, A. Reina Conde, S. Rosier-Lees, A. Rozhkov, D. Rozza, R. Sagdeev, S. Schael, S.M. Schmidt, A. Schulz von Dratzig, G. Schwering, E.S. Seo, B.S. Shan, J.Y. Shi, T. Siedenburg, C. Solano, J.W. Song, R. Sonnabend, Q. Sun, Z.T. Sun, M. Tacconi, X.W. Tang, Z.C. Tang, J. Tian, S.C.C. Ting, S.M. Ting, N. Tomassetti, J. Torsti, C. Tüysüz, T. Urban, I. Usoskin, V. Vagelli, R. Vainio, E. Valente, E. Valtonen, M. Vázquez Acosta, M. Vecchi, M. Velasco, J.P. Vialle, L.Q. Wang, N.H. Wang, Q.L. Wang, S. Wang, X. Wang, Z.X. Wang, J. Wei, Z.L. Weng, H. Wu, R.Q. Xiong, W. Xu, Q. Yan, Y. Yang, H. Yi, Y.J. Yu, Z.Q. Yu, M. Zannoni, C. Zhang, F. Zhang, F.Z. Zhang, J.H. Zhang, Z. Zhang, F. Zhao, Z.M. Zheng, H.L. Zhuang, V. Zhukov, A. Zichichi, N. Zimmermann, P. Zuccon (AMS Collaboration), The alpha magnetic spectrometer (AMS) on the international space station: part II - results from the first seven years. Phys. Rep. 894, 1–116 (2021)
ADS Google Scholar
F.A. Aharonian, A.G. Akhperjanian, K.M. Aye, A.R. Bazer-Bachi, M. Beilicke, W. Benbow, D. Berge, P. Berghaus, K. Bernlöhr, O. Bolz, C. Boisson, C. Borgmeier, F. Breitling, A.M. Brown, J. Bussons Gordo, P.M. Chadwick, V.R. Chitnis, L.M. Chounet, R. Cornils, L. Costamante, B. Degrange, A. Djannati-Ataï, L.O. Drury, T. Ergin, P. Espigat, F. Feinstein, P. Fleury, G. Fontaine, S. Funk, Y.A. Gallant, B. Giebels, S. Gillessen, P. Goret, J. Guy, C. Hadjichristidis, M. Hauser, G. Heinzelmann, G. Henri, G. Hermann, J.A. Hinton, W. Hofmann, M. Holleran, D. Horns, O.C. de Jager, I. Jung, B. Khélifi, N. Komin, A. Konopelko, I.J. Latham, R. Le Gallou, M. Lemoine, A. Lemière, N. Leroy, T. Lohse, A. Marcowith, C. Masterson, T.J.L. McComb, M. de Naurois, S.J. Nolan, A. Noutsos, K.J. Orford, J.L. Osborne, M. Ouchrif, M. Panter, G. Pelletier, S. Pita, M. Pohl, G. Pühlhofer, M. Punch, B.C. Raubenheimer, M. Raue, J. Raux, S.M. Rayner, I. Redondo, A. Reimer, O. Reimer, J. Ripken, M. Rivoal, L. Rob, L. Rolland, G. Rowell, V. Sahakian, L. Saugé, S. Schlenker, R. Schlickeiser, C. Schuster, U. Schwanke, M. Siewert, H. Sol, R. Steenkamp, C. Stegmann, J.P. Tavernet, C.G. Théoret, M. Tluczykont, D.J. van der Walt, G. Vasileiadis, P. Vincent, B. Visser, H.J. Völk, S.J. Wagner, High-energy particle acceleration in the shell of a supernova remnant. Nature 432(7013), 75–77 (2004). https://doi.org/10.1038/nature02960. astro-ph/0411533
ADS Article Google Scholar
F. Aharonian, R. Yang, E. de Oña Wilhelmi, Massive stars as major factories of galactic cosmic rays. Nat. Astron. 3, 561–567 (2019). https://doi.org/10.1038/s41550-019-0724-0. 1804.02331
ADS Article Google Scholar
A. Alexandrov, L. Bogdankevich, A. Rukhadze, Principles of Plasma Electrodynamics. Springer Series in Electronics and Photonics (Springer, Berlin, 2013). https://books.google.de/books?id=NuerngEACAAJ
Google Scholar
R.C. Allen, G.C. Ho, G.M. Mason, G. Li, L.K. Jian, S.K. Vines, N.A. Schwadron, C.J. Joyce, S.D. Bale, J.W. Bonnell, A.W. Case, E.R. Christian, C.M.S. Cohen, M.I. Desai, R. Filwett, K. Goetz, P.R. Harvey, M.E. Hill, J.C. Kasper, K.E. Korreck, D. Lario, D. Larson, R. Livi, R.J. MacDowall, D.M. Malaspina, D.J. McComas, R. McNutt, D.G. Mitchell, K.W. Paulson, M. Pulupa, N. Raouafi, M.L. Stevens, P.L. Whittlesey, M. Wiedenbeck, Radial Evolution of a CIR: Observations From a Nearly Radially Aligned Event Between Parker Solar Probe and STEREO A. Geophys. Res. Lett. 48(3), e91376 (2021)
ADS Google Scholar
E. Amato, The origin of galactic cosmic rays. Int. J. Mod. Phys. D 23(07), 1430, 013 (2014)
MathSciNet Google Scholar
W.I. Axford, E. Leer, G. Skadron, The acceleration of cosmic rays by shock waves, in Proc. 15th ICRC (Plovdiv), vol. 11 (1977), p. 132
Google Scholar
S.D. Bale, P.J. Kellogg, F.S. Mozer, T.S. Horbury, H. Reme, Measurement of the electric fluctuation spectrum of magnetohydrodynamic turbulence. Phys. Rev. Lett. 94(21), 215002 (2005)
ADS Google Scholar
S.J. Bame, D.J. McComas, B.L. Barraclough, J.L. Phillips, K.J. Sofaly, J.C. Chavez, B.E. Goldstein, R.K. Sakurai, The ULYSSES solar wind plasma experiment. Astron. Astrophys. Suppl. Ser. 92(2), 237–265 (1992)
ADS Google Scholar
A.R. Bell, The acceleration of cosmic rays in shock fronts. I. Mon. Not. R. Astron. Soc. 182, 147–156 (1978). https://doi.org/10.1093/mnras/182.2.147
ADS Article Google Scholar
A. Bell, Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Not. R. Astron. Soc. 353(2), 550–558 (2004)
ADS Google Scholar
E.G. Berezhko, G.F. Krymskiĭ, Reviews of topical problems: acceleration of cosmic rays by shock waves. Sov. Phys. Usp. 31, 27–51 (1988)
ADS Google Scholar
J.W. Bieber, W.H. Matthaeus, C.W. Smith, W. Wanner, M.B. Kallenrode, G. Wibberenz, Proton and electron mean free paths: the palmer consensus revisited. Astrophys. J. 420, 294–306 (1994)
ADS Google Scholar
R. Blandford, D. Eichler, Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154, 1–75 (1987)
ADS Google Scholar
R.D. Blandford, J.P. Ostriker, Particle acceleration by astrophysical shocks. Astrophys. J. 221, L29–L32 (1978)
ADS Google Scholar
P. Blasi, Acceleration of galactic cosmic rays. Nuovo Cimento Riv. Ser. 42(12), 549–600 (2019). https://doi.org/10.1393/ncr/i2019-10166-0
ADS Article Google Scholar
A.M. Bykov, Nonthermal particles and photons in starburst regions and superbubbles. Astron. Astrophys. Rev. 22, 77 (2014). https://doi.org/10.1007/s00159-014-0077-8. 1511.04608
ADS Article Google Scholar
A.M. Bykov, I.N. Toptygin, Effect of shocks on interstellar turbulence and cosmic-ray dynamics. Astrophys. Space Sci. 138(2), 341–354 (1987). https://doi.org/10.1007/BF00637855
ADS Article Google Scholar
A.M. Bykov, I. Toptygin, Particle kinetics in highly turbulent plasmas (renormalization and self-consistent field methods). Phys. Usp. 36(11), 1020–1052 (1993). https://doi.org/10.1070/PU1993v036n11ABEH002179
ADS Article Google Scholar
A.M. Bykov, A. Brandenburg, M.A. Malkov, S.M. Osipov, Microphysics of cosmic ray driven plasma instabilities. Space Sci. Rev. 178(2–4), 201–232 (2013a). https://doi.org/10.1007/s11214-013-9988-3. 1304.7081
ADS Article Google Scholar
A.M. Bykov, P.E. Gladilin, S.M. Osipov, Non-linear model of particle acceleration at colliding shock flows. Mon. Not. R. Astron. Soc. 429(3), 2755–2762 (2013b). https://doi.org/10.1093/mnras/sts553. 1212.1556
ADS Article Google Scholar
A.M. Bykov, D.C. Ellison, S.M. Osipov, Nonlinear Monte Carlo model of superdiffusive shock acceleration with magnetic field amplification. Phys. Rev. E. 95, 033,207 (2017). https://doi.org/10.1103/PhysRevE.95.033207
Article Google Scholar
A.M. Bykov, A.E. Petrov, A.M. Krassilchtchikov, K.P. Levenfish, S.M. Osipov, G.G. Pavlov, GeV-TeV cosmic-ray leptons in the solar system from the bow shock wind nebula of the nearest millisecond pulsar J0437-4715. Astrophys. J. Lett. 876(1), L8 (2019a). https://doi.org/10.3847/2041-8213/ab1922. 1904.09430
ADS Article Google Scholar
A.M. Bykov, F. Vazza, J.A. Kropotina, K.P. Levenfish, F.B.S. Paerels, Shocks and non-thermal particles in clusters of galaxies. Space Sci. Rev. 215(1), 14 (2019b). https://doi.org/10.1007/s11214-019-0585-y. 1902.00240
ADS Article Google Scholar
A.M. Bykov, A. Marcowith, E. Amato, M.E. Kalyashova, J.M.D. Kruijssen, E. Waxman, High-energy particles and radiation in star-forming regions. Space Sci. Rev. 216(3), 42 (2020). https://doi.org/10.1007/s11214-020-00663-0. 2003.11534
ADS Article Google Scholar
A.M. Bykov, A.E. Petrov, M.E. Kalyashova, S.V. Troitsky, PeV photon and neutrino flares from galactic gamma-ray binaries. Astrophys. J. Lett. 921(1), L10 (2021). https://doi.org/10.3847/2041-8213/ac2f3d. 2110.11189
ADS Article Google Scholar
D. Caprioli, D.T. Yi, A. Spitkovsky, Chemical enhancements in shock-accelerated particles: ab initio simulations. Phys. Rev. Lett. 119(17), 171101 (2017)
ADS Google Scholar
M. Caputo, Linear models of dissipation whose Q is almost frequency independent-II. Geophys. J. 13(5), 529–539 (1967)
ADS Google Scholar
F. Casse, M. Lemoine, G. Pelletier, Transport of cosmic rays in chaotic magnetic fields. Phys. Rev. D 65(2), 023,002 (2001)
Google Scholar
S.V. Chalov, H.J. Fahr, The role of solar wind electrons at the solar wind termination shock. Mon. Not. R. Astron. Soc. 433, L40–L43 (2013). https://doi.org/10.1093/mnrasl/slt052
ADS Article Google Scholar
I.V. Chashei, H.J. Fahr, On the electron temperature downstream of the solar wind termination shock. Ann. Geophys. 31(7), 1205–1212 (2013). https://doi.org/10.5194/angeo-31-1205-2013
ADS Article Google Scholar
F.F. Chen, Introduction to Plasma Physics and Controlled Fusion (Springer, Berlin, 2016). https://doi.org/10.1007/978-3-319-22309-4
Book Google Scholar
E.W. Cliver, A.G. Ling, Low-frequency type III bursts and solar energetic particle events. Astrophys. J. 690(1), 598–609 (2009). https://doi.org/10.1088/0004-637X/690/1/598
ADS Article Google Scholar
L. Comisso, L. Sironi, The interplay of magnetically dominated turbulence and magnetic reconnection in producing nonthermal particles. Astrophys. J. 886(2), 122 (2019). https://doi.org/10.3847/1538-4357/ab4c33. 1909.01420
ADS Article Google Scholar
N. Crooker, J. Gosling, V. Bothmer, R. Forsyth, P. Gazis, A. Hewish, T. Horbury, D. Intriligator, J. Jokipii, J. Kóta et al., Cir morphology, turbulence, discontinuities, and energetic particles. Space Sci. Rev. 89(1–2), 179–220 (1999)
ADS Google Scholar
R.B. Decker, S.M. Krimigis, E.C. Roelof, M.E. Hill, T.P. Armstrong, G. Gloeckler, D.C. Hamilton, L.J. Lanzerotti, Voyager 1 in the foreshock, termination shock, and heliosheath. Science 309(5743), 2020–2024 (2005). https://doi.org/10.1126/science.1117569
ADS Article Google Scholar
R.B. Decker, S.M. Krimigis, E.C. Roelof, M.E. Hill, T.P. Armstrong, G. Gloeckler, D.C. Hamilton, L.J. Lanzerotti, Mediation of the solar wind termination shock by non-thermal ions. Nature 454(7200), 67–70 (2008). https://doi.org/10.1038/nature07030
ADS Article Google Scholar
A. Dosch, A. Shalchi, Diffusive shock acceleration at interplanetary perpendicular shock waves: influence of the large scale structure of turbulence on the maximum particle energy. Adv. Space Res. 46(9), 1208–1217 (2010). https://doi.org/10.1016/j.asr.2010.07.001. https://www.sciencedirect.com/science/article/pii/S0273117710004588
ADS Article Google Scholar
J.F. Drake, M. Swisdak, H. Che, M.A. Shay, Electron acceleration from contracting magnetic islands during reconnection. Nature 443(7111), 553–556 (2006)
ADS Google Scholar
L.O. Drury, An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 46(8), 973 (1983)
ADS Google Scholar
F. Effenberger, F. Rubio da Costa, M. Oka, P. Saint-Hilaire, W. Liu, V. Petrosian, L. Glesener, S. Krucker, Hard X-ray emission from partially occulted solar flares: RHESSI observations in two solar cycles. Astrophys. J. 835(2), 124 (2017). https://doi.org/10.3847/1538-4357/835/2/124. 1612.02856
ADS Article Google Scholar
J. Egedal, J. Schroeder, E. Lichko, Parallel velocity mixing yielding enhanced electron heating during magnetic pumping. J. Plasma Phys. 87(2), 905870116 (2021). https://doi.org/10.1017/S0022377821000088. 2102.06300
Article Google Scholar
N. Engelbrecht, F. Effenberger, V. Florinski, M. Potgieter, D. Ruffolo, R. Chhiber, A. Usmanov, J. Rankin, P. Els, Theory of cosmic ray transport in the heliosphere. Space Sci. Rev. 218 (2022)
H.J. Fahr, H. Fichtner, Pick-up ion transport under conservation of particle invariants: how important are velocity diffusion and cooling processes? Astron. Astrophys. 533, A92 (2011). https://doi.org/10.1051/0004-6361/201116880
ADS Article Google Scholar
H.J. Fahr, M. Heyl, Probing the thermodynamic conditions of the heliosheath plasma by shock wave propagation. Astron. Astrophys. 642, A144 (2020). https://doi.org/10.1051/0004-6361/202038453
ADS Article Google Scholar
H.J. Fahr, G. Lay, Remote diagnostic of the heliospheric termination shock using neutralized post shock pick-up ions as messengers. Astron. Astrophys. 356, 327–334 (2000)
ADS Google Scholar
H.J. Fahr, M. Siewert, The multi-fluid pressures downstream of the solar wind termination shock. Astron. Astrophys. 558, A41 (2013). https://doi.org/10.1051/0004-6361/201322262
Article Google Scholar
H.J. Fahr, M. Siewert, Entropy generation at multi-fluid magnetohydrodynamic shocks with emphasis to the solar wind termination shock. Astron. Astrophys. 576, A100 (2015). https://doi.org/10.1051/0004-6361/201424485
Article Google Scholar
H.J. Fahr, D. Verscharen, Electrons under the dominant action of shock-electric fields. Astron. Astrophys. 587, L1 (2016). https://doi.org/10.1051/0004-6361/201527901. 1602.04263
ADS Article Google Scholar
H.J. Fahr, M. Siewert, I. Chashei, Phasespace transport of a quasi-neutral multi-fluid plasma over the solar wind MHD termination shock. Astrophys. Space Sci. 341(2), 265–276 (2012). https://doi.org/10.1007/s10509-012-1126-2
ADS Article MATH Google Scholar
H.J. Fahr, J.D. Richardson, D. Verscharen, The electron distribution function downstream of the solar-wind termination shock: where are the hot electrons? Astron. Astrophys. 579, A18 (2015). https://doi.org/10.1051/0004-6361/201525710. 1505.02676
ADS Article Google Scholar
H.J. Fahr, A. Sylla, H. Fichtner, K. Scherer, On the evolution of the $\kappa $ distribution of protons in the inner heliosheath. J. Geophys. Res. 121, 8203–8214 (2016). https://doi.org/10.1002/2016JA022561
Article Google Scholar
G. Ferrand, R.J. Danos, A. Shalchi, S. Safi-Harb, P. Edmon, P. Mendygral, Cosmic ray acceleration at perpendicular shocks in supernova remnants. Astrophys. J. 792(2), 133 (2014). https://doi.org/10.1088/0004-637x/792/2/133.
ADS Article Google Scholar
H. Fichtner, K. Scherer, M. Lazar, H.J. Fahr, Z. Vörös, Entropy of plasmas described with regularized $\kappa$ distributions. Phys. Rev. E 98(5), 053205 (2018). https://doi.org/10.1103/PhysRevE.98.053205. 1810.12645
ADS Article Google Scholar
L.A. Fisk, G. Gloeckler, The common spectrum for accelerated ions in the quiet-time solar wind. Astrophys. J. Lett. 640, L79–L82 (2006). https://doi.org/10.1086/503293
ADS Article Google Scholar
L.A. Fisk, G. Gloeckler, Particle acceleration in the heliosphere: implications for astrophysics. Space Sci. Rev. 173, 433–458 (2012). https://doi.org/10.1007/s11214-012-9899-8
ADS Article Google Scholar
L.A. Fisk, G. Gloeckler, The case for a common spectrum of particles accelerated in the heliosphere: observations and theory. J. Geophys. Res. 119, 8733–8749 (2014). https://doi.org/10.1002/2014JA020426
Article Google Scholar
L.A. Fisk, G. Gloeckler, The pump acceleration mechanism, J. Phys. Conf. Ser. 900 (2017), 012006. https://doi.org/10.1088/1742-6596/900/1/012006
Article Google Scholar
L.A. Fisk, M.A. Lee, Shock acceleration of energetic particles in corotating interaction regions in the solar wind. Astrophys. J. 237, 620–626 (1980)
ADS Google Scholar
T.K. Gaisser, Cosmic Rays and Particle Physics (Cambridge University Press, Cambridge, 1990)
Google Scholar
S.P. Gary, O. Chang, J. Wang, Forward cascade of whistler turbulence: three-dimensional particle-in-cell simulations. Astrophys. J. 755(2), 142 (2012)
ADS Google Scholar
J. Giacalone, Particle acceleration at shocks moving through an irregular magnetic field. Astrophys. J. 624(2), 765–772 (2005a)
ADS Google Scholar
J. Giacalone, The efficient acceleration of thermal protons by perpendicular shocks. Astrophys. J. 628(1), L37–L40 (2005b)
ADS Google Scholar
J. Giacalone, Energetic charged particles associated with strong interplanetary shocks. Astrophys. J. 761, 28 (2012). https://doi.org/10.1088/0004-637X/761/1/28
ADS Article Google Scholar
J. Giacalone, Cosmic-ray transport and interaction with shocks. Space Sci. Rev. 176(1–4), 73–88 (2013)
ADS Google Scholar
J. Giacalone, The acceleration of charged particles at a spherical shock moving through an irregular magnetic field. Astrophys. J. 848(2), 123 (2017)
ADS Google Scholar
J. Giacalone, J. Jokipii, The transport of cosmic rays across a turbulent magnetic field. Astrophys. J. 520(1), 204 (1999)
ADS Google Scholar
J. Giacalone, J.R. Jokipii, Magnetic field amplification by shocks in turbulent fluids. Astrophys. J. Lett. 663(1), L41–L44 (2007)
ADS Google Scholar
J. Giacalone, M. Neugebauer, The energy spectrum of energetic particles downstream of turbulent collisionless shocks. Astrophys. J. 673(1), 629–636 (2008)
ADS Google Scholar
J. Giacalone, J.F. Drake, J.R. Jokipii, The acceleration mechanism of anomalous cosmic rays. Space Sci. Rev. 173(1–4), 283–307 (2012)
ADS Google Scholar
J. Giacalone, H. Fahr, H. Fichtner, V. Florinksi, B. Heber, M. Hill, J. Kota, R. Leske, M.S. Potgieter, J. Rankin, Anomalous cosmic rays and other heliospheric energetic particles. Space Sci. Rev. 218, (2022)
J.P. Goedbloed, A. Lifschitz, Stationary symmetric magnetohydrodynamic flows. Phys. Plasmas 4(10), 3544–3564 (1997). https://doi.org/10.1063/1.872251
ADS MathSciNet Article Google Scholar
V.V. Grechnev, A.M. Uralov, I.V. Kuzmenko, A.A. Kochanov, I.M. Chertok, S.S. Kalashnikov, Responsibility of a filament eruption for the initiation of a flare, CME, and blast wave, and its possible transformation into a bow shock. Sol. Phys. 290(1), 129–158 (2015)
ADS Google Scholar
A. Greco, P. Chuychai, W.H. Matthaeus, S. Servidio, P. Dmitruk, Intermittent MHD structures and classical discontinuities. Geophys. Res. Lett. 35(19), L19111 (2008)
ADS Google Scholar
A. Greco, S. Servidio, W.H. Matthaeus, P. Dmitruk, Intermittent structures and magnetic discontinuities on small scales in MHD simulations and solar wind. Planet. Space Sci. 58(14–15), 1895–1899 (2010)
ADS Google Scholar
A. Greco, W.H. Matthaeus, S. Perri, K.T. Osman, S. Servidio, M. Wan, P. Dmitruk, Partial variance of increments method in solar wind observations and plasma simulations. Space Sci. Rev. 214(1), 1 (2018)
ADS Google Scholar
E. Grimaldo, A. Reimer, R. Kissmann, F. Niederwanger, K. Reitberger, Proton acceleration in colliding stellar wind binaries. Astrophys. J. 871(1), 55 (2019). https://doi.org/10.3847/1538-4357/aaf6ee. 1812.02960
ADS Article Google Scholar
L. Han-Thanh, K. Scherer, H. Fichtner, Relativistic regularized kappa distributions. Phys. Plasmas 29, 022901 (2022). https://doi.org/10.1063/5.0080293
ADS Article Google Scholar
K. Hasselmann, G. Wibberenz, A note on the parallel diffusion coefficient. Astrophys. J. 162, 1049 (1970). https://doi.org/10.1086/150736
ADS Article Google Scholar
J. Heerikhuisen, E.J. Zirnstein, N.V. Pogorelov, G.P. Zank, M. Desai, The effect of suprathermal protons in the heliosheath on the global structure of the heliosphere and heliotail. Astrophys. J. 874(1), 76 (2019). https://doi.org/10.3847/1538-4357/ab05e3
ADS Article Google Scholar
E.A. Helder, J. Vink, A.M. Bykov, Y. Ohira, J.C. Raymond, R. Terrier, Observational signatures of particle acceleration in supernova remnants. Space Sci. Rev. 173(1–4), 369–431 (2012). https://doi.org/10.1007/s11214-012-9919-8. 1206.1593
ADS Article Google Scholar
M. Hoshino, Stochastic particle acceleration in multiple magnetic islands during reconnection. Phys. Rev. Lett. 108(13), 135003 (2012)
ADS Google Scholar
E. Husidic, M. Lazar, H. Fichtner, K. Scherer, P. Astfalk, Linear dispersion theory of parallel electromagnetic modes for regularized Kappa-distributions. Phys. Plasmas 27(4), 042110 (2020). https://doi.org/10.1063/1.5145181. 2006.03308
ADS Article Google Scholar
M. Hussein, A. Shalchi, Simulations of energetic particles interacting with dynamical magnetic turbulence. Astrophys. J. 817(2), 136 (2016)
ADS Google Scholar
J.R. Jokipii, Cosmic-ray propagation. I. Charged particles in a random magnetic field. Astrophys. J. 146, 480 (1966)
ADS Google Scholar
J.R. Jokipii, Rate of energy gain and maximum energy in diffusive shock acceleration. Astrophys. J. 313, 842 (1987)
ADS Google Scholar
F.C. Jones, D.C. Ellison, The plasma physics of shock acceleration. Space Sci. Rev. 58, 259–346 (1991)
ADS Google Scholar
P. Kajdič, L. Preisser, X. Blanco-Cano, D. Burgess, D. Trotta, First observations of irregular surface of interplanetary shocks at ion scales by cluster. Astrophys. J. Lett. 874(2), L13 (2019)
ADS Google Scholar
H. Kang, D. Ryu, T.W. Jones, Diffusive shock acceleration simulations of radio relics. Astrophys. J. 756, 97 (2012). https://doi.org/10.1088/0004-637X/756/1/97. 1205.1895
ADS Article Google Scholar
H. Karimabadi, V. Roytershteyn, M. Wan, W.H. Matthaeus, W. Daughton, P. Wu, M. Shay, B. Loring, J. Borovsky, E. Leonardis, S.C. Chapman, T.K.M. Nakamura, Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Phys. Plasmas 20(1), 012303 (2013)
ADS Google Scholar
C.F. Kennel, H. Petschek, Limit on stably trapped particle fluxes. J. Geophys. Res. 71(1), 1–28 (1966)
ADS Google Scholar
C.F. Kennel, F.V. Coroniti, F.L. Scarf, W.A. Livesey, C.T. Russell, E.J. Smith, K.P. Wenzel, M. Scholer, A test of Lee’s quasi-linear theory of ion acceleration by interplanetary traveling shocks. J. Geophys. Res. 191(A11), 11,917–11,928 (1986). https://doi.org/10.1029/JA091iA11p11917
ADS Article Google Scholar
J.G. Kirk, P. Duffy, Y.A. Gallant, Stochastic particle acceleration at shocks in the presence of braided magnetic fields. Astron. Astrophys. 314, 1010–1016 (1996). astro-ph/9604056
ADS Google Scholar
J. Klafter, A. Blumen, M.F. Shlesinger, Stochastic pathway to anomalous diffusion. Phys. Rev. A 35, 3081–3085 (1987). https://doi.org/10.1103/PhysRevA.35.3081
ADS MathSciNet Article Google Scholar
J.A. Kropotina, L. Webster, A.V. Artemyev, A.M. Bykov, D.L. Vainchtein, I.Y. Vasko, Solar wind discontinuity transformation at the bow shock. Astrophys. J. 913(2), 142 (2021). https://doi.org/10.3847/1538-4357/abf6c7. 2106.06414
ADS Article Google Scholar
G.F. Krymskii, A regular mechanism for the acceleration of charged particles on the front of a shock wave. Akad. Nauk SSSR Dokl. 234, 1306–1308 (1977)
ADS Google Scholar
D. Lario, L. Berger, I.L.B. Wilson, R.B. Decker, D.K. Haggerty, E.C. Roelof, R.F. Wimmer-Schweingruber, J. Giacalone, Flat proton spectra in large solar energetic particle events, J. Phys. Conf. Ser. 1100 (2018), 012014. https://doi.org/10.1088/1742-6596/1100/1/012014
Article Google Scholar
M. Lazar, Towards realistic characterization of the solar wind suprathermal populations and their effects. Phys. Plasmas 24(3), 034501 (2017). https://doi.org/10.1063/1.4977899
ADS Article Google Scholar
M. Lazar, H. Fichtner (eds.), Kappa Distributions: From Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas (Springer, Berlin, 2021)
Google Scholar
M. Lazar, S. Poedts, H. Fichtner, Destabilizing effects of the suprathermal populations in the solar wind. A & A 582, A124 (2015). https://doi.org/10.1051/0004-6361/201526509
ADS Article Google Scholar
M. Lazar, H. Fichtner, P.H. Yoon, On the interpretation and applicability of $\kappa$-distributions. A & A 589, A39 (2016). https://doi.org/10.1051/0004-6361/201527593. 1602.04132
ADS Article Google Scholar
M. Lazar, V. Pierrard, S.M. Shaaban, H. Fichtner, S. Poedts, Dual Maxwellian-Kappa modeling of the solar wind electrons: new clues on the temperature of Kappa populations. A & A 602, A44 (2017). https://doi.org/10.1051/0004-6361/201630194. 1703.01459
ADS Article Google Scholar
A. Lazarian, H. Yan, Superdiffusion of cosmic rays: implications for cosmic ray acceleration. Astrophys. J. 784(1), 38 (2014)
ADS Google Scholar
J.A. le Roux, G.P. Zank, A focused transport-based kinetic fractional diffusion-advection equation for energetic particle trapping and reconnection-related acceleration by small-scale magnetic flux ropes in the solar wind. Astrophys. J. 913(2), 84 (2021). https://doi.org/10.3847/1538-4357/abf3c6
ADS Article Google Scholar
J.A. le Roux, G.P. Zank, G.M. Webb, O. Khabarova, A kinetic transport theory for particle acceleration and transport in regions of multiple contracting and reconnecting inertial-scale flux ropes. Astrophys. J. 801(2), 112 (2015)
ADS Google Scholar
M.A. Lee, Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J. Geophys. Res. 188(A8), 6109–6120 (1983). https://doi.org/10.1029/JA088iA08p06109
ADS Article Google Scholar
M.A. Lee, Coupled hydromagnetic wave excitation and ion acceleration at an evolving coronal/interplanetary shock. Astrophys. J. Suppl. Ser. 158(1), 38–67 (2005). https://doi.org/10.1086/428753
ADS Article Google Scholar
M.A. Lee, L.A. Fisk, Shock acceleration of energetic particles in the heliosphere. Space Sci. Rev. 32, 205–228 (1982). https://doi.org/10.1007/BF00225185
ADS Article Google Scholar
M.A. Lee, R.A. Mewaldt, J. Giacalone, Shock acceleration of ions in the heliosphere. Space Sci. Rev. 173(1–4), 247–281 (2012)
ADS Google Scholar
B. Lembège, P. Savoini, M. Balikhin, S. Walker, V. Krasnoselskikh, Demagnetization of transmitted electrons through a quasi-perpendicular collisionless shock. J. Geophys. Res. 108(A6), 1256 (2003). https://doi.org/10.1029/2002JA009288
Article Google Scholar
B. Lembège, J. Giacalone, M. Scholer, T. Hada, M. Hoshino, V. Krasnoselskikh, H. Kucharek, P. Savoini, T. Terasawa, Selected problems in collisionless-shock physics. Space Sci. Rev. 110(3), 161–226 (2004). https://doi.org/10.1023/B:SPAC.0000023372.12232.b7
ADS Article Google Scholar
M. Lemoine, Particle acceleration in strong MHD turbulence, arXiv e-prints (2021). arXiv:2104.08199
M.M. Leroy, A. Mangeney, A theory of energization of solar wind electrons by the Earth’s bow shock. Ann. Geophys. 2, 449–456 (1984)
ADS Google Scholar
E. Lichko, J. Egedal, Magnetic pumping model for energizing superthermal particles applied to observations of the Earth’s bow shock. Nat. Commun. 11, 2942 (2020). https://doi.org/10.1038/s41467-020-16660-4
ADS Article Google Scholar
R. Lin, Non-relativistic solar electrons. Space Sci. Rev. 16(1–2), 189–256 (1974)
ADS Google Scholar
R.P. Lin, Relationship of solar flare accelerated particles to solar energetic particles (SEPs) observed in the interplanetary medium. Adv. Space Res. 35(10), 1857–1863 (2005). https://doi.org/10.1016/j.asr.2005.02.087
ADS Article Google Scholar
Y.E. Litvinenko, H. Fichtner, D. Walter, Anomalous transport of cosmic rays in a nonlinear diffusion model. Astrophys. J. 841, 57 (2017). https://doi.org/10.3847/1538-4357/aa71ba
ADS Article Google Scholar
Y.E. Litvinenko, D. Walter, H. Fichtner, A nonlinear energetic particle diffusion model with a variable source. AIP Adv. 9(5), 055,005 (2019). https://doi.org/10.1063/1.5090953
Article Google Scholar
S. Liu, J.R. Jokipii, Acceleration of charged particles in astrophysical plasmas. Front. Astron. Space Sci. 8, 100 (2021). https://doi.org/10.3389/fspas.2021.651830
ADS Article Google Scholar
G. Livadiotis, Introduction to special section on origins and properties of kappa distributions: statistical background and properties of kappa distributions in space plasmas. J. Geophys. Res. Space Phys. 120, 1607–1619 (2015). https://doi.org/10.1002/2014JA020825
ADS Article Google Scholar
M.A. Malkov, L. Drury, Nonlinear theory of diffusive acceleration of particles by shock waves. Rep. Prog. Phys. 64, 429–481 (2001)
ADS Google Scholar
A. Marcowith, A. Bret, A. Bykov, M.E. Dieckman, L. O’C Drury, B. Lembège, M. Lemoine, G. Morlino, G. Murphy, G. Pelletier, I. Plotnikov, B. Reville, M. Riquelme, L. Sironi, A. Stockem Novo, The microphysics of collisionless shock waves. Rep. Prog. Phys. 79(4), 046901 (2016). https://doi.org/10.1088/0034-4885/79/4/046901. 1604.00318
ADS Article Google Scholar
S. Matsukiyo, M. Scholer, Modified two-stream instability in the foot of high Mach number quasi-perpendicular shocks. J. Geophys. Res. 108(A12), 1459 (2003). https://doi.org/10.1029/2003JA010080
Article Google Scholar
H. Matsumoto, Theoretical studies on Whistler mode wave-particle interactions in the magnetospheric plasma. PhD thesis, Kyoto University, Japan (1972)
W. Matthaeus, G. Qin, J. Bieber, G. Zank, Nonlinear collisionless perpendicular diffusion of charged particles. Astrophys. J. Lett. 590(1), L53 (2003)
ADS Google Scholar
R. Metzler, J. Klafter, The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1–77 (2000). https://doi.org/10.1016/S0370-1573(00)00070-3
ADS MathSciNet Article MATH Google Scholar
R. Metzler, J. Klafter, Topical review: the restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A, Math. Gen. 37, R161–R208 (2004). https://doi.org/10.1088/0305-4470/37/31/R01
ADS Article MATH Google Scholar
R.A. Mewaldt, New views of solar energetic particles from the Advanced Composition Explorer, in 26th International Cosmic Ray Conference, ICRC XXVI, ed. by B.L. Dingus, D.B. Kieda, M.H. Salamon. American Institute of Physics Conference Series, vol. 516 (2000), pp. 265–273
Google Scholar
M. Nauenberg, Critique of q-entropy for thermal statistics. Phys. Rev. E 67(3), 036114 (2003). https://doi.org/10.1103/PhysRevE.67.036114. cond-mat/0210561
ADS Article Google Scholar
M. Neugebauer, J. Giacalone, Multispacecraft observations of interplanetary shocks: nonplanarity and energetic particles. J. Geophys. Res. Space Phys. 110(A12), A12106 (2005)
ADS Google Scholar
C.K. Ng, D.V. Reames, A.J. Tylka, Modeling shock-accelerated solar energetic particles coupled to interplanetary Alfvén waves. Astrophys. J. 591(1), 461–485 (2003). https://doi.org/10.1086/375293
ADS Article Google Scholar
M. Oka, S. Ishikawa, P. Saint-Hilaire, S. Krucker, R.P. Lin, Kappa distribution model for hard X-ray coronal sources of solar flares. Astrophys. J. 764(1), 6 (2013). https://doi.org/10.1088/0004-637X/764/1/6. 1212.2579
ADS Article Google Scholar
S. Olbert, Summary of experimental results from M.I.T. detector on IMP-1, in Physics of the Magnetosphere. Astrophysics and Space Science Library, vol. 10, ed. by R.D.L. Carovillano, J.F. McClay (1968), p. 641
Google Scholar
I. Palmer, Transport coefficients of low-energy cosmic rays in interplanetary space. Rev. Geophys. 20(2), 335–351 (1982)
ADS Google Scholar
S. Perri, Superdiffusion of relativistic electrons at supernova remnant shocks. Plasma Phys. Control. Fusion 60(1), 014005 (2018). https://doi.org/10.1088/1361-6587/aa8602
ADS Article Google Scholar
S. Perri, G. Zimbardo, Evidence of superdiffusive transport of electrons accelerated at interplanetary shocks. Astrophys. J. Lett. 671(2), L177–L180 (2007)
ADS Google Scholar
S. Perri, G. Zimbardo, Superdiffusive transport of electrons accelerated at corotating interaction regions. J. Geophys. Res. Space Phys. 113, A03107 (2008). https://doi.org/10.1029/2007JA012695
ADS Article Google Scholar
S. Perri, G. Zimbardo, Ion superdiffusion at the solar wind termination shock. Astrophys. J. Lett. 693(2), L118–L121 (2009)
ADS Google Scholar
S. Perri, G. Zimbardo, Superdiffusive shock acceleration. Astrophys. J. 750(2), 87 (2012a)
ADS Google Scholar
S. Perri, G. Zimbardo, Magnetic variances and pitch-angle scattering times upstream of interplanetary shocks. Astrophys. J. 754(1), 8 (2012b)
ADS Google Scholar
S. Perri, G. Zimbardo, Evidence for superdiffusive shock acceleration at interplanetary shock waves, J. Phys. Conf. Ser. 642 012020 (2015a). https://doi.org/10.1088/1742-6596/642/1/012020
Article Google Scholar
S. Perri, G. Zimbardo, Short acceleration times from superdiffusive shock acceleration in the heliosphere. Astrophys. J. 815(1), 75 (2015b)
ADS Google Scholar
S. Perri, E. Yordanova, V. Carbone, P. Veltri, L. Sorriso-Valvo, R. Bruno, M. André, Magnetic turbulence in space plasmas: scale-dependent effects of anisotropy. J. Geophys. Res. Space Phys. 114(A2), A02102 (2009)
ADS Google Scholar
S. Perri, G. Zimbardo, F. Effenberger, H. Fichtner, Parameter estimation of superdiffusive motion of energetic particles upstream of heliospheric shocks. A & A 578, A2 (2015). https://doi.org/10.1051/0004-6361/201425295. 1505.07980
ADS Article Google Scholar
S. Perri, E. Amato, G. Zimbardo, Transport of relativistic electrons at shocks in shell-type supernova remnants: diffusive and superdiffusive regimes. Astron. Astrophys. 596, A34 (2016). https://doi.org/10.1051/0004-6361/201628767
ADS Article Google Scholar
S. Perri, F. Pucci, F. Malara, G. Zimbardo, On the power-law distribution of pitch-angle scattering times in solar wind turbulence. Sol. Phys. 294(3), 34 (2019)
ADS Google Scholar
S. Perri, G. Prete, F. Malara, F. Pucci, G. Zimbardo, The influence of magnetic turbulence on the energetic particle transport upstream of shock waves. Atmosphere 12(4), 508 (2021)
ADS Google Scholar
D. Perrone, R.O. Dendy, I. Furno, R. Sanchez, G. Zimbardo, A. Bovet, A. Fasoli, K. Gustafson, S. Perri, P. Ricci, F. Valentini, Nonclassical transport and particle-field coupling: from laboratory plasmas to the solar wind. Space Sci. Rev. 178(2–4), 233–270 (2013)
ADS Google Scholar
V. Petrosian, Particle acceleration in solar flares and associated CME shocks. Astrophys. J. 830(1), 28 (2016). https://doi.org/10.3847/0004-637X/830/1/28. 1605.04022
ADS Article Google Scholar
V. Petrosian, A.M. Bykov, Particle acceleration mechanisms. Space Sci. Rev. 134(1–4), 207–227 (2008). https://doi.org/10.1007/s11214-008-9315-6. 0801.0923
ADS Article Google Scholar
J.M. Pittard, G.E. Romero, G.S. Vila, Particle acceleration and non-thermal emission in colliding-wind binary systems. Mon. Not. R. Astron. Soc. 504(3), 4204–4225 (2021). https://doi.org/10.1093/mnras/stab1107. 2104.07399
ADS Article Google Scholar
P. Pommois, G. Zimbardo, P. Veltri, Anomalous, non-Gaussian transport of charged particles in anisotropic magnetic turbulence. Phys. Plasmas 14(1), 012311 (2007). https://doi.org/10.1063/1.2434795
ADS Article Google Scholar
M.H. Pope, D.B. Melrose, Diffusive shock acceleration by multiple shock fronts with differing properties. Publ. Astron. Soc. Aust. 11(2), 175–179 (1994)
ADS Google Scholar
M.S. Potgieter, The modulation of galactic cosmic rays in the heliosphere: theory and models. Space Sci. Rev. 83, 147–158 (1998)
ADS Google Scholar
P.L. Prinsloo, R.D. Strauss, J.A. le Roux, Acceleration of solar wind particles by traveling interplanetary shocks. Astrophys. J. 878(2), 144 (2019). https://doi.org/10.3847/1538-4357/ab211b. 1905.08458
ADS Article Google Scholar
V. Ptuskin, V. Zirakashvili, E.S. Seo, Spectra of cosmic-ray protons and helium produced in supernova remnants. Astrophys. J. 763(1), 47 (2013). https://doi.org/10.1088/0004-637X/763/1/47. 1212.0381
ADS Article Google Scholar
F. Pucci, F. Malara, S. Perri, G. Zimbardo, L. Sorriso-Valvo, F. Valentini, Energetic particle transport in the presence of magnetic turbulence: influence of spectral extension and intermittency. Mon. Not. R. Astron. Soc. 459, 3395–3406 (2016). https://doi.org/10.1093/mnras/stw877
ADS Article Google Scholar
B.R. Ragot, J.G. Kirk, Anomalous transport of cosmic ray electrons. Astron. Astrophys. 327, 432–440 (1997). astro-ph/9708041
ADS Google Scholar
S.P. Reynolds, B.M. Gaensler, F. Bocchino, Magnetic fields in supernova remnants and pulsar-wind nebulae. Space Sci. Rev. 166, 231–261 (2012). https://doi.org/10.1007/s11214-011-9775-y. 1104.4047
ADS Article Google Scholar
J.D. Richardson, J.C. Kasper, C. Wang, J.W. Belcher, A.J. Lazarus, Cool heliosheath plasma and deceleration of the upstream solar wind at the termination shock. Nature 454(7200), 63–66 (2008). https://doi.org/10.1038/nature07024
ADS Article Google Scholar
J.D. Riordan, A. Pe’er, Pitch-angle diffusion and Bohm-type approximations in diffusive shock acceleration. Astrophys. J. 873(1), 13 (2019). https://doi.org/10.3847/1538-4357/aaffd2. 1810.11817
ADS Article Google Scholar
D. Ruffolo, Effect of adiabatic deceleration on the focused transport of solar cosmic rays. Astrophys. J. 442, 861 (1995)
ADS Google Scholar
K. Scherer, H. Fichtner, M. Lazar, Regularized $\kappa $-distributions with non-diverging moments. Europhys. Lett. 120(50), 002 (2017). https://doi.org/10.1209/0295-5075/120/50002
Article Google Scholar
K. Scherer, M. Lazar, E. Husidic, H. Fichtner, Moments of the anisotropic regularized $\kappa$-distributions. Astrophys. J. 880(2), 118 (2019). https://doi.org/10.3847/1538-4357/ab1ea1. 1906.01406
ADS Article Google Scholar
K.M. Schure, A.R. Bell, L. O’C Drury, A.M. Bykov, Diffusive shock acceleration and magnetic field amplification. Space Sci. Rev. 173(1–4), 491–519 (2012). https://doi.org/10.1007/s11214-012-9871-7. 1203.1637
ADS Article Google Scholar
S.J. Schwartz, M.F. Thomsen, S.J. Bame, J. Stansberry, Electron heating and the potential jump across fast mode shocks. J. Geophys. Res. 93, 12,923–12,931 (1988). https://doi.org/10.1029/JA093iA11p12923
ADS Article Google Scholar
A. Shalchi, Applicability of the Taylor-Green-Kubo formula in particle diffusion theory. Phys. Rev. E 83(4), 046402 (2011). https://doi.org/10.1103/PhysRevE.83.046402
ADS Article Google Scholar
A. Shalchi, I. Kourakis, A new theory for perpendicular transport of cosmic rays. Astron. Astrophys. 470(2), 405–409 (2007)
ADS MATH Google Scholar
A. Shalchi, G.M. Webb, J.A. le Roux, Parallel transport of cosmic rays for non-diffusive pitch-angle scattering: I. Using the standard Fokker-Planck equation. Phys. Scr. 85(6), 065901 (2012)
ADS MATH Google Scholar
N. Sioulas, H. Isliker, L. Vlahos, A. Koumtzis, T. Pisokas, Superdiffusive stochastic Fermi acceleration in space and energy. Mon. Not. R. Astron. Soc. 491(3), 3860–3869 (2020)
ADS Google Scholar
L. Sironi, U. Keshet, M. Lemoine, Relativistic shocks: particle acceleration and magnetization. Space Sci. Rev. 191(1–4), 519–544 (2015). https://doi.org/10.1007/s11214-015-0181-8. 1506.02034
ADS Article Google Scholar
I.M. Sokolov, J. Klafter, From diffusion to anomalous diffusion: a century after Einstein’s Brownian motion. Chaos 15(2), 026103 (2005)
ADS MathSciNet MATH Google Scholar
B.U.Ö. Sonnerup, J.L.J. Cahill, Explorer 12 observations of the magnetopause current layer. J. Geophys. Res. 73(5), 1757 (1968)
ADS Google Scholar
C.D. Steenberg, H. Moraal, Form of the anomalous cosmic ray spectrum at the solar wind termination shock. J. Geophys. Res. 104(24), 24,879–24,884 (1999). https://doi.org/10.1029/1999JA900336.
ADS Article Google Scholar
R. Stern, F. Effenberger, H. Fichtner, T. Schäfer, The space-fractional diffusion-advection equation: analytical solutions and critical assessment of numerical solutions. Fract. Calc. Appl. Anal. 17(1), 171–190 (2014)
MathSciNet MATH Google Scholar
T. Sugiyama, D. Shiota, Sign for super-diffusive transport of energetic ions associated with a coronal-mass-ejection-driven interplanetary shock. Astrophys. J. Lett. 731, L34 (2011). https://doi.org/10.1088/2041-8205/731/2/L34
ADS Article Google Scholar
J.A. Tessein, W.H. Matthaeus, M. Wan, K.T. Osman, D. Ruffolo, J. Giacalone, Association of suprathermal particles with coherent structures and shocks. Astrophys. J. Lett. 776(1), L8 (2013)
ADS Google Scholar
J.A. Tessein, D. Ruffolo, W.H. Matthaeus, M. Wan, J. Giacalone, M. Neugebauer, Effect of coherent structures on energetic particle intensity in the solar wind at 1 AU. Astrophys. J. 812(1), 68 (2015). https://doi.org/10.1088/0004-637X/812/1/68
ADS Article Google Scholar
R.L. Tokar, C.H. Aldrich, D.W. Forslund, K.B. Quest, Nonadiabatic electron heating at high-Mach-number perpendicular shocks. Phys. Rev. Lett. 56, 1059–1062 (1986). https://doi.org/10.1103/PhysRevLett.56.1059
ADS Article Google Scholar
R.A. Treumann, W. Baumjohann, The differential cosmic ray energy flux in the light of an ultrarelativistic generalized Lorentzian thermodynamics. Astrophys. Space Sci. 363(2), 37 (2018). https://doi.org/10.1007/s10509-018-3255-8
ADS Article Google Scholar
D. Trotta, D. Burgess, G. Prete, S. Perri, G. Zimbardo, Particle transport in hybrid PIC shock simulations: a comparison of diagnostics. Mon. Not. R. Astron. Soc. 491, 580–595 (2020). https://doi.org/10.1093/mnras/stz2760
ADS Article Google Scholar
D. Trotta, F. Valentini, D. Burgess, S. Servidio, Phase space transport in the interaction between shocks and plasma turbulence. Proc. Natl. Acad. Sci. 118(21), 2026764118 (2021)
MathSciNet Google Scholar
C. Tsallis, Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 52, 479–487 (1988). https://doi.org/10.1007/BF01016429
ADS MathSciNet Article MATH Google Scholar
C. Tsallis, D.J. Bukman, Anomalous diffusion in the presence of external forces: exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 54, R2197–R2200 (1996). https://doi.org/10.1103/PhysRevE.54.R2197. cond-mat/9511007
ADS Article Google Scholar
D.L. Turner, L.B. Wilson, T.Z. Liu, I.J. Cohen, S.J. Schwartz, A. Osmane, J.F. Fennell, J.H. Clemmons, J.B. Blake, J. Westlake, B.H. Mauk, A.N. Jaynes, T. Leonard, D.N. Baker, R.J. Strangeway, C.T. Russell, D.J. Gershman, L. Avanov, B.L. Giles, R.B. Torbert, J. Broll, R.G. Gomez, S.A. Fuselier, J.L. Burch, Autogenous and efficient acceleration of energetic ions upstream of Earth’s bow shock. Nature 561(7722), 206–210 (2018). https://doi.org/10.1038/s41586-018-0472-9
ADS Article Google Scholar
R.J. Van Weeren, G. Brunetti, M. Brüggen, F. Andrade-Santos, G.A. Ogrean, W.L. Williams, H.J.A. Röttgering, W.A. Dawson, W.R. Forman, F. de Gasperin, M.J. Hardcastle, C. Jones, G.K. Miley, D.A. Rafferty, L. Rudnick, J. Sabater, C.L. Sarazin, T.W. Shimwell, A. Bonafede, P.N. Best, L. Bîrzan, R. Cassano, K.T. Chyży, J.H. Croston, T.J. Dijkema, T. Enßlin, C. Ferrari, G. Heald, M. Hoeft, C. Horellou, M.J. Jarvis, R.P. Kraft, M. Mevius, H.T. Intema, S.S. Murray, E. Orrú, R. Pizzo, S.S. Sridhar, A. Simionescu, A. Stroe, S. van der Tol, G.J. White, LOFAR, VLA, and Chandra observations of the Toothbrush Galaxy cluster. Astrophys. J. 818, 204 (2016). https://doi.org/10.3847/0004-637X/818/2/204. 1601.06029
ADS Article Google Scholar
I.Y. Vasko, O.V. Agapitov, F.S. Mozer, J.W. Bonnell, A.V. Artemyev, V.V. Krasnoselskikh, Y. Tong, Electrostatic steepening of whistler waves. Phys. Rev. Lett. 120(19), 195101 (2018). https://doi.org/10.1103/PhysRevLett.120.195101
ADS Article Google Scholar
V.M. Vasyliunas, A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 173, 2839–2884 (1968). https://doi.org/10.1029/JA073i009p02839
ADS Article Google Scholar
T. Vieu, S. Gabici, V. Tatischeff, Particle acceleration at colliding shock waves. Mon. Not. R. Astron. Soc. 494(3), 3166–3176 (2020). https://doi.org/10.1093/mnras/staa799. 2003.03411
ADS Article Google Scholar
L. Vlahos, H. Isliker, F. Lepreti, Particle acceleration in an evolving network of unstable current sheets. Astrophys. J. 608(1), 540–553 (2004)
ADS Google Scholar
L. Vlahos, T. Pisokas, H. Isliker, V. Tsiolis, A. Anastasiadis, Particle acceleration and heating by turbulent reconnection. Astrophys. J. Lett. 827(1), L3 (2016)
ADS Google Scholar
A. Vourlidas, S.T. Wu, A.H. Wang, P. Subramanian, R.A. Howard, Direct detection of a coronal mass ejection-associated shock in large angle and spectrometric coronagraph experiment white-light images. Astrophys. J. 598(2), 1392–1402 (2003)
ADS Google Scholar
D. Walter, H. Fichtner, Y. Litvinenko, A perturbative approach to a nonlinear advection-diffusion equation of particle transport. Phys. Plasmas 27(8), 082901 (2020). https://doi.org/10.1063/5.0003582
ADS Article Google Scholar
X. Wang, J. Giacalone, Y. Yan, M. Ding, C. Li, H. Lu, H. Shan, Particle acceleration at the pileup collision of the twin shock. Astrophys. J. 885(1), 66 (2019). https://doi.org/10.3847/1538-4357/ab4655
ADS Article Google Scholar
G. Webb, G. Zank, E.K. Kaghashvili, J. Le Roux, Compound and perpendicular diffusion of cosmic rays and random walk of the field lines. I. Parallel particle transport models. Astrophys. J. 651(1), 211 (2006)
ADS Google Scholar
R.L. White, W. Chen, Particle acceleration, X-rays, and gamma-rays from winds. Astrophys. Space Sci. 221(1–2), 295–307 (1994). https://doi.org/10.1007/BF01091161
ADS Article Google Scholar
W.J. Wykes, S.C. Chapman, G. Rowlands, Stochastic pitch angle diffusion due to electron-whistler wave-particle interactions. Phys. Plasmas 8(6), 2953–2962 (2001). https://doi.org/10.1063/1.1371953
ADS Article Google Scholar
P.H. Yoon, M. Lazar, K. Scherer, H. Fichtner, R. Schlickeiser, Modified $\kappa$-distribution of solar wind electrons and steady-state Langmuir turbulence. Astrophys. J. 868(2), 131 (2018). https://doi.org/10.3847/1538-4357/aaeb94
ADS Article Google Scholar
G.P. Zank, Y. Zhou, W.H. Matthaeus, W.K.M. Rice, The interaction of turbulence with shock waves: a basic model. Phys. Fluids 14(11), 3766–3774 (2002)
ADS MathSciNet MATH Google Scholar
G.P. Zank, J. Heerikhuisen, N.V. Pogorelov, R. Burrows, D. McComas, Microstructure of the heliospheric termination shock: implications for energetic neutral atom observations. Astrophys. J. 708(2), 1092–1106 (2010). https://doi.org/10.1088/0004-637X/708/2/1092
ADS Article Google Scholar
G.P. Zank, J.A. le Roux, G.M. Webb, A. Dosch, O. Khabarova, Particle acceleration via reconnection processes in the supersonic solar wind. Astrophys. J. 797(1), 28 (2014)
ADS Google Scholar
G.P. Zank, P. Hunana, P. Mostafavi, J.A. le Roux, G. Li, G.M. Webb, O. Khabarova, Particle acceleration by combined diffusive shock acceleration and downstream multiple magnetic island acceleration, J. Phys. Conf. Ser. 642, 012031 (2015a)
Google Scholar
G.P. Zank, P. Hunana, P. Mostafavi, J.A. Le Roux, G. Li, G.M. Webb, O. Khabarova, A. Cummings, E. Stone, R. Decker, Diffusive shock acceleration and reconnection acceleration processes. Astrophys. J. 814(2), 137 (2015b)
ADS Google Scholar
B. Zieger, M. Opher, G. Tóth, R.B. Decker, J.D. Richardson, Constraining the pickup ion abundance and temperature through the multifluid reconstruction of the Voyager 2 termination shock crossing. J. Geophys. Res. 120(9), 7130–7153 (2015). https://doi.org/10.1002/2015JA021437
Article Google Scholar
G. Zimbardo, S. Perri, Superdiffusive transport upstream of the solar wind termination shock, in Twelfth International Solar Wind Conference, ed. by M. Maksimovic, K. Issautier, N. Meyer-Vernet, M. Moncuquet, F. Pantellini. American Institute of Physics Conference Series, vol. 1216 (2010), pp. 584–587. https://doi.org/10.1063/1.3395933
Chapter Google Scholar
G. Zimbardo, S. Perri, From Lévy walks to superdiffusive shock acceleration. Astrophys. J. 778(1), 35 (2013)
ADS Google Scholar
G. Zimbardo, S. Perri, Non-Markovian pitch-angle scattering as the origin of particle superdiffusion parallel to the magnetic field. Astrophys. J. 903(2), 105 (2020). https://doi.org/10.3847/1538-4357/abb951
ADS Article Google Scholar
G. Zimbardo, P. Pommois, P. Veltri, Superdiffusive and subdiffusive transport of energetic particles in solar wind anisotropic magnetic turbulence. Astrophys. J. Lett. 639(2), L91 (2006)
ADS Google Scholar
G. Zimbardo, S. Perri, P. Pommois, P. Veltri, Anomalous particle transport in the heliosphere. Adv. Space Res. 49(11), 1633–1642 (2012)
ADS Google Scholar
G. Zimbardo, E. Amato, A. Bovet, F. Effenberger, A. Fasoli, H. Fichtner, I. Furno, K. Gustafson, P. Ricci, S. Perri, Superdiffusive transport in laboratory and astrophysical plasmas. J. Plasma Phys. 81(6), 495810601 (2015). https://doi.org/10.1017/S0022377815001117
Article Google Scholar
G. Zimbardo, S. Perri, F. Effenberger, H. Fichtner, Fractional Parker equation for the transport of cosmic rays: steady-state solutions. A & A 607, A7 (2017). https://doi.org/10.1051/0004-6361/201731179
ADS Article Google Scholar
G. Zumofen, J. Klafter, Scale-invariant motion in intermittent chaotic systems. Phys. Rev. E 47, 851–863 (1993). https://doi.org/10.1103/PhysRevE.47.851
ADS Article MATH Google Scholar

Download references

Acknowledgements

A.M.B. was supported by the RSF grant 21-72-20020. Some of the modeling was performed at the JSCC RAS and the “Tornado” subsystem of the St. Petersburg Polytechnic University supercomputing center. The work of Horst Fichtner was supported via the DFG grant FI 706/26-1. S.P. acknowledges discussions with G. Zimbardo.

Author information

Authors and Affiliations

Department of Physics, Universitá della Calabria, Rende, Italy
Silvia Perri
Ioffe Institute, St. Petersburg, 194223, Russia
Andrei Bykov
Argelander-Institute of Astronomy, University of Bonn, Bonn, Germany
Hans Fahr
Institut für Theoretische Physik, Ruhr-Universität, Bochum, Germany
Horst Fichtner
Lunar and Planetary Laboratory, University of Arizona, Tucson, USA
Joe Giacalone

Authors

Silvia Perri
View author publications
You can also search for this author in PubMed Google Scholar
Andrei Bykov
View author publications
You can also search for this author in PubMed Google Scholar
Hans Fahr
View author publications
You can also search for this author in PubMed Google Scholar
Horst Fichtner
View author publications
You can also search for this author in PubMed Google Scholar
Joe Giacalone
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Silvia Perri.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The Heliosphere in the Local Interstellar Medium: Into the Unknown

Edited by John D. Richardson, Andrei Bykov, Frederic Effenberger, Klaus Scherer, Veerle Sterken, Rudolf von Steiger and Gary P. Zank

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and Permissions

About this article

Cite this article

Perri, S., Bykov, A., Fahr, H. et al. Recent Developments in Particle Acceleration at Shocks: Theory and Observations. Space Sci Rev 218, 26 (2022). https://doi.org/10.1007/s11214-022-00892-5

Download citation

Received: 12 January 2022
Accepted: 15 April 2022
Published: 05 May 2022
DOI: https://doi.org/10.1007/s11214-022-00892-5

Keywords

Energetic particles
Space plasmas
Shock acceleration
Turbulence