Comparative Na and K Mercury and Moon Exospheres

Abstract

Sodium and, in a lesser way, potassium atomic components of surface-bounded exospheres are among the brightest elements that can be observed from the Earth in our Solar System. Both species have been intensively observed around Mercury, the Moon and the Galilean Moons. During the last decade, new observations have been obtained thanks to space missions carrying remote and in situ instrumentation that provide a completely original view of these species in the exospheres of Mercury and the Moon. They challenged our understanding and modelling of these exospheres and opened new directions of research by suggesting the need to better take into account the relationship between the surface-exosphere and the magnetosphere. In this paper, we first review the large set of observations of Mercury and the Moon Sodium and Potassium exospheres. In the second part, we list what it tells us on the sources and sinks of these exospheres focusing in particular on the role of their magnetospheres of these objects and then discuss, in a third section, how these observations help us to understand and identify the key drivers of these exospheres.

1 Observations

1.1 Seasonal/Diurnal Variation of the Lunar Exosphere

Sodium and potassium are the only two species within the lunar exosphere that can be readily measured remotely from the Earth. Na and K within the lunar exosphere produce visible wavelength emissions that are optically thin. Solar irradiance is invariant at the wavelengths of their bright D line transitions, so it is straightforward to determine the column density using the incident solar flux and the observation geometry. Scattered moonlight is so intense, however, that the weak exosphere signal can only be distinguished in off-disk measurements that sample the tangent column. The atmospheric scale height and tangent column together yields an estimate for the zenith column, being about $8\times 10^{8}$ atoms/cm² for Na at the subsolar point (Potter and Morgan 1988a,b). Based on two years of coronagraphic observations, Killen et al. (2021) obtained equatorial column abundances between $2\times 10^{8}$ and $2\times 10^{10}$ atoms/cm², strongly dependent on local time of day and position inside or outside of Earth’s magnetosphere. Ground-based measurements have estimated Na/K ratios from 4.4 to 5.7 (Potter and Morgan 1988a, 1988b; Hunten and Sprague 1997). More recently, the Lunar Atmosphere and Dust Environment Explorer (LADEE) determined a higher Na/K ratio—if ground-based scale heights are assumed—placing the exospheric Na/K ratio near the stoichiometric value of 7–9, as measured in lunar rocks returned by Apollo (Lodders and Fegley 1998; Colaprete et al. 2016).

Following discovery of the Moon’s Na exosphere by Potter and Morgan (1988a), decades of debate have ensued about the relative roles of each source process that sustains it. Sprague et al. (1998) conducted a comprehensive study of sodium’s atmospheric scale height. Although a collisionless surface-bound exosphere is not intrinsically thermal, scale heights are nonetheless a useful energy metric, and their measurements corresponded to characteristic energies of 985–1470 K. Concurrently, Potter and Morgan (1998) observations estimated 1280 K, in good agreement. Laboratory experiments by Yakshinskiy and Madey (1999) quickly pointed out that this is the characteristic energy for Na photo-desorption and that the mechanism is amply efficient to explain the observations.

Several measurements suggest that the lunar alkali exosphere cannot be explained by photo-desorption alone. Figure 1 shows the relative orbital variability in the LADEE UVS-derived column densities, averaged over four lunations. These columns are sampled near the subsolar point at tangent altitudes of 40 km. Na and K exhibit a similar and significant structure in Fig. 1 and such structure is unexpected from a photo-desorbed exosphere considering the viewing geometry. Szalay et al. (2016) showed that the potassium behaviour correlates with the local mineral inhomogeneity beneath the tangent point, as the local abundance tracks the K concentration in the lunar regolith measured by Lunar Prospector and Chang’E-2 (Prettyman et al. 2006; Zhu et al. 2013).

Fig. 1

Alkali column densities in the lunar exosphere as a function of orbital phase. Data are scaled to their dynamic range in radius and color, with blue to red showing increasing abundances. Orange wedges show nominal magnetotail passages, spanning phases of Full Moon ±30°. From Szalay et al. (2016)

Alternative interpretations exist for the orbital behaviour that LADEE measured in the exosphere. Orange regions in Fig. 1 denote lunar orbital phases that are nominally in the Earth’s magnetotail. From this perspective, one might infer that the Earth’s magnetotail passage primes the lunar surface by shielding it from the solar wind. Hence, Colaprete et al. (2016) theorized that alkali enhancements may reflect drivers in the Moon’s plasma environment. Their idea was supported by pre-LADEE models (Sarantos et al. 2010). The mechanism is for ions and electrons to catalyze solid state diffusion, regulating the supply available for release by photo-desorption after the Moon’s path through the Earth magnetotail (Fig. 1). These two possibilities exemplify an inherent challenge to understanding the lunar exosphere: since our Moon is tidally-locked, it is difficult to know whether observed properties of the exosphere during a lunation are a consequence of coupling from “above” (i.e., the lunar space environment) or from “below” (i.e. the lunar surface and gas-surface interactions).

1.2 Seasonal Variation of Mercury’s Exosphere

Whereas viable sodium and potassium measurements at the Moon are restricted to off-disk, emissions at Mercury are sufficiently bright for ground-based spectrographs to distinguish the signature above the planet’s dayside (Fig. 2). Mercury’s 3:2 spin-orbit resonance can effectively break the degeneracy described above for the Moon. Merkel et al. (2018) leveraged this fact in their study of exospheric Mg using MESSENGER. They showed enhancements in the Mg exosphere only appearing during alternating Mercury years, definitive evidence that these enhancements were coupled “from below” to Mg rich terrain, as opposed to the space environment.

Fig. 2

Na and K emissions over Mercury’s dayside at a true anomaly angle of 76°. Because the solar K absorption feature is narrower than that for Na, K scattering occurs in the continuum whereas Na remains partially within the solar absorption well. Emissions are slightly blue-shifted from rest, characteristic of gases leaving the surface (Courtesy, P. Lierle)

To understand the seasonal behaviour of Mercury’s alkali exosphere it is first necessary to understand how these atoms interact with sunlight. The planet’s eccentric orbit gives heliocentric radial velocities of up to ±10 km/s. This Doppler shifts the solar spectrum, changing the photon flux that excites the strong D line transitions in Mercury’s alkali gases. The Doppler shift is greatest at true anomaly angles of 90° and 270°, where photon excitation occurs not in deep wells of the solar alkali features, but in the strong solar continuum (Fig. 2). In addition to the Doppler shift, the heliocentric radial distance modulates the g-values, hence the maximum g-value is closer to 60° than to 90° (e.g. Killen et al. 2009). This effect strongly modulates the emission brightness over the Mercury year, independent of the actual column of gas that is being observed. Figure 3 nicely demonstrates this seasonal effect for Na. Although poorly characterized owing to the difficulty in making the observations, an even stronger modulation is expected in the potassium brightness because the solar K absorption lines are narrower (Fig. 2, cf. Smyth and Marconi 1995a). Killen et al. (2009) calculated g-values as a function of true anomaly angle for those emission lines expected to be observable by the MESSENGER MASCS spectrometer, including the 404.5 nm K line and the visible Na lines.

Fig. 3

Disk-averaged Na brightness from ground-based measurements. Adapted from Leblanc and Johnson (2010). Resonance scattering rates are seasonally modulated as the black solid line. Maximal heliocentric velocities occur at the dotted green lines. Maximal radiation pressure occurs at the dotted red lines. Black dotted lines bound the region near perihelion where rotation becomes slightly retrograde. Blue dotted lines correspond to the minimal heliocentric velocities

Consider the intensity at aphelion in Fig. 3 (true anomaly 180°). This season shows the faintest alkali emissions because resonance scattering occurs in the solar absorption core with Mercury farthest from the Sun. Note that these aphelion measurements are brighter than theory predicts from scattering rates alone, in some cases by a factor of two or three. This region represents a persistent seasonal enhancement in Mercury’s Na column that was not fully realized until after MESSENGER. Cassidy et al. (2015, 2016) analyzed 10 Mercury years of sodium equatorial limb scans with UVVS. They showed Na column peaks at aphelion (Fig. 21a), which is surprising because solar-driven sources of the exosphere are weakest here. They termed this feature the “cold-pole enhancement” because it extends above two geographic longitudes that have the coldest annual surface temperatures, points that alternately face the Sun at aphelion owing to Mercury’s 3:2 spin-orbit resonance.

Two interpretations could plausibly explain the cold-pole sodium enhancement. First, as a volatile, the sodium supply in the top-most soil could be sensitive to the maximum annual surface temperature. Na may have simply “baked-out” of the regolith grains, exhausting supplies in all but the coldest regions: high latitudes and cold-pole longitudes where surface temperatures peak ∼130 K below their hot-pole counterparts. Though longitudinal variation in the Na soil concentration remains unknown, variations in abundance within the top few cm of chemically-analogous potassium supports this perspective (Peplowski et al. 2012). A second interpretation involves the bouncing and sticking of exospheric atoms over the surface. Cold-pole longitudes are also located at the terminators during perihelion. Solar driven support of the exosphere peaks at perihelion and could send Na atoms bouncing across the ∼700 K dayside until they stick to the first cold surface they encounter behind the terminator. Surrounding perihelion, Mercury revolves nearly as fast as it rotates, so the progression of local time nearly stands still and the solar sidereal motion even becomes slightly retrograde. The terminators remain at nearly fixed longitudes in seasons between the black dotted lines in Fig. 3, about 15% of Mercury’s year. Cold-trapping here could locally enhance the Na reservoir within the topmost regolith, because alkalis are known to stick to ∼100 K surfaces (Yakshinskiy and Madey 2005). Over geological timescales, preferential deposition at cold poles may even explain the longitudinal asymmetries in soil concentration that Peplowski et al. reported. Either or both scenarios could be causal to the cold-pole longitudinal enhancements that UVVS observed in the Na exosphere and models have not yet determined which of these two influences dominates.

1.3 Lunar Linewidths & Altitude Profiles

Altitude profiles and linewidths are the two available means to estimate exospheric gas temperatures (or if the exosphere is intrinsically non-thermal, to place useful constrains on its velocity distribution function). As opposed to barometric scale heights, exospheric altitude profiles are traditionally fit using Chamberlain theory (cf. Chamberlain and Hunten 1989). A fit for temperature in this way can consider integrated densities that include contributions from all gas particles in ballistic, satellite and escaping orbits. Temperature retrievals based on alkali linewidths must account for hyperfine line structure in order to correctly interpret Doppler broadening, particularly if the gas is cold. Non-thermal treatments have also been made, but generally as forward models and not from analytical theory (Chaufray and Leblanc 2013). If the exosphere has multiple sources, e.g., sputtering and desorption at the Moon, the problem of temperature retrieval quickly becomes intractable. Disentangling a multiple-component thermal exosphere from a non-thermal energy distribution is a formidable undertaking, and even with high quality measurements, this is typically a problem with a non-unique solution. A best approach is of course to obtain concurrent measurements of both altitude and spectral line profiles, but observations of the lunar exosphere have yet not achieved this benchmark.

Reported exospheric temperatures inferred from altitude profiles vary extensively, even within individual publications. Sprague et al. (2012) reported 950 K to 20,000 K near the surface, depending on location and phase. Killen et al. (2019, 2021) reported 2250 K to 6750 K using a coronagraph that sampled higher altitudes above about 450 km. Their observations and others have reported the exosphere is most extended at high latitudes (e.g., Mendillo et al. 1993). Thus, not only is the exosphere not in thermal equilibrium with the surface, but it seems that in the gas-surface interactions superthermal atoms do not thermally accommodate towards local surface temperature. If sources of the exosphere originate predominately at the sub-solar point, however, larger scale heights at high latitudes could merely reflect transport, as only the most energetic atoms can reach the poles. Moreover, radiation pressure acceleration causes the scale height to be shorter on the dayside regardless of the temperature of the source.

Stern and Flynn (1995) have reported observations of a cold exospheric component near the lunar surface temperatures. This was achieved by observing a column just behind the terminator, where the gas is sunlit, but the surface is in shadow. They proposed a two-component exosphere: a cold population in thermal equilibrium with the surface and a spatially extended superthermal population. Potter and Morgan (1988a) also proposed a two component exosphere, with a “cold” component at 543 K above the subsolar limb. Subsequent studies have not yet confirmed this very cold component, but it can be broadly summarized that the scale heights appear more extended farther from the surface, as is expected for a very extended exosphere that is partially escaping.

Na linewidths reported by Potter and Morgan (1988a) are in good agreement with their atmospheric scale height temperatures of ∼540K. Although observations have not shown so explicitly, the linewidth, like the scale height, probably increases with altitude, because more energetic particles reach higher apex altitudes. Kuruppuaratchi et al. (2018) and Rosborough et al. (2019) have surveyed Na and K linewidths, respectively, using Fabry-Perot techniques. In a 3 arcminute field at tangent altitudes of several hundred km, their Na line profiles corresponded to 1700 K to 9000 K whereas K profiles corresponded to colder temperatures of 980 K–1920 K. Both species show an increase in temperature and a decrease in brightness between Quarter phases and Full Moon. Again, this behavior can be at least partly attributed to viewing geometry and transport; the exosphere’s concentration is highest at the subsolar point (Killen et al. 2019; Potter and Morgan 1998) and only the most energetic atoms will reach the limb. Still, kinetic models that account for this partitioning show that a single temperature cannot explain the observations (Fig. 4). Therefore, linewidth variations may reflect the true interplay between multiple sources: relatively cold photo-desorbed sources are diminished near Full Moon, causing the intensity to drop, while the relative contribution from hot sputtered sources becomes more evident. Of course, we are again confronted with the possibility of a single non-thermal source as a potentially viable alternate explanation.

Fig. 4

Linewidth derived Na gas velocities at the Moon compared to simulations at various temperatures to assess geometric effects. From Kuruppuaratchi et al. (2018)

1.4 Mercury Linewidths & Altitude Profiles

Unlike the Moon, ground-based altitude profiles of Mercury’s exosphere are not generally possible because the scale height is of smaller angular size than the limitations imposed by atmospheric seeing. Killen et al. (1999) found the Na to be several hundred K above the surface temperature using the Na D₂ linewidth, which were confirmed upon MESSENGER’s arrival (Cassidy et al. 2015). The MESSENGER UVVS wavelength range unfortunately did not include the potassium D lines. Furthermore, owing to operational constraints, the majority of the altitude profiles obtained by MESSENGER UVVS were confined to low latitudes, and sampling of profiles at the higher dayside latitudes where the magnetosphere’s cusps channel ions to the planet’s surface was limited. Leblanc et al. (2008, 2009) reported changes in linewidth alongside dynamic brightening in these regions, however, which together suggest significant contributions from a higher energy plasma sputtering population. MESSENGER did confirm a trace high-energy component above 1000 km altitudes in the low-altitude limb profiles, and Chamberlain models place temperatures of this component near 20,000 K. This is significantly hotter than is expected from meteorite vaporization, indicating a sputtered component or the photodissociation of vaporized molecules imparting extra energy to the released atoms (Burger et al. 2014) or/and a strong influence of the radiation pressure and particle transport on the apparent scale height. A review of these findings is presented in Chapter’s 14 and 15 of the book Mercury: The View after MESSENGER (eds. Solomon, Nittler, Anderson).

1.5 Lunar Na Tail

Whereas solar photons are incident from the sunward direction, photons interacting with alkalis are scattered nearly isotropically (we say ‘nearly’ because a small phase function occurs in the D₂ line, cf. Chamberlain 2011). Solar photons carry momentum, and so, on average, there is a net momentum in the anti-sunward direction transferred to the atoms. This effect is termed radiation pressure and it contributes significantly to particles overcoming gravity and achieving atmospheric escape. This effect shapes escaping alkalis into a comet-like “tail” pointing directly anti-sunward.

Measurements of the lunar tail are mostly indirect. Figure 5 shows the sole published image of the sodium lunar exo-tail; it has never been detected in potassium. Scattered moonlight from the bright surface competes with the faint tail and were it not for the projection of the Moon’s shadow, it would be difficult to discern. A surprising discovery was made by all-sky cameras that the lunar exo-tail can be measured much more readily using the Earth as a lens. The massive comet-like tail has been detected from its backscattered sodium emissions in a direction nearly opposite to New Moon (see Fig. 6). In this geometry, anti-sunward streaming atoms encounter the Earth’s gravity field. The trajectories of the Na atoms are bent as they pass by the Earth, and so the broad diffuse tail is focused into a narrow column where the trajectories cross. This forms a spot near the anti-lunar direction for about four days surrounding New Moon, while Earth passes through the lunar exo-tail.

Fig. 5

Image of the lunar sodium exosphere over a 7° field of view. Fifteen on-band/off-band filter pairs of one minute each are co-added, hence the trailing in the stellar residuals. A neutral density mask allows the Moon to be imaged at the same time as its atmosphere. The effect of the Moon’s shadow in blocking resonance fluorescence can be seen in the sodium exosphere. From Baumgardner and Mendillo (2009)

Fig. 6

Observations and modelling of the Moon’s sodium tail “spot”. Top-left: all-sky image with Na feature identified, with expanded view on top-right. Bottom-left: simulation results (to scale) showing the cloud of cloud of Na atoms passing Earth, gravitationally focused into the tail spot. (Smith et al. 1999; Wilson et al. 1999)

The Na spot’s brightness varies measurably with the Earth-Moon distance and its shape depends on the parallax of the observer’s topocentric location. Line et al. (2012) observed a mean gas velocity of 12.5 km/s in the spot with measurable emissions of up to 30 km/s originating from down-tail distances of 1.5 million km. Baumgardner et al. (2021) used an archive of all-sky imaging data to study the spot’s apparitions 2006-2019. Figure 7 shows the duration and brightness of the apparition. Brightness in the lower panel effectively represents a cross-section of the lunar tail at a down-tail distance of 60 R_Earth. This brightness does not peak at the time of New Moon but 5–6 hours later, with an asymmetrical light curve about this peak. A latitudinal asymmetry is also seen, wherein the spot is brighter when New Moon phases north of the ecliptic. Modelling is needed to clarify if these reflect true axial asymmetries in the exo-tail or merely geometric effects. It is unlikely that an analogous spot of potassium is bright enough to be measured given that the D₂ line is obscured by telluric O₂ absorption and K has both a shorter photo-ionization lifetime and lower escape rate than Na.

Fig. 7

Brightness of the focused lunar tail’s spot from 2006-2019 using an all-sky imager in El Leoncito Argentina. Colored dots highlight data within two days of a meteor shower’s peak, accounting for the Moon-Earth transit time. The pink plus sign marks the initial discovery of the feature, following the 1998 Leonids shower (Baumgardner et al. 2021)

Models of the Moon spot’s brightness demonstrate that a flux of $\sim 2 \times 10^{22}$ Na atoms/s, escape at New Moon phase (Wilson et al. 1999), which is perhaps 3–15% of the global surface supply (Smyth and Marconi 1995b). This is a minimum, however, of escape rates that are modulated during each lunation cycle. Radiation pressure that propels atmospheric escape has positive or negative feedback, depending on the sign of the lunar heliocentric velocity. Atoms accelerated anti-sunward encounter increasing sunlight as the Doppler shift moves up the solar well (heliocentric radial velocity away from the Sun, as occurs during 1st Quarter), which then further increases the acceleration from solar radiation pressure. Negative feedback occurs at 3rd Quarter, where atoms are Doppler shifted into the solar absorption well, stagnating their acceleration. This effect modulates the fraction of atmosphere stripped away during each phase of the lunation (e.g., Smyth and Marconi 1995b). At least in part, it can likely explain the 20% decrease in sodium surface abundance between 1st and 3rd Quarter that was reported from measurements by the SELENE (Kaguya) orbiter (Kagitani et al. 2010). By the time atoms have Doppler shifted into the continuum due to their increasing heliocentric radial velocity when moving away from the Moon, they also scatter up to 20 times more solar photons. This may explain the line-of-sight Doppler shifts that Kuruppuaratchi et al. (2018) reported between 1st and 3rd Quarter, again at least in part. Relating this back to Fig. 4 and the similar potassium finding (Rosborough et al. 2019), it can be deduced that line of sight near New Moon span the full column down the exo-tail. During this configuration, the confluence of surface-ejected gas toward the observer and gas escaping away from the observer naturally produce a broadened line. Still, kinetic models in Fig. 4 (Sarantos et al. 2010; Sarantos and Tsavachidis 2020) demonstrate that this geometric effect is only a partial explanation of the observed linewidth enhancement and consequently the Moon’s exosphere is hotter at New Moon phases. Killen et al. (2021) concluded that the largest measured scale heights are at dawn and dusk, and are correlated with local solar time. Observations of the lunar exosphere from Earth are limited to dawn and dusk terminators at both New Moon and Full Moon.

1.6 Mercury’s Alkali Tail

Mercury’s comet-like tail has been measured beyond 3 million km from the planet. Along with the sodium nebula of Io, it is among the largest structures in our solar system. Seasonal modulation of alkali escape is much stronger at Mercury than at the Moon, owing to the greater range of distances and velocities relative to the Sun experienced over the Mercury orbit. Na radiation pressure peaks near a true anomaly angle of 64°. This is indeed where the largest escape rates have been reported, about $1.3 \times 10^{24}$ Na atoms/s (Schmidt et al. 2010). This is ∼20% of the surface ejection rates modelled by Schmidt et al. (2012) who noted that a dropout from the expected brightness is evident at this true anomaly in Fig. 3. The sodium tail during Mercury’s inward bound orbit is far weaker and was not detected until MESSENGER’s arrival, emphasizing the importance of negative feedback in radiation acceleration when Mercury’s motion is inbound (Potter et al. 2007).

The sodium tail is a valuable observable for understanding Mercury’s exosphere overall. It shows a distinct width, as in Fig. 8, that depends on the gas velocity distribution function. This width is narrow, consistent with low energy photo-desorption, despite the fact that meteoroid vaporization and sputtering have a much higher fractional escape (Schmidt et al. 2012). Although the tail typically exhibits slow and regular changes in the escape flux, it also records a history up to 15 hours in duration, capturing any high-energy transient events like sputtering during a coronal mass ejection passage, or a vaporization from a large meteor impact.

Fig. 8

Image of Mercury’s Na tail at 35° true anomaly angle. The disk is visible through a high density filter that serves as a coronagraph. (Courtesy, J. Morgenthaler)

Despite photons—not plasma—being the source mechanism that supplies the escaping sodium tail, the influence of Mercury’s offset magnetosphere is imprinted in the tail’s structure. Cross-sections of the tail usually show an enhancement in the northern lobe (Potter and Killen 2008). Near Mercury, the north/south ratio in the tail is typically 1.2, but varies dynamically. Figure 9 shows an example of this asymmetry, which smooths out to a unity ratio beyond 10 R_M. The N/S asymmetry, combined with the tail’s width, is consistent with low-energy atoms originating near the footprint of the southern cusp (Schmidt 2013). The southern surface has a ∼4x larger region for open field lines to channel plasma precipitation, relative to the north (Winslow et al. 2012). Gases escaping from this region drift northward as a natural consequence of the balance between radiation pressure and gravitational forcing as atoms traverse the planet’s shadow. Only low-energy atoms that barely reach escape trajectories exhibit this “sloshing” behaviour.

Fig. 9

Cross-tail profiles of Mercury’s Na at 110° true anomaly angle. Note the dearth of emission in shadow and the enhancement in the northern lobe, both of which are less pronounced with distance (Potter and Killen 2008)

Because atmospheric escape partitions the gas near the escape velocity, the tail is where high-energy sources in Mercury’s exosphere should appear most prominently. Yet, the escaping tail show no signs of ion sputtering, imploring the question “if low-energy desorption is the dominant process and high-energy ion sputtering is absent then why does the magnetosphere affect the exosphere?” Again, this is thought to be evidence of indirect plasma effects. Low-energy desorption in the cusp regions could be sensitive to plasma bombardment because of gardening. Desorption is a surface process that would be depleted unless fresh alkali atoms are supplied from depth. Ion bombardment can create defects in the micro-structure of regolith grains and thereby catalyse solid-state diffusion. Modellers have independently concluded that this multi-step process is consistent with the available data, both at Mercury (Burger et al. 2010; Schmidt 2013) and at the Moon (Sarantos et al. 2010). However, this process remains hypothetical being not supported by detailed models of sputtering physics. Moreover, the low-energy solar wind particles won’t penetrate deeply into the regolith grains limiting the region impacted by enhanced diffusion.

Potassium radiation pressure peaks near 48° true anomaly (Smyth and Marconi 1995b). In this portion of the planet’s orbit, detections of the faint potassium tail have been reported at conference proceedings. Schmidt et al. (2017) observed a ∼95 Na/K ratio at 5 radii down-tail. Potassium escape remains poorly characterized and its gas velocity in Mercury’s exosphere is unknown. MESSENGER was unable to observe emissions at far red wavelengths. BepiColombo might be able to do so thanks to ViHI/SIMBIO-SYS, an observation that will need, however, specific pointing of MPO that may be difficult to obtain. Future ground-based observations can improve upon this, using instrumentation with high spectral resolution and long-slit capabilities.

1.7 Plasma Drivers in the Lunar Exosphere

Earth’s magnetotail provides a convenient experiment to test the influence of plasma bombardment on the lunar exosphere. This sheltered plasma environment is populated at roughly 1/500th the solar wind density. Observations of the exosphere’s passage through the magnetotail have differing results, however. Mendillo et al. (1999) showed the exospheric Na abundance was nearly unchanged between Quarter Moon, when the Moon is fully exposed to the solar wind and phases in the magnetosheath, when its surface is shielded from the solar wind. This lack of any response suggested solar wind ion sputtering is not an important driver. Potter et al. (2000) found from low altitude measurements (100–400 km) that the Na density decreased during passage through the magnetotail. Kaguya’s measurements showed similar behavior consistent with low altitude measurements, but again no evidence for a magnetotail influence was observed (Kagitani et al. 2010). As noted earlier, decreasing radiation pressure and scattering rates may partly explain these findings. Potter et al. argued that the decrease could be attributed to ion bombardment catalyzing solid-state diffusion, thereby regulating the Na supply available for desorption in the topmost regolith layer. A model by Sarantos et al. (2010) synthesizing multiple data sets agreed with this interpretation. However, the LADEE UVS results in Fig. 1 show quite the opposite effect: alkalis increasing throughout the orange phase in the magnetotail. This led Colaprete et al. (2016) to conclude that the topmost reservoir of alkali atoms accumulates in the absence of solar wind plasma, rather than in its presence. Killen et al. (2019) show, using high altitude measurements (>400 km), that the highest column abundance observed in a five-year long study was correlated with ion impact to the lunar surface measured by the Artemis spacecraft. Since observations from Earth are taken off the lunar limb, Killen et al. (2019) also showed that such observations probe local time variations. Viewing geometry and altitude range seems the most likely explanation for discrepancies between the results of this natural experiment, particularly when comparing in situ and remote observations taken at different altitude ranges.

Earth’s plasma sheet contains a distinct plasma population within the magnetosphere. It is both denser and more energetic than surrounding magnetotail lobes. Crossings of the Earth’s plasma sheet have been reported to significantly enhance the exosphere (Wilson et al. 2006). This phenomenon needs to be confirmed by new studies; the plasma sheet at 60 Earth radii is thin and dynamic so it is challenging to predict when crossings occur. The fractional time that our Moon spends in Earth’s plasma sheet varies on 18.6-year cycles because of the lunar orbital precession and there is also a weak dependence on lunation number (Hapgood 2007). Using a set of coronagraph observations during lunar eclipses, Wilson et al. (2006) discerned strong enhancements following recent plasma sheet crossings of the Moon (Fig. 10). With only five eclipses surveyed over seven years, statistics are far from robust though. Hapgood (2007) notes that the Wilson et al. study was ideally suited in time for the likelihood of plasma sheet crossings. Correlations between in-situ plasma measurements and ground-based monitoring of the exosphere may be the best way to ascertain the influence of the plasma sheet population.

Fig. 10

Observations of Na during two lunar eclipses in 1993 and 1996. A coronagraph mask remains necessary due to refracted light though Earth’s atmosphere. Left was taken when the Moon was near the magnetosheath boundary, two days after plasmasheet crossing. Three crossings occurred in such time preceding the image at right, with the last being ∼4 hours earlier (Mendillo et al. 1999)

1.8 Plasma Drivers in the Mercury Exosphere

Mercury’s magnetosphere offers more visibility to the effects of plasma drivers. Enhanced emissions associated with plasma precipitation in the magnetosphere’s cusps were first reported by Potter and Morgan (1990). MESSENGER later determined the planet’s field is, to good approximation, a dipole offset by 484 km northward from the planet’s center (Anderson et al. 2011). Consequently, Mercury’s weaker field in the southern hemisphere exposes the surface to greater plasma bombardment. This discovery of an offset magnetosphere has helped researchers understand the magnetosphere-exosphere connection. The finding explained multiple reports of persistent asymmetries in the exosphere exhibiting southern maxima as seen in Fig. 11 (e.g., Baumgardner et al. 2008; Leblanc et al. 2008; Mangano et al. 2009). Southern cusp precipitation is thought to occur over a surface area four times greater relative to the north, and the cusp latitudes are centered approximately at 64°S and 71–75°N (Winslow et al. 2012). However, Na enhancements generally appear equatorward of the magnetic cusps and the north-south ratio is often closer to unity (Fig. 12), or even enhanced in the northern hemisphere (Mangano et al. 2015), an observation which could be partly due to the atmospheric seeing (Killen 2020). It remains uncertain how planetary ions, which are more energetic and precipitate with a different pattern, can influence the exosphere as opposed to solar wind ions. A deeper discussion of exospheric plasma sources follows in Sect. 3 of this chapter. In any case, it is clearly evident that a coupled system between the magnetosphere and exosphere exists and this in turn establishes the capability to observe Mercury as a responsive and dynamic space weather system using the low-cost means of remote sensing.

Fig. 11

Enhancements in Mercury’s Na exosphere near the magnetic cusp regions (Mangano et al. 2013)

Fig. 12

Contours of Na column density, showing near symmetry between north and south, with peaks equatorward of the cusps near 50–60 latitude (Schmidt et al. 2020)

Several observers have reported short term changes in the exosphere’s structure (Potter et al. 1999; Leblanc et al. 2009; Mangano et al. 2013; Massetti et al. 2017). Exospheric structure, in particular the north/south asymmetry, appears sensitive to the interplanetary magnetic field’s clock angle, and probably also dynamic pressure (Mangano et al. 2015). Sodium and potassium emissions are therefore a powerful tool in understanding the planet’s response to space weather, but much more than a snapshot in time requires daytime observations. Solar telescopes have proven the optimal tool. In principle temporal changes could be on the order of ∼10 min, the ballistic flight time of the atoms, although few robust measurements on these timescales have been possible. Hourly changes are certainly evident. Winslow et al. (2015) catalogued coronal mass ejections (CMEs) at Mercury during the MESSENGER mission and Orsini et al. (2018) showed the exosphere rapidly reconfigures during a CME passage. The frequency of CMEs at Mercury is thought to be fairly high, and occasional extreme events are known where strong dynamic pressure pushes the magnetopause below the dayside surface, exposing it to the shocked solar wind (Slavin et al. 2019). BepiColombo will perform continuous observation from the orbit around Mercury using the Mercury sodium atmosphere spectral imager (MSASI) (Yoshikawa et al. 2007).

1.9 Meteoritoid Influence on the Lunar Exosphere

Several observers have reported that the lunar exosphere responds dynamically to strong meteoroid showers including the Leonids (Hunten et al. 1998; Smith et al. 1999), Perseids (Berezhnoy et al. 2014), Quadrantids (Verani et al. 2001) and Geminids (Colaprete et al. 2016). As an example, Na D₁ and D₂ lines in the lunar exosphere at distances of 90, 270, and 455 km from the surface were observed during maximum of the Perseid 2009 meteor shower (Berezhnoy et al. 2014). A rapid increase of the intensities of Na D1 and D2 resonance lines in the lunar exosphere near the north pole on August 12, 2009, 23:54 UT–August 13, 2009, 1:13 UT) was detected corresponding to an increase in the Na zenith column density of 40%. These observations were explained by numerous impacts of relatively small Perseid meteoroids with masses smaller than 1 kg and total mass flux of impacted meteoroids on the Moon of about 27 kg/hour. The zenith column density of Na atoms on August 13/14, 2009, about $(9.0\pm 0.2)\times 10^{8}$ cm⁻², was almost the same within error of measurements as the zenith column density of Na atoms on August 12 at 23:13-23:43 UT, $(8.2\pm 0.5)\times 10^{8}$ cm⁻², before the sudden increase of the Na zenith column density, suggesting a duration of the signature of this episode of meteoroid bombardment in the Na exosphere of less than one day. The photoionization lifetime of Na at the Moon is 2 days, which suggests that the impact-derived sodium exosphere is escaping kinetically.

Each of these streams impacts the lunar surface from a different radiant, so stream impact locations and velocities differ year to year. Both are important: the local alkali soil concentration probably determines its ejecta into the exosphere (Szalay et al. 2016) and energy deposited in the fireball is proportional to the square of the stream velocity. It is possible that higher energy impacts yield not only more ejecta, but ejecta at higher energies. Killen et al. (2010) assumed a 1000 K Na gas temperature to determine the mass of gas released from the low velocity, which is substantially colder than most vaporization studies predict. Temperatures associated with vaporization remain model-dependent. Higher temperatures have higher escape fractions into the anti-sunward tail. Given that several studies show exospheric enhancements during strong meteoroid showers, it is surprising that these events rarely produce measurable column enhancements in the tail spot (see coloured points in Fig. 7). The absence could indicate that vapour produced by showers is relatively cold or that meteoroid showers do not augment the overall bulk exosphere except on rare occasions. Baumgardner et al. (2021) found significant correlations between annual variations in the sporadic influx and the Na tail spot brightness, however, signifying that the sporadic meteor influx is more influential than transient meteoroid showers in driving atmospheric escape.

The LDEX dust detector and UVS on LADEE provided a good proxy to study correlations between meteoroid dust and gas ejecta, and the BepiColombo MDM dust monitor will bring such capabilities to Mercury. LADEE showed potassium was more responsive to meteoroid influx than sodium, as seen in Fig. 13. This might be attributed in part to transport effects: hot Na ejecta could escape the Moon, whereas heavier K remains bound. Berezhnoy et al. (2014) estimated Na temperatures of 3100 K during the Perseids shower. At this temperature, a significant portion of the Na velocity distribution is above the lunar escape speed. Laboratory measurements indicate K ejecta re-impacting the Moon would adsorb to the cold surface whereas Na would bounce (Yakshinskiy and Madey 2005). It is surprising therefore that K residence times in the exosphere are estimated to be several days (Szalay et al. 2016). This may imply re-ejection of adsorbed material, whereas bouncing removes particles from the exosphere via rapid migration to cold traps on the night side.

Fig. 13

Na and K column densities near noon during the entire LADEE mission (Colaprete et al. 2016). The lunation behaviour in Fig. 1 is evident, as well as long-term trends following the curve in blue. Three meteoroid streams (Leo, Gem, and Qua) are marked with the blue dashed lines. Red arrows mark the New Moon phase

1.10 Meteoroid Influence on Mercury’s Exosphere

A strong meteoroid influence on Mercury’s exosphere has been suggested for Ca (Burger et al. 2014), but the connection to alkalis is less evident. Comet Encke’s stream has been attributed to Ca enhancements near 30° true anomaly (Killen and Hahn 2015). Like the Moon, impacts preferentially strike Mercury’s dawn-side, and although Ca shows persistent enhancement at morning, other exospheric constituents show a more varied behaviour, indicating a mix of sources. Impactors strike Mercury with much higher velocity compared to the Moon. Models predict vaporization is dominated by impacting meteoroids >100 km/s, with a factor of five seasonal variation peaking just before perihelion (Pokorny et al. 2018). Detailed overview of this topic can be found in review (Grava et al. 2021). Christou et al. (2015) modelling of the Encke dust stream complicated the story: they found that the Encke dust, depending on its age, can hit nearly anywhere on Mercury’s surface except for the dawn hemisphere. Kameda et al. (2009) showed the potential correlation between Mercury sodium density and the interplanetary dust distribution (IPD), as suggested by Killen and Hahn (2015).

1.11 Na & K in Other Surface-Bound Exospheres

Europa is perhaps the best studied icy body with a surface-bound alkali exosphere. The Na/K ratio there is approximately 25, falling between that of the Moon and Mercury (Brown 2001). It has long been debated what fraction of these alkalis originate from the adjacent moon Io, which sprays neutral alkali jets and seeds the magnetosphere’s plasma. Simulations have determined that loss rates in Europa’s exosphere well exceed realistic implantation rates from Io and its plasma torus, suggesting Europa’s alkalis are a native product of its sub-surface ocean salinity (Leblanc et al. 2002). Surface spectroscopy shows signatures of irradiated NaCl (Trumbo et al. 2019) and helps strengthen this argument, because transport from external sources is doubtful in a molecular form. Na emission is too faint to be readily measured at Enceladus, but has been detected with in situ mass spectroscopy (Postberg et al. 2009; Schneider et al. 2009). Na and K exospheres have yet to be detected at asteroids, despite a dedicated search at C-type Ryugu by the Hayabusa2 sample and return mission.

2 Sources of Na/K: The Role of Magnetosphere

2.1 Release Processes at Mercury and the Moon

The release of atoms from the surface of Mercury and the Moon essentially occurs at the expense of the energy supplied by the precipitating plasma, neutral atoms, meteoroids, the flow of photons and by the thermal energy of the surface itself. The rate of release of neutral and, in a lesser extent, ion particles and the velocity distribution depend, to first approximation on the energy transferred.

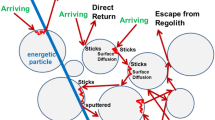
At Mercury, the first energetic process is the release by precipitating solid grains, which is called micro-meteoroid impact vaporization (MMIV) for impactors with the size of a few tens of microns, and meteoroid impact vaporization (MIV) for larger dimensions. The smallest particles precipitate more constantly and uniformly on the surface of Mercury, with an average speed of a few tens of km/s (Cintala 1992; Pokorny et al. 2017, 2018). As the size of impactors increases, events become rarer (and with more variable velocity). Very large meteoroids impact sporadically, but with a higher average velocity (Marchi et al. 2005). The contribution of these larger meteoroids to the Hermean exosphere is, globally, negligible, and their impact is expected to produce strong but localized temporary increases in exospheric density, enriched by species from deeper layers of the surface (Mangano et al. 2007). Regardless of the size of the impactor, refractory species contained in the surface are highly volatile during high-speed impacts owing to the high temperatures and pressures that are produced (Gerasimov et al. 1998). Therefore, atoms released by MIV or MMIV will be almost stoichiometrically representative of the surface composition. Regardless of the size of the impactor, the initial ejection will also be high-temperature vapor (∼5,000 K), followed by the “liquid and vapor” at a slightly lower temperature (2,500 K) (Killen et al. 2007). Hence, the velocity distribution of ejecta can be approximated by a Maxwellian function, with such a temperature parameter (please see Sect. 1.9 for further discussions of this parametrization). Details on the produced species and molecules at different stages of the involved vaporization process are described later in Sect. 2.1.1.

A second energetic release process is caused by the precipitation of plasma on Mercury’s surface and is called Ion Sputtering (IS) or electron sputtering (ES) for electron with energy larger than MeV. This causes the release of particles via momentum transfer and, similar to MMIV and MIV, reproduces more or less the local surface composition. At least in the case of MeV electrons and light solar wind ions, sputtering is a two-step process. First, the projectile impacts the surface target and is either implanted into the substrate or back-scattered. This impact can also lead to sputtered neutrals from the target due to either direct (from the initial impact) or secondary (from the collision cascade) sputtering. The ejected atom is neutral in most cases, but it could be ionized. The projectile can transmit only a fraction of its energy to the ejected particle:

$$ T_{m} = E_{1}\frac{4 m_{1}m_{2}}{\left ( m_{1} + m_{2} \right )^{2}} $$

where Tm is the maximum transmitted energy from the incident particle (mass $m_{1}$ and energy $E_{1}$) to the ejecta (mass $m_{2}$ and energy $T_{{m}}$). The distribution function ($f_{{S}}$) of the ejection energy can be empirically reproduced by the following function:

$$ f_{S}\left ( E_{e},T_{m} \right ) = c_{n}\frac{E_{e}}{\left ( E_{e} + E_{b} \right )^{3}} \left [ 1 - \left ( \frac{E_{e} + E_{b}}{T_{m}} \right )^{\frac{1}{2}} \right ] $$

where $E_{{b}}$ is the surface binding energy of the ejected atomic species, $E_{{e}}$ is the energy of the emitted particles, and $c_{{n}}$ is a normalization constant (Sigmund 1981; Sieveka and Johnson 1984; Johnson and Baragiola 1991; Wurz et al. 2021; Morrissey et al. 2021; see also Eckstein and Preuss 2003). The angular distribution of the ejected particles is difficult to define for space weathered surfaces. Heavy and energetic ions penetrate deeper than lighter and less energetic particle and have multiple scattering impacts (Mura et al. 2005). The resulting angular distribution of ejecta is also dependent on the porosity of the surface, and it may be approximated with a cosine law with an exponent larger than one (Cassidy and Johnson 2005). Angular distributions of sputtered atoms have been measured for H⁺ and He⁺ onto polycrystalline tungsten and nickel by Bay et al. (1980). For light ions, the angular distribution is related to the ion impact direction, and may exhibit a maximum close to the backscattering angle, with a complex dependence that is usually discarded in Mercury exospheric studies (e.g. Bay et al. 1980; Behrisch and Eckstein 2007), because the plasma precipitation angular distribution is quite wide (Mura et al. 2005; Massetti et al. 2003).

A less energetic release process is Photon-stimulated desorption (PSD), sometimes referred to as photon sputtering, which corresponds to the desorption of surface elements as a result of electron excitation of a surface atom by a photon or by electron of moderate energy (Madey et al. 1998). McGrath et al. (1986) first proposed that PSD was the major source of Na in the Hermean exosphere because the Na distribution peaks at the sub-solar point (Killen et al. 1990). It is nowadays assumed that it is, indeed, one of the major sources, but not for all exospheric species. In fact, this is not a stochiometric process, as it is supposed to release only more volatile species such as Sodium or Potassium. Laboratory measurements by Madey et al. (1998) have shown that this process efficiently releases alkalis from regolith surfaces. The same authors (Yakshinskiy and Madey 1999, 2004) also found that UV photons with energies greater than 5 eV cause desorption of “hot” Na atoms, whereas energies ≤4 eV caused little or no Na desorption. Yakshinskiy and Madey (2004) estimated that the cross section of the PSD at photon energies of ≈5 eV is about 10⁻²⁰ cm², which is about seven times larger than that used by other authors. Killen et al. (2001) claimed that the PSD yield at Mercury is diffusion limited and also reduced by porosity. Yakshinskiy and Madey (2004) also found from their experiments that desorbed Na atoms are super-thermal with a velocity peak in the PSD distribution of about 900 m/s. Cassidy and Johnson (2005) estimated that desorption from a regolith is reduced by about a factor of three compared to that on a flat surface. PSD is induced by electronic excitations rather than by thermal processes or momentum transfer, but the surface temperature is responsible for diffusion of material to the surface (Wurz and Lammer 2003). In fact, because the process is highly efficient, the volatile composition is quickly depleted in the uppermost surface layers, and some refilling mechanism from the innermost layers of the regolith grains is required (McGrath et al. 1986; Mura et al. 2009). The same authors suggested that enhanced diffusion or chemical sputtering is able to produce this refilling and is needed to explain observations of the dawn-dusk asymmetries (Schleicher et al. 2004). The velocity distribution of PSD particles can be either assumed Maxwellian with a temperature of 900–1200 K, or with a Weibull distribution (Johnson et al. 2002):

$$ f\left ( E \right ) = \beta \left ( 1 + \beta \right )\frac{EU^{\beta }}{\left ( E + U \right )^{2 + \beta }} $$

where $\beta$ is the shape parameter (0.7 for Na) and U is the characteristic energy, which is of the order of 0.05 eV, for Na (Wurz et al. 2021). The maximum ejection energy should be lower than the photon energy so that a cut-off function at about 10 eV should be included. Mura et al. (2009) found that this second approximation fits much better with Doppler velocity distribution measurements by Schleicher et al. (2004).

Finally, thermal energy of the surface is able to desorb most volatile elements (Thermal desorption, TD). This is the least energetic process and basically results in a population of low-altitude neutrals that are in thermal equilibrium with the surface, and that bounce or stick to the grains in the regolith. In Fig. 14 we show examples of the energy distributions, trajectories and exospheric densities for different sources. However, temperature programmed desorption results of Poston et al. (2015) show high temperature of water desorption, 550 K, for Apollo lunar sample 72501, indicating activation energies approaching 1.5 eV for water. Activation energies for other species on simulated lunar and hermean soils should be examined, particularly to determine the activation energies under the harsh conditions at Mercury.

Fig. 14

Energy distribution (left), example of trajectory (center) and exospheric density simulations (right) for three different release mechanism: TD (top), PSD (middle) and IS (bottom)

2.1.1 Meteoroid Bombardment as a Source of Na and K Atoms in the Exospheres of the Moon and Mercury

Chemical processes in hot clouds produced after impacts of meteoroids with the Moon and Mercury have been studied through quenching theory (Berezhnoy and Klumov 2008; Berezhnoy 2013, 2018). Namely, the chemical composition of an impact-produced cloud is in equilibrium soon after an impact when the temperature and pressure in the cloud are high and chemical reactions occur quickly in comparison with the typical timescale of hydrodynamic processes. During the cloud’s expansion, the temperature and pressure decrease and, at the moment of quenching, the timescales of chemical reactions and hydrodynamic processes are comparable. It is assumed that the chemical composition of the cloud remains unchanged after quenching. Such a simple model has some limitations, as discussed in detail by Berezhnoy and Klumov (2008); however, it can be used as a first step for modelling of very complex processes during impact events.

Timescales of the main chemical reactions with participation of Na- and K-containing species are comparable with hydrodynamic timescales during impacts of 1 mm–3 cm meteoroids at about 2500–3500 K (Berezhnoy 2013). Thermodynamic calculations show that atomic Na and K atoms are the main Na-, K- containing species in clouds formed during collisions of meteoroids with the Moon and Mercury at a temperature range between 3500 and 5500 K. The KOH equilibrium content at 2000–3000 K is higher than that of atomic K whereas atomic Na and NaOH contents are comparable at 2500–3000 K (Berezhnoy 2013). NaO and KO molecules are the second or third most abundant Na-, K-containing species at the range of temperatures considered (see Fig. 15). Another important feature of the behavior of alkali metals during impact events is that condensation of atomic Na and K as well as oxides and hydroxides of Na and K does not occur during expansion of impact-produced clouds (Berezhnoy 2013, 2018).

Fig. 15

Equilibrium chemical composition of Na-, K-, Li- containing species during adiabatic cooling of an impact-produced cloud. Initial temperature is 10000 K, initial pressure is 10000 bar, the ratio of specific heats $\gamma$ is 1.2. This figure is taken from Berezhnoy (2013)

When estimating the probability of photolysis and release of photolysis-generated atoms of alkali metals to the exosphere, the photolysis lifetimes of molecules should be compared with their ballistic flight times. Based on the results of ab-initio calculations of the dependence of photolysis cross sections on wavelength, NaO, KO, NaCl, and KCl photolysis lifetimes at 1 A.U. for quiet Sun conditions were estimated as 5, 14, 42, and 52 s (Valiev et al. 2020). Based on experimental data, NaOH and NaO photolysis lifetimes are estimated as 11 and 42 s (Self and Plane 2002). Ballistic flight times at 3000 K (typical temperature of impact-produced species) of considered species are about 1000 s and much longer than photolysis lifetimes of these species. It means that the probability of photolysis of the main impact-produced Na-, K- containing species during their first ballistic flight in the exospheres of the Moon and Mercury should be close to unity. Therefore, the delivery efficiency of Na and K into the exospheres of the Moon and Mercury should be large contrary to the one of refractory elements (Grava et al. 2021).

2.1.2 Velocity Distribution Function of Na and K Atoms Produced During Photolysis of NaO, KO, NaOH

It is generally accepted that meteoroid bombardment is responsible for production of quite hot Na and K atoms with temperatures of about 2500 to 5000 K in planetary exospheres (see Sect. 2.1). Let us note that a Maxwellian distribution of velocities is valid for the case of atoms produced directly in impact-produced clouds because such atoms were thermalized during numerous collisions before the start of the collisionless regime.

Considering the typical photolysis lifetimes of Na, K-containing species (about 10 s) and the expansion velocities of the impact-produced clouds (about 2 km/s), the photolysis should occur when the size of the impact-produced clouds reaches about 20 km. For the typical radius of impactors (about 0.02 cm), the number density of the impact-produced species decreases down to about 1 cm⁻³ when the photolysis of the molecules occurs. Therefore, the velocity distribution of Na and K atoms produced during photolysis of parent molecules is not Maxwellian because the photolysis occurs during the collisionless regime of the expansion of the impact-produced cloud. Experimental studies of the velocity distribution of Na and K atoms produced during photolysis of Na-, K-containing species are limited. Photolysis cross sections of NaO and NaOH at 200 and 300 K were measured by Self and Plane (2002). Based on these experimental data and taking into account solar flux from Huebner et al. (1992), the velocity distribution of Na atoms produced during NaO and NaOH photolysis were obtained by Berezhnoy (2010). Namely, the velocity of Na atoms produced during NaO photolysis has a maximum at 2200 ± 200 m/s whereas the velocity of Na atoms produced during NaOH photolysis has a broader maximum at 1800 ± 400 m/s. Based on ab-initio calculations of the photolysis process, it was found that peaks of the velocity distribution of photolysis-generated Na and K atoms occur at 1200 ± 200, 1700 ± 200, 1200 ± 200, and 850 ± 100 m/s for photolysis of NaO, NaCl, KO, and KCl, respectively (Valiev et al. 2020). These estimates were performed by assuming that the velocity of parent molecules before photolysis equal to 0. Taking into account the initial velocity of parent molecules can lead to significant increase of velocities of photolysis-generated atoms (Pezzella et al. 2021). So a significant fraction of photolysis-generated Na atoms has velocities exceeding the escape velocity from the Moon, 2380 m/s. For this reason, photolysis-generated Na atoms may be quite abundant in Na lunar tail especially during the maxima of the strong meteoroid showers.

Detection of impact-produced and photolysis-generated Na and K atoms is a difficult task. Such atoms can be seen in the lunar exosphere only during the first ballistic flight time, about 1000 s, because such atoms quickly lose their energy during inelastic collisions with the surface. For this reason, observations of Na and K atoms in the lunar exosphere should be performed during the maxima of the strong meteoroid showers with the highest possible temporal resolution (at least less than 1000 s) and spatial resolution as it was already done during observations of Na plume formed after the LCROSS impact (Killen et al. 2010).

2.2 The Role of the Magnetosphere as a Source of the Exosphere (Focus on Na)

The interaction of energetic charged particles in Mercury’s environment with the surface can induce particle release. Evidence of correlation between the dayside regions of plasma precipitation and exospheric Na intensification have been reported from several ground-based observations (Potter and Morgan 1990; Killen et al. 2001; Leblanc et al. 2008; Mangano et al. 2015; Orsini et al. 2018), with temporal variability as small as a few minutes (Leblanc et al. 2009; Massetti et al. 2017).

2.2.1 Solar Wind and Magnetosphere Coupling

The interaction of the solar wind with the dipolar magnetic field of Mercury creates a magnetosphere, structurally analogous to that of the Earth’s but smaller in size, even with respect to the planetary radius $R_{{M}}$ (Fig. 16; see Milillo et al. 2020 and references therein). Recent data from the MAG instrument onboard MESSENGER show that the dipole moment is about 190 nT $R_{{M}}^{3}$, nearly anti-aligned with the rotation axis (that is, pointing southward), and displaced by 484 km northward with respect the equator (Anderson et al. 2011; Johnson et al. 2012). Computation of the internal magnetic field is complicated by the fact that both magnetic reconnection and magnetic induction affect the amount of magnetic flux above the surface of Mercury (Jia et al. 2019). Consequently, interplanetary transients (as CMEs) can be associated with a variation of the dipolar magnetic moment up to about 25% (Slavin et al. 2019). Under average solar wind conditions, the magnetopause—the current sheet separating Mercury’s internal magnetic field from the external Interplanetary Magnetic Field (IMF) dragged by the solar wind—has an average stand-off distance of about 1.4–1.5 $R_{{M}}$ in the upstream direction. The magnetotail has a diameter of about 5 $R_{{M}}$ at 3 $R_{{M}}$ downstream of Mercury (Slavin et al. 2009a; Winslow et al. 2013).

Fig. 16

Schematic of Mercury’s magnetosphere (Adapted from Slavin et al. 2009b)

Owing to its heliocentric distance, Mercury’s space environment is characterized by a high solar wind density (N_SW between 34 to 83 cm⁻³) and strong IMF ($B \sim 15$–30 nT), with typical values at 1 AU of ∼5–6 cm⁻³ and ∼5 nT, respectively. The Parker spiral IMF angle is about 20° at Mercury (that is, half the average value at 1 AU of 45°) with the radial IMF component usually dominating. The solar wind dynamic pressure at Mercury is on average ∼10 times larger than at 1 AU. As the solar wind impacts on the planetary magnetosphere it is decelerated and heated, and the IMF moving with the plasma piles up within the magnetosheath region which is between the upstream shock (bow shock) and the magnetopause. The Hermean shock is much weaker than Earth’s, as the solar wind has lower plasma $\beta$ (ratio of the plasma pressure (nk_BT) to the magnetic pressure ($B^{2}$/2$\mu _{0}$)) and Mach number than at Earth. The solar wind Alfvénic Mach number ($M_{{A}} = B/(\mu _{0}\rho )^{1/2}$, where $\mu _{0}$ is the permeability of vacuum, and $\rho$ is the solar wind density) at Mercury ranges between about 2 and 5 (Slavin and Holzer 1981; Gershman et al. 2013), and it is much lower than at the other magnetized planets, because $M_{{A}}$ is typically ∼7–10 at 1 AU and it increases with heliocentric distance. Low $M_{{A}}$ solar wind interaction drives a low plasma $\beta$ condition in the Hermean magnetosheath, promoting the development of a strong plasma depletion layer (PDL) just upstream the magnetopause, during nearly any IMF orientation (Gershman et al. 2013). Such a PDL allows magnetic reconnection to frequently occur between magnetic field of similar magnitude for any non-zero shear-angles, and with a higher rate than at the Earth (DiBraccio et al. 2013), driving a series of fast flux transfer events (FTEs) at the magnetopause (Slavin et al. 2012a; Imber and Slavin 2017; Zhong et al. 2020b), as well as flux ropes and plasmoid in the magnetotail (Slavin et al. 2012b; DiBraccio et al. 2015a; Zhong et al. 2020a).

The Dungey convection cycle in the Hermean magnetosphere takes places within only a few minutes (Slavin et al. 2010), which is about 1/60 of the duration observed at Earth where the cycle lasts several hours. The pileup of newly opened magnetic field lines and consequent magnetic merging events in Mercury’s magnetotail (loading-unloading cycle) is comparable in duration to the convection cycle as estimated from the reconnection rate at the dayside magnetopause (Slavin et al. 2009b; DiBraccio et al. 2013).

On the basis of the solar wind dynamic pressure distribution at the orbit of Mercury, and including the effect of low latitude erosion on the dayside magnetopause caused by the high reconnection rate (Slavin and Holzer 1979), the solar wind would be expected to impact directly onto the surface frequently. On the other hand, increases of the solar wind pressure were shown to drive induction currents in Mercury’s core (Hood and Schubert 1979; Suess and Goldstein 1979) that have the effect to intensify the global dipolar magnetic field of the planet (intrinsic field + induction field). On the dayside, the increased magnetic field acts against the compression caused by the dynamical pressure variation, and also increases the magnetic flux that is available to reconnect with the IMF, thus possibly mitigating—at least in part—the effect of the magnetopause erosion. By analyzing the dependence of the magnetopause compressibility as a function of the distance of Mercury from the Sun, Zhong et al. (2015) found that at the perihelion, where solar wind pressure is higher and Mach number, $M_{{A}}$, is lower, the more effective magnetic reconnection counterbalances the effect of the induction, whereas at aphelion the lower solar wind pressure and higher $M_{{A}}$ cause magnetic induction to prevail over reconnection effects.

During extreme solar wind events, such as CMEs, high dynamic pressure was observed to push the magnetopause close to the surface, especially in the southern hemisphere where the intrinsic dipolar field is weaker, thus allowing the direct impact of the solar wind onto the surface. A very low-altitude bow shock was observed when such high solar wind dynamic pressure events ($P_{SW}\sim 140 \div 290$ nPa) are also associated with intense southward magnetic fields ($B_{{Z}} \sim -100 \div -400$ nT). The high reconnection-driven erosion of the dayside magnetosphere traced by frequent FTEs indicates that the solar wind should be able to impact a wide portion of the sunlit hemisphere (Slavin et al. 2019). During this class of extreme events, termed “disappearing dayside magnetosphere” (DDM), no dayside magnetopause or magnetosphere signatures were found in MESSENGER data, only magnetosheath plasma was observed down to altitude of about 300 km from the surface of Mercury (four DDM events were identified from the four years of MESSENGER data set; Slavin et al. 2019).

During normal interplanetary conditions, as predicted by numerical modelling studies (e.g.: Sarantos et al. 2001; Kallio and Janhunen 2003, Massetti et al. 2003, 2007), the solar wind plasma can impact on the surface after the magnetic reconnection on the dayside magnetopause injects the plasma into the magnetospheric cusps. Protons in Mercury’s (northern) cusp were observed to flow toward the surface (Raines et al. 2014). These protons with energies around 1 keV likely moved into the cusp from the magnetosheath or the dayside reconnection. In the latter case, the protons should have experienced an acceleration along the magnetic field (Cowley and Owen 1989). The pitch-angle distribution shows the existence of a loss cone ($\alpha \geq 40$°), that strongly indicates a fraction of these protons are actually precipitating onto the surface at the footprint of the cusp (Raines et al. 2014). Furthermore, higher magnetic field magnitudes in the IMF are more likely to inject protons with field-aligned pitch-angles, making them more likely to precipitate onto the surface of Mercury rather than mirror in the cusp and travel downtail into the plasma mantle (Jasinski et al. 2017). This occurs because higher magnetic fields magnitudes in the IMF will produce more intense parallel electric fields at the reconnection site, accelerating the particles in the field aligned direction (Egedal et al. 2012; Li et al. 2017).

A clear north-south asymmetry on the night side of Mercury was found by mapping the plasma pressure to invariant latitude (Korth et al. 2014). Because of the northward shifted planetary magnetic dipole and correspondingly a wider southern cusp, an increased particle loss through precipitation in the southern hemisphere is expected. From the analysis of many cusp transits Winslow et al. (2014) found best fit solutions of 121° and 43° pitch angle for the loss cone of the northern and southern cusp, respectively. These observations support the idea that space weathering is actually occurring in the cusp areas.

The planetary ions released from the surface or resulting from the exosphere photo-ionization, circulate and are accelerated in the magnetosphere. They can be convected back onto the surface mainly on the night side at middle latitudes (Raines et al. 2013, 2014; Wurz et al. 2019). Therefore, these charged particles of solar wind or planetary origin can impact onto the surface over a wide range of local times releasing atoms and molecules from the surface.

Not only positive ions circulate and impact onto the surface of Mercury; in fact, the signature of electron precipitation has been observed through the detection of X-ray emission from Mercury’s nightside surface, located mainly between 0 and 6 h local time (Lindsay et al. 2016). Although presently unobserved at Mercury, electron stimulated desorption (ESD, see Sect. 2.1) is likely to occur during these electron precipitation events generally associated with reconnection events in the magnetotail (Starr et al. 2012). This precipitation could provide another possible driver for Na exospheric refilling via the process of ESD.

2.2.2 Magnetosphere–Exosphere–Surface Coupling at Mercury

Despite evidence of the effect of plasma precipitation on the exospheric Na distributions at Mercury (see Sect. 1.8), the details of the mechanism responsible for the surface release of these atoms has still not been identified. In fact, although ion sputtering is the first process that has been advocated, the expected release rate from this process is about two orders of magnitude less than what is needed to explain the observed quantity of Na atoms in Mercury’s exosphere. The Na yield, number of released atoms for single impacting ion, for a 1 keV- proton sputtering onto a regolith is between $Y=0.01$ and 0.1 (Lammer et al. 2003; Johnson and Baragiola 1991). The surface concentration of Na is about C = 3% in the hotter (low latitudes) regions, and up to 6% in northern smooth plains (Peplowski et al. 2014). The expected Na release due to ion sputtering is $F(\mbox{Na}_{sp})=F_{ion}\times Y\times C$, where $F_{ion}$ is the impacting ion flux. If we consider a typical solar wind density of 60 cm⁻³ and a velocity of 400 km/s at Mercury’s orbit, the flux of solar wind protons at the magnetopause is 2.5×10¹³ m⁻² s⁻¹, but it can reach higher values in specific conditions. Only 10% of this flux reaches the surface (Massetti et al. 2003), precipitating through the magnetic field lines in the cusps, so that, the impacting ion flux is $F_{ion}=(2\mbox{--}20)\times 10^{12}$ m⁻² s⁻¹ on a surface which area below the cusp is of the order of $A=10^{13}$ m². Therefore, $F(\mathrm{Na}_{sp})= (2\mbox{--}20)\times 10^{12} \times 0.1\times (0.03\mbox{--}0.06) = (8\mbox{--}200)\times 10^{9}$ m⁻² s⁻¹ leading to a release rate of $f(\mbox{Na}_{Sp}) = F(\mbox{Na}_{Sp})\times A = (8\mbox{--}200)\times 10^{22}$ s⁻¹.

The expected induced density at the surface is $n_{\mathrm{Na}} = F(\mbox{Na}_{Sp})/v_{sp} = (3\mbox{--}70)\times 10^{6}$ m⁻³ where $v_{sp} = 3\times 10^{3}$ m/s which is the typical velocity of the sputtered Na atoms ejected with a bulk energy around 2 eV (Mura et al. 2007), i.e. about 2 to 4 orders of magnitude less than the typical observed Na equal to $10^{10}$ m⁻³ (Cassidy et al. 2015).

But ion bombardment can contribute to the formation of the Na exosphere in a different way than direct sputtering. Indeed, Wilson et al. (2006) and Sarantos et al. (2008, 2010) presented an analysis of the Na observations during the Moon’s passage in the Earth magnetotail. When the surface is exposed to magnetospheric ions and electrons of the plasma sheet, a significant increase of the Na ejected flux by a factor between 20 and 60 is observed with respect to the period before the path through the magnetospheric plasma sheet. These authors explained these observations by the precipitation-induced diffusion of volatiles inside the regolith up to the upper surface leading to an increase of the reservoir of volatiles available for ejection into the exosphere through other processes. A similar effect was suggested to occur at Mercury (McGrath et al. 1986). Mura et al. (2009) proposed a different mechanism operating at Mercury, being the combined effect of first; ion sputtering onto the surface that would produce a chemical alteration of the surface, and then, second, the reduced binding energy of surface minerals that could allow the Na atoms to be released more efficiently by solar UV photons via PSD. The two mechanisms together may produce the increase of Na release in regions typical of IS, but with the high efficiency and lower energy distribution typical of PSD. This combined mechanism would be active only for volatile species (and not for refractories), which could explain why MESSENGER did not detect a mid-latitude enhancement of Mg and Ca.

Nevertheless, the suggestion that the observed Na exospheric distribution is strongly correlated with the plasma precipitation seem not to fully agree with statistical observations of Sodium distribution. In fact, the northward magnetospheric dipole shift should cause a wider southern region exposed to solar wind impacts. On the contrary, statistical studies based on ground based observations (with limited imaging capabilities owing to the atmospheric seeing) suggested that the southern peaks seen in Na are not more frequent or more extended than the northern ones (Potter et al. 1999; Mangano et al. 2015; Milillo et al. 2021). Milillo et al. (2021) found that the asymmetries in the latitudinal peaks also seem to be related to Mercury’s orbital phase, more specifically, the northern peak is more frequent during the outbound leg (roughly coinciding with positions above the ecliptic plane) whereas the southern peak in the inbound leg (coincident with positions below the ecliptic plane). This analysis seems to indicate that the solar effects on the Na exosphere are possibly influenced by another effect due to Mercury’s motion or heliocentric position (radiation pressure or distance from the interplanetary dust disk).

A statistical analysis of the Na exospheric distributions obtained by the THEMIS solar telescope by Mangano et al. (2015) concluded that there is not a clear relation between the IMF orientation and the profiles of the Na exosphere, even if double-peak patterns are observed more frequently during positive IMF B_X and negative IMF B_Z components, whereas positive IMF B_Z values are more frequently associated with single-peak equatorial Na emission. This is consistent with the high reconnection rate observed at Mercury not being strongly driven by the IMF orientation (DiBraccio et al. 2013; Slavin et al. 2012a, 2012b).

Short term Na variabilities accounting for about 10–20% of the total disk intensities have been identified from ground-based observations with time scales of hours down (Killen et al. 1999; Leblanc et al. 2009; Mangano et al. 2013; Massetti et al. 2017). In spite of the rapid changes in the precipitating proton flux related to the fast magnetospheric activity (time scales of 10 s of seconds) and magnetic reconnection processes (DiBraccio et al. 2013; Slavin et al. 2012a,b), the exosphere should show a much smoother response, because of the time delay of the exosphere transport. In fact, the ballistic time scale is about 10 minutes after MIV (Mangano et al. 2007) and the exosphere is expected to recover after a major impulsive ion precipitation event in some hours (Mangano et al. 2013; Mura 2012).

Orsini et al. (2018) reported the unique event of simultaneous in-situ observations of MESSENGER magnetic field (MAG) and ions (FIPS) with the ground-based observations (THEMIS) of the Na exosphere on September 20, 2012 during two strong iCMEs arrivals at Mercury (separated approximately eight hours from each other). Their analysis showed that during solar wind nominal conditions (IMF intensities ∼25 nT) the double peak configuration was regularly observed with a Na intensity that seems to be proportional to the ion fluxes observed inside the cusps. During the iCME passage the magnetic field intensity reached values >50 nT and the ion fluxes were so intense that they saturated the FIPS detector. During these events the Na exosphere assumed a more uniform distribution over the whole dayside, and the double peaks were no longer visible. This abrupt change seemed to be an evidence of the effect of plasma precipitation over a wide subsolar region of the Mercury surface, related to the increase of solar wind pressure able to push the magnetopause close to the Mercury surface, as in the cases described above (Slavin et al. 2019). According to this result, the major driver of the Na exosphere configuration may not be the IMF orientation, but the plasma $\beta$ (the ratio between thermal and magnetic pressures). A possible additional effect occurring during an iCME arrival, is that the iCME plasma is generally rich in heavy and highly charged ions (von Steiger et al. 2000). The yield of multi-charged heavy ion sputtering is higher than the yield of the average solar wind proton (Aumayr and Winter 2003); this fact may increase the surface release and, as a consequence, also the neutral atom, ion and electron density near the surface. The exosphere observed by Orsini et al. (2018) peaked at the subsolar point—this was thought to be unusual, given that Mercury’s Na is usually reported to peak at mid to high latitudes. However, the survey of ground-based (THEMIS) data by Milillo et al. (2021) put the observation of the iCME passage in its seasonal context. They found that for that time of year (true anomaly of 128°), exosphere emission peaks frequently near the equator.

2.3 The Lunar Exospheric and Plasma Environment

Na and K exospheres at the Moon were identified from Earth-based telescopes in late 1980 s (Potter and Morgan 1988a,b). In a manner similar to that at Mercury, the two species, though minor, assume the important role of tracers of the exospheric morphology and its dynamics. In particular, the Na component was identified in two components (thermal and suprathermal) with a long and variable tail in the antisunward direction, observed through its gravitational interaction with the Earth, especially at New Moon phase, when it surrounds the Earth and is gravitationally ‘refocused’ on the night-side (see Sect. 1.5, and references therein). Major lunar exospheric species also include Ar, He and Ne; H is a minor species.

The Neutral population at the Moon has been measured more recently by in-situ missions (Bhardwaj et al. 2005, 2010; Barabash et al. 2009; McComas et al. 2009). In particular, the spacecrafts Chandrayaan-1 and IBEX identified ENAs (Energetic Neutral Atoms) as derived from neutralization of solar wind protons after interaction with the surface. Though the energy spectrum distribution (whether Maxwellian or a power law) (Futaana et al. 2012; Allegrini et al. 2013), and also the dependence or not on solar wind and IMF characteristics are still debated, the intensity of such high energy neutral atoms is clearly related to the solar zenith angle (decreasing as SZA increases) (Wieser et al. 2009).

The Moon primarily differs from Mercury in the fact that it does not possess a global intrinsic magnetic field. Nevertheless, it possesses a series of mini-magnetospheres associated with the numerous magnetic anomalies spread over the surface (Coleman et al. 1972; Hood et al. 2001). A detailed map of magnetic anomalies over the Moon was produced from Kaguya and Lunar Prospector and can be found on Tsunakawa et al. (2015). Magnetic anomalies produce a shielding of specific surface regions, acting on all ionized particles present in the close lunar environment; as a consequence, they cause the double effect of deflecting impinging particles over the core region of the anomaly and of intensifying the flux impinging on the surrounding region (in an annular shape) (Vorburger et al. 2013; Saul et al. 2013). In fact, typical annular regions of higher ENA albedo have been identified almost perfectly superposed over the mini-magnetosphere map. As a consequence, the lunar surface also experiences an inhomogeneous space weathering effect, as well as a differential charging of the different regions of each mini-magnetosphere (Poppe et al. 2016).

The situation is different when the Moon crosses the Earth’s magnetotail: during these periods, the plasma in the Earth’s magnetosheath has higher velocity and the impacts produce higher ENA flux (and albedo) (Allegrini et al. 2013).

The lunar dayside ion population appears to be composed of three different families of particles: 1. Solar wind protons backscattered from the surface (and not neutralized as ENAs); 2. Protons scattered from the anomalies, and 3. Endogenic ions (Bhardwaj et al. 2015 and references therein). The first family accounts for up to the 1% of backscattered solar wind; the second family shows a scattering efficiency of scattering up to 10% and produces a broadening of the energy spectrum; collisionless shocks are also observed. The third family is composed of heavier ions of lunar origin such as He⁺, C⁺, O⁺, Na⁺ and K⁺. Low energy measurements by Kaguya showed an evident dawn-dusk asymmetry in Na⁺ ions (dusk side being lower by 50%), probably related to higher emission from the surface on the dawn side. Dawn side plasmas were attributed to micrometeoroid impact by Poppe et al. (2021). Pickup ions (probably He²⁺) are observed when the Moon is in the Earth’s magnetotail lobes and also upstream. Pickup ions at dawn with a peak at 16 amu mass have been identified too (probably originating from Earth’s OH, CH₄ and O₂).

Nightside protons were identified at an altitude of 100–200 km (in the wake, originally thought not to contain plasma) with trajectories both perpendicular and parallel to the IMF (Halekas et al. 2015). Electron fluxes are also observed, with enhancements in the wake region (Halekas et al. 2011). An overview of the interactions between the solar wind, plasma and the Moon to produce ions and neutrals is shown in Fig. 17.

Fig. 17

Overview of the processes known to occur around the Moon and on its surface, owing to interaction with the solar wind (from Bhardwaj et al. 2015)

To conclude, the processes acting on the Moon are similar to those observed at Mercury, with the main difference being that the Moon regularly passes into the Earth’s magnetosphere, which produces additional production through the interaction between the surface, the exosphere and the different ion (and electron) populations. Better understanding of the processes involved and of their relative roles, together with the influence of the surface potential and mini-magnetospheres of the magnetic anomalies, can give a global overview of the Lunar environment.

3 Exospheric Circulation: The Na Example at Mercury

3.1 The Key Observation of the Dawn/Dusk Asymmetry at Mercury and Its Orbital Variability

Sprague (1992) analyzed several set of observations (Sprague et al. 1990; Potter and Morgan 1986, 1990; Killen et al. 1990) and found that Mercury’s Na exosphere was spatially organized with systematic brighter emissions when observing the dawn side of Mercury than when looking to the dusk side. These authors explained it as a process of sodium and potassium ions from the dayside being accelerated to energies in excess of 1 keV by electric fields in the plasma sheet, striking the nightside Mercurian surface and being implanted to depths up to it few hundred Angstroms. This recycling of the dayside Na via ion implantation on the nightside could therefore induce a preferential release of the Na atoms in the morning when the surface moved to the dayside. These conclusions were criticized by Killen and Morgan (1993) who argued that the observations did not clearly show a dawn/dusk asymmetry nor could the ion recycling model really explain this asymmetry. These authors also showed that grain/regolith diffusion from depth to the surface is not intense enough to explain the needed supply rate of the exosphere.

Sprague et al. (1997) presented new set of observations, confirming the existence of a dawn/dusk asymmetry. This work was followed by Hunten and Sprague (1997), who suggested that the neutral Na exosphere could follow a cycle similar to that of the lunar Ar. However, Killen and Ip (1999) argued that the two species and environments were significantly different and that a Na cycle like that of Ar should not be expected.

Schleicher et al. (2004) published the first reconstructed image of the sodium exosphere as observed during the May 2003 transit of Mercury. This observation (reproduced in Fig. 18, panel a) clearly showed a strong dawn/dusk asymmetry with a much stronger absorption by the sodium exosphere on the dawn side than on the dusk. During the following transit in 2006, Potter et al. (2013) also observed the sodium exosphere in absorption, producing an image similar to the one published by Schleicher et al. (2004). Contrary to Schleicher et al. (2004), these authors did not observe a dawn/dusk asymmetry (Fig. 18, panel b). A third transit has been observed on 9 September 2016 by Schmidt et al. (2020) at an orbital position very close to that during Schleicher et al. (2004) observation and again displaying a clear dawn/dusk asymmetry. A striking feature of the 2016 transit is that the spatial distribution of the absorption equivalent width is similar to the one observed thirteen years before, consistent with the sodium exosphere being highly repeatable from one year to another as demonstrated by MESSENGER observations (Cassidy et al. 2015).

Fig. 18

Reconstructed image of the sodium exosphere as observed during three Mercury transits. Equivalent width above the limb observed during the (a) 7 May 2003 transit (Schleicher et al. 2004) at a TAA=149°, (b) the 8 November 2006 transit (Potter et al. 2013) at a TAA=328°, and (c) the 9 May 2016 transit (Schmidt et al. 2020) at a TAA=149°

Given this year-to-year consistency, why didn’t Potter et al. (2013) observe a similar dawn/dusk asymmetry? A key difference from the two other transit observations is the orbital position of Mercury. The three transit observations correspond to two different orbital positions associated to two different speeds of rotation of Mercury’s surface with respect to the Sun, as explained by Potter et al. (2006, 2013). Indeed, the rate of rotation of the surface in solar local time drastically changes along Mercury’s orbit, with a much faster prograde rotation at aphelion near TAA=180° (case of Figs. 18 a and c) compared to a much slower retrograde rotation at perihelion near TAA=0° (Fig. 18 b case). Potter et al. (2006, 2013) and Leblanc and Johnson (2003) thus explained this asymmetry by the rotation of Mercury’s nightside surface into the dayside. MESSENGER observations showed a definite TAA correlation in the dawn/dusk ratio of Na in the exosphere. This explains the Potter et al. (2013) observation of the 2006 transit at a TAA of 323° (Fig. 18b). The ratio of Na column abundance at 6 AM to that at 18:00, dusk, measured during the outbound leg of the MESSENGER orbit (TAA<180°) shows a strong dawn enhancement, whereas the inbound portion of the orbit (TAA>180°) shows no such dawn/dusk asymmetry.

A preferential bombardment by meteoroids of the trailing hemisphere with respect to the leading could also produce an asymmetry, as actually observed for the Ca exosphere (Burger et al. 2014; Killen and Hahn 2015; Christou et al. 2015). This would produce a permanent dawn/dusk asymmetry, changing along Mercury’s orbit. Furthermore, it would produce an equatorial maximum as for Ca and not high-latitude maxima as displayed in Fig. 18 a and c. Finally, the Na released by meteoroid vaporization should be ejected with significantly more energy (with a temperature larger than 3000 K) than as suggested by the altitude profile near the equator observed during these transits (around 1600 K according to Potter et al. 2013). Therefore, Meteoroid Impact Vaporization, MIV, is unlikely to be responsible for any dawn/dusk asymmetry in the Na exosphere.

Another potential explanation is that the release of a significant portion of the exospheric sodium atoms from the surface is controlled by the Sun. In order to induce a dawn/dusk asymmetry this way, at least during a portion of Mercury’s orbit, it would be necessary that the interaction between the surface and the Sun ejects a solar local time-dependent amount of sodium atoms into the exosphere with the release of more sodium in the exosphere in the morning than in the evening to yield a dawn peak. The mechanisms of ejection, such as photo-stimulated desorption or thermal desorption, would become less efficient with increasing local time; however this can only be explained by a change in the surface, the solar radiation being the same on both sides of the dayside and the surface temperature as well. This brings us to the second possible explanation which is a change in the upper surface from which the sodium atoms are released. Such a change could be either a variation in the quantity of sodium atom available for ejection (as suggested by Hunten and Sprague 1997) or in the way these atoms are adsorbed in the regolith (a typical signature of space weathering). Both explanations are equivalent, inducing a gradual impoverishment of the surface in sodium atoms available for ejection into the exosphere with increasing solar local time. Moreover, because MESSENGER and transit observations suggest that the sodium exosphere is steady from one year to another, it also implies that a Na-depleted evening surface would need to path back to a Na-enriched surface before rotating back to the dayside, after 88 Earth days in the nightside, to once again produce the observed dawn/dusk asymmetry.

The question of the existence of a TAA dependent dawn/dusk asymmetry is therefore that it provides us an important clue about the fate of the sodium exospheric atoms. As explained before, the best explanation today is that the asymmetry is produced by a permanent but TAA-dependent day to night cycle of the sodium exosphere, involving a layer of the upper surface and release from this layer into the exosphere.

The situation is more complicated than this, however, as shown in Fig. 18 where the dawn/dusk asymmetry is observed to change along Mercury’s orbit. Several decades of ground-based observations have led to large set of data allowing us to investigate this variability. Potter et al. (2006) analyzed several years of observations of Mercury’s sodium exosphere and extracted the ratio between the limb dayside emission and the terminator, either dawn or dusk, emission from the 94 useful days of observation. These authors further corrected these ratios by dividing them by a theoretical value for a uniformly spatially distributed exosphere, taking into account the phase angle of the observation. As shown in Fig. 19 panel b, the variations of these two ratios during the Mercury year display clear variability and are not always close to one as would be expected for a uniform exosphere. These variations are in good agreement with Leblanc and Johnson (2010), who simulated the dawn-to-dusk ratio (Fig. 19, panel a) and found values close to one around perihelion (below 30°) and which gradually increased up to values significantly larger than one up to 100 to 140° TAA before then being close to one the rest of the orbit. However, they are not in agreement during the second half of Mercury’s orbit between 180 to 330° with the model predicting significantly larger dawn-to-dusk asymmetry (panel a) as compared to the observations (panel b; see also panel c of Fig. 21).

Fig. 19

Panel a: Dawn side (upper) and dusk side (lower) emission intensity in kilo-Rayleigh ($kR$) per Mercury’s disk area along an annual cycle (true anomaly angle) as simulated by Exospheric Global Model—EGM (averaged on half a day period and for a phase angle of 90°). Circles: ground based observations. The size of the circles follows the sine of the phase angle. Increasing size of the circle corresponds to increasing observed proportion of Mercury’s exosphere. Vertical blue lines: perihelion and aphelion of Mercury. Vertical dark lines: reversal of the apparent motion of the Sun at Mercury. Vertical red lines: peak of solar radiation pressure and of solar photon scattering efficiency. Vertical green lines: peak of heliocentric radial velocity (Leblanc and Johnson (2010)). Panel b: Variation of the corrected terminator-to-limb ratio with true anomaly angle, black dots: dawn-to-limb ratio, red dots: dusk-to-limb ratio. Green line: ratio between the solar radiation pressure and the gravity surface intensity (Potter et al. 2006)

Leblanc and Johnson (2010) predicted an almost permanent strong dawn-to-dusk asymmetry because of the cycling of the sodium atoms from dayside to nightside and their accumulation in the nightside surface, leading to a persistent peak of sodium release in the morning, except during the phase of retrograde increase of the local time around perihelion. The intensity of this cycling should be partly influenced by the solar radiation pressure, as explained by Potter et al. (2007), because between the inbound and outbound orbital legs, the net effect of this force changes, in an opposite way, the intensity of the solar continuum seen by the sodium atoms (as modelled in Leblanc and Johnson 2010). Mura et al. (2009) added the surface rotation to their Monte Carlo exospheric model and found that the above mentioned mechanism of nightside refilling and dawn release could almost perfectly fit the first available observations at transit (Schleicher et al. 2004) (Fig. 20). The Doppler measurements made during transit and the observed enhancements of sodium column density above the poles also constrained the release mechanism to PSD, partially boosted by solar wind precipitation. It is worth noting, however, that to properly reproduce the transit observation, Mura et al. needed to simulate the evolution of Mercury for more than one Mercury orbit (see Fig. 20), and found that the dawn enhancement is a stationary state, contrary to what is observed along the orbit.

Fig. 20

Panel a: Comparison between transit observations (Schleicher et al. 2004, left) and modelling (Mura et al. 2009, right). The solar wind conditions at the time of the observation were modelled to obtain the proton precipitation onto the cusps, which in turn produces the polar enhancements observed via the mechanism proposed by Sarantos et al. (2008). The Doppler measurements (panel b, solid line) of Na particles’ velocity distribution can be properly fitted if the ejection source has a temperature above 1000 K (dashed line)

However, this picture of the sodium cycle has been partially contradicted by the long-term observations of the sodium exosphere by MESSENGER (Cassidy et al. 2016). As shown in Fig. 21 panels a, c and d, MESSENGER MASCS instrument reported a persistent peak of the exospheric sodium column density associated with the planetary cold longitudes, see Fig. 21, panel d. The cold longitudes (90° and 270° East longitudes in panel d) are the two planetary longitudes at the dawn and dusk terminators when Mercury is at perihelion. They are called cold longitudes because they received less solar flux than the other planetary longitudes when averaged over one Mercury year (Soter and Ulrichs 1967). Cassidy et al. (2016) explained these observations by a combination of cold surface and solar radiation pressure during a large portion of Mercury’s orbit around the perihelion leading to a maximum of surface absorption of exospheric sodium atoms at these specific longitudes. The building of a large surface reservoir around perihelion would then lead to a release of the sodium atoms all along the rest of Mercury’s year.

Fig. 21

a: Observed sodium limb column density (with line-of-sight tangent points below 30° in latitude) projected onto Mercury’s equatorial plane over the course of one Mercury year. The white dashed lines indicate the position of the cold longitudes as Mercury rotates (Cassidy et al. 2016). b: EGM-simulated vertical column density along one Mercury year. Each insert represents the vertical column density with respect to longitude (horizontal axis) and latitude (vertical axis) as simulated at the same true anomaly angle (TAA) as in panel a. The two vertical dashed lines in each insert are for the terminators. The centre of the insert corresponds to the subsolar point. c: Observed sodium limb column density with respect to True anomaly angle and local time at 300 km altitude. d: Observed sodium limb column density at 300 km altitude with respect to East longitude and local time

Both adsorption by the cold surface and solar radiation pressure are included in the EGM model (Leblanc and Johnson 2010) and the one developed by Mura et al. (2009). As shown in Fig. 21, panel b, in the case of an EGM-simulated spatial distribution of the vertical column density, the cycle of Na exospheric atoms occurs throughout the Mercury year, so there is always a cycle of Na atoms from the exosphere onto the nightside surface. This in turn leads to the preferential enrichment of the surface pre-dawn regions in sodium atoms and to the existence of a release of Na atoms from the surface into the exosphere at dawn over the majority of Mercury’s orbit. As shown in panel b of Fig. 21, the peak of the simulated vertical column density seems to follow the evolution displayed in panel a during the first half of Mercury’s orbit, from a true anomaly angle of 0° up to 180°, but continues to appear at dawn during the second part of the orbit, in contradiction with the observations that display no dawn enhancement at TAA=220° and 250°. What could affect the cycle as depicted in panel b during this portion of the orbit remains an open question. Several potential mechanisms that could influence this cycle are discussed in the following sections.

3.2 Surface Abundance as a Signature or a Driver of the Na Cycle?

The surface of Mercury, because of the absence of an atmosphere, has evolved mainly under external forces during the last few billion years. It is saturated with small impact craters and covered by regolith, which is defined as “the entire unconsolidated or secondarily recemented cover that overlies more coherent bedrock, that has been formed by weathering, erosion, transport, and/or deposition of the older material” (Eggleton 2001). In many aspects, the study of the surface of Mercury inherits concepts from that of the Moon, even if the regolith of Mercury is probably more mature than the lunar regolith, with smaller grain sizes and larger proportions of glassy particles (Langevin 1997). This is because some differences exist in the size distribution of micrometeoroids/meteoroids (with relatively more micrometeoroids at Mercury, which also have higher impact energies; Janches et al. 2021), in the solar wind flux, solar cosmic rays’ flux and surface temperature.

Mercury’s surface is continuously modified by loss processes and by replenishment of new material. Every agent precipitating on the surface transmits energy to bound particles and may produce their release: plasma (IS, ES); photons (PSD), and micrometeoroids (MIV; see Sect. 2.1). Different studies (i.e. Wurz and Lammer 2003; Leblanc and Johnson 2003; Mura et al. 2007) have shown that the particles extracted by the surface just by thermal energy (TD) do not have sufficient energy to escape from the planet; hence, this process may be assumed to be negligible in terms of net surface erosion, although it causes some redistribution of particles over the surface, and it is necessary to take it into account as well. The material on the surface may be characterized in two groups: volatiles (those species with a relatively small equilibrium condensation temperature) and refractories (all others). Compared to refractories, which are primarily sensitive only to very energetic processes such as IS and MIV, volatiles may be extracted by all processes and are more exposed to variations in surface concentration, sometimes in a rapid way. Understanding such short-term variabilities is a key factor in understanding the long-term history of the surface and, hence, of Mercury’s planetary evolution. Among volatiles, sodium is the most natural candidate for studying these phenomena, because in addition to being relatively abundant in the exosphere of Mercury, it is also observable from the ground with relative ease.

We therefore assume that volatiles such as Na are extracted by all the surface processes that extract and modify the surface composition of Mercury, and although they mostly reprecipitate, partially they are lost to space. In particular, Na neutral particles in the exosphere are subject to the radiation pressure of the Sun and this increases the escape probability. To add some complexity, the radiation pressure is not constant but varies over the Mercurian year (Fig. 19b). A long tail of escaping sodium particles can be observed (Potter et al. 2002; Fig. 8), and knowing the order of magnitude of the speed (by Doppler measurements—see Schleicher et al. 2004 —or by numerical simulations), it is possible to approximately quantify the amount of sodium that is lost instantly. Some sodium is also lost from the exosphere by Jeans escape, or by photoionization and escape of ions, governed by magnetospheric processes and solar wind pickup. This represents a net loss of sodium, which is, in a small fraction, replenished by that contained in the precipitating micro-meteoroids (Genge et al. 2008).

On a geological timescale, impacts are the dominant mechanism in terms of their effect on the surfaces of the airless bodies of the solar system. The frequency, geographic distribution and type of impact control the evolution of the finer-grained superficial heterogeneous regolith. In addition, larger impacts have an influence on the orography of the terrain. The long-term implications of this net are discussed in Orsini et al. (2013), whereas annual variabilities have been discussed in several studies, as more observational data have become available (e.g. Leblanc and Johnson 2010; Milillo et al. 2021). In any case, to achieve some sort of short-term stability on a yearly cycle, a mechanism that refills the uppermost surface layer is needed. Impacts remix the material in the first layers of the surface in a process called “impact gardening”. We may consider that as a “blending” or “tipping” because it repeatedly and stochastically reverses the depth distribution of materials that, otherwise, would be a distinct stratigraphy with depth. Killen et al. (2004) calculated the outward diffusion rates from inside the regolith grains and compared them with the gardening scale times, which are the typical “annealing” timescale for the surface to lose memory of the previous state. The diffusion scale times—to completely unload the grain—must be longer, otherwise the grain empties completely. This implies a threshold for the net outward flux, which is also calculated in Killen et al. (2004), and it is mostly a function of grain size and diffusion coefficient. However, the large uncertainties on these two latter quantities makes the evaluation quite difficult. Particle precipitation, and the effects of plasma impacts, also adds some complexity to the physics. Sarantos et al. (2008) using plasma and exospheric Na measurements at the Moon, speculated that the plasma bombardment may increase the diffusion rate (enhanced diffusion) by supplying energy to the deepest layers of the grains. At Mercury, that would result in an excess of Na release where solar wind precipitates (dayside magnetospheric cusps), leading to distinct bulges of Na excess in the Northern and Southern dayside exosphere as observed (Schleicher et al. 2004; Mangano et al. 2015). It was also suggested by the observations performed by the Gamma-Ray Spectrometer onboard MESSENGER, that the enrichment in Na of the high latitude surface with respect to the equatorial surface (Fig. 22b) could be a signature of the relation between upper surface composition and exospheric circulation as suggested by the exospheric models (Fig. 22a). On the other hand, the high-latitude enhancement in Na follows the north volcanic plains unit which is a geologic feature. Better sampling of the southern hemisphere by the BepiColombo mission will hopefully provide new insight into this circulation versus geology aspect of the Na exosphere.

Fig. 22

Left: Example of Na/Si abundance ratio in the Northern hemisphere of Mercury’s surface for three different scenario of forward modelling of the observations performed by the Gamma Ray Spectrometer of MESSENGER (see Peplowski et al. 2014, for details). Top-right: Simulated sodium surface density (in log₁₀ of Na/$\mbox{cm}^{2}$) in Mercury’s surface as modelled by EGM; bottom-right: longitudinal variability of surface Na abundance, as simulated by using the same model as in Mura et al. 2009, and averaged over all latitudes. The two maxima at 90° and 270° are the effect of the updated temperature map with “cold poles” at these longitudes

A schematic illustration of a model of surface accumulation and release of Na is shown in Fig. 23. Solar wind (or magnetospheric) plasma precipitates onto a surface element and causes immediate ion sputtering or enhanced diffusion of sodium, from deep in the regolith layer (up to fraction of μm). If the element is in the dayside, PSD and TD release Na from the uppermost surface layer, but because these processes are highly efficient at Mercury, the net flux is basically limited by the amount of free Na in that element, which is provided by diffusion and ion-enhanced diffusion. Particles released by TD have low energy and quickly return to a (maybe different) surface element; particles release by PSD have longer ballistic lifetimes, and they may either fall back farther away or be lost to space, depending on the combination of multiple effects (radiation pressure, release energy, etc.). Thus, we expect the free Na content in the surface to be a function of the local time (see as an example Fig. 22b), because surface elements that are brought to the nightside by planetary rotation ceases to release Na particles, so that their Na content can be replenished. Models following Fig. 22 (Mura et al. 2009; Leblanc and Johnson 2010) are in fact able to explain the yearly variability or the excess of Na column density observed close to the dawn terminator during transit measurements (Schleicher et al. 2004), for which the local-time surface Na abundance profile should always peak close to dawn. However, MESSENGER observations show that the picture is more complicated than this. Cassidy et al. (2015) observed that the sodium exosphere is enhanced above Mercury’s cold-pole longitudes (Fig. 21a). This stems from the fact that, owing to the 3:2 spin/orbit resonance, the longitudes at 90° and 270° are always at the subsolar point at aphelion. On long timescales, this leads to a smaller average temperature close to these longitudes, and smaller temperature means less Na release on average, which will result in the formation of two sodium reservoirs at 90° and 270°. According to Cassidy et al. (2016) the reservoirs are filled during periods of anti-sunward sodium transport, when the cold poles are near the terminator.

Fig. 23

Scheme of Sodium circulation between Mercury’ surface and exosphere

To account for the presence of cold poles, one approach could be to adapt the surface temperature models. In most work before the MESSENGER observations, surface temperature was modelled with simple local-time functions with no longitudinal variability. However, although it is straightforward that such reservoirs would work for the surface abundance, it is still debated why the accumulation of Na particles at the cold pole at 270° would, at the same time, result in an enhancement of exospheric sodium over the same region, which seems counterintuitive. For example, we may assume that surface composition maps such as those in Fig. 22 (right), with maxima at 90° and 270°, are valid for all TAAs, and run a typical exospheric model. The result will be similar to Fig. 24, with almost correct asymmetries. The main problem with this approach is that the actual instantaneous surface map is not the average one; in other words, the available models are able to explain the MESSENGER observation in Cassidy et al. (2016) only if we assume that the cold-pole enhancement has worked for ages in the past, causing an excess of sodium at 90° and 270° that is now eroded by PSD release. Because observations from ground are not able to disentangle the yearly variability from the local-time ones, it is likely that a big improvement of our knowledge of the surface variability of sodium will come when BepiColombo orbital data are available.

Fig. 24

Simulated Sodium column density at different TAAs and projected onto the equatorial plane of Mercury, to be compared with MESSENGER observations in Fig. 21a (see text for details)

3.3 What Else Could Control the Na Cycle?

3.3.1 The Role of the Meteoroid Bombardment

The meteoroids arriving on Mercury may have many different sources, from the Main Belt Asteroids (MBA) to comets (Janches et al. 2021). Within the comet populations, these may further break down into Jupiter-family (JFC, short-period) and long-period (LPC) comets, with the LPCs being divided into Halley-type comets (HTC) and Oort Cloud comets (OCC). Small particles originating from MBAs ($D<2$ cm) were revisited by Borin et al. (2009, 2016a, 2016b) who showed that the circularization of their orbits by Poynting-Robertson drag results in narrow impact velocity distributions. The analytic velocity distribution of Cintala (1992) is 20.50 km s⁻¹ as compared to 16.81 km s⁻¹ from Borin et al. (2009, 2016a, 2016b). Large MBA meteoroids ($D>2$ cm) have been treated by Marchi et al. (2005) and provide a much broader impact velocity distribution at Mercury, ranging from 20 to 80 km s⁻¹. These higher velocities are due to the fact that larger particles are influenced only by gravitational forces. The impact of large meteoroids are rare events, with low probability that one might occur during the BepiColombo mission (Mangano et al. 2007) and are briefly described towards the end of this subsection.

More recent models focus on demonstrating that the directionality of the meteoroid influx plays a major role in the characteristics of the Hermean exosphere (Pokorny et al. 2017). This adds a strong dependence of impact characteristics and fluxes with respect to the planet’s TAA, which is true for all planets and satellites (Janches et al. 2018, 2020) but is particularly extreme at Mercury owing to the planet’s high eccentricity and orbital inclination (Pokorny et al. 2017). Such dependency also influences the impact velocity distributions (Pokorny et al. 2018), which can vary from $V_{imp} <70$ km s⁻¹ at perihelion and $V_{imp} <50$ km s⁻¹ at aphelion for meteoroids originating from MBAs and JFCs. Nesvorny et al. (2010) argued that JFC-released meteoroids represent the majority of the flux incoming into Earth’s atmosphere, both in number and mass, emphasizing their importance in the inner solar system. Both Borin et al. (2016a, 2016b, 2017) and Pokorny et al. (2017, 2018) considered for the first time this population as part of the influx at Mercury. Owing to the high eccentricity of Mercury and low impact velocities of these meteoroids compared to Mercury’s orbital velocity, the impact directions of JFC and MBA meteoroids are expected to experience significant motion in the local reference time frame during Mercury’s orbit.

Similar to that of MBA meteoroids (see Pokorny et al. 2018), there is a shift in the radiant distribution of JFC meteoroids as Mercury moves toward or away from the Sun, caused by the nonzero eccentricity and inclination of Mercury’s orbit and a consequent drift of the planet’s velocity vector from the ecliptic plane and its perpendicular orientation with regard to the radial vector.

The influence of meteoroids originating from long-period comets, such as HTCs or OCCs, was only treated recently by Pokorny et al. (2017, 2018). These play an essential role in the formation of Mercury’s exosphere, even though they represent a small fraction of the meteoroid input budget. This is because they are dynamically less evolved than MBA or JFC meteoroids and are released into highly eccentric orbits intersecting Mercury faster and at high speeds, thus making them the dominant source of physical phenomena regarding the formation and morphology of Mercury’s exosphere. Specifically, the mass flux of LPC meteoroids at Mercury compared to JFC meteoroids could be as small as 5% but their impact velocities reach values over 100 km s⁻¹ and make them the dominant source in terms of the impact vaporization or the impact yield (Pokorny et al. 2017, 2018).

Recent estimates on the mass accretion of meteoroids (Pokorny et al. 2018), averaged on the Mercury orbit, provided the following values: MBA meteoroids 0.26±0.15 tons per day, JFC meteoroids 7.84±3.13 tons per day, HTC meteoroids 1.69±0.91 tons per day, and OCC meteoroids 2.37±1.38 tons per day (Janches et al. 2021).

The vaporization flux averaged over a Hermean year then results in $F_{\mathit{orbit}}= (200\pm 16)\times 10^{16}$ g cm² s⁻¹, with maximum value of $(436\pm 57)\times 10^{16}$ g cm² s⁻¹ occurring at TAA=337°, and a minimum value of $(82\pm 12)\times 10^{16}$ g cm² s⁻¹ occurring at TAA=188°. Pokorny et al. (2018) state that only ∼1% of the estimated total vapor appears to contribute neutrals to Mercury’s exosphere. Moreover, the model of Pokorny et al. (2018) predicts an important perihelion-to-aphelion ratio in the impact vaporization rate (Fig. 25).

Fig. 25

Total vaporization flux as a function of TAA and the impact velocity. The units are g cm⁻² s⁻¹ per 2 km s⁻¹ bin (Pokorny et al. 2018)

The meteoroids discussed so far are usually very small in size (<cm) and their vaporization at the surface of Mercury provide a mostly continuous source to the exosphere of Mercury. Large impactors do not contribute significantly to the long-term state of the exosphere but instead can provide transient enhancements. A 1 m sized meteoroid is expected to impact the Earth at a rate of 10 per year, and this estimate is an order of magnitude lower for Mercury (Marchi et al. 2005). Mangano et al. (2007) modelled the transient effects to the exosphere of a 1 m and 10 cm sized meteoroid surface impact. It should be noted that the modelled exospheric densities from the impact reported by Mangano et al. (2007) would most likely be an order of magnitude larger for sodium, when adjusted for the surface sodium abundance that has since been updated from MESSENGER observations (McCoy et al. 2019). Mangano et al. (2007) found that an impact by such meteoroids would be noticeable to the exosphere for Al, Mg, Si and Ca, and more likely to be noticeable on the nightside for Na and K owing to the higher background exospheric levels on the dayside. Recently, an observation by MESSENGER of planetary ions that had been detected in the solar wind from an inferred large meteoroid impact was reported by Jasinski et al. (2020). The ions were estimated to be mostly Na⁺ and Si⁺, just photoionized and picked-up by the solar wind. The neutral densities of the plume at high altitudes of ∼5000 km were inferred from the measured ion fluxes to be ${<}10^{2}$ cm⁻³. Such exospheric neutral enhancements are expected to be transient in nature, and only expected to last for ∼20 minutes (Mangano et al. 2007).

Meteoroid showers, caused by fresh meteoroids ejected from comet nuclei into heliocentric orbit, represent a significant, but short-lived, enhancement of the flux incident on a planet (Janches et al. 2020). During a shower, the meteoroid velocity distribution and direction remain fixed. Christou et al. (2015) (see also Killen and Hahn 2015) showed that the stream belonging to short-period comet 2P/Encke crosses Mercury’s orbit twice, once at TAA≳0° with the meteoroids arriving on the planetary nightside and a second time at TAA≲180° on the dayside (but much farther from Mercury and therefore probably of lesser importance), with a speed of ∼35 km s⁻¹ in both cases. The authors estimated the mass influx on Mercury to be 10.5 g s⁻¹ or ∼0.9 tons per day, which compares favourably with other sources. However, owing to a shower’s spatially restricted nature, this influx is only sustained for a short period of time, typically no more than a few tens of degrees of TAA; therefore, the resulting fluence over the entire orbit is likely less significant than that from other sources.

LADEE was the first mission to directly observe the link between meteoroid bombardment and exosphere formation (Elphic et al. 2014) because, in addition to the LDEX dust experiment, it also carried an Ultraviolet-Visible Spectrometer (UVS; Colaprete et al. 2014) and a Neutral Mass Spectrometer (NMS; Mahaffy et al. 2014). The comparison between the observations of LDEX and UVS identified a correlation between the meteoroid influx and the Na and K abundances in the lunar exosphere, in particular with shower activity. Specifically, Colaprete et al. (2016) and Szalay et al. (2016) found a strong correlation of exospheric potassium and meteoroid ejecta during the Geminids meteoroid shower, exhibiting a much stronger response than sodium (Fig. 3). With the exception of the Geminids, the authors found a weak correlation between the meteoroid influx as measured by LDEX and exospheric density of alkalis as measured by UVS. To fully understand why these two species respond differently to meteoritic bombardment, requires to better identify the differences of their reservoirs, sources and sinks on the lunar surface. Similarly, with NMS, Benna et al. (2019) reported detections of water vapor released into the lunar exosphere. The timing of 29 water release events agreed with periods when the Moon encountered known meteoroid streams. The authors used these measurements to constrain the hydration state of the lunar soil, arguing that by heating the soil meteoroids release water that is buried below a layer of dry regolith at depths of a few centimeters.

3.3.2 The Role of the Surface Interaction with the Exosphere

Our inability to explain the observed Na cycle suggests that current models of the surface-exosphere interaction may be incomplete. Some progress towards a better specification of the boundary conditions for models was contained in the recent work of Sarantos and Tsavachidis (2020). To understand how the microstructure of soil affects the exospheric reservoir for alkalis, a simulation of a porous soil (1 mm in depth) was produced in that work using spherical grains sampled with a distribution of grain sizes from Apollo Lunar Soil Sample 72141, a typical mature soil (keeping in mind that Mercury’s regolith is probably different from Moon’s regolith, as an example, in composition). The competition between desorption and thermal diffusion was studied with a Monte Carlo code, in which the trajectories of 16,000 test particles were tracked in such beds for up to 90 days. Repeated desorption and re-adsorption events were simulated using parameters obtained from thin-film experiments until adsorbates escaped to vacuum or time expired. Diffusion both through the spaces between grains as well as diffusion along the grain surface (surface diffusion) was included in this simulation. The temperature of the soil was adjusted from 100 K, typical of the nightside, up to 590 K, the noon temperature at Mercury’s aphelion.

The soil structure was found to change the residence time of atoms on the surface, and the evolution of the surface reservoir, in two ways not previously appreciated: the effect of 1) microshadows and 2) soil thermal gradients. When adsorbed alkalis cannot thermally desorb, as it occurs at lunar temperatures for the usually assumed binding energies, atoms that are not in illuminated areas of grains are trapped unless adsorbate mobility is posited (Fig. 26a). This is to say that if adsorbates are assumed to be “frozen” on a grain between the arrivals of UV photons, about half the adsorbates comprising the exosphere reservoir (i.e. equivalent to the porosity of the soil) are trapped in microscopic shadows (the underside of grains) and do not contribute to desorption. Only at different True Anomaly angles, when the soil becomes warmer, would the remaining particles contribute to desorption when thermal desorption or increased mobility along the grain boundary dislodged atoms from shadows. This is different than the assumption in global models of the Na reservoir (e.g., Leblanc and Johnson 2003, 2010; Mura et al. 2009) that all particles returning to the surface are susceptible to UV photons. The simulation suggests that if thermal desorption is suppressed, e.g., when the assumed pre exponential factor is reduced or when the binding energy is increased owing to surface weathering, there is a possibility for increased lags in surface outgassing because half the adsorbates are unavailable for desorption. If the lag is considerable, we would err in our present models of the Na reservoir. A second finding was that the monotonic increase in temperature expected within the first 1-2 cm of the soil helped reduce losses of adsorbates to the subsurface by “biasing” the random walk. This gradient actually increased the ability of adsorbates to enrich the reservoir. In summary, the temperature at which the surface turns from retentive to emissive is a function of the assumed parameters for thermal desorption, the adsorbate mobility, and the soil thermal gradients. More work is required to quantify at which temperature the porous surface starts evaporating when these complications are considered.

Fig. 26

Simulated desorption of alkali adsorbates from a porous soil. (a) Desorbed versus initially adsorbed particles as a function of time for soil temperature $T=350$ K. Adsorbates that are not on illuminated grains are trapped unless high mobility is considered; (b) Effective photodesorption rate for constant and temperature-dependent yield and different mobilities. Mobility in these simulations is defined by a barrier for surface diffusion (Ediff). Figure from Sarantos and Tsavachidis (2020)

In this closer look at the microphysics of soil, diffusion and re-adsorption reduced desorption rates and affected their temperature dependence. The photodesorption rate from an ensemble of grains had a different dependence on temperature than the rate from a single grain as it was found to combine the dependence of photodesorption yield, measured by thin-film experiments for sodium, the sticking coefficient, which is temperature-dependent for sodium, and the diffusion rate. In fact, for high diffusivity of adsorbates the photodesorption rate could be a non-monotonic function of temperature (Fig. 26b). Second, re-adsorption to adjacent grains combined with diffusion was shown to slow thermal desorption at Hermean temperatures as if the effective binding energy from the soil is higher, ∼2 eV/atom from the sphere packing as opposed to 1.85 eV/atom used to describe desorption from a single grain. It is clear from these results that 1) parameters from thin-film experiments must be modified when adopted in exosphere models in more ways than the usual assumption of a reduction of the rate for porosity (i.e. the porosity reduction is temperature-dependent), and 2) thermal desorption rates too are subject to this reduction owing to soil porosity. These are additional improvements that we must strive to incorporate in models of the surface reservoir.

3.3.3 Ion Circulation

The picture of planetary ion circulation at Mercury has been assembled from observations, modelling, and intuition gained through decades of research at Earth. The first measurements of these ions were made by MESSENGER’s Fast Imaging Plasma Spectrometer (FIPS, Andrews et al. 2007), as the ion instrument on Mariner 10 failed to deploy. These observations quickly revealed that Mercury’s magnetosphere is dominated by solar wind plasma that is concentrated mostly in the magnetospheric cusps and central plasma sheet (CPS), much like at Earth (Zurbuchen et al. 2008, 2011; Raines et al. 2011). FIPS observed Na⁺ ions on every orbit, reported as part of a group of ions in the mass per charge range 21–30 amu/e, including Mg⁺ and Si⁺ (Raines et al. 2013). No detection of K⁺ has been reported from FIPS in the orbital mission, as identification of counts in that mass per charge range was found to be complicated by an instrument background signature. Though most modelling studies have focused on Na⁺, it is likely that heavier ions, such as K⁺, behave in a similar manner dynamically, though their source(s) may be different. A wealth of ion measurements was returned from the instrument. Na⁺ ions at Mercury mostly originate from the exosphere, where photoionization of the neutral exospheric sodium mass-loads the plasma in Mercury’s magnetosphere with Na⁺. Owing to the variation of density and scale height of Mercury’s exosphere with the planet’s eccentric orbit around the Sun, the Na⁺ content at Mercury’s magnetosphere is also found to largely follow the same trend as the exosphere (Jasinski et al. 2021). Calculations using neutral observations from MESSENGER, estimate that the dayside Na⁺ production rate from photoionization is ∼10²⁴ ions s⁻¹ (Jasinski et al. 2021). With their ∼1 eV initial energy, Na⁺ photoions born in Mercury’s dayside magnetosphere remain largely trapped on closed planetary magnetic field lines. Their gyroradius is small enough, of order 10 s of km, that they are tightly locked to the dipole-like magnetic field, bouncing between the magnetic mirrors formed in the increasing field near the surface. Those that are very close to the magnetopause may be able to gyrate into that boundary layer, though it would be difficult for them to cross into the magnetosheath as the magnetopause is ∼100 km thick (DiBraccio et al. 2013). In some cases, they may acquire enough energy to gyrate out of the dayside. Ions that cross into the magnetosheath, will be picked up by the magnetosheath plasma flow and rapidly energized up to hundreds of eV or even up to several keV (Fig. 27, right). Most of these ions would be lost, carried downstream in the magnetosheath on the flanks of Mercury’s magnetotail. A small fraction may be injected into the magnetosphere through the cusps. Ions entering the magnetospheric cusp will either precipitate onto the surface or magnetically mirror and continue travelling away from the planet, forming the plasma mantle in the magnetotail (DiBraccio et al. 2015a; Jasinski et al. 2017). One of the surprises of MESSENGER’s first ion measurements was the observation of keV Na⁺ ions in Mercury’s northern cusp (Zurbuchen et al. 2011; Raines et al. 2014). The energization of these ions is not yet well understood, but it is likely to include pickup into the magnetosheath flow prior to cusp entry or energization by reconnection by parallel electric fields. Na⁺ photoions originating in the cusp may gain energy owing to the curvature of their E x B drift paths (Delcourt et al. 2002), resulting from the combined effect of electrostatic (E) and magnetostatic (B) forces on individual ions. This behaviour was shown convincingly by test particle simulations, tracing trajectories in an analytical model of Mercury’s magnetospheric magnetic field by numerical integration of an adiabatic, guiding-center (Delcourt et al. 2002; Delcourt 2013) or full equation of motion (Delcourt et al. 2003). Na⁺ ions were found to gain energy logarithmically in great arcing trajectories through the northern magnetospheric lobe and into the central plasma sheet (CPS, Fig. 28). Modeled ions were energized from initial energies of 0.1 eV up to several hundred eV through their <10 min. travel time to the CPS (Delcourt et al. 2012). The much smaller size of Mercury’s magnetosphere relative to that of the Earth results in substantially increased curvature and thus stronger energization (Delcourt et al. 2002) than in Earth’s cleft (high-altitude cusp) ion fountain (Horwitz 1984; Lockwood et al. 1985). Observational evidence of acceleration local to the cusp is very limited. A small portion of Na⁺-group ions observed by MESSENGER in the northern cusp were found to be moving away from the surface (Fig. 28, left), anti-parallel to the magnetic field, which is mostly radial there (Raines et al. 2014). These ions had energies in the 200–300 eV range, higher than test-particle model predictions but possibly consistent with wave-particle energization mechanisms that may occur in the cusp (see Raines et al. 2014, and references therein).

Fig. 27

Two possible sources for Na⁺ ions in the cusp: (left) Na⁺ ions are generated in the cusp, both by solar wind impact and photoionization, and are accelerated by processes there. (Right) Neutral Na atoms are ionized near the magnetopause, picked up in the magnetosheath flow and swept into the cusp. Adapted from Raines et al. (2014)

Fig. 28

Model Na⁺ trajectories: (Left) projections in the noon-midnight meridian plane (top) and in the equatorial plane (bottom), (right) kinetic energy versus time. The test ions are launched from 65° latitude with 0.1 eV energy on the noon meridian. Three distinct cross-electric magnetospheric potentials are considered: 1 kV, 10 kV, and 30 kV (coded in grey, blue, and red, respectively). Adapted from Delcourt (2013)

Na⁺ ions arrive preferentially on the pre-midnight side of the CPS, a feature shown both in observations (Raines et al. 2013; Jasinski et al. 2017) and test-particle modelling (Delcourt et al. 2003; Delcourt 2013). Once in the CPS, Na⁺ ions are likely accelerated further, from several keV to up over 10 keV depending on the cross-polar cap potential (Delcourt et al. 2003), which is determined largely by the rate of magnetic reconnection at the dayside magnetopause. Motion of Na⁺ ions there is complicated and varies periodically with distance from the planet, owing to the magnetic field geometry and their large and varying gyroradii, of order 0.6–1.3 $R_{{M}}$ (2440 km) for 1–5 keV energies. They can undergo quasi-adiabatic, Speiser-type orbits (Speiser 1965), where they gain substantial energy from the dawn-to-dusk electric field as they oscillate around the magnetic field reversal in the central current sheet. At other distances, Na⁺ ions behave non-adiabatically, their large gyroradii causing them to be partially demagnetized and drifting substantially across the magnetic field. Gershman et al. (2014) estimated the temperature of Na⁺-group ions in the CPS to be predominately in the 5–40 MK range, with a small number of values going higher, up to ∼55 MK (4.7 keV). O⁺-group ions are found at about the same temperatures, indicating a heating mechanism that is not mass-proportional, consistent with energization in the potential drop of an electric field. Although it is not clear if planetary ions strongly affect the dynamics of the magnetotail, Na⁺-group ions were found to make up to 15% of the plasma thermal pressure and 50% of the mass density (Gershman et al. 2014), so clearly that potential exists.

Loss of Na⁺ ions from the magnetotail occurs through several processes. Ions travelling downtail and forming the plasma mantle (having previously mirrored in the cusp) will either be lost downtail or will drift equatorward into the plasma sheet (Jasinski et al. 2017). Na⁺, owing to its higher mass, will more likely drift into the plasma sheet in comparison to protons—although owing to the observed velocity distributions, most of the ions observed in the plasma mantle are expected to be lost downtail (Jasinski et al. 2017). Reconnection in the CPS creates fast plasma flows that carry heavy ions toward the nightside surface. These flows have been estimated at ∼200–300 km/s on average, using a statistical reconstruction from FIPS measurements (Dewey et al. 2018). This plasma may impact broadly across the nightside surface, or be slowed and deflected around the dipolar magnetic field to impact at mid-latitudes near the open-closed field line boundary (like the auroral region at Earth). Studies of reconnection events have shown evidence of the flow breaking that would be associated with this plasma deflection (Poh et al. 2017; Dewey et al. 2020). Energetic electrons (∼100–200 keV) have been shown to be associated with magnetotail reconnection signatures, such as magnetic field dipolarizations (Dewey et al. 2018). When mapped to the surface in a dipolar field, these electrons arrive at magnetic latitudes 10–40°, just below the estimated location of the open-closed field boundary. X-ray fluorescence measurements show substantial enhancements around this region, and are thus attributed to the impact of these energetic electrons upon the surface (Lindsay et al. 2016). Ions that do not precipitate are likely carried around the dusk side of the planet, where their keV-energies result in large gyroradii (∼100–300 km) that likely cause them to be lost either to impact on the surface or crossing into the magnetosheath (Raines et al. 2014). When not carried planetward by magnetotail reconnection, Na⁺ ions are likely lost to the tail magnetosheath, either being carried out directly by their large gyroradii or by Kelvin-Helmholtz (K-H) vortices on the magnetopause boundary. Magnetotail plasma is also lost owing to magnetic reconnection and plasmoid formation (DiBraccio et al. 2015a), though Na+ has not yet been observed in these structures. K-H vortices result from the large difference in flow speed across the magnetopause, like the fluid instability of the same name. They have been observed in over 145 orbits, about 6% of those examined, with 93% occurring on the dusk side (Liljeblad et al. 2014). In several large amplitude cases, Na⁺-group ions have been found in the K-H vortices themselves (Sundberg et al. 2012). Observations of magnetic field fluctuations, associated with K-H activity, near the Na⁺ gyrofrequency indicates that these ions might have a role in determining the size of the vortices (Gershman et al. 2015). Test-particle simulations of Na⁺ ions on MHD-generated K-H vortices showed that the Na⁺ ions can be energized by the electric field within the vortices in cases where the IMF is southward (Aizawa et al. 2020a, 2020b). This effect is unique for heavy ions (like Na⁺) because of their large gyroradii; protons in the study were not energized in this way. However, when compared to observations of Na⁺-group ions from FIPS, the results indicated that these ions might actually lose energy in K-H vortices under some conditions, highlighting the complex behavior of heavy ions in Mercury’s magnetotail.

4 Future Steps

Future steps to progress in our understanding of surface-bounded exospheres has been described in the final section of the Chapter “Volatiles and refractories in surface-bounded exospheres in the inner Solar System” by Grava et al. (2021). In the following, we described what is specific to the Na/K environments of these objects, in particular in terms of new directions of developments and efforts in the fields of ground based observations, modeling and laboratory measurements.

4.1 Na & K Ground Based Observations

Mercury and the Moon are ideal targets for small aperture telescopes with specialized instrumentation. Numerous studies agree that both bodies possess exospheres that are exceptionally dynamic. Monitoring of their Na and K emissions can therefore provide valuable insights to time-dependent drivers like solar wind and meteoroid influx. An exosphere’s response to events like an ICME, a meteor shower, or even individual meteoroid impacts can quantify a wealth of information like yields, temperatures and timescales for exosphere-surface interactions. Such parameters are challenging to constrain from snapshots of an exosphere with multiple sources and losses. Observations of dynamic phenomena in our solar system enables cause-and-effect relationships to be established and characterized, but monitoring with any regularity can become impractical where space-based observation or large aperture telescopes are needed, e.g. for studies of gas giant aurorae. Dedicated monitoring of these exospheres with small and medium-size telescopes at optical wavelengths is low cost means to leverage significant science return, particularly during missions when in situ measurements can be compared to better inform our interpretation of both datasets.

4.2 Modeling Development

The spatial organization, composition and temporal evolution of surface-bounded exospheres are highly dependent of their interaction with the surface. The upper layer of the surface of these objects, the regolith, being permanently space weathered by the Sun, the exospheres are an almost direct signature of this surface ageing process. But, the permanent recycling of these exospheres into the surface tends also to modify the upper layer of the regolith. Therefore, to develop a precise description of the interaction between exosphere and regolith is essential to address the formation and evolution of both. Its importance has been highlighted in particular when discussing the modelling of the orbital evolution of the Na and K exospheres at Mercury which does not agree with the observations by MESSENGER discussed in Sect. 3. The discrepancies between the data and models suggests that some additional physical parameters need to be taken into account or updated. For example, a better understanding of the surface-exosphere interaction, especially on a space-weathered surfaces, is necessary. Data from Bepi-Colombo on interplanetary dust flux at Mercury, ion flux and its temporal and spatial variability, and more information on the surface composition in the southern hemisphere will be a definite boon. Calculations and the help of new laboratory experiments regarding parameters such as photon-stimulated desorption and electron-stimulated desorption as well as space weathering are desired.

The complexity of this task is increased by the need to take into account all the environmental parameters that could influence this interaction. As an example, this interaction depends on the existence or not of an intrinsic magnetosphere, on the composition and structure of the upper layer of the surface in direct interaction with these atmospheres, on the solar local time, topography, on the distance to the Sun, on the environment of these objects (embedded or not in the magnetosphere of a larger planetary objects, like our Moon within the Earth’s magnetosphere), on the meteoroid environment and its variability and on the variability of the solar conditions either due to the solar cycle or to solar energetic events or due to the orbit of these objects. But more challenging is to take into account the regolith structure and composition. Indeed, the upper surface is not a simple rocky surface but rather a complex assembly of grains whose size, density and microstructure will depend on the depth, solar illumination and residence time in the upper layer as a first order (see Sect. 3.3.2).

Therefore, to meet the present challenge of reconciling models of the exosphere of these objects with the observations, we must integrate in these models: 1) the description of the fate of the exosphere during its interaction with the surface; 2) its dependency on the location at the surface but also the particularities of the planetary environment, 3) to describe the regolith taking into account all the mechanisms that could weather it (solar illumination, radiation, temperature profile with depth, structure and size of the grains, impact gardening...); and 4) to describe how the surface controls the exosphere.

Such type of models integrating both the description of the exosphere and of the fate of its atomic and molecular contents through the regolith remains to be developed for Mercury and the Moon and represents the next step in our capability to describe these environments.

4.3 Towards Unprecedented New Achievements Thanks to BepiColombo

ESA/JAXA BepiColombo mission, with its two spacecraft and a much larger set of instruments, is much better equipped and conceived to address the questions related to the relations between our Sun and Mercury’s system than was MESSENGER. BepiColombo mission, with its unprecedented capability to distinguish spatial and temporal variabilities, will be able to track the various signatures of the solar activities in Mercury’s magnetosphere, exosphere, ionosphere and surface. As a matter of facts and illustrated in this paper, the Na and K exospheres are among the easiest observable signatures of these relations from both an orbiter and/or ground based telescopes.

We can list two main advantages for BepiColombo mission with respect to what has been done so far by previous space missions at Mercury. First, two spacecraft able to observe simultaneously the far and close environments of Mercury, second a set of instruments with a much better coverage of the different regions of Mercury thanks also to MIO and MPO orbital coverages and also able to observe the Na and K exospheres with various approaches (see Milillo et al. 2020 for a description of BepiColombo instruments):

• BepiColombo will be able to track the solar environment, thanks to SIXS for the radiative environment but more importantly for the exosphere, thanks to MDM for the dust environment, and because the use of two spacecraft will occasionally allow for the simultaneous measurement of conditions in the upstream solar wind and inside the magnetosphere.

• With two spacecraft inside Mercury’s magnetosphere, BepiColombo will be able to follow the propagation of solar perturbations through the magnetosphere up to the surface and exosphere/ionosphere, characterizing the magnetospheric response to solar events.

• BepiColombo two spacecraft have an unprecedented set of instruments dedicated to the observation of Mercury’s exosphere, from in situ instruments with MPO/SERENA/STROFIO able to in situ measure the Na and K exospheres to UV spectrometer with MPO/PHEBUS, potentially able to measure the Na exosphere, up to the visible imager MIO/MSASI specifically dedicated to the Na exospheric component.

• Tracking Mercury’s exospheric variability will be also possible by observing its signatures in its ionosphere and vice-versa, thanks to a much larger set of plasma dedicated instruments as MPO/SERENA/PICAM and MPO/SERENA/MIPA and to MIO/MPPE, all able to measure the Na⁺ and K⁺ ions as previously observed by MESSENGER/FIPS.

• Thanks to MESSENGER observations, we also know that there are direct observable signatures of Mercury’s surface composition in its exosphere. Clearly the many instruments dedicated to the observations of the surface, SIMBIO-SYS, MIXS, BELA, MERTIS and MGN on board MPO, will provide a completely new view on the surface composition and will be essential to complete our view of Mercury’s exosphere. Actually, Mercury’s surface volatile abundance is also known to be potentially related to Mercury’s exospheric circulation.

• At the end, a description of the exosphere won’t be completed without considering the relations between Mercury’s magnetosphere and its internal structure, in particular without considering the induced currents in Mercury’s core.

Few years after the completely new view provided by MESSENGER on Mercury’s exosphere, BepiColombo clearly provides us the rare opportunity to pursue MESSENGER achievements by significantly improving our view and understanding of Mercury’s exosphere. Moreover, with its two spacecrafts and comprehensive set of instruments, it will provide us a unique capability to observe the complex relations between Mercury’s exosphere, surface, magnetosphere and environments.

5 On the Importance to Further Observe, Analyse and Model the Moon and Mercury Na and K Exospheres

Mercury and the Moon Na and K exospheres appear more and more clearly as a complex and intrinsic component of the environments of these objects. Our current view of the Moon and Mercury presents their Na and K exosphere as a product and potential driver of the interaction with their plasma environment, a product and signature of the meteoritic environments and a product, signature but probably also driver of their surface composition.

This complexity is actually what makes so crucial the observations of these two components of Mercury or the Moon exospheres. The exosphere has an obvious role in the formation and variability of the magnetosphere. It contains direct signatures of Mercury and of the Moon interaction with our Sun and the Earth magnetosphere in the case of the Moon. Observing the exosphere was shown to provide an original and highly useful view on how the solar wind interacts with the Moon’s crustal magnetic fields or to track the energy and mass exchanges between the solar wind and Mercury’s magnetosphere. Mercury and the Moon’s ionized environments are essentially formed from their respective exospheres. These newly created ions are then further interacting with the solar wind contributing to shape the electric and magnetic environments of these objects.

These ions are also one of the most easily measurable signatures of Mercury and Moon’s surface space weathering. Thanks to the observations of the Moon exosphere, it has been possible to track the effects of the surface bombardment by the meteoroid and by the solar wind but also to use these observations to probe the very uppermost layer of these objects and also to infer the composition of some large size terrains at both the Moon and Mercury. To understand the surface/exosphere cycle is also essential to properly interpret some remote observations of the surface composition, the exosphere readsorption by the surface being potentially one of the explanations for the unusual surface composition on Mercury. Therefore, observing the exosphere helps us to explore the composition of some specific regions of the surface of these objects, the cusps region at Mercury, the locally magnetized regions at the Moon and the permanently shaded regions at Mercury and the Moon.

The exosphere of weakly magnetized objects without thick atmospheres is therefore an intrinsic component of these objects which characteristics contribute to shape the surface, electric and magnetic environments of these objects. Integrating the exosphere as one of the targets of our efforts to understand these objects is therefore essential to properly tackle their complexity.