Abstract
Solar flare emission is detected in all EM bands and variations in flux density of solar energetic particles. Often the EM radiation generated in solar and stellar flares shows a pronounced oscillatory pattern, with characteristic periods ranging from a fraction of a second to several minutes. These oscillations are referred to as quasi-periodic pulsations (QPPs), to emphasise that they often contain apparent amplitude and period modulation. We review the current understanding of quasi-periodic pulsations in solar and stellar flares. In particular, we focus on the possible physical mechanisms, with an emphasis on the underlying physics that generates the resultant range of periodicities. These physical mechanisms include MHD oscillations, self-oscillatory mechanisms, oscillatory reconnection/reconnection reversal, wave-driven reconnection, two loop coalescence, MHD flow over-stability, the equivalent LCR-contour mechanism, and thermal-dynamical cycles. We also provide a histogram of all QPP events published in the literature at this time. The occurrence of QPPs puts additional constraints on the interpretation and understanding of the fundamental processes operating in flares, e.g. magnetic energy liberation and particle acceleration. Therefore, a full understanding of QPPs is essential in order to work towards an integrated model of solar and stellar flares.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Flares constitute one of the most impressive manifestations of solar and stellar activity. They appear as a sudden increase of radiated flux, detectable in a broad range of wavelengths, going from gamma rays to radio. Since the first observations of a solar flare by Carrington (1859) and Hodgson (1859), countless detections were reported of flares on the Sun as well as on other stars (Hertzsprung is credited of the first stellar flare detection in 1924). However, flares have not yet revealed all their secrets.
According to the most often invoked flare model, the CSHKP (Carmichael 1964; Sturrock 1968; Hirayama 1974; Kopp and Pneuman 1976; Svestka and Cliver 1992)—or standard—model, flares have their origin in magnetic reconnection that takes place in a coronal current sheet. The reconnection process accelerates particles in both the upwards and downward directions to non-thermal speeds. The latter, after propagating collisionlessly along magnetic field lines through the corona, eventually reach the denser chromosphere. There, they dissipate part of their energy by radiating (e.g. bremsstrahlung processes that produce hard X-rays) and by heating the ambient plasma, which results in the so-called chromospheric evaporation. This evaporated plasma, while cooling, will produce thermal emission essentially in the EUV and soft X-ray ranges. This model, although providing a detailed phenomenological description of most of the flare characteristics, keeps the main quantitative aspects elusive. In particular, the way the energy produced at the reconnection site is transported to the chromosphere remains highly debated. Obviously, the accelerated electron beam is a good energy propagation agent, but it is not clear whether it suffices to explain the huge amount of energy released during the flare process. Some authors suggested that part of the flare energy could rather be transported downward by Alfvén waves (e.g. Fletcher and Hudson 2008) or by thermal conduction (e.g. Antiochos and Sturrock 1978; Cargill et al. 1995; Milligan et al. 2006).
The occurrence of waves and pulsations associated with flares puts additional constraints on the interpretation and understanding of the fundamental processes operating in both solar and stellar flares (e.g. particle acceleration, magnetic energy liberation). In this way, one can consider waves as both an integral part of flare dynamics as well as a potential diagnostic of the flare process. The overarching goal of solar and stellar flare modelling is thus to create an integrated plasma model which will, ultimately, create a coherent vision of reconnection, waves and particle acceleration processes in flares. This review paper considers one of these three key components: the modelling of waves and pulsations in solar and stellar flares. Specifically, we focus on quasi-periodic pulsations (QPPs)—see Sect. 1.3—but also briefly review other important wave processes in the Appendices A and B.
Note that this paper focuses on modelling QPPs, and their possible production by waves and pulsations, and thus is primarily a theoretical modelling review. For a comprehensive observational overview of solar flares see, e.g. Fletcher et al. (2011). Detailed reviews of observational and forward modelling aspects of QPPs are summarised in Nakariakov and Melnikov (2009); Nakariakov et al. (2010); Van Doorsselaere et al. (2016), while the theoretical aspect, mainly the mechanisms based on standing MHD oscillations, is covered there too. In this paper we address the QPP mechanisms developed in recent years, such as periodic reconnection, the magnetic tuning fork, and self-oscillatory processes, as well as some well-known mechanisms, e.g. the equivalent LCR contour and dispersive wave trains, which recently obtained observational support, but have not obtained sufficient attention in previous reviews.
1.1 Oscillations, Self-Oscillations, Waves and Pulsations
Let us start with some terminology and definitions. According to the common knowledge, an oscillation is any motion, effect or change of state that varies periodically between two values, i.e. there is a repetitive nature. However, clearly, this definition does not include a number of constraints, such as the finite duration of the oscillatory pattern, possible amplitude modulation, e.g., the decay, and frequency drifts. In the Fourier spectral domain, an oscillation is usually associated with a statistically significant peak, or a group of peaks in the case of an anharmonic pattern. But, again, this approach does not take into account the oscillation life time and the modulations. Thus, it is difficult to produce a mathematically rigorous definition of an oscillation in real data. In flaring signals, this difficulty is magnified by the intrinsic localisation of the quasi-oscillatory patterns in a certain time interval that is determined not only by the properties of the oscillation itself, but also by the duration of the emission in the flare. For example, in the gyrosynchrotron emission an oscillatory pattern is seen only during the operation of this mechanism, i.e. when there are non-thermal electrons in the oscillating plasma. Thus, we usually intuitively consider a quasi-periodic pulsation (QPP) to be a quasi-repetitive pattern in the signal, which has at least three or four iterations—the QPP cycles.
It is easier to define an oscillation in theoretical modelling. From this point of view, an oscillation is a quasi-periodic variation of certain physical parameters in the vicinity of a certain equilibrium. For example, it is the (quasi)-periodic dynamics of a load of the pendulum, or, in the case of solar flares, a (quasi)-periodic variation of the plasma density with respect to the equilibrium in a flaring loop. It should be pointed out that the equilibrium itself may vary during the oscillation, for example the equilibrium value of the density in the loop may change because of the ongoing chromospheric evaporation, or gradual variation of the loop length or width. Parameters of an oscillation, such as the amplitude and phase, are determined by the initial excitation. In general, in an oscillation there is a (quasi)-periodic transformation of the kinetic, potential, magnetic and thermal energy into each other. There is also the continuous sinking of the oscillation energy to the internal energy, and possibly radiation of the energy outward the oscillating system. Thus, an oscillation can be considered as a (quasi)-periodic competition between an effective restoring force and inertia. The oscillation period is determined by the properties of the oscillating system, an oscillator. In a certain time interval, oscillations may be driven by an external time-dependent force, resupplying the oscillation with energy. In this case the response of an oscillator to the external force consists of a combination of the natural oscillation and the driven oscillation. When the frequencies of the natural and driven oscillations are close to each other, the phenomenon of resonance occurs.
An important class of oscillatory motions in dissipative and activeFootnote 1 media are self-sustained oscillations, also called self-oscillations, auto-oscillations or oscillatory dissipative structures. Self-oscillations occur in essentially non-conservative systems because of the competition between the energy supply and losses. In particular, in electronics self-oscillations are associated with the process of the conversion of the direct current in the alternate current of a certain frequency. Self-oscillatory motions are common in a number of dynamical systems, and the well-known examples are various musical instruments, radio-frequency generators, the heart, the clock (see Jenkins 2013, for a comprehensive review). Usually, the self-oscillation period depends on the amplitude. Despite the presence of dissipative and/or radiative losses, a self-oscillation may be decayless, because of the continuous extraction of the energy from the medium. This behaviour should not be confused with the driven oscillations mentioned above, as in the case of self-oscillations this energy supply comes from an essentially non-periodic source, e.g. the DC battery in a watch, or the steady wind causing the periodic shedding of aerodynamic vortices. In solar flares, a steady inflow of the magnetic flux towards the reconnection site could result in repetitive magnetic reconnection (“magnetic dripping”, Nakariakov et al. 2010) that should be considered as a self-oscillatory process.
In contrast with regular oscillations, properties of self-oscillations, such as the period, shape of the signal, and amplitude are uniquely determined by the parameters of the system they are supported by, and are independent of the initial conditions. It makes them an excellent tool for seismological probing of the media and physical processes operating there. Hence, the search for and identification of self-oscillatory processes in solar and stellar impulsive energy releases is an interesting research avenue.
A wave is a perturbation that propagates through space and time, which is usually accompanied by energy transference. Despite the common knowledge that a wave should be “wavy”, it is not necessary for the wave signal to be periodic. The main property of a wave is its propagation that is characterised by its phase and group speeds. More rigorously, a wave is a signal that, in the simplest, one-dimensional case, is described by the general solution to the wave equation, \(f(z-Ct)\), where \(z\) and \(t\) are the spatial coordinate and time, and \(C\) is the phase speed of the propagation. The function \(f\) that describes the wave shape is an arbitrary, sufficiently smooth function that is determined by the excitation. In particular, it may be periodic, e.g. harmonic, or aperiodic, e.g. Gaussian.
In a more general case the function \(f\) can also gradually vary in time and space, as it is, e.g. in the presence of dissipation, mode conversion, or non-plane effects. If nonlinear effects are important, the speed \(C\) may become a function of the amplitude, and the wave evolution is described by a certain evolutionary equation, e.g. the Burgers equation for magnetoacoustic waves, or the Cohen–Kulsrud equation for Alfvén waves. Nonlinear evolution of a wave usually leads to the deformation of the wave shape, e.g. the formation of the characteristic saw-tooth pattern in the case of nonlinear magnetoacoustic waves. Shock waves are a specific class of nonlinear wave motions, with the functions \(f\) having an infinite gradient.
In dispersive media or systems, signals with different frequencies have different phase and group speeds, for example a fast magnetoacoustic wave propagating within a system with a field-aligned inhomogeneity. In this case, different spectral components that are the results of the Fourier decomposition of the function \(f\) propagate at different speeds, and an initially broadband signals evolves into a locally harmonic signal. This situation occurs, in particular, in the case of the waves on the surface of water, which leads to our everyday experience that a wave should be “wavy”.
Similarly to self-oscillations, there could be “self-waves”, more often called autowaves that appear in active media, when the passage of the wave causes the energy release that reinforces the wave. An example of an autowave is the wave of flame. The speed, amplitude and other parameters of autowaves are determined by the properties of the medium. In solar physics, autowaves could occur, for example, as the “wave”of sympathetic flares: an energy release in the first flare ignites the next one that, in turn, ignites the third, etc., i.e. a “domino effect”. The progression of the quasi-periodic energy release site along the neutral line in a two-ribbon flare could also be produced by an autowave.
Waves and oscillations are closely related to each other. A standing wave that is a linear superposition of two oppositely propagating waves of the same amplitude, is usually called an oscillation in solar physics. Examples of these oscillations are the fundamental magnetoacoustic harmonics of coronal loops, such as kink, sausage, fluting, torsional and acoustic modes (see, e.g. De Moortel and Nakariakov 2012; Nakariakov et al. 2016, for comprehensive reviews).
1.2 Waves and Pulsations Generated by Flares
The dramatic energy release in flares can generate waves and pulsations in the elastic and compressive solar atmosphere. Firstly, there is the impulsive energy release of the flare itself; this can act as an impulsive driver for waves and pulsations. Additionally, during the huge magnetic restructuring that accompanies the reconnection, the magnetic field below the reconnection site is believed to collapse in an “implosion” process (Hudson 2000) that would very likely trigger waves too. Simply put, the flare is converting stored energy into various forms which we observe both directly and indirectly, and waves/pulsations/outflows are part of that energy conversion process (see, e.g. §3.3 of Hudson 2011).
Thus, there is a rich tapestry of wave-related phenomena associated with solar (and stellar) flares. This review focuses on QPPs, but other types of waves and pulsations associated with solar and stellar flares are discussed briefly in the appendices, where Appendix A considers global waves generated by CMEs and flares (including shock waves, blast waves, EIT waves, Moreton waves and ‘flare waves’) and Appendix B considers sunquakes (another wave-like global phenomenon associated with flares).
1.3 Quasi-Periodic Pulsations
Quasi-repetitive patterns have been detected in a variety of signals generated by flares. These are referred to as quasi-periodic pulsations (QPPs), and have been observed in radio, optical and X-ray emission of solar flares (e.g. Kane et al. 1983; Kiplinger et al. 1983; Dennis 1985; Asai et al. 2001; Inglis et al. 2008; Inglis and Nakariakov 2009; Nakariakov and Melnikov 2009; Hayes et al. 2016; Van Doorsselaere et al. 2016; Zhang et al. 2016) and stellar flares (e.g. Mathioudakis et al. 2003; Mathioudakis et al. 2006; Mitra-Kraev et al. 2005). These are not, rigorously speaking, oscillations or waves (see Sect. 1.1 for terminology), rather they are oscillation trains (short bursts of oscillations) or, in some cases, modulated oscillations, i.e. time-varying (in amplitude or period) oscillations.
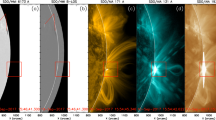
An example of QPPs is illustrated in Fig. 1 for the X4.9 flare of 25 February 2014. QPP oscillations with a period of ∼35 s are clearly visible as an oscillatory train in all displayed time series that cover the radio (Nobeyama Radio Polarimeters 17 GHz), the EUV (PROBA-2/Lyra 1–20 nm, see Dominique et al. 2013) and the HXR ranges (RHESSI 50–100 keV, see Lin et al. 2002). Despite the very different ranges of energy considered, the oscillations are remarkably synchronous.
Example of QPPs for the X4.9 flare of 25 February 2014. Top panel: the normalised flare time series from GOES 0.1–0.8 nm (black), Lyra 1–20 nm (blue), RHESSI 50–100 keV (red) and Nobeyama 17 GHz. Second, third and fourth panels: the same time series for respectively RHESSI, Lyra, and Nobeyama, detrended with a 50 s window. The QPPs appear to be remarkably synchronous. The data gap in the Lyra time series from 00:50 UT onwards is caused by a spacecraft manoeuvre
In the top panel of Fig. 1, the green and red curves show the clear oscillatory pattern that is often displayed in the flare non-thermal emission. At the end of the 1960s, those oscillations were known to correlate well in the X-ray and radio bands, and a possible wave-origin had already been invoked (Parks and Winckler 1969). Since then, numerous observations of these QPPs have been reported during solar flares, not only in non-thermal (see e.g. Kane et al. 1983; Inglis et al. 2008), but also in thermal emission, with example cases in the visible (e.g. Jain and Tripathy 1998; McAteer et al. 2005), in the soft X-rays/EUV (e.g. Dolla et al. 2012; Brosius and Daw 2015) and in the ultraviolet ranges (e.g. Tian et al. 2016), as well as simultaneously in both thermal and non-thermal emission (e.g. Brosius et al. 2016). Such a global wavelength coverage tends to indicate that QPPs affect all layers of the solar atmosphere from the chromosphere to the corona.
The web-pageFootnote 2 presents a catalogue that contains information about QPPs in solar flares, detected in various bands and with various instruments. The catalogue is based on the information provided in already published papers by various authors, is continuously updated, and at the moment contains 278 QPP events reported in the literature. Figure 2 illustrates the distribution of the detected QPPs in time and by the periods. In the cases of drifting periods we took the mean value of the period. We attribute an event to a QPP in the thermal emission if it was detected in EUV and/or soft X-rays, while QPPs in radio, microwave, visible light and white light (see below), hard X-ray and gamma-ray bands are considered as QPPs in the non-thermal emission. This separation is rather artificial, but may be useful for the choice of appropriate instrumentation for further studies of this phenomenon.
Properties of 278 QPP events reported in the literature. The top panel shows the time distribution, with the bin size being the calendar year. The bottom panel shows the distribution of detected periods. The blue colour shows QPPs detected in the non-thermal emission, red in thermal, and green detected in both thermal and non-thermal emissions simultaneously
We note that white light emission in flares is associated with non-thermal particles, whereas visible light includes various lines that could be more sensitive to thermal effects (for example, H\(\upalpha\) is dependent mainly on temperature, not directly on the non-thermal process). Thus, we have attributed QPPs detected in visible light as non-thermal emission, but we emphasise that certain types of visible light could be classed as either thermal or non-thermal emission (as stated, the separation is rather artificial, but potentially useful). The classification is clearer for white light: with regards to white light and hard X-ray light curves, it has been observed that both behave in a similar manner in many flares (e.g. Hudson et al. 1992) and that both of these emissions in the impulsive phase of flares are caused by non-thermal electrons (e.g. Fletcher et al. 2007; Watanabe et al. 2010).
The statistics of the QPP detections clearly correlates with the solar cycle, which is not a surprise, as the frequency of flares depends on the phase of the cycle. The recent increase in the detection of QPPs in the thermal emission is explained in the availability of EUV and soft X-ray instruments. The increase in the number of QPPs detected simultaneously in both thermal and non-thermal emission reflects also the growing interest in multi-instrumental studies of the QPP phenomenon, necessary for the exclusion of instrumental artefacts. The distribution of the detected periodicities is partly affected by the time resolution of the available instruments. These statistics confirms that QPPs are a rather common phenomenon that is intensively studied observationally. Detected periods range from a fraction of a second to several minutes, which means QPPs are detectable with the majority of modern solar instruments.
Stellar flares, far more energetic than typical solar flares have been observed on solar-like stars (Maehara et al. 2012) leading to predictions of ‘superflares’. QPPs have been reported in stellar flares throughout the whole spectrum (see e.g. Pugh et al. 2016 and references therein). Obviously, QPPs are neither a rare phenomenon, nor one that is limited only to the Sun. Karoff et al. (2016) analysed 48 superflare stars using the LAMOST telescope (Cui et al. 2012) and suggested that solar flares and superflares most likely share the same underlying mechanism.Footnote 3
Furthermore, there has been a wealth of QPP detections in stellar flares using NASA’s Kepler mission (Borucki et al. 2010), e.g. Davenport et al. (2014) investigated the temporal morphology of white-light flares in Kepler data (Davenport 2016 complied a Kepler catalogue of stellar flares). Anfinogentov et al. (2013) analysed the signal in the decay phase of the U-band light curve of a stellar megaflare and reported that the oscillation was well approximated by an exponentially-decaying harmonic function. Balona et al. (2015) analysed data from 257 flares in 75 stars to search for QPPs in the flare decay branch. Pugh et al. (2015) presented an analysis of a white-light stellar superflare observed by Kepler and detected a multi-period QPP pattern. Pugh et al. (2016) studied QPPs in the decay phase of white-light stellar flares and looked for correlations between QPP periods and parameters of the host star. For the 56 flares with QPP signatures detected, no correlation was found between the QPP period and the stellar temperature, radius, rotation period or surface gravity, suggesting that QPPs are independent of global stellar parameters and are likely to be determined by the local parameters, e.g. of the flaring active region.
Systematic statistical studies of solar QPPs have also been performed. Kupriyanova et al. (2010) analysed twelve ‘single-loop’ flares observed in the microwave band (i.e. in the non-thermal emission) and found statistically significant QPPs in ten of them. Simões et al. (2015) found that 80% of X-class flares from Cycle 24 (so far) display QPPs in thermal emission. More recently, Li et al. (2017) reported on QPPs with periods that change depending on whether the pulsations have thermal or non-thermal components.
While Inglis et al. (2015) claimed that QPPs are not statistically rigorous oscillations, Inglis et al. (2016) performed a large-scale search for evidence of signals consistent with QPPs in solar flares, focusing on the 1–300 second timescale, and concluded that 30% of thermal events (GOES) and 8% of non-thermal events (Fermi/GBM) show strong signatures consistent with the classical interpretation of a QPP, based on the significance level of the corresponding peak in the Fourier power spectrum. These estimations are rather conservative, as they address the search for stationary periodicities in the spectrum, while QPPs are often non-stationary, wavelet-like signals. There is a clear need for a definition of a QPP, which would account for the effects of coloured noises, regular trend and the intrinsic non-stationary nature of the quasi-oscillatory patterns in flaring light curves.
QPP observations cover a wide range of periodicities (see Fig. 2). If sub-second periodicities are usually attributed to cyclic behaviours of self-organising systems driven by wave-wave or wave-particle interactions (see the reviews by Aschwanden 1987; Zaitsev and Stepanov 2008, as well as Chernov et al. 1998 for a specific example), QPPs with periodicities from a few seconds to several minutes have often been attributed to MHD waves. Fast sausage modes are usually considered here, especially when dealing with sub-minute QPPs (e.g. Nakariakov et al. 2003; Melnikov et al. 2005), although slow magnetoacoustic (Van Doorsselaere et al. 2011; Su et al. 2012) and fast kink modes (Foullon et al. 2005) have been sometimes invoked to explain longer periodicities.
However, MHD waves are not the only possible explanation for QPPs (see Nakariakov and Melnikov 2009 for a discussion). The initial electron acceleration process, if being itself quasi-periodic, would also result in a spectrally broad modulation of the observed flux, both thermal and non-thermal. This mechanism was for example invoked by Kane et al. (1983) to explain the well-known Seven–Sisters Flare of 7 June 1980.
2 Physical Mechanisms Underpinning QPP Generation
The motivation to understand the physical mechanism(s) responsible for QPPs is clear: the frequent occurrence of QPPs in flaring light curves puts additional constraints on the interpretation and understanding of fundamental flare physics. Thus, the rest of this review focuses on the discussion of the physical mechanisms proposed for the generation of QPPs in solar and stellar flares.
Whether QPPs are caused by MHD waves or an alternative mechanism(s) is a highly debated question and might depend on the considered range of periodicities. This section summarises the state-of-the-art understanding of each of those processes and aims to pin-point the spectral and temporal characteristics of the QPPs that each of them would produce, so as to help diagnosing the origin of QPPs in the various observational cases.
2.1 MHD Oscillations
Some of the observed periods of QPPs coincide with the order of magnitude of MHD waves and oscillations that are abundantly detected in the corona (and well resolved both spatially and temporally).
Coronal plasma flows or rearrangement of magnetic fields can cause the displacement of coronal loops, filaments and streamers, which can result, for example, in transverse oscillations of these coronal structures. The initial energy deposition must come from somewhere, and the dramatic energy deposition from a flare could be the origin of such a driver (there are other potential origins, of course). In this sense, the flare is invoked as an impulsive perturbation, and that impulsive energy release could be modelled as a thermal pressure pulse as well as a magnetic, velocity and/or heat perturbation to the system. Such perturbations can be external to a loop system (e.g. Ofman and Thompson 2002; McLaughlin and Ofman 2008) or internal to a loop system. For example, in the latter case, Nakariakov et al. (2004a) studied the evolution of a coronal loop in response to an impulsive energy release and found that the evolution of the loop density exhibits quasi-periodic oscillations associated with the second standing harmonics of an acoustic wave (note that the slow magnetoacoustic oscillations—since their study was limited to 1D—could also be interpreted as the second, standing slow magnetoacoustic mode of the loop). Here, the perturbation was modelled as the response of the loop to a flare-like impulsive heat deposition at a chosen location. Tsiklauri et al. (2004) extending this work to look at how the locations of the heat deposition affects the mode excitation; it was found that excitation of such oscillations is independent of the heat-deposition location within the loop. On the other hand, numerical simulations of the response of a coronal loop to an impulsive heat deposition at one chromospheric footpoints demonstrates the effective excitation of the fundamental acoustic mode (Taroyan et al. 2005). Pinto et al. (2016) developed a model of the thermal and non-thermal emission produced during the evolution of kink-unstable twisted coronal loops in a flare. Their modelling showed post-flare oscillations, which could be interpreted as QPPs, in the soft X-ray emission, see Fig. 3. Cho et al. (2016) investigated QPPs observed in the decay phase of solar and stellar flares in X-rays, and proposed that the underlying mechanism responsible for the stellar QPPs is a natural MHD oscillation in the flaring or adjacent coronal loops.
Light curves of the soft X-ray emission (black and red lines) and hard X-ray emission (blue and green lines) at different photon energy bands (see the inset legend). A few post-flare oscillations are visible in the soft X-ray light curves. From Pinto et al. (2016); their Fig. 12, model V
In this sense, the flare is invoked as a justification for a source region and energy provider, but that once the finite-duration internal/external excitation occurs, we will get free MHD oscillations of the emitting plasma. Thus, we are now within the field of coronal seismology and so the observed parameters tell us diagnostic information about the medium and the oscillating structure itself (e.g. the magnetic field strength of an oscillating coronal loop; information about the heating function, transport coefficients, and fine sub-resolution structuring) rather than about the driver (be that a flare or other). In other words, the period will be independent of the flare energy and so coronal seismology tells us about the local conditions in flaring active regions, rather than the flare itself. Coronal seismology is a significant field in its own right and readers are recommended to consult the comprehensive reviews in this area (e.g. see De Moortel 2005; De Moortel and Nakariakov 2012, and references therein).
2.2 QPPs Periodically Triggered by External Waves
In the previous subsection, the flare is invoked as an impulsive forcing term, hence the periodicity comes from the global parameters of the oscillating loop, not from the driver. However, in some cases MHD waves and oscillations may affect, or back-react on, the flaring process. Let us consider the trigger mechanism for flares. The pre-flare stage, i.e. before the primary energy release (the impulsive phase), is one of energy storage. By definition, flares are the rapid release of energy stored previously in the magnetic field, and the total flare energy is of the same order of magnitude as the amount of magnetic free energy, while the specific fraction is still debated in the literature (e.g. Emslie et al. 2012 reports that for large solar eruptive events, approximately 30% of the available non-potential magnetic energy is released). Reconnection must be at the heart of this energy release and thus waves must play a role here, namely that it is known that steady-state reconnection models generate not only outflows/waves but also require inflows/waves (e.g. Parker 1957; Sweet 1958; Petschek 1964). This is for example the case in the CSHKP standard flare model which has a null point—a location where the magnetic field, and hence the Alfvén speed, is zero, at least in a certain plane—as part of its magnetic topology.
In order to model and understand the pre-flare stage, one must understand how a stable magnetic configuration (which has sufficient stored magnetic free energy) becomes unstable in such a way as to produce a rapid and dramatic energy release. There are many models of how a magnetic topology can store magnetic energy (e.g. Régnier 2013; Kleint et al. 2015) or emerge with sufficient magnetic free energy (e.g. Heyvaerts et al. 1977; Török et al. 2014) and here we focus specifically on the triggering of flares by MHD waves.
McLaughlin and Hood (2004) investigated the behaviour of an aperiodic fast magnetoacoustic pulse about a 2D X-type null point and found that the fast wave refracts into the vicinity of the null point and, ultimately, accumulates at the null point itself. As it approaches the null, the refraction effect causes the pulse amplitude to be amplified and the length scales (which can be thought of as the distance between the leading and trailing edges of the wave pulse) to rapidly decrease. This leads to an increase of the electric current density associated with the pulse, which manifests as exponential growth near the null point. The phenomenon, i.e. fast waves accumulate at null points is entirely general and has been shown to work for double X-type neutral points (McLaughlin and Hood 2005) as well as 3D null points (e.g. Thurgood and McLaughlin 2012, and see McLaughlin et al. 2011 for a review). Crucially, McLaughlin et al. (2009) showed that this accumulation of wave energy at the null is enough to induce reconnection, i.e. wave-driven reconnection (see Sect. 2.3 for full details).
Nakariakov et al. (2006) investigated this phenomenon further by simulating the interaction of a periodic fast magnetoacoustic wave with a magnetic null point. This causes the periodic occurrence of highly steep spikes of the electric current density. The current variations can, in turn, periodically induce current-driven plasma micro-instabilities which are known to cause anomalous resistivity. This can then periodically trigger reconnection. The modulation depth of these current variations is a few orders of magnitude greater than the amplitude of the driving wave, and thus this may be a suitable mechanism for QPPs (see Sect. 1.3 above). Nakariakov et al. (2006) postulated that this initial wave driver come from an oscillating coronal loop outside (but close to) the flaring arcade. Thus, an external evanescent or leaking part of the oscillation could reach the null point in the arcade. A sketch of the mechanism can be seen in Fig. 4. Here, the period is determined by the period of the oscillating loop, which corresponds approximately to the ratio of the loop length to the average magnetoacoustic speed. Moreover, in this scenario the inducing wave may be freely propagating or guided by a plasma non-uniformity, with the periodicity appearing because of its dispersive evolution (see Sect. 2.6 below).
The cool (shaded) loop experiences fast magnetoacoustic oscillations (e.g. kink or sausage mode). A segment of the oscillating loop is situated nearby a flaring arcade. An external evanescent or leaking part of the oscillation can reach the null point(s) in the arcade, inducing quasi-periodic modulations of the electric current density. Via plasma micro-instabilities this cause anomalous resistivity which triggers reconnection. This then accelerates particles periodically, which follow the field lines and precipitate in the dense atmosphere, causing quasi-periodic emission in radio, optical and X-ray bands. From Nakariakov et al. (2006)
Chen and Priest (2006) performed MHD simulations of transition-region explosive events driven by five-minute solar p-mode oscillations. The authors considered an anti-parallel magnetic field with a stratified atmosphere. Five-minute oscillations are imposed at the photospheric base and this leads to periodically triggered reconnection. Specifically, it was found that density variations in the vicinity of the reconnection site result in a periodic variation in the electron drift speed, which switches on/off anomalous resistivity, and thus accelerates the process of reconnection periodically. Thus the reconnection rate is modulated with a period of approximately five minutes. The corresponding UV light curve indicates impulsive bursty behaviour, which each spiky burst lasting for approximately one minute (for the parameters considered). Thus, this is an example of the periodic triggering of reconnection due to MHD oscillations, specifically longitudinal, slow magnetoacoustic (i.e. p-modes). In addition, this mechanism could readily explain the observed association of QPPs of the microwave emission in solar flares with the slow magnetoacoustic waves leaking from a sunspot in the corona (Sych et al. 2009). Thus, both fast and slow magnetoacoustic waves could act as periodic triggers of magnetic reconnection, transferring their periodicities in QPPs.
2.3 Oscillatory Reconnection (Reconnection Reversal)
Section 2.2 considered periodic flare triggering via MHD oscillations, but alternatively the reconnection itself can be repetitive and even periodic. Traditionally, magnetic reconnection and MHD wave theory have been viewed as separate topics. However, this is a misconception: it is known that steady-state reconnection models generate not only outflows/waves but also require inflows/waves (e.g. Parker 1957; Sweet 1958; Petschek 1964). This point-of-view has been challenged by several authors via the mechanism of spontaneous oscillatory reconnection which is a time-dependent magnetic reconnection mechanism that naturally produces periodic outputs from aperiodic drivers. From the point of view of oscillation theory, this process is a self-oscillation (see Sect. 1.1 for details).
The process was first reported by Craig and McClymont (1991) who investigated the relaxation of a 2D X-point magnetic field disturbed from equilibrium. They found that the additional free magnetic energy was released by oscillatory reconnection, which coupled the resistive diffusion at the null point to global advection of the outer field.
The process is named oscillatory since inertial overshoot of the plasma carries more flux through the null than is required for equilibrium and the plasma undergoes several oscillations through the null point. The oscillation period scales as \(\ln {\eta }\), with \(\eta \) being the resistivity. The reconnection rate was found to scale as \({|\ln {\eta }|}^{2}\), i.e. ‘fast’ (as opposed to ‘slow’ which depends upon a power of \(\eta \)). In the theoretical set-up of Craig and McClymont (1991), the free magnetic energy is dissipated across approximately 100 Alfvén times and thus, for typical solar parameters, the dissipation time scale is of the order of several minutes to an hour. The authors note that this is sufficiently rapid to account for thermal energy release in the decay phase but may be too slow to explain the impulsive phase flare timescale. This work was expanded upon by Craig and Watson (1992), Hassam (1992) and Craig and McClymont (1993) who suggested that for large-amplitude disturbances the structure of current flattens out into a quasi-1D current sheet. Thus, fast dissipation results in the formation of flux pile-up at the edges of the current layer, and so the bulk of the magnetic energy is released as heat rather than kinetic energy (of bulk mass flows). These works were limited to cylindrical geometries with artificial field line manipulation on the boundary, e.g. imposing a closing-up of the angle of the separatrix field lines, as well as reflective boundaries; thus all the outgoing wave energy was reflected and focused at the null point. Note that the gradients in the spatially-varying, equilibrium Alfvén-speed profile lead to fast magnetoacoustic waves being refracted into the null anyway (see McLaughlin and Hood 2004 for details).
McLaughlin et al. (2009) were the first demonstration of reconnection naturally driven by MHD wave propagation, via the process of oscillatory reconnection. These authors investigated the behaviour of nonlinear fast magnetoacoustic waves near a 2D X-type neutral point and found that the incoming wave deforms the null point into a cusp-like point which in turn collapses to a current sheet. Specifically, it was found that the incoming (fast) wave propagates across the magnetic field lines and the initial annulus profile contracts as the wave approaches the null. This can be seen in Fig. 5a. The incoming wave was observed to develop discontinuities (for a physical explanation, see Appendix B of McLaughlin et al. 2009 or, alternatively, Gruszecki et al. 2011), and these discontinuities form fast oblique magnetic shock waves, where the shock makes \(\mathbf{{B}}\) refract away from the normal. Interestingly, the shock locally heats the initially plasma \(\upbeta = 0\) plasma, creating plasma \(\upbeta \neq 0\) locally. Subsequently, the shocks overlap and form a shock-cusp, which leads to the development of hot jets and in turn these jets substantially heat the local plasma and significantly deform the local magnetic field (Fig. 5b). When the shock waves reach the null, the initial X-point field has been deformed such that the separatrices now touch one another rather than intersecting at a non-zero angle (called ‘cusp-like’ by Priest and Cowley 1975). The osculating field structure continues to collapse; forming a horizontal current sheet. However, the separatrices continue to evolve: the jets at the ends of the (horizontal) current sheet continue to heat the local plasma, which in turn expands. This expansion squashes/shortens the current sheet, forcing the separatrices apart. The (squashed) current sheet thus returns to a ‘cusp-like’ null that, due to the continuing expansion of the heated plasma, in turn forms a vertical current sheet. This is the manifestation of the overshoot reported by Craig and McClymont (1991). The phenomenon then repeats: jets heat the plasma at the ends of this newly-formed (vertical) current sheet, the local plasma expands, the (vertical) current sheet is shortened, the system attempts to return itself to equilibrium, overshoots and forms a (second) horizontal current sheet. The evolution proceeds periodically through a series of horizontal/vertical current sheets. The oscillatory nature can be clearly seen by looking at the time evolution of the current (in McLaughlin et al. 2009, this was \(j_{z}(0,0)\)) as shown in Fig. 5c. We also note that there is nothing unique about the orientation of the first current sheet being horizontal followed by a vertical, this simply results from the particular choice of initial condition, and McLaughlin et al. (2012a) use the more general terminology: orientation 1 and orientation 2. McLaughlin et al. (2009) also present evidence of reconnection; reporting both a change in field line connectivity as well as changes in the vector potential which directly showed a cyclic increase and decrease in magnetic flux on either side of the separatrices.
Contours of \(v_{\perp }\) (i.e. velocity across the magnetic field) for a fast wave pulse initially located at a radius \(r=5\) and its resultant propagation at (a) time \(t=1\) and (b) time \(t=2.6\) (measured in Alfvén times). Black lines denote the separatrices and null is located at their intersection. Note in (b) the separatrices have been deformed and now form a ‘cusp-like’ field structure. Subfigure have their own colour bars since \(v_{\perp }\) amplitude varies substantially throughout the evolution. (c) Time evolution of \(j_{z} (0,0)\) for \(0 \le t \le 60\). Insert shows time evolution of \(j_{z} (0,0)\) for \(25 \le t \le 60\) (i.e. same horizontal but different vertical axis). Dashed lines indicate maxima (red) and minima (blue). Green line shows limiting value of \({{j_{z}}(0,0)=0.8615}\). Adapted from McLaughlin et al. (2009)
McLaughlin et al. (2012b) quantified and measured the periodic nature of oscillatory reconnection. They identified two distinct periodic regimes: the (transient) impulsive phases and a longer-lived stationary phase. In the stationary phase, for driving amplitudes 6.3–126.2 km/s, they measured (stationary-phase) periods in the range 56.3–78.9 s. In particular, a driving amplitude of 25.2 km/s corresponds to a stationary period of 69.0 s. McLaughlin et al. (2012b) highlighted that the system acts akin to a damped harmonic oscillator (in the stationary phase). Thus, the greater the initial amplitude, the longer and stronger the current sheets at each stage, and thus the greater restoring force, leading to shorter periods (compared to smaller initial amplitude, shorter resultant current sheets, weaker restoring force and thus longer periods).
The physics behind oscillatory reconnection has been investigated by McLaughlin et al. (2009), Murray et al. (2009) and Threlfall et al. (2012). The restoring force of oscillatory reconnection has been shown to be a dynamic competition between the thermal-pressure gradients and the Lorentz force (i.e. a local imbalance of forces) with each in turn restoring an overshoot of the equilibrium brought on by the other (see Sect. 3.3 of McLaughlin et al. 2009; Sect. 3.2 of Murray et al. 2009; Fig. 7 of Threlfall et al. 2012). In other words, the reconnection occurs in distinct bursts: the inflow/outflow magnetic fields of one reconnection burst become the outflow/inflow fields in the following burst. With the Lorentz force, it is magnetic pressure that dominates (Threlfall et al. 2012) whereas magnetic tension only aids the compression of field lines as the current sheet forms. Note that in consecutive bursts of reconnection, the contrast between the thermal-pressure gradients and magnetic pressure decreases. Thus, each successive overshoot is smaller than the last and so the system is ultimately able to relax back to equilibrium.
2.3.1 Periodic Signals Associated with Magnetic Flux Emergence
An important example of oscillatory reconnection was found in the work of Murray et al. (2009) who utilised a stratified atmosphere permeated by a unipolar magnetic field (to represent a coronal hole) and investigated the emergence of a buoyant flux tube. Flux emerging into a pre-existing field had been studied in detail before, but Murray et al. (2009) were the first to investigate the long-term evolution of such a system, i.e. previous simulations ended once reconnection was first initiated. Murray et al. found that a series of “reconnection reversals” take place as the system searches for equilibrium, i.e. a cycle of inflow/outflow bursts followed by outflow/inflow bursts. Thus, the system demonstrates oscillatory reconnection in a self-consistent manner.
This seminal work was generalised by McLaughlin et al. (2012a) who detailed the oscillatory outputs and outflows of the system. They found that the physical mechanism of oscillatory reconnection naturally generates quasi-periodic vertical outflows with a transverse/swaying aspect. The vertical outflows consist of both a periodic aspect and a positively-directed flow of 20–60 km/s. Parametric studies show that varying the magnetic strength of the initial-submerged, buoyant flux tube \(\mathbf{B}_{\mathrm{buoyant}}\) yield a range of associated periodicities of 105–212.5 s for \(2.6 \times 10^{3}~\mbox{G} \le \mathbf{B}_{\mathrm{buoyant}} \le 3.9 \times 10^{3}~\mbox{G}\), where the stronger the initial flux tube strength, the longer the period of oscillation. Note that if the flux tube strength is too low (for McLaughlin et al. 2012a, this was \(\mathbf{B}_{\text{buoyant}} < 2.6 \times 10^{3}~\mbox{G}\)) the tube cannot fully emerge into the atmosphere since the buoyancy instability criterion is not satisfied (failed emergence). If the initial-submerged flux was too high (\(\mathbf{{B}}_{\mathrm{{buoyant}}} > 3.9 \times 10^{3}~\mbox{G}\)) then plasmoids are ejected from the ends of the current sheet. These ejected plasmoids change the properties of the X-point, e.g. taking magnetic flux with them. Thus, even though there is still oscillatory behaviour, this represents a fundamentally different regime than that of burst of reconnection without plasmoids. Thus, there are natural limitations placed on the periods generated by oscillatory reconnection in such a system. As before, the mechanism naturally generates periodic outputs even though no periodic driver is imposed on the system. Note that the transverse behaviour seen in the periodic jets originating from the reconnection region of the inverted Y-shaped structure is specifically due to the oscillatory reconnection mechanism, and would be absent for a single, steady-state reconnection jet.
Thus, oscillations associated with magnetic flux emergence (as well as the continuous emergence of the magnetic flux) show promise as a physical mechanism for QPPs, for example McLaughlin et al. (2012a) could not generate periodicities shorter than 105 seconds since this was restricted by the buoyancy instability criterion (i.e. failed emergence): lower periods could have been generated by changing the equilibrium parameters, such as modifying the strength of the pre-existing coronal field in the model. Longer periods are also possible for different equilibrium set-ups, e.g. Lee et al. (2014) saw 30-min oscillations during the interaction of an emerging magnetic flux with a pre-existing coronal magnetic configuration, see Fig. 6 (Fig. 9 from Lee et al. 2014).
Variations of the magnetic rope speed and temperature at the X-point below the flux rope, caused by the interaction of an emerging magnetic flux with a pre-existing magnetic configuration. From Lee et al. (2014)
2.3.2 Periodicities Generated
McLaughlin et al. (2012b) also ask what determines the (stationary) period (post-transients) and what determines the exponentially-decaying timescale. They recall the work of Craig and McClymont (1991) who derived an analytical prediction for two timescales:
where \(S\) is the Lundquist number and we identify \(t_{\mathrm{{oscillation}}}\) as our stationary period and \(t_{\mathrm{{decay}}}\) as our decay time. From McLaughlin et al. (2012b), for a driving amplitude of 25.2 km s−1, this gives \(t_{\mathrm{{oscillation}}} = 109.6~\mbox{s}\) and \(t_{\mathrm{{decay}}}=76.7~\mbox{s}\), compared to the measured stationary period of 69.0 s and decay time of 66.7 s. These estimates are in fair agreement given the simplicity of the Craig and McClymont (1991) model and hence we could conclude that the periodicity is determined by the Lundquist number, \(S\), or equivalently the magnetic Reynolds number, \(R_{m}\), since everything in McLaughlin et al. (2012b) is non-dimensionalised with respect to the Alfvén speed.
However, the model of Craig and McClymont (1991) is a closed system, whereas McLaughlin et al. (2012b) is an open system. Thus, the period of Craig and McClymont (1991) is better interpreted as the signal travel time from their outer boundary to the diffusion region (see, e.g. §7.1 of Priest and Forbes 2000 for further discussion). Craig and McClymont (1991) also neglect both nonlinear and thermal-pressure effects and so, in that sense, the similarity in periods between Craig and McClymont (1991) and McLaughlin et al. (2012b) could be simply coincidental. Thus, what dictates the period of oscillatory reconnection remains an open question.
The periodicities generated by the oscillatory reconnection mechanism are promising: around a lone null point, periodicities of 56.3–78.9 s have been found, and via flux emergence scenarios, periodicities of 105–212.5 s have arisen in a self-consistent manner. Flares unlock the stored non-potential magnetic energy in magnetic fields and, by releasing energy, a stressed magnetic system can return to a lower energy state. As noted by Murray et al. (2009) flares, therefore, are perfect events in which to search for signs of oscillatory reconnection.
Crucially for the mechanism these oscillations are generated with an exponentially-decaying signature for both the flux emergence scenario (McLaughlin et al. 2012a) and single null (McLaughlin et al. 2012b). QPPs with these properties have been detected in soft X-ray light curves of both solar and stellar flares (e.g. Cho et al. 2016Footnote 4). What is important to note is that the oscillations caused by this mechanism would be decaying not due to a particular dissipative mechanism, but due to the generation mechanism itself. Physically, this can be thought of as injecting a finite amount of energy into the oscillatory reconnection mechanism and so, intuitively, the resultant periodic behaviour must be finite in duration. Clearly this is a dynamic reconnection phenomena as opposed to the classical steady-state, time-independent reconnection models. This means that the oscillatory reconnection mechanism will struggle to explain decayless oscillations.
Only specific examples of oscillatory reconnection have been investigated so far but, given that the underlying physical mechanism in the dynamic competition between gas and magnetic pressure searching for equilibrium, the mechanism looks to be a robust, general phenomenon that may be observed in other systems that demonstrate finite-duration reconnection. The mechanism could occur at all scales. Recently, Thurgood et al. (2017) demonstrated how the oscillatory reconnection mechanism works about a three-dimensional null point, and now parametric studies are needed to investigate the full range of periodicities possible, as well as an investigation into how plasmoid generation modifies the system. Further studies should focus on heat conduction which is expected to reduce the temperature of the outflow jets. However, to ensure force balance in the current sheet, the density of outflows may actually be increased by heat conduction, which may make the outflow jet more observable. Another interesting question is whether this mechanism can produce QPPs in flaring light curves, if in the flare site there are several or a number of plasmoids and hence, elementary null points, as has been suggested in the fractal reconnection model (Shibata and Takasao 2016).
2.4 Thermal Over-Stability
In the solar coronal plasma there is a continuous competition between the radiative losses and the energy supply, that constitutes the coronal heating problem (see, e.g. Parnell and De Moortel 2012, for a recent review). The misbalance of the radiative losses and heating can lead to the appearance of oscillatory regime of thermal instability, and variations of thermodynamical properties of the plasma and induced flows. In particular, the dispersion relation describing acoustic oscillations along the field is:
where \(\omega \) is the cyclic frequency, \(k\) is the wave number, \(C_{\mathrm{s}}\) is the sound speed, \(\overline{\kappa }\) and \(\overline{\nu }\) are the parallel thermal conductivity and bulk viscosity, respectively, and \(\tilde{a_{\rho }}={\partial Q}/{\partial \rho }\) and \(\tilde{a_{p}}={\partial Q}/{\partial p}\) are the derivatives of the combined plasma heating/cooling function \(Q(p,\rho )\) at the thermal equilibrium with the pressure \(p_{0}\) and density \(\rho_{0}\), and other notations are standard (see Kumar et al. 2016, for details). The heating mechanism is not specified, and is assumed to be stationary. The radiation is assumed to be optically thin. In the case of weakly non-adiabatic effects, one can readily separate the real and imaginary parts of dispersion relation (1), obtaining:
respectively. The sign and specific value of \(\tilde{a}_{\rho }/C_{ \mathrm{s}}^{2}+\tilde{a}_{p}\) is determined by the dependence of the radiative and heating function on thermodynamical variables. If the value is positive, the misbalance of the radiative losses and plasma heating counteracts the dissipation because of thermal conduction and viscosity. Moreover, if this value is sufficiently large, the acoustic oscillation becomes undamped and even growing (see Fig. 7). In the case of the negative value, this effect enhances the oscillation damping. In the over-stable regime, the oscillation amplitude experiences the saturation because of nonlinear effects. The oscillation frequency is determined by the wavelength, e.g. the distance between the footpoints along the magnetic field line (e.g. Tsiklauri et al. 2004). This phenomenon is acoustic over-stability that can occur in flaring regions. As the second term on the right hand side of Eq. (3) depends on \(k^{2}\), the acoustic over-stability is most pronounced for long wavelength perturbations, for example, fundamental modes of long loops. Typical periods of the quasi-periodic pulsations of thermal emission, generated by acoustic self-oscillations, are determined by the length of the oscillating loop and the plasma temperature. For typical flaring loops the periods of these oscillations range from a few to several minutes, and may be longer in the case of these oscillations in long, cold pre-flare loops or filaments.
Different regimes of the evolution of the fundamental acoustic oscillation of a coronal loop, determined by the misbalance of radiative cooling and plasma heating. The plasma speed is normalised at double the initial amplitude. The time is normalised at half the oscillation period. The spatial coordinate is normalised at the loop length \(L\). Top raw, left: a decaying linear oscillation in the absence of radiative cooling and heating; right: undamped oscillation occurring when radiative and dissipative losses are compensated by heating. Bottom raw, left: a growing oscillation; right: an over-damped oscillation. Adapted from Kumar et al. (2016)
Examples of the decayless and growing oscillations detected in the Doppler shifts of hot coronal emission lines (possibly, incorrectly best-fitted by a decaying harmonic function) could be seen in Fig. 3 of Mariska et al. (2008). The recently detected very long period pulsations of the plasma temperature before the onset of flares (8–30 min “preflare-VLPs”, Tan et al. 2016) may perhaps be linked to this effect too. In addition, this effect may be responsible for the high-quality oscillatory patterns of the thermal X-ray emission, with the intermittent variation of the amplitude, detected in the time derivative of the GOES light curves of X-class flares by Simões et al. (2015) (see also Hayes et al. 2016 and Dennis et al. 2017).
An interesting research avenue is the investigation of the effect on the misbalance between the radiative losses and (quasi-)steady heating on another highly compressive mode, the sausage oscillation. Damping of this mode is known to be connected with the finite transport coefficients, i.e. the ion viscosity and electron thermal conductivity, and also by leakage of the fast magnetoacoustic oscillations across the field, in the external medium (e.g. Stepanov and Zaitsev 2014; Nakariakov et al. 2012). On the other hand, observations show the presence of high-quality compressive QPP with the periods typical for the sausage mode. For example, 25-s intensity and Doppler shift oscillations were recently detected in the thermal emission by Tian et al. (2016), and interpreted as the sausage mode. In these oscillations, the dissipative, radiative and leaky losses should be compensated by some energy supply that could be the thermal over-stability.
Longer period variations of the thermal emission intensity could be associated with entirely thermodynamical processes, for example the evaporation-condensation cycles (e.g. Froment et al. 2017, and references therein). These cycles include recurrent plasma condensations and temperature variations, followed by high-speed plasma flows (Müller et al. 2004), even in the case of a time-independent heating function. In this regime the QPP patterns are usually highly anharmonic, and resemble relaxation oscillations. It is found that this effect gives a wide range of periods, while we are not aware of any systematic studies of the dependence of the oscillation period upon the plasma parameters. Similar quasi-oscillatory variations are observed in laboratory plasma devices, in particular the phenomenon of the multifaceted asymmetric radiation from the edge (“MARFE”, DePloey et al. 1994).
2.5 MHD Flow Over-Stability
In the self-oscillation scenario, the energy supply can also be associated with steady flows of the plasma. Ofman and Sui (2006) considered the dynamical reconnection in a current sheet with a steady plasma flow localised near its plane. The profiles of all equilibrium quantities were taken to be smoothly non-uniform in the transverse direction. The profile of the flow had the transverse spatial scale about one order of magnitude smaller than the transverse non-uniformity of the magnetic field. The plasma density and temperature was initially constant. In the vicinity of the current sheet the plasma \(\upbeta \) was taken to be high, of about 4. Such a plasma configuration could appear because of, for example, the interaction between an emerging flaring loop and the overlying magnetic field. In this scenario, the plasma flow is caused by the chromospheric evaporation, which can be taken as steady if its time scale is much longer than the period of QPPs.
For a sufficiently high speed of the plasma flow, e.g. about the Alfvén speed, the plasma configuration was found to be unstable to the coupled Kelvin–Helmholtz and tearing instabilities, giving rise to the over-stable, i.e. oscillating, modes. During the evolution, the integrated Ohmic heating rate was found to vary quasi-periodically, see Fig. 8. The oscillation period is about 50 Alfvénic transit times across the current sheet. In the numerical simulations of Ofman and Sui (2006), for a macroscopic current sheet of the half-width about 1500 km, and the Alfvén speed of 500 km/s, the oscillation period is about 150 s.
Variation of the integrated Ohmic heating rate, \(\Delta H _{r}\), in a reconnecting current sheet with a non-uniform steady flow of the plasma. The dotted curve corresponds to the case without the flow, the dashed curve shows the case when the flow speed is equal to the local Alfvén speed, and the solid line to the case when the flow speed is 1.5 of the local Alfvén speed. The time unit is the transverse Alfvén time that is the ratio of the current sheet half-width and the Alfvén speed. From Ofman and Sui (2006)
This mechanism can naturally produce QPPs of the thermal emission, by the variation of the plasma heating rate. In addition, as the over-stability leads to the development of magnetic islands (plasmoids), there appear strong oscillating electric field that can readily exceed the Dreicer field. Hence, the over-stability is accompanied by the periodic acceleration of non-thermal electrons and associated QPP of non-thermal emission.
A parametric study of this mechanism, in particular the investigation of the effect of the specific values of the transport coefficients, the steepness of the transverse profiles of the flow, the electric current and plasma densities, temperature, magnetic field, and the anomalous resistivity, on the oscillation period, would be an interesting future task. Also, the over-stability could be associated not with the Kelvin–Helmholtz instability, but with one of the negative energy instabilities that have a much lower shear flow threshold, e.g. Joarder et al. (1997).
2.6 Waves and Plasmoids in a Current Sheet
Neutral current sheets are common structures both in the solar corona and in magnetosphere of the Earth. In the solar atmosphere, we can find these structures, for example, above the helmet structures, in coronal streamers, at the boundary between closed and open fields, or between coronal loop systems which have opposite magnetic polarity. A macroscopic current sheet is the key ingredient of the standard model of a solar flare. Neutral current sheets can be formed in one of three possible ways: the interaction of topologically different regions (this may give rise to a solar flare), the loss of equilibrium of a force-free field, and X-point collapse (see Priest 2014). Owing to their enhanced density, neutral current sheets are the structures that can guide the MHD waves. A Harris-type current sheet structure can support several kinds of guided magnetoacoustic waves, in particular, both kink and sausage modes. In the sausage mode, the current sheet pulsates like a blood vessel, with the central axis remaining undisturbed. In the kink mode the central axis moves back and forth during the wave motion. In a continuously non-uniform current sheet, three types of mode can exist: body, surface and hybrid, depending on the transverse structure of the perturbation (Smith et al. 1997). Hybrid modes contain elements of both body and surface waves, see e.g. Cramer (1994), Smith et al. (1997) and references therein. The nature of the mode determines its dispersion, i.e. the dependence of the phase speed on wavenumber. MHD waves and oscillations of current sheets can be excited by various processes where one of the most probable, providing either single or multiple sources of disturbances, is the impulsive energy release in a flare. In turn, these oscillations, e.g. the quasi-periodic signals appearing because of the dispersion, can be the sources of QPPs.
The analysis of group speeds of the guided modes shows that the long-wavelength spectral components propagate faster than the medium- and short-wavelength ones. This suggested that an impulsively-generated fast wave train has a characteristic wave signature with three distinct phases: the periodic phase, followed by quasi-periodic phase and then a decay phase (Roberts et al. 1983, 1984). Nakariakov et al. (2004b) simulated the formation of a quasi-periodic wave train in fast magnetoacoustic waveguides with the transverse plasma density profiles of different steepness. It was established that the dispersive evolution of fast wave trains leads to the appearance of characteristic “crazy” tadpole wavelet signatures, which was also confirmed by the observations. The key element of this mechanism is the broadband excitation, in other words, by a pulse that could occur because of a flaring energy release.
Pascoe et al. (2013) simulated numerically the dispersive evolution of fast waves in an expanding magnetic field generated by an impulsive, spatially localised energy release with a field-aligned density structures. The numerical results were found to be consistent with the observations, see Yuan et al. (2013). Jelínek and Murawski (2013) numerically studied magnetoacoustic-gravity waves in an open magnetic structure. They found that a pulse of the horizontal velocity both below and above the transition region could trigger oscillations with the periods in the range of three minutes, which correspond with those observed above the sunspots e.g. in UV/EUV emission by the Solar Dynamics Observatory (SDO)/Atmospheric Imaging Assembly (AIA) and in radio emission by the Nobeyama Radioheliograph (NoRH). The propagation of fast magnetoacoustic waves along coronal magnetic funnels has been studied numerically in Yang et al. (2015). The waves are excited impulsively by plasmoids formed in the X-point in the coronal magnetic funnel structure followed by the collision between them and the magnetic field in the outflow region. Nisticò et al. (2014) found good agreement of the numerical simulations of rapidly propagating fast wave trains with the observations of quasi-periodic rapidly-propagating waves of the EUV intensity observed with SDO/AIA. It was found out that an impulsive energy release could generate a quasi-periodic propagating fast wave train with a high signal quality from a single impulsive source. All the above mentioned studies modelled the fast wave propagation in a plasma slab. However, the results are not sensitive to the direction of the magnetic field as long as it is parallel to the slab’s boundaries. Hence, these results could be applied to the case of a neutral current sheet, provided it remains stable on the time scale of the wave evolution.
The widely used current sheet model satisfying the MHD equilibrium, \(\nabla p = \mathbf{j} \times \mathbf{B}\), is the so-called Harris model given by the magnetic configuration:
where \(B_{{0}}\) is external magnetic field and \(w_{\mathrm{cs}}\) is the semi-width of the current sheet. This formula was first derived by Harris (1962) in terms of the kinetic Vlasov theory.
It is well known that magnetoacoustic waves can be triggered easily during reconnection of magnetic field lines. In Kliem et al. (2000) the authors present a 2D MHD numerical model of pulsating decimetric continuum radio bursts, caused by quasi-periodic particle acceleration, resulting from the dynamic phase of magnetic reconnection in a large-scale current sheet. By means of this model, where the formation of plasmoids, their coalescence and repeated formation of next plasmoids, they explain the presence of quasi-periodic pulses with the characteristic periods ranging in \(0.5\mbox{--}10~\mbox{s}\).
Radio spikes, defined as a group of very short and narrowband bursts, are observed during solar flares and are believed to be generated during the reconnection process (Bárta and Karlický 2001). Karlický et al. (2011), Bárta et al. (2011) demonstrated that narrowband dm spikes could be associated with fast magnetoacoustic waves, numerically modelling the waves excited by turbulent reconnection outflows in a neutral Harris current sheet. The dispersively evolved waves were found to have the same wavelet spectral signatures as detected in the radio observations. It was concluded that narrowband dm spikes are generated by driven coalescence and fragmentation processes in turbulent reconnection outflows. The propagating magnetoacoustic waves (indicated by tadpole wavelet spectral signatures) modulate these coalescence processes via a modulation of current densities in interaction regions between colliding plasmoids. These waves modulate an acceleration of electrons and generation of plasma and electromagnetic waves that produce the spikes. The narrowband dm spikes can thus be considered as a radio signature of the fragmented reconnection in solar flares.
Jelínek and Karlický (2012) performed a more extended and detailed study of fast sausage waves in a current sheet. The specific interest has been placed on the parameters of the current sheets, such as the width, plasma \(\upbeta \), and the distance between the wave initiation and detection sites, that influence the detected signal and its corresponding wavelet spectrum, see Fig. 9. The wave period, similarly as in the case of simple mass density slab, can be expressed as:
where \(v_{\mathrm{Ae}}\) is the external Alfvén speed.
Comparison of wave signals (left column) and corresponding wavelet tadpole shapes (right column) for two different widths of the Harris current sheet; \(w_{\mathrm{cs}} = 0.50~\mbox{Mm}\) (first row) and \(w_{\mathrm{cs}} = 1.50~\mbox{Mm}\) (second row). From Jelínek and Karlický (2012)
Assuming that fast magnetoacoustic waves guided by current sheets modulate the radio fluxes (or even UV fluxes) at various locations, Jelínek and Karlický (2012) proposed that this knowledge can be helpful for estimating physical parameters of flare current sheets—another example of MHD seismology. From the point-of-view of the diagnostics of either flare current sheets or flare loops, the most important measurements and findings were: (a) the periods of the fast waves, which give information about the half-width of the Harris current sheet, and (b) that the wavelet tadpoles become longer and their heads are detected later in time when increasing the distance between the detection and perturbation points. Thus, it is possible to estimate the distance between the radio source at which the modulated signal is detected, and the region where the modulating magnetoacoustic wave is initiated. For example, the magnetoacoustic wave can propagate along the current sheet upwards in the solar atmosphere, and modulate the radio emission (produced by the plasma emission mechanism) at lower radio frequencies. The wavelet spectra of the signals at these frequencies would then show how the wavelet tadpoles have shifted in time, corresponding to the propagating magnetoacoustic wave train. Each tadpole corresponds to a specific plasma frequency, i.e. to the specific plasma density. Using models of the density stratification it is possible to determine the height. In particular, the recent detection of a quasi-periodic sequence of short radio ‘sparks’ (finite-bandwidth, short-duration isolated radio spikes) revealed that their repetition rate, 100 s, coincides with the periodicity in a quasi-periodic rapidly-propagating train of the EUV emission, detected in the low corona (Goddard et al. 2016).
There also exist several important differences between the propagation of fast magnetoacoustic waves in a vertical flare current sheet in a gravitationally-stratified solar atmosphere and a gravity-free case. The authors (Galsgaard and Roussev 2002; Jelínek et al. 2012) implemented in their 2D numerical simulations for the altitude-variant current sheet in the gravitational-stratified solar atmosphere an additional horizontal component of the magnetic field, contrary to the gravity-free case and altitude-invariant current sheet:
where the coefficient \(H_{0}\) denotes the magnetic scale height.
As a consequence of this modification, waveguiding properties of the current sheet can change significantly (Jelínek et al. 2012). At very low altitudes of the vertical current sheets the parameters are the same in both cases. However, in the stratified case the width of the current sheet grows with height (Jelínek et al. 2012). By this fact the authors in their 2D numerical simulations explained (according to Eq. (5)) the longer wave periods of propagating fast magnetoacoustic waves in the gravitationally-stratified solar atmosphere compared to the gravity-free case, see Fig. 10.
Temporal evolution of wavelet tadpoles for the three detection points: \(L_{\mathrm{D}} = 50~\mbox{Mm}\), \(60~\mbox{Mm}\), and \(70~\mbox{Mm}\) (upper, middle, and lower panel, respectively) for the gravity-free (left panels) and gravitationally stratified (right panels) solar atmosphere. The semi-width of the current sheet is \(w_{\mathrm{cs}} = 1.0~\mbox{Mm}\). From Jelínek et al. (2012)
Variations of the wave signal and their wavelet tadpoles are more irregular in the case with gravity (altitude-variant current sheet) than in the gravity-free case (altitude-invariant current sheet), which result from the variation with height of the dispersive properties and group velocities of the propagating magnetoacoustic waves in the gravitational case. As the gravitationally-stratified atmosphere is more realistic than gravity-free, it allows one to make a direct comparison with observational data. The most frequently measurable parameters of these waves in solar events are the wave periods and their temporal changes (i.e. the period modulation). Combining these data with the possible determination of the wave types and their wavelengths (from spatially-resolving measurements) together with independent estimates of the Alfvén speed at these locations (e.g. by the magnetic field extrapolation or UV and optical spectroscopy methods), it could be possible to directly compare these results with the observational findings.
Fiber bursts are fine structures of broadband type IV radio bursts, manifested by a certain frequency drift. In the wavelet spectra of the fiber bursts computed at different radio frequencies, wavelet tadpole features were found, whose head maxima have the same frequency drift as the drift of fiber bursts, see Fig. 11. It indicates that the drift of these fiber bursts can be explained by the propagating fast sausage wave train, which modulates the radio emission produced by non-thermal electrons trapped in a flare loop or current sheet. Karlický et al. (2013) presented a model for fiber bursts in the dm band, based on assuming fast sausage wave trains that propagate along a dense vertical current sheet to support this idea. They found that the frequency drift of the wavelet tadpoles corresponds to the drift of individual fiber bursts and they suggested the use of this information for the determination of the density profiles of the propagating magnetoacoustic wave from the fiber burst profiles measured along the radio frequency at some specific times.
Upper panels: examples of the fiber bursts at 12:01:05–12:01:16 UT (November 23, 1998, left panel) and 8:35:05–8:35:17 UT (November 18, 2003, right panel). Bottom part: corresponding wavelet power spectra showing the tadpoles with the period \(P = 1.4~\mbox{s}\). In both spectra, at selected frequencies the times of the tadpoles head maxima were determined (\(t1\)–\(t6\)) and also shown in the upper dynamic radio spectra (upper panels). The tadpole head maxima drift as the fiber bursts. From Karlický et al. (2013)
Jelínek et al. (2017) advanced the above-mentioned studies by performing high-resolution numerical simulations of the oscillatory processes during magnetic reconnection in a vertical, gravitationally-stratified current sheet. Development of magnetic reconnection leads to appearance of plasmoids that under the gravitational and buoyancy forces move upward or downward along the current sheet. These plasmoids collide with each other, as well as with the underlining magnetic arcade. After the collisions the plasmoids oscillate with the periods determined by the Alfvén travel time within the plasmoids. These oscillations could be responsible for the drifting pulsating structure (DPS) with distinct quasi-periodic oscillations in frequency, detected in the radio spectrum (Karlický et al. 2016).
Finally, efforts have been made using kinetic theory to model pulsations and periodicities generated by the plasma-emission mechanism of radio waves. For example, quasi-periodic generation of Langmuir waves and radio emission due to density inhomogeneities (Kontar 2001) and radio-emission pulsations produced via nonlinear oscillations (see Ratcliffe and Kontar 2014; Fonseca-Pongutá et al. 2016; and references therein).
2.7 “Magnetic Tuning Ork” Oscillation Driven by Reconnection Outflow
Magnetic reconnection, the central engine of solar flares, can drive supersonic Alfvénic flows. Such fast reconnection outflows can be an exciter of oscillations through the collision with the ambient plasma. The oscillations excited by the reconnection outflows may have the potential to tell us about the in situ physical quantities of flares. However, the oscillation process will be highly nonlinear, because the supersonic reconnection outflows will form nonlinear waves and shocks. Therefore, direct MHD simulations are necessary for a complete understanding.
Takasao and Shibata (2016) performed a set of 2D MHD simulations of a solar flare and studied oscillations excited by the reconnection outflow. Unlike previous models for quasi-periodic propagating fast-mode magnetoacoustic waves (QPFs), their model includes essential physics for solar flares such as magnetic reconnection, heat conduction, and chromospheric evaporation. From the simulations, they discovered the local oscillation above the loops filled with evaporated plasma (above-the-loop-top region) and the generation of QPFs from such oscillating region. In this section, we will introduce the physical process found in their study.
Figure 12a displays snapshots of the density distribution in the site of the simulated flare. Magnetic reconnection drives the narrow reconnection outflow. The reconnected fields pile up and form a loop system which is eventually filled with the hot dense plasma coming from the chromosphere (chromospheric evaporation). The loops filled with evaporated plasma correspond to the soft X-ray flare loops, and therefore the authors call the region above the loops “above-the-loop-top region” (an enlarged image of this is shown in Fig. 12a).
Quasi-periodic propagating fast-mode waves (QPFs) in a simulation of Takasao and Shibata (2016). (a) Top: density map. The solid lines denote magnetic field lines. An enlarged image of the above-the-loop-top region is also displayed. Bottom: the normalized running difference of the density. (b) Snapshots of the above-the-loop-top region. The colour contour indicates the density
Takasao and Shibata (2016) discovered an oscillation in the flaring region even without imposing any oscillatory perturbations. The normalised running difference image of the density (\(\Delta \rho / \rho \)) in Fig. 12a clearly shows the recurrent generation of isotropic waves. These waves are identified as fast-mode MHD waves. A noticeable point is that these waves are emitted from the oscillating above-the-loop-top region. Thus, the wave source of the fast-mode waves (QPFs) or “quasi-periodic flows” is very small compared to the system size (less than 10% of the system size in this simulation).
The above-the-loop-top region is found to be full of shocks and waves (see Fig. 12a), which is different from the previous expectations based on a standard flare model and previous simulations (Yokoyama and Shibata 2001). These shocks and waves are formed as a result of the collision of the supersonic reconnection outflow with the reconnected loops piled up below. In the standard flare model, a standing horizontal fast-mode shock is expected to be formed at the termination site of the outflow and is often referred to as a “termination shock” (Priest and Forbes 2002). However, the simulation shows that a V-shaped pattern is formed by two oblique fast-mode shocks and later by two oblique shocks and a single horizontal fast-mode shock (Fig. 12b). Moreover, the multiple termination shocks are never stationary and the structure changes drastically with time. We note that the very dynamic shocked region can be formed even in the case of steady reconnection (the localised resistivity is fixed in time and space in this study). It can be shown that this is a natural consequence of the termination of the reconnection outflow (see Takasao et al. 2015 and Takasao and Shibata 2016 for more details).
The above-the-loop-top region shows a pair of the sharply bent magnetic field structures (see Fig. 12b). Looking at the temporal evolution, one finds that the distance between the two arms changes quasi-periodically. The oscillation is displayed in Fig. 13. The left panels show snapshots of the plasma \(\upbeta \) of the above-the-loop-top region. The right panels indicate time-sequenced images of plasma \(\upbeta \) and normalised running difference of the total pressure \(\Delta p_{\mathrm{tot}}/p_{ \mathrm{tot}}\) obtained along the slit shown in the left panels, where the total pressure is the sum of the gas and magnetic pressures. The slit is positioned just below the V-shaped termination shocks. The figure shows that the two arms, shown as the two narrow high-\(\upbeta \) regions at the left and right edges, are oscillating with a period of ∼40 s (top and bottom rows show the timings when the two arms are closed and open, respectively).
Above-the-loop-top oscillation or magnetic tuning fork oscillation. Left: snapshots of the distribution of the plasma \(\upbeta \) of the above-the-loop-top region. Right: time-sequenced images of the plasma \(\upbeta \) and normalised running difference of the total pressure along the slit shown in the left panels. The horizontal lines in the time-sequenced images denote the timings of the snapshots in the left panels
Time-sequenced images of \(\Delta p_{\mathrm{tot}}/p_{\mathrm{tot}}\) in Fig. 13 indicate that outward-propagating fast-mode waves are excited quasi-periodically when the outward motion of the arms terminates. These fast-mode waves are what we have already displayed in Fig. 12a. Thus, it is clarified that the QPFs in the simulations are excited by the oscillatory motion of the above-the-loop-top region.
What is the generation mechanism of the oscillation and QPFs? Looking at Fig. 14a, one will find a fast backflow of the reconnection outflow in the small above-the-loop-top region. It was found that this backflow is the exciter of the oscillation. Figure 14b illustrates how the backflow controls the oscillation. The backflow (more exactly, the gradient of the dynamic pressure by backflow) pushes the two arms outward and compresses the magnetic field around the arms. This leads to the generation of outward-propagating fast-mode waves. Once the magnetic field there becomes strong enough to overcome the backflow, the arms start to move inward. The same process repeats and the oscillation is maintained as long as there is a strong backflow. The generation process of fast-mode waves by the backflow-driven oscillatory motion of the two arms is similar to the generation process of sound waves by an externally-driven tuning fork. For this reason, Takasao and Shibata (2016) name the two arms (a pair of the sharply bent magnetic field structures) “magnetic tuning fork”. For the rest of this section, the oscillation is called the “magnetic tuning fork oscillation”.
The shock structure is essential for maintaining the oscillation. The oscillation stops when a horizontal fast-mode shock appears in between the two oblique shocks (right panel of Fig. 13b). The timing of the appearance is also indicated in Fig. 13. The horizontal shock more significantly decelerates the reconnection outflow than oblique shocks. Therefore, the backflow should become slower after the formation of the horizontal shock. This leads to the disappearance of the oscillation. Thus, the termination shock structure is key for the maintenance of the oscillation.
The magnetic tuning fork oscillation generates not only QPFs but also the quasi-periodic oscillation of the termination shock strength. It has been argued that termination shocks could be a promising site for particle acceleration (Tsuneta and Naito 1998; Nishizuka and Shibata 2013; Chen et al. 2015) and could be related to the above-the-loop-top hard X-ray source (Masuda et al. 1994; Krucker et al. 2010; Oka et al. 2015), although the detailed acceleration process in such low Mach number and high-\(\upbeta \) shocks should be studied in more detail (for recent studies about electron acceleration at such shocks, see Matsukiyo et al. 2011; Guo et al. 2014). If this is correct, it is possible that the quasi-periodic oscillation of the multiple termination shocks found in their study leads to QPPs in non-thermal emissions through the quasi-periodic variation of the efficiency of particle acceleration. In addition, the simulations showed that the oscillation of multiple termination shocks and QPFs can have a common origin. On this basis, the authors suggest a new picture in which QPFs and QPPs in the non-thermal emissions have a common origin. Thermal emissions may also respond to the variation of the efficiency of acceleration through the thermalisation of non-thermal particles, showing QPPs.
What underlying physics determines the periodicity? Since the magnetic tuning fork oscillation is controlled by the backflow of the reconnection outflow in the above-the-loop-top region, we expect that the oscillation period \(P\) is proportional to the timescale determined by the backflow in this region: \(P\propto w/v_{\mathrm{bf}}\), where \(w\) is the size of the above-the-loop-top region and \(v_{\mathrm{bf}}\) is the backflow speed. This expectation is supported by a set of numerical simulations with different magnetic field strength \(B\) (equivalently, different plasma \(\upbeta \) in their study). Therefore, the problem is to clarify what determines the dependencies of the backflow speed \(v_{\mathrm{bf}}\) and the size \(w\).
The simulations show that the backflow speed is of the order of the Alfvén speed, as expected. This indicates that \(v_{\mathrm{bf}}\propto B\propto \beta^{-1/2}\). The dependence of the size \(w\) could be determined by the balance between the mass flux of the reconnection outflow and the mass flux carried horizontally by the backflow. Considering the fundamentals of reconnection and shock theories, gives \(w \propto \beta^{4/7}L^{9/7}\) (see Takasao and Shibata 2016 for details). From these results, we obtain the following scaling relation:
Numerical results are consistent with this predicted scaling relation. This further supports the fact that the oscillation is controlled by the backflow of the reconnection outflow.
It is noteworthy that the period is sensitive to the magnetic field strength (see Eq. (8)). In the typical case of a flare with the size of 60 Mm and plasma \(\upbeta \) of 0.08, the oscillation has a period of ∼40 s. Since the real coronal field strength will vary from flare to flare, typically from a few G to several tens G or larger, the magnetic tuning fork oscillation can create a large range of periods. This is consistent with the fact that QPFs and QPPs have a wide range of periods. Attention must be paid when one directly applies the scaling relation to observations, because the effects of the 3D global magnetic field structure and time-dependent magnetic reconnection, which are not considered in the study, can make the process more complex. Investigating these effects will be important for advancing the theory.
Recently, Takahashi et al. (2017) performed a series high-resolution 2D simulations of magnetic reconnection which occurs below an erupting CME. They showed that the oscillation in the above-the-loop-top region operates even in the case of plasmoid-dominated reconnection, although the oscillation tends to be asymmetric and the dynamics in the current sheet becomes turbulent in this case. Since the reconnection jets are bi-directional, two oscillation periods from the two termination shock regions emerge in their simulations. Takahashi et al. (2017) presents an observational example of a flare associated with a CME which shows two distinct periods in the QPPs. Another important finding is that the magnetic tuning fork oscillation at the bottom of a CME can cause quasi-periodic oscillations of the CME. Since such oscillations of CMEs have been reported (e.g. Krall et al. 2001), it will be interesting to statistically investigate the relationship between oscillations of CMEs and QPPs in emissions.
The above-the-loop-top region is very small, and therefore resolving a detailed structure of this region is observationally challenging. Nevertheless, confirming the key features of the magnetic tuning fork oscillation from observations is necessary to validate this mechanism. It is important to affirm the presence of the fast backflow from spectroscopic observations. The oscillation can lead to a quasi-periodic pulsations of emissions from the above-the-loop-top region. Therefore, investigating the temporal evolution of emissions from this region may allow us to infer whether the magnetic tuning fork oscillation actually operates. If the pulsations in the above-the-loop-top region and QPFs have a similar period, then this can be strong supporting evidence.
Direct identification of the magnetic tuning fork oscillation is very challenging. Therefore, it is necessary to accumulate pieces of indirect supporting evidence. For this aim, the following (and probably more) considerations will be useful. Bursts in non-thermal emissions, which seem to occur quasi-periodically in some cases, are sometimes attributed to the electron acceleration associated with plasmoid dynamics (Drake et al. 2006; Nishizuka et al. 2015; Takasao et al. 2016). One has to check if QPPs are accompanied by plasmoid ejections/dark downflows from coronal images and/or dynamic radio spectra (since plasmoids may be seen as drifting pulsating signatures in dynamic radio spectra, Karlický 2004). The quasi-periodic change of the magnetic reconnection rate is also a possible cause for QPPs, and plasmoid-dominated reconnection and oscillatory reconnection have been discussed in this context (Kliem et al. 2000; McLaughlin et al. 2009). If the change in reconnection rate is the main cause of QPPs, then QPPs in emissions and the reconnection rate estimated from e.g. flare ribbon separation (e.g. Isobe et al. 2005) will correlate well. These do not necessarily correlate in the case of the magnetic tuning fork oscillation (of course this is also true for many other cases). We need to examine if standing MHD waves in flare loops (e.g. Chen et al. 1999; Nakariakov et al. 2004a) are irrelevant to the observed oscillations or not. This may be done by tracking the motion of reconnected field lines or hard X-ray loop top source (Li and Gan 2006) and from Doppler observations (Mariska 2005). We are aware that the amplitude of the oscillation in Li and Gan (2006) is estimated to be only approximately 300 km (\({\sim} 0.4^{\prime \prime }\)) which is much smaller than the spatial resolution of RHESSI, \({\sim }7^{ \prime \prime }\). Therefore, there needs to be caution with regards to the interpretation of such a result.
2.8 Wave-Driven Reconnection in the Taylor Problem
As mentioned in Sect. 2.3, the seminal reconnection models of Sweet–Parker (Parker 1957; Sweet 1958) and Petschek (Petschek 1964) are steady-state models. Apart from the obvious problem of applying steady-state theory to dynamic flaring events, there is a subtler issue here: steady-state models can only provide one timescale, that of steady reconnection; proportional to \(S^{1/2}\) for Sweet–Parker, and to \(\ln {S}\) for Petschek (Bhattacharjee 2004). However, flares require a growth rate that is not only fast, but also exhibits a sudden increase in its time derivative. This is referred to as the ‘trigger problem’; the magnetic topology evolves slowly for an extended duration, only to then undergo a sudden change over a shorter timescale. Sweet–Parker and Petschek cannot account for the time evolution of the reconnection rate. Instead, time-dependent reconnection rates are referred to as impulsive or bursty. In addition, magnetic reconnection can be broadly classified into two types: free or spontaneous, i.e. caused by an intrinsic instability which taps into the magnetic free energy stored within the equilibrium topology, or forced, which is driven by perturbations (e.g. from a boundary) that induce a change in connectivity to an equilibrium or a sudden increase in the anomalous resistivity in the reconnection site.
An interesting forced, impulsive mechanism has been investigated with regards to the so-called ‘Taylor’ problem, which was proposed by J.B. Taylor in a private communication to Hahm and Kulsrud (1985) who then carried out the analysis themselves. Hahm and Kulsrud (1985) considered a slab plasma equilibrium that is suddenly subjected to imposed, small-amplitude boundary perturbations such as to drive magnetic reconnection at the centre of the slab. The so-called ‘Taylor’ problem has then been developed by several authors, including Wang and Bhattacharjee (1992), Wang et al. (1996) and Fitzpatrick (2003), who all consider slight variations on the initial and boundary conditions of the fundamental system, and Comisso et al. (2015) who extended the theory into the plasmoid-unstable regime. A self-consistent solution for the continuous plasma-heating was derived by Vekstein and Jain (1999) within a similar system undergoing forced external driving. The authors found that the plasma-heating rate displayed a relaxation-type dependency on the driving frequency, leading to a discussion whether forced magnetic reconnection can be interpreted as an Alfvén resonance with zero frequency (Uberoi and Zweibel 1999) or not (Vekstein 2000).
As an illustrative example, here we adopt the conditions of Fitzpatrick et al. (2003). Initial conditions are chosen such that \(\mathbf{{B}} = ( 0, B_{0} x , B_{T} ) \), where \(B_{0}\) and \(B_{T}\) are constants, and \(\mathbf{{A}}= [ 0,0,\phi (x,y,t) ] \) is the vector potential. The plasma is stable to tearing modes. The plasma is bounded by perfectly conducting walls (located at \(x=\pm a\)) and is periodic in the \(y\)-direction with periodicity length \(L\). The conducting walls are subject to displacement \(\varXi (t)\cos { ( k y ) }\) at \(x=a\) where \(k=2\pi / L\). An equal and opposite displacement is applied at \(x=-a\). Here \(\varXi (t)\propto 1- \exp { ( {t/\tau } ) }- ( t/\tau ) \exp { ( {-t/\tau } ) }\) is a ramp-up term. At early times, the plasma builds up a concentration of current (surface current) along \(x=0\) (the resonant surface). Subsequently, reconnection of flux across the resonant surface occurs, forming a chain of magnetic islands. As the reconnection proceeds, the surface current decreases and the plasma tends towards equilibrium. The process evolves through multiple stages in the reconnection process, labelled \(A\), \(B\), \(C\), \(D\) and \(E\) by Hahm and Kulsrud (1985). Phases \(A\) to \(C\) are governed by linear boundary-layer physics, phase \(D\) corresponds to Sweet-Parker reconnection (under certain circumstances, see Wang and Bhattacharjee 1992) and phase \(E\) corresponds to the nonlinear magnetic island dynamics of Rutherford (1973).
Hahm and Kulsrud (1985), Wang and Bhattacharjee (1992), Wang et al. (1996) and Fitzpatrick (2003) investigated the Taylor problem using Laplace Transforms and solved the resulting equations via asymptotic matching, equivalent to a boundary-layer problem. Essentially, there is an assumption that the plasma is divisible into two regions: an inner region (non-ideal, time-dependent, narrow) around the \(x=0\) resonant surface and an outer region (ideal, steady) consisting of the rest of the plasma (see, e.g. Bhattacharjee 2004). The inner and outer solutions are then matched asymptotically; referred to conventional asymptotic theory. Fitzpatrick et al. (2003) developed an improved Laplace Transform approach, which does not involve asymptotic matching, to investigate the early time response of the plasma; which is missed by the boundary-layer approach.
If the wall perturbation is switched on slowly compared to the Alfvén time, then the plasma response eventually asymptotes to that predicted by conventional asymptotic theory. However, at early times there is a compressible Alfvén wave driven contribution to the reconnection rate which leads a significant increase in the reconnection rate. If the wall perturbation is switched on rapidly compared to the Alfvén time then strongly localised compressible Alfvén wave pulses are generated which bounce back and forth between the walls several times. Each time these wave-pulses cross the resonant surface, they generate a transient surge in the reconnection rate. The maximum pulse-driven reconnection rate is much larger than that from conventional asymptotic theory. The evolution of the current density is dominated by a series of spikes in the reconnection rate. This can be seen in Fig. 15.
Evolution of the magnetic reconnection rate, \(J(t)\). Solid curve shows numerical solution generated by the FLASH code. Long-dashed curve shows the solution produced by conventional asymptotic matching theory. The short-dashed curve shows the solution generated by the improved Laplace Transform approach (and has been shifted downwards slightly to make it more visible). Reproduced from Fitzpatrick et al. (2003)
Fitzpatrick et al. (2003) derive an expression for the evolving current (see their equation 30) that involves integrating over the Bromwich contour. The numerator of the integrand contains multiple poles which correspond to those of the function \(\partial Y / \partial x|_{x=0}\) where \(Y(x,g)\) is a solution of the linearised, Laplace-transformed MHD equations governing the system. The poles can be written \(g=\pm i \omega_{n}\) where \(\omega_{n}\) (which are real) represents the oscillation frequencies associated with the natural Alfvénic modes of oscillation of the plasma. The plasma response emanating from these poles can be thought of as due to compressible Alfvén waves excited by the sudden imposition of the wall perturbation (Fitzpatrick et al. 2003).
Note that Fitzpatrick et al. (2003) uses the terminology compressible and compressional Alfvén wave. In the solar literature, compressional (or, actually, compressive) Alfvén waves are usually called fast magnetoacoustic waves, even in the case of gas pressure being neglected and the wave is driven by the magnetic pressure gradient (so as to avoid confusion with the incompressive shear Alfvén wave or, in cylindrical geometry, torsional Alfvén wave which are both sustained solely by magnetic tension). Thus, in accordance with the solar literature, for the rest of this section we use the terminology fast magnetoacoustic.
Simulations by Fitzpatrick et al. (2003) show that this manifests such that the sudden switch-on of the wall perturbation generates two strongly localised pulses which propagate towards the resonant surface, pass through one another and reflect off the walls. The two pulses then subsequently bounce back and forth several times. The arrival time of the pulses at \(x=0\) correlates with the spikes in the reconnection rate. The authors conclude that the strong spikes in \(J(t)\), i.e. the amplitude of the current sheet driven at the resonant surface, represent magnetic reconnection driven by fast magnetoacoustic waves which are excited by the sudden onset of the wall perturbation. The physical mechanism as to why the reconnection rate increases sharply as the fast magnetoacoustic wave pulse transits the resonant layer is not reported, although we may speculate that this is related to an increase in gradients of \(\mathbf{B}\) and therefore \(\nabla \times \mathbf{B}\) and \(J(t)\) as the wave passes through the resonant layer.
The period is governed by the fast magnetoacoustic speed and the distance between the walls \(2a\), i.e. the travel time. For example, increasing the central pressure increases the (fast magnetoacoustic) propagation speed and hence decreases the period between the spikes in \(J(t)\). Since this is a theoretical model solely, a broad range of periods, e.g. from seconds to minutes, can be obtained by tuning the fast magnetoacoustic speed and \(a\).
We note that the pulses only remain coherent over several transits where \(k \ll 1\), equivalent to \(L \gg a\). This is equivalent to the wavelength of the wall perturbation \(\propto k^{-1}\) being much greater than the wall separation \(\propto a\), which places limitations on the applicability of the model.
All the Taylor problem models considered so far are restricted to 2D nonlinear MHD and so a natural progression would be to extend the modelling to three-dimensions. In addition, the periodicity of the model is based on reflections between opposing solid boundaries and thus its applicability to solar and stellar atmospheres is unclear (whereas its applicability to, e.g., tokamaks is more obvious). In the solar atmosphere, the requirement for solid boundaries is usually achieved via, say, bouncing repeatedly between two footpoints in a wave-guiding coronal loop. However, in such systems, the fast magnetoacoustic waves would take a different form and one would require a resonant layer (as defined in the Taylor problem, not resonant absorption) to be located at the loop apex. It is unclear how this could be achieved topologically, let alone the wave generation aspect. This is of course not the only scenario; one can imagine a reconnection region might be bounded by a strong magnetic field, which would act as walls enveloping a cavity. As an example for stellar objects, Gao et al. (2008) reported on a periodicity in the flaring rate of binary star YY Gem and proposed that magnetic reconnection (responsible for the flaring) is modulated by fast magnetoacoustic waves which are trapped between the surfaces of the two stars, so that the reconnection rate presents a periodic behaviour. Regardless of specific applicability, from a forced, impulsive reconnection mechanism point-of-view, these papers are seminal.
2.9 Two Loop Coalescence
It has been widely believed that a current sheet with a high (\({>}10^{4}\)) Lundquist number is subject to fragmentation (Shibata and Takasao 2016). This instability is called the plasmoid instability and leads to the formation of plasmoids in a current sheet (Tanuma et al. 2001; Loureiro et al. 2007; Bhattacharjee et al. 2009), where plasmoids are magnetically-confined plasma. Plasmoids in the current sheet will contain the electric current in almost the same direction with each other, because the plasmoid formation results in the discretization of the electric current in the current sheet. Therefore an attracting Lorentz force will operate between these plasmoids, which will lead to the coalescence of plasmoids. This process, known as the coalescence instability (Finn and Kaw 1977; Pritchett and Wu 1979), is considered as a key process for the bursty, impulsive energy release during solar flares (Biskamp and Welter 1980; Bhattacharjee et al. 1983). The coalescence of plasmoids were actually observed (Takasao et al. 2012).
Previous nonlinear simulations revealed that the coalescing plasmoids show quasi-periodic oscillations in fields and other particle quantities (Pritchett and Wu 1979; Tajima et al. 1987). Since the particle acceleration is expected during the coalescence (Tajima et al. 1982; Oka et al. 2010; Karlický and Bárta 2011), QPPs seen in emissions originated from non-thermal, high-energy particles could be caused by the oscillations associated with the coalescence instability (an observational example is given by Takasao et al. 2016). On this basis, Tajima et al. (1987) investigated the characteristics of the oscillations in detail and compared their results with observations. As a representative work on the oscillations caused by the coalescence of plasmoids, we here briefly introduce their study in the following. This work has been generalised by Kolotkov et al. (2016), which will be also mentioned later.
Tajima et al. (1982, 1987) was motivated particularly by the observations of the (Seven–Sisters) flare on 7 June 1980 that showed seven successive pulses with a quasi-periodicity of ∼8 s (Nakajima et al. 1983). This flare was observed in hard X-ray, gamma-ray, and microwave emissions. All of the pulses in these bands were almost synchronous within ±2.2 s and have a similar shape. The observations suggest a quasi-periodic acceleration of both electrons and ions. An interesting feature of the pulsation is that a few of the pulses of microwaves at 17 GHz showed double subpeaks. It seems that the first subpeak coincides with the peak of the corresponding hard X-ray, while the second subpeak coincides with the peak of the corresponding gamma-ray pulse. To understand the observational characteristics, the authors investigated the coalescence of plasmoids numerically and theoretically in detail. They performed both particle and MHD simulations in 2.5D (two spatial dimensions \(x,y\) and three velocity and field dimensions), but here we only focus on the results of the particle simulations to see the relation between the oscillation and particle acceleration. The initial setup of their typical simulations assumes two plasmoids that are attracted by the Lorentz force by each other. A uniform external magnetic field, \(B_{z}\), is applied. A more detailed explanation for the setup is given in Leboeuf et al. (1982).
Figure 16 displays the temporal evolution of particle and field quantities during the coalescence process. Looking at the magnetic energy (thick line in Fig. 16a), one sees three peaks clearly. Corresponding to these peaks, the electrostatic field \(\mathbf {E}_{L}\) and ion and electron temperatures show double subpeaks. Strong particle acceleration in the \(z\)-direction occurs at the subpeaks of \(\mathbf {E}_{L}\) through the \(\mathbf {E}_{L}\times \mathbf {B}\) acceleration.
Temporal profiles of particle and field quantities for the coalescence process. (a) The thick line represents the magnetic energy, the thin one the ion temperature in the \(x\)-direction. (b) Electrostatic field energy in time. (c) Ion temperature in the \(z\)-direction. (d) Electron temperature in the \(x\)-direction. (e) Electron temperature in the \(z\)-direction. (f) Inductive electric field (\(E_{z}\)). From Tajima et al. (1987)
This oscillation process is schematically described in Fig. 17. When the coalescence starts, a strong acceleration of ions by the Lorentz force takes place. At \(t=t_{1}\), the acceleration reaches a maximum, leading to a strong compression at the far sides of the two plasma blobs. This compression causes the first temperature peak. In addition, the difference in inertia between ions and electrons results in charge separation at the compressed regions. The charge separation generates the electrostatic field \(\mathbf {E}_{L}\). The \(\mathbf {E}_{L} \times \mathbf {B}\) acceleration, together with the magnetic acceleration, produces high energy particles in the \(z\)-direction. At time \(t=t_{2}\) when two plasma blobs totally merge, the inductive electric field (\(\mathbf {v}\times \mathbf {B}\)) vanishes. The direction of the acceleration of electrons and ions along the \(z\)-direction is reversed at this moment. At time \(t=t_{3}\), the overshooting plasma blob motions result in the generation of the reverse electrostatic field. The temperature again reaches a maximum. This is the mechanism’s interpretation of the formation of the double peaks in the electrostatic field and temperature.
Schematic sequence of snapshots of the plasma and electric and magnetic fields during the coalescence process. Note that the direction of the electric field is defined in the opposite way as usual. From Tajima et al. (1987)
Tajima et al. (1987) developed a theoretical model of the coalescence of two plasmoids. They assume that \(\partial /\partial x \gg \partial /\partial y, \partial /\partial z\), where \(x\) is the direction of coalescence so that the dynamics of the coalescence is treated as a one-dimensional problem. To separately deal with the dynamics of ions and electrons, they start from the two-fluid ideal MHD equations.
Since no specific scale length appears in this one-dimensional coalescence process, we expect the presence of a self-similar solution for this problem. They introduced scale factors \(a(t)\) and \(b(t)\) in the following way to look for self-similar solutions:
where a dot represents the time derivatives and \(v_{ex}\) and \(v_{ix}\) are the electron and ion velocities in the \(x\)-direction, respectively. An ansatz imposed here is that the velocities are linear in \(x\). Further assuming quasi-neutrality (\(n_{i}=n_{e}\)), we get \(a=b\). As a result, it is found that a self-similar solution for the fields and particle quantities can be written as a function of the scale factor \(a(t)\).
The equation that governs the temporal evolution of the scale factor \(a(t)\) can be written as follows:
where the effective potential \(V(a)\) has essentially the same functional form as that of the effective potential for the gravitational force (see Fig. 18a). Thus, this means that the scale factor \(a\) (and therefore the other quantities) oscillates within a finite range. The minimum oscillation period \(P_{\mathrm{min}}\) is estimated as:
where \(C_{\mathrm{s}}\) and \(v_{\mathrm{A}}\) are the sound and Alfvén speeds, respectively, and \(\lambda \) is a characteristic scale length of the magnetic field in the interaction region (typically the size of plasmoids). One can see that the period increases as the plasma \(\upbeta \) increases. More detailed investigation implies that the period also depends on the magnetic twist of the plasmoids (namely, the ratio of the toroidal to poloidal magnetic fields) and the colliding velocity of the plasmoids.
Schematic behaviour of the explosive collapse. (a) The Sagdeev potential for the scale factor of the explosive coalescence. (b) The temporary behaviour of the magnetic field energy constructed from the Sagdeev potential. (c) The temporal behaviour of the electrostatic field energy constructed from the Sagdeev potential. (d) The temporal behaviour of the ion temperature in the \(x\)-direction (in the direction of coalescence) constructed from the Sagdeev potential. From Tajima et al. (1987)
Figure 18 shows a schematic temporal behaviour of (b) the electrostatic field \(E_{x}^{2}\) (\(E_{L}^{2}\)), (c) magnetic energy \(B_{y}^{2}\), and (d) ion temperature \(T_{ix}\). The double subpeak is prominent in the \(E_{x}^{2}\) and \(T_{ix}\) profiles, although \(E_{x}^{2}\) shows another small peak. The triple-peak profile will be a double-peak profile when the plasma \(\upbeta \) is sufficiently small.
From numerical and analytical investigations, it is found that the coalescence results in the quasi-periodic particle acceleration as seen in the observations of a flare on 7 June 1980. The double-peak profiles of the electrostatic field and ion and electron temperatures are likely to be relevant to the double subpeaks in emissions. If one looks at the electron energy spectrum, it can be fitted by a double power law with a break. This is consistent with the observations (Kane et al. 1983).
The theoretical discussion of Tajima et al. (1987) is based on the quasi-neutrality assumption, which is valid only at the non-kinetic scale (current sheet thickness is larger than the Debye length—We are aware that this assumption may not be consistent with the interpretation where the charge separation at a kinetic scale is discussed, see Fig. 17). Kolotkov et al. (2016) generalised the discussion to cover both the kinetic and non-kinetic scales. When the current sheet is thicker than the kinetic scale, the electrostatic field \(E_{x}\) is produced by the mechanical effects (coming from the momentum equations). This \(E_{x}\) appears from the equation of motion for ions. On the other hand, when the current sheet is comparable to or thinner than the kinetic scale, \(E_{x}\) is mainly produced by the charge separation. Kolotkov et al. (2016) found that the double-peak structure in \(E_{x}\) will be a general feature and can be found in both the kinetic and non-kinetic scales, although the shape of the profile is different from that in Tajima et al. (1987). In addition to this, the anharmonicity of the oscillations is also a distinct feature of the nonlinear large amplitude regime of the coalescence. The anharmonicity is clearly seen only in the nonlinear regime. The theory of Tajima et al. (1987) is constructed under the assumption that the gas pressure can be ignored during the implosion, but the gas pressure significantly increases at the center of the current sheet and produces two MHD fast-mode shocks (Forbes 1982; Takeshige et al. 2015).
Now numerical modelling of plasmoid coalescence is an essential method to advance our understanding of particle acceleration associated with plasmoid dynamics. Drake et al. (2006) pointed out that contracting plasmoids can be an efficient accelerator via Fermi acceleration. Guidoni et al. (2016) applied the idea to plasmoid-dominated reconnection in a simulated eruptive flare using a 2.5D MHD simulation, and found that energy gain of electrons in plasmoids can be higher than the previous estimation by Drake et al. (2006) due to strong plasma compression that occurs at the flare current sheet. However, Oka et al. (2010) performed 2D particle-in-cell simulations of magnetic reconnection with multiple plasmoids and found that the key process for electron acceleration is the secondary magnetic reconnection at merging points formed between coalescing plasmoids. The idea around the interaction between plasmoids and shocks by Nishizuka and Shibata (2013) has not been examined numerically. Therefore, our knowledge regarding electron acceleration has not been established yet. More detailed numerical modelling and comparison with observations should be important for understanding the origin of QPPs in non-thermal emissions.
2.10 Equivalent LCR Contour
An alternative, non-hydrodynamic mechanism for QPPs, based upon the consideration of a flaring magnetic configuration as an equivalent LCR contour was proposed by Zaitsev et al. (1998). The model is based on the difference in the values of the electrical conductivity in the coronal and chromospheric parts of the flaring region. In the corona, the parallel conductivity is much higher than across the field, and the electric current should go along the magnetic field lines. In the partly-ionised photospheric plasma, the electric current could go across the field. Hence there appears a closed electrical circuit formed in a coronal loop by a field-aligned current, which goes from one footpoint to the other, and the cross-field current between the footpoints in the photosphere.
Dynamics of the electric current ℐ in such a contour is described by the equation:
where \(c\) is the speed of light,
are the effective circuit capacitance and inductance, respectively; where \(B_{z0}\) is the magnetic field along the axis of the loop; \(r_{\mathrm{c}}\) and \(l_{\mathrm{c}}\) are the minor radius and length of the coronal part of the loop, respectively; \(\rho_{0}\) is the mass density in the coronal part of the loop (Khodachenko et al. 2009) and \(\varLambda = \mathrm{ln} \frac{4l_{\mathrm{c}}}{\pi r_{\mathrm{c}}} - \frac{7}{4}\). The nonlinear term \(\mathcal{R}(\mathcal{I})\) represents the effective resistance. It combines the resistance connected with the ion-neutral collisions in the photosphere, proportional to \(\mathcal{I}^{2}\), and the electromotive force associated with the photospheric convection. For sufficiently large photospheric convective flows the expression for \(\mathcal{R}( \mathcal{I})\) can become negative, inducing the alternate current in the system. This effect is more pronounced in the loops with a lower equilibrium electric current.
In the linear regime, when the effective resistance ℛ and capacitance \(\mathcal{C}\) are independent of the amplitude of the alternate current, equation (12) is a damped harmonic oscillator equation. It describes an alternate electric current with the period:
where \(\mathcal{I}_{0}\) is the equilibrium electric current in the loop, which is connected with the azimuthal component of the equilibrium magnetic field. For different values of the parameters, the model gives periods from a fraction of a second to a few minutes (e.g. Zaitsev and Stepanov 2008).
The LCR oscillations of a flaring magnetic loop can produce QPPs of both thermal and non-thermal emission. In particular, the intensity of the microwave emission produced by the gyrosynchrotron mechanism, is proportional to the angle between the line-of-sight and the local magnetic field. Thus, periodic variations of the field-aligned electric current that can be considered as the periodic appearance of the azimuthal component of the magnetic field, should result in the modulation of the gyrosynchrotron emission. The Ohmic heating of the alternate current would lead to a periodic variation of the plasma temperature. The temperature variation period is two times shorter than the period of the electric current oscillations, as it is proportional to the current amplitude squared. The associated variation of the electric field may result in periodic acceleration of charged particles, provided the electric field exceeds the Dreicer field. The periodic acceleration will lead to the periodic non-thermal emission. Another possibility is the transverse perturbation of the axis of the loop, caused by the periodic twisting of the loop by the alternate electric current. Indeed, twisting leads to the deformation of the loop’s plane, i.e. making the loop having an S-shape. Hence, periodic alternate twisting should periodically deform the loop’s plane, resembling a kink oscillation, with the structure resembling the second or higher harmonics. The interaction of this oscillation with a magnetic X-point situated nearby, could lead to the periodic modulation of the reconnection rate.
This mechanism may also easily explain drifts of the QPP periods, that are often observed in flares. For example, Dennis et al. (2017) detected high-quality oscillations of the time derivative of the soft X-ray emission of the decay phase of a flare, with the period gradually increasing from 25 s to 100 s. If the detected QPPs are produced by the alternate current, a gradual decrease in the equilibrium current \(\mathcal{I}_{0}\), caused, for example, by Ohmic dissipation, would lead to the increase in the oscillation period, see Eq. (13).
Similar ideas could be applied to the oscillatory interaction of two or several current-carrying loops, via the variation of the mutual inductance (e.g. Khodachenko et al. 2005, 2009). This interaction would result in variation of the electric currents, and also of the geometrical parameters of the magnetic configuration, for example the variation of the loop plane, the distance between individual loops, etc., which would look like transverse oscillations. It was shown that the inductive interaction inside a flaring active region may lead to longer period oscillations, of several minutes. The observational manifestation of these oscillations could, in particular, lead to QPPs in flaring light curves, either directly, by the effect of the alternate electric current, or indirectly, by, for example, periodically induced magnetic reconnection.
As was emphasised by Khodachenko et al. (2009), the equivalent LCR circuit approach ignores the fact that changes of the magnetic field and related electric current propagate as torsional Alfvén waves at the Alfvén speed, assuming the instant changes of the electric current in the whole circuit. Therefore, this model describes adequately the oscillations and evolution with time scales longer than the Alfvén travel time along the loop.
2.11 Autowave Processes in Flares
The effect of autowaves has not been directly addressed in the context of solar flares so far. However, the possibility of the triggering of flaring energy release by an MHD wave, and the subsequent excitation of the wave by the flare, creates a theoretical ground for the occurrence of autowave processes.
One possible manifestation of such a process is connected with the well-established progression of the flaring hard X-ray and EUV brightenings along the photospheric neutral line in two-ribbon flares. The typical speed of this progression along the ribbons is a few tens of km/s (e.g. Krucker et al. 2003, 2005; Bogachev et al. 2005; Grigis and Benz 2005; Yang et al. 2009; Inglis and Gilbert 2013).Footnote 5 Nakariakov and Zimovets (2011) suggested that this value of the speed is well consistent with the perpendicular group speed of a highly oblique slow magnetoacoustic wave. It was found that the perpendicular group speed has a rather sharp maximum reaching about 10–20% of the sound speed for the propagation angles of about 25–28 degrees to the magnetic field. In a typical flaring plasma of temperature 107 K and with Alfvén speed of 1000 km/s, the highest perpendicular group speed of a slow magnetoacoustic wave is about 40 km/s.
In the proposed scenario a primary energy release occurring somewhere above the neutral line, in the flaring arcade, excites a slow magnetoacoustic pulse that propagates downward. The pulse gets reflected from the chromosphere and returns back to the top of the flaring arcade, slightly offset from the location of the primary energy release along the neutral line (Gruszecki and Nakariakov 2011). There the wave triggers another energy release by one of the mechanisms described in Sect. 2.2. This energy release excites another slow wave, causing the next cycle of this autowave mechanism. Along the field, the pulse propagates at a speed close to the sound speed, while across the field its group speed is 10–20% which is consistent with the observed speed of the brightening progression along the neutral line. In addition, this mechanism explains readily the quasi-periodic nature of the energy releases. The oscillation period would be determined by the acoustic travel time from the footpoints to the arcade top, e.g. 30–80 s for typical solar flares. This value is consistent with the quasi-periodic progression of hard X-ray sources along the neutral line, observed by Grigis and Benz (2005). An important element of this mechanism is that, in contrast with the fast magnetoacoustic waves propagating in a non-uniform plasma (see Sect. 2.6), slow waves experience very weak dispersion, and hence the initial pulse does not evolve in a quasi-periodic wave train.
This mechanism could be modified. For example, the excitation of the slow magnetoacoustic pulse could occur not near the energy release site, but at the chromosphere, by the precipitating non-thermal particles accelerated by the energy release near the top of the arcade. Some asymmetry of the footpoints with respect to the arcade top would cause some difference in the acoustic travel time in the opposite magnetic legs. It would produce the double-peak structure of the emission peaks in the flare light curve, which is a frequently detected feature of QPPs.
3 Conclusions
There are quasi-periodic patterns in solar and stellar flaring energy releases. Often the EM radiation generated in flares shows a pronounced oscillatory pattern, with characteristic periods ranging from a fraction of a second to several minutes, or even longer in the case of stellar superflares. These are referred to as quasi-periodic pulsations (QPPs) to emphasise that they often contain apparent amplitude and period modulation. QPPs have been detected in all EM bands (including radio, microwave, white-light, H\(\upalpha \), UV, EUV, soft X-ray, hard X-ray and gamma-ray) and occur in all stages of the flare. QPPs are detected across multiple instruments, so they are not an instrumental effect, and are observed in a significant fraction of flares. This review paper is primarily a theoretical modelling review and details the possible physical mechanisms underpinning QPPs, with an emphasis on the physical processes that generate the resultant range of periodicities.
We have reviewed eleven potential physical mechanisms underpinning QPP generation (Sect. 2). These can be classed according to the nature of the underlying physical process:
-
Oscillatory processes of the emitting plasma, including MHD oscillations (Sect. 2.1), QPPs triggered periodically by external waves (Sect. 2.2), dispersive wave trains (Sect. 2.6), the magnetic tuning fork (Sect. 2.7) and the equivalent LCR contour (Sect. 2.10). Oscillations are (quasi-)periodic motions around an equilibrium, connected with the competition between inertia and an effective restoring force. Properties of oscillations (spectrum, amplitudes, phases, etc) are prescribed by the initial perturbation. The advantage of the MHD oscillation explanation is the observation of multiple periodicities.
-
Self-oscillatory processes, including the “load-unload” model and relaxation processes. This includes periodic or repetitive spontaneous reconnection, including oscillatory reconnection (Sect. 2.3), thermal overstabilities (Sect. 2.4) and wave-flow overstabilities (Sect. 2.5), wave-driven reconnection in the Taylor problem (Sect. 2.8) as well as the coalescence of two magnetic flux tubes (Sect. 2.9). Mathematically, self-oscillations are associated with a limit cycle. Usually self-oscillations have properties that are independent of the initial excitation and occur in essentially non-conservative systems. The self-oscillation period may depend upon the amplitude. In flares, a steady inflow of magnetic flux towards a reconnection site could result in repetitive magnetic reconnection (“magnetic dripping”) that should be considered a self-oscillatory process. The energy supply for self-oscillations comes from an essentially non-periodic source. In the “load-unload” model, QPPs are a side-effect of the transient energy release, connected with the relationship of the energy load-and-then-unload balance. The advantage of the time-dependent reconnection model is the natural explanation of the simultaneity of QPPs in different bands (as they are produced by the same cause: the time-varying rate of the electron acceleration).
-
We also considered autowave processes in flares (Sect. 2.11). Properties of autowaves are independent or weakly-dependent on the initial excitation, and so they are determined only by the parameters of the system.
Terminology and definitions were given in Sect. 1.1.
3.1 Future Directions and Key Unanswered Questions
There remain key unanswered questions concerning QPPs, including:
-
Is there any statistical relationship between QPP parameters (periods, decay times, relative and absolute amplitudes, modulations, etc) with the parameters of the host flare?
-
The observed periods of QPPs coincide by the order of magnitude with the MHD oscillations and waves detected abundantly in the solar corona (and well resolved in time and space). These MHD oscillations and waves typically have a few percent relative amplitude. In contrast, QPPs can reach a modulation depth of up to 100%. If QPP are caused by MHD oscillations, how can the oscillatory signal be amplified?
-
Are QPPs detected in different phases of the flare fundamentally different? Are QPPs detected in thermal and non-thermal emission different?
-
Can we distinguish between different classes of QPPs (if indeed there are different classes)?
-
Are the QPPs detected in stellar superflares, that are much more powerful than the strongest detected solar flares, produced by the same mechanisms as in solar flares?
The occurrence of QPPs puts additional constraints on the interpretation and understanding of the fundamental processes operating in both solar and stellar flares, e.g. particle acceleration and magnetic energy liberation. Simply put, there must be a physical reason for the flaring emission being arranged in a sequence of quasi-periodic bursts. The importance of a full understanding of QPPs is essential in order to work towards an integrated model of solar and stellar flares, as well as unlocking a potential diagnostic of the flare process.
When reviewing the QPP physical mechanisms in this paper, we have emphasised (where possible) the following details: (i) What range of periods can the mechanism generate? (ii) What underlying physics determines these periodicities? (iii) How much can this mechanism be proven/identified in observations? All the QPP physical mechanisms detailed in Sect. 2 require further study and refinement, e.g. parametric studies and forward modelling of produced observables. There is currently no physical mechanism that can unambiguously explain all QPPs, and conclusive proof will require identification of multiple characteristics in a single observed event with a favourable magnetic configuration. In this context, the main advantage of solar observations, the availability of spatial information about the plasma and magnetic structures in the flaring region, and also of the sources of different emissions, opens up very interesting perspectives and needs full exploitation. Another important feature of QPP, the non-stationarity of the period and amplitude of the oscillatory patterns, in other words, the “quasi”-ness, requires the development of new analytical techniques addressing the intrinsically non-stationary nature of QPPs.
Notes
The medium could be considered as active if certain perturbations provoke the medium to release energy.
Note that this propagation along the ribbons is a different phenomenon to the gradual separation motion of the flare ribbons, which is (also) typically of the order of tens of km/s.
References
S. Anfinogentov, V.M. Nakariakov, M. Mathioudakis, T. Van Doorsselaere, A.F. Kowalski, The decaying long-period oscillation of a stellar megaflare. Astrophys. J. 773, 156 (2013). https://doi.org/10.1088/0004-637X/773/2/156
S.K. Antiochos, P.A. Sturrock, Evaporative cooling of flare plasma. Astrophys. J. 220, 1137–1143 (1978). https://doi.org/10.1086/155999
A. Asai, M. Shimojo, H. Isobe, T. Morimoto, T. Yokoyama, K. Shibasaki, H. Nakajima, Periodic acceleration of electrons in the 1998 November 10 solar flare. Astrophys. J. Lett. 562, 103–106 (2001). https://doi.org/10.1086/338052
M.J. Aschwanden, Theory of radio pulsations in coronal loops. Sol. Phys. 111, 113–136 (1987). https://doi.org/10.1007/BF00145445
L.A. Balona, A.-M. Broomhall, A. Kosovichev, V.M. Nakariakov, C.E. Pugh, T. Van Doorsselaere, Oscillations in stellar superflares. Mon. Not. R. Astron. Soc. 450, 956–966 (2015). https://doi.org/10.1093/mnras/stv661
M. Bárta, M. Karlický, Turbulent plasma model of the narrowband dm-spikes. Astron. Astrophys. 379, 1045–1051 (2001). https://doi.org/10.1051/0004-6361:20011375
M. Bárta, J. Büchner, M. Karlický, J. Skála, Spontaneous current-layer fragmentation and cascading reconnection in solar flares. I. Model and analysis. Astrophys. J. 737, 24 (2011). https://doi.org/10.1088/0004-637X/737/1/24
T.M. Belloni, A. Sanna, M. Méndez, High-frequency quasi-periodic oscillations in black hole binaries. Mon. Not. R. Astron. Soc. 426, 1701–1709 (2012). https://doi.org/10.1111/j.1365-2966.2012.21634.x
A. Bhattacharjee, Impulsive magnetic reconnection in the Earth’s magnetotail and the solar corona. Annu. Rev. Astron. Astrophys. 42, 365–384 (2004). https://doi.org/10.1146/annurev.astro.42.053102.134039
A. Bhattacharjee, F. Brunel, T. Tajima, Magnetic reconnection driven by the coalescence instability. Phys. Fluids 26, 3332–3337 (1983). https://doi.org/10.1063/1.864070
A. Bhattacharjee, Y.-M. Huang, H. Yang, B. Rogers, Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16(11), 112102 (2009). https://doi.org/10.1063/1.3264103
D. Biskamp, H. Welter, Coalescence of magnetic islands. Phys. Rev. Lett. 44, 1069–1072 (1980). https://doi.org/10.1103/PhysRevLett.44.1069
S.A. Bogachev, B.V. Somov, T. Kosugi, T. Sakao, The motions of the hard X-ray sources in solar flares: images and statistics. Astrophys. J. 630, 561–572 (2005). https://doi.org/10.1086/431918
W.J. Borucki, D. Koch, G. Basri, N. Batalha, T. Brown, D. Caldwell, J. Caldwell, J. Christensen-Dalsgaard, W.D. Cochran, E. DeVore, E.W. Dunham, A.K. Dupree, T.N. Gautier, J.C. Geary, R. Gilliland, A. Gould, S.B. Howell, J.M. Jenkins, Y. Kondo, D.W. Latham, G.W. Marcy, S. Meibom, H. Kjeldsen, J.J. Lissauer, D.G. Monet, D. Morrison, D. Sasselov, J. Tarter, A. Boss, D. Brownlee, T. Owen, D. Buzasi, D. Charbonneau, L. Doyle, J. Fortney, E.B. Ford, M.J. Holman, S. Seager, J.H. Steffen, W.F. Welsh, J. Rowe, H. Anderson, L. Buchhave, D. Ciardi, L. Walkowicz, W. Sherry, E. Horch, H. Isaacson, M.E. Everett, D. Fischer, G. Torres, J.A. Johnson, M. Endl, P. MacQueen, S.T. Bryson, J. Dotson, M. Haas, J. Kolodziejczak, J. Van Cleve, H. Chandrasekaran, J.D. Twicken, E.V. Quintana, B.D. Clarke, C. Allen, J. Li, H. Wu, P. Tenenbaum, E. Verner, F. Bruhweiler, J. Barnes, A. Prsa, Kepler planet-detection mission: introduction and first results. Science 327, 977 (2010). https://doi.org/10.1126/science.1185402
J.W. Brosius, A.N. Daw, Quasi-periodic fluctuations and chromospheric evaporation in a solar flare ribbon observed by IRIS. Astrophys. J. 810, 45 (2015). https://doi.org/10.1088/0004-637X/810/1/45
J.W. Brosius, A.N. Daw, A.R. Inglis, Quasi-periodic fluctuations and chromospheric evaporation in a solar flare ribbon observed by Hinode/EIS, IRIS, and RHESSI. Astrophys. J. 830, 101 (2016). https://doi.org/10.3847/0004-637X/830/2/101
J.C. Buitrago-Casas, J.C. Martínez Oliveros, C. Lindsey, B. Calvo-Mozo, S. Krucker, L. Glesener, S. Zharkov, A statistical correlation of sunquakes based on their seismic and white-light emission. Sol. Phys. 290, 3151–3162 (2015). https://doi.org/10.1007/s11207-015-0786-9
P.J. Cargill, J.T. Mariska, S.K. Antiochos, Cooling of solar flares plasmas. 1: Theoretical considerations. Astrophys. J. 439, 1034–1043 (1995). https://doi.org/10.1086/175240
H. Carmichael, A process for flares. NASA Spec. Publ. 50, 451 (1964)
R.C. Carrington, Description of a singular appearance seen in the Sun on September 1, 1859. Mon. Not. R. Astron. Soc. 20, 13–15 (1859). https://doi.org/10.1093/mnras/20.1.13
P.F. Chen, The relation between EIT waves and solar flares. Astrophys. J. Lett. 641, 153–156 (2006). https://doi.org/10.1086/503868
P.F. Chen, Global coronal waves, in Low-Frequency Waves in Space Plasmas. Geophysical Monograph Series, vol. 216 (Willey, New York, 2016), pp. 381–394. https://doi.org/10.1002/9781119055006.ch22, Washington DC American Geophysical Union
P.F. Chen, E.R. Priest, Transition-region explosive events: reconnection modulated by p-mode waves. Sol. Phys. 238, 313–327 (2006). https://doi.org/10.1007/s11207-006-0215-1
P.F. Chen, C. Fang, Y.H. Tang, M.D. Ding, Simulation of magnetic reconnection with heat conduction. Astrophys. J. 513, 516–523 (1999). https://doi.org/10.1086/306823
P.F. Chen, S.T. Wu, K. Shibata, C. Fang, Evidence of EIT and Moreton waves in numerical simulations. Astrophys. J. Lett. 572, 99–102 (2002). https://doi.org/10.1086/341486
B. Chen, T.S. Bastian, C. Shen, D.E. Gary, S. Krucker, L. Glesener, Particle acceleration by a solar flare termination shock. Science 350, 1238–1242 (2015). https://doi.org/10.1126/science.aac8467
G.P. Chernov, A.K. Markeev, M. Poquerusse, J.L. Bougeret, K.-L. Klein, G. Mann, H. Aurass, M.J. Aschwanden, New features in type IV solar radio emission: combined effects of plasma wave resonances and MHD waves. Astron. Astrophys. 334, 314–324 (1998)
I.-H. Cho, K.-S. Cho, V.M. Nakariakov, S. Kim, P. Kumar, Comparison of damped oscillations in solar and stellar X-ray flares. Astrophys. J. 830, 110 (2016). https://doi.org/10.3847/0004-637X/830/2/110
L. Comisso, D. Grasso, F.L. Waelbroeck, Extended theory of the Taylor problem in the plasmoid-unstable regime. Phys. Plasmas 22(4), 042109 (2015). https://doi.org/10.1063/1.4918331
I.J.D. Craig, A.N. McClymont, Dynamic magnetic reconnection at an X-type neutral point. Astrophys. J. Lett. 371, 41–44 (1991). https://doi.org/10.1086/185997
I.J.D. Craig, A.N. McClymont, Linear theory of fast reconnection at an X-type neutral point. Astrophys. J. 405, 207–215 (1993). https://doi.org/10.1086/172354
I.J. Craig, P.G. Watson, Fast dynamic reconnection at X-type neutral points. Astrophys. J. 393, 385–395 (1992). https://doi.org/10.1086/171512
N.F. Cramer, Magneto-acoustic surface waves on current sheets. J. Plasma Phys. 51, 221–232 (1994). https://doi.org/10.1017/S0022377800017530
X.-Q. Cui, Y.-H. Zhao, Y.-Q. Chu, G.-P. Li, Q. Li, L.-P. Zhang, H.-J. Su, Z.-Q. Yao, Y.-N. Wang, X.-Z. Xing, X.-N. Li, Y.-T. Zhu, G. Wang, B.-Z. Gu, A.-L. Luo, X.-Q. Xu, Z.-C. Zhang, G.-R. Liu, H.-T. Zhang, D.-H. Yang, S.-Y. Cao, H.-Y. Chen, J.-J. Chen, K.-X. Chen, Y. Chen, J.-R. Chu, L. Feng, X.-F. Gong, Y.-H. Hou, H.-Z. Hu, N.-S. Hu, Z.-W. Hu, L. Jia, F.-H. Jiang, X. Jiang, Z.-B. Jiang, G. Jin, A.-H. Li, Y. Li, Y.-P. Li, G.-Q. Liu, Z.-G. Liu, W.-Z. Lu, Y.-D. Mao, L. Men, Y.-J. Qi, Z.-X. Qi, H.-M. Shi, Z.-H. Tang, Q.-S. Tao, D.-Q. Wang, D. Wang, G.-M. Wang, H. Wang, J.-N. Wang, J. Wang, J.-L. Wang, J.-P. Wang, L. Wang, S.-Q. Wang, Y. Wang, Y.-F. Wang, L.-Z. Xu, Y. Xu, S.-H. Yang, Y. Yu, H. Yuan, X.-Y. Yuan, C. Zhai, J. Zhang, Y.-X. Zhang, Y. Zhang, M. Zhao, F. Zhou, G.-H. Zhou, J. Zhu, S.-C. Zou, The large sky area multi-object fiber spectroscopic telescope (LAMOST). Res. Astron. Astrophys. 12, 1197–1242 (2012). https://doi.org/10.1088/1674-4527/12/9/003
J.R.A. Davenport, The Kepler catalog of stellar flares. Astrophys. J. 829, 23 (2016). https://doi.org/10.3847/0004-637X/829/1/23
J.R.A. Davenport, S.L. Hawley, L. Hebb, J.P. Wisniewski, A.F. Kowalski, E.C. Johnson, M. Malatesta, J. Peraza, M. Keil, S.M. Silverberg, T.C. Jansen, M.S. Scheffler, J.R. Berdis, D.M. Larsen, E.J. Hilton, Kepler flares. II. The temporal morphology of white-light flares on GJ 1243. Astrophys. J. 797, 122 (2014). https://doi.org/10.1088/0004-637X/797/2/122
I. De Moortel, An overview of coronal seismology. Philos. Trans. R. Soc. Lond. Ser. A 363, 2743–2760 (2005). https://doi.org/10.1098/rsta.2005.1665
I. De Moortel, V.M. Nakariakov, Magnetohydrodynamic waves and coronal seismology: an overview of recent results. Philos. Trans. R. Soc. Lond. Ser. A 370, 3193–3216 (2012). https://doi.org/10.1098/rsta.2011.0640
B.R. Dennis, Solar hard X-ray bursts. Sol. Phys. 100, 465–490 (1985). https://doi.org/10.1007/BF00158441
B.R. Dennis, A.K. Tolbert, A. Inglis, J. Ireland, T. Wang, G.D. Holman, L.A. Hayes, P.T. Gallagher, Detection and interpretation of long-lived X-ray quasi-periodic pulsations in the X-class solar flare on 2013 May 14. Astrophys. J. 836, 84 (2017). https://doi.org/10.3847/1538-4357/836/1/84
A. DePloey, M. Goossens, R.A.M.V. der Linden, Multifaceted asymmetric radiation from the edge (MARFEs): a general magnetohydrodynamic study in a one-dimensional tokamak model. Phys. Plasmas 1(8), 2623 (1994)
L. Dolla, C. Marqué, D.B. Seaton, T. Van Doorsselaere, M. Dominique, D. Berghmans, C. Cabanas, A. De Groof, W. Schmutz, A. Verdini, M.J. West, J. Zender, A.N. Zhukov, Time delays in quasi-periodic pulsations observed during the X2.2 solar flare on 2011 February 15. Astrophys. J. Lett. 749, 16 (2012). https://doi.org/10.1088/2041-8205/749/1/L16
M. Dominique, J.-F. Hochedez, W. Schmutz, I.E. Dammasch, A.I. Shapiro, M. Kretzschmar, A.N. Zhukov, D. Gillotay, Y. Stockman, A. BenMoussa, The LYRA instrument onboard PROBA2: description and in-flight performance. Sol. Phys. 286, 21–42 (2013). https://doi.org/10.1007/s11207-013-0252-5
A. Donea, Seismic transients from flares in solar cycle 23. Space Sci. Rev. 158, 451–469 (2011). https://doi.org/10.1007/s11214-011-9787-7
A.-C. Donea, C. Lindsey, Seismic emission from the solar flares of 2003 October 28 and 29. Astrophys. J. 630, 1168–1183 (2005). https://doi.org/10.1086/432155
A.-C. Donea, D. Besliu-Ionescu, P.S. Cally, C. Lindsey, V.V. Zharkova, Seismic emission from a M9.5-class solar flare. Sol. Phys. 239, 113–135 (2006). https://doi.org/10.1007/s11207-006-0108-3
J.F. Drake, M. Swisdak, H. Che, M.A. Shay, Electron acceleration from contracting magnetic islands during reconnection. Nature 443, 553–556 (2006). https://doi.org/10.1038/nature05116
A.G. Emslie, B.R. Dennis, A.Y. Shih, P.C. Chamberlin, R.A. Mewaldt, C.S. Moore, G.H. Share, A. Vourlidas, B.T. Welsch, Global energetics of thirty-eight large solar eruptive events. Astrophys. J. 759, 71 (2012). https://doi.org/10.1088/0004-637X/759/1/71
J.M. Finn, P.K. Kaw, Coalescence instability of magnetic islands. Phys. Fluids 20, 72–78 (1977). https://doi.org/10.1063/1.861709
G.H. Fisher, R.C. Canfield, A.N. McClymont, Flare loop radiative hydrodynamics—part six—chromospheric evaporation due to heating by nonthermal electrons. Astrophys. J. 289, 425 (1985). https://doi.org/10.1086/162902
R. Fitzpatrick, A numerical study of forced magnetic reconnection in the viscous Taylor problem. Phys. Plasmas 10, 2304–2312 (2003). https://doi.org/10.1063/1.1574516
R. Fitzpatrick, A. Bhattacharjee, Z.-W. Ma, T. Linde, Wave driven magnetic reconnection in the Taylor problem. Phys. Plasmas 10, 4284–4290 (2003). https://doi.org/10.1063/1.1617983
L. Fletcher, H.S. Hudson, Impulsive phase flare energy transport by large-scale Alfvén waves and the electron acceleration problem. Astrophys. J. 675, 1645–1655 (2008). https://doi.org/10.1086/527044
L. Fletcher, I.G. Hannah, H.S. Hudson, T.R. Metcalf, A TRACE white light and RHESSI hard X-ray study of flare energetics. Astrophys. J. 656, 1187–1196 (2007). https://doi.org/10.1086/510446
L. Fletcher, B.R. Dennis, H.S. Hudson, S. Krucker, K. Phillips, A. Veronig, M. Battaglia, L. Bone, A. Caspi, Q. Chen, P. Gallagher, P.T. Grigis, H. Ji, W. Liu, R.O. Milligan, M. Temmer, An observational overview of solar flares. Space Sci. Rev. 159, 19–106 (2011). https://doi.org/10.1007/s11214-010-9701-8
E.C. Fonseca-Pongutá, L.F. Ziebell, R. Gaelzer, P.H. Yoon, Two dimensional kinetic analysis of electrostatic harmonic plasma waves. Phys. Plasmas 23(6), 062310 (2016). https://doi.org/10.1063/1.4953898
T.G. Forbes, Implosion of a uniform current sheet in a low-beta plasma. J. Plasma Phys. 27, 491–505 (1982). https://doi.org/10.1017/S002237780001103X
C. Foullon, E. Verwichte, V.M. Nakariakov, L. Fletcher, X-ray quasi-periodic pulsations in solar flares as magnetohydrodynamic oscillations. Astron. Astrophys. 440, 59–62 (2005). https://doi.org/10.1051/0004-6361:200500169
C. Froment, F. Auchère, G. Aulanier, Z. Mikić, K. Bocchialini, E. Buchlin, J. Solomon, Long-period intensity pulsations in coronal loops explained by thermal non-equilibrium cycles. Astrophys. J. 835, 272 (2017). https://doi.org/10.3847/1538-4357/835/2/272
P.T. Gallagher, D.M. Long, Large-scale bright fronts in the solar corona: a review of “EIT waves”. Space Sci. Rev. 158, 365–396 (2011). https://doi.org/10.1007/s11214-010-9710-7
K. Galsgaard, I. Roussev, Magnetic reconnection in 2D stratified atmospheres. I. Dynamical consequences. Astron. Astrophys. 383, 685–696 (2002). https://doi.org/10.1051/0004-6361:20011733
D.H. Gao, P.F. Chen, M.D. Ding, X.D. Li, Simulations of the periodic flaring rate on YY Gem. Mon. Not. R. Astron. Soc. 384, 1355–1362 (2008). https://doi.org/10.1111/j.1365-2966.2007.12830.x
C.R. Goddard, G. Nisticò, V.M. Nakariakov, I.V. Zimovets, S.M. White, Observation of quasi-periodic solar radio bursts associated with propagating fast-mode waves. Astron. Astrophys. 594, 96 (2016). https://doi.org/10.1051/0004-6361/201628478
P.C. Grigis, A.O. Benz, The evolution of reconnection along an arcade of magnetic loops. Astrophys. J. Lett. 625, 143–146 (2005). https://doi.org/10.1086/431147
M. Gruszecki, V.M. Nakariakov, Slow magnetacoustic waves in magnetic arcades. Astron. Astrophys. 536, 68 (2011). https://doi.org/10.1051/0004-6361/201117549
M. Gruszecki, S. Vasheghani Farahani, V.M. Nakariakov, T.D. Arber, Magnetoacoustic shock formation near a magnetic null point. Astron. Astrophys. 531, 63 (2011). https://doi.org/10.1051/0004-6361/201116753
S.E. Guidoni, C.R. DeVore, J.T. Karpen, B.J. Lynch, Magnetic-island contraction and particle acceleration in simulated eruptive solar flares. Astrophys. J. 820, 60 (2016). https://doi.org/10.3847/0004-637X/820/1/60
X. Guo, L. Sironi, R. Narayan, Non-thermal electron acceleration in low mach number collisionless shocks. I. Particle energy spectra and acceleration mechanism. Astrophys. J. 794, 153 (2014). https://doi.org/10.1088/0004-637X/794/2/153
T.S. Hahm, R.M. Kulsrud, Forced magnetic reconnection. Phys. Fluids 28, 2412–2418 (1985). https://doi.org/10.1063/1.865247
E.G. Harris, On a plasma sheath separating regions of oppositely directed magnetic field. Il Nuovo Cimento (1955–1965) 23(1), 115–121 (1962). https://doi.org/10.1007/BF02733547.
A.B. Hassam, Reconnection of stressed magnetic fields. Astrophys. J. 399, 159–163 (1992). https://doi.org/10.1086/171911
L.A. Hayes, P.T. Gallagher, B.R. Dennis, J. Ireland, A.R. Inglis, D.F. Ryan, Quasi-periodic pulsations during the impulsive and decay phases of an X-class flare. Astrophys. J. Lett. 827, 30 (2016). https://doi.org/10.3847/2041-8205/827/2/L30
E. Hertzsprung, Note on a peculiar variable star or nova of short duration. Bull. Astron. Inst. Neth. 2, 87 (1924)
J. Heyvaerts, E.R. Priest, D.M. Rust, An emerging flux model for the solar flare phenomenon. Astrophys. J. 216, 123–137 (1977). https://doi.org/10.1086/155453
T. Hirayama, Theoretical model of flares and prominences. I: Evaporating flare model. Sol. Phys. 34, 323–338 (1974). https://doi.org/10.1007/BF00153671
R. Hodgson, On a curious appearance seen in the Sun. Mon. Not. R. Astron. Soc. 20, 15–16 (1859). https://doi.org/10.1093/mnras/20.1.15
H. Hudson, The global dynamics of the high-temperature corona. Sol. Phys. 190, 91–106 (1999). https://doi.org/10.1023/A:1005246501003
H.S. Hudson, Implosions in coronal transients. Astrophys. J. Lett. 531, 75–77 (2000). https://doi.org/10.1086/312516
H.S. Hudson, Global properties of solar flares. Space Sci. Rev. 158, 5–41 (2011). https://doi.org/10.1007/s11214-010-9721-4
H.S. Hudson, L.W. Acton, T. Hirayama, Y. Uchida, White-light flares observed by YOHKOH. Publ. Astron. Soc. Jpn. 44, 77–81 (1992)
H.S. Hudson, G.H. Fisher, B.T. Welsch, Flare energy and magnetic field variations, in Subsurface and Atmospheric Influences on Solar Activity, ed. by R. Howe, R.W. Komm, K.S. Balasubramaniam, G.J.D. Petrie. Astronomical Society of the Pacific Conference Series, vol. 383 (2008), p. 221
A.R. Inglis, H.R. Gilbert, Hard X-ray and ultraviolet emission during the 2011 June 7 solar flare. Astrophys. J. 777, 30 (2013). https://doi.org/10.1088/0004-637X/777/1/30
A.R. Inglis, V.M. Nakariakov, A multi-periodic oscillatory event in a solar flare. Astron. Astrophys. 493, 259–266 (2009). https://doi.org/10.1051/0004-6361:200810473
A.R. Inglis, V.M. Nakariakov, V.F. Melnikov, Multi-wavelength spatially resolved analysis of quasi-periodic pulsations in a solar flare. Astron. Astrophys. 487, 1147–1153 (2008). https://doi.org/10.1051/0004-6361:20079323
A.R. Inglis, J. Ireland, M. Dominique, Quasi-periodic pulsations in solar and stellar flares: re-evaluating their nature in the context of power-law flare Fourier spectra. Astrophys. J. 798, 108 (2015). https://doi.org/10.1088/0004-637X/798/2/108
A.R. Inglis, J. Ireland, B.R. Dennis, L. Hayes, P. Gallagher, A large-scale search for evidence of quasi-periodic pulsations in solar flares. Astrophys. J. 833, 284 (2016). https://doi.org/10.3847/1538-4357/833/2/284
H. Isobe, H. Takasaki, K. Shibata, Measurement of the energy release rate and the reconnection rate in solar flares. Astrophys. J. 632, 1184–1195 (2005). https://doi.org/10.1086/444490
R. Jain, S.C. Tripathy, Detection of H\(\upalpha\) intensity oscillations in solar flares. Sol. Phys. 181, 113–120 (1998). https://doi.org/10.1023/A:1005056908646
P. Jelínek, M. Karlický, Magnetoacoustic waves in diagnostics of the flare current sheets. Astron. Astrophys. 537, 46 (2012). https://doi.org/10.1051/0004-6361/201117883
P. Jelínek, K. Murawski, Numerical simulations of magnetoacoustic-gravity waves in the solar coronal curved magnetic field lines structure. Mon. Not. R. Astron. Soc. 434, 2347–2354 (2013). https://doi.org/10.1093/mnras/stt1178
P. Jelínek, M. Karlický, K. Murawski, Magnetoacoustic waves in a vertical flare current-sheet in a gravitationally stratified solar atmosphere. Astron. Astrophys. 546, 49 (2012). https://doi.org/10.1051/0004-6361/201219891
P. Jelínek, M. Karlický, T. Van Doorsselaere, M. Bárta, Oscillations excited by plasmoids formed during magnetic reconnection in vertical gravitationally stratified current-sheet. Astrophys. J. 847(2), 98 (2017)
A. Jenkins, Self-oscillation. Phys. Rep. 525, 167–222 (2013). https://doi.org/10.1016/j.physrep.2012.10.007
P.S. Joarder, V.M. Nakariakov, B. Roberts, A manifestation of negative energy waves in the solar atmosphere. Sol. Phys. 176, 285–297 (1997). https://doi.org/10.1023/A:1004977928351
P.G. Judge, L. Kleint, A. Donea, A. Sainz Dalda, L. Fletcher, On the origin of a sunquake during the 2014 March 29 X1 flare. Astrophys. J. 796, 85 (2014). https://doi.org/10.1088/0004-637X/796/2/85
S.R. Kane, K. Kai, T. Kosugi, S. Enome, P.B. Landecker, D.L. McKenzie, Acceleration and confinement of energetic particles in the 1980 June 7 solar flare. Astrophys. J. 271, 376–387 (1983). https://doi.org/10.1086/161203
M. Karlický, Series of high-frequency slowly drifting structures mapping the flare magnetic field reconnection. Astron. Astrophys. 417, 325–332 (2004). https://doi.org/10.1051/0004-6361:20034249
M. Karlický, M. Bárta, Successive merging of plasmoids and fragmentation in a flare current sheet and their X-ray and radio signatures. Astrophys. J. 733, 107 (2011). https://doi.org/10.1088/0004-637X/733/2/107
M. Karlický, P. Jelínek, H. Mészárosová, Magnetoacoustic waves in the narrowband dm-spikes sources. Astron. Astrophys. 529, 96 (2011). https://doi.org/10.1051/0004-6361/201016171
M. Karlický, H. Mészárosová, P. Jelínek, Radio fiber bursts and fast magnetoacoustic wave trains. Astron. Astrophys. 550, 1 (2013). https://doi.org/10.1051/0004-6361/201220296
M. Karlický, K. Jiřička, M. Bárta, Frequency oscillations of drifting pulsating structures. Cent. Eur. Astrophys. Bull. 40, 93–96 (2016)
C. Karoff, M.F. Knudsen, P. De Cat, A. Bonanno, A. Fogtmann-Schulz, J. Fu, A. Frasca, F. Inceoglu, J. Olsen, Y. Zhang, Y. Hou, Y. Wang, J. Shi, W. Zhang, Observational evidence for enhanced magnetic activity of superflare stars. Nat. Commun. 7, 11058 (2016). https://doi.org/10.1038/ncomms11058
M.L. Khodachenko, V.V. Zaitsev, A.G. Kislyakov, H.O. Rucker, S. Urpo, Low-frequency modulations in the solar microwave radiation as a possible indicator of inductive interaction of coronal magnetic loops. Astron. Astrophys. 433, 691–699 (2005). https://doi.org/10.1051/0004-6361:20041988
M.L. Khodachenko, V.V. Zaitsev, A.G. Kislyakov, A.V. Stepanov, Equivalent electric circuit models of coronal magnetic loops and related oscillatory phenomena on the sun. Space Sci. Rev. 149, 83–117 (2009). https://doi.org/10.1007/s11214-009-9538-1
A.L. Kiplinger, B.R. Dennis, K.J. Frost, L.E. Orwig, Recurrent pulse trains in the solar hard X-ray flare of 1980 June 7. Astrophys. J. 273, 783–794 (1983). https://doi.org/10.1086/161413
L. Kleint, M. Battaglia, K. Reardon, A. Sainz Dalda, P.R. Young, S. Krucker, The fast filament eruption leading to the X-flare on 2014 March 29. Astrophys. J. 806, 9 (2015). https://doi.org/10.1088/0004-637X/806/1/9
B. Kliem, M. Karlický, A.O. Benz, Solar flare radio pulsations as a signature of dynamic magnetic reconnection. Astron. Astrophys. 360, 715–728 (2000)
D.Y. Kolotkov, V.M. Nakariakov, G. Rowlands, Nonlinear oscillations of coalescing magnetic flux ropes. Phys. Rev. E 93(5), 053205 (2016). https://doi.org/10.1103/PhysRevE.93.053205
E.P. Kontar, Dynamics of electron beams in the solar corona plasma with density fluctuations. Astron. Astrophys. 375, 629–637 (2001). https://doi.org/10.1051/0004-6361:20010807
R.A. Kopp, G.W. Pneuman, Magnetic reconnection in the corona and the loop prominence phenomenon. Sol. Phys. 50, 85–98 (1976). https://doi.org/10.1007/BF00206193
A.G. Kosovichev, Properties of flares-generated seismic waves on the Sun. Sol. Phys. 238, 1–11 (2006). https://doi.org/10.1007/s11207-006-0190-6
A.G. Kosovichev, Advances in global and local helioseismology: an introductory review, in The Pulsations of the Sun and the Stars, ed. by J.-P. Rozelot, C. Neiner. Lecture Notes in Physics, vol. 832 (Springer, Berlin, 2011), p. 3. https://doi.org/10.1007/978-3-642-19928-8_1
A.G. Kosovichev, Sunquakes and starquakes, in Precision Asteroseismology, ed. by J.A. Guzik, W.J. Chaplin, G. Handler, A. Pigulski. IAU Symposium, vol. 301 (2014a), pp. 349–352. https://doi.org/10.1017/S1743921313014579
A.G. Kosovichev, Sunquakes: helioseismic response to solar flares. ArXiv e-prints (2014b)
A.G. Kosovichev, V.V. Zharkova, Seismic response to solar flares: theoretical predictions, in Helioseismology. ESA Special Publication, vol. 376 (1995), p. 341
A.G. Kosovichev, V.V. Zharkova, X-ray flare sparks quake inside Sun. Nature 393, 317–318 (1998). https://doi.org/10.1038/30629
N.D. Kostiuk, S.B. Pikelner, Gasdynamics of a flare region heated by a stream of high-velocity electrons. Sov. Astron. 18, 590–599 (1975)
J. Krall, J. Chen, R.T. Duffin, R.A. Howard, B.J. Thompson, Erupting solar magnetic flux ropes: theory and observation. Astrophys. J. 562, 1045–1057 (2001). https://doi.org/10.1086/323844
S. Krucker, G.J. Hurford, R.P. Lin, Hard X-ray source motions in the 2002 July 23 gamma-ray flare. Astrophys. J. Lett. 595, 103–106 (2003). https://doi.org/10.1086/378840
S. Krucker, M.D. Fivian, R.P. Lin, Hard X-ray footpoint motions in solar flares: comparing magnetic reconnection models with observations. Adv. Space Res. 35, 1707–1711 (2005). https://doi.org/10.1016/j.asr.2005.05.054
S. Krucker, H.S. Hudson, L. Glesener, S.M. White, S. Masuda, J.-P. Wuelser, R.P. Lin, Measurements of the coronal acceleration region of a solar flare. Astrophys. J. 714, 1108–1119 (2010). https://doi.org/10.1088/0004-637X/714/2/1108
P. Kumar, D.E. Innes, Multiwavelength observations of an eruptive flare: evidence for blast waves and break-out. Sol. Phys. 288, 255–268 (2013). https://doi.org/10.1007/s11207-013-0303-y
S. Kumar, V.M. Nakariakov, Y.-J. Moon, Effect of a radiation cooling and heating function on standing longitudinal oscillations in coronal loops. Astrophys. J. 824, 8 (2016). https://doi.org/10.3847/0004-637X/824/1/8
E.G. Kupriyanova, V.F. Melnikov, V.M. Nakariakov, K. Shibasaki, Types of microwave quasi-periodic pulsations in single flaring loops. Sol. Phys. 267, 329–342 (2010). https://doi.org/10.1007/s11207-010-9642-0
L.D. Landau, E.M. Lifshitz, Fluid Mechanics (1959)
J.N. Leboeuf, T. Tajima, J.M. Dawson, Dynamic magnetic x points. Phys. Fluids 25, 784–799 (1982). https://doi.org/10.1063/1.863833
E. Lee, V.S. Lukin, M.G. Linton, On flux rope stability and atmospheric stratification in models of coronal mass ejections triggered by flux emergence. Astron. Astrophys. 569, 94 (2014). https://doi.org/10.1051/0004-6361/201423739
W.H.G. Lewin, J. van Paradijs, M. van der Klis, A review of quasi-periodic oscillations in low-mass X-ray binaries. Space Sci. Rev. 46, 273–378 (1988). https://doi.org/10.1007/BF00212242
Y.P. Li, W.Q. Gan, The oscillatory shrinkage in TRACE 195 Å loops during a flare impulsive phase. Astrophys. J. Lett. 644, 97–100 (2006). https://doi.org/10.1086/505576
D. Li, Q.M. Zhang, Y. Huang, Z.J. Ning, Y.N. Su, Quasi-periodic pulsations with periods that change depending on whether the pulsations have thermal or nonthermal components. Astron. Astrophys. 597, 4 (2017). https://doi.org/10.1051/0004-6361/201629867
R.P. Lin, B.R. Dennis, G.J. Hurford, D.M. Smith, A. Zehnder, P.R. Harvey, D.W. Curtis, D. Pankow, P. Turin, M. Bester, A. Csillaghy, M. Lewis, N. Madden, H.F. van Beek, M. Appleby, T. Raudorf, J. McTiernan, R. Ramaty, E. Schmahl, R. Schwartz, S. Krucker, R. Abiad, T. Quinn, P. Berg, M. Hashii, R. Sterling, R. Jackson, R. Pratt, R.D. Campbell, D. Malone, D. Landis, C.P. Barrington-Leigh, S. Slassi-Sennou, C. Cork, D. Clark, D. Amato, L. Orwig, R. Boyle, I.S. Banks, K. Shirey, A.K. Tolbert, D. Zarro, F. Snow, K. Thomsen, R. Henneck, A. McHedlishvili, P. Ming, M. Fivian, J. Jordan, R. Wanner, J. Crubb, J. Preble, M. Matranga, A. Benz, H. Hudson, R.C. Canfield, G.D. Holman, C. Crannell, T. Kosugi, A.G. Emslie, N. Vilmer, J.C. Brown, C. Johns-Krull, M. Aschwanden, T. Metcalf, A. Conway, The Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI). Sol. Phys. 210, 3–32 (2002). https://doi.org/10.1023/A:1022428818870
C. Lindsey, D.C. Braun, Basic principles of solar acoustic holography—(invited review). Sol. Phys. 192, 261–284 (2000). https://doi.org/10.1023/A:1005227200911
C. Lindsey, A.-C. Donea, Mechanics of seismic emission from solar flares. Sol. Phys. 251, 627–639 (2008). https://doi.org/10.1007/s11207-008-9140-9
W. Liu, L. Ofman, N.V. Nitta, M.J. Aschwanden, C.J. Schrijver, A.M. Title, T.D. Tarbell, Quasi-periodic fast-mode wave trains within a global EUV wave and sequential transverse oscillations detected by SDO/AIA. Astrophys. J. 753, 52 (2012). https://doi.org/10.1088/0004-637X/753/1/52
M.A. Livshits, O.G. Badalian, A.G. Kosovichev, M.M. Katsova, The optical continuum of solar and stellar flares. Sol. Phys. 73, 269–288 (1981). https://doi.org/10.1007/BF00151682
D.M. Long, P.T. Gallagher, R.T.J. McAteer, D.S. Bloomfield, Deceleration and dispersion of large-scale coronal bright fronts. Astron. Astrophys. 531, 42 (2011). https://doi.org/10.1051/0004-6361/201015879
D.M. Long, D.R. Williams, S. Régnier, L.K. Harra, Measuring the magnetic-field strength of the quiet solar corona using ”EIT waves”. Sol. Phys. 288, 567–583 (2013). https://doi.org/10.1007/s11207-013-0331-7
D.M. Long, D.S. Bloomfield, P.T. Gallagher, D. Pérez-Suárez, CorPITA: an automated algorithm for the identification and analysis of coronal “EIT waves”. Sol. Phys. 289, 3279–3295 (2014). https://doi.org/10.1007/s11207-014-0527-5
D.M. Long, D.S. Bloomfield, P.F. Chen, C. Downs, P.T. Gallagher, R.-Y. Kwon, K. Vanninathan, A.M. Veronig, A. Vourlidas, B. Vršnak, A. Warmuth, T. Žic, Understanding the physical nature of coronal “EIT waves”. Sol. Phys. 292, 7 (2017). https://doi.org/10.1007/s11207-016-1030-y
N.F. Loureiro, A.A. Schekochihin, S.C. Cowley, Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14(10), 100703 (2007). https://doi.org/10.1063/1.2783986
H. Maehara, T. Shibayama, S. Notsu, Y. Notsu, T. Nagao, S. Kusaba, S. Honda, D. Nogami, K. Shibata, Superflares on solar-type stars. Nature 485, 478–481 (2012). https://doi.org/10.1038/nature11063
J.T. Mariska, Observations of solar flare Doppler shift oscillations with the Bragg crystal spectrometer on Yohkoh. Astrophys. J. Lett. 620, 67–70 (2005). https://doi.org/10.1086/428611
J.T. Mariska, H.P. Warren, D.R. Williams, T. Watanabe, Observations of Doppler shift oscillations with the EUV imaging spectrometer on Hinode. Astrophys. J. Lett. 681, 41 (2008). https://doi.org/10.1086/590341
J.C. Martínez-Oliveros, H. Moradi, A.-C. Donea, Seismic emissions from a highly impulsive M6.7 solar flare. Sol. Phys. 251, 613–626 (2008). https://doi.org/10.1007/s11207-008-9122-y
S. Masuda, T. Kosugi, H. Hara, S. Tsuneta, Y. Ogawara, A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection. Nature 371, 495–497 (1994). https://doi.org/10.1038/371495a0
M. Mathioudakis, J.H. Seiradakis, D.R. Williams, S. Avgoloupis, D.S. Bloomfield, R.T.J. McAteer, White-light oscillations during a flare on II Peg. Astron. Astrophys. 403, 1101–1104 (2003). https://doi.org/10.1051/0004-6361:20030394
M. Mathioudakis, D.S. Bloomfield, D.B. Jess, V.S. Dhillon, T.R. Marsh, The periodic variations of a white-light flare observed with ULTRACAM. Astron. Astrophys. 456, 323–327 (2006). https://doi.org/10.1051/0004-6361:20054752
S. Matsukiyo, Y. Ohira, R. Yamazaki, T. Umeda, Relativistic electron shock drift acceleration in low mach number galaxy cluster shocks. Astrophys. J. 742, 47 (2011). https://doi.org/10.1088/0004-637X/742/1/47
S.A. Matthews, L.K. Harra, S. Zharkov, L.M. Green, Spectroscopic signatures related to a sunquake. Astrophys. J. 812, 35 (2015). https://doi.org/10.1088/0004-637X/812/1/35
R.T.J. McAteer, P.T. Gallagher, D.S. Brown, D.S. Bloomfield, R. Moore, D.R. Williams, M. Mathioudakis, A. Katsiyannis, F.P. Keenan, Observations of H\(\upalpha\) intensity oscillations in a flare ribbon. Astrophys. J. 620, 1101–1106 (2005). https://doi.org/10.1086/427084
J.A. McLaughlin, A.W. Hood, MHD wave propagation in the neighbourhood of a two-dimensional null point. Astron. Astrophys. 420, 1129–1140 (2004). https://doi.org/10.1051/0004-6361:20035900
J.A. McLaughlin, A.W. Hood, MHD wave propagation in the neighbourhood of two null points. Astron. Astrophys. 435, 313–325 (2005). https://doi.org/10.1051/0004-6361:20042361
J.A. McLaughlin, L. Ofman, Three-dimensional magnetohydrodynamic wave behavior in active regions: individual loop density structure. Astrophys. J. 682, 1338–1350 (2008). https://doi.org/10.1086/588799
J.A. McLaughlin, I. De Moortel, A.W. Hood, C.S. Brady, Nonlinear fast magnetoacoustic wave propagation in the neighbourhood of a 2D magnetic X-point: oscillatory reconnection. Astron. Astrophys. 493, 227–240 (2009). https://doi.org/10.1051/0004-6361:200810465
J.A. McLaughlin, A.W. Hood, I. De Moortel, Review article: MHD wave propagation near coronal null points of magnetic fields. Space Sci. Rev. 158, 205–236 (2011). https://doi.org/10.1007/s11214-010-9654-y
J.A. McLaughlin, G. Verth, V. Fedun, R. Erdélyi, Generation of quasi-periodic waves and flows in the solar atmosphere by oscillatory reconnection. Astrophys. J. 749, 30 (2012a). https://doi.org/10.1088/0004-637X/749/1/30
J.A. McLaughlin, J.O. Thurgood, D. MacTaggart, On the periodicity of oscillatory reconnection. Astron. Astrophys. 548, 98 (2012b). https://doi.org/10.1051/0004-6361/201220234
V.F. Melnikov, V.E. Reznikova, K. Shibasaki, V.M. Nakariakov, Spatially resolved microwave pulsations of a flare loop. Astron. Astrophys. 439, 727–736 (2005). https://doi.org/10.1051/0004-6361:20052774
R.O. Milligan, P.T. Gallagher, M. Mathioudakis, F.P. Keenan, Observational evidence of gentle chromospheric evaporation during the impulsive phase of a solar flare. Astrophys. J. Lett. 642, 169–171 (2006). https://doi.org/10.1086/504592
U. Mitra-Kraev, L.K. Harra, D.R. Williams, E. Kraev, The first observed stellar X-ray flare oscillation: constraints on the flare loop length and the magnetic field. Astron. Astrophys. 436, 1041–1047 (2005). https://doi.org/10.1051/0004-6361:20052834
G.E. Moreton, H\(\upalpha\) observations of flare-initiated disturbances with velocities 1000 km/sec. Astron. J. 65, 494 (1960). https://doi.org/10.1086/108346
G.E. Moreton, H.E. Ramsey, Recent observations of dynamical phenomena associated with solar flares. Publ. Astron. Soc. Pac. 72, 357 (1960). https://doi.org/10.1086/127549
D. Moses, F. Clette, J.-P. Delaboudinière, G.E. Artzner, M. Bougnet, J. Brunaud, C. Carabetian, A.H. Gabriel, J.F. Hochedez, F. Millier, X.Y. Song, B. Au, K.P. Dere, R.A. Howard, R. Kreplin, D.J. Michels, J.M. Defise, C. Jamar, P. Rochus, J.P. Chauvineau, J.P. Marioge, R.C. Catura, J.R. Lemen, L. Shing, R.A. Stern, J.B. Gurman, W.M. Neupert, J. Newmark, B. Thompson, A. Maucherat, F. Portier-Fozzani, D. Berghmans, P. Cugnon, E.L. van Dessel, J.R. Gabryl, EIT observations of the extreme ultraviolet Sun. Sol. Phys. 175, 571–599 (1997). https://doi.org/10.1023/A:1004902913117
D.A.N. Müller, H. Peter, V.H. Hansteen, Dynamics of solar coronal loops. II. Catastrophic cooling and high-speed downflows. Astron. Astrophys. 424, 289–300 (2004). https://doi.org/10.1051/0004-6361:20040403
M.J. Murray, L. van Driel-Gesztelyi, D. Baker, Simulations of emerging flux in a coronal hole: oscillatory reconnection. Astron. Astrophys. 494, 329–337 (2009). https://doi.org/10.1051/0004-6361:200810406
H. Nakajima, T. Kosugi, K. Kai, S. Enome, Successive electron and ion accelerations in impulsive solar flares on 7 and 21 June 1980. Nature 305, 292–294 (1983). https://doi.org/10.1038/305292a0
V.M. Nakariakov, V.F. Melnikov, Quasi-periodic pulsations in solar flares. Space Sci. Rev. 149, 119–151 (2009). https://doi.org/10.1007/s11214-009-9536-3
V.M. Nakariakov, I.V. Zimovets, Slow magnetoacoustic waves in two-ribbon flares. Astrophys. J. Lett. 730, 27 (2011). https://doi.org/10.1088/2041-8205/730/2/L27
V.M. Nakariakov, V.F. Melnikov, V.E. Reznikova, Global sausage modes of coronal loops. Astron. Astrophys. 412, 7–10 (2003). https://doi.org/10.1051/0004-6361:20031660
V.M. Nakariakov, D. Tsiklauri, A. Kelly, T.D. Arber, M.J. Aschwanden, Acoustic oscillations in solar and stellar flaring loops. Astron. Astrophys. 414, 25–28 (2004a). https://doi.org/10.1051/0004-6361:20031738
V.M. Nakariakov, T.D. Arber, C.E. Ault, A.C. Katsiyannis, D.R. Williams, F.P. Keenan, Time signatures of impulsively generated coronal fast wave trains. Mon. Not. R. Astron. Soc. 349, 705–709 (2004b). https://doi.org/10.1111/j.1365-2966.2004.07537.x
V.M. Nakariakov, C. Foullon, E. Verwichte, N.P. Young, Quasi-periodic modulation of solar and stellar flaring emission by magnetohydrodynamic oscillations in a nearby loop. Astron. Astrophys. 452, 343–346 (2006). https://doi.org/10.1051/0004-6361:20054608
V.M. Nakariakov, A.R. Inglis, I.V. Zimovets, C. Foullon, E. Verwichte, R. Sych, I.N. Myagkova, Oscillatory processes in solar flares. Plasma Phys. Control. Fusion 52(12), 124009 (2010). https://doi.org/10.1088/0741-3335/52/12/124009
V.M. Nakariakov, C. Hornsey, V.F. Melnikov, Sausage oscillations of coronal plasma structures. Astrophys. J. 761, 134 (2012). https://doi.org/10.1088/0004-637X/761/2/134
V.M. Nakariakov, V. Pilipenko, B. Heilig, P. Jelínek, M. Karlický, D.Y. Klimushkin, D.Y. Kolotkov, D.-H. Lee, G. Nisticò, T. Van Doorsselaere, G. Verth, I.V. Zimovets, Magnetohydrodynamic oscillations in the solar corona and Earth’s magnetosphere: towards consolidated understanding. Space Sci. Rev. 200, 75–203 (2016). https://doi.org/10.1007/s11214-015-0233-0
N. Nishizuka, K. Shibata, Fermi acceleration in plasmoids interacting with fast shocks of reconnection via fractal reconnection. Phys. Rev. Lett. 110(5), 051101 (2013). https://doi.org/10.1103/PhysRevLett.110.051101
N. Nishizuka, M. Karlický, M. Janvier, M. Bárta, Particle acceleration in plasmoid ejections derived from radio drifting pulsating structures. Astrophys. J. 799, 126 (2015). https://doi.org/10.1088/0004-637X/799/2/126
G. Nisticò, D.J. Pascoe, V.M. Nakariakov, Observation of a high-quality quasi-periodic rapidly propagating wave train using SDO/AIA. Astron. Astrophys. 569, 12 (2014). https://doi.org/10.1051/0004-6361/201423763
L. Ofman, L. Sui, Oscillations of hard X-ray flare emission observed by RHESSI: effects of super-Alfvénic beams? Astrophys. J. Lett. 644, 149–152 (2006). https://doi.org/10.1086/505622
L. Ofman, B.J. Thompson, Interaction of EIT waves with coronal active regions. Astrophys. J. 574, 440–452 (2002). https://doi.org/10.1086/340924
M. Oka, T.-D. Phan, S. Krucker, M. Fujimoto, I. Shinohara, Electron acceleration by multi-island coalescence. Astrophys. J. 714, 915–926 (2010). https://doi.org/10.1088/0004-637X/714/1/915
M. Oka, S. Krucker, H.S. Hudson, P. Saint-Hilaire, Electron energy partition in the above-the-looptop solar hard X-ray sources. Astrophys. J. 799, 129 (2015). https://doi.org/10.1088/0004-637X/799/2/129
E.N. Parker, Sweet’s mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520 (1957). https://doi.org/10.1029/JZ062i004p00509
G.K. Parks, J.R. Winckler, Sixteen-second periodic pulsations observed in the correlated microwave and energetic X-ray emission from a solar flare. Astrophys. J. Lett. 155, 117 (1969). https://doi.org/10.1086/180315
C.E. Parnell, I. De Moortel, A contemporary view of coronal heating. Philos. Trans. R. Soc. Lond. Ser. A 370, 3217–3240 (2012). https://doi.org/10.1098/rsta.2012.0113
D.J. Pascoe, V.M. Nakariakov, E.G. Kupriyanova, Fast magnetoacoustic wave trains in magnetic funnels of the solar corona. Astron. Astrophys. 560, 97 (2013). https://doi.org/10.1051/0004-6361/201322678
H.E. Petschek, Magnetic field annihilation. NASA Spec. Publ. 50, 425 (1964)
R.F. Pinto, M. Gordovskyy, P.K. Browning, N. Vilmer, Thermal and non-thermal emission from reconnecting twisted coronal loops. Astron. Astrophys. 585, 159 (2016). https://doi.org/10.1051/0004-6361/201526633
E. Priest, Magnetohydrodynamics of the Sun (Cambridge University Press, Cambridge, 2014)
E.R. Priest, S.W.H. Cowley, Some comments on magnetic field reconnection. J. Plasma Phys. 14, 271–282 (1975). https://doi.org/10.1017/S0022377800009569
E. Priest, T. Forbes, Magnetic Reconnection (Cambridge University Press, Cambridge, 2000), p. 612
E.R. Priest, T.G. Forbes, The magnetic nature of solar flares. Astron. Astrophys. Rev. 10, 313–377 (2002). https://doi.org/10.1007/s001590100013
P.L. Pritchett, C.C. Wu, Coalescence of magnetic islands. Phys. Fluids 22, 2140–2146 (1979). https://doi.org/10.1063/1.862507
C.E. Pugh, V.M. Nakariakov, A.-M. Broomhall, A multi-period oscillation in a stellar superflare. Astrophys. J. Lett. 813, 5 (2015). https://doi.org/10.1088/2041-8205/813/1/L5
C.E. Pugh, D.J. Armstrong, V.M. Nakariakov, A.-M. Broomhall, Statistical properties of quasi-periodic pulsations in white-light flares observed with Kepler. Mon. Not. R. Astron. Soc. 459, 3659–3676 (2016). https://doi.org/10.1093/mnras/stw850
H.E. Ramsey, S.F. Smith, Flare-initiated filamei it oscillations. Astron. J. 71, 197 (1966). https://doi.org/10.1086/109903
H. Ratcliffe, E.P. Kontar, Plasma radio emission from inhomogeneous collisional plasma of a flaring loop. Astron. Astrophys. 562, 57 (2014). https://doi.org/10.1051/0004-6361/201322263
S. Régnier, Magnetic field extrapolations into the corona: success and future improvements. Sol. Phys. 288, 481–505 (2013). https://doi.org/10.1007/s11207-013-0367-8
B. Roberts, P.M. Edwin, A.O. Benz, Fast pulsations in the solar corona. Nature 305, 688–690 (1983). https://doi.org/10.1038/305688a0
B. Roberts, P.M. Edwin, A.O. Benz, On coronal oscillations. Astrophys. J. 279, 857–865 (1984). https://doi.org/10.1086/161956
A.J.B. Russell, M.K. Mooney, J.E. Leake, H.S. Hudson, Sunquake generation by coronal magnetic restructuring. Astrophys. J. 831, 42 (2016). https://doi.org/10.3847/0004-637X/831/1/42
P.H. Rutherford, Nonlinear growth of the tearing mode. Phys. Fluids 16, 1903–1908 (1973). https://doi.org/10.1063/1.1694232
K. Shibata, S. Takasao, Fractal reconnection in solar and stellar environments, in Astrophys. Space Sci. Library, ed. by W. Gonzalez, E. Parker. Astrophys. Space Sci. Library, vol. 427 (2016), p. 373. https://doi.org/10.1007/978-3-319-26432-5_10
P.J.A. Simões, H.S. Hudson, L. Fletcher, Soft X-ray pulsations in solar flares. Sol. Phys. 290, 3625–3639 (2015). https://doi.org/10.1007/s11207-015-0691-2
J.M. Smith, B. Roberts, R. Oliver, Magnetoacoustic wave propagation in current sheets. Astron. Astrophys. 327, 377–387 (1997)
L. Stella, M. Vietri, Lense-Thirring precession and quasi-periodic oscillations in low-mass X-ray binaries. Astrophys. J. Lett. 492, 59–62 (1998). https://doi.org/10.1086/311075
A.V. Stepanov, V.V. Zaitsev, Quasi-periodic pulsations and diagnostics of flaring plasma. Geomagn. Aeron. 54, 969–981 (2014). https://doi.org/10.1134/S0016793214080167
P.A. Sturrock, A model of solar flares, in Structure and Development of Solar Active Regions, ed. by K.O. Kiepenheuer. IAU Symposium, vol. 35, (1968), p. 471
J.T. Su, Y.D. Shen, Y. Liu, Y. Liu, X.J. Mao, Imaging observations of quasi-periodic pulsations in solar flare loops with SDO/AIA. Astrophys. J. 755, 113 (2012). https://doi.org/10.1088/0004-637X/755/2/113
Z. Svestka, E.W. Cliver, History and basic characteristics of eruptive flares, in IAU Colloq. 133: Eruptive Solar Flares, ed. by Z. Svestka, B.V. Jackson, M.E. Machado. Lecture Notes in Physics, Berlin Springer Verlag, vol. 399 (1992), p. 1. https://doi.org/10.1007/3-540-55246-4_70
P.A. Sweet, The neutral point theory of solar flares, in Electromagnetic Phenomena in Cosmical Physics, ed. by B. Lehnert. IAU Symposium, vol. 6 (1958), p. 123
R. Sych, V.M. Nakariakov, M. Karlicky, S. Anfinogentov, Relationship between wave processes in sunspots and quasi-periodic pulsations in active region flares. Astron. Astrophys. 505, 791–799 (2009). https://doi.org/10.1051/0004-6361/200912132
T. Tajima, F. Brunel, J. Sakai, Loop coalescence in flares and coronal X-ray brightening. Astrophys. J. Lett. 258, 45–48 (1982). https://doi.org/10.1086/183827
T. Tajima, J. Sakai, H. Nakajima, T. Kosugi, F. Brunel, M.R. Kundu, Current loop coalescence model of solar flares. Astrophys. J. 321, 1031–1048 (1987). https://doi.org/10.1086/165694
T. Takahashi, J. Qiu, K. Shibata, Quasi-periodic oscillations in flares and coronal mass ejections associated with magnetic reconnection. Astrophys. J. 848(2), (2017)
S. Takasao, K. Shibata, Above-the-loop-top oscillation and quasi-periodic coronal wave generation in solar flares. Astrophys. J. 823, 150 (2016). https://doi.org/10.3847/0004-637X/823/2/150
S. Takasao, A. Asai, H. Isobe, K. Shibata, Simultaneous observation of reconnection inflow and outflow associated with the 2010 August 18 solar flare. Astrophys. J. Lett. 745, 6 (2012). https://doi.org/10.1088/2041-8205/745/1/L6
S. Takasao, T. Matsumoto, N. Nakamura, K. Shibata, Magnetohydrodynamic shocks in and above post-flare loops: two-dimensional simulation and a simplified model. Astrophys. J. 805, 135 (2015). https://doi.org/10.1088/0004-637X/805/2/135
S. Takasao, A. Asai, H. Isobe, K. Shibata, Observational evidence of particle acceleration associated with plasmoid motions. Astrophys. J. 828, 103 (2016). https://doi.org/10.3847/0004-637X/828/2/103
S. Takeshige, S. Takasao, K. Shibata, A theoretical model of a thinning current sheet in the low-\(\upbeta\) plasmas. Astrophys. J. 807, 159 (2015). https://doi.org/10.1088/0004-637X/807/2/159
B. Tan, Z. Yu, J. Huang, C. Tan, Y. Zhang, Very long-period pulsations before the onset of solar flares. Astrophys. J. 833, 206 (2016). https://doi.org/10.3847/1538-4357/833/2/206
S. Tanuma, T. Yokoyama, T. Kudoh, K. Shibata, Two-dimensional magnetohydrodynamic numerical simulations of magnetic reconnection triggered by a supernova shock in the interstellar medium: generation of X-ray gas in the galaxy. Astrophys. J. 551, 312–332 (2001). https://doi.org/10.1086/320058
Y. Taroyan, R. Erdélyi, J.G. Doyle, S.J. Bradshaw, Footpoint excitation of standing acoustic waves in coronal loops. Astron. Astrophys. 438, 713–720 (2005). https://doi.org/10.1051/0004-6361:20052794
B.J. Thompson, S.P. Plunkett, J.B. Gurman, J.S. Newmark, O.C. St. Cyr, D.J. Michels, SOHO/EIT observations of an Earth-directed coronal mass ejection on may 12, 1997. Geophys. Res. Lett. 25, 2465–2468 (1998). https://doi.org/10.1029/98GL50429
B.J. Thompson, B. Reynolds, H. Aurass, N. Gopalswamy, J.B. Gurman, H.S. Hudson, S.F. Martin, O.C. St. Cyr, Observations of the 24 September 1997 coronal flare waves. Sol. Phys. 193, 161–180 (2000). https://doi.org/10.1023/A:1005222123970
J. Threlfall, C.E. Parnell, I. De Moortel, K.G. McClements, T.D. Arber, Nonlinear wave propagation and reconnection at magnetic X-points in the hall MHD regime. Astron. Astrophys. 544, 24 (2012). https://doi.org/10.1051/0004-6361/201219098
J.O. Thurgood, J.A. McLaughlin, Linear and nonlinear MHD mode coupling of the fast magnetoacoustic wave about a 3D magnetic null point. Astron. Astrophys. 545, 9 (2012). https://doi.org/10.1051/0004-6361/201219850
J.O. Thurgood, D.I. Pontin, J.A. McLaughlin, Three-dimensional oscillatory magnetic reconnection. Astrophys. J. 844, 2 (2017). https://doi.org/10.3847/1538-4357/aa79fa
H. Tian, P.R. Young, K.K. Reeves, T. Wang, P. Antolin, B. Chen, J. He, Global sausage oscillation of solar flare loops detected by the interface region imaging spectrograph. Astrophys. J. Lett. 823, 16 (2016). https://doi.org/10.3847/2041-8205/823/1/L16
T. Török, J.E. Leake, V.S. Titov, V. Archontis, Z. Mikić, M.G. Linton, K. Dalmasse, G. Aulanier, B. Kliem, Distribution of electric currents in solar active regions. Astrophys. J. Lett. 782, 10 (2014). https://doi.org/10.1088/2041-8205/782/1/L10
R. Tousey, The solar corona, in Space Research Conference, ed. by M.J. Rycroft, S.K. Runcorn. Space Research Conference, vol. 2 (1973), pp. 713–730
D. Tsiklauri, V.M. Nakariakov, T.D. Arber, M.J. Aschwanden, Flare-generated acoustic oscillations in solar and stellar coronal loops. Astron. Astrophys. 422, 351–355 (2004). https://doi.org/10.1051/0004-6361:20040299
S. Tsuneta, T. Naito, Fermi acceleration at the fast shock in a solar flare and the impulsive loop-top hard X-ray source. Astrophys. J. Lett. 495, 67–70 (1998). https://doi.org/10.1086/311207
C. Uberoi, E.G. Zweibel, Alfvén resonances and forced reconnection. J. Plasma Phys. 62, 345–350 (1999). https://doi.org/10.1017/S0022377899007813
Y. Uchida, Propagation of hydromagnetic disturbances in the solar corona and Moreton’s wave phenomenon. Sol. Phys. 4, 30–44 (1968). https://doi.org/10.1007/BF00146996
T. Van Doorsselaere, A. De Groof, J. Zender, D. Berghmans, M. Goossens, LYRA observations of two oscillation modes in a single flare. Astrophys. J. 740, 90 (2011). https://doi.org/10.1088/0004-637X/740/2/90
T. Van Doorsselaere, E.G. Kupriyanova, D. Yuan, Quasi-periodic pulsations in solar and stellar flares: an overview of recent results (invited review). Sol. Phys. 291, 3143–3164 (2016). https://doi.org/10.1007/s11207-016-0977-z
G. Vekstein, On the correspondence between forced magnetic reconnection and Alfvén resonances. Phys. Plasmas 7, 3808–3810 (2000). https://doi.org/10.1063/1.1286802
G. Vekstein, R. Jain, On plasma heating by reconnective magnetic relaxation. Phys. Plasmas 6, 2897–2902 (1999). https://doi.org/10.1063/1.873247
B. Vršnak, E.W. Cliver, Origin of coronal shock waves. Invited review. Sol. Phys. 253, 215–235 (2008). https://doi.org/10.1007/s11207-008-9241-5
B. Vršnak, A. Warmuth, R. Brajša, A. Hanslmeier, Flare waves observed in Helium I 10 830 Å. A link between H\(\upalpha\) moreton and EIT waves. Astron. Astrophys. 394, 299–310 (2002). https://doi.org/10.1051/0004-6361:20021121
X. Wang, A. Bhattacharjee, Forced reconnection and current sheet formation in Taylor’s model. Phys. Fluids, B 4, 1795–1799 (1992). https://doi.org/10.1063/1.860035
X. Wang, Z.W. Ma, A. Bhattacharjee, Fast magnetic reconnection and sudden enhancement of current sheets due to inward boundary flows. Phys. Plasmas 3, 2129–2134 (1996). https://doi.org/10.1063/1.871665
A. Warmuth, Large-scale globally propagating coronal waves. Living Rev. Sol. Phys. 12, 3 (2015). https://doi.org/10.1007/lrsp-2015-3
A. Warmuth, B. Vršnak, H. Aurass, A. Hanslmeier, Evolution of two EIT/H\(\upalpha\) Moreton waves. Astrophys. J. Lett. 560, 105–109 (2001). https://doi.org/10.1086/324055
A. Warmuth, B. Vršnak, J. Magdalenić, A. Hanslmeier, W. Otruba, A multiwavelength study of solar flare waves. I. Observations and basic properties. Astron. Astrophys. 418, 1101–1115 (2004a). https://doi.org/10.1051/0004-6361:20034332
A. Warmuth, B. Vršnak, J. Magdalenić, A. Hanslmeier, W. Otruba, A multiwavelength study of solar flare waves. II. Perturbation characteristics and physical interpretation. Astron. Astrophys. 418, 1117–1129 (2004b). https://doi.org/10.1051/0004-6361:20034333
K. Watanabe, S. Krucker, H. Hudson, T. Shimizu, S. Masuda, K. Ichimoto, G-band and hard X-ray emissions of the 2006 December 14 flare observed by Hinode/SOT and Rhessi. Astrophys. J. 715, 651–655 (2010). https://doi.org/10.1088/0004-637X/715/1/651
C.L. Wolff, Free oscillations of the sun and their possible stimulation by solar flares. Astrophys. J. 176, 833 (1972). https://doi.org/10.1086/151680
Y.-H. Yang, C.Z. Cheng, S. Krucker, R.P. Lin, W.H. Ip, A statistical study of hard X-ray footpoint motions in large solar flares. Astrophys. J. 693, 132–139 (2009). https://doi.org/10.1088/0004-637X/693/1/132
L. Yang, L. Zhang, J. He, H. Peter, C. Tu, L. Wang, S. Zhang, X. Feng, Numerical simulation of fast-mode magnetosonic waves excited by plasmoid ejections in the solar corona. Astrophys. J. 800, 111 (2015). https://doi.org/10.1088/0004-637X/800/2/111
T. Yokoyama, K. Shibata, Magnetohydrodynamic simulation of a solar flare with chromospheric evaporation effect based on the magnetic reconnection model. Astrophys. J. 549, 1160–1174 (2001). https://doi.org/10.1086/319440
D. Yuan, Y. Shen, Y. Liu, V.M. Nakariakov, B. Tan, J. Huang, Distinct propagating fast wave trains associated with flaring energy releases. Astron. Astrophys. 554, 144 (2013). https://doi.org/10.1051/0004-6361/201321435
V.V. Zaitsev, A.V. Stepanov, Coronal magnetic loops. Phys. Usp. 51, 1123–1160 (2008). https://doi.org/10.1070/PU2008v051n11ABEH006657
V.V. Zaitsev, A.V. Stepanov, S. Urpo, S. Pohjolainen, LRC-circuit analog of current-carrying magnetic loop: diagnostics of electric parameters. Astron. Astrophys. 337, 887–896 (1998)
Q.M. Zhang, D. Li, Z.J. Ning, Chromospheric condensation and quasi-periodic pulsations in a circular-ribbon flare. Astrophys. J. 832, 65 (2016). https://doi.org/10.3847/0004-637X/832/1/65
V.V. Zharkova, S.I. Zharkov, On the origin of three seismic sources in the proton-rich flare of 2003 October 28. Astrophys. J. 664, 573–585 (2007). https://doi.org/10.1086/518731
V. Zharkova, S. Zharkov, On the generation of hydrodynamic shocks by mixed beams and occurrence of sunquakes in flares. Sol. Phys. 290, 3163–3188 (2015). https://doi.org/10.1007/s11207-015-0813-x
H. Zirin, S. Werner, Detailed analysis of flares, magnetic fields and activity in the sunspot group of Sept. 13 26, 1963. Sol. Phys. 1, 66–100 (1967). https://doi.org/10.1007/BF00150304
Acknowledgements
This review arose from discussions at a workshop on ‘Integrated Plasma Modelling of Solar Flares’ at the Lorentz Center, University of Leiden (May 2015). JAM acknowledges generous support from the Leverhulme Trust and this work was funded by a Leverhulme Trust Research Project Grant: RPG-2015-075. JAM also acknowledges this material is based upon work supported by the US Air Force Office of Scientific Research, Air Force Material Command, USAF under Award No. FA9550-16-1-0032. JAM acknowledges IDL support provided by STFC. VMN acknowledges the support from the European Research Council under the SeismoSun Research Project No. 321141, and the BK21 plus program through the National Research Foundation funded by the Ministry of Education of Korea. This work was supported in part by the Russian Foundation for Basic Research grant No. 17-52-80064 (VMN). MD acknowledges the IAP P7/08 CHARM programme as well as the SIDC Data exploitation programma from PRODEX. PJ acknowledges support from grant 16-13277S of the Grant Agency of the Czech Republic. JAM and VMN acknowledge the support of ISSI. ST acknowledges support by the Research Fellowship of the Japan Society for the Promotion of Science (JSPS).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Global Waves Generated by Flares: Shock Waves, Blast Waves and ‘Flare Waves’
On the global scale, we can consider flares to be enormous impulsive energy releases in an elastic and compressive medium surrounding the flaring site. Simply put, we expect MHD waves and shocks to propagate away from the flaring region. Vršnak and Cliver (2008) provide an excellent review of the origin of large-scale coronal shock waves, and detail the physical mechanisms capable of launching MHD shocks. Of relevance, Vršnak and Cliver (2008) review the idea of a shock wave driven by a 3D piston effect, where the expanding driver pushes the plasma in all directions (piston-shock). As a special case, when the driver is of finite duration (temporary piston) this generates a freely-propagating simple-wave shock, also known as a blast wave. Thus, a flare modelled as a (explosion-like) pressure pulse would generate a blast wave or shocked simple-wave (i.e. the driver has an acceleration phase, deceleration phase and then stops). Whereas a CME-driven shock is a piston-shock in its early stages (and in later stages, a piston-shock in combination with a bow shock). The physical difference is that the piston-driven shock wave is drawing additional energy from the piston (source region) whereas in a blast wave the shock is freely propagating and there is no additional energy input (see also Landau and Lifshitz 1959).
Global-scale propagating disturbances have been observed directly in the corona initially with the SoHO/EIT instrument and became known as EIT waves. These are bright, wave-like (pulse) features propagating globally across the solar disk through the corona (Moses et al. 1997; Thompson et al. 1998). After being observed by different instruments, EIT waves later became known as large-scale Coronal Bright Fronts (CBFs, see reviews by Gallagher and Long 2011; Warmuth 2015) and also as Global Coronal Waves (Hudson 1999; Chen 2016).
In addition to EIT waves, there are Moreton waves (Moreton 1960; Moreton and Ramsey 1960). These are propagating, bright fronts in H\(\upalpha \) line center and blue wing (and dark fronts in H\(\upalpha \) red wing) and, given that the H\(\upalpha \) spectral line is formed in the chromosphere, are a chromospheric phenomenon. The study of EIT waves and their association, or not, with chromospheric Moreton waves is a subject of active research (e.g. Long et al. 2011; Long et al. 2013; Long et al. 2014) and readers are referred to a comparison of different EIT wave models (Long et al. 2017). What seems to be clear is that Moreton waves are related to CMEs (Chen et al. 2002; Chen 2016). But what about the link to flares, specifically? Since Moreton waves were discovered before CMEs were discovered (Tousey 1973) solar flares were initially thought to be the cause of Moreton waves (Ramsey and Smith 1966). Uchida (1968) proposed that the pressure pulse in the solar flare generates a fast wave propagating in the corona. As the wavefront sweeps through the chromosphere, it pushes chromospheric material downward and this is how a Moreton wavefront is formed. Thus, Moreton waves were thought to be blast waves (freely-propagating shock wave). Moreover, chromospheric Moreton waves were given the specific terminology flare waves (e.g. Zirin and Werner 1967; Warmuth et al. 2001; Warmuth et al. 2004a; Warmuth et al. 2004b). Note that under this interpretation, the chromospheric Moreton wave is the footprint of the fast-mode EIT wave. This coronal counterpart (i.e. the fast-mode EIT wave) then also took on the terminology coronal flare wave and coronal Moreton wave (e.g. Thompson et al. 2000; Vršnak et al. 2002).
However, this interpretation has now been superseded by the link to CMEs, rather than driven by flares. E.g. Chen et al. (2002) replace the blast wave (initiated by the solar-flare pressure pulse) by a piston-driven shock wave from a CME (see Vršnak and Cliver 2008 and §2.2 of Warmuth 2015 for further details). Furthermore, Chen (2006) selected 14 M-class and X-class flares that were not associated with CMEs and found that none of the flares was associated with any EIT waves. Chen et al. conclude that it is unlikely that pressure pulses from flares generate EIT waves. Thus, even though the current evidence favours CMEs as the origin of EIT waves rather than flares, there is still the possibility that some waves are generated by flare-associated pressure pulses (e.g. Liu et al. 2012; Kumar and Innes 2013; and see §5.1 of Warmuth 2015). It is seen that there are many types of waves in the corona, some are driven by CMEs, and some are by flares. Even for CME-associated waves, it seems that there are two distinct types of EUV coronal global waves, where the faster EUV global waves are interpreted as nonlinear fast waves (driven by the impulsive expansion of an erupting CME) and that there also exists a slower type of EUV wave (see reviews by Warmuth 2015; Chen 2016; Long et al. 2017, and references therein).
Appendix B: Global, Flare-Generated Waves in the Solar Interior: Sunquakes
Another global wave-like phenomenon associated with flares is that of sunquakes. Wolff (1972) proposed that solar flares could excite free global oscillations inside the Sun similar to earthquakes, i.e. that flares should deliver acoustic impulses to the solar interior (Hudson 2011). These seismic transients were modelled by Kosovichev and Zharkova (1995) and then were first discovered by Kosovichev and Zharkova (1998). Sunquakes are seismic (acoustic) waves generated by flares and manifest themselves at the photospheric solar surface, as a quasi-circular pattern of ripples moving away from the flare epicentre. Donea (2011) reports that the manifestation of this acoustic energy is seen 20–50 Mm from the source when it refracts back to the solar surface within about an hour after the commencement of the flare. This refraction is a result of the increasing sound speed with increasing depth in the solar interior. Thus, flare-driven sunquakes open the prospect of using seismology (helioseismic analysis) to study the solar interior structure (Lindsey and Donea 2008) as well as informing the general topic of MHD wave behaviour in inhomogeneous media. See Kosovichev (2011) for a comprehensive review of the basic principles of global and local helioseismology and see Kosovichev (2006) for a review of the properties of sunquakes. For examples of sunquakes see, e.g., Martínez-Oliveros et al. (2008) and examples by Judge et al. (2014), Matthews et al. (2015), and Buitrago-Casas et al. (2015).
Kosovichev (2014b) reports that the excitation impact strongly correlates with the impulsive flare phase and is caused by the energy/momentum transported from the energy-release site(s) but that the physical mechanism is currently uncertain. These seismic transients have been explained via a ‘thick-target’ hydrodynamic model (see e.g. Kostiuk and Pikelner 1975; Livshits et al. 1981; Fisher et al. 1985). Here, a beam of high-energy particles is accelerated in the corona, heats the chromosphere, which results in a compression of the lower chromosphere. This compression produces chromospheric evaporation and a downward-propagating shock wave (velocity impulse) which impacts the photosphere (i.e. a hydrodynamic impact) causing the seismic response (Kosovichev and Zharkova 1998; Kosovichev 2014b; Zharkova and Zharkov 2015).
Donea (2011) details several alternative generation mechanisms for sunquakes that have been proposed, including a generation mechanism based on the direct interaction of high-energy particles (electrons or protons) with the photosphere (Donea and Lindsey 2005; Zharkova and Zharkov 2007); pressure transients related to photospheric backwarming by enhanced chromospheric radiation (Lindsey and Braun 2000; Donea and Lindsey 2005); flare acoustic emission due to impulsive heating of the low photosphere and radiative backwarming (Donea et al. 2006); and a magnetic jerk that manifests as a seismic response occurring during the re-organisation of the magnetic topology, specifically a change in field line inclination at the footpoints (Hudson et al. 2008, and see recent extension by Russell et al. 2016).
Donea (2011) reports that (with current instruments) sunquakes are a rare phenomenon and most flares do not generate detectable seismic emission in the p-mode spectrum. However, Kosovichev (2014b) speculates that perhaps all flares generate some seismic response, but if the amplitude is not high enough the signal may be lost in the background noise. ‘Starquakes’ resulting from stellar flares have also been detected on other stars (Kosovichev 2014a), while other studies are less optimistic (e.g. Balona et al. 2015). If detected confidently, starquakes could provide new asteroseismic information and impose rigorous constraints on stellar flare mechanisms.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
McLaughlin, J.A., Nakariakov, V.M., Dominique, M. et al. Modelling Quasi-Periodic Pulsations in Solar and Stellar Flares. Space Sci Rev 214, 45 (2018). https://doi.org/10.1007/s11214-018-0478-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-018-0478-5