Abstract
Charged particle acceleration takes place ubiquitously in the Universe including the near-Earth heliospheric environment. Typical in situ spacecraft measurements made in the solar wind show that the charged particle velocity distribution contains energetic components with quasi scale-free power-law velocity dependence, f∼v −α, for high velocity range. In this Review a theory of quiet-time solar-wind electrons that contain a suprathermal component is discussed, in which these electrons are taken to be in dynamical equilibrium with Langmuir turbulence. This Review includes an overview of the Langmuir turbulence theory, as well as a discussion on asymptotic equilibrium solution of Langmuir turbulence/suprathermal electron system. Theoretical predictions of high-energy electron velocity power-law distribution index is then compared against the recent observations of the superhalo electron velocity distribution made by instruments onboard WIND and STEREO spacecraft. It is shown that the theoretical prediction of velocity power-law index is intermediate to the observed range.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Turbulent and/or nonlinear processes as well as the charged particle acceleration are fundamental and mutually related processes that take place in many laboratory and astrophysical environments. The present Review is concerned with the Langmuir turbulence and suprathermal electron acceleration in the solar wind. In situ spacecraft measurements of the space environment became available in the 1960s. Observations of charged particles in the solar wind showed that they featured suprathermal components (Feldman et al. 1975; Gosling et al. 1981; Armstrong et al. 1983), characterized by velocity distribution function (VDF), f∝v −α, for high-velocity regime. Vasyliunas was one of the first to employ the kappa distribution in order to phenomenologically describe the spacecraft observation of electron VDF (Vasyliunas 1968),
where v Te =(2T e /m e )1/2 is the Maxwellian electron thermal speed, and where the temperature T e is defined without the Boltzmann constant, since it is customary in plasma physics to define T e in the unit of eV. The quantity m e is the electron mass. Of course, the limit κ→∞ corresponds to the classic Maxwell-Boltzmann distribution, \(f_{e}(v)\sim\exp(-v^{2}/v_{Te}^{2})\).
The kappa model facilitates the data analysis, but as far as their physical origin is concerned, there is no clear understanding. Of course, if one is judicious, then one may reproduce the kappa distribution by non self-consistent methods. That is, if the turbulence spectrum of a given wave mode is simply assumed, then the particle kinetic equation can be solved to obtain the power-law or kappa-like solutions. For instance, adopting such an approach (Hasegawa et al. 1985) obtained an analytical kappa distribution in the presence of a high-intensity radiation field. Ma and Summers (1998) employed stationary whistler turbulence to obtain the power-law electron distribution function. Similarly, Roberts and Miller (1998) and Leubner (2004a) solved particle diffusion equation to obtain power-law type of distributions when the diffusion coefficients are given by non self-consistent means.
By phenomenologically coupling the strong-turbulence theory (which does not have the wave-particle interaction in its original form) and the particle diffusion equation (Galeev et al. 1975; Papadopoulos 1975; Gorev et al. 1976; Kingsep 1978, and Pelletier 1982) addressed the problem of the formation of high-energy electrons when these electrons interact with long wavelength (small k) Langmuir condensate mode, whose dynamical evolution is described by strong turbulence theory.
There are alternative approaches to explain the origin of suprathermal electron acceleration. For example Collier (1993) applied the Lévy flights probability concept to show that the kappa distribution can form under such a condition. One of the most interesting recent alternative approaches rely on the “non-extensive” thermo-statistical concept to show that kappa-like distribution corresponds to the most probable state in the non-extensive statistical system (Tsallis 1988, 2009; Treumann 1999a, 1999b; Treumann and Jaroschek 2008; Leubner 2000, 2002, 2004a, 2004b, 2005; Livadiotis and McComas 2009).
Yoon et al. (2005, 2006), Rhee et al. (2006), Gaelzer et al. (2008) on the other hand, were the first to show that the kappa-like electron VDF can form as a result of self-consistent wave-particle interaction between the Langmuir turbulence and the energetic electrons. They concretely demonstrated this by numerically solving the complete equations of the weak turbulence theory. In order to confirm the numerical solution of the weak turbulence equation (Ryu et al. 2007) performed one-dimensional particle-in-cell simulation with a large number of particles to show that the long time simulation of the electron beam-plasma interaction process and the ensuing Langmuir turbulence generation leads to the formation of kappa-like electron velocity distribution function.
The above works are, however, based either on numerical initial value solution of the weak turbulence equation or by direct particle-in-cell simulation method in one-dimension. It is not evident that the formation of kappa-like state, which was demonstrated during the long-time evolution of the system, does indeed correspond to the rigorous asymptotically steady-state solution or not in a mathematical sense. Moreover, it is not clear whether the kappa fit of the final stage of the accelerated electrons obtained by these means is the true asymptotic value of the kappa parameter or not. Furthermore, the numerical demonstrations of the formation of kappa-like state was obtained only in the simplifying one-dimensional approximation.
Two- or higher-dimensional numerical solutions to the complete equations of weak turbulence theory applicable for electron-Langmuir/ion-sound turbulence problems have recently become available (Ziebell et al. 2008a, 2008b; Pavan et al. 2009a, 2009b, 2010a, 2010b; Ziebell et al. 2011a, 2011b, 2011c). The solutions indicate that indeed, the wave-particle interaction involving Langmuir turbulence and electrons does lead to quasi-isotropic acceleration, accompanied by two- or three-dimensional Langmuir turbulence spectrum. However, as the higher-dimensional numerical solutions demand high computational resources these solutions could not be numerically integrated long enough to demonstrate quasi asymptotic state. Numerical simulations in two- or higher-dimensions (Rhee et al. 2009; Yi et al. 2010) face the same problem of limited computational resources such that these runs cannot reach the true quasi asymptotic state.
For these reasons, the issue of whether the basic set of coupled electron-Langmuir turbulence equations do indeed lend themselves to an asymptotically steady-state solution or not, especially in higher-dimensions, deserves separate discussions based upon analytical approach. Yoon (2011, 2012a, 2012b) addressed this issue. Yoon (2011) discusses one-dimensional steady-state self-consistent asymptotic solution of the electron-Langmuir turbulence system, and show that the non-Maxwellian kappa-like VDF does indeed correspond to a rigorous solution. In subsequent papers Yoon (2012a, 2012b) extend the analysis to three-dimensional situation. Physically, the one-dimensional approach may be justified when there exists a sufficiently strong ambient magnetic field so that implicitly, field-aligned beam-plasma interaction can be described by the one-dimensional approximation. Three-dimensional solution is applicable to the situation where the ambient magnetic field is weak (Yoon 2012a) or absent (Yoon 2012b).
As noted already, the electron VDFs detected in the solar wind deviate considerably from the Maxwellian model at high-energy tail (Lin et al. 1981, 1986; Ergun et al. 1998). The solar wind VDF is typically described as thermal core plus suprathermal halo populations. Recently, a third component, the superhalo distribution, was identified by WIND spacecraft (Lin 1998). In the solar wind, there exist quasi-stationary electrostatic (Langmuir wave) fluctuations called the quasi-thermal noise (Couturier et al. 1981; Meyer-Vernet et al. 1986; Maksimovic et al. 1995). In the literature, most theories of suprathermal electrons rely on the consideration of the altitude-dependent collisional dynamics (Scudder and Olbert 1979; Pierrard et al. 1999). The present Review shall not be concerned with such an approach, although this does not mean that the altitude-dependent collisional dynamics is unimportant. The present Review shall be concerned with local wave-particle (i.e., collective) dynamical processes of energetic electron acceleration. We envision that the dynamical steady-state will be that of kappa-like electron VDF and enhanced quasi-thermal noise-like Langmuir turbulence spectrum.
We claim that such a system corresponds to the theoretical asymptotic quasi-steady state equilibrium solution for the weak turbulence theory. In order to verify this claim, we shall compare the theoretical predictions of high-energy electron velocity power-law distribution index against the observed value. For the observation, we make use of the velocity power-law index derived from the superhalo electron velocity distribution made by instruments onboard WIND and STEREO spacecraft. As it will be discussed subsequently, we find that the comparison is rather good. Specifically, it will be shown that the theoretical prediction of velocity power-law index is intermediate to the observed range. From this, we conclude that the Langmuir turbulence may indeed be responsible for the suprathermal electron acceleration near 1 AU.
The organization of the present Review is as follows: In Sect. 2, we present a brief overview of the history of Langmuir turbulence. The purpose is to provide a rationale for employing the weak turbulence approach to discuss the Langmuir turbulence problem. In Sect. 3, we present a self-contained discussion of the weak turbulence theory. On the basis of the equations of the weak turbulence theory derived in Sect. 3, we discuss numerical solution in 1D and 2D (or 3D with cylindrical symmetry) in Sect. 4. In order to facilitate the discussion, we consider the problem of bump-in-tail instability, although in the quiet-time solar wind, no electron beam with positive gradient in velocity space is observed at 1 AU. However, the solar wind contains energetic, highly field-aligned component called the strahl. In any case, we are concerned with time-asymptotic state associated with the Langmuir turbulence so that how Langmuir turbulence is generated is not too important. We shall thus demonstrate that over the long time scale the electrons are accelerated to suprathermal energies by Langmuir turbulence. In Sect. 5, we present the rigorous analysis of steady-state Langmuir turbulence and electron acceleration problem by solving the set of coupled electron-Langmuir turbulence equations. On the basis of such an analysis, it shall be shown that the steady-state suprathermal electron should behave as F e ∼v −6.5. In order to verify this, we shall compare the quiet-time solar wind electron distribution and show that the observation indicates ∼v −5.0 to v −8.7 dependence associated with the suprathermal electrons, while the theory predicts v −6.5. In the remainder of this Review, we shall systematically expound on the various issues discussed above.
2 A Brief History of Langmuir Turbulence
Serious investigations of (high-frequency) plasma turbulence began with the works of the scientists largely from the former Soviet Union in the early 1960s. Standard monographs on the subject are: Kadomtsev (1965), Sitenko (1967, 1982), Vedenov (1968), Sagdeev and Galeev (1969), Tsytovich (1970, 1977a, 1977b), Davidson (1972), Kaplan and Tsytovich (1973), Hasegawa (1975), Akhiezer et al. (1975), Melrose (1980). Efforts by these pioneers, which came to be known as the plasma weak turbulence theory, continued on through the 1970s and 1980s. It should be noted that although the weak turbulence formalism is quite general, and in principle it can be applied to a wide variety of problems, in practice however, it is almost exclusively applied to the bump-in-tail (or weak beam-plasma) instability problem, which is one of the simplest plasma instabilities. Hence, the Langmuir turbulence problem became the test bed for various plasma turbulence theories.
During the trail-blazing days, scientists in the West were largely following the Soviet scientists’ lead, but a few made important contributions of their own. For instance, Dupree (1966, 1972), Weinstock (1969), and others, suggested the renormalized turbulence theories, which is an effort to go beyond the weak turbulence perturbation scheme and take the higher-order terms into account. In the early days, the renormalized kinetic theories were called “strong turbulence” theories, but we use the term “renormalized” to distinguish them from the later theory of the same name by Zakharov (1972). In contrast to the mostly theoretical works spearheaded by the Soviet scientists, the American scientists such as Dawson and Buneman pioneered the powerful particle-in-cell numerical simulation method (Dawson 1983). By employing such a scheme, coherent nonlinear effects such as particle trapping by large-amplitude waves were discovered and were shown to play an important, if not the dominant, role (Dawson and Shanny 1968; Morse and Nielson 1969).
However, Dum (1990a, 1990b, 1990c) carried out detailed particle-in-cell simulations to show that the dominant particle trapping behavior observed in early simulations were partly owing to the insufficient mode resolution and small system size. He proceeded to demonstrate with his refined simulations that quasilinear/weak turbulence theories are actually quite good for certain parameter regime. Specifically, for a weak and warm beam, the weak turbulence theory provided an acceptable first-order description of the nonlinear behavior of the system. For a more recent discussions on the preponderance of incoherent versus coherent nonlinear effects in beam-plasma interactions, see the discussion by Omura et al. (1996).
In 1972, Zakharov proposed a semi-phenomenological theory of plasma turbulence, which came to be known as the strong turbulence theory. In his theory, the collapse of intense Langmuir wave packet plays the prominent role. The strong turbulence theory ignores the wave-particle effect, and is a macroscopic theory. Even though Zakharov’s strong turbulence theory continues to be investigated by many researchers (see the reviews by Goldman 1984 and Robinson 1997), the theory remains controversial to this date, and various numerical simulations and experiments to confirm the theory are inconclusive (Robinson and Newman 1990; Vyacheslavov et al. 2002; Erofeev 2002).
Here, it should be noted that Zakharov-type of highly nonlinear and coherent theory of Langmuir waves plays a prominent role in high power radio wave experiment in the ionosphere, and such a theory enjoys many successes there (Dubois et al. 2001; Cheung et al. 2001). However, the present discussion is concerned with incoherent turbulence problem where the nonlinearity is relatively weak. For such a weakly turbulent situation, the Zakharov theory remains controversial, and renormalized theory is unnecessary. For reasons discussed above, we do not consider particle trapping effects in our discussion either. Consequently, the present Review is focused on weak turbulence theory of Langmuir turbulence.
3 An Overview of Weak Turbulence Theory
The starting point of the present analysis is the self-consistent Klimontovich equation in the absence of external fields, under electrostatic approximation,
where \(N_{a}=\sum_{i=1}\delta[\mathbf{r}-\mathbf{r}_{i}^{a}(t)]\,\delta[\mathbf{v}-\mathbf{v}_{i}^{a}(t)]\) stands for the exact one-particle phase-space distribution function for species a (=e,i denotes the electrons and the ions, respectively) and E stands for the self-consistent electrostatic field. If we denote the ensemble average of the Klimontovich function by \(\hat{n}f_{a}=\langle N_{a}\rangle\), where \(\hat{n} =\hat{n}_{e} =\hat{n}_{i}\) stands for the ambient plasma density, and the deviation of the Klimontovich function from its average by \(\delta N_{a}=N_{a}-\hat{n}f_{a}\), then the hierarchy of equations can be obtained in the standard manner. We are concerned with spatially uniform plasmas with no average fields. Consequently we may represent the total electric field by the fluctuating part only, E=δ E. The ensemble average 〈⋯〉 can also be viewed as the random-phase average. As such the averages of all fluctuations, i.e., quantities preceded by δ, are zero. The random-phase approximation precludes coherent nonlinear effects at the outset.
Let us employ the shortcut two-time scale approximation in which physical quantities are decomposed in the customary sense of Fourier-Laplace transformation with respect to the fast time scale of the fluctuations, while the spectral coefficients and the average particle distribution evolve in the slow time. This reduces (2) to a set of hierarchical equations,

where 〈⋯〉 denotes ensemble averages over the phases of the perturbation, and we have made use of the spectral property associated with the stationary and homogeneous turbulence, \(\langle\delta a_{\mathbf{k},\omega}\,\delta a_{\mathbf{k}',\omega'}\rangle=\delta(\mathbf{k}+\mathbf{k}')\;\delta(\omega+\omega')\,\langle\delta a^{2}\rangle_{\mathbf{k},\omega}\). The first equation in the above represents the formal particle kinetic equation, the second describes the evolution of perturbed particle distribution function, and the third equation represents Poisson equation for the field perturbation.
Obviously the above set of equations is not closed, since the solution for \(\delta N_{\mathbf{k},\omega}^{a}\) requires the knowledge of the two-body correlation \(\langle\delta N_{\mathbf{k},\omega}^{a}\delta N_{\mathbf{k}',\omega'}^{a}\rangle\), which depends on the tertiary correlation, \(\langle\delta N_{\mathbf{k},\omega}^{a}\delta N_{\mathbf{k}',\omega'}^{a}\) \(\delta N_{\mathbf{k}'',\omega''}^{a}\rangle\), and so on. In order to break the hierarchy and obtain a closure we shall represent the fourth-order correlation in terms of products of two-body correlations by ignoring the irreducible four-body correlations,

This is known as the quasi-normal closure in fluid turbulence theory, and it corresponds to the simplest closure scheme.
The quantity \(\delta N_{\mathbf{k},\omega}^{a0}\) in (3) represents the perturbed phase space distribution owing to pure particle effects. The ensemble average of the correlation of this quantity is of interest to us,
In the purely collisionless Vlasov theory, the above quantity is set equal to zero. However, such an approximation is strictly speaking, invalid, since the above quantity leads to the various spontaneous thermal effects, and in the subsequent equations of weak turbulence theory that shall be derived, the presence of the above “source fluctuation” gives rise to the proper balance of various spontaneous and induced processes.
Note that the arguments, (k′,ω′) and (k−k′,ω−ω′), in (3) are not symmetrized yet, since these can be interchanged. Eventually these dummy arguments should be fully symmetrized by considering all possible permutations. Also in (3), note that we have retained the slow adiabatic time derivative i (∂/∂t) on the left-hand side of the equation for the perturbed distribution. In solving for \(\delta N_{\mathbf{k},\omega}^{a}\), this slow time derivative is tentatively ignored, but is reintroduced later. Such a treatment is the essence of the two-time step approximation. Another way to look at the present two-time step approach is to imagine the factor i (∂/∂t) as being absorbed in the “new” definition of the angular frequency, ω→ω+i ∂/∂t. Then the equation for perturbed distribution δN k,ω can be solved iteratively up to third order in electric field strength, δE k,ω . After the desired iterative solution has been obtained, then the solution is inserted into the perturbed Poisson equation, and appropriate ensemble averages are taken under the assumption of random phases associated with the fluctuations. This results in the nonlinear spectral balance equation, as has been discussed in the standard literature. At this stage, the slow time derivative i (∂/∂t) is reintroduced. This is the essence of the two-time step approximation, which bypasses the mathematical rigor in the full multiple-time scale analysis (Davidson 1972).
After manipulating the set of equations (3) under the closure scheme (4) and making use of the source fluctuation (5), one may derive an equation, known as the nonlinear spectral balance equation, as given below (Yoon 2005):

where

In the above, ϵ(k,ω)=1+χ(k,ω), is the linear dielectric response function, χ(k,ω)=∑ a χ a (k,ω) being the linear dielectric susceptibility, \(\chi^{(2)}(\mathbf{k}_{1},\allowbreak\omega_{1} |\mathbf{k}_{2},\omega_{2})=\sum_{a}\chi_{a}^{(2)}(\mathbf{k}_{1},\allowbreak\omega_{1} |\mathbf{k}_{2},\omega_{2})\) is the second-order nonlinear susceptibility, and \(\bar{\chi}^{(3)}\) \((\mathbf{k}_{1},\omega_{1} |\mathbf{k}_{2},\omega_{2} |\mathbf{k}_{3},\omega_{3})=\sum_{a}\bar{\chi}_{a}^{(3)} (\mathbf{k}_{1},\omega_{1} |\mathbf{k}_{2},\omega_{2}|\mathbf{k}_{3},\omega_{3})\) is the partial third-order nonlinear susceptibility. The fully symmetric nonlinear third-order susceptibility is defined by \({\chi}^{(3)}(\mathbf{k}_{1},\omega_{1} |\mathbf{k}_{2},\omega_{2}|\mathbf{k}_{3},\omega_{3}) =(1/3)\,[\,\bar{\chi}^{(3)}(\mathbf{k}_{1},\omega_{1}|\mathbf{k}_{2},\omega_{2} |\mathbf{k}_{3},\omega_{3}) +\bar{\chi}^{(3)}(\mathbf{k}_{2},\omega_{2} |\mathbf{k}_{1},\omega_{1} |\mathbf{k}_{3},\omega_{3})+\bar{\chi}^{(3)}(\mathbf{k}_{3},\omega_{3} |\mathbf{k}_{2},\omega_{2}|\mathbf{k}_{1},\omega_{1})\,]\), which one encounters in theories of coherent nonlinear processes, but is not used in the current turbulent nonlinear kinetic theory. The specific definitions for various susceptibility functions for particle species a are given by

where
The formal result (6), which was known in one form or another in the literature, but recently systematically rederived in Yoon (2005), forms the basis for plasma weak turbulence theory.
The common procedure in plasma kinetic theory is to assume that |Im ϵ(k,ω)| ≪|Re ϵ(k,ω)|. In general, this assumption limits the applicability of the customary weak turbulence theory to weakly unstable modes where the real part of linear response in (6) leads to the dispersion relation, while the imaginary terms determine how the wave intensity evolves in time, i.e., the wave kinetic equation.
In the standard weak turbulence theory, simple quasilinear diffusion equation is adopted for the particle kinetic equation, although it is possible to obtain a more general formal particle kinetic equation in which various nonlinear wave coupling terms are incorporated to the same degree of perturbation expansion as in the wave kinetic equation. However, doing so is not only unnecessary but under certain circumstances, it leads to divergences. For this reason it is better to limit oneself to the simple first-order iterative solution for \(\delta N_{\mathbf{k},\omega}^{a}\) when it comes to the particle kinetic equation. Then, we arrive at the familiar formal particle kinetic equation:

where the repeated indices imply summation (i.e., Einstein convention).
3.1 Wave Kinetic Equation
The nonlinear spectral balance equation (6) provides the platform upon which the wave kinetic equation that describes nonlinear interaction among plasma eigenmodes, i.e., Langmuir (denoted with L) and ion-sound (S) waves, as well as particle may be formulated. For plasma eigenmodes, if one retains only the linear response in the real part of the spectral balance equation, then we have
If one is interested in the region of (k,ω) space for which Re ϵ(k,ω)≠0, then one obtains the familiar expression for the spontaneous fluctuation formula found in the literature (Sitenko 1967),
The right-hand side of the above expression diverges near the mode transparency domain, Re ϵ(k,ω)→0 and Im ϵ(k,ω)→0, where one must exclude such regions.
For the present purpose, we are interested in the region of (k,ω) space for which Re ϵ(k,ω)=0, i.e., the plasma eigenmodes. In this case, the roots of the equation Re ϵ(k,ω)=0 can be represented by \(\omega=\omega_{\mathbf{k}}^{\alpha}\), α=L, S, where L and S denote Langmuir and ion-sound modes. In this case, the quantity
is nonzero, and in general, it is an eigenfunction which may be represented as
If we ignore the thermal fluctuation owing to single-particle effects, i.e., \(\langle\delta E^{2}\rangle_{\mathbf{k},\omega}^{0}\), which provides finite level of electric field in the spectral range outside the eigenmode solution, \((\mathbf{k},\omega\neq\pm\omega_{\mathbf{k}}^{\alpha})\), then Ψ k,ω ≈〈δE 2〉 k,ω , and the wave intensity can simply be approximated by
In the above σ=±1 represents the direction of the wave phase velocity.
Inserting this to the imaginary part of (6), we obtain, after some algebraic manipulations, the following:

where

This is the formal wave kinetic equation. Many early treatises on nonlinear plasma kinetic theory would often develop the formulation only up to the stage equivalent to the above formal equation. However, as one can see, unless the various nonlinear susceptibilities are explicitly worked out, the above equation is not very informative. In the literature, the first and second terms on the right-hand side are designated as the induced and spontaneous emission terms, respectively, while the third and fourth terms are called the induced and spontaneous scattering, respectively. The final term is said to depict the decay processes, but the first two terms within large parenthesis are said to be responsible for the induced decay process, while the final term corresponds to the spontaneous decay. The reason for these terminologies becomes eminently self-evident if one starts from the principle of detailed balance, which is based upon concepts of quantum field theory (Tsytovich 1970, 1977a, 1977b; Melrose 1980). However, within the context of the present statistical mechanical approach, there is no a priori reason why we should call these terms as such. Note that spontaneous emission and scattering terms would be absent had we resorted to the purely Vlasov approximation in which the source fluctuation (5) is set equal to zero.
It turns out that the induced and spontaneous emission processes are dictated by linear wave-particle resonant interaction governed by the condition, \(\sigma\omega_{\mathbf{k}}^{\alpha}-\mathbf{k}\cdot\mathbf{v}=0\), the induced and spontaneous scattering processes are dictated by nonlinear wave-particle resonant interaction, \(\sigma\omega_{\mathbf{k}}^{\alpha}-\sigma'\omega_{\mathbf{k}'}^{\beta}-(\mathbf{k}-\mathbf{k}')\cdot\mathbf{v}=0\), and the induced and spontaneous decay processes are dictated by nonlinear wave-wave resonance, \(\sigma\omega_{\mathbf{k}}^{\alpha}-\sigma'\omega_{\mathbf{k}'}^{\beta}-\sigma''\omega_{\mathbf{k}-\mathbf{k}'}^{\gamma}=0\). Examining the various terms in (16) and (17), one may realize that these resonance conditions are not apparent in all the terms. The reason is that some of the resonance conditions are hidden within the definitions of the various susceptibilities and only reveal themselves after the response functions are explicitly computed.
3.2 Induced and Spontaneous Emissions
Induced emission terms for L and S modes are well-known in the literature and also discussed in Yoon (2000),
where \(\omega_{pe}=(4\pi\hat{n}e^{2}/m_{e})^{1/2}\) is the electron plasma frequency; m e and m i are the electron and ion masses, respectively; and we have made use the familiar dispersion relations,
and the properties of the linear dielectric, \(1/\epsilon'(\mathbf{k},\sigma\omega_{\mathbf{k}}^{L})=\sigma\omega_{\mathbf{k}}^{L}/2\), \(1/\epsilon'(\mathbf{k},\sigma\omega_{\mathbf{k}}^{S})= \mu_{\mathbf{k}}\,\sigma\omega_{\mathbf{k}}^{L}/2\), where
Here, v te =(2T e /m e )1/2 is the thermal speed of the background electrons. Induced emission process is variously called the (quasi) linear or Landau growth/damping process.
Spontaneous emission terms for these modes can also be computed in a straightforward manner on the basis of the dielectric constant;
3.3 Induced and Spontaneous Decay Processes
The expression for decay processes is discussed by Yoon (2000), and can also be found in standard literature,

where
The first terms within the parentheses on the right-hand sides of (22) are called the spontaneous decay while the remaining terms depict the induced decay processes.
It is interesting to observe that the following conservation relation for the “plasmon number densities” exists within the context of the above three-wave coupling equations:
Note that \(N_{\mathbf{k}}^{\sigma L}=I_{\mathbf{k}}^{\sigma L}/\hbar\omega_{\mathbf{k}}^{L}\) and \(N_{\mathbf{k}}^{\sigma S}=I_{\mathbf{k}}^{\sigma S}/\hbar\mu_{\mathbf{k}}\omega_{\mathbf{k}}^{L}\), where ħ is the Planck constant, can be conceived of as the “quantum mechanical” plasmon number densities, although the present formalism is strictly classical. In the literature, sometimes the quantities \(N_{\mathbf{k}}^{\sigma L}\) and \(N_{\mathbf{k}}^{\sigma S}\) are used as the fundamental quantities instead of intensities, \(I_{\mathbf{k}}^{\sigma L}\) and \(I_{\mathbf{k}}^{\sigma S}\). Since the three-wave decay/coalescence process involves two Langmuir waves and an ion-sound wave, the total plasmon number density of conserved Langmuir mode equals twice that of the ion-sound mode.
3.4 Induced and Spontaneous Scattering Processes
For nonlinear scattering processes, we keep only the most important term, namely the scattering of L mode off another L mode mediated by the ions (sometimes called the scattering off thermal ions), as discussed in standard literature. Consequently, the induced scattering process is dictated by

In Yoon (2000) the induced scattering of an ion-sound wave off another ion-sound wave was discussed. Moreover, the same L−L scattering as depicted by the above but mediated by the electrons (also known as the electron nonlinear Landau damping in the literature) was also considered. However, the former process is an extremely slow process, and the latter process becomes almost totally irrelevant owing to the electron’s low mass, when compared with the scattering off thermal ions. Spontaneous scattering terms were derived in Yoon (2005),

3.5 Electron Kinetic Equation
The electron kinetic equation (10) reduces to the following upon making use of (15):

In the present discussion the ions shall be treated as quasi-stationary, so that we do not need to consider the kinetic equation for the ion distribution function.
Before we move on to the main discussion of electron acceleration by weak Langmuir turbulence, it is instructive to discuss the difference between the above kinetic equation for the particles and the Balescu-Lénard collisional kinetic equation (Balescu 1960; Lénard 1960). Note that the general form of particle kinetic equation is given by (10). The kinetic equation (27) is the result of ignoring the thermal fluctuation \(\langle\delta E^{2}\rangle_{\mathbf{k},\omega}^{0}\) in (13). In contrast, Balescu-Lénard equation results from the opposite limit where the total electric field eigenfunction Φ k,ω is approximated by \(\langle\delta E^{2}\rangle_{\mathbf{k},\omega}^{0}\). Thus, if we approximate the electric field fluctuation by
and insert this result to (10), then we have

which is the desired Balescu-Lénard collisional kinetic equation. Clearly, the approximation (28) breaks down near (k,ω) space where ϵ(k,ω)=0. As a result, when applying (28) one must exclude those portions of (k,ω) space for which ϵ(k,ω)=0. If we determine the electric field by the above form, then by definition, we are assuming that the contributions from the zeros of ϵ(k,ω), i.e., the collective modes, are insignificant. That is, in this regime collective oscillations (such as arising from instabilities) are not assumed to play any dominant role, but the electric field is predominantly determined by spontaneous emission from bulk particles. Physically, such an assumption is valid when the plasma is close to thermal equilibrium state.
In short, Balescu-Lénard kinetic equation is appropriate for long-term particle evolution when the system deviates slightly from thermal equilibrium. When the plasma system contains highly non-thermal features such as energetic electron beam, then the collective oscillation arising from the zeros of linear dielectric, ϵ(k,ω) will become far more important than thermal emission from the bulk particles, such that the electric field can no longer be simply given by (28), but rather, in this case, the approximation (13) is more appropriate. Then, the appropriate particle kinetic equation is (27).
4 Electron Acceleration by Langmuir Turbulence
We now apply the weak turbulence formalism derived in the previous section to the problem of electron acceleration to suprathermal energies by Langmuir turbulence. In the numerical analysis, it is more convenient to absorb the factor μ k in the definition for the ion-sound turbulence intensity,

This is largely for mathematical convenience as doing so removes certain superficial singularity. Physically, the quantity \(I_{\mathbf{k}}^{\sigma S}/\mu_{\mathbf{k}}\) is related to the so-called semi-classical “plasmon” density, \(N_{\mathbf{k}}^{\sigma S}\propto I_{\mathbf{k}}^{\sigma S}/(\mu_{\mathbf{k}}\omega_{\mathbf{k}}^{L})\). For Langmuir waves, we simply have \(N_{\mathbf{k}}^{\sigma L}\propto I_{\mathbf{k}}^{\sigma L}/\omega_{\mathbf{k}}^{L}\)—see the discussion immediately following (24). Consequently, the redefined ion-sound turbulence intensity (30) has a specific physical basis. In plotting the numerical results, however, we shall resort to the original definition of ion-sound turbulence intensity, by multiplying the factor μ k to the redefined quantity \(I_{\mathbf{k}}^{\sigma S}\) computed from the wave equation for the ion sound mode.
Let us rewrite the entire set of weak turbulence equations in dimensionless form on the basis of the following normalization scheme:

The quantity g is an effective plasma parameter
For typical laboratory beam-plasma experiment, the density is \(\hat{n}\approx10^{9}\) per c.c., and the electron temperature can be a few tens of eV’s. In this case, the plasma parameter can be of the order of 10−4–10−3. For interplanetary space, the plasma density is typically \(\hat{n}\approx1\) per c.c., and \(T_{e}\approx\mathcal{O}(10)~\mathrm{eV}\). For such an environment, we find that \(1/(\hat{n}\lambda_{De}^{3})\approx10^{-5}\sim10^{-4}\). Further examples are that for glow discharge experiment \(1/(\hat{n}\lambda_{De}^{3})\approx3.33\times10^{-3}\), and for chromosphere \(1/(\hat{n}\lambda_{De}^{3})\approx5\times10^{-4}\). The above shows that \(1/(\hat{n}\lambda_{De}^{3})\) in the range of ∼10−4 to ∼10−3 is typical for many plasma environments in which the Langmuir turbulence process may be operative. For thermonuclear fusion experimental devices, on the other hand, \(1/(\hat{n}\lambda_{De}^{3})\) can be as low as 2×10−8. For such a high-temperature plasma, the purely collisionless theory is indeed justifiable, but as we have briefly overviewed, for other situations the effects of spontaneous thermal fluctuations may not be completely ignorable.
In terms of the above normalization, the electron particle kinetic equation is given in the following dimensionless form:

Note that the collisional drag term A i has an overall factor g on the right-hand side, showing clearly that the drag effect is related to spontaneous thermal fluctuations and that for purely collisionless plasmas this term is absent.
The dimensionless Langmuir wave equation is given by

In the above, terms that possess the factor g owe their existence to the spontaneous effects. They are spontaneous emission and scattering terms. The normalized ion-sound wave equation, given in terms of redefined intensity (30), is given by

The dimensionless expressions for wave dispersion relation and the auxiliary quantity μ q are given by
4.1 One-Dimensional Case
In what follows, we consider a simple one-dimensional (1D) situation. The 1D approximation may be justifiable if the implicit ambient magnetic field is sufficiently strong such as that both the electron and Langmuir wave dynamics is restricted along the direction of the ambient magnetic field. As noted, the ions are assumed to be quasi-stationary in time. The initial electron and stationary ion distributions are given by the following:

In (37), we have introduced additional dimensionless quantities,
namely, the ratio of average beam speed to thermal speed, and the ratios of beam-to-background temperatures and densities. Here v Tb =(2T b /m e )1/2 is the beam thermal speed. We assume that we consider 1% beam-to-background density ratio, δ=0.01, equal thermal spreads for the beam and background electrons, ρ=1, electron-to-ion temperature ratio of τ=1/7, average beam drift speed equal to four time higher than thermal speed, U 0=4, and of course, the real ion-to-electron mass ratio, M=1836. We also consider the value for the plasma parameter equal to \(g=1/\hat{n}\lambda_{De}^{3}=5\times10^{-3}\). Of course the above choice of parameters represents only a sample case and that variations of input parameters are possible. However, the purpose of the numerical examples to be displayed below is to demonstrate that a quasi-power law tail population can result in the long-time nonlinear evolution of the electron beam-Langmuir turbulence system. To serve such a purpose, it is sufficient to consider one representative example.
Shown in Fig. 1 are Langmuir and ion-sound wave intensities, I L (q) and μ q I S (q), plotted versus normalized wave number q, and normalized time T. The portion of the wave intensity corresponding to positive q space belongs to σ=+1, while q<0 space corresponds to σ=−1. We have combined both σ’s using the entire q space by making use of the symmetry property, I σL (−q)=I σL (q) and I σS (−q)=I σS (q), and omitted σ after we have plotted the results. The forward-propagating Langmuir waves, I +L (q), with the range of q centered around ∼0.3 are designated as primary Langmuir waves, while the backscattered L modes possess opposite q values, I −L (|q|). The excitation of long wavelength Langmuir modes (i.e., small q) is the so-called Langmuir condensation phenomenon, which is noticeable for long time range. The time shown in Fig. 1 correspond to the normalized time T=1×104. Note that the ion-sound waves are first excited as a result of decay instability, but as time goes by, the decay process eventually diminishes such that the ion-sound turbulence level diminishes also. The fact that Langmuir spectrum remains robust indicates that the scattering off quasi-stationary ions persists.
The time evolution of the electron distribution f e (u) versus u starting from initial time T=0 and the final computational time T=2×104, is shown in Fig. 2. For relatively early time, the familiar quasilinear plateau formation associated with the initial beam distribution can be seen. However, over long time scale a significant heating of the electrons in the suprathermal range can be seen. The primary reason for the acceleration of electrons is the formation of Langmuir condensate mode, q≪1, by nonlinear mode coupling processes. Small q allows electrons with increasingly higher speeds to participate in the wave-particle resonance, and thus, get energized.
From space observation the energetic electron distributions are often modeled by the kappa distribution (1), as discussed already. The kappa model in 1D with proper normalization constant is given by
Superposed in Fig. 2 is the kappa distribution (41) with index κ=3.5. Observe the rather good fit of the numerical solution at T=2×104 with the model kappa distribution. However, whether such a kappa value is indeed the asymptotic value or not cannot be determined on the basis of the numerical solution. As it will be shown in later discussion, the true asymptotic kappa value (for T→∞) is much lower than 3.5. To sum up the present 1D Langmuir turbulence and electron acceleration problem, we find that it is the nonlinear mode coupling which leads to the inverse cascade of Langmuir turbulence, which in turn, leads to the acceleration of electrons to suprathermal energies.
4.2 Higher-Dimensional Situation
The preceding discussion with the simplifying assumption of 1D may be applicable when the implicit ambient magnetic field is strong. However, for weak magnetic field the dynamics may be quasi-isotropic. To discuss such an effect, we have developed a numerical code to solve the set of (33)–(35) in two-dimensional (2D) wave number and velocity space. With cylindrical symmetry, our result can also be viewed as essentially a three-dimensional (3D) calculation as well.
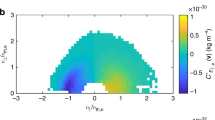
In Fig. 3 we show the time evolution of the electron distribution function by plotting f e vs u ⊥=v ⊥/v Te and u ∥=v ∥/v Te at t=0, \(t=2000 \omega_{p}^{-1}\), and \(t=5000 \omega_{p}^{-1}\). The well-known quasilinear plateau formation along parallel direction can be seen, but the result also displays perpendicular broadening of the beam distribution accompanied by the production of the backward tail, which becomes prominent at \(t=5000 \omega_{p}^{-1}\). We thus conclude that the energetic tail formation takes place in higher dimensions as well, although we have not solved the set of equations long enough to demonstrate the asymptotic stage.
Figure 4 shows the Langmuir spectrum vs q ⊥=k ⊥ v e /ω p and q ∥=k ∥ v e /ω p , at ω p t=500, 2000, and 5000. Figure 2 shows that the higher-dimensional Langmuir turbulence spectrum forms a circular ring-like structure in 2D wave number space. Of course, we have also solved the S wave spectrum but the result is not shown.
To recap the discussion in the present section, we have shown, by numerically solving the entire set of equations of weak turbulence theory, either in 1D or higher dimensions, that the Langmuir turbulence generated by the beam-plasma instability leads to the acceleration of electrons to suprathermal energies. However, these discussions are based upon numerical initial value solution. It is not evident that the formation of kappa-like state, which was clearly demonstrated in 1D and implied in 2D, does indeed correspond to the rigorous asymptotically steady-state solution or not in a mathematical sense. Also, it is not clear whether the kappa index κ=3.5, which provided a reasonable fit in 1D case, is indeed the asymptotic value or not.
To address the issue of whether the basic set of coupled electron-Langmuir turbulence equations do indeed lend themselves to an asymptotically steady-state solution or not, we next turn to the problem of self-consistent, steady-state, asymptotic solution of the electrons-Langmuir turbulence system, i.e., the problem of finding a dynamic equilibrium for suprathermal electron-Langmuir turbulence system.
5 Turbulent Quasi-Equilibrium for Suprathermal Electrons
5.1 One-Dimensional Situation
Let us consider the electron kinetic equation (27) in steady-state (∂/∂t=0). In one-dimensional limit (27) reduces to
From this it is straightforward to see that the formal solution is given by Hasegawa et al. (1985)
where C is the normalization constant. It should be noted, however, that the diffusion coefficient D contains the wave intensity, the asymptotic form of which must be determined by solving the wave kinetic equation. Consequently, despite its apparent simplicity, (41) is a rather convoluted mathematical object.
Suppose that the asymptotically steady-state solution is a kappa-like distribution,

where (42) is different from the customary kappa distribution (see, for example, Vasyliunas 1968) in that we adopt two different kappa parameters, namely, κ and κ′. Note that the kappa velocity distribution functions found in the literature are either given by f e ∼(1+m e v 2/2κT e )−κ or f e ∼(1+m e v 2/2κT e )−κ−1. In contrast, the present model (42) allows two independent kappa indices. It is well known that the effective temperature for the kappa model differs from Maxwellian temperature. The relation between the effective temperature and the Maxwellian temperature in the case of (42) is T eff=T e κ′/(κ−3/2). The question is what kind of wave spectrum I L (k) will be consistent with (42)? To answer this question, we proceed as follows: Upon taking the logarithm of (40), making use of the integral identity,
and upon approximating \(\omega_{k}^{L}\approx\omega_{pe}\), we obtain
From this, by virtue of the resonance condition, |v|=ω pe /k, we readily obtain the turbulence intensity that leads to the kappa-like steady-state particle distribution (42),
where \(v_{Te}^{2}=2T_{e}/m_{e}\) is the Maxwellian thermal speed. It is important to note that the above Langmuir turbulence intensity is the result of simply requiring that the steady-state electron distribution be given by (42). There is, however, no a priori reason why (45) should also correspond to the asymptotically steady-state solution of the nonlinear wave kinetic equation. The remaining task is, therefore, to see whether the turbulence spectrum (45) is indeed the asymptotic self-consistent solution of the wave kinetic equation as well. So, we now turn to the discussion of the waves.
Before we consider the turbulent wave kinetic equation, we must modify the dispersion relations so that the bulk electron velocity distribution is given by (42) rather than the customary Maxwellian model. Yoon (2011) obtained the modified Langmuir mode dispersion relation when the electron distribution is given by the kappa-like model (42). The result is the following:
With the generalized dispersion relation we now move on to the discussion of the wave kinetic equation.
The wave kinetic equations must also be slightly modified since the derivation of specific forms of nonlinear susceptibilities depends on the assumption that the electron distribution is given by the Maxwellian form. Yoon (2011) also provides the modified wave kinetic equation suitable for the present discussion of asymptotic steady-state equilibrium. Yoon (2011) shows that of the nonlinear terms, namely, three-wave decay and nonlinear wave-particle scattering processes, the decay terms can be ignored when compared with the scattering terms. As a result, the steady-state weak turbulence equation for Langmuir waves is given by

Taking the 1D limit, upon explicitly writing out various terms associated with different signs of σ′,σ″=±1 and discarding those terms that do not satisfy the resonance conditions we find that (47) reduces to

In (48) we have made use of linear dispersion relation (46).
Let us consider the first term on the right-hand side of (48), namely, the terms depicting the balance of spontaneous and induced emission processes. Upon making use of (42) we have

From this, we readily obtain the Langmuir turbulence spectrum,
which is none other than (45). We remind the readers that (45) was deduced purely from the requirement that the asymptotic distribution be given by (42) without considering the wave dynamics. The balance of spontaneous and induced emission terms proves that (45) is indeed correct. From this, it is clear that, at least (42) and (45) are consistent with the balance of spontaneous and induced emission processes. However, the remaining question is whether electron kappa-like distribution, (42), and the corresponding Langmuir turbulence spectrum, (45) or equivalently (50), are also consistent with the balance of nonlinear terms in the steady-state wave kinetic equation (48).
Making use of

we may rewrite the nonlinear terms in (48) as follows:

The k′ integral may be evaluated by writing k′=k+δk′ and expanding the integrand for small δk′. This is justified by the fact that the integrand contains the exponential factor with the argument proportional to −(m i /m e )(k−k′)2, which shows that unless k∼k′ the integrand becomes exceedingly small. Thus proceeding, we have

Setting the quantities within the large parenthesis equal to zero leads to an alternative expression for the asymptotically steady-state Langmuir turbulence intensity,

The above equation enjoys an exact solution,
On the other hand, we know the stationary kappa-like distribution (42) has a self-consistent turbulence spectrum given by (45), or equivalently, (50). Consequently, upon equating (45) and (55), we obtain
That is, if κ and κ′ are given by (56), then the time-asymptotic solution of the wave kinetic equation produces a consistent solution whether we balance spontaneous and induced emissions, or whether we balance spontaneous and induced scattering processes, and the resulting time-asymptotic turbulence spectrum is also consistent with the kappa-like electron velocity distribution function. Note that under the present result (56), the suprathermal electrons behave as
whereas the empirical fit shown in Fig. 2 implies f e ∝v −9.0. This shows that the numerical solution shown in Fig. 2 has not approached the true asymptotic state, and this also justifies the present analytical approach for determining the true asymptotic steady-state equilibrium.
5.2 Three-Dimensional Case
The previous discussion pertaining to the simple one-dimension may be justified when the implicit ambient magnetic field is strong. Such a situation may be envisioned, for example, near the Solar corona. However, for situations near 1 AU where the ambient magnetic field is weak, one must relax the assumption of one-dimensionality and consider fully three-dimensional case. From numerical solutions shown in Sect. 4.2, we also know that Langmuir turbulence in 2D or 3D (with cylindrical symmetry) involves quasi-three dimensional velocity distribution function for the electrons and a quasi-three dimensional Langmuir turbulence spectrum. For this reason, we now discuss the problem of three-dimensional isotropic electron distribution and three-dimensional (but not necessarily isotropic, as it will turn out) Langmuir turbulence spectrum.
Let us consider the electron kinetic equation (27) again. We may decompose the wave vector and the velocity into components perpendicular and parallel with respect to a reference axis (say, the weak ambient magnetic field), \(\mathbf{k}=k_{\perp}\hat{\mathbf{e}}_{\perp}+k_{\parallel}\hat{\mathbf{e}}_{\parallel}\) and \(\mathbf{v}=v_{\perp}\hat{\mathbf{e}}_{\perp}+v_{\parallel}\hat{\mathbf{e}}_{\parallel}\). Then, if we allow an approximate wave-particle resonance condition, ω−k⋅v≈ω−k ∥ v ∥=0, then one may show that the perpendicular component of A i and the off-diagonal elements of D ij vanish,

Let us define the reduced distribution,
Then, by integrating the particle kinetic equation (27) over perpendicular velocity, \(2\pi\int_{0}^{\infty}dv_{\perp}\,v_{\perp}\), we obtain a reduced particle kinetic equation in the steady-state,
where

Note that technically the quantity \(\mathcal{H}(k_{\parallel}^{2})\) diverges. However, if we introduce a suitable upper limit in the k ⊥ integral, say limit the integral range to 0<k ⊥<k 0, then we may formally perform the integration and obtain the result, \(\mathcal{H}(k_{\parallel}^{2})=\pi\ln(1+k_{0}^{2}/k_{\parallel}^{2})\). On the basis of the above consideration, the time-asymptotic state for the reduced distribution is given by
where C is the normalization constant.
If we suppose that 3D isotropic asymptotically steady-state solution is given by a kappa-like distribution,

then the reduced distribution is given by a similar 1D kappa-like distribution except that the power-law (or kappa) index is reduced by 1,

Note that the effective temperature for the present kappa-like model (63) is given in terms of the Maxwellian temperature by T eff=T e κ′/(κ−5/2).
Following the procedure outlined in the previous subsection, the reduced wave spectrum \(\mathcal{I}(k_{\parallel}^{2})\) that is consistent with (64) can be obtained as follows:
Note that (65) implies, by virtue of the definition (61), that
Solving the above integral equation for I L we obtain the asymptotic three-dimensional Langmuir turbulence intensity, which is consistent with the 3D isotropic electron distribution (63),
where \(\mathcal{H}(k_{\parallel}^{2})=\pi\,\ln (1+k_{0}^{2}/k_{\parallel}^{2})\), provided a suitable upper limit k 0 can be defined. For instance, k 0 can be defined by \(k_{0}\lambda_{De}\sim\mathcal{O}(1)\), where λ De =T e /(4πne 2)1/2 is the electron Debye length. It is important to note, however, the detailed definition for k 0 is immaterial to the present discussion since we are dealing with the reduced electron distribution, \(\bar{F}_{e}\), and reduced Langmuir turbulence spectrum, \(\mathcal{I}\).
In the subsequent analysis, following the previous discussion for 1D case, we now discuss whether the (reduced) turbulence spectrum (65) does indeed correspond to the asymptotic self-consistent solution of the wave kinetic equation. Following the previous discussion, we may ignore the three-wave decay processes at the outset. The resulting steady-state Langmuir turbulence wave equation is given by Yoon (2012a)

Let us consider the first term on the right-hand side of (68), namely, the terms depicting the balance of spontaneous and induced emission processes, which may be written in terms of the reduced distribution as

Upon integrating the above equation by \(2\pi\int_{0}^{\infty}dk_{\perp}\,k_{\perp}/k^{2}\), we readily obtain,

The necessary condition for the equality to be satisfied is when \(\mathcal{I}(k_{\parallel}^{2})\) is given exactly by (65). This shows again that, even for 3D case, the balance of spontaneous and induced emission processes leads to the self-consistent reduced turbulence intensity.
Let us consider the nonlinear terms in (68). Upon ignoring those terms that do not satisfy the resonance condition, namely those that involve the sum of two frequencies, \(\omega_{\mathbf{k}}^{L}+\omega_{\mathbf{k}'}^{L}\), we are left with non-vanishing nonlinear terms in (68), which are set equal to zero,

Following the discussion for 1D, we may write k′=k+δ k and expand the integrand for small δ k. Then we have

One may obtain the necessary equality upon setting the quantities within the large parenthesis to zero,
We are, however, interested only in the reduced turbulence intensity. We thus consider only the parallel component and integrate the result by \(2\pi\int_{0}^{\infty}dk_{\perp}\,k_{\perp}/k^{2}\),

which can be solved as
Of course, upon comparison with (65), we immediately obtain the necessary values of κ and κ′,
To recap the present result, we have now generalized the 1D solution to 3D case, and the result is the following:

Here \(\mathcal{H}(k_{\parallel}^{2})\) is the form factor associated with the spontaneous effects, which can be estimated as \(\mathcal{H}(k_{\parallel}^{2})=\pi\,\ln(1+k_{0}^{2}/k_{\parallel}^{2})\), with \(k_{0}\lambda_{De}\sim\mathcal{O}(1)\). According to the present result, the suprathermal electrons behave as
for v≫v Te .
Note that in a recently submitted paper (Yoon 2012b), the issue of three-dimensional turbulent equilibrium was revisited in order to formulate the problem for genuinely field-free situation. This is because, while the one-dimensional solution discussed in Sect. 5.1 and Yoon (2011) is rigorously correct, the three-dimensional solution discussed here and in Yoon (2012a), which is obtained using the cylindrical coordinate representation, is based upon the assumption that the resonance condition can be approximated by ω−k⋅v≈ω−k ∥ v ∥, which is not the most general condition. Also, while the electron distribution is isotropic in velocity, the Langmuir turbulence intensity depends on k ∥ [see (77)]. While these features may describe the situation in which an implicit ambient magnetic field is assumed to be present, they are not applicable if the plasma is genuinely unmagnetized since the field-free medium has no preferential direction. To address this issue, Yoon (2012b) reformulated the problem using a spherical coordinate system in a truly free-field plasma, and obtained isotropic electron distribution and Langmuir turbulence intensity. Although the derivation is somewhat different (which we shall not repeat here) the final solution for truly field-free plasmas is given by Yoon (2012b)

It is important to note that the asymptotic behavior f e ∝v −2κ∼v −6.5 remains unchanged. On the basis of this we believe that the turbulent equilibrium between suprathermal electrons and Langmuir waves is characterized by the power-law velocity tail with the index close to −6.5. To test this prediction, we now turn to the solar wind data.
6 Solar Wind Electrons
Wang et al. (2012) did a statistical survey of ∼2–20 keV superhalo electron observations during quiet times in the interplanetary medium in 2007-2008, from the SupraThermal Electron (STE) instrument (Lin et al. 2008) onboard the STEREO A & B spacecraft. The observed quiet-time VDFs of superhalo electrons fit well to a power-law, f∝v −b, from 2 to 20 keV, with b ranging from 5 to 8.7 with average of 6.69±0.90 (1-sigma) and about half of the points in a peak at 6.5<b<7.5. Figure 5 shows that on 9 January 2007 when WIND and two STEREO spacecrafts were close together (<140R E or ∼0.06 AU), the observed superhalo VDFs show similar power-laws, f∼v −7.3. About 10 month later when the STEREO spacecrafts were ∼42∘ ecliptic longitude (∼0.7 AU) apart, the superhalo electrons (Fig. 5, insert) show significantly different power-laws (exponents of −5.3 and −6.3) at the two spacecraft, indicating variations on that spatial scale, and possibly temporal variation on a scale of months.
Omnidirectional electron velocity distribution function (VDF) measured from ∼106 m/s (∼ 5eV) to ∼108 m/s (∼60 keV) during a quiet period in the interplanetary medium on 9 January 2007, The black line gives the Maxwellian fit to the solar wind (SW) core and Kappa fit to the SW halo, measured by the Wind spacecraft. The pink and blue lines are power-law fit to the solar wind superhalo measured by the STEREO A & B spacecraft. The three spacecraft are located within ∼140 R E (0.06 AU) of each other, near L1, ∼200 R E upstream of the Earth. The inset shows the superhalo electron spectra measured on 30 November 2007 by STEREO A & B, separated by ∼0.7 AU (20.6∘ ahead of, and 21.1∘ ecliptic longitude behind, the Earth, respectively)
Such a variation is not unexpected since the real solar wind is not in exact dynamical equilibrium. Nevertheless, judging from the fact that theoretical prediction of f e ∼v −6.5 is intermediate between observed range of power-law indices (∼v −5.0 to v −8.7 with average v −6.69), we find that the agreement is quite remarkable.
7 Conclusions and Discussion
The purpose of the present Review had been to put forth a self-contained treatise on the problem of (local) acceleration of suprathermal electrons by Langmuir turbulence. In order to achieve that purpose, we have first presented a brief overview of the history of Langmuir turbulence. The rationale was to provide the justification for the use of weak turbulence approach in view of the historical development associated with various approaches in dealing with the Langmuir turbulence problem.
For the sake of completeness, we have also presented a self-contained discussion of the weak turbulence theory. On the basis of the equations of the weak turbulence theory, we discussed numerical solution in 1D and 2D (or 3D with cylindrical symmetry). In order to facilitate the discussion, we chose the problem of bump-in-tail instability so that the free energy associated with the electron beam leads to the rapid excitation of Langmuir turbulence and subsequent saturation.
Of course in the quiet-time solar wind, no electron beam with positive gradient in velocity space is observed at 1 AU. However, the solar wind contains the energetic, highly field-aligned component called the strahl. The enhanced Langmuir fluctuation excited by these strahl’s may drive the system to time-asymptotic steady-state turbulence for the Langmuir wave spectrum. However, we have considered the beam-driven Langmuir turbulence problem in order to facilitate the discussion. It should be noted, however, that we are concerned largely with the time-asymptotic state associated with the Langmuir turbulence. We have thus demonstrated that over the long time range the electrons are seen to be accelerated to suprathermal energies as a result of wave-particle interaction with long-wavelength portion of the Langmuir turbulence spectrum.
It should be noted on the basis of numerical solutions that for quasi-asymptotic, long-time stage, both the Langmuir turbulence intensity and electron distribution function evolve into quasi-symmetric forms in wave number and velocity, respectively, owing to nonlinear mode coupling processes, such that the directionality associated with the original beam is lost. We expect a similar situation with the enhanced Langmuir fluctuation excited by strahl electrons.
In any situation, the numerical demonstrations are insufficient in that they are based upon numerical initial value solution. It is not evident that the formation of kappa-like state does indeed correspond to the rigorous asymptotically steady-state solution or not in a mathematical sense. Also, it is not clear whether the empirical kappa fit reasonably represents the true asymptotic value or not. To address the issue, we have presented the rigorous analysis of steady-state Langmuir turbulence and electron acceleration problem by solving the set of coupled electron-Langmuir turbulence equations. On the basis of such an analysis, we found that the steady-state suprathermal electron should behave as f e ∼v −6.5.
In order to verify this theoretical prediction against observation, we have taken the quiet-time solar wind electrons as a representative example of quasi-steady state particle population, and have compared the velocity power-law spectral indices predicted by both theory and observation. We found a reasonable agreement between the theory (v −6.5) and observation (∼v −5.0 to v −8.7 with average v −6.69). On the basis of this finding we believe that the local acceleration of energetic electrons by Langmuir turbulence may indeed take place in the solar wind, and that similar turbulent acceleration processes involving other types of wave modes and charged particles of different species may take place in other space environments.
References
A.I. Akhiezer, I.A. Akhiezer, R.V. Polovin, A.G. Sitenko, K.N. Stepanov, Plasma Electrodynamics (Pergamon, New York, 1975)
T.P. Armstrong, M.T. Paonessa, E.V. Bell II, S.M. Krimigis, J. Geophys. Res. 88, 8893 (1983)
R. Balescu, Phys. Fluids 3, 52 (1960)
P.Y. Cheung, M.P. Sulzer, D.F. Dubois, D.A. Russell, Phys. Plasmas 8, 802 (2001)
M.R. Collier, Geophys. Res. Lett. 20, 1531 (1993)
P. Couturier, S. Hoang, N. Meyer-Vernet, J.L. Steinberg, J. Geophys. Res. 86, 11127 (1981)
R.C. Davidson, Methods in Nonlinear Plasma Theory (Academic Press, New York, 1972)
J.M. Dawson, Rev. Mod. Phys. 55, 403 (1983)
J.M. Dawson, R. Shanny, Phys. Fluids 11, 1506 (1968)
D.F. Dubois, D.A. Russell, P.Y. Cheung, M.P. Sulzer, Phys. Plasmas 8, 791 (2001)
C.T. Dum, J. Geophys. Res. 95, 8095 (1990a)
C.T. Dum, J. Geophys. Res. 95, 8111 (1990b)
C.T. Dum, J. Geophys. Res. 95, 8123 (1990c)
T.H. Dupree, Phys. Fluids 9, 1773 (1966)
T.H. Dupree, Phys. Fluids 15, 334 (1972)
R.E. Ergun, D. Larson, R.P. Lin et al., Astrophys. J. 503, 435 (1998)
V.I. Erofeev, J. Plasma Phys. 68, 1 (2002)
W.C. Feldman, J.R. Asbridge, S.J. Bame, M.D. Montgomery, S.P. Gary, J. Geophys. Res. 80, 4181 (1975)
A.A. Galeev, R.Z. Sagdeev, Yu.S. Sigov, V.D. Shapiro, V.I. Shevchenko, Sov. J. Plasma Phys. 1, 5 (1975)
R. Gaelzer, L.F. Ziebell, A.F. Viñas, P.H. Yoon, C.-M. Ryu, Astrophys. J. 677, 676 (2008). doi:10.1086/527430
M.V. Goldman, Rev. Mod. Phys. 56, 709 (1984)
V.V. Gorev, A.S. Kingsep, V.V. Yan’kov, Sov. Phys. JETP 43, 479 (1976)
J.T. Gosling, J.R. Asbridge, S.J. Bame, W.C. Feldman, R.D. Zwickl, G. Paschmann, N. Sckopke, R.J. Hynds, J. Geophys. Res. 86, 547 (1981)
A. Hasegawa, Plasma Instabilities and Nonlinear Effects (Springer, New York, 1975)
A. Hasegawa, K. Mima, M. Duong-van, Phys. Rev. Lett. 54, 2608 (1985)
B.B. Kadomtsev, Plasma Turbulence (Academic Press, New York, 1965)
S.A. Kaplan, V.N. Tsytovich, Plasma Astrophysics (Pergamon, Oxford, 1973)
A.S. Kingsep, Sov. Phys. JETP 47, 51 (1978)
A. Lénard, Ann. Phys. 10, 390 (1960)
M.P. Leubner, Planet. Space Sci. 48, 133 (2000)
M.P. Leubner, Astrophys. Space Sci. 282, 573 (2002)
M.P. Leubner, Phys. Plasmas 11, 1308 (2004a)
M.P. Leubner, Astrophys. J. 604, 469 (2004b)
M.P. Leubner, Nonlinear Process. Geophys. 12, 171 (2005)
R.P. Lin, Space Sci. Rev. 86, 61 (1998)
R.P. Lin, D.W. Potter, D.A. Gurnett, F.L. Scarf, Astrophys. J. 251, 364 (1981)
R.P. Lin, W.K. Levedahl, W. Lotko, D.A. Gurnett, F.L. Scarf, Astrophys. J. 308, 954 (1986)
R.P. Lin, D.W. Curtis, D.E. Larson, J.G. Luhmann, S.E. McBride, M.R. Maier, T. Moreau, C.S. Tindall, P. Turin, L. Wang, Space Sci. Rev. 136, 241–255 (2008)
G. Livadiotis, D.J. McComas, J. Geophys. Res. 114, A11105 (2009). doi:10.1029/2009JA014352 and references therein
C. Ma, D. Summers, Geophys. Res. Lett. 25, 4099 (1998)
M. Maksimovic, S. Hoang, N. Meyer-Vernet, M. Moncuquet, J.-L. Bougeret, J.L. Phillips, P. Canu, J. Geophys. Res. 100, 19881 (1995)
D.B. Melrose, Plasma Astrophysics (Gordon & Breach, New York, 1980)
N. Meyer-Vernet, P. Couturier, S. Hoang, J.L. Steinberg, R.D. Zwickl, J. Geophys. Res. 91, 3294 (1986)
R.L. Morse, C.W. Nielson, Phys. Fluids 12, 2418 (1969)
Y. Omura, H. Matsumoto, T. Miyake, H. Kojima, J. Geophys. Res. 101, 2685 (1996)
K. Papadopoulos, Phys. Fluids 18, 1769 (1975)
J. Pavan, L.F. Ziebell, P.H. Yoon, R. Gaelzer, Plasma Phys. Control. Fusion 51, 095011 (2009a). doi:10.1088/0741-3335/51/9/095011
J. Pavan, L.F. Ziebell, R. Gaelzer, P.H. Yoon, J. Geophys. Res. 114, A01106 (2009b). doi:10.1029/2008JA013557
J. Pavan, L.F. Ziebell, P.H. Yoon, R. Gaelzer, J. Geophys. Res. 115, A02310 (2010a). doi:10.1029/2009JA014448
J. Pavan, L.F. Ziebell, P.H. Yoon, R. Gaelzer, J. Geophys. Res. 115, A01103 (2010b). doi:10.1029/2009JA014447
G. Pelletier, Phys. Rev. Lett. 49, 782 (1982)
V. Pierrard, M. Maksimovic, J. Lemaire, J. Geophys. Res. 104, 17021 (1999)
T. Rhee, C.-M. Ryu, P.H. Yoon, J. Geophys. Res. 111, A09107 (2006)
T. Rhee, C.-M. Ryu, M. Woo, H.H. Kaang, S. Yi, P.H. Yoon, Astrophys. J. 694, 618 (2009). doi:10.1088/0004-637X/694/1/618
C.-M. Ryu, T. Rhe, T. Umeda, P.H. Yoon, Y. Omura, Phys. Plasmas 14, 100701 (2007). doi:10.1063/1.2779282
D.A. Roberts, J.A. Miller, Geophys. Res. Lett. 25, 607 (1998)
P.A. Robinson, Rev. Mod. Phys. 68, 507 (1997)
P.A. Robinson, D.L. Newman, Phys. Fluids B 2, 2999 (1990)
R.Z. Sagdeev, A.A. Galeev, Nonlinear Plasma Theory (Benjamin, New York, 1969)
J.D. Scudder, S. Olbert, J. Geophys. Res. 84, 2755 (1979)
A.G. Sitenko, Electromagnetic Fluctuations in Plasmas (Academic, New York, 1967)
A.G. Sitenko, Fluctuations and Nonlinear Wave Interactions in Plasmas (Pergamon, New York, 1982)
R.A. Treumann, Phys. Scr. 59, 19 (1999a)
R.A. Treumann, Phys. Scr. 59, 204 (1999b)
R.A. Treumann, C.H. Jaroschek, Phys. Rev. Lett. 100, 155005 (2008). doi:10.1103/PhysRevLett.100.155005
C. Tsallis, J. Stat. Phys. 52, 479 (1988)
C. Tsallis, Introduction to Nonextensive Statistical Mechanics (Springer, New York, 2009)
V.N. Tsytovich, Nonlinear Effects in a Plasma (Plenum, New York, 1970)
V.N. Tsytovich, An Introduction to the Theory of Plasma Turbulence (Pergamon, New York, 1977a)
V.N. Tsytovich, Theory of Plasma Turbulence (Consultants Bureau, New York, 1977b)
V.M. Vasyliunas, J. Geophys. Res. 73, 2839 (1968)
A.A. Vedenov, Theory of Turbulent Plasma (Elsevier, New York, 1968)
L.N. Vyacheslavov, V.S. Burmasov, I.V. Kandaurov, É.P. Kruglyakov, O.I. Meshkov, A.L. Sanin, JETP Lett. 75, 41 (2002)
L. Wang, R.P. Lin, C.S. Salem, M.P. Pulupa, Quiet-time interplanetary ∼2–20 keV superhalo electrons at solar minimum (2012, in preparation)
J. Weinstock, Phys. Fluids 12, 1045 (1969)
S. Yi, T. Rhee, C.-M. Ryu, P.H. Yoon, Phys. Plasmas 17, 122318 (2010). doi:10.1063/1.3529359
P.H. Yoon, Phys. Plasmas 7, 4858 (2000)
P.H. Yoon, Phys. Plasmas 12, 042306 (2005). doi:10.1063/1.1864073
P.H. Yoon, T. Rhee, C.-M. Ryu, Phys. Rev. Lett. 95, 215003 (2005)
P.H. Yoon, Phys. Plasmas 18, 122303 (2011). doi:10.1063/1.3662105
P.H. Yoon, Phys. Plasmas 19, 012304 (2012a). doi:10.1063/1.3676159
P.H. Yoon, Three-dimensional turbulent equilibrium for field-free plasmas, Phys. Plasmas (2012b, submitted)
P.H. Yoon, T. Rhee, C.-M. Ryu, J. Geophys. Res. 111, A09106 (2006)
V.E. Zakharov, Sov. Phys. JETP 35, 908 (1972)
L.F. Ziebell, R. Gaelzer, P.H. Yoon, Phys. Plasmas 15, 032303 (2008a). doi:10.1063/1.2844740
L.F. Ziebell, R. Gaelzer, J. Pavan, P.H. Yoon, Plasma Phys. Control. Fusion 50, 085011 (2008b). doi:10.1088/0741-3335/50/8/085011
L.F. Ziebell, P.H. Yoon, J. Pavan, R. Gaelzer, J. Geophys. Res. 116, A03320 (2011a). doi:10.1029/2010JA016147
L.F. Ziebell, P.H. Yoon, J. Pavan, R. Gaelzer, Plasma Phys. Control. Fusion 53, 085004 (2011b). doi:10.1088/0741-3335/53/8/085004
L.F. Ziebell, P.H. Yoon, J. Pavan, R. Gaelzer, Astrophys. J. 727, 16 (2011c). doi:10.1088/0004-637X/727/1/16
Acknowledgements
P. H. Y. acknowledges support from NSF grants ATM0837878 and AGS0940985, and NASA grant NNX09AJ81G to the University of Maryland. P.H.Y. and R.P.L. acknowledge WCU grant No. R31-10016 from the Korean Ministry of Education, Science and Technology to the Kyung Hee University, Korea. L.F.Z. and R.G. acknowledge support from Brazilian agencies CNPq and FAPERGS.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yoon, P.H., Ziebell, L.F., Gaelzer, R. et al. Langmuir Turbulence and Suprathermal Electrons. Space Sci Rev 173, 459–489 (2012). https://doi.org/10.1007/s11214-012-9867-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-012-9867-3