1 Introduction

Solar activity is involved in studies of different scientific fields such as solar physics, climate change, and space-mission planning (Haigh, 2007; Hanslmeier, 2007; Usoskin, 2023). Solar activity can potentially affect our society, which is becoming increasingly dependent on technological systems. Some of the problems that can be traced to solar activity are, for example, disruptions of navigation systems, communications, and electric-power distribution grids on the ground. Thus space-weather effects can lead to different social and economic losses (Pulkkinen, 2007). For that reason, the interest in solar-activity behavior and its prediction has been increasing in recent times, not only in the scientific field, but also in society (Overbye, 2021).

Petrovay (2020) classified different types of solar-activity prediction methods. On the one hand, there are methods based on precursors, that is methods that use the statistical relationship between an observed variable and the next maximum of the solar cycle. Obviously, the variable must be available prior to the maximum solar activity. The statistical relationship between the two variables may have an explanation based on our understanding of solar physics, or it may have been found purely statistically. On the other hand, there are prediction methods based on physical models, such as the well-known surface flux-transport models. In addition, we have methods that use extrapolations (see Section 4 of the review by Petrovay, 2020).

Logically, solar physicists prefer to use prediction models created from physical laws. However, the complexity of these models means that other methods continue to be used, even purely statistical ones (which do not contain a physical basis, or, at least, it is not known). However, we must point out the interesting result proposed by Nandy (2021): predictions based on various techniques present a wide variety of results, yet predictions based on physical models are converging for Solar Cycle 25. Therefore it is now more interesting than ever to make predictions with various techniques, including purely statistical, so that intercomparisons can be carried out.

In addition, the prediction of the current Solar Cycle 25 is especially interesting. Whereas different methods used to predict Solar Cycle 25 generally predict an amplitude cycle below the average (Nandy, 2021; Jiang, Zhang, and Petrovay, 2023), some forecasts have predicted an above-average amplitude (Han and Yin, 2019; McIntosh et al., 2020). Note that the forecast made by McIntosh et al. (2020) was recently revised by McIntosh, Leamon, and Egeland (2023) to be a solar cycle with maximum amplitude around the average. In any case, the data observed so far are showing Solar Cycle 25 as a below-average cycle (Carrasco and Vaquero, 2021, 2022).

The objective of this work is to provide a prediction of the maximum amplitude of Solar Cycle 25 from a method that uses the inflection point of the ascending part of the solar cycle, which was first proposed by Lantos (2000). Note that the prediction of Solar Cycle 25 using this method could not be made so far, since the inflection point had not yet occurred during this cycle. In Section 2, we describe the data and methodology employed in this work. The prediction for Solar Cycle 25 obtained from this method is shown and compared with those of other works in Section 3. The main conclusions of this work are discussed in Section 4, including some additional comments and suggestions about this method.

2 Inflection-Point Method and the New Sunspot Number

The inflection-point method (Lantos, 2000) is based on finding a linear relationship between the maximum amplitude of each solar cycle and the slope at the inflection point that occurs in the rising curve to the maximum. The 13-month smoothed sunspot-number series (which uses weights of 0.5 for the first and last value of the running averages) is used as dataset. The inflection point is defined as the point of the ascending part of the solar cycle where the slope is maximum. Note that, following the methodology by Lantos (2000), the slopes are calculated from the 13-month smoothed sunspot-number series. Then, the series of slopes is smoothed through 3-month running averages. The values of those smoothed slopes are the ones referred to, shown, and used for analysis in this work. As an example, for a standard solar cycle, the slope is zero at the solar minimum. Subsequently, the sunspot number and the slope start growing whereas the curve remains concave upward. After a few months, the slope reaches its maximum value (this is the inflection point), and the curve becomes concave downward until it reaches its maximum value of sunspot number (where the slope is zero).

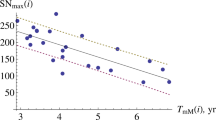
We followed the methodology of Lantos (2000) and reproduced his results using the Solar Influences Data Analysis Center (SILSO) Sunspot Number (version 1). However, version 2 of the Sunspot Number was released in 2015 (Clette et al., 2014; Clette and Lefèvre, 2016), so we have implemented the Lantos (2000) methodology to this latest version and expanded the temporal coverage to the two latest complete solar cycles (Figure 1). Data of the sunspot number are available at the website of the Sunspot Index and Long-term Solar Observations (www.sidc.be/silso).

Figure 1
figure 1

Relationship between the sunspot number of the solar-cycle maximum and the inflection-point slope for Solar Cycles 9 – 22 (red dots) and 9 – 24 (red dots plus blue diamonds). The red continuous and blue dashed lines represent the best linear fits regarding Solar Cycles 9 – 22 and 9 – 24, respectively.

Full size image

Considering Solar Cycles 9 – 22, we obtain the following relationship between the maximum value of the 13-month smoothed sunspot number for a solar cycle [SNmax] and the inflection point slope [IPS] of the ascending part of that solar cycle in units of sunspot number per month: SNmax = (14.0 ± 2.8) IPS + (59.4 ± 27.0), \(r = 0.82\), \(p\)-value < 0.001. The estimated standard error for the linear regression is 30.0. If we expand the temporal coverage to include the latest complete cycles (i.e. we consider Solar Cycles 9 – 24), we obtain a new relationship: SNmax = (13.9 ± 2.9) IPS + (58.2 ± 27.1), \(r = 0.79\), \(p\)-value < 0.001 with an estimated standard error equal to 31.9.

Note that the addition of Solar Cycles 23 and 24 reduces the quality of the linear least-squares fit a bit. This is a typical situation for statistical methods and shows how difficult it is to improve them. However, the mentioned addition is far from changing the correlation fit by more than one standard error. All the relevant parameters used in the present study, which we have computed from the 13-month smoothed sunspot-number series, are listed in Table 1.

Table 1 Parameters used in the present study (computed from version 2 of the 13-month smoothed sunspot-number series). Column 1: solar-cycle number. Column 2: date of the solar-cycle minimum [month/year]. Column 3: sunspot number of the solar-cycle minimum. Column 4: date of the solar-cycle maximum [month/year]. Column 5: months between the solar-cycle minimum and the solar-cycle maximum. Column 6: sunspot number of the solar-cycle maximum. Column 7: date of the inflection point [month/year]. Column 8: months between the solar-cycle minimum and the inflection point. Column 9: sunspot number of the inflection point. Column 10: slope of the inflection point in units of sunspot number per month.
Full size table

3 Prediction of the Solar Cycle 25 Amplitude and Discussion

Using the equation of the best linear fit between SNmax and IPS obtained in the previous section (considering Solar Cycles 9 – 24), the prediction for Solar Cycle 25 is 131 ± 32. This is a typical value for a below-average solar cycle (taking into account that the average of existing solar-cycle amplitudes is SNmax = 180).

We compare the prediction obtained in this work with others for Solar Cycle 25 (Figure 2). The forecast obtained in this work is similar to the predicted value by Upton and Hathaway (2023) of 134 ± 8, who revised the maximum amplitude made by the Solar Cycle 25 Prediction Panel of 115 ± 10 (Biesecker and Upton, 2019). Moreover, the inflection-point method provides a maximum amplitude for Solar Cycle 25 (131 ± 32) close to the average of the predictions analyzed by Nandy (2021), which is 136 ± 42.

Figure 2
figure 2

Representation of the observed 13-month smoothed sunspot number (red line) and the inflection point for Solar Cycle 25 (black dot and vertical line). The prediction of the monthly sunspot number for Solar Cycle 25 (including its upper and lower limits) provided by Upton and Hathaway (2023) [updated May 2023] is depicted in blue (source: solarcyclescience.com/). The prediction made in this work with their error bars is represented by the green dot. Note that to compare results, we considered the same date of the maximum as that by Upton and Hathaway (2023). Vertical dashed lines depict the date of the solar minimum and maximum.

Full size image

The prediction obtained in the present work using the inflection point is generally consistent with predictions made by model-based methods (Bhowmik and Nandy, 2018; Jiang, Zhang, and Petrovay, 2023). However, the forecast of Solar Cycle 25 made by Labonville, Charbonneau, and Lemerle (2019) based also on a model method predicts a significantly below-average cycle. Predictions made using neural networks and machine-learning techniques are generally similar to our result (Okoh et al., 2018). However, that is not the case for Covas, Peixinho, and Fernandes (2019), who predicted a significantly below-average cycle. Regarding predictions made by authors using precursor methods, we find that the predictions of Solar Cycle 25 range between values significantly below the average solar cycle (Hawkes and Berger, 2018), below the average solar cycle (Petrovay et al., 2018; Pesnell and Schatten, 2018), and around the average cycle (McIntosh, Leamon, and Egeland, 2023). Lastly, there is a wide range of predictions using statistical methods. For example, we found similar prediction to our result (Kakad, Kumar, and Kakad, 2020), but there are forecasts significantly different, such as those by Singh and Bhargawa (2017) and Han and Yin (2019), whose predictions are 103 and 229 for Solar Cycle 25. A comparison of the above predictions for Solar Cycle 25 using different methods is listed in Table 2.

Table 2 Some predictions of the maximum amplitude of Solar Cycle 25 by different authors based on different types of prediction methods.
Full size table

4 Conclusions

In this work, we have updated the method for predicting the maximum amplitude of a solar cycle using the slope of the inflection point during the rising phase of the solar cycle. The update includes the use of the current version 2 of the Sunspot Number and the addition of two more solar cycles. The value obtained for the maximum amplitude of Solar Cycle 25 in terms of the 13-month smoothed sunspot number is 131 ± 32, which corresponds to a below-average cycle. Although this result is significantly different from some predictions (such as Han and Yin, 2019; McIntosh et al., 2020; McIntosh, Leamon, and Egeland, 2023), it agrees with most of the predictions analyzed by Nandy (2021), including the methods based on, for example, physics-based models, precursors, and other statistical methods.

This inflection-point method is based on an empirical linear relationship between the value of the sunspot number at the peak of the cycle and the slope at the inflection point in the rising phase. As with most methods based on empirical relationships, the physical basis of this relationship is unknown, except that it coincides with Waldmeier’s phenomenological rules (Waldmeier, 1935). From our point of view, the prediction of solar activity should be made from models based on known physical laws. However, predictions based on statistics and precursors are interesting since we can compare their results and try to unravel the physical bases that support these phenomenological relationships. In addition, the use of more complex statistical tools, such as Bayesian statistics, could help to improve and correctly interpret this type of predictions, as Arregui (2022) showed.