Abstract
We present a combined study of a coronal mass ejection (CME), revealed in a unique orbital configuration that permits the analysis of remote-sensing observations on 27 June 2007 from the twin Solar Terrestrial Relations Observatory (STEREO)-A and -B spacecraft and of its subsequent in situ counterpart outside the ecliptic plane, the interplanetary coronal mass ejection (ICME) observed on 04 July 2007 by Ulysses at 1.5 AU and heliographic-Earth-ecliptic coordinates system (HEE) 33° latitude and 49° longitude. We apply a triangulation method to the STEREO Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI) COR2 coronagraph images of the CME, and a self-similar expansion fitting method to STEREO/SECCHI Heliospheric Imager (HI)-B. At Ulysses we observe: a preceding forward shock, followed by a sheath region, a magnetic cloud, a rear forward shock, followed by a compression region due to a succeeding high-speed stream (HSS) interacting with the ICME. From a minimum variance analysis (MVA) and a length-scale analysis we infer that the magnetic cloud at Ulysses, with a duration of 24 h, has a west-north-east configuration, length scale of ≈0.2 AU, and mean expansion speed of 14.2 km s−1. The relatively small size of this ICME is likely to be a result of its interaction with the succeeding HSS. This ICME differs from the previously known over-expanding types observed by Ulysses, in that it straddles a region between the slow and fast solar wind that in itself drives the rear shock. We describe the agreements and limitations of these observations in comparison with 3D magneto-hydrodynamic (MHD) heliospheric simulations of the ICME in the context of a complex solar-wind environment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coronal mass ejections (CMEs) are large, dynamically evolving structures of plasma and magnetic field, propagating outwards from the Sun into interplanetary space. They are observed using remote-sensing instruments including coronagraphs and heliospheric imagers. When observed in situ, in the solar wind, they are referred to as interplanetary coronal mass ejections (ICMEs), (e.g. Rouillard, 2011; Bothmer and Mrotzek, 2017; Weiss et al., 2021). (I)CMEs are key drivers of space weather throughout the heliosphere, expanding as they travel large distances through the interplanetary medium, and are known to cause a global response of the heliosphere (von Steiger and Richardson, 2006). Observational studies of (I)CMEs are therefore key to understanding their evolution and for developing existing models and theory.
Coronagraphs allow the measurement of some of the large-scale properties of CMEs in the corona, in particular by tracking part(s) of the CME through a set of images and creating a height–time diagram from which their velocity and acceleration can be derived. However, when using single spacecraft data, these observations are in the plane-of-sky and have unresolved projection effects (Lugaz, Manchester, and Gombosi, 2005; Howard and Tappin, 2009). In situ observations provide complementary measurements of the ICME magnetic-field, bulk plasma and particle signatures. The first confirmed association between solar-wind disturbances, specifically that of interplanetary shocks, and ICMEs was established by Gosling et al. (1975). ICMEs can be identified as magnetic clouds by distinct in situ magnetic-field signatures (e.g. Burlaga et al., 1981; Bothmer and Schwenn, 1998; Kilpua, Koskinen, and Pulkkinen, 2017), which may be approximated as cylindrically symmetric force-free flux ropes (e.g. Goldstein, 1983; Marubashi, 1986; Démoulin, Janvier, and Dasso, 2016). Single spacecraft in situ observations are limited by the single track through the ICME as it passes over the spacecraft, resulting in incomplete knowledge of the global structure and composition of an ICME (Russell and Mulligan, 2002; Howard, 2011; DiBraccio et al., 2015).
Multi-spacecraft investigations not only provide additional data but also multiple observer points that permit more accurate estimation of CME properties and give an idea of the structure of ICMEs along different tracks, permitting the development of a more accurate implied 3D structure (e.g. Foullon et al., 2007; Möstl et al., 2009; Palmerio et al., 2019). Multi-spacecraft studies are therefore essential to developing more in-depth understanding of (I)CME (sub)structures (e.g. Cabello et al., 2016; Cremades, 2018), and to disentangling (I)CMEs from the surrounding complex solar-wind environments (e.g. Rouillard et al., 2009; Winslow et al., 2021), that include interactions with the heliospheric current sheet (HCS) or a high-speed stream (HSS).
Outside of the ecliptic plane, observations of overexpanding ICMEs (Gosling et al., 1994a,b) raised important questions about the characteristics and modelling of CMEs embedded in different solar-wind speeds (e.g. Forsyth et al., 1996; Schmidt and Cargill, 2001). Further studies, at mid-latitudes, supported the notion that CMEs receive the same minimum acceleration outwards as the ambient solar wind (Gosling et al., 1994b).
A survey of events observed during the one year overlap between the twin Solar Terrestrial Relations Observatory (STEREO; Kaiser et al., 2008) and Ulysses (Wenzel et al., 1992) missions revealed only one event where the CME was observed in both STEREO Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI; Howard and et al., 2008) coronagraphs and the associated ICME detected in situ by Ulysses. The CME was observed on 27 June 2007 by the twin STEREO/SECCHI/COR2 coronagraphs (Howard and et al., 2008), which have a field of view (FOV) of 2 – 15 \(\textrm{R}_{\odot}\), and by the STEREO/SECCHI Heliospheric Imager (HI; Eyles et al., 2009)) on board STEREO-B, which comprises two cameras, HI1 and HI2, with respective elongation ranges of 4 – 24∘ and 18 – 88∘ in the ecliptic plane and allows CMEs to be tracked further through interplanetary space. The subsequent ICME was observed in situ on 4 July 2007 by Ulysses. We use data sets from the Vector Helium Magnetometer (VHM) (Balogh and et al., 1992) and the plasma Solar Wind Observations Over the Poles of the Sun (SWOOPS) experiment (Bame et al., 1992).
The STEREO and Ulysses orbital positions at the times they observed the (I)CME are given in the heliographic-Earth-ecliptic coordinate system (HEE) in Table 1. Their positions as seen from (panel a) above the north pole and (panel b) from 90∘ [HEE] to the east of the Sun–Earth line at this time are depicted in Figure 1. At this time, the two STEREO spacecraft have a separation angle of 15∘.
Spacecraft positions at the time of the (I)CME observations: STEREO-A (purple), -B (dark blue) on 27 Jun 2007, and Ulysses (light blue) on 04 July 2007, the Sun (yellow, panels a and b), Earth (green, panels a and b), and the Sun–Earth line (green, panel b) are plotted for reference in (a) as viewed from above the solar north, (b) as viewed from 90∘ longitude to the east of the Sun–Earth line.
This rare dataset allows for multi-spacecraft analysis through the application of a triangulation method to STEREO/SECCHI/COR2-A and -B images, and a self-similar expansion fitting (SSEF) method to heliospheric images from STEREO/SECCHI/HI-B (Section 2) before presenting the in situ measurements from Ulysses (Section 3). We perform a minimum variance analysis (MVA), and a length-scale analysis to develop a clearer understanding of how the ICME evolves. We present a discussion of its geometry and topology before a comparison of our observational analysis against results from the Enlil 3D magneto-hydrodynamic model of the ICME in the heliosphere (Section 4). We conclude with a brief summary of our findings (Section 5).
2 Remote-Sensing Observations
2.1 STEREO/SECCHI/COR2
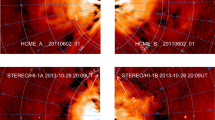
Figure 2 shows the STEREO/SECCHI/COR2 images on 27 June 2007 (at 19:07 and 19:08 UT, -A and -B, respectively). The CME was observed by COR2-A in the south-west quadrant at around 10:46 UT. The CME was then observed by COR2-B, also in the south-west, but somewhat later, at around 14:01 UT the same day, due to an instrumental feature obscuring the CME earlier on (likely a result of increased occulter misalignment after launch, resulting in increased stray-light levels and affecting vignetting around the occulter pylon, which was more severe for COR2-B and prevented the detection of faint coronal structures around the southern rim of the occulter up to ≈4.1 \(\textrm{R}_{\odot }\); see Howard and et al., 2008 and Frazin et al., 2012). The CME was faintly visible in STEREO/SECCHI/COR1-A and -B on the south-west limb at around 09:40 UT the same day.
The CME appeared in the COR2 field of view (FOV) in (top) background subtracted and (bottom) difference images; it propagated from ≈ 4.2 to 14.5 \(\textrm{R}_{\odot}\) above the solar surface in the plane of the sky. The CME main axis was located southward of the ecliptic plane, and its structure can be interpreted as a magnetic flux rope, based on the 3D scheme of configuration proposed by Cremades and Bothmer (2004).
The COR2 data points are obtained by tracking the CME front in time–elongation maps, or j-maps, constructed at a fixed position angle (PA) of 240∘ (e.g. Sheeley et al., 1999), Figure 3. The time–height profiles of the CME estimated in the plane-of-sky are plotted as symbols in Figure 4a. Second-order polynomial fits on each dataset are interpolated to a regular time array and the 3D propagation direction of the CME is determined by applying a triangulation method (Mierla et al., 2008). This provides a more accurate estimation than plane-of-sky measurements, (e.g. Foullon et al., 2011b). To ensure we are accurately tracking the CME apex, we only include points with an elongation of more than 1.5∘. This method makes two assumptions: (1) the distance of the spacecraft from the ecliptic is neglected, (2) and affine geometry is used instead of projective geometry.
Propagation direction analysis of the CME with: (a) plane-of-sky height–time profiles (symbols) from STEREO/SECCHI/COR2-A and -B and after triangulation (thick line), (b) velocity–height profile after triangulation, (c) longitude [HEE] of the triangulated feature (thick line), (d) latitude [HEE] of the triangulated feature.
Panel a of Figure 4 also shows the triangulated height–time profile of the CME (solid thick line), which gives a mean radial speed of 187 km s−1 and acceleration of 5.4 km s−2. The inferred velocity–height profile in panel b shows more clearly that the CME is accelerating, with speeds starting at 83.8 km s−1 at a height of 7.4 \(R_{\odot}\) and reaching 290 km s−1 at a height of 17.6 \(R_{ \odot}\) above the solar surface. For comparison, Table 2 lists the projected (plane-of-sky) speeds and the 3D triangulated speeds following the second-order polynomial fits.
Time series of the longitude and latitude (HEE coordinates) of the triangulated CME are plotted as the solid thick lines in panels c and d of Figure 4, respectively. The longitudinal position, panel c, changes initially almost linearly with radial distance, until it reaches a near-constant longitude from about 20:00 UT; the CME starts at 42.7∘ and moves to 63.7∘ in longitude, giving an average rate of deflection of 2.1∘ per \(R_{\odot}\) (21.0∘ over 10.2 \(R_{\odot}\)). In the latitudinal direction, in panel d, there is a small deflection away from the equator, again initially almost linear with radial distance and then reaching a near-constant latitude from about 20:00 UT; starting at −21.6∘ and ending at −28.6∘ in latitude with a rate of deflection of approximately −0.7∘ per \(R_{\odot}\) (−7.0∘ over 10.2 \(R_{\odot}\)). Deflections are common in the corona; CMEs are known to deflect towards the equator at solar minimum (Cremades and Bothmer, 2004). CME interactions with other magnetic structures may also change the CME trajectories (e.g. Gopalswamy et al., 2009; Liewer et al., 2015) as CMEs tend to move away from open fields to escape the corona through weak fields near the HCS (Kay, Opher, and Evans, 2015; Sieyra et al., 2020).
The assumptions made in order to apply this method result in: (1) a small error in latitude and longitude of the order of the rotation angles, that is increased for a small angle of separation between spacecraft; (2) a distance error that increases farther from the Sun (Mierla et al., 2008). These relative errors (shown as error bars on Figure 4) are calculated using: (1) \(atan\,2(z_{scA}-z_{scB})/d_{AB}\) and \(atan\,(z_{scA}+z_{scB})/2d_{sc})\), for the latitudinal (±0.66 ∘) and longitudinal (±0.16 ∘) errors respectively, where \(z_{scA}\) \(z_{scB}\) are the spacecraft distances off the ecliptic, \(d_{AB}\) is their mutual distance and \(d_{sc}\) is their distance from the Sun centre; (2) \((d_{obj} - d_{sc})/d_{sc}\), where \(d_{obj}\) is the true distance of the CME from the spacecraft, which gives an approximate height error of ± 1.8 – 1.9 \(R_{\odot}\) (Mierla et al., 2008).
Notwithstanding this, these errors are much smaller than the overall deflections obtained and a comparison of the triangulation results with the Ulysses observations confirms the association of events and therefore the main trajectory of the (I)CME. The CME had a mean calculated latitude of −27.0∘ and longitude of 61.8∘ and was last observed with a latitude of −28.6∘ and longitude of 58.6∘.
2.2 STEREO/SECCHI/HI
The CME is clearly visible in HI images from STEREO-B (Figure 5) and may be tracked to an elongation of approximately 40∘ into the HI-2 FOV. However, due to its westward propagation direction in COR2 images, as seen in Figure 2, the CME does not enter the FOV of HI on STEREO-A. Thus, the triangulation method could not be applied to the STEREO heliospheric images.
STEREO/SECCHI/HI-1B images of the CME taken at 12:50 UT on 28 June 2007. The image in panel a is the level 2 (background-subtracted) HI data provided by the UK Solar System Data Centre (UKSSDC). These data have had additional smoothing applied to them in order to remove some of the background star field. The image in panel b is produced using a running difference between consecutive level 2 images, which serves to highlight moving structures. The PA at 245∘ is over-plotted in both images, representing the PA at which the CME is tracked, as can be seen in Figure 6.
However, observations from a single spacecraft allow the speed of the CME and the 3D propagation direction to be estimated using the self-similar expansion fitting (SSEF) method of Davies et al. (2012). The SSEF method works by assuming that the CME front possesses a circular cross-section that expands with a constant half-width, \(\lambda\), which can be set from 0∘ to 90∘ (see Davies et al., 2012; Barnes et al., 2020). These extreme values equate to the Fixed Phi Fitting (FPF: Kahler and Webb, 2007; Rouillard et al., 2008; Sheeley et al., 2008) and Harmonic Mean Fitting (HMF: Lugaz, Vourlidas, and Roussev, 2009; Lugaz, 2010), respectively. In order to fit the CME geometry to HI observations, the technique assumes that it travels in a constant direction and at a constant radial speed, both of which are reasonable assumptions for the majority of CMEs in the HI FOV. Tracking the CME front is achieved by constructing a time–elongation map, or j-map, from HI data at a fixed PA (Davies et al., 2009), the results of which can be seen in Figure 6. The J-maps in Figure 6 were constructed at a PA of 245∘, which is taken from the HELCATS HIGeoCAT catalogue (Barnes et al., 2019) where the PA is chosen to be as close to the CME apex as is practicable and close to the PA of 240∘ used to track the CME apex in COR2 data. HIGeoCAT is compiled by applying the SSEF to HI data with \(\lambda = 0\), 30, and 90∘.
(a) Time–elongation map constructed using STEREO/SECCHI/HI-1 and HI-2 data at a PA of 245∘ from STEREO-B from 27 June to 01 July 2007. The COR2B data are also included in both panels for reference, however, the CME fronts are only tracked using HI. (b) The same time–elongation map with the manually identified time–elongation data over-plotted in red.
The observed leading edge, close to the apex, is used to constrain the solution to the SSEF model fit along a track at 245∘ PA, and from this the CME speed, direction, and launch time may be derived. The SSEF technique is applied to the track along the PA, using a half-width of 90∘, which equates to the HMF technique. The SSEF has been found to work better with a wider half-width (Barnes et al., 2020), although for this CME geometry, the assumed half-width has little impact on the resulting speeds and direction of propagation. The technique results in a propagation direction of −28.8∘ latitude, 55.1∘ longitude (HEE coordinates) for the tracked front at 245∘ PA, which is close to the CME apex.
There is a difference of 0.2∘ and 8.6∘ in latitude and longitude, respectively, between this and the inferred 3D direction of propagation of the CME apex obtained via triangulation using the STEREO COR2 images (at −28.6∘, 63.7∘, see Section 2.1). The SSEF results give a (single) predicted speed of 328 km s−1, derived from observations, at distances (from the Sun centre) of ≈ 0.09 AU to 0.71 AU, in comparison to the calculated speed from the triangulation of 290 km s−1 at a height of 17.7 \(R_{\odot}\) (0.07 AU, Table 2).
The latitudes are consistent and give confidence in both techniques. The larger difference (8.6∘) in the calculated longitudes is reasonable and may have various causes: it could be due to the CME deflection (slow CMEs are more likely to be deflected, e.g. Wang et al., 2004; Lugaz et al., 2010), it could also arise from variations in the CME front location (e.g. as a result of feature tracking, Braga and Vourlidas, 2021), or from the small (5∘) difference in the fixed PAs used in each technique and inherent differences in instrumentation.
The coordinates of the CME apex direction of propagation from the SSEF analysis match closely to the position of Ulysses (−32.5∘, 48.6∘), when the magnetic cloud associated to CME was first observed in situ at 13:00 UT on 04 July. Assuming the CME was heading towards Ulysses at the constant speed of 328 km s−1, we estimate the impact time of the CME front at Ulysses as 12:13UT on 05 July 2007.
3 In Situ Observations: Ulysses
The ICME is sampled in the form of a magnetic cloud at Ulysses at 13:00 UT on 04 July, shown in Figure 7. We observe a preceding forward shock (FS1), the leading edge of the magnetic cloud (MC). A high-speed stream (HSS) then runs into the back of the ICME, creating an interaction region where the resulting compression drives a forward shock (FS2) and a subsequent reverse shock (RS).
The ICME observed on 04 – 05 July 2007 by Ulysses. The panels show: (a) the magnitude and (b–d) normalised components of the magnetic field vector, with blue lines plotted at 0 for reference to allow easy identification of rotation; (e) the proton velocity; (f) the observed proton temperature (black), the expected temperature calculated from the observed solar-wind speed (blue), and half the calculated expected proton temperature (purple); (g) the observed proton density; (h) the calculated total pressure, combining the proton and magnetic pressures; (i) the \(\alpha\) particle to proton ratio and the typical threshold of 4% observed in the solar wind (blue); (j) the calculated proton plasma \(\beta\) with a threshold of 1 (blue); (k) the electron pitch angles at 312 eV. Magenta vertical lines labelled ‘MC’ and ‘FS2’ represent the front of the magnetic cloud and the shock created by the fast wind propagating into the back of the cloud, respectively, black vertical lines labelled ‘FS1’ and ‘RS2’ represent the shock in front of the forward sheath and the reverse shock preceding the compression region, respectively.
Panels a–d show the magnitude and normalised components of the magnetic field vector, presented in the heliographic radial-tangential-normal (RTN) system of reference (Burlaga, 1984). In the RTN coordinate system, \(\boldsymbol {R}\) points from the Sun to the spacecraft, \(\boldsymbol {T}\) is the transverse component, the Sun’s rotation vector crossed into \(\boldsymbol {R}\) (thus towards west for a spacecraft near the ecliptic), and \(\boldsymbol {N}\) is the normal component that completes the right-handed system. The magnetic cloud is identified by a strongly enhanced magnetic field and a distinct, smooth rotation in the \(\boldsymbol {B_{T}}\) and \(\boldsymbol {B_{N}}\) components (e.g. Burlaga et al., 1981; Burlaga, 2001). The magnetic cloud has a mean magnetic field intensity \(\langle \boldsymbol {B}\rangle= 11.5\) nT.
In panel e, the magnetic cloud is characterised by a consistently declining (from 396 to 368 km s−1) solar-wind speed, indicative of magnetic-cloud expansion (e.g. Klein and Burlaga, 1982). The magnetic cloud is relatively slow (Richardson and Cane, 2010; Kilpua, Koskinen, and Pulkkinen, 2017), with a mean solar-wind speed (and standard deviation) of 378 (±11.2) km s−1. The proton temperature, in panel f, is less than the expected temperature \(T_{ex}\) (overplotted in blue, Richardson and Cane, 1995; Lopez, 1987) for the first part of the proposed magnetic-cloud interval.
The low proton density, panel g, and low total pressure, panel h are again consistent with the passage of a magnetic cloud (Gosling, 1994; Gosling et al., 1994a). The observed proton temperature, density, and total pressure, in panels f, g, and h, all exhibit an approximately smooth profile, in line with other Ulysses observations of ICMEs (Gosling and Forsyth, 2001; von Steiger and Richardson, 2006). Panel i presents the observed \(\alpha\) particle to proton ratio sampled by Ulysses. The helium abundance of the ICME is significantly lower than the typical \(4\% \) observed in the solar wind, again consistent with a magnetic cloud (Borrini et al., 1982). The proton-beta, \(\beta_{p}\) in panel j, is consistently less than 1 (between 0.01 and 0.56) in the proposed magnetic-cloud time interval, (e.g. Burlaga et al., 1981; Burlaga, 2001). The suprathermal electron pitch-angle distribution at 312 eV, in panel k, shows evidence of counter-streaming in the last section of the ICME passage; this counter-streaming may be interpreted as an indicative signature of a magnetic cloud (e.g. Gosling and McComas, 1987a; Riley, Gosling, and Crooker, 2004).
The ICME is preceded by a distinct forward shock (FS1), characterised by an increase in total magnetic field, solar-wind speed, density and temperature (Gosling et al., 1975); the subsequent region that precedes the ICME (FS1-MC) has a higher temperature and density, and large magnetic field variations consistent with a sheath (Gosling and McComas, 1987b; Temmer and Bothmer, 2022).
The second forward shock (FS2) is the result of a HSS propagating directly into the back of the magnetic cloud. Here, the succeeding compression region of interaction is the result of the back of the cloud being caught-up by the HSS behind. We observe variations >8\(\%\) in the \(\alpha\) particle to proton ratio in both the sheath and interaction regions, confirming one of the best signatures for tracking ICMEs at increasing heliographic distances (since relative helium abundances remain constant at large distances from the Sun, von Steiger and Richardson, 2006). The HSS is also characterised by the presence of large-amplitude Alfvén waves independent of the interaction (Richardson, 2018). RS (see Figure 7) marks the end of the compressed interaction region and the start of the HSS.
At this point in July 2007 Ulysses had completed its third traverse of southern high latitudes and was making its first subsequent encounter with the streamer-belt slow wind, thus the ICME is close to the transition region between the southern heliospheric (away) sector defined by the continuous fast stream wind from the solar south pole and the HCS. For an overview of the ICME events observed by Ulysses during the solar maximum fast latitude scan, see Forsyth et al. (2003). This event is listed in Richardson’s (2014) Ulysses ICME statistical study of average magnetic and plasma properties and in Ebert et al.’s (2009) study of bulk properties of the slow and fast solar wind and ICMEs measured by Ulysses. For an in-depth review of magnetic clouds and their sheath regions see Kilpua, Koskinen, and Pulkkinen (2017).
4 Geometry and Topology of the ICME
4.1 Flux-Rope Interpretation and Minimum Variance Analysis
We interpret the magnetic cloud as a flux rope through which the spacecraft passes. The primary direction of propagation of the CME aligns closely with the position of Ulysses. Thus, we expect that Ulysses samples the nose of the ICME, the near-centre of the magnetic cloud. For a spacecraft passing through the flux-rope centre, the minimum distance between the (rectilinear) trajectory of the spacecraft and the flux-rope axis is much lower than the typical flux-rope size and thus we observe a large and coherent rotation of the magnetic field vector. The (normalised) \(\boldsymbol {B_{R}}\) component of the magnetic field is positive, which implies an axis orientation away from the Sun. By adapting the method proposed by Bothmer and Schwenn (1998) and Mulligan, Russell, and Luhmann (1998), we deduce that the magnetic cloud has a west-north-east (WNE) axis configuration suggesting that the flux rope has a right-handed (positive) helicity/chirality, a measure of the entanglement of a magnetic field (see, e.g., Dasso et al., 2006; Foullon et al., 2007; Kilpua, Koskinen, and Pulkkinen, 2017, for similar applications). Examination of the electron pitch-angle characteristics show that before the ICME, we observe streaming predominately away from the Sun before the event with some evidence of counter-streaming during the event, which is evidence of a closed magnetic topology, consistent with the flux-rope interpretation.
A minimum variance analysis (MVA) is used to determine the flux-rope axis orientation, by calculating the eigenvectors and eigenvalues of a covariance matrix of the magnetic field components (e.g. Goldstein, 1983; Sonnerup and Scheible, 1998; Davies et al., 2020). The intermediate variance eigenvector provides an approximate cloud-axis orientation of [0.1, 0.6, 0.8] in RTN. When the technique is applied to a planar magnetic structure of the sheath regions, it provides a good estimate of the normal to the ICME front (e.g. Jones et al., 2002; Palmerio, Kilpua, and Savani, 2016), and to the succeeding interaction (compression) region to determine their normal directions. This gives an approximate shock normal to the front sheath and to the rear compression region of [0.86, 0.14, 0.50] and [0.96, −0.07, 0.27] in RTN, respectively. This suggests that both planes of the ICME front (FS1) and rear (FS2) lie predominantly in the RN-plane, and the cloud axis is predominately in the TN-plane, this is shown schematically in Figure 8.
4.2 Expansion
Single spacecraft methods for estimating the expansion of an ICME include: considering the duration and radial extent of ICMEs (e.g. Bothmer and Schwenn, 1998; Gosling and Forsyth, 2001; Palmerio et al., 2021), expansion speed comparing leading and trailing edges (e.g. Owens et al., 2005; Davies et al., 2020), and the dimensionless expansion parameter (e.g. Démoulin and Dasso, 2009; Gulisano et al., 2010). We calculate the length scale of the magnetic cloud by taking the mean velocity across the region multiplied by the duration of the region (with the standard deviation included for reference). This gives an estimate of 32.6 \(\pm1.0 \times10^{6}\) km (≈0.2 AU) at Ulysses, which is typical for slower ICMEs (Lepping, Jones, and Burlaga, 1990). The length scale of the preceding sheath is 6.8 \(\pm0.3\times10^{6}\) km and that of the succeeding compression caused by the HSS interaction is 12.2 \(\pm1.5 \times10^{6}\) km, giving a length scale of 51.7 \(\pm4.3 \times10^{6}\) km (≈0.3 AU) for the whole disturbance. This may be compared with the remote-sensing analysis in which the CME propagated a distance of ≈ 7.1 \(\times10^{6}\) km (10.2 \(R_{ \odot}\), 0.004 AU) in the corona and ≈0.62 AU in the inner heliosphere.
The duration of the magnetic cloud is 24 hours; this is somewhat short at 1.48 AU but expected, since the HSS is propagating directly into the back of the magnetic cloud and prevents its trailing edge from decelerating and thus the cloud from expanding. The mean speed across the cloud is relatively slow, at 378 km s−1 (Richardson and Cane, 2010; Kilpua, Koskinen, and Pulkkinen, 2017); this is likely due to interaction with the preceding slow wind. The mean expansion speed, 14.2 km s−1, calculated as half of the difference between the speed of the leading and trailing edge is much less than the typical expansion rate (one third the speed of propagation; Kilpua, Koskinen, and Pulkkinen, 2017), again likely as a result of the HSS propagating into the back of the magnetic cloud, preventing its expansion.
We note that contrary to the estimated impact time and speed from the SSEF (12:13UT on 05 July 2007 and 328 km s−1) the event arrives almost a day earlier and 68 km s−1 faster (13:00 UT on 04 July and 396 km s−1). This is likely a consequence of the simple fit to a constant speed and the assumption of a self-similar expansion (see Riley and Crooker, 2004; Savani et al., 2011), which does not account for the CME interaction with the succeeding HSS.
The ICME shares some common characteristics with the over-expanding ICMEs observed by Ulysses (Gosling et al., 1994b), including: a magnetic-cloud structure including a clear rotation of the magnetic field vector, consistent with a flux-rope structure, and a nearly monotonically declining flow speed from forward to reverse shock (Gosling and Forsyth, 2001). However, the ICME in our event does not exhibit the roughly symmetrical pressure profile about the minimum at the ICME centre, nor the abnormally low proton densities and temperatures considered to be product of prolonged expansion. What we observe is a low expansion speed, small length scale and short duration. The ICME propagates into much slower preceding solar wind, driving a shock front, and is succeeded by a HSS that propagates directly into the back of the flux rope. This HSS prevents the trailing edge of the magnetic cloud from decelerating and drives a shock bounding the compressed region of interaction between the two.
Previous observations of complex ICMEs resulting from CME interactions demonstrate that ICMEs can have relatively simple speed profiles but complicated internal structure in which the identity of the individual CMEs can be lost (Burlaga, Plunkett, and St. Cyr, 2002), and the magnetic field structure can differ between remote-sensing and in situ derived orientations (Bothmer and Mrotzek, 2017). Here, the magnetic cloud is well preserved, although limited in its expansion, and its boundaries are well defined by distinct northward shocks: (FS1) the result of the ICME propagating into the slow wind in front of it, and (FS2) the result of the HSS propagating directly into the back of the ICME. Shock pairs generated by other types of dynamic plasma interactions between ICMEs and the surrounding solar wind include erosion from magnetic reconnection (e.g. Dasso et al., 2007; Ruffenach et al., 2015), and Kelvin–Helmholtz waves driven by flow shear (e.g. Foullon et al., 2011a). Observations of ICME interactions with complex solar-wind streams include Odstrčil and Pizzo (1999), Schmidt and Cargill (2001), and Jian et al. (2008). A similar CME–HSS interaction was investigated using heavy-ion composition by Rodkin et al. (2018); similarities with the ICME under study include a slow rising CME speed (in coronagraph images), comparable speed and magnetic field profiles (in situ) and the ICME–HSS interaction impeding expansion.
To summarise and assist in the interpretation of this ICME and its geometry, we developed an illustration of an ICME that has been prevented from expanding by a succeeding HSS (Figure 9). We show the CME (purple) as it propagates towards Ulysses, the preceding sheath and subsequent compression region of interaction (light blue) and the HSS (yellow).
4.3 Enlil Simulation
The (I)CME propagation in the heliosphere is simulated using Enlil, a time-dependent 3D MHD, which solves equations for plasma mass, momentum, energy density, and magnetic field, with a Flux-Corrected-Transport (FCT) algorithm to model the ICME (Odstrčil, 2003). The choice of geometric input parameters is guided by the STEREO/SECCHI COR2 and HI analysis alongside the observed properties of the magnetic cloud at Ulysses, and the simulation results (available via the Community Coordinated Modelling Centre, model run id: Megan_Maunder_062322_SH_2)Footnote 1 show the ICME propagating towards Ulysses, as shown in panel a of Figure 10, which corresponds to a disturbance seen at Ulysses (panel b). The simulated ICME is consistent in duration (approximately one day), radial impact velocity (≈400 km s−1), the rotation of \(\boldsymbol {B_{T}}\) (from positive to negative), and in temperature profile in the CME centre (≈105 K) with the observations at Ulysses.
(a) A snapshot at 05 July 2007 of the solar-wind radial flow velocity in the heliosphere within 1.7 AU simulated with ENLIL in the ecliptic plane. The simulated CME is shown as a black contour. The HCS is shown as a white line, the IMF as a black and white dashed line; spacecraft and planet positions, including Ulysses, are projected into the FOV. (b) The simulated solar-wind and CME properties plotted in blue, and the CME as a vertical orange section.
However, the simulated ICME does not show a decrease in radial speed, the simulated magnetic field strength is underestimated by ≈10 nT, and arrives approximately 1 day earlier than observed at Ulysses. In comparison, the SSEF estimated the ICME impact 1 day late. The distinct shocks we observe in situ are not present in the simulations, thus we infer that the model does not account for the distinct difference in background solar-wind speeds that we observe in situ and the model underestimates the succeeding fast, background solar wind from the HSS that impacts the expansion and evolution of the ICME (see Figure 9). This is likely as the model is idealised and does not show the complexity of the interaction with the surrounding solar-wind structures. Nevertheless, overall the model supports our understanding of the ICME, in that it is a large, slow ICME that is launched towards Ulysses.
5 Summary
We have investigated an unusual type of CME observed on 27 June 2007 and its subsequent ICME observed outside the ecliptic plane on 04 July 2007; this is the only study, to our knowledge, that examines an (I)CME using both the STEREO/SECCHI/COR2 images and Ulysses in situ data. This event was isolated and occurred during a period of solar minimum when coronal-hole regions and therefore sources of the fast solar wind extended towards the lower latitudes. Through comparison and analysis of the remote-sensing observations from the STEREO/SECCHI suite, and in situ data at Ulysses we have shown that the observations relate to the same structure. A triangulation method is applied to the STEREO/SECCHI/COR2-A and -B images, and a SSEF to STEREO/SECCHI/HI-images. The in situ magnetic field data at Ulysess is analysed using an MVA method and length-scale analysis to infer the ICME structure and magnetic field properties. Enlil, a time-dependant 3D MHD model, is employed to assist in the interpretation of the (I)CME evolution.
Using this combined multi-point analysis, we deduce the following:
-
i)
The estimated direction of propagation of the CME is consistent between the stereoscopic and SSEF techniques and points towards the orbital position of Ulysses where the ICME is observed.
-
ii)
The ICME includes a magnetic cloud with a west-north-east orientation, confirmed by MVA, and provides a well-preserved example of a magnetic cloud outside of the ecliptic plane.
-
iii)
The ICME is bounded by shocks driven by a distinct difference between the speed of the CME and the surrounding solar wind, resulting in two distinct forward shocks: (FS1) the result of the ICME propagating into the slow wind in front of it, and (FS2) the result of the HSS propagating directly into the back of the ICME.
-
iv)
The ICME is short in duration, with a small length scale, and slow expansion rate. This is a result of the HSS propagating directly into the back of the ICME, preventing its trailing edge from decelerating, and the magnetic cloud from expanding.
-
v)
A comparison of the observations against the SSEF and ENLIL solar-wind model demonstrates the continued challenge of modelling and fitting the propagation of (I)CMEs embedded in complex solar-wind environments in the heliosphere, for which complex interactions between structures are unaccounted for.
This study provides a clear example of the impact of the local solar-wind environment on the (I)CME evolution and the need for observational case studies in addition to statistical studies. Further analysis of (I)CMEs out of the ecliptic plane will be possible with Solar Orbiter and complemented by Parker Solar Probe; together they will provide a complete view of the equatorial corona and new vantage points from which to investigate additional large-scale effects of ICMEs and a global view of (I)CME activity.
Data Availability
The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Balogh, A., et al.: 1992, The magnetic field investigation on the ULYSSES mission – instrumentation and preliminary scientific results. Astron. Astrophys. Suppl. 92(2), 221. ADS.
Bame, S.J., McComas, D.J., Barraclough, B.L., Phillips, J.L., Sofaly, K.J., Chavez, J.C., Goldstein, B.E., Sakurai, R.K.: 1992, The ULYSSES solar wind plasma experiment. Astron. Astrophys. Suppl. 92, 237.
Barnes, D., Davies, J.A., Harrison, R.A., Byrne, J.P., Perry, C.H., et al.: 2019, CMEs in the heliosphere: II. A statistical analysis of the kinematic properties derived from single-spacecraft geometrical modelling techniques applied to CMEs detected in the heliosphere from 2007 to 2017 by STEREO/HI-1. Solar Phys. 294(5), 57. DOI.
Barnes, D., Davies, J.A., Harrison, R.A., Byrne, J.P., Perry, C.H., et al.: 2020, CMEs in the heliosphere: III. A statistical analysis of the kinematic properties derived from stereoscopic geometrical modelling techniques applied to CMEs detected in the heliosphere from 2008 to 2014 by STEREO/HI-1. Solar Phys. 295(11), 150. DOI. ADS.
Borrini, G., Gosling, J.T., Bame, S.J., Feldman, W.C.: 1982, Helium abundance enhancements in the solar wind. J. Geophys. Res. 87, 7370. DOI. ADS.
Bothmer, V., Mrotzek, N.: 2017, Comparison of CME and ICME structures derived from remote-sensing and in situ observations. Solar Phys. 292(11), 157. DOI. ADS.
Bothmer, V., Schwenn, R.: 1998, The structure and origin of magnetic clouds in the solar wind. Ann. Geophys. 16(1), 1. DOI. https://www.ann-geophys.net/16/1/1998/.
Braga, C.R., Vourlidas, A.: 2021, Coronal mass ejections observed by heliospheric imagers at 0.2 and 1 au. The events on April 1 and 2, 2019. Astron. Astrophys. 650, A31. DOI. ADS.
Burlaga, L.F.: 1984, Magnetohydrodynamic processes in the outer heliosphere. Space Sci. Rev. 39(3-4), 255. DOI. ADS.
Burlaga, L.F.: 2001, Terminology for ejecta in the solar wind. EOS Trans. 82, 433. DOI. ADS.
Burlaga, L.F., Plunkett, S.P., St. Cyr, O.C.: 2002, Successive CMEs and complex ejecta. J. Geophys. Res. 107(A10), 1266. DOI. ADS.
Burlaga, L., Sittler, E., Mariani, F., Schwenn, R.: 1981, Magnetic loop behind an interplanetary shock: Voyager, Helios, and IMP 8 observations. J. Geophys. Res. 86(A8), 6673. DOI. ADS.
Cabello, I., Cremades, H., Balmaceda, L., Dohmen, I.: 2016, First simultaneous views of the axial and lateral perspectives of a coronal mass ejection. Solar Phys. 291(6), 1799. DOI. ADS.
Cremades, H.: 2018, Pursuing forecasts of the behavior and arrival of coronal mass ejections through modeling and observations. In: Foullon, C., Malandraki, O.E. (eds.) Space Weather of the Heliosphere: Processes and Forecasts, IAU Symp. 335, 58. DOI. ADS.
Cremades, H., Bothmer, V.: 2004, On the three-dimensional configuration of coronal mass ejections. Astron. Astrophys. 422, 307. DOI. ADS.
Dasso, S., Mandrini, C.H., Démoulin, P., Luoni, M.L.: 2006, A new model-independent method to compute magnetic helicity in magnetic clouds. Astron. Astrophys. 455(1), 349. DOI. ADS.
Dasso, S., Nakwacki, M.S., Démoulin, P., Mandrini, C.H.: 2007, Progressive transformation of a flux rope to an ICME. Comparative analysis using the direct and fitted expansion methods. Solar Phys. 244(1-2), 115. DOI. ADS.
Davies, J.A., Harrison, R.A., Rouillard, A.P., Sheeley, N.R., Perry, C.H., Bewsher, D., Davis, C.J., Eyles, C.J., Crothers, S.R., Brown, D.S.: 2009, A synoptic view of solar transient evolution in the inner heliosphere using the heliospheric imagers on STEREO. Geophys. Res. Lett. 36, L02102. DOI. ADS.
Davies, J.A., Harrison, R.A., Perry, C.H., Möstl, C., Lugaz, N., Rollett, T., Davis, C.J., Crothers, S.R., Temmer, M., Eyles, C.J., Savani, N.P.: 2012, A self-similar expansion model for use in solar wind transient propagation studies. Astrophys. J. 750, 23. DOI. ADS.
Davies, E.E., Forsyth, R.J., Good, S.W., Kilpua, E.K.J.: 2020, On the radial and longitudinal variation of a magnetic cloud: ACE, wind, ARTEMIS and Juno observations. Solar Phys. 295(11), 157. DOI. ADS.
Démoulin, P., Dasso, S.: 2009, Causes and consequences of magnetic cloud expansion. Astron. Astrophys. 498(2), 551. DOI. ADS.
Démoulin, P., Janvier, M., Dasso, S.: 2016, Magnetic flux and helicity of magnetic clouds. Solar Phys. 291(2), 531. DOI. ADS.
DiBraccio, G.A., Slavin, J.A., Imber, S.M., Gershman, D.J., Raines, J.M., Jackman, C.M., Boardsen, S.A., Anderson, B.J., Korth, H., Zurbuchen, T.H., McNutt, R.L., Solomon, S.C.: 2015, MESSENGER observations of flux ropes in Mercury’s magnetotail. Planet. Space Sci. 115, 77. DOI. ADS.
Ebert, R.W., McComas, D.J., Elliott, H.A., Forsyth, R.J., Gosling, J.T.: 2009, Bulk properties of the slow and fast solar wind and interplanetary coronal mass ejections measured by Ulysses: three polar orbits of observations. J. Geophys. Res. 114(A1), A01109. DOI. ADS.
Eyles, C.J., Harrison, R.A., Davis, C.J., Waltham, N.R., Shaughnessy, B.M., Mapson-Menard, H.C.A., Bewsher, D., Crothers, S.R., Davies, J.A., Simnett, G.M., Howard, R.A., Moses, J.D., Newmark, J.S., Socker, D.G., Halain, J.-P., Defise, J.-M., Mazy, E., Rochus, P.: 2009, The heliospheric imagers onboard the STEREO mission. Solar Phys. 254, 387. DOI. ADS.
Forsyth, R.J., Balogh, A., Horbury, T.S., Erdoes, G., Smith, E.J., Burton, M.E.: 1996, The heliospheric magnetic field at solar minimum: ULYSSES observations from pole to pole. Astron. Astrophys. 316, 287. ADS.
Forsyth, R.J., Rees, A., Reisenfeld, D.B., Lepri, S.T., Zurbuchen, T.H.: 2003, ICME observations during the Ulysses fast latitude scan. In: Velli, M., Bruno, R., Malara, F., Bucci, B. (eds.) Solar Wind Ten, AIP Conf. Ser. 679, 715. DOI. ADS.
Foullon, C., Owen, C.J., Dasso, S., Green, L.M., Dandouras, I., Elliott, H.A., Fazakerley, A.N., Bogdanova, Y.V., Crooker, N.U.: 2007, Multi-spacecraft study of the 21 January 2005 ICME. Evidence of current sheet substructure near the periphery of a strongly expanding, fast magnetic cloud. Solar Phys. 244, 139. DOI. ADS.
Foullon, C., Verwichte, E., Nakariakov, V.M., Nykyri, K., Farrugia, C.J.: 2011a, Magnetic Kelvin-Helmholtz instability at the Sun. Astrophys. J. Lett. 729(1), L8. DOI. ADS.
Foullon, C., Lavraud, B., Luhmann, J.G., Farrugia, C.J., Retinò, A., Simunac, K.D.C., Wardle, N.C., et al.: 2011b, Plasmoid releases in the heliospheric current sheet and associated coronal hole boundary layer evolution. Astrophys. J. 737(1), 16. DOI. ADS.
Frazin, R.A., Vásquez, A.M., Thompson, W.T., Hewett, R.J., Lamy, P., Llebaria, A., Vourlidas, A., Burkepile, J.: 2012, Intercomparison of the LASCO-C2, SECCHI-COR1, SECCHI-COR2, and Mk4 coronagraphs. Solar Phys. 280(1), 273. DOI. ADS.
Goldstein, H.: 1983, On the field configuration in magnetic clouds. In: NASA Conf Pub. 228, 0.731. ADS.
Gopalswamy, N., Mäkelä, P., Xie, H., Akiyama, S., Yashiro, S.: 2009, CME interactions with coronal holes and their interplanetary consequences. J. Geophys. Res. 114(A3), A00A22. DOI. ADS.
Gosling, J.T.: 1994, Coronal mass ejections in the solar wind at high solar latitudes: an overview. In: Hunt, J.J. (ed.) Solar Dynamic Phenomena and Solar Wind Consequences, The Third SOHO Workshop, ESA SP 373, 275.
Gosling, J.T., Forsyth, R.J.: 2001, CME-driven solar wind disturbances at high heliographic latitudes. Space Sci. Rev. 97, 87.
Gosling, J.T., McComas, D.J.: 1987a, Field line draping about fast coronal mass ejecta: a source of strong out-of-the-ecliptic interplanetary magnetic fields. Geophys. Res. Lett. 14(4), 355. DOI. ADS.
Gosling, J.T., McComas, D.J.: 1987b, Field line draping about fast coronal mass ejecta: a source of strong out-of-the-ecliptic interplanetary magnetic fields. Geophys. Res. Lett. 14(4), 355. DOI. ADS.
Gosling, J.T., Hildner, E., MacQueen, R.M., Munro, R.H., Poland, A.I., Ross, C.L.: 1975, Direct observations of a flare related coronal and solar wind disturbance. Solar Phys. 40, 439. DOI.
Gosling, J.T., Bame, S.J., McComas, D.J., Phillips, J.L., Scime, E.E., Pizzo, V.J., Goldstein, B.E., Balogh, A.: 1994a, A forward-reverse shock pair in the solar wind driven by over-expansion of a coronal mass ejection: Ulysses observations. Geophys. Res. Lett. 21(3), 237. DOI.
Gosling, J.T., Bame, S.J., McComas, D.J., Phillips, J.L., Goldstein, B.E., Neugebauer, M.: 1994b, The speeds of coronal mass ejections in the solar wind at mid heliographic latitudes: Ulysses. Geophys. Res. Lett. 21(12), 1109. DOI. ADS.
Gulisano, A.M., Démoulin, P., Dasso, S., Ruiz, M.E., Marsch, E.: 2010, Global and local expansion of magnetic clouds in the inner heliosphere. Astron. Astrophys. 509, A39. DOI. ADS.
Howard, T.: 2011, Coronal Mass Ejections: An Introduction 376, Springer, New York. 978-1-4419-8789-1. DOI. ADS.
Howard, T.A., Tappin, S.J.: 2009, Interplanetary coronal mass ejections observed in the heliosphere: 1. Review of theory. Space Sci. Rev. 147(1-2), 31. DOI. ADS.
Howard, R.A., et al.: 2008, Sun Earth connection coronal and heliospheric investigation (SECCHI). Space Sci. Rev. 136(1-4), 67. DOI. ADS.
Jian, L.K., Russell, C.T., Luhmann, J.G., Skoug, R.M., Steinberg, J.T.: 2008, Stream interactions and interplanetary coronal mass ejections at 5.3 AU near the solar ecliptic plane. Solar Phys. 250(2), 375. DOI. ADS.
Jones, G.H., Rees, A., Balogh, A., Forsyth, R.J.: 2002, The draping of heliospheric magnetic fields upstream of coronal mass ejecta. Geophys. Res. Lett. 29(11), 1520. DOI. ADS.
Kahler, S.W., Webb, D.F.: 2007, V arc interplanetary coronal mass ejections observed with the Solar Mass Ejection Imager. J. Geophys. Res. 112, A09103. DOI. ADS.
Kaiser, M.L., Kucera, T.A., Davila, J.M., St. Cyr, O.C., Guhathakurta, M., Christian, E.: 2008, The STEREO mission: an introduction. Space Sci. Rev. 136(1-4), 5. DOI. ADS.
Kay, C., Opher, M., Evans, R.M.: 2015, Global trends of CME deflections based on CME and solar parameters. Astrophys. J. 805(2), 168. DOI. ADS.
Kilpua, E., Koskinen, H.E.J., Pulkkinen, T.I.: 2017, Coronal mass ejections and their sheath regions in interplanetary space. Living Rev. Solar Phys. 14, 5. DOI. ADS.
Klein, L.W., Burlaga, L.F.: 1982, Interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 87, 613. DOI. ADS.
Lepping, R.P., Jones, J.A., Burlaga, L.F.: 1990, Magnetic field structure of interplanetary magnetic clouds at 1 AU. J. Geophys. Res. 95(A8), 11957. DOI. ADS.
Liewer, P., Panasenco, O., Vourlidas, A., Colaninno, R.: 2015, Observations and analysis of the non-radial propagation of coronal mass ejections near the Sun. Solar Phys. 290(11), 3343. DOI. ADS.
Lopez, R.E.: 1987, Solar cycle invariance in solar wind proton temperature relationships. J. Geophys. Res. 92(A10), 11189. DOI. ADS.
Lugaz, N.: 2010, Accuracy and limitations of fitting and stereoscopic methods to determine the direction of coronal mass ejections from heliospheric imagers observations. Solar Phys. 267(2), 411. DOI. ADS.
Lugaz, N., Manchester, I.W.B., Gombosi, T.I.: 2005, The evolution of coronal mass ejection density structures. Astrophys. J. 627(2), 1019. DOI. ADS.
Lugaz, N., Vourlidas, A., Roussev, I.I.: 2009, Deriving the radial distances of wide coronal mass ejections from elongation measurements in the heliosphere – application to CME-CME interaction. Ann. Geophys. 27, 3479. DOI. ADS.
Lugaz, N., Hernandez-Charpak, J.N., Roussev, I.I., Davis, C.J., Vourlidas, A., Davies, J.A.: 2010, Determining the azimuthal properties of coronal mass ejections from multi-spacecraft remote-sensing observations with STEREO SECCHI. Astrophys. J. 715(1), 493. DOI. ADS.
Marubashi, K.: 1986, Structure of the interplanetary magnetic clouds and their solar origins. Adv. Space Res. 6(6), 335. DOI. ADS.
Mierla, M., Davila, J., Thompson, W., Inhester, B., Srivastava, N., Kramar, M., St. Cyr, O.C., Stenborg, G., Howard, R.A.: 2008, A quick method for estimating the propagation direction of coronal mass ejections using stereo-COR1 images. Solar Phys. 252(2), 385. DOI.
Möstl, C., Farrugia, C.J., Miklenic, C., Temmer, M., Galvin, A.B., Luhmann, J.G., Kilpua, E.K.J., Leitner, M., Nieves-Chinchilla, T., Veronig, A., Biernat, H.K.: 2009, Multispacecraft recovery of a magnetic cloud and its origin from magnetic reconnection on the Sun. J. Geophys. Res. 114(A4), A04102. DOI. ADS.
Mulligan, T., Russell, C.T., Luhmann, J.G.: 1998, Solar cycle evolution of the structure of magnetic clouds in the inner heliosphere. Geophys. Res. Lett. 25(15), 2959. DOI. ADS.
Odstrčil, D.: 2003, Modeling 3-D solar wind structure. Adv. Space Res. 32(4), 497. DOI. ADS.
Odstrčil, D., Pizzo, V.J.: 1999, Three-dimensional propagation of coronal mass ejections in a structured solar wind flow 2. CME launched adjacent to the streamer belt. J. Geophys. Res. 104(A1), 493. DOI. ADS.
Owens, M.J., Cargill, P.J., Pagel, C., Siscoe, G.L., Crooker, N.U.: 2005, Characteristic magnetic field and speed properties of interplanetary coronal mass ejections and their sheath regions. J. Geophys. Res. 110(A1), A01105. DOI. ADS.
Palmerio, E., Kilpua, E.K.J., Savani, N.P.: 2016, Planar magnetic structures in coronal mass ejection-driven sheath regions. Ann. Geophys. 34(2), 313. DOI. ADS.
Palmerio, E., Scolini, C., Barnes, D., Magdalenić, J., West, M.J., Zhukov, A.N., Rodriguez, L., Mierla, M., Good, S.W., Morosan, D.E., Kilpua, E.K.J., Pomoell, J., Poedts, S.: 2019, Multipoint study of successive coronal mass ejections driving moderate disturbances at 1 au. Astrophys. J. 878(1), 37. DOI. ADS.
Palmerio, E., Kilpua, E.K.J., Witasse, O., Barnes, D., Sánchez-Cano, B., Weiss, A.J., Nieves-Chinchilla, T., Möstl, C., Jian, L.K., Mierla, M., Zhukov, A.N., Guo, J., Rodriguez, L., Lowrance, P.J., Isavnin, A., Turc, L., Futaana, Y., Holmström, M.: 2021, CME magnetic structure and IMF preconditioning affecting SEP transport. Space Weather 19(4), e02654. DOI. ADS.
Richardson, I.G.: 2014, Identification of interplanetary coronal mass ejections at Ulysses using multiple solar wind signatures. Solar Phys. 289, 3843. DOI. ADS.
Richardson, I.G.: 2018, Solar wind stream interaction regions throughout the heliosphere. Living Rev. Solar Phys. 15(1), 1. DOI. ADS.
Richardson, I.G., Cane, H.V.: 1995, Regions of abnormally low proton temperature in the solar wind (1965 – 1991) and their association with ejecta. J. Geophys. Res. 100(A12), 23397. DOI.
Richardson, I.G., Cane, H.V.: 2010, Near-Earth interplanetary coronal mass ejections during solar cycle 23 (1996 – 2009): catalog and summary of properties. Solar Phys. 264(1), 189. DOI. ADS.
Riley, P., Crooker, N.U.: 2004, Kinematic treatment of coronal mass ejection evolution in the solar wind. Astrophys. J. 600(2), 1035. DOI. ADS.
Riley, P., Gosling, J.T., Crooker, N.U.: 2004, Ulysses observations of the magnetic connectivity between coronal mass ejections and the Sun. Astrophys. J. 608(2), 1100. DOI. ADS.
Rodkin, D., Slemzin, V., Zhukov, A.N., Goryaev, F., Shugay, Y., Veselovsky, I.: 2018, Single ICMEs and complex transient structures in the solar wind in 2010 – 2011. Solar Phys. 293(5), 78. DOI. ADS.
Rouillard, A.P.: 2011, Relating white light and in situ observations of coronal mass ejections: a review. J. Atmos. Solar-Terr. Phys. 73(10), 1201. DOI. ADS.
Rouillard, A.P., Davies, J.A., Forsyth, R.J., Rees, A., Davis, C.J., Harrison, R.A., Lockwood, M., Bewsher, D., Crothers, S.R., Eyles, C.J., Hapgood, M., Perry, C.H.: 2008, First imaging of corotating interaction regions using the STEREO spacecraft. Geophys. Res. Lett. 35, L10110. DOI. ADS.
Rouillard, A.P., Savani, N.P., Davies, J.A., Lavraud, B., Forsyth, R.J., Morley, S.K., Opitz, A., Sheeley, N.R., Burlaga, L.F., Sauvaud, J.-A., Simunac, K.D.C., Luhmann, J.G., Galvin, A.B., Crothers, S.R., Davis, C.J., Harrison, R.A., Lockwood, M., Eyles, C.J., Bewsher, D., Brown, D.S.: 2009, A multispacecraft analysis of a small-scale transient entrained by solar wind streams. Solar Phys. 256(1-2), 307. DOI. ADS.
Ruffenach, A., Lavraud, B., Farrugia, C.J., Démoulin, P., Dasso, S., Owens, M.J., Sauvaud, J.-A., Rouillard, A.P., Lynnyk, A., Foullon, C., Savani, N.P., Luhmann, J.G., Galvin, A.B.: 2015, Statistical study of magnetic cloud erosion by magnetic reconnection. J. Geophys. Res. 120(1), 43. DOI. ADS.
Russell, C.T., Mulligan, T.: 2002, The true dimensions of interplanetary coronal mass ejections. Adv. Space Res. 29, 301. DOI.
Savani, N.P., Owens, M.J., Rouillard, A.P., Forsyth, R.J., Kusano, K., Shiota, D., Kataoka, R.: 2011, Evolution of coronal mass ejection morphology with increasing heliocentric distance. I. Geometrical analysis. Astrophys. J. 731(2), 109. DOI. ADS.
Schmidt, J.M., Cargill, P.J.: 2001, Magnetic cloud evolution in a two-speed solar wind. J. Geophys. Res. 106(A5), 8283. DOI. ADS.
Sheeley, N.R. Jr., Herbst, A.D., Palatchi, C.A., Wang, Y.-M., Howard, R.A., Moses, J.D., Vourlidas, A., Newmark, J.S., Socker, D.G., Plunkett, S.P., Korendyke, C.M., Burlaga, L.F., Davila, J.M., Thompson, W.T., St Cyr, O.C., Harrison, R.A., Davis, C.J., Eyles, C.J., Halain, J.P., Wang, D., Rich, N.B., Battams, K., Esfandiari, E., Stenborg, G.: 2008, Heliospheric images of the solar wind at Earth. Astrophys. J. 675, 853. DOI. ADS.
Sheeley, N.R., Walters, J.H., Wang, Y.-M., Howard, R.A.: 1999, Continuous tracking of coronal outflows: two kinds of coronal mass ejections. J. Geophys. Res. 104, 24739. DOI. ADS.
Sieyra, M.V., Cécere, M., Cremades, H., Iglesias, F.A., Sahade, A., Mierla, M., Stenborg, G., Costa, A., West, M.J., D’Huys, E.: 2020, Analysis of large deflections of prominence-CME events during the rising phase of solar cycle 24. Solar Phys. 295(9), 126. DOI. ADS.
Sonnerup, B.U.Ö., Scheible, M.: 1998, Minimum and Maximum Variance Analysis, ISSI Scientific Rep. Ser. 1, 185. ADS.
Temmer, M., Bothmer, V.: 2022, Characteristics and evolution of sheath and leading edge structures of interplanetary coronal mass ejections in the inner heliosphere based on Helios and Parker Solar Probe observations. Astron. Astrophys. 665, A70. DOI. ADS.
von Steiger, R., Richardson, J.D.: 2006, ICMEs in the outer heliosphere and at high latitudes: an introduction. Space Sci. Rev. 123, 111. DOI. ADS.
Wang, Y., Shen, C., Wang, S., Ye, P.: 2004, Deflection of coronal mass ejection in the interplanetary medium. Solar Phys. 222(2), 329. DOI. ADS.
Weiss, A.J., Möstl, C., Davies, E.E., Amerstorfer, T., Bauer, M., Hinterreiter, J., Reiss, M.A., Bailey, R.L., Horbury, T.S., O’Brien, H., Evans, V., Angelini, V., Heyner, D., Richter, I., Auster, H.-U., Magnes, W., Fischer, D., Baumjohann, W.: 2021, Multi-point analysis of coronal mass ejection flux ropes using combined data from Solar Orbiter, BepiColombo, and wind. Astron. Astrophys. 656, A13. DOI. ADS.
Wenzel, K.P., Marsden, R.G., Page, D.E., Smith, E.J.: 1992, The ULYSSES mission. Astron. Astrophys. Suppl. 92, 207. ADS.
Winslow, R.M., Lugaz, N., Scolini, C., Galvin, A.B.: 2021, First simultaneous in situ measurements of a coronal mass ejection by Parker Solar Probe and STEREO-A. Astrophys. J. 916(2), 94. DOI. ADS.
Acknowledgments
The authors would like to thank the anonymous reviewers for their time and constructive feedback. M.L.M would like to thank Emma E. Davies (Imperial College, London/University of New Hampshire) for useful discussions about ICMEs. Data analysis was performed with the AMDA science analysis system provided by the Centre de Données de la Physique des Plasmas (CDPP) supported by CNRS, CNES, Observatoire de Paris and Université Paul Sabatier, Toulouse, France. The Enlil Model was developed by D. Odstrčil, George Mason University; simulation results have been provided by the Community Coordinated Modeling Center at Goddard Space Flight Center through their publicly available simulation services (https://ccmc.gsfc.nasa.gov). The HI instruments on STEREO were developed by a consortium that comprised the Rutherford Appleton Laboratory (UK), the University of Birmingham (UK), Centre Spatial de Liège (CSL, Belgium), and the Naval Research Laboratory (NRL, USA). The STEREO/SECCHI project, of which HI is a part, is an international consortium led by NRL. We recognise the support of the UK Space Agency for funding STEREO/HI operations in the UK.
Funding
M.L.M. acknowledges financial support from the UK Science and Technology Facilities Council (STFC) studentship ST/S505389/1, grant number: 2072927.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Maunder, M.L., Foullon, C., Forsyth, R. et al. Multi-Spacecraft Observations of an Interplanetary Coronal Mass Ejection Interacting with Two Solar-Wind Regimes Observed by the Ulysses and Twin-STEREO Spacecraft. Sol Phys 297, 148 (2022). https://doi.org/10.1007/s11207-022-02077-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-022-02077-3