Abstract
A new method to reconstruct the high-rigidity part (≥ 1 GV) of the spectral fluence of solar energetic particles (SEP) for GLE events, based on the world-wide neutron monitor (NM) network data, is presented. The method is based on the effective rigidity \(R_{\mathrm{eff}}\) and scaling factor \(K_{\mathrm{eff}}\). In contrast to many other methods based on derivation of the best-fit parameters of a prescribed spectral shape, it provides a true non-parametric (viz. free of a priori assumptions on the exact spectrum) estimate of fluence. We reconstructed the SEP fluences for two recent GLE events, #69 (20 Jan. 2005) and #71 (17 May 2012), using four NM yield functions: (CD00 – Clem and Dorman in Space Sci. Rev. 93, 335, 2000), (CM12 – Caballero-Lopez and Moraal in J. Geophys. Res. 117, A12103, 2012), (Mi13 – Mishev, Usoskin, and Kovaltsov in J. Geophys. Res. 118, 2783, 2013), and (Ma16 – Mangeard et al. in J. Geophys. Res. 121, 7435, 2016b). The results were compared with full reconstructions and direct measurements by the PAMELA instrument. While reconstructions based on Mi13 and CM12 yield functions are consistent with the measurements, those based on CD00 and Ma16 ones underestimate the fluence by a factor of 2 – 3. It is also shown that the often used power-law approximation of the high-energy tail of SEP spectrum does not properly describe the GLE spectrum in the NM-energy range. Therefore, the earlier estimates of GLE integral fluences need to be revised.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
While galactic cosmic rays (GCRs) always bombard the Earth’s atmosphere, with the intensity being somewhat modulated by solar activity in the course of the 11-year solar cycle (see, e.g. a review by Potgieter, 2013), sometimes sporadic fluxes of solar energetic particles (SEPs) can impinge on the Earth’s atmosphere, as caused by solar eruptive events like solar flares or coronal mass ejections (e.g., Vainio et al., 2009; Desai and Giacalone, 2016). During SEP events, fluxes of lower-energy particles (below several hundred MeV) can get enhanced over the GCR background by many orders of magnitude during several to tens of hours. It is important to study such events for different reasons, from purely academic, viz. studying solar eruptive events and probing the inner heliosphere, to very practical ones, since these fluxes pose serious radiation hazards for space-based technologies and even to high-latitude commercial jet flights (Gopalswamy, 2018; Shea and Smart, 2012).
Variability of SEPs is continuously monitored by space missions, such as GOES (Geostationary Operational Environmental Satellites), SoHO (Solar-Heliospheric Observatory), etc. over the last several decades. However, due to natural limitations, most space missions are able to measure mainly the low-energy range of particles, ≤ 100 MeV. A few instruments can detect higher energies, GOES/HEPAD (High Energy Proton and Alpha Detector) can extend the energy range to 700 MeV (P10 channel) and to the integrated flux above 700 MeV (P11 channel). In addition, the SoHO/EPHIN (Electron Proton and Helium Instrument) can measure SEPs up to 500 MeV (Kühl et al., 2017). Two missions are/were able to measure more energetic particles in space, PAMELA (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics, Adriani et al., 2014) was in operation June 2006 through January 2016, while AMS-02 (Alpha Magnetic Spectrometer, Aguilar et al., 2017) is in operation since 2011. Despite their excellent performance and sensitivity, both these missions are not well suited for SEP monitoring because of their low orbits, whose major fraction is located inside the geomagnetic field and is thus protected from low-energy cosmic particles. Therefore, the only type of detectors able to continuously monitor the energy range above several hundred MeV is a ground-based neutron monitor (NM; see Simpson, 2000). On one hand, NM is an energy-integrating detector unable to directly measure the particle energy/rigidity spectrum. On the other hand, there is the world-wide network of NMs, located in different places with different geomagnetic rigidity cutoffs, which makes it possible to roughly assess the spectrum of energetic particles during SEP events. The key here is the knowledge of the yield function of a NM that quantifies the response of a NM to a monoenergetic unit flux of primary energetic particles on the top of the atmosphere (e.g., Clem and Dorman, 2000). Usually, the spectrum of SEPs is reconstructed parametrically, so that the best-fit parameters of a prescribed SEP spectral shape are defined by fitting the modeled responses of several NMs to the measured ones (e.g., Cramp et al., 1997; Vashenyuk, Balabin, and Stoker, 2007; Mishev, Kocharov, and Usoskin, 2014), explicitly considering also the SEP pitch-angle anisotropy, which can be large in the initial impulsive phase of the event. This method, while allowing for estimate of the time-variable spectral and angular distributions of SEPs during the events, is very laborious and not always stable, and may lead to large uncertainties (Bütikofer and Flückiger, 2015), mostly due to differences in NM yield functions. Of course, the NM-based estimates can be made only for hard-spectrum SEP events, which can initiate atmospheric cascades and be detected by ground-based NMs. This class of events is called Ground-Level Enhancements or GLEs (Poluianov et al., 2017). At present there are known 72 such events (a list can be found at https://gle.oulu.fi ).
For practical applications, it is often sufficient to know not the peak flux and its temporal/angular distributions, but the integral fluence (flux integrated over the entire event). Determination of the event fluence is more robust and is usually done under an assumption of the isotropic distribution of SEP particles near Earth. A detailed method for that was proposed by Tylka and Dietrich (2009), who fitted a power law in rigidity tail of the Band-function spectral shape to the measured NM responses for most of the GLEs (see Raukunen et al., 2018, – called R18 henceforth). However, this method is parametric, viz. based on an explicit assumption of the power-law spectral shape. In addition, it uses an outdated yield function of Clem and Dorman (2000).
Here we propose a further development of the method by Tylka and Dietrich (2009), by introducing the effective rigidity of a NM, which enables one to make a non-parametric (viz. free of explicit assumptions of the spectral shape) reconstructions of the GLE integral fluence, based on the data from the NM network.
2 Assessment of the Integral SEP Fluence from NM Data
2.1 General Approach
A solid method of an assessment of the integral fluence of SEPs for a GLE event, using the data from the world-wide NM network was developed by Tylka and Dietrich (2009) and updated in R18. According to the method, the integral omnidirectional fluence of SEP is assumed as a power-law dependence of the proton rigidity (in the NM energy range of above several hundred MeV):
Then, the SEP fluence in the Earth’s vicinity can be defined via the measured response of a given \(i\)th NM, characterized by the effective vertical geomagnetic cutoff rigidity, \(P_{\mathrm{c}_{i}}\), to the SEP event (GLE) as
where the first term is the measured (asterisks denote the measured values henceforth) relative increase of the \(i\)th NM count rate due to SEPs, integrated over the entire duration of the event, with respect to the background count rate caused by GCR; the second term is the theoretically expected response of an ideal NM to GCR (see Equation 5); and the last term is the scaling (corresponding to the ’correction’ term in Tylka and Dietrich, 2009) factor, which is defined as
where \(\gamma \) is the spectral index and \(Y\) is the yield function of the ideal NM at the atmospheric depth (height) \(h_{i}\), and integration is over the particle’s rigidity \(R\). It is important that the value of the scaling factor depends on the SEPs’ spectral shape, viz. the spectral index \(\gamma \). Using data from several NMs with different geomagnetic cutoffs \(P_{\mathrm{c}_{i}}\), the best-fit values of \(F_{0}\) and \(\gamma \) were found by means of the \(\chi ^{2}\) method, along with their uncertainties. By applying this method, integral SEP fluences were estimated for most of the GLE events (R18).
The method described above contains two important simplifications: first, it ignores the angular distribution of SEPs, and second, it is based on a prescribed spectral shape (power law in rigidity). While the former one is reasonable as the integral fluence is largely defined for the main isotropic phase of the event, the latter assumption makes the method parametric (viz., not the spectrum per se is estimated but parameters of a prescribed shape, without validation whether this shape is applicable) and may lead to a significant systematic uncertainty.
Here we propose a non-parametric method of SEP fluence assessment that is free of strict assumptions of the SEPs’ spectral shape. The proposed method leads to a true non-parametric spectrum reconstruction rather than to estimation of some prescribed spectral parameters. We have modified the method of Tylka and Dietrich (2009) by introducing the concept of the effective rigidity \(R_{\mathrm{eff}}\) and the scaling factor \(K_{\mathrm{eff}}\) so that the SEP event-integrated fluence is defined as (cf. Equation 2)
The values of \(R_{\mathrm{eff}_{i}}\) and \(K_{\mathrm{eff}_{i}}\) are constant characteristics of each (\(i\)th) NM. They are calculated once and do not depend on the SEPs’ spectral shape. Accordingly, this method allows one to directly relate the NM response to the integral SEP fluence for a GLE event, without any a priori assumptions on its spectral shape. In other words, instead of fitting a model to different observational points, one can plot each NM response as a single point (with error bars) on an \(F\)–\(R\) diagram. Details are discussed later in Section 2.3.
The theoretically expected response of an ideal NM (characterized by the geomagnetic cutoff rigidity \(P_{\mathrm{c}}\) and the height \(h\) of its location) to GLE or GCR can be calculated as
where \(Y_{j}(R,h)\) is the yield function of the NM (located at height \(h\)) for primary cosmic-ray particles of type \(j\) (protons, helium, heavier species), and \(J_{j}\) is the differential intensity of primary particles of type \(j\) at the Earth’s orbit but outside the magnetosphere and atmosphere. The spectrum can be either GCR or SEP. In the case of SEP only protons are considered, so that there is no summation over the different types of primary particles. We used the force-field parameterization (Caballero-Lopez and Moraal, 2004; Usoskin et al., 2005) of the GCR spectra near Earth based on an updated local interstellar spectrum for protons (Vos and Potgieter, 2015) as constrained by recent measurements of Voyager (Stone et al., 2013) and PAMELA (Adriani et al., 2013) in-situ data. The methodology is described elsewhere (Koldobskiy, Kovaltsov, and Usoskin, 2018a; Koldobskiy et al., 2019). The values of the modulation potential \(\phi \) in the force-field parameterization were calculated for each GLE pre-increase interval from polar NM data, using the methodology described in Usoskin et al. (2017).
2.2 NM Yield Function
The NM is a ground-based detector, where secondary nucleonic particles produced in the atmospheric cascade are detected instead of the primary energetic cosmic rays. Thus, the process of the atmospheric cascade needs to be properly modeled in order to study the cosmic-ray variability. Successful efforts in modeling the cosmic-ray induced atmospheric cascade were made over 60 years (e.g., Debrunner and Brunberg, 1968), but only during the last decades it became possible, thanks to the improving computer performance and development of appropriate full-target Monte-Carlo packages, to conduct detailed simulations. This led to the concept of the yield function (YF) of a NM defined as the response of the detector (in terms of counts) to the unit flux of primary cosmic-ray particles outside the Earth’s atmosphere and magnetosphere (e.g., Clem and Dorman, 2000).
At present, four yield functions for the standard NM64 detector (Simpson, 2000) are used in the research community:
-
CD00 (Clem and Dorman, 2000) YF was computed numerically as a first detailed Monte-Carlo simulation, using the FLUKA (FLUktuierende KAscade or Fluctuating Cascade – Fassò et al., 2001; Ballarini et al., 2006) package, of the cosmic-ray induced atmospheric cascade in the atmosphere;
-
CM12 (Caballero-Lopez and Moraal, 2012) YF was empirically constructed based on latitudinal surveys of a NM, and thus defined only for the rigidities below 15 GV, it was extended to higher energies/rigidities theoretically;
-
Mi13 (Mishev, Usoskin, and Kovaltsov, 2013) YF was computed using the PLANETOCOSMICS GEANT-4 simulation tool (Desorgher et al., 2005, 2009), considering, for the first time, the finite lateral size of the atmospheric cascade and the NM’s electronic dead time;
-
Ma16 (Mangeard et al., 2016b,a) YF was also computed using the FLUKA package (release 2011; see Böhlen et al., 2014).
We note that the method of R18 was based solely on the CD00 YF, which may be outdated and does not agree with the NM latitudinal surveys (Caballero-Lopez and Moraal, 2012; Mishev, Usoskin, and Kovaltsov, 2013). Figure 1 shows these YFs and their ratios to the CD00 one. One can see that while they generally agree, within \(\pm 10\)%, with each other for high rigidities \({>}\,20\) GV, there is a significant discrepancy between them in the low-rigidity range \({<}\,10\) GV. Ma16 and CD00 YFs appear to be quite close for \(R<2\) GV, whereas CM12 and Mi13 YFs are significantly, by a factor of two – three, lower. This has been noted by Koldobskiy et al. (2019), who, using the direct in-situ cosmic-ray measurements by PAMELA and AMS-02 over a solar cycle, showed that Mi13 YF is the most consistent with the data, while CD00 and Ma16 tend to overestimate the sensitivity of a NM to low-energy cosmic rays. CM12 YF lies close to Mi13 but gives slightly larger uncertainties. That result was based on an analysis of GCR data related to a higher energy/rigidity range. Here we re-analyze the response of a NM to SEPs, which are less energetic and thus make it possible to study the low-energy part of the NM YF in greater details.
Panel A: Yield functions of NM64 sea-level neutron monitors for primary protons, used in this study (denoted in the legend as Mi13 (Mishev, Usoskin, and Kovaltsov, 2013), Ma16 (Mangeard et al., 2016b), CM12 (Caballero-Lopez and Moraal, 2012) and CD00 (Clem and Dorman, 2000)), normalized to the unity at 100 GV rigidity. Panel B: Ratios of the yield functions shown in panel A to that of CD00.
We note that YF is usually defined for the intensity of primary energetic particles, \(J\) (see Equation 5), while SEPs are typically presented via the omnidirectional flux/fluence \(F\). For the isotropic case, the two quantities are related as \(F=4\pi \cdot J\) (Grieder, 2001, Chapter 1.6).
2.3 NM Effective Rigidity for GLE
The NM is an energy-integrating detector that cannot directly measure the differential energy spectrum of cosmic rays. However, it can record the integral spectrum. The ideal integral particle detector would have a step-like YF (viz., zero below the threshold energy \(E_{\mathrm{th}}\), and constant above it). The response of such an ideal detector is directly proportional to the integral flux of primary particles with energy above this threshold energy \(E_{\mathrm{th}}\). While the YF of NM is not ideal, it is close to that (very sharp, nearly step-like rise, especially for non-polar NMs followed by a gradual increase roughly proportional to the energy; see Figure 1a). This makes it possible to define the effective energy/rigidity of a NM for the given typical spectrum of primary particles, GCR or GLE. The effective energy/rigidity, \(E_{\mathrm{eff}}/R_{\mathrm{eff}}\), is such that the integral flux of primary particles above this threshold is nearly proportional to the count rate of the detector, viz. an analog of \(E_{\mathrm{th}}\).
The concept of the effective energy/rigidity for NM has been used in application to study GCR variability (e.g., Alanko et al., 2003; Asvestari et al., 2017). The same concept was applied also to such integral ‘detectors’ as production of cosmogenic isotopes in the Earth’s atmosphere (Kovaltsov et al., 2014; Asvestari et al., 2017) and lunar rocks (Poluianov, Kovaltsov, and Usoskin, 2018). Such an effective energy/rigidity was recently introduced for the sea-level polar NMs for detection of GLEs (Koldobskiy, Kovaltsov, and Usoskin, 2018b).
This approach makes it possible to assess the SEP energy-integrated spectrum directly, without making any a priori assumption of the spectral shape. Let us assume that there is an effective rigidity \(R_{\mathrm{eff}}\) such that the integral fluence of SEPs above this rigidity \(F(>R_{\mathrm{eff}})\), is proportional to the NM response to GLE \(N_{\mathrm{GLE}}\):
where \(K_{\mathrm{eff}}\) is a scaling factor for a given NM, which is ideally a constant irrespectively of the strength and energy/rigidity spectrum of the analyzed event (Koldobskiy, Kovaltsov, and Usoskin, 2018b). The expected response of a NM to GLE is calculated using Equation 5. Here we assume that SEPs causing the GLE consist of protons only, otherwise a term accounting for heavier species needs to be considered. This assumption is valid for large SEP events, where helium composes typically about 0.01 of protons (Torsti et al., 2002), but not for GCR, where helium and heavier species should be explicitly considered.
We consider the modified power law in rigidity as the spectral shape of SEP fluence (e.g. Cramp et al., 1997; Mishev et al., 2018):
where \(R\) is rigidity in GV, \(\gamma \) is the spectral index, and \(\delta \gamma \) in GV−1 is the rate of the spectrum steepening. In the forthcoming analysis we varied the value of \(\gamma \) in a range from five to nine, which corresponds to typical GLE spectra. The rate of the spectrum steepening \(\delta \gamma \) was considered in the range from 0 (no steepening of the spectrum, viz. the power law) to 1 GV−1 (strong steepening). The analyzed range of \(\gamma \) and \(\delta \gamma \) corresponds to a wide range spectra of real SEP events. For each value of \(\gamma \) and \(\delta \gamma \) from these ranges we calculated the value of \(K\) for different values of \(R\),
where \(N_{\mathrm{GLE}}\) is defined using Equation 5. This forms a ribbon in the \(K\)-vs-\(R\) diagram (see Figure 2). We considered the vertical full-range width of the ribbon, for a given \(R\) as \(\Delta K\). Next we found such a value of \(R\), called the effective rigidity \(R_{\mathrm{eff}}\), which minimizes the value of \(\delta K(R) \equiv \Delta K/\langle K\rangle \), where \(\langle K\rangle \) is a mean value of \(K\) for the given value of \(R\). The value of \(\langle K \rangle \) is called the effective scaling factor \(K_{\mathrm{eff}}\). Full-scale uncertainties for both values \(R_{\mathrm{eff}}\) and \(K_{\mathrm{eff}}\) were evaluated as illustrated by the red error bars in Figure 2. For the standard near-sea-level polar 1NM64 we found, for the Mi13 YF, that \(R_{ \mathrm{eff}}=1.43_{-0.11}^{+0.05}\) GV and \(K_{\mathrm{eff}}=5.44_{-1.45} ^{+1.07}\) (cm2 count)−1. The value of \(K_{\mathrm{eff}}\) is defined for 1NM64 throughout the paper.
Diagram of the scaling factor \(K\) versus rigidity \(R\) for the standard near-sea-level polar 1NM64 (\(P_{\mathrm{c}}=0.1\) GV, \(h=1000\) g cm−2), using the Mi13 YF, for the spectral indices (Equation 7) \(\gamma \) and \(\delta \gamma \) ranging between 5 – 9 and 0 – 1, respectively. \(R_{\mathrm{eff}}\) and the corresponding value of \(K_{\mathrm{eff}}\), with full-range uncertainties are denoted by the red dot. The right-hand panel is a zoom to the left-hand panel around the red dot.
In a similar way we have defined effective rigidities and scaling factors for different geomagnetic rigidity cutoffs \(P_{\mathrm{c}}\) and altitudes \(h\), as shown in Figures 3 and 4 and summarized in Tables 1 and 2, respectively, for Mi13 YF. Since the Mi13 yield function was computed only for the sea-level NMs, we used the altitudinal dependence according to Flückiger et al. (2008) applied to the Mi13 yield function. One can see that the effective rigidity \(R_{\mathrm{eff}}\) is very close to the geomagnetic rigidity cutoff \(P_{\mathrm{c}}\) for low- and mid-latitude locations (\(P_{\mathrm{c}}>3\) GV) but saturates at 1.3 – 1.5 GV (depending on the atmospheric depth) for high-latitude sites. The value of the \(K_{\mathrm{eff}}\) varies with the geomagnetic cutoff depicting a shoulder at high-latitude locations and a nearly exponential decrease with \(P_{\mathrm{c}}\) for low latitudes and mid-latitudes. This relation is shaped by two different processes, viz. the atmospheric cutoff (particles must possess sufficient energy of a several hundred MeV to initiate an atmospheric cascade reaching the ground) and the geomagnetic cutoff (particles must possess sufficient rigidity to be able to enter the atmosphere). While the geomagnetic cutoff dominates at low latitudes and mid-latitudes, the atmospheric cutoff becomes crucial at high latitudes.
The effective rigidity \(R_{\mathrm{eff}}\) of a NM, using the Mi13 YF, as a function of the cutoff rigidity \(P_{\mathrm{c}}\) for different atmospheric depths as denoted in the legend. Error bars represent the full-range uncertainties. Values are tabulated in Table 1.
It is important that the effective rigidity and scaling factor are defined robustly for a wide range of the geomagnetic rigidity cutoffs, and they are independent of the exact SEP spectrum, in a reasonable range of parameters. Thus, for each GLE and each NM, one can estimate, using Equation 6, the integral fluence \(F(>R_{ \mathrm{eff}})\) of SEPs, and a set of such NMs with different values of \(R_{\mathrm{eff}}\) makes it possible to perform a non-parametric reconstruction (i.e., one without an explicit assumption on the spectral shape) of the event’s integral spectrum.
3 Test of the Effective-Rigidity Method
In this section we test the \(R_{\mathrm{eff}}\) method for two well-studied events: GLE #69 and #71. The relative measured response of \(i\)th NM to a GLE, integrated over the entire event is defined as
where \(X_{i}\) is the event-integrated relative intensity of GLE in units of percent-hours (Asvestari et al., 2017), where percents are with respect to the pre-increase NM count rate due to GCR. The value of \(X_{i}\) was computed (see column 5 in Table 3) as time integration of the relative (%) increase in time profiles obtained from the international GLE database ( https://gle.oulu.fi ). These values were defined here and thus may differ from those used in R18. Geomagnetic cutoff rigidities \(P_{\mathrm{c}}\) were taken from the NMDB database.
The theoretically expected response of a NM to GLE \(N_{\mathrm{GLE}}\), which enters Equation 6, is
whose statistical uncertainties have two independent sources: the accuracy of the determination of \(X_{i}\) considered as 1% hr and the statistical uncertainty of the GCR count rate:
Another source of uncertainties of the final reconstruction is also the uncertainties in the definition of \(R_{\mathrm{eff}}\) and \(K_{ \mathrm{eff}}\) (Section 2.3). All the uncertainties were accounted for in the following analysis.
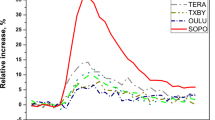
3.1 GLE #69, 20 Jan. 2005
As the first test of the method we considered GLE #69, which occurred on 20 January 2005 and was the strongest event over the last cycles and the second strongest ever directly observed. It was an impulsive event with the high peak (\({\approx} \,3350\) and 4800% for the SOPB and SOPO NMs, respectively) and was characterized by a very strong anisotropy of its initial phase (e.g., Plainaki et al., 2007; Matthiä et al., 2009). Since the effects of anisotropy and temporal evolution of fluxes cannot be considered by the effective-rigidity approach, we can only provide a rough estimate, while the exact spectral reconstruction requires a laborious and complicated method with particle tracing (e.g., Plainaki et al., 2007; Mishev and Usoskin, 2016).
For the comparison we use four NM yield functions as mentioned before. The corresponding values of the \(R_{\mathrm{eff}}\) and \(K_{ \mathrm{eff}}\) were computed for all the YFs, but shown only for Mi13 in Table 3.
Thus, for each NM we can estimate one value of the integral fluence \(F(>R_{\mathrm{eff}})\), that yields a spectral estimate for a set of NMs with different cutoff rigidities (ignoring the anisotropy effects). This was done for the GLE #69 as shown in Figure 5 for the four different YFs, along with the integral fluence (using the Band-function parameterization) estimated for the same event by R18. One can see that the results obtained here by using the effective-rigidity concept (viz., no explicit fitting of the spectral shape) generally agree with the Band-function fitting R18 using NM network and spacecraft data and also ignoring the possible anisotropy, but there are also significant differences. In order to study it in more detail we show in Figure 6 the ratio of the fluences reconstructed here using different YFs from that provided by R18 for GLE #69. Two main features can be observed.
Reconstruction of the omnidirectional integral SEP fluence for GLE #69 (20 Jan. 2005) using Mi13 (panel a), Ma16 (panel b), CM12 (panel c) and CD00 (panel d) yield functions. Error bars represent the final uncertainties, including the uncertainties in \(R_{\mathrm{eff}}\) (horizontal bars – see Section 2.3) and both the uncertainties in \(K_{\mathrm{eff}}\) (Section 2.3) and the errors of the definition of the GLE strength (Equation 11). The integral fluence, reconstructed by Raukunen et al. (2018) in the Band-function form and using the CD00 YF, is depicted with the blue line.
Ratio of the integral fluences reconstructed for the GLE #69 (20 Jan. 2005) here, using different YFs from that provided by Raukunen et al. (2018) using the Band-function approximation.
First, the overall shape of the spectrum, reconstructed here, is robust for different YFs and disagrees with the Band-function shape (note that in this energy/rigidity range the Band function is close to a simple power law with the index \(\gamma _{2}\), following the notations of R18): while all spectra merge at the high-rigidity tail of 6 – 7 GV and low-rigidity head (\({<}\,1\) GV), they have an essential excess in the mid-rigidity range of several GV. We note that the wide spread of low-rigidity points is caused by the anisotropic impulsive phase observed by polar NMs. This suggests that the single power-law tail of the Band-function shape is not well representative of such spectrum. Despite the discrepancy in the absolute calibration of the reconstructed spectrum, all YF-based calculations agree in that the spectrum rolls off at high rigidities, above 5 GV, with respect to a purely power-law high-energy tail of the Band function. In order to exclude a possibility that the roll-off is an artifact related to the ‘training’ of the method on the modified power-law spectral shape (Equation 7), we have tested the method also for the pure power law (\(\delta \gamma =0\)) and found that it does not have any significant effect on the values of \(R_{\mathrm{eff}}\) and \(K_{\mathrm{eff}}\). Accordingly, the roll-off of the spectrum is realistic and should be taken into account either using the modified power law (Equation 7) or the Ellison–Ramaty spectra shape (Ellison and Ramaty, 1985), which is a power law over energy with an exponential cutoff.
Second, the mid-rigidity excess ranges for different yield functions between 1.5 – 2 for CD00 and Ma16 YFs to 2.5 – 4 for CM12 and Mi13 YFs. Overall, the fluence reconstructed here with the use of the CD00 and Ma16 YF is comparable to that of R18 which was also based on the CD00 YF. In the case of Mi13 and CM12, the reconstructed fluence above a few GV rigidity is a factor of 2 – 3 higher than that proposed by R18. Considering that CM12 and Mi13 YFs better represent the low-energy part (Koldobskiy et al., 2019), particularly CM12 one which was empirically constructed from the latitudinal survey data, these estimates look more realistic.
Figure 7 focuses on the spectral fluence reconstruction for GLE #69. The reconstruction (red dots) is based on the effective-rigidity method introduced here, using the Mi13 YF. The full reconstruction, based on the full inversion of the NM responses, which accounts for the anisotropy of the impulsive phase and temporal evolution of the SEP energy spectrum throughout the events (e.g., Mishev et al., 2018), using the same Mi13 YF, is shown as the blue dashed line. One can observe that, while the shapes of the spectra are nearly identical within the error bars, the full reconstruction agrees within 10% with respect to the method presented here. Since this event was strongly anisotropic during the impulsive phase and both methods use the same Mi13 YF, we consider this as the uncertainty related to the anisotropy of the SEP flux, since the method assumes the SEP flux to be isotropic. On the other hand, the R18 fluence is significantly lower than the full reconstruction, which is caused largely by the use of the CD00 YF (Bütikofer and Flückiger, 2015).
3.2 GLE #71: 17 May 2012
We have also applied the effective-rigidity method of spectrum reconstruction to GLE #71 (17 May 2012). While the event was moderate in strength, much weaker (peak 15 – 17 % in South Pole, Apatity and Oulu NM count rates) than that #69, it was also highly anisotropic and relatively hard in the impulsive phase (Mishev et al., 2015). Peak fluxes and temporal evolution of SEPs for that event have been studied in detail (e.g. Mishev, Kocharov, and Usoskin, 2014; Plainaki et al., 2014), however, here we focus on the event-integrated fluence. Most importantly, the event was observed by the PAMELA experiment, which directly measured the SEP integral fluence (Bruno et al., 2018). In Figure 8 we confront the spectra reconstructed here, using different YFs, with that measured directly in space. One can see that the spectra, reconstructed using the \(R_{\mathrm{eff}}\) method, are fully consistent with the direct data (gray area) in the spectral shape, but those based on CD00 and Ma16 YFs tend to underestimate the low-energy range of the spectrum. On the other hand the Band-function approximation (R18) systematically underestimates, by the factor 2 – 3, the fluence in the rigidity range of about 2 GV (energy about 1 GeV). The full NM-based reconstruction based on Mi13 YF (dashed red line) demonstrates the excellent agreement with the spectrum reconstructed here, and a fair agreement, within the uncertainties, with the directly observed one.
Reconstruction of the integral SEP fluence for GLE #71 (17 May 2012) by the method with the effective-rigidity \(R_{\mathrm{eff}}\) (colored points) using different yield functions as denoted in the legend (errors bars are shown only for the Mi13 YF, for clarity), along with that by Raukunen et al. (2018) (blue line) and full spectrum reconstruction based on the Mi13 YF (red dashed line). Direct measurements by the PAMELA experiment parameterized via the Ellison–Ramaty form with 1\(\sigma \) uncertainties are shown with the gray-filled area (Bruno et al., 2018).
4 Summary
Here we presented a new fast method for assessment of the high-rigidity part (above 1 GV) of the spectral fluence of SEPs for GLE events based on the data from the world-wide NM network. The method is based on the effective rigidity \(R_{\mathrm{eff}}\) and scaling factor \(K_{ \mathrm{eff}}\), calculated for each NM, where the SEP integral fluence is directly related to the NM response to the event. This method is non-parametric so that it provides an estimate of the spectrum without any explicit assumption of the spectral shape. This is an important difference to most of the other methods which fit a prescribed spectral shape into the data by finding the best-fit parameters for that shape, often without a proper validation. This method is simple and fast avoiding laborious computations needed for the full reconstruction, but it neglects the possible anisotropy of the impulsive phase of the event.
We tested the method for two recent GLE events, #69 (20 Jan. 2005), which was the second strongest observed one and had a very anisotropic SEP distribution during the impulsive phase of the event, and #71 (17 May 2012), which was a moderate, but also strongly anisotropic event, whose spectrum was directly measured by PAMELA instrument. For both events we found a good qualitative agreement between the spectral shape of the reconstructed here, on one hand, and that for fully reconstructed spectra, on the other hand. By confronting the spectra assessed here with those obtained via a full NM-based reconstruction, we estimated the uncertainty related to the anisotropy as being within 10%.
Next, we compared our present reconstructions with the directly measured spectrum for GLE #71. Only the reconstructions based on Mi13 and CM12 YFs appear quantitatively consistent with the measurements, while the results based on CD00 and Ma16 lead to an underestimate of the spectrum by a factor 2 – 3 in the lower-rigidity range. This is most probably related to the fact that the latter two YFs tend to overestimate the NM response to lower-energy particles, as was found by Koldobskiy et al. (2019) from an analysis of GCR spectra measured directly by AMS-02 and PAMELA experiments. In particular, the CD00 YF is known to fail reproducing the observed NM latitudinal surveys (Clem and Dorman, 2000; Caballero-Lopez and Moraal, 2012; Mishev, Usoskin, and Kovaltsov, 2013) implying that it overestimates the sensitivity of a NM to the lower-energy particles. Since the model by R18 is based on the CD00 YF, it may underestimate the SEP fluence by a factor of two to three. It is also shown that the power-law approximation of the high-energy tail, used in particular in the Band-function parameterization, does not properly describe the form of the GLE spectrum in the NM-energy range. Therefore, the earlier estimates of GLE integral fluences need to be revised. A proper reconstruction of the SEP integral fluence for the known GLE events is planned for a forthcoming work.
References
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A., Bellotti, R., Boezio, M., Bogomolov, E.A., Bongi, M., Bonvicini, V., Borisov, S., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carbone, R., Carlson, P., Casolino, M., Castellini, G., De Pascale, M.P., De Santis, C., De Simone, N., Di Felice, V., Formato, V., Galper, A.M., Grishantseva, L., Karelin, A.V., Koldashov, S.V., Koldobskiy, S., Krutkov, S.Y., Kvashnin, A.N., Leonov, A., Malakhov, V., Marcelli, L., Mayorov, A.G., Menn, W., Mikhailov, V.V., Mocchiutti, E., Monaco, A., Mori, N., Nikonov, N., Osteria, G., Palma, F., Papini, P., Pearce, M., Picozza, P., Pizzolotto, C., Ricci, M., Ricciarini, S.B., Rossetto, L., Sarkar, R., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y.I., Vacchi, A., Vannuccini, E., Vasilyev, G., Voronov, S.A., Yurkin, Y.T., Wu, J., Zampa, G., Zampa, N., Zverev, V.G., Potgieter, M.S., Vos, E.E.: 2013, Time dependence of the proton flux measured by PAMELA during the 2006 July – 2009 December solar minimum. Astrophys. J. 765, 91. DOI . ADS .
Adriani, O., Barbarino, G.C., Bazilevskaya, G.A., Bellotti, R., Boezio, M., Bogomolov, E.A., Bongi, M., Bonvicini, V., Bottai, S., Bruno, A., Cafagna, F., Campana, D., Carbone, R., Carlson, P., Casolino, M., Castellini, G., De Pascale, M.P., De Santis, C., De Simone, N., Di Felice, V., Formato, V., Galper, A.M., Giaccari, U., Karelin, A.V., Kheymits, M.D., Koldashov, S.V., Koldobskiy, S., Krut’kov, S.Y., Kvashnin, A.N., Leonov, A., Malakhov, V., Marcelli, L., Martucci, M., Mayorov, A.G., Menn, W., Mikhailov, V.V., Mocchiutti, E., Monaco, A., Mori, N., Munini, R., Nikonov, N., Osteria, G., Papini, P., Pearce, M., Picozza, P., Pizzolotto, C., Ricci, M., Ricciarini, S.B., Rossetto, L., Sarkar, R., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y.I., Vacchi, A., Vannuccini, E., Vasilyev, G.I., Voronov, S.A., Wu, J., Yurkin, Y.T., Zampa, G., Zampa, N., Zverev, V.G.: 2014, The PAMELA mission: heralding a new era in precision cosmic ray physics. Phys. Rep. 544, 323. DOI . ADS .
Aguilar, M., Ali Cavasonza, L., Alpat, B., Ambrosi, G., Arruda, L., Attig, N., Aupetit, S., Azzarello, P., Bachlechner, A., Barao, F., Barrau, A., Barrin, L., Bartoloni, A., Basara, L., Başe ǧmez-du Pree, S., Battarbee, M., Battiston, R., Becker, U., Behlmann, M., Beischer, B., Berdugo, J., Bertucci, B., Bindel, K.F., Bindi, V., de Boer, W., Bollweg, K., Bonnivard, V., Borgia, B., Boschini, M.J., Bourquin, M., Bueno, E.F., Burger, J., Burger, W.J., Cadoux, F., Cai, X.D., Capell, M., Caroff, S., Casaus, J., Castellini, G., Cervelli, F., Chae, M.J., Chang, Y.H., Chen, A.I., Chen, G.M., Chen, H.S., Cheng, L., Chou, H.Y., Choumilov, E., Choutko, V., Chung, C.H., Clark, C., Clavero, R., Coignet, G., Consolandi, C., Contin, A., Corti, C., Creus, W., Crispoltoni, M., Cui, Z., Dadzie, K., Dai, Y.M., Datta, A., Delgado, C., Della Torre, S., Demakov, O., Demirköz, M.B., Derome, L., Di Falco, S., Dimiccoli, F., Díaz, C., von Doetinchem, P., Dong, F., Donnini, F., Duranti, M., D’Urso, D., Egorov, A., Eline, A., Eronen, T., Feng, J., Fiandrini, E., Fisher, P., Formato, V., Galaktionov, Y., Gallucci, G., García-López, R.J., Gargiulo, C., Gast, H., Gebauer, I., Gervasi, M., Ghelfi, A., Giovacchini, F., Gómez-Coral, D.M., Gong, J., Goy, C., Grabski, V., Grandi, D., Graziani, M., Guo, K.H., Haino, S., Han, K.C., He, Z.H., Heil, M., Hoffman, J., Hsieh, T.H., Huang, H., Huang, Z.C., Huh, C., Incagli, M., Ionica, M., Jang, W.Y., Jia, Y., Jinchi, H., Kang, S.C., Kanishev, K., Khiali, B., Kim, G.N., Kim, K.S., Kirn, T., Konak, C., Kounina, O., Kounine, A., Koutsenko, V., Kulemzin, A., La Vacca, G., Laudi, E., Laurenti, G., Lazzizzera, I., Lebedev, A., Lee, H.T., Lee, S.C., Leluc, C., Li, H.S., Li, J.Q., Li, Q., Li, T.X., Li, Y., Li, Z.H., Li, Z.Y., Lim, S., Lin, C.H., Lipari, P., Lippert, T., Liu, D., Liu, H., Lordello, V.D., Lu, S.Q., Lu, Y.S., Luebelsmeyer, K., Luo, F., Luo, J.Z., Lyu, S.S., Machate, F., Mañá, C., Marín, J., Martin, T., Martínez, G., Masi, N., Maurin, D., Menchaca-Rocha, A., Meng, Q., Mikuni, V.M., Mo, D.C., Mott, P., Nelson, T., Ni, J.Q., Nikonov, N., Nozzoli, F., Oliva, A., Orcinha, M., Palmonari, F., Palomares, C., Paniccia, M., Pauluzzi, M., Pensotti, S., Perrina, C., Phan, H.D., Picot-Clemente, N., Pilo, F., Pizzolotto, C., Plyaskin, V., Pohl, M., Poireau, V., Quadrani, L., Qi, X.M., Qin, X., Qu, Z.Y., Räihä, T., Rancoita, P.G., Rapin, D., Ricol, J.S., Rosier-Lees, S., Rozhkov, A., Rozza, D., Sagdeev, R., Schael, S., Schmidt, S.M., Schulz von Dratzig, A., Schwering, G., Seo, E.S., Shan, B.S., Shi, J.Y., Siedenburg, T., Son, D., Song, J.W., Tacconi, M., Tang, X.W., Tang, Z.C., Tescaro, D., Ting, S.C.C., Ting, S.M., Tomassetti, N., Torsti, J., Türko ǧlu, C., Urban, T., Vagelli, V., Valente, E., Valtonen, E., Vázquez Acosta, M., Vecchi, M., Velasco, M., Vialle, J.P., Vitale, V., Vitillo, S., Wang, L.Q., Wang, N.H., Wang, Q.L., Wang, X., Wang, X.Q., Wang, Z.X., Wei, C.C., Weng, Z.L., Whitman, K., Wu, H., Wu, X., Xiong, R.Q., Xu, W., Yan, Q., Yang, J., Yang, M., Yang, Y., Yi, H., Yu, Y.J., Yu, Z.Q., Zannoni, M., Zeissler, S., Zhang, C., Zhang, F., Zhang, J., Zhang, J.H., Zhang, S.W., Zhang, Z., Zheng, Z.M., Zhuang, H.L., Zhukov, V., Zichichi, A., Zimmermann, N., Zuccon, P.: 2017, Observation of the identical rigidity dependence of He, C, and O cosmic rays at high rigidities by the alpha magnetic spectrometer on the international space station. Phys. Rev. Lett. 119, 251101. DOI .
Alanko, K., Usoskin, I.G., Mursula, K., Kovaltsov, G.A.: 2003, Heliospheric modulation strength: effective neutron monitor energy. Adv. Space Res. 32, 615. DOI .
Asvestari, E., Willamo, T., Gil, A., Usoskin, I.G., Kovaltsov, G.A., Mikhailov, V.V., Mayorov, A.: 2017, Analysis of Ground Level Enhancements (GLE): extreme solar energetic particle events have hard spectra. Adv. Space Res. 60, 781. DOI .
Asvestari, E., Gil, A., Kovaltsov, G.A., Usoskin, I.G.: 2017, Neutron monitors and cosmogenic isotopes as cosmic ray energy-integration detectors: effective yield functions, effective energy, and its dependence on the local interstellar spectrum. J. Geophys. Res. 122, 9790. DOI . ADS .
Ballarini, F., Battistoni, G., Campanella, M., Carboni, M., Cerutti, F., Empl, A., Fassò, A., Ferrari, A., Gadioli, E., Garzelli, M.V., Lantz, M., Liotta, M., Mairani, A., Mostacci, A., Muraro, S., Ottolenghi, A., Pelliccioni, M., Pinsky, L., Ranft, J., Roesler, S., Sala, P.R., Scannicchio, D., Trovati, S., Villari, R., Wilson, T., Zapp, N., Vlachoudis, V.: 2006, The FLUKA code: an overview. J. Phys. Conf. Ser. 41, 151. DOI . ADS .
Böhlen, T.T., Cerutti, F., Chin, M.P.W., Fassò, A., Ferrari, A., Ortega, P.G., Mairani, A., Sala, P.R., Smirnov, G., Vlachoudis, V.: 2014, The FLUKA code: developments and challenges for high energy and medical applications. Nucl. Data Sheets 120, 211. DOI . ADS .
Bruno, A., Bazilevskaya, G.A., Boezio, M., Christian, E.R., de Nolfo, G.A., Martucci, M., Merge’, M., Mikhailov, V.V., Munini, R., Richardson, I.G., Ryan, J.M., Stochaj, S., Adriani, O., Barbarino, G.C., Bellotti, R., Bogomolov, E.A., Bongi, M., Bonvicini, V., Bottai, S., Cafagna, F., Campana, D., Carlson, P., Casolino, M., Castellini, G., De Santis, C., Di Felice, V., Galper, A.M., Karelin, A.V., Koldashov, S.V., Koldobskiy, S., Krutkov, S.Y., Kvashnin, A.N., Leonov, A., Malakhov, V., Marcelli, L., Mayorov, A.G., Menn, W., Mocchiutti, E., Monaco, A., Mori, N., Osteria, G., Panico, B., Papini, P., Pearce, M., Picozza, P., Ricci, M., Ricciarini, S.B., Simon, M., Sparvoli, R., Spillantini, P., Stozhkov, Y.I., Vacchi, A., Vannuccini, E., Vasilyev, G.I., Voronov, S.A., Yurkin, Y.T., Zampa, G., Zampa, N.: 2018, Solar energetic particle events observed by the PAMELA mission. Astrophys. J. 862, 97. DOI . ADS .
Bütikofer, R., Flückiger, E.: 2015, What are the causes for the spread of GLE parameters deduced from NM data? J. Phys. Conf. Ser. 632, 012053. DOI . ADS .
Caballero-Lopez, R.A., Moraal, H.: 2004, Limitations of the force field equation to describe cosmic ray modulation. J. Geophys. Res. 109, A01101. DOI . ADS .
Caballero-Lopez, R.A., Moraal, H.: 2012, Cosmic-ray yield and response functions in the atmosphere. J. Geophys. Res. 117, A12103. DOI .
Clem, J.M., Dorman, L.I.: 2000, Neutron monitor response functions. Space Sci. Rev. 93, 335. DOI . ADS .
Cramp, J.L., Duldig, M.L., Flückiger, E.O., Humble, J.E., Shea, M.A., Smart, D.F.: 1997, The October 22, 1989, solar cosmic ray enhancement: an analysis of the anisotropy and spectral characteristics. J. Geophys. Res. 102, 24237. DOI . ADS .
Debrunner, H., Brunberg, E.Å.: 1968, Monte Carlo calculation of the nucleonic cascade in the atmosphere. Can. J. Phys. 46, 1069. ADS .
Desai, M., Giacalone, J.: 2016, Large gradual solar energetic particle events. Living Rev. Solar Phys. 13, 3. DOI . ADS .
Desorgher, L., Flückiger, E.O., Gurtner, M., Moser, M.R., Bütikofer, R.: 2005, Atmocosmics: a GEANT 4 code for computing the interaction of cosmic rays with the Earth’s atmosphere. Int. J. Mod. Phys. A 20, 6802. DOI . ADS .
Desorgher, L., Kudela, K., Flueckiger, E.O., Buetikofer, R., Storini, M., Kalegaev, V.: 2009, Comparison of Earth’s magnetospheric magnetic field models in the context of cosmic ray physics. Acta Geophys. 57(1), 75. DOI .
Ellison, D.C., Ramaty, R.: 1985, Shock acceleration of electrons and ions in solar flares. Astrophys. J. 298, 400. DOI . ADS .
Fassò, A., Ferrari, A., Sala, P.R., Ranft, J.: 2001, FLUKA: status and prospective of hadronic applications. In: Kling, A., Barão, F., Nakagawa, M., Távora, L., Vaz, P. (eds.) Advanced Monte Carlo for Radiation Physics, Particle Transport Simulation and Applications, Springer, Berlin, 955.
Flückiger, E.O., Moser, M.R., Pirard, B., et al.: 2008, A parameterized neutron monitor yield function for space weather applications. In: Caballero, R., D’Olivo, J.C., Medina-Tanco, G., Nellen, L., Sánchez, F.A., Valdés-Galicia, J.F. (eds.) 30th Proc. Internat. Cosmic Ray Conf. 2007 1, Universidad Nacional Autónoma de México, Mexico City, Mexico, 289. ADS .
Gopalswamy, N.: 2018, Chapter 2 – extreme solar eruptions and their space weather consequences. In: Buzulukova, N. (ed.) Extreme Events in Geospace, Elsevier, Amsterdam, 37. 978-0-12-812700-1. DOI .
Grieder, P.K.F.: 2001, Cosmic Rays at Earth, Elsevier Science, Amsterdam.
Koldobskiy, S.A., Kovaltsov, G.A., Usoskin, I.G.: 2018a, A solar cycle of cosmic ray fluxes for 2006 – 2014: comparison between PAMELA and neutron monitors. J. Geophys. Res. 123, 4479. DOI . ADS .
Koldobskiy, S.A., Kovaltsov, G.A., Usoskin, I.G.: 2018b, Effective rigidity of a polar neutron monitor for recording ground-level enhancements. Solar Phys. 293, 110. DOI . ADS .
Koldobskiy, S.A., Bindi, V., Corti, C., Kovaltsov, G.A., Usoskin, I.G.: 2019, Validation of the neutron monitor yield function using data from AMS-02 experiment 2011 – 2017. J. Geophys. Res. 124, 2367. DOI .
Kovaltsov, G.A., Usoskin, I.G., Cliver, E.W., Dietrich, W.F., Tylka, A.J.: 2014, Fluence ordering of solar energetic proton events using cosmogenic radionuclide data. Solar Phys. 289, 4691. DOI . ADS .
Kühl, P., Dresing, N., Heber, B., Klassen, A.: 2017, Solar energetic particle events with protons above 500 MeV between 1995 and 2015 measured with SOHO/EPHIN. Solar Phys. 292(1), 10. DOI . ADS .
Mangeard, P.-S., Ruffolo, D., Sáiz, A., Nuntiyakul, W., Bieber, J.W., Clem, J., Evenson, P., Pyle, R., Duldig, M.L., Humble, J.E.: 2016a, Dependence of the neutron monitor count rate and time delay distribution on the rigidity spectrum of primary cosmic rays. J. Geophys. Res. 121(A10), 11620. DOI . ADS .
Mangeard, P.-S., Ruffolo, D., Sáiz, A., Madlee, S., Nutaro, T.: 2016b, Monte Carlo simulation of the neutron monitor yield function. J. Geophys. Res. 121, 7435. DOI . ADS .
Matthiä, D., Heber, B., Reitz, G., Meier, M., Sihver, L., Berger, T., Herbst, K.: 2009, Temporal and spatial evolution of the solar energetic particle event on 20 January 2005 and resulting radiation doses in aviation. J. Geophys. Res. 114. DOI .
Mishev, A.L., Usoskin, I.G.: 2016, Analysis of the ground-level enhancements on 14 July 2000 and 13 December 2006 using neutron monitor data. Solar Phys. 291, 1225. DOI . ADS .
Mishev, A.L., Kocharov, L.G., Usoskin, I.G.: 2014, Analysis of the ground level enhancement on 17 May 2012 using data from the global neutron monitor network. J. Geophys. Res. 119, 670. DOI . ADS .
Mishev, A.L., Usoskin, I.G., Kovaltsov, G.A.: 2013, Neutron monitor yield function: new improved computations. J. Geophys. Res. 118, 2783. DOI . ADS .
Mishev, A.L., Adibpour, F., Usoskin, I., Felsberger, E.: 2015, Computation of dose rate at flight altitudes during ground level enhancements no. 69, 70 and 71. Adv. Space Res. 55, 354. DOI . ADS .
Mishev, A.L., Usoskin, I., Raukunen, O., Paassilta, M., Valtonen, E., Kocharov, L., Vainio, R.: 2018, First analysis of Ground-Level Enhancement (GLE) 72 on 10 September 2017: spectral and anisotropy characteristics. Solar Phys. 293, 136. DOI . ADS .
Plainaki, C., Belov, A., Eroshenko, E., Mavromichalaki, H., Yanke, V.: 2007, Modeling ground level enhancements: event of 20 January 2005. J. Geophys. Res. 112(A11). DOI . ADS .
Plainaki, C., Mavromichalaki, H., Laurenza, M., Gerontidou, M., Kanellakopoulos, A., Storini, M.: 2014, The ground-level enhancement of 2012 May 17: derivation of solar proton event properties through the application of the NMBANGLE PPOLA model. Astrophys. J. 785(2), 160. DOI . ADS .
Poluianov, S., Kovaltsov, G.A., Usoskin, I.G.: 2018, Solar energetic particles and galactic cosmic rays over millions of years as inferred from data on cosmogenic 26Al in lunar samples. Astron. Astrophys. 618, A96. DOI . ADS .
Poluianov, S.V., Usoskin, I.G., Mishev, A.L., Shea, M.A., Smart, D.F.: 2017, GLE and sub-GLE redefinition in the light of high-altitude polar neutron monitors. Solar Phys. 292, 176. DOI . ADS .
Potgieter, M.: 2013, Solar modulation of cosmic rays. Living Rev. Solar Phys. 10, 3. DOI . ADS .
Raukunen, O., Vainio, R., Tylka, A.J., Dietrich, W.F., Jiggens, P., Heynderickx, D., Dierckxsens, M., Crosby, N., Ganse, U., Siipola, R.: 2018, Two solar proton fluence models based on ground level enhancement observations. J. Space Weather Space Clim. 8(27), A04. DOI . ADS .
Shea, M.A., Smart, D.F.: 2012, Space weather and the ground-level solar proton events of the 23rd solar cycle. Space Sci. Rev. 171, 161. DOI . ADS .
Simpson, J.A.: 2000, The cosmic ray nucleonic component: the invention and scientific uses of the neutron monitor. Space Sci. Rev. 93, 11. DOI . ADS .
Stone, E.C., Cummings, A.C., McDonald, F.B., Heikkila, B.C., Lal, N., Webber, W.R.: 2013, Voyager 1 observes low-energy galactic cosmic rays in a region depleted of heliospheric ions. Science 341, 150. DOI . ADS .
Torsti, J., Kocharov, L., Laivola, J., Pohjolainen, S., Plunkett, S.P., Thompson, B.J., Kaiser, M.L., Reiner, M.J.: 2002, Solar particle events with helium-over-hydrogen enhancement in the energy range up to 100 MeV nucl–1. Solar Phys. 205, 123. DOI . ADS .
Tylka, A., Dietrich, W.: 2009, A new and comprehensive analysis of proton spectra in Ground-Level Enhanced (GLE) solar particle events. In: 31th International Cosmic Ray Conference, Universal Academy Press, Lodź, icrc0273.
Usoskin, I.G., Alanko-Huotari, K., Kovaltsov, G.A., Mursula, K.: 2005, Heliospheric modulation of cosmic rays: monthly reconstruction for 1951 – 2004. J. Geophys. Res. 110, A12108. DOI . ADS .
Usoskin, I.G., Gil, A., Kovaltsov, G.A., Mishev, A.L., Mikhailov, V.V.: 2017, Heliospheric modulation of cosmic rays during the neutron monitor era: calibration using PAMELA data for 2006 – 2010. J. Geophys. Res. 122, 3875. DOI . ADS .
Vainio, R., Desorgher, L., Heynderickx, D., Storini, M., Flückiger, E., Horne, R.B., Kovaltsov, G.A., Kudela, K., Laurenza, M., McKenna-Lawlor, S., Rothkaehl, H., Usoskin, I.G.: 2009, Dynamics of the Earth’s particle radiation environment. Space Sci. Rev. 147, 187. DOI .
Vashenyuk, E.V., Balabin, Y.V., Stoker, P.H.: 2007, Responses to solar cosmic rays of neutron monitors of a various design. Adv. Space Res. 40, 331. DOI . ADS .
Vos, E.E., Potgieter, M.S.: 2015, New modeling of galactic proton modulation during the minimum of Solar Cycle 23/24. Astrophys. J. 815, 119. DOI . ADS .
Acknowledgements
Open access funding provided by University of Oulu including Oulu University Hospital. Data of GLE recorded by NMs were obtained from the International GLE database http://gle.oulu.fi and NMDB database ( www.nmdb.eu , founded under the European Union’s FP7 programme, contract no. 213007). PIs and teams of all the ground-based neutron monitors whose data were used here, are gratefully acknowledged. This work was partially supported by the ReSoLVE Centre of Excellence (project no. 307411) and HEAIM Project (no. 314982 and no. 316223) of Academy of Finland, by the grant no. MK-6160.2018.2 of the President of the Russian Federation and MEPhI Academic Excellence Project (contract 02.a03.21.0005).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure of Potential Conflicts of Interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Koldobskiy, S.A., Kovaltsov, G.A., Mishev, A.L. et al. New Method of Assessment of the Integral Fluence of Solar Energetic (> 1 GV Rigidity) Particles from Neutron Monitor Data. Sol Phys 294, 94 (2019). https://doi.org/10.1007/s11207-019-1485-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-019-1485-8