1 Introduction

“Almost 25 years ago, [...] we thought 19¢ was a fair price for one banana. Decades later, Bananas are still only 19¢ each, every day, in every store.”Trader Joe’s (2022)

The Internet has reduced the barriers to search, enabling consumers to explore products and prices at a lower cost. One might imagine that this has led to vast price transparency and convergence within and across firms. However, at the same time, the Internet has fostered information and communications technologies (ICTs) that exploit customization opportunities.

This paper documents pricing patterns for grocery products in online and offline channels. We collect price data from the leading online grocery retailers in the United States: AmazonFresh and WalmartGrocery. Importantly, (a) we collect data for identical products, and (b) prices for the same product are collected at nearly the same time across retailers and across delivery zipcodes. To facilitate a comparison with the offline channel, we utilize NielsenIQ’s scanner data, specifically selecting the same products and cities. This approach allows us to examine three fundamental aspects of price dispersion: across locations, across retailers, and over time. To the best of our knowledge, this paper is the first to study grocery pricing with such detailed granularity.

Price dispersion is significantly higher among online retailers than among offline retailers. More specifically, online grocery retailers exacerbate price dispersion by utilizing algorithmic pricing—defined as the practice of automating price setting via a computer.Footnote 1 Our data reveals that price algorithms for online groceries are characterized by three novel stylized facts:

  1. (i)

    Extremely frequent price changes. We document a remarkably high temporal price variation. The average probability of a price change within two consecutive days exceeds 17% and, moreover, sometimes products have multiple price chances within a single day. For a retailer offering 20K products in a delivery zipcode, it means 2 price changes per minute.

  2. (ii)

    Pronounced price discrimination across markets. Price algorithms set different prices for an identical product across different delivery zipcodes within the same retailer. That is, online grocers exhibit less uniform pricing than seen across the physical stores of offline retailers.

  3. (iii)

    Persistent price disparities across rival firms. Amazon’s and Walmart’s price algorithms are able to track and match each other’s prices in real-time (for a specific product x delivery zipcode x day). Yet, price-matching occurs rarely. We generally observe significant price disparities across sellers for identical products in the same delivery zipcode. Moreover, this dispersion is larger than in the offline channel.

Fig. 1
figure 1

Algorithmic Pricing — Diet Coke. Notes: Prices of a Diet Coke 12 fl oz 12 Pack over the course of one month on AmazonFresh and WalmartGrocery. Prices are collected in 6- to 12-hour time intervals. Data details are discussed in Section 2

Full size image

Figure 1, displaying the prices of a 12-Pack Diet Coke, illustrates the three facts. First, algorithms update prices at a given location with high frequency, as captured by the constant fluctuations in the price of Diet Coke over time. Second, algorithms charge different relative prices across markets at a given point in time, and these relative prices are time-varying. For example, Walmart’s prices are sometimes $5.5 in New York and $3.4 in Atlanta, but sometimes both prices are $5.5. Lastly, there are significant price differences between Walmart and Amazon in a given zipcode and point in time. Amazon’s price in New York is $6.5 but Walmart’s price there is $5.5.

The three stylized facts collectively indicate that algorithmic pricing amplifies price dispersion. (1) Price algorithms increase price dispersion over time through frequent price changes. Algorithms exacerbate this variability by triggering numerous price updates in shorter time spans. (2) Price algorithms also lift price dispersion across markets. For example, AmazonFresh sets different prices for an identical item based on the delivery zipcode. Algorithms’ finer granularity of product x timestamp x zipcode level exacerbate price differences across locations. Finally, (3) price algorithms maintain persistent price disparities for the same item across sellers in the same delivery zipcode. As a result, algorithms increase price dispersion across sellers.

The remainder of the paper is organized as follows. Section 1.1 reviews the literature. Section 2 describes the data. Sections 3, 4, and 5 document the stylized facts. And Section 6 reviews our findings and suggests avenues for future research.

1.1 Related literature

There exists an extensive body of literature in economics and marketing that studies price dispersion. The availability of scanner data from offline supermarket chains throughout the U.S. (typically provided by NielsenIQ or IRI) has opened up new avenues for empirical research. Recent studies point out that prices tend to be more “uniform” across stores than across chains (Nakamura, 2008; Anderson et al., 2015; DellaVigna & Gentzkow, 2019; Arcidiacono et al., 2020; Hitsch et al., 2021). Nevertheless, price uniformity is not absolute. Indeed, these studies still observe some retailer-level price variation across different markets. Most notably, there is compelling evidence that retail chains engage in price discrimination across locations through “price zones” (Hoch et al., 1995; Chintagunta et al., 2003; Khan & Jain, 2005; Besanko et., 2005; Ellickson & Misra, 2008; Li et al., 2018; Adams & Williams, 2019). Additionally, there is evidence that offline prices across sellers (chains) are dispersed (Kaplan et al., 2019; Arcidiacono et al., 2020; Eizenberg et al., 2021).

In a similar vein, with the increasing availability of online data, it has become possible to examine the role, or lack thereof, of Internet frictions and price dispersion. While some studies document relatively high levels of uniform pricing in online markets, particularly as online transparency or competition intensify (Brown & Goolsbee, 2002; Cavallo, 2017, 2019; Ater & Rigbi, 2023; Jo et al., 2022; Aparicio , Rigobon, 2023), it is clear that price dispersion still exists online, especially across sellers (Brynjolfsson & Smith, 2000; Baylis & Perloff, 2002; Chevalier & Goolsbee, 2003; Baye et al., 2004; Orlov, 2011; Overby & Forman, 2015; Gorodnichenko & Talavera, 2017; Gorodnichenko et al., 2018; Cavallo, 2019; González & Miles-Touya, 2018).

Another area of research related to the online channel has examined the rising frequency of price changes, often associated with the surge in artificial intelligence tools such as algorithms. Generally speaking, these tools reduce “menu costs” and intensify price variability (Chen, 2016; Cavallo, 2018; Seim & Sinkinson, 2016; Cavallo, 2019; Brown & MacKay, 2023; Hillen & Fedoseeva, 2021; Assad et al., 2020; Huang, 2022; Aparicio et al., 2022; Aparicio & Misra, 2023).

Although estimating time-series price variation using scanner data presents some obstacles (Campbell & Eden, 2014; Eichenbaum et al., 2014), our matched-product approach allows us to estimate comparable measures of price dispersion in both the online and offline channels. The importance of a matched-product approach has been highlighted in previous work. Hwang et al. (2010), for instance, examine store clientele and competitive structure using store assortment overlap. Moreover, Seim and Sinkinson (2016); Cavallo (2017); Ater and Rigbi (2023); Martinez-de et al. (2023) use matched-product datasets to investigate various retailing and pricing behaviors.

Most previous studies have primarily analyzed only one dimension of price dispersion and have tended to ignore the impact of price algorithms. Thus, to the best of our knowledge, this work is the first to examine three dimensions of price dispersion using a matched-product approach at the chain–product–zipcode level in the context of online groceries; plus, it is first to construct comparable measures for offline supermarkets. More specifically, we contribute to the literature by documenting novel facts about within-chain and cross-chain price dispersion, price variability over time, and differences between online and offline channels.

2 Data

The market for groceries is the largest retail category in the United States, with estimated sales of $1.1 trillion, representing a meaningful portion of both CPI expenditures and the economy. While online grocery accounts for 12% of total grocery retail sales (i.e., $160 billion), its market value is growing rapidly: from 3% ($26 billion) in 2018 to 12% in just four years.Footnote 2

In this paper, we focus on the leading online grocery retailers in the United States: AmazonFresh and WalmartGrocery. As of 2019, the two e-commerce giants held a combined market share of at least 50%. We conduct additional analyses using FreshDirect, Peapod, Jet, and Instacart.Footnote 3

The data encompasses a wide range of products, including fresh produce, packaged food items, and cleaning and personal care products. Importantly, we matched identical products across all retailers to ensure comparability. To collect the data, we developed scripts that entered zipcodes into the retailers’ websites and then collected prices. A random VPN was also used to check robustness from different originating IP addresses. Appendix A.1 provides further details on the products and Appendix A.2 provides methodological information on collecting online data.

Fig. 2
figure 2

Delivery zipcodes of the online grocery retailers

Full size image

We examine three dimensions of price dispersion: (a) variation within a retailer–location over time, (b) variation within a retailer across different locations, and (c) variation across rival retailers within a specific location. For dimension (a), we collected price data at high-frequency intervals (hourly differences within a day) for 8 zipcodes. For dimensions (b) and (c), we collected data for 50 zipcodes (in major cities across the U.S.) on a single day each month and with observations taken within minutes.Footnote 4 To the best of our knowledge, this empirical strategy to study algorithmic pricing is the most comprehensive to date, allowing us to recover pricing patterns at the granular level of product x zipcode x time. Figure 2 shows the delivery locations.

The second dataset used is NielsenIQ’s Retail Scanner (RMS) data provided by the Kilts Center at the University of Chicago. This data covers sales and prices at the store x week x UPC level. Importantly, we manually match products in the online data with those in the scanner data. We then narrow down the sample to matched products and stores located in the same cities as the online data (NielsenIQ includes the city but not the zipcode), as well as to grocery chains. A matched-product approach (and in matched cities) allows us to account for differences that may arise due to assortment composition or geographic coverage. Further methodological details are described in Appendix A.3.Footnote 5

Table 1 presents an overview of the data. The monthly online data consists of 16,317 price observations for 74 matched online products across 50 zipcodes, 33 cities, and 14 states. The hourly online data covers 122,170 price observations for 70 products across 6 cities. The scanner data covers 418,477 price observations for 82 matched products across 37 retail chains and 32 cities.

Table 1 Data description
Full size table

3 Stylized fact 1: online prices change very frequently

Our analysis of price dispersion begins with the following question: How often do prices change in online groceries? To explore this, we compute the frequency of price changes across various time intervals.

Let L denote the time interval of interest. For a given product i at time t, sold by retailer r in delivery zipcode d, a price change occurs when the current price, \(p_{t}^{r,d,i}\), differs from at least one of the prices collected within the last L weeks. More formally: \(\textit{Price Change}_{t}^{r,d,i} = 1 \textit{ } \text { if } \textit{ } \exists h: 1\le h \le L \text { such that } p_{t}^{r,d,i} \ne p_{t-h}^{r,d,i} \). For instance, a weekly indicator of a price change takes the value 1 if the price of a retailer–zipcode–product has experienced at least one change during the previous 168 hours (7 days).

We then proceed to compare the online frequencies with those obtained using the offline data. To ensure comparability, (a) we use scanner data from grocery stores, (b) restrict the product sample to identical matched products, and (c) limit the sample to stores located in the same cities. We calculate the indicator of a price change for retailer r and store d between consecutive weeks w and \(w-1\) (or for the last 4 weeks). We note that scanner prices are weekly volume-weighted averages at the store x product level, which tends to overstate the frequencies of price changes (Eichenbaum et al., 2014; Campbell & Eden, 2014; Cavallo, 2018). To better account for measurement error, liquidation, or fractional prices in the scanner data, we bin prices in 10-cent intervals and exclude price changes smaller (in absolute value) than 5%.Footnote 6 We report robustness results in Appendix C.3.

Table 2 Price Stickiness: Online vs. Offline
Full size table

The results are shown in Table 2. We find a significantly lower “stickiness” in the online data—that is, online prices exhibit far more variability than offline prices. Observe the weekly and monthly frequencies of price changes, which allow for a direct comparison between the online and offline channels. The probability of an (online) retailer–zipcode–product experiencing a price change within a week and a month is 44% and 75%, respectively. In contrast, the analogous measures for a chain–store–product are 31% and 43%, respectively.

These findings are robust using alternative frequency measures. The median duration is 1.1 weeks for online prices, whereas it is 3.1 weeks for offline prices. The third column shows that the differences are statistically significant. Appendix C.1 and C.2 report robustness results using a fixed-effects model and using all retail formats in the scanner data, respectively.Footnote 7

The availability of online data enables us to recover price changes at even finer time intervals: daily and intra-day price changes. Here, once again, we estimate remarkable pricing flexibility. The probability of a price change between two consecutive days is 17% and the intra-day probability is 8% (i.e., within hours of the same day). Furthermore, roughly 73% of the products at a given online retailer experienced at least one price change (across all zipcodes) in a random week. This temporal price variation surpasses most comparable statistics reported in the literature.

These facts indicate that online grocery retailers in our dataset utilize price algorithms to set prices. It is implausible that a “manager” could manually implement so many price changes each day across multiple delivery zipcodes. In fact, for a retailer offering 20,000 items in a single zipcode, it means 2 price changes in 1 minute or 3,400 price changes in 1 day.Footnote 8 To accomplish this price variability, algorithmic pricing automates the pricing decision and enables firms to trigger an unprecedented number of price changes—a key characteristic associated with the adoption or usage of algorithmic pricing (Chen, 2016; Brown & MacKay, 2023; Assad et al., 2020; Aparicio et al., 2022). For a literature review of AI and pricing, we refer the reader to Aparicio and Misra (2023).

An alternative approach to identify algorithmic pricing is to observe whether a retailer’s prices quickly respond to the prices set by another retailer. Chen (2016)’s study of Amazon marketplace (not AmazonFresh) states that “sellers using algorithmic pricing are likely to base their prices at least partially on the prices of other sellers.” Therefore, we run their correlation test to confirm that price algorithms are setting prices. Specifically, we find the lowest price of Amazon and Walmart for the same zipcode–product within the past 2 days, and then estimate a correlation between these two prices at the retailer–zipcode–product–date level. We find a correlation of 90% (and similar in a fixed-effects regression), providing further evidence of algorithmic pricing.

Fig. 3
figure 3

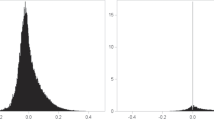
Histogram of size of price changes. Notes: Panels (a) and (b) display the histogram of the size of the daily price changes across all product-zipcode-timestamp combinations (conditional on a price change), expressed in percentage terms and in dollar terms, respectively. Values are restricted to an absolute value of 50% (or $2) for better visualization

Full size image

In line with the notion that algorithmic pricing overcomes traditional “menu cost” and stickiness frictions, we also observe a substantial portion of tiny price changes. Conditional on a price change, approximately 50% of the changes are within 3.7%, and 25% are within 5 cents. Once again, it only makes sense to update prices by a few cents when pricing is automated. Panels (a) and (b) of Fig. 3 show the histogram of the size of the price change in percentage terms and in dollar terms, respectively.

Fig. 4
figure 4

Pricing Heterogeneity — Experimentation vs. Hi-Lo. Notes: Panels (a) to (c) display Amazon’s prices in one week. Panels (d) to (f) display Walmart’s prices in one week. The unit of analysis is a retailer–zipcode–product

Full size image

There is heterogeneity in the characteristics of algorithmic pricing. We make two key observations. First, Fig. 4 captures two typical, yet contrasting, patterns when algorithms trigger price changes: grid exploration (“experimentation”) vs. high-low (“Hi-Lo”). In both cases, there is a high frequency of price changes—and higher than offline stores, which rarely update prices multiple times during the same week. The distinction lies in the menu of prices. Panels (a) to (c) exemplify situations where the algorithm constantly explores different price points. For instance, in Panel (a), we observe 8 distinct prices for Colavita Olive Oil within a single week. In contrast, Panels (d) to (f) showcase instances where the algorithm alternates between a high price and a low price, resulting in a saw-tooth or Hi-Lo pattern. Hi-Lo pricing has been documented in the scanner data (Hitsch et al., 2021), but not with this velocity. We note that while these two pricing patterns are common, not all product–zipcode–weeks experience such high variability. Panel (a) of Fig. 5 shows the distribution of the probability of a daily price change and reports strong heterogeneity across products.

The second observation is that Amazon and Walmart employ one of those strategies but not both. Amazon’s algorithms tend to explore many distinct prices (e.g., Panels (a) to (c)), whereas Walmart’s algorithms exhibit a Hi-Lo pattern (e.g., Panels (d) to (f)).Footnote 9 Indeed, Amazon utilizes five times more distinct prices for the same matched product–zipcode than Walmart. To see this, we compute the number of distinct prices for each matched product–zipcode (separately by retailer), and then calculate the ratio of Amazon’s distinct prices to Walmart’s distinct prices. Panel (b) displays the ratios for a sample of products. For example, a ratio of 10 for Ben & Jerry’s indicates that, in a given zipcode, Amazon uses 10 times more distinct prices than Walmart. Panel (c) displays the distribution of such ratios. Appendix E reports additional results comparing Amazon vs. Walmart, and Appendix F describes additional pricing patterns by time of day and day of the week.

Thus far, we have established that the leading online grocery retailers (Amazon and Walmart) use algorithmic pricing to set prices, leading to an extremely high frequency of price changes (Fact 1). Next, we explore the role of algorithms in another dimension of price dispersion: across markets.

Fig. 5
figure 5

Heterogeneity in pricing strategies

Full size image

4 Stylized fact 2: retailer-level price dispersion across markets

In Fig. 1, we noticed that algorithms set different prices for an identical Diet Coke across various delivery locations at a given point in time. This suggests that price algorithms might reduce uniform pricing across markets within a retail chain. However, do these observations extend more broadly to other products? Here, we proceed to document the extent to which retailer-level price dispersion across markets is more pronounced in the online data compared to the offline data.

To measure price dispersion across markets, we collect prices for an identical product from a specific online retailer for different delivery zipcodes at nearly the same time. Price dispersion is measured across cities. Said differently, we compare the prices of Pebbles’ cereal in a Miami zipcode vs. a Chicago zipcode. We then compare online vs. offline price dispersion, as follows: (a) restrict NielsenIQ’s data to the same set of products, (b) select offline stores located in the same cities, and (c) select offline chains with stores in multiple cities. While we strive to closely mimic the online process, it is important to acknowledge that our empirical strategy is not perfect (e.g., we lack Amazon offline prices).

Fig. 6
figure 6

Zipcode price personalization — examples

Full size image

Figure 6 illustrates the operationalization of price discrimination across markets by online grocery retailers. When users access the AmazonFresh website, they are prompted to enter a delivery zipcode or address. This means that prices (or assortments) are not visible unless a delivery zipcode is entered. Notably, Fig. 6 reveals a price difference for Pebbles’ cereal: $4.99 in Wynwood and $5.29 in Little Havana (two zipcodes within Miami). This translates to a 6% price difference for a 4-mile walking distance.

To formalize the analysis of price dispersion, we compute pairwise price differentials at the product x time x retailer level across all locations (in different cities). The unit of analysis is the same in the online and offline datasets.Footnote 10 Next, we compute the percentage difference in absolute value between two prices:

$$\begin{aligned} \textit{Price Difference}_{d,d'}^{t,i,r} = \frac{ | p_{d,r}^{t,i} - p_{d',r}^{t,i} | }{( p_{d,r}^{t,i} + p_{d',r}^{t,i})/2 }*100 \end{aligned}$$
(1)

where \(p_{d,r}^{t,i}\) denotes the price of item i for retailer r, in location d, at time t. To simplify notation, we define a retailer x location as a retailer–zipcode (retailer–store) in the case of online (offline) data. Note that t stands for nearly the same timestamp in the online data, whereas t stands for the same week in the scanner data.

An alternative measure of uniform pricing is the share of identical prices. It can be defined as follows: \( \mathbbm {1}_{d,d'}^{t,i,r} = 1 \text { if } p_{d,r}^{t,i} = p_{d',r}^{t,i} ; 0 \text { otherwise} \). In the case of within-retailer pairs, the indicator \(\mathbbm {1}_{d,d'}^{t,i,r}\) takes the value 1 when the price of the item i, in retailer r, at time t is the same across locations d and \(d'\). As before, we bin offline prices to 10 cents.

Table 3 Price dispersion across markets: Online vs. Offline
Full size table

The results are shown in Table 3. We find that online retailers exhibit substantially higher price dispersion. For instance, the mean share of identical prices across cities is 35.5% online, compared to 61.0% offline. The median and average percent difference in online pairwise prices is 7.4% and 11.6%, respectively, whereas the equivalent measures in the offline data are 0% and 7.5%. Furthermore, this pattern is consistent across product categories (fresh items, packaged food, and personal and cleaning products).Footnote 11

The results remain similar using various robustness checks. Appendix C.1 reports similar results in a regression model controlling for product fixed effects. Appendix C.2 shows results using all retail formats in the scanner data (not just grocery chains). Appendix C.4 shows similar results using seven online grocers. Lastly, Appendix G ’s variance decomposition indicates that retailer x zipcodes account for a sizable portion of online price dispersion.

There is heterogeneity in the intensity of price dispersion. Panel (a) of Fig. 7 displays the histogram of the price differences. An observation in the plot is the price difference for a given product, within a retailer, between two markets at a given point in time. Roughly 30% of the products have little to no price dispersion, whereas 25% have price differences across delivery zipcodes exceeding 20% in absolute value. For visual intuition, Panel (b) provides examples for AmazonFresh (more examples are reported in Appendix H).

Fig. 7
figure 7

Heterogeneity in price dispersion across markets

Full size image

Our analysis has focused on retailer-level price dispersion across different cities in the U.S., rather than across zipcodes within a city. Our data is limited to examine retailer-level within-city price dispersion.Footnote 12 Nevertheless, we collected data for a few within-city zipcodes for AmazonFresh to inform the following question: Do online prices vary within a city? We find that price algorithms can charge different prices, for an identical product, across neighborhoods within a single city (as illustrated in Fig. 6). However, such within-city variations occur infrequently (roughly for 5% of the price pairs) and, interestingly, are less common than in the offline data. We report more detailed results in Appendix I.

We have established that price algorithms also amplify retailer-level price dispersion across markets (Fact 2). Next, we delve into another dimension of price dispersion: across sellers.

5 Stylized fact 3: price dispersion across local retailers

One might expect online markets to exhibit a higher cross-chain price elasticity compared to offline markets. Intuitively, the ease of finding the lowest deal online could result in lower price dispersion and overall prices. However, Fig. 8 paints a different picture: the price of Ritz Crackers is $4.59 on Amazon but $3.58 on Walmart. (Importantly, for the same delivery zipcode in San Francisco and at the same point in time.) This price disparity prompts us to examine whether price algorithms also amplify price dispersion across sellers, compared to offline stores.

As explained previously, we collect price data for identical products sold by multiple online grocery retailers, for the same delivery zipcodes at nearly the same time. To mimic this analysis for offline stores, we subset to the same items and to the same cities in the scanner data. We then proceed to measure price dispersion within a location and across sellers using Eq. 1: a price pair for the same product between two online retailers, in the same zipcode at the same time (or between two offline stores of different chains).Footnote 13

Fig. 8
figure 8

Ritz Crackers 13.7 Oz — Amazon vs. Walmart

Full size image

The estimates of market-level price dispersion across sellers are shown in Table 4. Once again, we find significantly higher price dispersion across retailers in the online channel, compared to the offline channel. For instance, the share of identical prices is 1.7% and the median price difference is 18.8% in the online data. In contrast, the equivalent measures in the scanner data are 30.2% and 13.3%, respectively. Once again, this pattern is consistent across product categories. The third column of Table 4 shows that the difference across all these measures is strongly significant.

Table 4 Price Disparities: Online vs. Offline
Full size table

The results are similar in various robustness checks. Appendix C.1 reports higher online price dispersion in a regression model controlling for product fixed effects. Appendix C.2 shows similar results using all retail formats in the scanner data. Appendix C.4 reports similar results using seven online grocers. While our estimates compare the same locations and products in the online and offline channels, we provide a caveat that we are unable to compare the same chain in both channels. Still, our findings overall indicate that price dispersion across sellers in online groceries is substantial. In fact, price dispersion across chains in the same location is close to twice the price dispersion within chains across locations: the median price difference is 7.4% within chains vs. 18.8% across chains.

There is substantial heterogeneity in price dispersion across sellers. Panel (a) of Fig. 9 provides examples of price differences for the same delivery zipcode and date. For instance, Wonderbread is +31% more expensive on Amazon compared to Walmart. Panel (b) displays the distribution of price differences. A point in the plot represents the price difference between Amazon and Walmart for a specific product, in the same market, and at a given point in time. A right-skewed distribution indicates that Amazon is consistently more expensive than Walmart.Footnote 14

Our findings regarding price differences across sellers might raise another question related to competition: Are online price levels cheaper than offline prices? To answer this, we compare prices between the online and offline channels for an identical product in the same city. We find that online prices are 4% lower. However, this effect is primarily driven by Walmart: Walmart’s prices are consistently lower than offline scanner prices, whereas Amazon’s prices are consistently higher than offline prices. More detailed results are discussed in Appendix K.

Fig. 9
figure 9

Heterogeneity in price dispersion across sellers

Full size image

It is possible that online prices exhibit significant disparities across sellers simply because they set prices in isolation. One might ask: Are price algorithms not mindful of competitors’ prices? This does not appear to be the case, though. We use high-frequency online data (Section 3) to detect whether retailers price-match each other’s price for the same product x delivery zipcode x day. Specifically, we define a price-matching event when Amazon and Walmart set prices within 1 cent of each other, for the same product x zipcode and in a window of 24 hours.

Figure 10 presents several compelling examples of price-matching. While both Amazon and Walmart explore the price space relatively frequently, they occasionally match each other’s prices. We emphasize the target granularity at which these events occur: a price-match for an identical product in the same delivery zipcode and same day. Although this evidence indicates that algorithms input competitors’ prices, price-matching is not the norm. Only around 4% of the zipcode–product–date prices experience a price-matching event. When considering the share of price-matching events out of all the zipcode–product prices, the distribution is clustered at 0%. In fact, 75% of the zipcode–product prices exhibit no price-matching at all. More details are discussed in Appendix L.Footnote 15

To summarize, we have shown that price algorithms lead to persistent price disparities across sellers, resulting in higher levels of price dispersion than in the offline channel (Fact 3). The following section recaps our findings about the role of algorithmic pricing in online groceries and discusses their implications for economic and marketing research.

Fig. 10
figure 10

Algorithmic price-matching: Amazon vs. Walmart

Full size image

6 Discussion

Our work is the first to empirically document the algorithmic pricing patterns of the leading online grocery retailers in the U.S. We examine three dimensions of price dispersion that are rarely studied in combination with one another: across time, across locations, and across sellers. Furthermore, we compare online and offline prices by leveraging NielsenIQ’s scanner data and matching the same set of products and cities. We organize our findings into three core facts.

The first fact is that online grocers automate price setting using algorithmic pricing—a technology traditionally used by airlines, ride-hailing, and online platforms for durable goods. We document a remarkably high frequency of price changes, which exceeds what has been observed in previous studies using offline or online supermarket data. Furthermore, the scope of price algorithms is noteworthy: they trigger multiple price changes a day at the product x zipcode level.

Our second fact reveals that price algorithms charge different prices across locations. This practice can be thought of as “personalizing prices” at the delivery zipcode level. Recall Fig. 6, showing that prices even vary across two zipcodes in Miami. In fact, customers are required to enter a delivery zipcode before they can gain access to the assortment and prices of an online grocery retailer. It is plausible that zipcode-specific online stores facilitate algorithms in implementing price discrimination strategies.

The third stylized fact regarding the use of price algorithms is the presence of persistent price disparities across sellers. This means that prices for the exact same product, on the same day, and in the same delivery zipcode, can vary significantly between rival retailers. This observation challenges the notion that the Internet’s transparency and the availability of price comparison websites lead to lower search costs and tighter price competition. Once again, online price dispersion is higher than what is observed in the offline channel.

There are several implications of the documented algorithmic pricing for the U.S. retail grocery industry.

  • Price experimentation. Algorithmic pricing allows firms to run price experiments. Indeed, Fig. 4 documented several examples in which algorithms explore at least 6 distinct prices in just 1 week. Algorithms can launch countless simultaneous experiments in which prices in test markets (i.e., zipcodes) are updated in various ways to dynamically learn demand and optimal prices, while prices remain flat in other control markets (Misra et al., 2019; Dubé & Misra, 2023; Aparicio & Misra, 2023). Zipcode-specific online stores are convenient A/B testing laboratories because customers are not exposed to (and cannot arbitrage) prices from different delivery zipcodes. From a managerial point of view, the gains from experimentation can be economically meaningful given the complexities of choosing prices for grocery products: the market is characterized by large and time-varying assortments, substitution/complementarity patterns, and stock-outs. Algorithmic pricing is a scalable way to learn optimal prices for many products (and cross-product elasticities) and bundles. Note that this kind of experimentation is prohibitively costly in brick-and-mortar stores, explaining why price dispersion is considerably lower.

  • Price discrimination. Algorithmic pricing enables firms to price-discriminate across customer segments. Algorithms can price-discriminate across customers depending on their address, namely their delivery zipcode. Charging different prices across stores (price zones) is a form of third-degree price discrimination (Khan & Jain, 2005) and is further amplified by algorithms’ finer granularity of product x timestamp x zipcode level. For instance, algorithms can utilize browsing and purchasing patterns by neighborhoods to then partition the assortment space and set heterogeneous relative expensiveness rules (i.e., relative prices across markets can greatly vary across products). Indeed, online price dispersion across markets is substantially higher than across offline stores. Algorithms may also enable inter-temporal price discrimination between deal-seekers and high-valuation customers. In the words of Hendel and Nevo (2003), “help the seller discriminate between the less intense buyer, who more frequently will end up paying the modal price, and the more intense buyer who is willing to wait for promotions.” Fig. 4 showed various examples of Hi-Lo promotional strategies. Nonetheless, we lack purchase records to tease out whether/what transactions occur at which prices, and which sets of customers purchase at those prices. In the offline channel, price promotions last for several days and are advertised using features and display—thus, price-sensitive households are unlikely to miss them. In contrast, we document online price drops which last for a short time, and it is unclear if the intent of the algorithm is to capture price-sensitive households—in order not to miss such promotion, households would have to search fairly frequently. These differences may affect the set of consumers who want to use an online or offline channel, may segment one-stop vs. multi-stop customers (Bell & Lattin, 1998), and may also affect the long-run equilibrium of online promotional practices.

  • Price competition. An important concern of algorithmic pricing for policy is collusion (Miklós-Thal & Tucker, 2019; Hansen et al., 2021; Aparicio & Misra, 2023). This is particularly relevant for groceries because rival online grocers sell identical products in the same delivery zipcodes. Our data covers a relatively short period and therefore cannot shed light on the extent to which algorithms may facilitate collusive prices. At the very least, Fig. 10 showcased that competing algorithms are mindful of each other’s prices—and have the ability to price-match at the product x zipcode level within hours. Future work should examine long-term implications for price competition, such as price levels over time, coordination of price discounts, and customer segmentation.

The pricing strategies we have considered in this study are specific to the online grocery market and to leading (and sophisticated) retailers—especially Amazon and Walmart. Accordingly, our findings may not directly apply to other markets or sellers. We therefore encourage scholars to build upon our empirical approach and collect matched-product data to further advance our understanding of price algorithms as technology evolves and their implementation becomes more prevalent in the economy. We also note that our data is unable to compare the same retailer in the online and offline channels, and so further research should examine the scope of algorithms in multi-channel settings. Other research questions going forward should cover thinner price customizations beyond the zipcode-level, multi-product or multi-location optimization algorithms, and forms of collusive prices.