Abstract
Firms in durable good product markets face incentives to intertemporally price discriminate, by setting high initial prices to sell to consumers with the highest willingness to pay, and cutting prices thereafter to appeal to those with lower willingness to pay. A critical determinant of the profitability of such pricing policies is the extent to which consumers anticipate future price declines, and delay purchases. I develop a framework to investigate empirically the optimal pricing over time of a firm selling a durable-good product to such strategic consumers. Prices in the model are equilibrium outcomes of a game played between forward-looking consumers who strategically delay purchases to avail of lower prices in the future, and a forward-looking firm that takes this consumer behavior into account in formulating its optimal pricing policy. The model outlines first, a dynamic model of demand incorporating forward-looking consumer behavior, and second, an algorithm to compute the optimal dynamic sequence of prices given these demand estimates. The model is solved using numerical dynamic programming techniques. I present an empirical application to the market for video-games in the US. The results indicate that consumer forward-looking behavior has a significant effect on optimal pricing of games in the industry. Simulations reveal that the profit losses of ignoring forward-looking behavior by consumers are large and economically significant, and suggest that market research that provides information regarding the extent of discounting by consumers is valuable to video-game firms.








Similar content being viewed by others
Notes
Competition with used-games is also unlikely to be an issue. The trade-press suggests that used-games sales in the US during the period 1998–2000 constituted only a small fraction of overall industry sales. For instance, FuncoLand, the only used-game retailer in the US with a national presence, reports annual dollar sales of $0.16 million in 1998 (Serlin 1998). In comparison, overall new video-game dollar sales in 1998 in the US was $5.5 billion (IDSA 2001).
Motivated by the empirical application to video-games, depreciation in product quality, and the potential for resale in the future are ignored.
For technical convenience I assume that ɛ rt and ɛ r0t are mean zero extreme value variates with location parameter -Γ, and scale parameter 1 (where, Γ is Euler’s constant.) Assuming that the location parameter is -Γ rather than 0 (as is standard in the literature) does not change the choice probabilities, but eliminates the Euler’s constant from the value function equation in Eq. 3 (see Rust 1987.)
Let h t = {s τ ,p τ , τ = 1,..,t − 1} denote the history of the game till period t. A policy is Markov at time t if there is a function p*: \({\text{R}}^{{{\left( {{\text{r + 1}}} \right)}}}_{{\text{ + }}} \to R_{ + } \) such that p t (h t ) = p t *(s t ) for all s t, and f(s t |h t ) ≡ f(s t |s t − 1,p t−1). A sequence of policies p t (h t ), is said to be a subgame perfect equilibrium if at any time t > 0, V(p t (h t )) ≥ V(p t ′(h t )), where p t ′(h t ) is any alternate policy. If a sequence of Markov policies {p t *} is a subgame perfect equilibrium, the equilibrium is said to be Markov-perfect. A sequence of Markov policies {p t *} is said to be stationary if p t * ≡ p* for all t ≥ 0.
BW establish analytically the existence and uniqueness of a subgame perfect Nash equilibrium in prices in the context of a related, stylized demand model with uniformly distributed consumers and no uncertainty (i.e. no shocks to demand).
One way to explicitly account for such “novelty” effects may be to include a flexible function of the time since game-introduction into consumer utility, so as to capture the decline in utility with the age of the game in a reduced form way (e.g. Einav 2006, and the regressions presented in Appendix D). One computational difficulty associated with introducing functions of time in this manner is that “calendar time” then explicitly becomes a relevant state variable for the firm’s pricing problem. This implies that we can no longer solve for a stationary pricing policy function. Further, one can get different pricing patterns depending on the chosen functional form for the decay.
With forward-looking consumers, the Jacobian terms in the associated likelihood function will involve numerical derivatives of the consumer value function W r (.) with respect to the demand shocks ξ. These tend to be unstable unless W r (.) is approximated very finely over the grid of ξ, which is computationally expensive.
This implies that we assume that the distribution of valuations for video-games in the population adopting the console is stationary (e.g. Conlisk et al. 1984; Narasimhan 1989). Stationarity implies that the distribution of (α jr ,β r ) in entering cohorts of consumers is constant over time. This assumption could be violated if consumers adopting the hardware console later in the life-cycle also have correspondingly lower valuations for compatible games. Incorporating this effect would require modeling the consumers’ joint decision to adopt the console and the set of compatible games, which is beyond the scope of the current analysis. Given the short time series in the video-game data (1.5 years), I expect the stationarity assumption to be a reasonable approximation. Further, I do not find any evidence in the data that games released later in the life-time of the consoles have lower levels or higher rates of decline in prices. Reflecting my empirical application to this industry, I also model the number of new consumers entering the market as exogenous to prices of game j. Given the large number of games for each console (over 600 for the Sony PlayStation), prices of any one game do not tend to shift aggregate sales of the hardware console. In the data, PlayStation console sales do not correlate significantly with prices of any one game. Further, after controlling for hardware console prices and game availability, game prices do not significantly explain console sale variation over time. This suggests that conditional on availability, to a first approximation, console sales can be treated exogenous to prices of any one game.
That is, we have assumed in Eq. 16 that the transition density of (p j,t + 1,ξ jt + 1 )|p t ,ξ jt can be factored as \( f_{{p\xi }} {\left( {p_{{t + 1}} ,\xi _{{t + 1}} \left| {p_{t} ,\xi _{t} } \right.} \right)} = f_{{\xi \left| p \right.}} {\left( {\xi _{{t + 1}} \left| {p_{{t + 1}} } \right.} \right)}f_{p} {\left( {p_{{t + 1}} \left| {p_{t} } \right.} \right)} \). Implicitly, while p and ξ can be contemporaneously correlated, I make the assumption that the realization of ξ t does not contain any information about p t + 1 or ξ t + 1 except through p t . The assumption implies that (a) ξ is iid across time, and (b) p t + 1 is a function of ξ t only through p t . In principle, conditional independence can be relaxed (e.g. Keane and Wolpin 1994), albeit at much larger computational cost.
To see this, note that with logit errors, the option value of waiting satisfies the functional equation: W rj (p jt ,ξ jt ;Θ) \( \begin{array}{*{20}c} { = \delta _{c} {\int\limits_p {{\int\limits_\xi {{\text{In}}{\left[ {\exp {\left( {\alpha _{{rj}} - \beta _{r} p_{{jt + 1}} + \xi _{{jt + 1}} } \right)} + \exp {\left( {W_{{rj}} {\left( {p_{{jt + 1}} ,\xi _{{jt + 1}} ;\Theta } \right)}} \right)}} \right]}f_{{p\xi }} {\left( {\left. {p_{{jt + 1}} ,\xi _{{jt + 1}} } \right|p_{{jt}} ,\xi _{{jt}} } \right)}{\text{d}}p_{{jt + 1}} {\text{d}}\xi _{{jt + 1}} } }} }} \\ { = \delta _{c} {\int\limits_p {{\int\limits_\xi {{\text{In}}{\left[ {\exp {\left( {\alpha _{{rj}} - \beta _{r} p_{{jt + 1}} + \xi _{{jt + 1}} } \right)} + \exp {\left( {W_{{rj}} {\left( {p_{{jt + 1}} ,\xi _{{jt + 1}} ;\Theta } \right)}} \right)}} \right]}f_{{\left. p \right|\xi }} {\left( {\left. {p_{{jt + 1}} } \right|p_{{jt}} ,\xi _{{jt + 1}} } \right)}f_{\xi } {\left( {\xi _{{jt + 1}} } \right)}{\text{d}}p_{{jt + 1}} {\text{d}}\xi _{{jt + 1}} } }} }} \\ \end{array} \).Its clear that the RHS is not a function of ξ jt , and hence, W rj (p jt ,ξ jt ;Θ) ≡ W rj (p jt ;Θ).
I thank Wes Hartmann for suggesting this example. Chintagunta (1999) (section 3), and Song and Chintagunta (2003) (section 4.1) provide Monte Carlo evidence for parametric identification of heterogeneity in static and dynamic logit-based aggregate demand systems respectively, with 1 brand and an outside good.
I do not consider games released after March 2000, to avoid pricing issues related to expectations that game publishers could have had about the release of the next generation Playstation 2 console in October 2000.
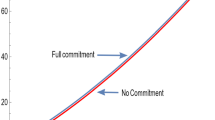
The results also indicate that both the slope and level of prices contain information about the consumer discount factor. In particular, it suggests that, while computationally burdensome, imposing the equilibrium pricing policy in a joint model of demand and pricing will be informative in pinning down the consumer’s discount factor. This is relevant given the difficulties that past literature has documented in reliably estimating the consumer’s discount factor from observed data.
However, if the proportion of new consumers is high enough, we see that it is possible that the probability that a consumer belongs to high-valuation segment does not fall over time. Then, the optimal pricing policy for the firm is cyclic: to keep prices high for many periods to sell mainly to high-valuation new consumers, and then cut price to clear the market of the low-valuation consumers (Conlisk et al. 1984; Narasimhan 1989).
More sophisticated estimation approaches for the Bass model (e.g. non-linear least squares) gave comparable estimates for the market potential.
References
Balachander, S., & Srinivasan, K. (1998). Modifying customer expectations of price decreases for a durable product. Management Science, 44(6), 776–786.
Bass, F. (1969). A new-product growth model for consumer durables. Management Science, 15, 215–227.
Benýtez-Silva, H., Hall, G., Hitsch, G., Pauletto, G., & Rust, H. (2000). A comparison of discrete and parametric approximation methods for continuous-state dynamic programming problems. Working paper, SUNY-Stony Brook.
Benkard, L. (2004). A dynamic analysis of the market for wide-bodied commercial aircraft. Review of Economic Studies, 71, 581–611.
Berry, S. (1994). Estimating discrete choice models of product differentiation. Rand Journal of Economics, 25(2), 242–261.
Berry, S., Levinsohn, J., & Pakes, A. (1995). Automobile prices in market equilibrium. Econometrica, 60(4), 841–890.
Besanko, D., Dubé, J. P., & Gupta, S. (2003). Competitive price discrimination strategies in a vertical channel with aggregate data. Management Science, 49(9), 1121–1138.
Besanko, D., & Winston, W. (1990). Optimal price skimming by a monopolist facing rational consumers. Management Science, 36(5), 555–567.
Bulow, J. (1982). Durable goods monopolists. Journal of Political Economy, 90, 314–332.
Chevalier, J., & Goolsbee, A. (2005). Are durable good consumers forward looking? Evidence from college textbooks. Working paper, University of Chicago.
Ching, A. (2005). Consumer learning and heterogeneity: Dynamics of demand for prescription drugs after patent expiration. Working paper, Rotman School of Management, University of Toronto.
Chintagunta, P. (1999). A flexible aggregate logit model. Working paper, University of Chicago.
Chintagunta, P., Dube, J.-P., & Goh, K.-Y. (2005). Beyond the endogeneity bias: The effect of unmeasured brand characteristics on household-level brand choice models. Management Science, 51(2).
Coase, R. (1972). Durability and monopoly. Journal of Law and Economics, 15, 143–149.
Conlisk, J. Gerstner, E., & Sobel, J. (1984). Cyclic pricing by a durable good monopolist. Quarterly Journal of Economics, 99(3), 489–505 (August).
Coughlan, P. (2001). Competitive dynamics in home video-games. J, K: Harvard Business School Cases.
Desai, P., & Purohit, D. (1999). Competition in durable goods markets: The strategic consequences of leasing and selling. Marketing Science, 18(1), 42–58.
Dolan, R., & Jeuland, A. (1981). Experience curves and dynamic demand models: Implications for optimal pricing strategies. Journal of Marketing, 45, 52–62.
Dubé, J. P., Hitsch, G., & Manchanda, P. (2005). An empirical model of advertising dynamics. Quantitative Marketing and Economics, 3(2), 107–144.
Einav, L. (2006). Seasonality in the U.S. motion picture industry. RAND Journal of Economics, (forthcoming).
Erdem, T., Keane, M. P., & Strebel, J. (2005). Learning about computers: An analysis of information search and technology choice. Quantitative Marketing and Economics, 3(3), 207–247.
Godfrey, L. G. (1978). Testing against general autoregressive and moving average error models when the regressors include lagged dependent variables. Econometrica, 46, 1293–1302.
Gowrisankaran, G., & Rysman, M. (2006). Dynamics of consumer demand for new durable goods. Working paper, Washington University at St. Louis.
Gul, F., Sonneenschein, H., & Wilson, R. (1986). Foundations of dynamic monopoly and the coase conjecture. Journal for Economic Theory, 39, 155–190.
Hitsch, G. (2006). An empirical model of optimal dynamic product launch and exit under demand uncertainty. Marketing Science, 25(1), 25–50.
Horsky, D. (1990). A diffusion model incorporating product benefits, price, income, and information. Marketing Science, 9(Fall), 342–365.
Interactive Digital Software Association (IDSA) (2001). State of the Industry Report: 2000–2001. http://www.idsa.com/pressroom.html, accessed July 21, 2004.
Judd, K. (1998). Numerical methods in economics. Cambridge: MIT Press.
Kahn, C. (1986). The durable good monopolist and consistency with increasing costs. Economterica, 54, 275–294.
Kalish, S. (1983). Monopolistic pricing with dynamic demand and production cost. Marketing Science, 2, 135–160.
Kalish, S. (1985). A new product adoption model with pricing, advertising and uncertainty. Management Science, 31, 1569–1585.
Kamakura, W. A., & Russell, G. (1989). A probabilistic choice model for market segmentation and elasticity structure. Journal of Marketing Research, 26, 379–390.
Keane, M. P., & Wolpin, K. I. (1994). The solution and estimation of discrete choice dynamic programming models by simulation and interpolation: Monte Carlo evidence. Review of Economics and Statistics, 76, 648–672.
Krishnan, T., Bass, F., & Jain, D. (1999). Optimal pricing strategy for new products. Management Science, 45(12), 1650–1663.
Landsberger, M., & Meilijson, I. (1985). Intertemporal price discrimination and sales strategy under incomplete information. Rand Journal of Economics, 16(3), 424–430.
Lazear, E. (1986). Retail pricing and clearance sales. American Economic Review, 76(1), 14–32.
Ljung, G. M., & Box, G. E. P. (1978). On a measure of lack of fit in time series models. Biometrika, 65, 297–303.
Mahajan, V., Muller, E., & Kerrin, R. A. (1984). Introduction strategy for new products with positive and negative word-of-mouth. Management Science, 30, 1389–1404.
Melnikov, O. (2000). Demand for differentiated durable products: The case of the U.S. computer printer market. Working paper, Yale University.
Moorthy, K. S. (1988). Consumer expectations and the pricing of durables. In T. Devinney (Ed.), Issues in pricing. Lexington, MA: Lexington Books.
Narasimhan, C. (1989). Incorporating consumer price expectations in a diffusion model. Marketing Science, 8(4), 343–357.
Pashigian, B. P. (1988). Demand uncertainty and sales: A study of fashion and markdown pricing. American Economic Review, 78, 936–953.
Petrin, A., & Train, K. (2004). Omitted product attributes in discrete choice models. Working paper. Graduate School of Business, University of Chicago.
Robinson, B., & Lakhani, C. (1975). Dynamic pricing models for new product planning. Management Science, 10, 1113–1122.
Rust, J. (1987). Optimal replacement of GMC bus engines: An empirical model of Harold Zurcher. Econometrica, 55(5), 999–1033.
Rust, J. (1996). Numerical dynamic programming in economics. In H. Amman, D. Kendrick, & J. Rust (Eds.), Handbook of computational economics. North Holland: Elsevier.
Serlin, J. (1998). “FuncoLand Inc.,” Cornell Equity Research. Johnson School of Management, Cornell University. http://parkercenter.johnson.cornell.edu/docs/other_research/1998_fall/fnco.pdf, July 2004.
Song, I., & Chintagunta, P. (2003). A micromodel of new product adoption with heterogeneous and forward-looking consumers: Application to the digital camera category. Quantitative Marketing and Economics, 1(4), 371–407.
Stokey, N. (1979). Intertemporal price discrimination. Quarterly Journal of Economics, 93(3), 355–371.
Stokey, N. (1981). Rational expectations and durable goods pricing. Bell Journal of Economics, 12, 112–128.
Tirole, J. (1988). The theory of industrial organization. Cambridge: MIT Press.
Villas-Boas, M., & Winer, R. (1999). Endogeneity in brand choice models. Management Science (45), 1324–1338.
Williams, D. (2002). Structure and competition in the U.S. home video game industry. International Journal on Media Management, 4(1), 41–54.
Yang, S., Chen, Y., & Allenby, G. M. (2003). Bayesian analysis of simultaneous demand and supply. Quantitative Marketing and Economics, 1, 251–304.
Acknowledgement
I thank my dissertation committee, Pradeep Chintagunta, Jean-Pierre Dubé, Günter Hitsch, and Peter Rossi for their guidance. I am grateful to Ester Han, Karen Sperduti and Sima Vasa of the NPD group, and R. Sukumar of IPSOS-Insight for their help in making available the data used in this research. I thank Dan Alderman of the Microsoft Xbox group, and Norman Basch of Reservoir Labs for sharing with me their insights on the video-game industry. I also received useful feedback from Tim Conley, Ulrich Doraszelski, Liran Einav, Wes Hartmann, Puneet Manchanda, Peter Reiss, Alan Sorensen two anonymous referees and seminar participants at Berkeley, CMU, Columbia, Cornell, Dartmouth, HKUST, ISB, MIT, Northwestern, Purdue, Stanford, UCLA, UConn, UMaryland, UPenn, UToronto, UWisconsin, Washington St. Louis and Yale.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is based on my dissertation. All errors in the paper are my own.
Appendices
Appendix A Numerical computation of the equilibrium
I solve for the equilibrium numerically using policy iteration. The algorithm is summarized below:
-
(a)
Discretize the state space into G s points, and choose a tolerance value ɛ.
-
(b)
Let S denote an {M 1,M 2 ,..,M R ,ξ } combination. Choose guesses for the optimal policy, p (n)(S), and the consumer’s equilibrium waiting functions \(W^{{{\left( {n,k} \right)}}}_{r} {\left( S \right)}\), r = 1,..,R.
-
(c)
Given, \(W^{{{\left( {n,k} \right)}}}_{r} {\left( S \right)}\), compute \( s^{{{\left( {n,k} \right)}}}_{r} {\left( {\user2{S}} \right)} = \frac{{e^{{\alpha _{r} - \beta _{r} p^{{{\left( n \right)}}} {\left( s \right)} + \xi }} }} {{e^{{W^{{{\left( {n,k} \right)}}}_{r} {\left( S \right)}}} + e^{{\alpha _{r} - \beta _{r} p^{{{\left( n \right)}}} {\left( s \right)} + \xi }} }},r = 1,..,R \)
-
(d)
Given \( s^{{{\left( {n,k} \right)}}}_{r} {\left( {\user2{S}} \right)} \), set up evolution of endogenous state variables for each segment as:
$$ M^{{{\left( {n,k} \right)}}}_{r} = M_{r} {\left[ {1 - s^{{{\left( {n,k} \right)}}}_{r} {\left( {\user2{S}} \right)}} \right]} + \varphi _{r} N,r = 1,..,R $$ -
(e)
Given \( M^{{{\left( {n,k} \right)}}}_{r} \), r = 1..,R, solve consumer’s problem to compute the new guess of equilibrium waiting functions for the R segments, \( W^{{{\left( {n,k + 1} \right)}}}_{r} {\left( {\user2{S}} \right)} \), r = 1, R:
$$ W^{{{\left( {n,k + 1} \right)}}}_{r} {\left( {\user2{S}} \right)} = \delta _{c} {\int {\log {\left[ {e^{{\alpha _{r} - \beta _{r} p{\left( {M^{{\prime {\left( {n,k} \right)}}}_{1} ,..M^{{\prime {\left( {n,k} \right)}}}_{R} ,\xi \prime } \right)} + \xi \prime }} + e^{{W^{{{\left( {n,k + 1} \right)}}}_{r} {\left( {M^{{\prime {\left( {n,k} \right)}}}_{1} ,..,M^{{\prime {\left( {n,k} \right)}}}_{r} \xi \prime } \right)}}} } \right]}} }{\text{d}}F{\left( {\left. {\xi \prime } \right|\xi } \right)},r = 1,..,R $$ -
(f)
Iterate on (c–e) till \({\left| {W^{{{\left( {n,k + 1} \right)}}}_{r} {\left( {\user2{S}} \right)} - W^{{{\left( {n,k} \right)}}}_{r} {\left( {\user2{S}} \right)}} \right|} < \varepsilon ,for\,r = 1,..,R\). This gives the equilibrium waiting functions given the guess of the pricing policy p (n)(S).
-
(g)
Solve for firm’s value function V (n) that satisfies (policy valuation step):\( V^{{{\left( n \right)}}} {\left( S \right)} = \pi {\left( {S,p^{{{\left( n \right)}}} {\left( S \right)}} \right)} + \delta _{f} {\int {V^{{{\left( n \right)}}} } }{\left( {S\prime } \right)}f{\left( {\left. {\xi \prime } \right|\xi } \right)}d{\left( {\xi \prime } \right)}\, \) where
$$ \begin{array}{*{20}l} {{\pi {\left( {S,p^{{{\left( n \right)}}} {\left( S \right)}} \right)} = \widetilde{Q}{\left( S \right)}{\left( {p^{{{\left( n \right)}}} {\left( S \right)} - c} \right)} - F} \hfill} \\ {{\widetilde{Q}{\left( S \right)} = {\sum\limits_{r = 1}^R {M^{{{\left( {n,k + 1} \right)}}}_{r} } }s^{{{\left( {n,k + 1} \right)}}}_{r} {\left( S \right)}} \hfill} \\ {{s^{{{\left( {n,k + 1} \right)}}}_{r} {\left( S \right)} = \frac{{e^{{\alpha _{r} - \beta _{r} p^{{{\left( n \right)}}} {\left( S \right)} + \xi }} }} {{e^{{W^{{{\left( {n,k + 1} \right)}}}_{r} {\left( S \right)}}} + e^{{\alpha _{r} - \beta _{r} p^{{{\left( n \right)}}} {\left( S \right)} + \xi }} }},r = 1,..,R} \hfill} \\ \end{array} $$ -
(h)
Given V (n) compute the improved policy using: \( p^{{{\left( {n + 1} \right)}}} {\left( S \right)} = {\mathop {\arg \max }\limits_{p> 0} }{\left[ {\pi {\left( {S,p} \right)} + \delta _{f} {\int {V^{{{\left( n \right)}}} {\left( {S\prime } \right)}f{\left( {\left. {\xi \prime } \right|\xi } \right)}d{\left( {\xi \prime } \right)}} }} \right]} \), with p (n)(S) as starting value.
-
(i)
If \( {\left| {p^{{{\left( {n + 1} \right)}}} {\left( S \right)} - p^{{{\left( n \right)}}} {\left( S \right)}} \right|} < \varepsilon \), stop, and set p*(S) = p (n + 1)(S), and W r *(S) = W r (n,k+1)(S), r = 1,..,R; else go back to (b) with p (n + 1)(S) and W r (n,k+ 1)(S) as initial guesses.
I approximate the firm’s value function V(S), the consumer’s waiting functions W r (S), and the pricing policy p(S), using the tensor product of a Chebychev polynomial basis of order 5 in each state dimension (Judd 1998, chapter 6, provides a discussion of Chebychev approximation methods). The state space is discretized using 15 points in each dimension and the state points chosen as the corresponding Chebychev zeros. I allow for the complete set of interactions between polynomial terms of the segment size {M 1,M 2,..,M R } state variables and ξ for approximating p(S) and W r (S), and set interactions between {M 1,M 2,..,M R } and ξ to zero in approximating V(S). Once the corresponding Chebychev parameters are computed, the functions are trivially interpolated to other parts of the state space. The integral in step (e) is computed using Monte-Carlo integration using 30 draws, and the integral in step in (i) is computed using Gauss–Hermite quadrature using 8 nodes.
Appendix B Incentives to cut prices
Equation 7 shows how the sizes of each segment in the potential market evolve over time. If the number of new consumers is low relative to the existing market size, this generates a shift in the distribution of heterogeneity in the potential market toward lower valuations, implying that a firm that takes this into account should optimally cut prices over time. To see this, consider the probability that a consumer chosen at random in period t + 1 belongs to segment r, μ r,t+1, given the corresponding probability μ rt for period t. Let η jr ≡ (α jr ,β r ) denote the parameters characterizing segment r and let w rjt = 1 denote the event that consumer type r chooses to not purchase game j in period t, and waits for period (t + 1). We first note that the probability that a consumer chosen at random from among those that waited for time t + 1 belongs to segment r, is given as:
Noting that the share of new consumers in time (t + 1) is \( \lambda _{{t + 1}} = N \mathord{\left/ {\vphantom {N {{\left( {{\sum\nolimits_{r = 1}^R {M_{{r,t + 1}} } }} \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {{\sum\nolimits_{r = 1}^R {M_{{r,t + 1}} } }} \right)}} \), the distribution of valuations in the entire potential market for the game in period (t + 1) is given by the mixture:
It is easy to see that the probability that a consumer belongs to a given segment r, falls at a faster rate \( {\left( {{\widetilde{\mu }_{{r,t + 1}} } \mathord{\left/ {\vphantom {{\widetilde{\mu }_{{r,t + 1}} } {\mu _{{r,t + 1}} }}} \right. \kern-\nulldelimiterspace} {\mu _{{r,t + 1}} }} \right)} \) for segments with higher valuations (α r ) and lower price sensitivities (β r ). Hence, if λ t is low, over time, the mix of consumers in the potential market will be composed of those with lower valuations and higher price sensitivities, and the firm would cut prices.Footnote 14
Appendix C Computation of market sizes
To estimate demand, I also need to develop measures of the initial market size for each game (M 0 in Eq. 7). A firm using the model is likely to have information on the initial market potential for its product, or can obtain a measure of it through market research. However, as a researcher, I need to somehow infer this from the observed data. A simple option is to use the entire installed base of the hardware at the time of introduction of the game as the initial market. A problem with this approach is the large size of the hardware installed base relative to the total sales of each game. In the data, the average installed base of Sony Playstation consoles at the time of game introduction was 16.5 million—while the maximum sales across all games in the data stood at around 1 million. The corresponding market shares are very small (of the order of 1E-5), and result in large negative fixed effects for each game when estimating demand. This effectively implies that even at the time of exit from the market, the size of each segment in the potential market for the game would remain virtually unchanged from the time of introduction. The state variables for the firm (i.e. the segment sizes) therefore do not change over time, and all variation in prices will have to be explained by changes in the realized demand shock ξ. To fix this issue, I adopt an alternative method to infer the size of each game’s potential market prior to estimating demand.
Specifically, the diffusion literature starting with Bass (1969) shows how it is possible to infer the size of the potential market of a product from data on the sales path. I use the Bass diffusion model to estimate the market size for each game. An approximation to the discrete-time version of the model implies an estimation equation in which current sales are related linearly to cumulative sales, and (cumulative sales)2 . Specifically, letting q jt and Q jt denote the sales and cumulative of game j in month t respectively, I estimate the pooled regression:
Given the regression coefficients, the Bass model implies that the market sizes for each game are given as \( \overline{M} _{j} = {a_{j} } \mathord{\left/ {\vphantom {{a_{j} } {p_{j} }}} \right. \kern-\nulldelimiterspace} {p_{j} } \), where p j is the positive root of the equation: \( p^{2}_{j} + p_{j} b + a_{j} c = 0 \). The mean market size so computed is 1.52 million, which corresponds to an average market share of 0.0802 across games and months.Footnote 15 The market shares are then used for estimating demand.
Appendix D Derivation of the Jacobian
I compute the Jacobian, \(J_{{{\left\{ {\xi ,\eta } \right\}} \to {\left\{ {q,p} \right\}}}} \) as follows. Suppose we can invert the aggregate demand function \( {\mathbf{q}}_{{jt}} = \widetilde{{\mathbf{Q}}}_{{jt}} {\left( \Theta \right)} = {\sum\nolimits_{r = 1}^R {{\mathbf{M}}_{{rjt}} {\mathbf{S}}_{{rjt}} {\left( {{\mathbf{p}}_{{jt}} ,\xi _{{jt}} } \right)}} } \) in Eq. 6 to obtain ξ jt . Denote this inversion mapping G 1. Denote the inversion of the price process to obtain η t as G 2. That is,
By definition, the Jacobian is:
To compute the derivative, let \( G = {\sum\nolimits_{r = 1}^R {M_{{rjt}} } }s_{{rjt}} {\left( {p_{{jt}} ,\xi _{{jt}} ;\Theta } \right)} \)-q jt = 0. By the implicit function theorem,
Appendix E Falling costs and competition
I discuss the role of declining marginal costs and increased competition in explaining price declines of the video-games. I first consider the falling-cost explanation. While economies-of-scale in the production of consoles imply that cost-related considerations play a role on the hardware-side, this is not the case on the software-side. The cost structure of video-games involves a fixed cost of game development and constant marginal costs thereafter. The latter correspond to royalty fees paid by the game manufacturer to the hardware platform provider, and also the costs of producing and packaging each CD-ROM title. The royalty fee for the 32-bit Sony Playstation compatible games in the data was pre-announced and held fixed at $10 by Sony throughout the life-cycle. Further, Coughlan (2001) reports that production/packaging costs for 32-bit CD-ROM games remained roughly constant at $1.5 per disc. Thus, I rule out falling costs and experience curve effects as a motive for price-cutting.
I now consider the role of competition. Several features of the data indicate that competition alone is inadequate in explaining the declining path of prices. In particular, I find that (a) cross-price effects across games are very low, indicating that games are not very substitutable for one another; these hold after accounting for potentially strategic behavior by game-manufacturers who may release games so as to minimize cannibalization from similar games existing in the market, (b), the pricing predictions from a demand model that ignores substitution effects are comparable to ones that explicitly account for these effects, (c) intertemporal price effects within narrowly defined game genres are statistically insignificant, (d) entry of hit games do not have significant effects on sales and prices of games within the genre, and (e) the rates at which prices fall are independent of competitive conditions in the market. I discuss these in sequence below.
1.1 Small cross-price effects and comparable margins between nested-logit, multinomial-logit and binary-logit specifications
We can expect substitution effects in the video-game market to be small for two reasons. First, there are a large number of games in the market. Between October 1998 and March 2000, there was an average of 665 titles available in the market per month for the Sony Playstation console. Second, each game is fairly unique, having its own distinct features, characters and idiosyncrasies: other than the genre-membership, there are few common tangible attributes by which to measure game “quality.” A priori, the large number of games in the market and the wide differentiation of game titles suggest that video-game titles are imperfect substitutes for each other.
We can test these formally by measuring cross-price effects among games. A concern is that cross-price substitution effects may be understated if game-manufacturers release games strategically so as to minimize cannibalization from similar games existing in the market. To address this, I estimate specifications similar to Einav (2006) that tries to control for the endogeneity of release times of games. This specification is a static nested-logit model of demand with nests corresponding to the video-game genres. The benchmark specification is:
where, t indexes month, r j is the release date of game j, p jt is the price, s jt is the market share of game j in month t, s 0t is the share of the outside good and s jt|g is the share of units sales of the game within its genre, g. A large σ indicates strong correlation in utilities of games within genre g; a small σ closer to zero indicates little within-genre correlation. The larger the σ, the larger the cross-price effects among games within each genre. The parameter λ captures the rate of decay of game sales from introduction.
The concern regarding introduction timing arises here because game manufacturers may be unlikely to release a new game in periods with very high-quality games or with games that are very similar. If “quality” or “similarity” of other games within the genre is included in the unobservable component of demand in period t, this may make r j endogenous and λ biased. I can address this issue fully by including game-fixed effects. By including a full set of fixed effects, all variation in demand arising from aspects of game-quality is already controlled for. To estimate the above model, I also need instruments for the within-genre share and prices. I use the number of games available in each genre each month as an instrument for within-genre share. More games within each genre are likely associated with more intense competition, and therefore should be negatively related to the within genre share. Analogous to Einav (2006), the identifying assumption here is that the number of games in a genre in a month is not correlated with the part of decay pattern that is specific to game j (ξ jt ). I use lagged prices as instruments for current period prices. These instruments are admittedly imperfect: I present specifications with and without including instruments for prices to demonstrate that these are not fully driving the results.
I estimate the nested-logit specification on the sample of new games in my data. Results are presented in Table 8. OLS and 2SLS specifications with and without including instruments for prices, as well as adding quadratic and cubic polynomials in age (i.e. t − r j ), are reported. In general, the price coefficient goes up in absolute magnitude after instrumenting. The within-genre correlation σ is close to zero after instrumenting. The value of σ does not change if I drop lagged prices from the instrument matrix. These regressions suggest that within a genre, games are not perceived to be very close substitutes by consumers.
I repeat the same regressions for multinomial-logit and nested logit specifications. These are presented in Table 9. To compare whether accounting for substitution effects as well as within-genre effects makes a qualitatively significant difference for pricing, I compare the percentage markups corresponding to these specifications. Using the estimates for each model, I first compute markup-s using the first-order conditions corresponding to static profit-maximization (e.g. for the nested logit model, the mark-up is as in equation 33 in Berry 1994.) While these are only static estimates, strong substitution effects if present, are likely to result in large differences between the markups corresponding to the multinomial versus the binomial logit specifications. If substitution effects are strong within genre, these differences are likely to be even larger between the nested versus the binomial logit specifications. The top panel of Fig. 9 presents the histogram of the difference in % markups between the nested-logit and the binary logit models, across all game-months within each genre. The bottom panel presents the corresponding plots for the multinomial-logit and the binary logit models. I find that the differences are small. These results suggest that the primary aspect of substitution is with the outside good—i.e. whether to buy now or to delay purchase; the binary logit demand model I have used captures this reasonably. Leaving out the substitution effects, while limiting, does not seem a priori to result in huge biases in predicting pricing policies for this industry.
1.2 Small Intertemportal price-effects
I now test whether there is evidence in the data for intertemporal substation across games. Such intertemporal price effects would imply that lagged prices of games within the same genre would have a significant effect on current demand. Presumably, a low price yesterday for say, action games would attract consumers who were on the lookout for such games, take them out of the market for this genre for awhile, and thus reduce demand for action games today. Likewise, a high price yesterday, may likely leave more potential buyers of that genre in the market, thus raising its demand today. To check for some evidence of these effects in the data, I estimate OLS specifications of binary-logit models in which lagged prices of other games within the same genre are included as repressors. The results are presented in Table 10. Full sets of game and age-fixed effects are included. Columns [1–4] adds the lagged minimum, median and maximum prices within the genre (excluding the focal game) as regressors. These variables are not significant. In columns [5–6] I find the best-selling game (across all months in the data) in the genre, and add its lagged price as a regressor. These are not significant. These suggest that intertemporal cross-price effects may not be a first-order issue for these data.
1.3 Small Intertemportal substitution effects
Do sales/prices fall when a hit game is to be released? To test this empirically, I first find the best selling game within each genre across all the months in the data. I then include the number of months to release of this game as a regressor into binary-logit specifications of demand. Table 11 presents estimates of this model. I find that the included variable is not significant. The last columns of Table 8 allows for this effect to vary by genre. I do not find a significant effect on demand. These results suggest that that current demand is not significantly shifted down as best-sellers are closer to being released. To check whether prices decline at a faster rate when a hit game is closer to being released, I also estimate regressions of prices on game-fixed effects, game-age and game-age*Tg, where Tg is the number months to the release of the best-seller in that game’s genre’s. A significant negative coefficient on game-age*Tg would indicate that the release affects the rate of decline of prices. This regression gave a coefficient of −1.7 on age (t = −2.96) and 0.0444 on age*Tg (t = 0.193), i.e. not significant; further, the interactions with genre fixed effects were not significant. To summarize, I do not find much evidence of sales or prices falling in anticipation of hit-game releases into the market.
1.4 Rate of fall of prices not affected by competitive conditions
I now explore whether the rate at which prices fall is affected by the degree of competition in the market. The number of games in the market is increasing over the months in the data, and hence the market is getting more competitive over time. Hence, if game manufacturers are responding to the increased competition by cutting prices, I should find that the rate at which prices fall is higher during the later months in the data. Testing this however, is confounded by the fact that games released in the later months in the data are also likely to be of better “quality,” and hence, less likely to cut prices. I resolve the issue as follows. Stacking the data across all games and months, I regress prices on game-fixed effects, game-age (i.e. time since introduction), and interactions of game-age with month fixed effects. Thus, I measure the rate at which prices fall (as the coefficient on age) while fully controlling for quality using game-fixed effects. Statistically significant interactions between game-age and month fixed effects will indicate that the rate at which prices fall is affected by completive conditions in the market. Table 12 (columns 1–4) shows the results from the regression. Controlling for game-age and game-quality, I find that the interactions are not significant. In columns 5 and 6, I also report on the results from regressing the change in prices on month fixed effects, where as before, I control for game-quality using game-specific intercepts. Again, I find that changes in prices are not statistically significantly explained by month-specific effects. Further, the month fixed effects explain a negligible percentage (less than 1%) of the variation in price cuts. Finally, in other specifications (not reported) I allow the effect of age to be genre-specific and interact the age of the game with month and genre-fixed effects. The interactions of age with month-fixed effects are not significant for each genre in this specification.
1.5 Plots
A visual examination of pricing patterns of incumbent games in response to entry provides additional evidence that is consistent with these results. Figure 10 plots the prices of the three games that were introduced into the “Action-oriented Racing” genre during the time-frame of the data. “Castrol Honda Spr. Bike” by Electronic Arts is the first entrant, followed by “Monaco Grand Prix” from UBI Soft, and “Championship Motorcross” from THQ. We see that neither the entry by the potentially close substitute, “Monaco Grand Prix,” not its price cuts till month 58 triggers a price-cut in “Castrol Honda Spr. Bike.” While both games cut prices post month 58, these price cuts do not induce the newer entrant, “Championship Motorcross” to lower prices. Figure 11 presents plots of prices and sales for the “Role Playing Game” genre. We see that prices of “Legend of Legaia,” the best-selling incumbent in the genre, and “'Shadow Madness,” one of least selling games, do not drop in response to the entry by “Jade Cocoon” and “Star Ocean: Second Story.” This, in spite of the fact that “Star Ocean: Second Story” is the best seller in the genre after entry. The pattern suggests that that competition from newer and better games is not the driving force behind falling prices.
Appendix F Pricing by a forward looking firm facing a “shrinking market”
Consider a two period model. My goal is to show that a forward looking (“dynamic”) monopolist would be even more likely than a “static” monopolist to set prices in the elastic region of the demand curve. This result depends on the fact that in the durable good context, a higher price by the firm today is likely to result in a higher demand tomorrow (since fewer consumers buy today and hence, more are in the market for the product tomorrow.) In other contexts, e.g. dynamic monopoly pricing under goodwill effects or brand-loyalty, or under learning-by-doing (e.g. Tirole 1988, section 1.1.2.1 and 1.1.2.2), low prices today increases demand (or lowers costs) for the firm in the future. For these cases, the dynamic monopoly has an incentive to set prices that are lower than the corresponding myopic case, and could optimally price in the inelastic region of the demand curve.
I consider a two period model that incorporates the essence of the shirking market induced by the durable nature of the good. Let D(p) denote the demand for the game given price p such that D′(p) < 0. Let c denote the marginal cost, δ the firm’s discount factor, and p 1 and p 2 denote the prices in the two periods. To capture the shrinking market effect, I assume that given the first period price p 1, the firm faces a residual demand curve in the second period that is shifted downward by a factor α(p 1), such that 0 ≤ α(.) ≤ 1, and α′(.) > 0. Thus, the higher the firm’s first period price, the more will be the residual demand in the next period. The firm’s problem is to choose prices p 1 and p 2 that maximize discounted profits:
The first-order conditions imply that the optimal prices satisfy:
The optimal prices for the myopic case are:\( p^{*}_{{1 - c}} = { - D{\left( {p^{*}_{1} } \right)}} \mathord{\left/ {\vphantom {{ - D{\left( {p^{*}_{1} } \right)}} {D\prime {\left( {p^{*}_{1} } \right)}}}} \right. \kern-\nulldelimiterspace} {D\prime {\left( {p^{*}_{1} } \right)}} \), \( p^{*}_{2} - c = { - D{\left( {p^{*}_{2} } \right)}} \mathord{\left/ {\vphantom {{ - D{\left( {p^{*}_{2} } \right)}} {D\prime {\left( {p^{*}_{2} } \right)}}}} \right. \kern-\nulldelimiterspace} {D\prime {\left( {p^{*}_{2} } \right)}} \). We see that if the firm is forward looking, it has an added incentive to keep p 1 higher than the myopic price by a value \( {\delta \alpha {\left( {p^{*}_{1} } \right)}D^{2} {\left( {p^{*}_{2} } \right)}} \mathord{\left/ {\vphantom {{\delta \alpha {\left( {p^{*}_{1} } \right)}D^{2} {\left( {p^{*}_{2} } \right)}} {D\prime {\left( {p^{*}_{1} } \right)}D\prime {\left( {p^{*}_{2} } \right)}}}} \right. \kern-\nulldelimiterspace} {D\prime {\left( {p^{*}_{1} } \right)}D\prime {\left( {p^{*}_{2} } \right)}} \). Further, the more the firm cares about the future (i.e. the higher the δ) the higher will be the first period price. Intuitively, the firm takes into account the fact that a lower period 1 price would cut into period 2 profits, and this reduces the firm’s incentive to set the period 1 price as low as the myopic case.
Denote the elasticity of demand in period 1, \( {D\prime {\left( {p^{*}_{1} } \right)}p^{*}_{1} } \mathord{\left/ {\vphantom {{D\prime {\left( {p^{*}_{1} } \right)}p^{*}_{1} } {D{\left( {p^{*}_{1} } \right)}}}} \right. \kern-\nulldelimiterspace} {D{\left( {p^{*}_{1} } \right)}} \) as η 1. Since costs are non-negative, Eq. 23 implies:
Some algebra yields:
implying the price skimming monopolist would always price on the elastic region of the demand curve.
Rights and permissions
About this article
Cite this article
Nair, H. Intertemporal price discrimination with forward-looking consumers: Application to the US market for console video-games. Quant Market Econ 5, 239–292 (2007). https://doi.org/10.1007/s11129-007-9026-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11129-007-9026-4
Keywords
- Durable-good pricing
- Forward-looking consumers
- Markov-perfect equilibrium
- Numerical dynamic programming
- Video-game industry