Shrinkage priors for high-dimensional demand estimation

Abstract

Estimating demand for large assortments of differentiated goods requires the specification of a demand system that is sufficiently flexible. However, flexible models are highly parameterized so estimation requires appropriate forms of regularization to avoid overfitting. In this paper, we study the specification of Bayesian shrinkage priors for pairwise product substitution parameters. We use a log-linear demand system as a leading example. Log-linear models are parameterized by own and cross-price elasticities, and the total number of elasticities grows quadratically in the number of goods. Traditional regularized estimators shrink regression coefficients towards zero which can be at odds with many economic properties of price effects. We propose a hierarchical extension of the class of global-local priors commonly used in regression modeling to allow the direction and rate of shrinkage to depend on a product classification tree. We use both simulated data and retail scanner data to show that, in the absence of a strong signal in the data, estimates of price elasticities and demand predictions can be improved by imposing shrinkage to higher-level group elasticities rather than zero.

1 Introduction

Measuring price and promotional effects from store-level transaction data is a mainstay of economics and marketing research. However, many challenges arise in model specification and inference when the product space is large. For example, demand models for many goods should be flexible so as to not impose strong prior restrictions on cross-price effects, but flexible models contain many parameters so some form of dimension reduction or regularization is needed to avoid overfitting. While there is a large literature on regularized estimation, existing methods typically assume that the underlying parameter vector is sparse and so shrinkage points are fixed at zero. In this paper, we demonstrate the value of non-sparse, data-driven shrinkage in high-dimensional demand models.

Our primary contribution is to develop Bayesian shrinkage priors for pairwise product substitution parameters that may not be sparse but instead conform to a low-dimensional structure. We propose a hierarchical extension of the class of global-local priors (Polson & Scott, 2010) that is parameterized using information from a product classification tree. Typical retail scanner panel data sets, such as those provided by IRI and Nielsen, include product classification tables where goods are partitioned into broad categories (e.g., “Salty Snacks”), subcategories (“Potato Chips”), brands (“Lay’s”), and ultimately UPCs (“Lay’s Classic Potato Chips 20 oz.”). We explicitly use this tree structure to parameterize: (i) prior means, so that substitution between two goods will depend on the nature of substitution between their respective subcategories and categories; (ii) prior variances, so that shrinkage can propagate down through the tree. We also consider different forms of shrinkage at each level of the tree—e.g., ridge (Hoerl & Kennard, 1970) vs. horseshoe (Carvalho et al., 2010)—and provide novel results on the shrinkage behavior of the induced marginal priors.

We apply the proposed hierarchical shrinkage priors to a log-linear demand system with hundreds of goods and thousands of cross-price elasticity parameters. Log-linear models remain widely used in elasticity-based pricing applications because of their simple yet flexible functional form. In practice, however, researchers typically only allow a small subset of “within category” cross-price effects to enter the demand equation for any good (e.g., Hausman et al., 1994; Montgomery, 1997; Hitsch et al., 2021; Semenova et al., 2021) or even omit cross effects altogether (e.g., DellaVigna & Gentzkow, 2019). We contribute to this literature by allowing a more complete, high-dimensional set of prices to enter each demand equation and then use the proposed shrinkage priors to do data-driven regularization on price elasticity parameters. We also propose a posterior computational strategy that partially mitigates the curse of dimensionality arising from estimating log-linear demand systems at scale.

We use both simulated and actual retail scanner data to highlight the value of hierarchical non-sparse shrinkage. In our simulation experiments, we show that the proposed priors are especially useful in settings where the true elasticity matrix is either: (i) dense, meaning all pairs of goods have a non-zero cross-price elasticity; (ii) dense but becomes sparse after subtracting off the prior mean, meaning all pairs of product groups have a non-zero cross-price elasticity and many product-level elasticities are exactly equal to the group-level elasticity; or (iii) group-wise sparse, meaning many group-level cross elasticities are zero and this sparsity is inherited by product-level elasticities. In our empirical application, we use store-level data to estimate a high-dimensional log-linear demand system with 275 products that span 28 subcategories and nine categories. We show improvements in demand predictions and estimated elasticities from imposing non-sparse hierarchical shrinkage. Relative to the best-performing sparse prior, the best-performing hierarchical prior leads to a 4.5% improvement in predictions across all products, a 5.7% improvement for products with extrapolated price levels in the holdout sample, and a 6.8% improvement for products with limited price variation. In addition, we find that imposing hierarchical shrinkage leads to larger and more dispersed cross-price elasticities as well as more negative and precisely estimated own-price elasticities. We believe that being able to produce more economically reasonable elasticity estimates by simply imposing shrinkage to higher-level category elasticities is a strength of our approach. Finally, we produce competitive maps from each estimated 275 × 275 price elasticity matrix and show that hierarchical shrinkage priors lead to a more interpretable analysis of product competition and market structure.

1.1 Related literature

Methodologically, our work relates to the literature on Bayesian shrinkage priors for high-dimensional regression models (Polson & Scott, 2012a; Bhadra et al., 2019). This literature has largely focused on the problem of sparse signal recovery in which the parameter vector is assumed to be zero except for a few possibly large components. Our goal is to illustrate how many existing shrinkage technologies can still be used for detecting deviations from some non-zero mean structure. Because our prior is hierarchical in nature, it also relates to the hierarchical penalties of Bien et al. (2013) and hierarchical priors of Griffin and Brown (2017) developed to control shrinkage in linear regression models with interaction terms. These penalties/priors control the rate of shrinkage of regression effects at different levels of the hierarchy, allowing for higher-order interactions to be present only when the main effects are present. In contrast, our priors control both the rate and direction of shrinkage and have applications beyond regression models with many interactions.

We also contribute to a rich literature on shrinkage estimation of price and promotional elasticities. For example, Blattberg and George (1991), Montgomery (1997), and Boatwright et al. (1999) estimate Bayesian hierarchical models that pool information across stores to improve elasticity estimates. Rather than exploiting a hierarchical structure over stores, we impose a hierarchical structure over products in order to estimate high-dimensional regression-based demand systems. Moreover, Montgomery and Rossi (1999), Fessler and Kasy (2019), and Smith et al. (2019) demonstrate the benefits of constructing priors that shrink towards economic theory. Relative to Smith et al. (2019), who also consider group-wise restrictions on price elasticity parameters in a log-linear demand system, we explicitly focus on a high-dimensional setting in which there are more prices and cross-price effects than there are observations. For example, while Smith et al. (2019) estimate demand for up to 32 goods spanning eight subcategories and one category, we estimate demand for 275 goods spanning 28 subcategories and nine categories. Smith et al. (2019) also impose group-wise equality restrictions on elasticity parameters, which is a very dogmatic form of shrinkage. Ensuring shrinkage points are correctly specified is a first-order concern and motivates their approach of estimating the grouping structure from the data. While this offers the ability to uncover boundaries in substitution, it comes at a severe cost of scalability and would not be feasible in our high-dimensional setting. Although the mean structure of our hierarchical prior is not explicitly derived from microeconomic theory, the idea of group-wise shrinkage is similar in spirit to the dimension reduction offered by the theory of separable preferences and multi-stage budgeting (Goldman and Uzawa, 1964; Gorman, 1971; Deaton & Muellbauer, 1980; Hausman et al., 1994).

Lastly, we contribute to a growing literature on large-scale demand estimation. One strand of literature has focused on modeling consumer choice among a high-dimensional set of substitutes from one product category. A variety of large-scale discrete choice models have been proposed and made tractable through regularization (Bajari et al., 2015), random projection (Chiong & Shum, 2018), and the use of auxiliary data on consumer consideration sets and search (Amano et al., 2019; Morozov, 2020). A second strand has focused on modeling demand for wider assortments spanning multiple categories and has exploited the flexibility of deep learning (Gabel & Timoshenko, 2021) and representation learning methods such as word embeddings (Ruiz et al., 2020) and matrix factorization (Chen et al., 2020; Donnelly et al., 2021).¹ There is also a well-established literature on economic models of multi-category demand (e.g., Manchanda et al., 1999; Song & Chintagunta, 2006; Mehta, 2007; Thomassen et al., 2017; Ershov et al., 2021). However, with the exception of Ershov et al. (2021), microfounded multi-category models become intractable at scale and have only been estimated on data with relatively small choice sets spanning a few categories.

There are a few ways in which the methods in this paper differ from, and potentially complement, existing large-scale methods. The first difference is in the data required. Our estimation framework—comprising a log-linear demand system with hierarchical shrinkage priors on price elasticity parameters—uses aggregate store-level data while most papers discussed above use household-level purchase basket data. Although granular purchase data sets are becoming more ubiquitous, many marketing researchers continue to rely on store-level data to estimate price and promotional effects (Hitsch et al., 2021). Our framework thus adds to the toolkit for anyone wanting to forecast demand and estimate large cross-price elasticity matrices with aggregate data.

The second difference is in the assumptions about functional forms and the consumer choice process. Log-linear models do not require explicit assumptions about the functional form of consumer utility and can instead be viewed as a first-order approximation to some Marshallian demand system (Diewert, 1974; Pollak and Wales, 1992).² Log-linear models are also directly parameterized by price elasticities, which is convenient when elasticities are focal objects of interest. That said, log-linear models do not allow for inferences about preference heterogeneity, are not guaranteed to satisfy global regularly conditions, and are less scalable—at least when modeled in a joint, seemingly unrelated regression system—than many existing machine learning methods.

Finally, we note that the novel contribution of this paper is not in the specification of demand, but instead in the approach to regularize high-dimensional demand parameters within a given functional form. We see at least two ways in which this paper can complement existing methods. First, estimating substitution patterns requires sufficient variation in key marketing variables such as price, which can be challenging in many retail settings. One common solution in empirical work is to exclude goods from the analysis whose prices either do not vary or perfectly covary with other prices (e.g., Donnelly et al., 2021). In contrast, our hierarchical shrinkage approach pools information across goods to produce reasonable estimates of cross-price elasticities for all products, even those with little to no price variation. Second, while we use log-linear demand as a leading case, we believe that hierarchical shrinkage priors can facilitate the estimation of many other demand systems at scale. Examples include models based on quadratic utility functions (Wales and Woodland, 1983; Thomassen et al., 2017) and discrete choice over product bundles (Gentzkow, 2007; Song & Chintagunta, 2006; Ershov et al., 2021), both of which contain sets of pairwise substitution parameters that grow quadratically in the number of goods.

The remainder of this paper is organized as follows. Section 2 defines the log-linear demand system and outlines existing approaches for imposing sparse shrinkage, including global-local priors. Section 3 develops hierarchical global-local priors. Section 4 discusses posterior computation strategies. Section 5 presents results from a set of simulation experiments and Section 6 presents results of an empirical application to store-level scanner data. Section 7 concludes.

2 Background: Regularizing high-dimensional demand

In this paper we propose a non-sparse, hierarchical shrinkage approach to improve the estimation of high-dimensional demand models. Our priors apply to demand models characterized by a set of pairwise product substitution parameters whose dimension grows non-linearly in the number of goods. Throughout the paper, we use log-linear demand as a leading example. Before introducing our shrinkage framework, we first outline the specification of a log-linear demand system and standard existing approaches for regularization.

2.1 Demand specification

Consider an assortment of products indexed by $i=1,\dotsc ,p$. For each product, we observe its unit sales q_it and price p_it across weeks $t=1,\dotsc ,n$. In a log-linear demand system, the log of unit sales of product i at time t is regressed on its own log price, the log prices of all other products, and a vector of controls which can include product intercepts, seasonal trends, and promotional activity:

$$ \log q_{it} = \beta_{ii}\log p_{it} + \sum\limits_{j\ne i}\beta_{ij}\log p_{jt} + c_{it}^{\prime}\phi_{i} + \varepsilon_{it}. $$

(1)

The p × 1 error vector $\varepsilon _{t}=(\varepsilon _{1t},\dotsc ,\varepsilon _{pt})$ is assumed to follow a N(0,Σ) distribution where the covariance matrix Σ captures any unobserved, contemporaneous correlations between goods.

Log-linear demand systems are attractive for a few reasons. First, the price coefficients represent own and cross-price elasticities, which are often focal economic objects in the analysis of market structure and pricing/promotion schedules. Second, the functional form is simple and admits tractable estimators of all model parameters. Third, the model is flexible in that there are no restrictions imposed on β_ij’s so we can accommodate both substitutes (β_ij > 0) and complements (β_ij < 0). Log-linear models are also flexible in the sense that they possess enough parameters to serve as a first-order approximation to a valid Marshallian demand system (Diewert, 1974; Pollak & Wales, 1992). However, because there are p² elasticities in a system with p goods, regularization is needed at scale.

2.2 Sparse shrinkage and global-local priors

We now outline a standard sparse approach to regularizing parameters in the log-linear demand system in Eq. 1 which will both lay the groundwork for, and also serve as a benchmark against, the hierarchical priors we construct in the following section. We take a Bayesian approach to estimation and so regularization will be imparted by way of the prior. There are now many prior specifications that can be used for elasticity parameters β_ij, each having different tail behavior and thus inducing different forms of shrinkage (see, e.g., Bhadra et al., 2019). We specifically focus on global-local priors (Polson & Scott, 2010), which are scale mixtures of normals:

$$ \begin{array}{@{}rcl@{}} \beta_{ij} |\lambda_{ij}^{2},\tau^{2}\!&\!\sim& \text{N}(0,\tau^{2}\lambda_{ij}^{2}),\\ \lambda_{ij}^{2}\!&\!\sim& G. \end{array} $$

(2)

Here τ² is the “global” variance that controls the overall amount of shrinkage across all elasticity parameters β_ij while $\lambda _{ij}^{2}$ is a “local” variance that allows for component-wise deviations from the shrinkage imposed by τ². The local variances are distributed according to a mixing distribution G, which is often assumed to be absolutely continuous and will thus admit an associated density g(⋅).³

One of the reasons that global-local priors are attractive is that, given an appropriate choice of mixing density, they can exhibit two useful properties for sparse signal recovery: (i) a spike of mass at zero to encourage sparsity for small noisy observations; and (ii) heavy tails to leave large signals unshrunk (Polson & Scott, 2010). Together, (i) and (ii) induce shrinkage behavior that mimics the hard selection rules of Bayesian two-group, spike-and-slab priors (Mitchell & Beauchamp, 1988; George & McCulloch, 1993; Ishwaran & Rao, 2005) while admitting much more efficient posterior computation strategies.

The global-local structure is also very general and nests many common Bayesian shrinkage priors. For example, ridge regression (Hoerl & Kennard, 1970) arises when $\lambda _{ij}^{2}=1$, the Bayesian lasso (Park & Casella, 2008; Hans, 2009) arises when $\lambda _{ij}^{2}$ follows an exponential distribution, and the horseshoe (Carvalho et al., 2010) arises when λ_ij follows a half-Cauchy distribution. The priors can be compared using their shrinkage profiles, which measure the amount by which the posterior mean shrinks the least squares estimate of a regression coefficient to zero, and is related to the shape of the mixing density g(⋅). For example, the tails of an exponential mixing density are lighter than the polynomial tails of the half-Cauchy, suggesting that the Bayesian lasso may tend to over-shrink large regression coefficients and under-shrink small ones relative to the horseshoe (Polson & Scott, 2010; Datta & Ghosh, 2013; Bhadra et al., 2016).

Although the tail behavior and associated shrinkage properties of global-local priors have now been studied extensively, existing work typically considers the problem of sparse signal recovery and so the prior means in Eq. 2 are assumed to be fixed at zero. However, economic theory offers many reasons for why sparse shrinkage may not be appropriate for price elasticity parameters. First, own-price effects should be negative by the law of demand and cross-price effects in a Marshallian demand system need not be zero even if true substitution effects are zero. Second, the property of Cournot aggregation (or “adding-up”) implies that demand must become more elastic as the set of available substitutes increases. If cross-effects are arbitrarily shrunk towards zero, then the magnitude of the own effects must fall, which would lead to estimates of own-price effects that are biased downward in magnitude. Third, line pricing can produce highly correlated prices among substitutable goods, which would lead to heavy shrinkage on the associated cross-price effects in estimation. However, fixing the shrinkage points to zero would suggest that varieties within the product line are unrelated even though the very nature of price correlation reflects a high degree of substitution. Together, these examples suggest that care must be taken when regularizing price effect parameters, which motivates our development of non-sparse shrinkage priors.

3 Hierarchical global-local priors

In this section, we develop hierarchical global-local priors with two goals in mind. The first is to allow own and cross-price elasticities to be shrunk towards higher-level group elasticities (rather than zero), where the hierarchy of groups is defined using a pre-specified product classification tree. The second is to allow shrinkage to propagate down through the tree. To this end, we extend the standard global-local specification by adding a hierarchical mean structure to connect shrinkage points across levels in the tree, as well as a hierarchical product structure on the local variances to connect the degree of shrinkage across levels in the tree.

3.1 Notation

We first define a minimum of notation. We assume that the researcher has access to an L-level product classification tree where levels are indexed by $\ell =0,1,\dotsc ,L-1$ and are ordered such that ℓ = 0 is the lowest level corresponding to products, ℓ = 1 corresponds to most granular definition of product groups, and ℓ = L − 1 corresponds to the highest level and most coarse definition of product groups. Further define n_ℓ to be the number of nodes (groups) on level ℓ where n₀ > n₁ > ⋯ > n_L− 1.

The indexing notation we introduce is slightly more complicated than the usual indexing for graphical models because, in our case, the target parameters are always defined with respect to two nodes (e.g., the price elasticity between two products), not one. So instead of considering the parent of node i, we must consider the parent of (i,j), which itself will be a pair of nodes. We now define the indexing function that will be used throughout.

Definition 1

Let (i,j) denote a pair of nodes at the lowest level (level 0) of the classification tree. Then let π(ij|ℓ) denote the parent index function which produces the level-ℓ parent nodes of (i,j).

To build intuition, consider the following two products: (i) Lay’s potato chips, which belongs to the “Potato Chip” subcategory (level 1) and “Salty Snack” category (level 2); and (ii) Heineken beer, which belongs to the “Imported Beer” subcategory (level 1) and “Beer” category (level 2). Then the parents of (Lay’s, Heineken) on levels 1 and 2 are as follows.

$$ \begin{array}{@{}rcl@{}} \pi(\text{Lay's},\text{Heineken}|1)&=&(\text{Potato Chips},\text{Imported Beer})\\ \pi(\text{Lay's},\text{Heineken}|2)&=&(\text{Salty Snacks},\text{Beer}) \end{array} $$

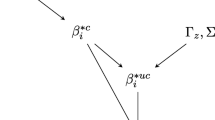
Given a product-level elasticity β_ij, we let 𝜃_π(ij|m) represent the relationship between the level-m ancestors of i and j. An example of this lineage of parameters is shown in Fig. 1. The darkest square in the left-hand-side grid denotes β_ij. The level-1 parent of (i,j) is π(ij|1) = (4,2) and the level-2 parent of (i,j) is π(ij|2) = (2,1). The idea is to then direct shrinkage of β_ij towards 𝜃_π(ij|1) (grid in the middle), which is in turn shrunk towards 𝜃_π(ij|2) (grid on the right).

Fig. 1

Visualization of hierarchical shrinkage using a three-level classification tree. The focal product pair is (i,j) which has level-1 parent π(ij|1) = (4,2) and level-2 parent π(ij|2) = (2,1). The parameter β_ij (darkest shaded square in the left grid) will be shrunk towards the level-1 parent 𝜃_π(ij|1) (darkest shaded region of 4 squares in the middle grid), which will in turn be shrunk towards the level-2 parent 𝜃_π(ij|2) (shaded region of 16 squares in the right grid)

3.2 Prior construction

Using the indexing notation above, we now introduce a sequence of prior distributions on the elasticity parameters of the log-linear demand model in Eq. 1. Starting at the lowest level of the tree, define the prior on the (i,j) product pair as:

$$ \beta_{ij} \sim \text{N}\left( \theta_{\pi(ij|1)},\tau_{\beta}^{2}{\Psi}_{ij}\right) $$

(3)

which is a global-local prior with global variance $\tau _{\beta }^{2}$, local variance Ψ_ij, and prior mean 𝜃_π(ij|1). Note that this notation holds for any (i,j) pair including the own elasticities where i = j. However, in order to account for differences in the expected signs of own and cross-price elasticities, we will ultimately build up two separate hierarchical structures: one for the β_ii’s and one for the β_ij’s. The former will shrink the product-level own elasticities towards higher-level own-price elasticities whereas the latter will shrink product-level cross elasticities towards higher-level cross-price elasticities. For ease of exposition, we will focus our prior construction on the case where i≠j and the β_ij’s are cross elasticities.

Hierarchy of means

We specify global-local priors on the higher-level group elasticities:

$$ \theta_{\pi(ij|\ell)} \sim \text{N}\left( \theta_{\pi(ij|\ell+1)},\tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell)}\right), \qquad \ell=1,\dotsc,L-1, $$

(4)

where $\tau _{\ell }^{2}$ is the global variance across all level-ℓ elasticities 𝜃_π(ij|ℓ), Ψ_π(ij|ℓ) is a local variance, and 𝜃_{π(ij|ℓ+ 1)} is the parent cross-group elasticity to 𝜃_π(ij|ℓ). This hierarchical mean structure allows the direction of shrinkage to be governed by the classification tree. That is, in the absence of a strong signal in the data, elasticities will be shrunk towards higher-level elasticity parameters instead of zero.

Hierarchy of variances

We also impose a hierarchical structure on the local variance parameters. At the product level, we have:

$$ {\Psi}_{ij}=\lambda_{ij}^{2} \prod\limits_{k=\ell+1}^{L-1} \lambda_{\pi(ij|k)}^{2}, \quad \lambda_{ij}^{2} \sim G_{\beta}, $$

(5)

and at higher levels in the tree, we have:

$$ {\Psi}_{\pi(ij|\ell)}=\lambda_{\pi(ij|\ell)}^{2} \prod\limits_{k=\ell+1}^{L-1} \lambda_{\pi(ij|k)}^{2}, \quad \lambda_{\pi(ij|\ell)}^{2} \sim G_{\ell}, \quad \ell=1,\dotsc,L-1. $$

(6)

Here $\lambda _{ij}^{2}$ and $\lambda _{\pi (ij|\ell )}^{2}$ are variances associated with β_ij and 𝜃_π(ij|ℓ), respectively, and represent local variances absent any hierarchical structure connecting variances across levels. That is, without a hierarchy of variances we would simply have ${\Psi }_{ij}=\lambda _{ij}^{2}$ and ${\Psi }_{\pi (ij|\ell )}=\lambda _{\pi (ij|\ell )}^{2}$. With the product hierarchy of variances, the induced local variances Ψ will be small whenever either $\lambda _{\pi (ij|\ell )}^{2}$ is small or any $\lambda _{\pi (ij|s)}^{2}$ is small for s > ℓ (i.e., higher levels in the tree), which allows shrinkage to propagate down through the tree. Taken together with the hierarchical mean structure, the hierarchal variance structure implies that, in the absence of a strong signal in the data, price elasticities will be strongly shrunk towards higher-level elasticities and these higher-level group elasticities will be strongly shrunk towards each other.

Examples

A summary of model parameters is provided in Table 1. Below we provide examples of the complete hierarchical prior specification for trees different numbers of levels. A single-level tree corresponds to a prior for β_ij that has a fixed mean $\bar {\theta }$ and does not encode any information about product groups. If the tree has at least two levels, then β_ij will be shrunk towards its parent elasticity and shrinkage will be allowed to propagate. Note that the level at which shrinkage begins to propagate is also a choice of the researcher. In the examples below, shrinkage starts to propagate at the top level (ℓ = L − 1) of the tree.

• (a) One-level prior

  $$ \beta_{ij} \sim \text{N}\left( \bar{\theta},\tau_{\beta}^{2}{\Psi}_{ij}\right), \quad {\Psi}_{ij}=\lambda_{ij}^{2} $$

• (b) Two-level prior

  $$ \begin{array}{@{}rcl@{}} \beta_{ij} \sim \text{N}\left( \theta_{\pi(ij|1)},\tau_{\beta}^{2}{\Psi}_{ij}\right), &&\quad {\Psi}_{ij}=\lambda_{ij}^{2}\lambda_{\pi(ij|1)}^{2}\\ \theta_{\pi(ij|1)} \sim \text{N}\left( \bar{\theta},{\tau_{1}^{2}}{\Psi}_{\pi(ij|1)}\right), &&\quad {\Psi}_{\pi(ij|1)}=\lambda_{\pi(ij|1)}^{2} \end{array} $$

• (c) Three-level prior

  $$ \begin{array}{@{}rcl@{}} \beta_{ij} \sim \text{N}\left( \theta_{\pi(ij|1)},\tau_{\beta}^{2}{\Psi}_{ij}\right), &&\quad {\Psi}_{ij}=\lambda_{ij}^{2}\lambda_{\pi(ij|1)}^{2}\lambda_{\pi(ij|2)}^{2}\\ \theta_{\pi(ij|1)} \sim \text{N}\left( \theta_{\pi(ij|2)},{\tau_{1}^{2}}{\Psi}_{\pi(ij|1)}\right), &&\quad {\Psi}_{\pi(ij|1)}=\lambda_{\pi(ij|1)}^{2}\lambda_{\pi(ij|2)}^{2}\\ \theta_{\pi(ij|2)} \sim \text{N}\left( \bar{\theta},{\tau_{2}^{2}}{\Psi}_{\pi(ij|2)}\right), &&\quad {\Psi}_{\pi(ij|2)}=\lambda_{\pi(ij|2)}^{2} \end{array} $$

Table 1 Summary of notation

3.3 Choice of mixing densities

The hierarchical priors outlined above endow each product-level elasticity and group-level elasticity with a local variance $\lambda _{\pi (ij|\ell )}^{2}$ which is distributed according to a level-specific mixing distribution G_ℓ. As discussed in Section 2.2, the tails of the associated densities g_ℓ(⋅) will play a key role in shaping the shrinkage imposed by the prior. Although there are now many possible choices for g_ℓ(⋅), we confine our attention to three forms of shrinkage: (i) ridge, where the mixing density is a degenerate distribution and local variances are fixed to one; (ii) lasso, with an exponential mixing density; and (iii) horseshoe, with a half-Cauchy mixing density. These three types of priors remain common choices in empirical work and have very different shrinkage profiles (Bhadra et al., 2019).

Our hierarchical global-local priors also require the specification of a mixing density for each level of the tree. We can therefore conceive of using different forms of shrinkage across different levels (e.g., ridge at the subcategory level and horseshoe at the product level). However, this also raises questions of whether properties of g_ℓ(⋅) at higher levels in the tree affect shrinkage behavior at the product level, which we address in the following section.

3.4 Some theory on shrinkage properties

The typical strategy for characterizing shrinkage in global-local models is to examine the shape—specifically, the tails—of the marginal prior for regression coefficients β_ij. Because global-local priors are scale mixtures of normals, the heaviness of the tails of this marginal prior will be determined by the tails of the mixing density (Barndorff-Nielsen et al., 1982). However, in our setting this analysis is complicated by the fact that the marginal prior for β_ij will depend on multiple mixing densities in the hierarchical global-local structure.

In this section, we provide three results to characterize shrinkage properties of hierarchical global-local priors. First, we show that the marginal prior for β_ij still retains a scale mixtures of normals representation and so the mixing densities will continue to play a key role in shaping the shrinkage profile for β_ij. Second, we show that if the same heavy-tailed mixing density is specified at each level of the tree, then its heaviness will be preserved under the hierarchical product structure that we impose on local variances. Finally, we show that even if a combination of heavy and light-tailed mixing densities are specified across different levels, the heavy-tailed mixing densities will ultimately dominate and shape the product-level shrinkage profile.

We focus on two specific forms of shrinkage. The first is the shrinkage of β_ij to 𝜃_π(ij|m), which is the shrinkage of the product-level elasticity to its level-m parent elasticity. This type of “vertical” shrinkage allows us to assess how quickly product-level elasticities can be pulled towards higher-level elasticities. Here we can write β_ij as a function of its parent mean and error term:

$$ \beta_{ij} = \theta_{\pi(ij|1)} + \xi_{ij}, \qquad \xi_{ij} \sim \text{N}\left( 0,\tau_{\beta}^{2}{\Psi}_{ij}\right) $$

(7)

where, again, for any $\ell =1,\dotsc ,L-1$:

$$ \theta_{\pi(ij|\ell)} = \theta_{\pi(ij|\ell+1)}+ \xi_{\pi(ij|\ell)}, \qquad \xi_{\pi(ij|\ell)} \sim \text{N}\left( 0,\tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell)}\right). $$

(8)

We can therefore write β_ij as a function of its level-m parent elasticity and a sum of errors across levels:

$$ \beta_{ij} = \theta_{\pi(ij|m)} + \sum\limits_{\ell=1}^{m-1}\xi_{\pi(ij|\ell)} + \xi_{ij}, $$

(9)

which yields the prior distribution:

$$ \beta_{ij}-\theta_{\pi(ij|m)}\sim \text{N}\left( 0, \sum\limits_{\ell=1}^{m-1} \tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell)} + \tau_{\beta}^{2}{\Psi}_{ij}\right). $$

(10)

This prior is a scale mixture of normals where the scales are sums over each level’s local variance Ψ_π(ij|ℓ), which is in turn a product of $\lambda _{\pi (ij|\ell )}^{2}, \dots , \lambda _{\pi (ij|L-1)}^{2}$. Thus, the local variances will be a sum of products and if there is a value of s (for s ≤ m) for which $\lambda _{\pi (ij|s)}^{2}$ is “small” then β_ij will tend to be very close to 𝜃_π(ij|m).

We also consider the shrinkage of β_ij to $\beta _{i^{\prime }j^{\prime }}$ (for i≠j, $i^{\prime }\ne j^{\prime }$, and $i\ne i^{\prime }$), which is the shrinkage between two product-level elasticities. This type of “horizontal” shrinkage allows us to assess the extent to which elasticities become more similar as they become closer in the tree. Formally define $m^{\star }=\min \limits \{m:\pi (ij|m)=\pi (i^{\prime }j^{\prime }|m)\}$ to be the lowest level in the tree such that all four products ($i,j,i^{\prime },j^{\prime }$) share a common ancestor (i.e., belong to the same group at some level in the tree), where m^⋆ = L if no common parent node exists for within the tree. Then we can write

$$ \beta_{ij}-\beta_{i^{\prime}j^{\prime}} = {\sum}_{s=\ell}^{m^{\star}-1}\Big(\xi_{\pi(ij|s)}-\xi_{\pi(i^{\prime}j^{\prime}|s)}\Big) $$

(11)

so the prior distribution of the difference is

$$ \beta_{ij}-\beta_{i^{\prime}j^{\prime}} \sim \text{N}\left( 0,\sum\limits_{s=\ell}^{m^{\star}-1} \Big({\Psi}_{\pi(ij|s)}+ {\Psi}_{\pi(i^{\prime}j^{\prime}|s)} \Big) {\tau_{s}^{2}}\right). $$

(12)

Like the marginal distribution of the cross elasticities, the marginal prior distribution of the difference will be a scale mixtures of normals, where the scales are sums of products of $\lambda _{\pi (ij|s)}^{2}$ and $\lambda _{\pi (i^{\prime }j^{\prime }|s)}^{2}$. The number of terms in the sum is m^⋆ − 1 − ℓ and so the variance of differences will be tend to be larger if m^⋆ is larger (i.e., the products are less similar). The form of the variances in Eq. 12 implies that if Ψ_π(ij|m) is “small” on level m then Ψ_π(ij|s) and ${\Psi }_{\pi (i^{\prime }j^{\prime }|s)}$ will tend to be small for s < m and so the variance of the difference will tend to be smaller further down the tree. This allows shrinkage to propagate down the tree with subsequent sub-categorizations of products tending to have similar cross-elasticities.

The results above show that the priors on β_ij and the differences $(\beta _{ij} - \beta _{i^{\prime }j^{\prime }})$ can be expressed as normal scale mixtures and so, like in sparse signal detection settings, the shape of the marginal prior will again be determined by the mixing density (Barndorff-Nielsen et al., 1982). However, while there is only one mixing density in traditional regression priors, the marginal priors for β_ij and $(\beta _{ij} - \beta _{i^{\prime }j^{\prime }})$ involve a “scaled sum of products” transformation over many mixing densities. It is therefore not clear whether the heaviness of the mixing density specified level ℓ is: (i) preserved under the scaled sum of products transformations; or (ii) tarnished by mixing densities with lighter tails at higher levels in the tree. We clarify both points in the following two propositions.

Definition 2

The random variable ζ has an L-sum of scaled products distribution if it can be written as $\zeta = {\sum }_{\ell =1}^{L} \tau _{\ell }^{2} {\prod }_{s=1}^{\ell } {\lambda _{s}^{2}}$ with fixed ${\tau _{1}^{2}},\dots ,{\tau _{L}^{2}}$.

Proposition 1

Suppose ζ has an L-sum of scaled products distribution where $\lambda _{\ell }^{2}\stackrel {iid}{\sim } G$ for $\ell =1,\dotsc ,L$ and G is a regularly varying distribution with index α. Then ζ is regularly varying with index α.

Proof

Because the ${\lambda _{s}^{2}}$’s are all independent and regularly varying with index α, then ${\Psi }_{\ell }={\prod }_{s=1}^{\ell }{\lambda _{s}^{2}}$ is also regularly varying with index α (Cline, 1987). Then the closure property of regularly varying functions guarantees that $\zeta = {\sum }_{\ell =1}^{L} \tau _{\ell }^{2} {\prod }_{s=1}^{\ell } {\lambda _{s}^{2}}$ is also regularly varying with index α. □

This first result shows that the heaviness of the mixing density at level ℓ is preserved under the scaled sum of products transformation. For example, if every λ_s has a half-Cauchy prior then each ${\lambda _{s}^{2}}$ is an inverted-beta random variable with density g(λ²) ∝ (λ²)^− 1/2(1 + λ²)^− 1 (Polson & Scott, 2012b), which is regularly varying with index -3/2 and so ${\lambda _{s}^{2}}$ is regularly varying with index 1/2 (Bingham et al., 1987). Then by Proposition 1, the sum of products would also have regularly varying tails, and the different forms of shrinkage in Eqs. 10 and 12 will all have tails of the same heaviness as a standard horseshoe prior.

Proposition 2

Suppose ζ has an L-sum of scaled products distribution with $\lambda _{\ell }^{2}\sim G_{\ell }$ for $\ell =1,\dotsc ,L$ and let RV = {ℓ : G_ℓisregularlyvaryingwithindexα} be non-empty. If there exists an 𝜖 such that G_s has a finite α + 𝜖 moment for all s∉RV then ζ is regularly varying with index α.

Proof

If at level ℓ at least one of ${\lambda _{1}^{2}}, \dots , \lambda _{\ell }^{2}$ is regularly varying with index α then ${\Psi }_{\ell }={\prod }_{s=1}^{\ell } {\lambda _{s}^{2}}$ is regularly varying with index α. If none of ${\lambda _{1}^{2}}, \dots , \lambda _{\ell }^{2}$ are regularly varying, then by assumption Ψ_ℓ has a finite α + 𝜖 moment. Since, by assumption, at least one of ${\lambda _{1}^{2}},\dots , {\lambda _{L}^{2}}$ is regularly varying then at least one ${\Psi }_{1},\dotsc ,{\Psi }_{L}$ is regularly varying while the others are guaranteed to have a finite α + 𝜖 moment. Therefore, the closure properties of regularly varying random variables implies that ζ is also regularly varying with index α (Bingham et al., 1987). □

Proposition 2 shows that the sum of products has regular variation if at least one element is regularly-varying. This suggests that sparsity shrinkage of the cross-elasticities at the lowest level of the tree does not require sparsity shrinkage at all levels. For example, we know by Proposition 1 that if $\lambda _{ij}^{2},\lambda _{\pi (ij|1)}^{2},\dotsc ,\lambda _{\pi (ij|L-1)}^{2}$ are all regularly varying with index α, then their product is also regularly varying with index α. Now by Proposition 2, we know that even if $\lambda _{\pi (ij|s)}^{2}$ is not regularly varying for s > ℓ but has a finite α + 𝜖 moment for some 𝜖 > 0, then the product is again regularly varying. Examples of non-regularly varying distributions with a finite α + 𝜖 moment are a degenerate distribution (i.e., ridge shrinkage with λ² = 1) and an exponential distribution (i.e., lasso shrinkage). Therefore, heavy tails at any level of the tree are all that is required to get sparsity shrinkage at for the product-level elasticities. We explore different combinations of shrinkage in the simulations and empirical applications below.

4 Posterior computation

Given the log-linear demand system defined in Section 2.1 and hierarchical priors outlined in Section 3, we now turn to our posterior sampling strategy. Note that the presence of product-specific control variables and general error structure in Eq. 1 leads to a seemingly unrelated regression (SUR) model:

$$ \begin{pmatrix} y_{1}\\ y_{2}\\\vdots\\y_{p} \end{pmatrix} = \begin{pmatrix} X & 0 & {\cdots} & 0\\ 0 & X & {\cdots} & 0\\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ 0 & 0 & {\cdots} & X\\ \end{pmatrix} \begin{pmatrix} \beta_{1}\\\beta_{2}\\\vdots\\\beta_{p} \end{pmatrix} + \begin{pmatrix} C_{1} & 0 & {\cdots} & 0\\ 0 & C_{2} & {\cdots} & 0\\ {\vdots} & {\vdots} & {\ddots} & \vdots\\ 0 & 0 & {\cdots} & C_{p}\\ \end{pmatrix} \begin{pmatrix} \phi_{1}\\\phi_{2}\\\vdots\\\phi_{p} \end{pmatrix} + \begin{pmatrix} \varepsilon_{1}\\ \varepsilon_{2}\\\vdots\\ \varepsilon_{p} \end{pmatrix} $$

(13)

where y_i is the n × 1 vector of log sales for product i, X is the n × p matrix of log prices, β_i is the p × 1 vector of own and cross-price elasticities associated with product i, and C_i is a n × d matrix of control variables with coefficients ϕ_i. In vector form, we have

$$ y = \text{X}\beta + \text{C}\phi + \varepsilon, \qquad \varepsilon \sim\text{N}(0,{\Sigma}\otimes I_{n}) $$

(14)

where $y=(y_{1}^{\prime }, y_{2}^{\prime }, \dots , y_{p}^{\prime })'$, $\text {X}=\text {diag}(X,X,\dotsc ,X)$, $\beta = (\beta _{1}^{\prime }, \beta _{2}^{\prime }, \dots , \beta _{p}^{\prime })'$, $\text {C}=\text {diag}(C_{1},C_{2},\dotsc ,C_{p})$, $\phi = (\phi _{1}^{\prime }, \phi _{2}^{\prime }, \dots , \phi _{p}^{\prime })'$ and $\varepsilon = (\varepsilon _{1}^{\prime }, \varepsilon _{2}^{\prime }, \dots , \varepsilon _{p}^{\prime })'$.

Sampling from the posterior of a SUR model first requires transforming the model in Eq. 14 into one with homogeneous unit errors. Let U denote the upper triangular Cholesky root of Σ and define $\tilde {y} = (U^{-1}\otimes I_{n})y$, $\tilde {\text {X}} = (U^{-1}\otimes I_{n})\text {X}$, and $\tilde {\text {C}} = (U^{-1}\otimes I_{n})\text {C}$. Then the following transformed system represents a standard normal linear regression model.

$$ \tilde{y} = \tilde{\text{X}}\beta + \tilde{\text{C}}\phi + \tilde{\varepsilon}, \qquad \tilde{\varepsilon}\sim \text{N}(0,I_{np}). $$

(15)

The full set of model parameters includes the elasticities β, the coefficients on controls ϕ, the error variance Σ, and the set of hierarchical prior parameters ${\Omega }=\big (\{\theta _{\pi (ij|\ell )}\},\{\lambda _{\pi (ij|\ell )}^{2}\},\{\tau _{\ell }^{2}\}\big )$.

Priors

The priors for β and all hierarchical hyperparameters are given in Section 3.2. We write the p² × p² prior covariance matrix for β as ${\Lambda }_{*}=\tau _{\beta }^{2}\text {diag}(\text {vec}({\Lambda }))$, where Λ is a p × p matrix of local variances Ψ_ij as defined in Eq. 5. Note that for a standard global-local prior, the (i,j)th element of Λ would be $\lambda _{ij}^{2}$. We place $\text {N}(\bar {\phi },A_{\phi }^{-1})$ priors on the control variable coefficients, which are conditionally conjugate to the normal likelihood given Σ. Inverse Wishart priors are commonly used for covariance matrices in Bayesian SUR models, however if p > n then Σ will be rank deficient. One approach would be to also regularize Σ (Li et al., 2019; Li et al., 2021). We instead impose a diagonal restriction ${\Sigma }=\text {diag}({\sigma _{1}^{2}},\dotsc ,{\sigma _{p}^{2}})$ and place independent IG(a,b) priors on each ${\sigma _{j}^{2}}$.

Full Conditionals

We construct a Gibbs sampler that cycles between the following full conditional distributions.

$$ \begin{array}{@{}rcl@{}} &&{\Omega}|\beta,\text{data} \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} &&{\Sigma}|\beta,\phi,{\Omega},\text{data} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} &&\beta,\phi|{\Sigma},\beta,{\Omega},\text{data} \end{array} $$

(18)

The first full conditional represents the posterior of all global/local variances and higher-level group elasticities. Sampling from these distributions is computationally inexpensive. The elements of 𝜃 each have independent normal posteriors conditional on all variance parameters. Both local variances λ² and global variances τ² can also be sampled independently, but the form of their respective posteriors will depend on the choice of prior. Under ridge shrinkage, each λ² = 1 so no posterior sampling is necessary. Under lasso shrinkage, each λ² follows an independent exponential distribution and so the full conditionals of 1/λ² have independent inverse Gaussian distributions (Park & Casella, 2008). Under horseshoe shrinkage, each λ follows an independent half-Cauchy distribution. We follow Makalic and Schmidt (2015) and represent the half-Cauchy as a scale mixture of inverse gammas, which is conjugate to the normal density so the target full conditional can be sampled from directly. Details are provided in Appendix A.1.

The second full conditional represents the posterior of the observational error covariance matrix. Assuming ${\Sigma }=\text {diag}({\sigma _{1}^{2}},\dotsc ,{\sigma _{p}^{2}})$ with independent IG(a,b) priors yields the following posterior:

$$ {\sigma_{j}^{2}}|\beta,\phi,{\Omega},\text{data} \sim\text{IG}\Big(a + n/2,b + (y_{j} - X\beta_{j} - C_{j}\phi_{j})'(y_{j} - X\beta_{j} - C_{j}\phi_{j})/2\Big) $$

(19)

where the j subscript denotes all elements of the given vector or matrix associated with product j. Note that the case of p > n calls for a judicious choice of (a,b) given that diffuse priors will yield barely proper posteriors. If n > p and Σ is unrestricted, typical inverse Wishart priors can be used.

The last full conditional represents the joint posterior of the regression coefficients (β,ϕ). One approach to sampling from the joint posterior is to iterate between each full conditional. For example, the posterior of β conditional on ϕ is:

$$ \beta|\phi,{\Sigma},{\Omega},\text{data} \sim \text{N}\Big((\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}(\tilde{\text{X}}^{\prime}\tilde{y}_{\phi}^{*} + {\Lambda}_{*}^{-1}\bar{\beta}(\theta)),(\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\Big) $$

(20)

where $\tilde {y}_{\phi }^{*}= \tilde {y} - \tilde {\text {C}}\phi$. Similarly, the posterior of ϕ conditional on β is:

$$ \phi|\beta,{\Sigma},{\Omega},\text{data}\sim \text{N}\Big(\big(\tilde{\text{C}}^{\prime}\tilde{\text{C}}+A_{\phi}\big)^{-1}\big(\tilde{\text{C}}^{\prime}\tilde{y}_{\beta}^{*}+A_{\phi}\bar{\phi}\big),\big(\tilde{\text{C}}^{\prime}\tilde{\text{C}}+A_{\phi}\big)^{-1}\Big) $$

(21)

where $\tilde {y}_{\beta }^{*}=\tilde {y}-\tilde {\text {X}}\beta$. However, note that these two Gibbs steps can be improved through blocking. For example, β can be integrated out of the conditional posterior of ϕ:

$$ \phi|{\Sigma},{\Omega},\text{data}\sim \text{N}\Big(\big(\tilde{\text{C}}^{\prime}\text{P}\tilde{\text{C}}+A_{\phi}\big)^{-1}\big(\tilde{\text{C}}^{\prime}\text{P}\tilde{y}+A_{\phi}\bar{\phi}\big),\big(\tilde{\text{C}}^{\prime}\text{P}\tilde{\text{C}}+A_{\phi}\big)^{-1}\Big) $$

(22)

where $\text {P}=I_{np}-\tilde {\text {X}}(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})^{-1}\tilde {\text {X}}^{\prime }$ is an orthogonal projection matrix. Marginalizing over β will yield improvements in convergence and mixing, and comes at virtually no additional cost since the inverse contained in the projection matrix must be computed to sample from Eq. 21. It should also be noted that the posterior precision matrix in Eq. 21 requires the inversion of a p² × p² matrix which is computationally expensive when p is large. We therefore present two strategies to facilitate scalability in the following subsections.

4.1 Diagonal restriction on Σ

As with all Bayesian regression models, a computational bottleneck arises in inverting the posterior precision matrix $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$. This especially true for Bayesian SUR models since the design matrix X contains p stacked copies of the multivariate regression design matrix. If Σ is unrestricted, then $\tilde {\text {X}}^{\prime }\tilde {\text {X}}$ is a dense p² × p² matrix and any sampler that directly inverts this matrix will be hopeless for large p. For example, even a sampler that calculates the inverse using Cholesky decompositions has complexity $\mathcal {O}(p^{6})$. If instead Σ is assumed to be diagonal then both $\tilde {\text {X}}^{\prime }\tilde {\text {X}}$ and $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$ will have block diagonal structures, with each of the p blocks containing an p × p matrix. Computing the inverse of $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$ then amounts to inverting each p × p block, which has computational complexity $\mathcal {O}(p^{4})$ using Cholesky decompositions. While this is better than inverting $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$ directly, it can still be prohibitively expensive for large p.

4.2 Fast sampling normal scale mixtures

Bhattacharya et al. (2016) present an alternative approach for sampling from the posteriors of linear regression models with normal scale mixture priors. The idea is to use data augmentation and a series of linear transformations to avoid the inversion of $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$. Instead, their algorithm replaces the inversion of $\tilde {\text {X}}^{\prime }\tilde {\text {X}}$ with the inversion of $\tilde {\text {X}}\tilde {\text {X}}^{\prime }$. For a multiple regression model, this means the matrix being inverted is n × n instead of p × p and the proposed algorithm has complexity that is linear in p. In the context of our SUR model, the fast sampling algorithm has complexity $\mathcal {O}(n^{2}p^{2})$ if Σ is diagonal or $\mathcal {O}(n^{2}p^{4})$ if Σ is unrestricted.

Since the original algorithm was also developed for typical shrinkage priors centered at zero, we present a modified algorithm to allow for the nonzero mean structure, which we denote as $\bar {\beta }(\theta )$, in the proposed hierarchical priors:

• 1. Sample $u\sim \text {N}(\bar {\beta }(\theta ),{\Lambda }_{*})$ and $\delta \sim \text {N}(0,I_{np})$;

• 2. Set $v=\tilde {\text {X}}u + \delta$;

• 3. Compute $w=(\tilde {\text {X}}{\Lambda }_{*}\tilde {\text {X}}^{\prime }+I_{np})^{-1}(\tilde {y}-v)$;

• 4. Set $\beta =u+{\Lambda }_{*} \tilde {\text {X}}^{\prime }w$.

A constructive proof that β retains the posterior in Eq. 21 is provided in Appendix A.2. Note that the computational gains come from the third step, which requires inverting the np × np matrix $(\tilde {\text {X}}{\Lambda }_{*}\tilde {\text {X}}^{\prime }+I_{np})$ rather than the original p² × p² precision matrix $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$. This also shows that the computational gains are largest when p is much larger than n.

4.3 Scalability

To provide practical insights into the computational gains afforded by fast sampling algorithm above, we draw from the posterior of the elasticity vector β using data generated with n = 100 and $p\in \{100,200,300,\dotsc ,1000\}$. In addition to the fast sampler of Bhattacharya et al. (2016), we also provide results for a “standard” sampler that inverts the p² × p² precision matrix $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})$ via Cholesky decompositions (see, e.g., chapters 2.12 and 3.5 of Rossi et al., 2005). In both cases we assume Σ is diagonal. The samplers are coded in Rcpp (Eddelbuettel and François, 2011) and run on a MacBook Pro laptop with 32GB of RAM and an Apple M1 Max processor. Figure 2 plots the computation time in log seconds against the number of products p. We find that the fast sampler offers significant computational savings: it is roughly two times faster when p = 200, 10 times faster when p = 500, and 30 times faster when p = 1000.

Fig. 2

Computation time associated with taking one draw from the posterior of the product-level elasticities β with fixed sample size n = 100 and varying numbers of products p

5 Simulation experiments

We first explore the performance of hierarchical global-local priors using simulated data. We generate data from price elasticity matrices that have different underlying structures in order to illustrate differences between sparse and non-sparse shrinkage, as well as differences in the heaviness of shrinkage used across levels in the tree. Each of these structures is described in detail below.

• (I) Hierarchical + Dense: A dense vector of elasticities β_ij is generated from a three-level hierarchical prior. The top-level coefficients 𝜃_π(ij|2) are sampled from a uniform distribution over the interval {-3,-1}∪{1,3} and we fix $\lambda _{\pi (ij|\ell )}^{2}=1$ and $\tau _{\ell }^{2}=1$ for all (i,j) and across all levels. The middle-level coefficients 𝜃_π(ij|1) and product elasticities β_ij are generated through the model outlined in Section 3.2. In this specification, all pairs of goods have a non-zero cross-price elasticity.

• (II) Hierarchical + Sparse After Transformation: A dense vector of elasticities β_ij is generated from a three-level hierarchical prior where 75% of the product-level local variances Ψ_ij are set to zero so that the corresponding product-level elasticity β_ij is exactly equal to its prior mean. Thus, all pairs of product groups have a non-zero cross-price elasticity and many product-level elasticities are exactly equal to the group-level elasticity. This creates a structure where β appears dense, but is sparse after subtracting off the prior mean parameters 𝜃_π(ij|1).

• (III) Hierarchical + Group-Wise Sparse: A “group-wise” sparse vector of elasticities β_ij is generated from a three-level hierarchical prior where 75% of the level-1 coefficients 𝜃_π(ij|1) and local variances Ψ_π(ij|1) are both set to zero. This allows the product-level elasticities to inherit their sparsity from higher levels in the tree, which in turn produces blocks of cross elasticities that are either all dense or exactly equal to zero.

• (IV) Sparse: A sparse vector of elasticities β_ij is generated from a non-hierarchical prior with 95% of all elasticities set to zero.

For each specification above, we generate data from the regression model in Eq. 1 with dimensions (n = 50, p = 100) and (n = 100, p = 300). For specifications (I)–(III), we use a three-level classification tree with five equal-sized groups on the top level and 10 equal-sized groups in the middle level. Across all specifications, we simulate the own elasticities from a Unif(-5,-1) distribution, fix ϕ_i = 0, define ${\Sigma }=\text {diag}({\sigma _{1}^{2}},\dotsc ,{\sigma _{p}^{2}})$ with ${\sigma _{j}^{2}}=1$, and generate elements of data matrices X and C_j from a N(0,1) distribution. We generate 25 data sets from each specification. Examples of the resulting elasticity matrices are shown in Fig. 3.

Fig. 3

Examples of simulated 100 × 100 cross elasticity matrices from the following specifications: (I) hierarchical + dense; (II) hierarchical + sparse after transformation; (III) hierarchical + group-wise sparse; and (IV) sparse. Darker tiles indicate larger elasticities in magnitude. Color version: red tiles represent negative elasticities and green tiles represent positive elasticities

We take a total of nine models to the data. The first three models impose standard shrinkage with fixed shrinkage points set to zero. The second three models include a hierarchical prior on β with ridge shrinkage for the upper-level parameters 𝜃. The final three models include a hierarchical prior on β with horseshoe shrinkage at the upper level. Within each batch, we specify three types of mixing distributions on $\lambda _{ij}^{2}$ which in turn induce three types of shrinkage for β: ridge, lasso, and horseshoe. All models are fit using the MCMC sampling algorithms outlined in Section 4. In Appendix B.1, we plot the posterior means and 95% credible intervals for elasticity parameters in the (𝜃-Ridge, β-Ridge) model to demonstrate that parameters can be accurately recovered.

Model fit statistics are reported in Table 2. The top panel reports results from the (n = 50, p = 100) data sets and the bottom panel reports results from the (n = 100, p = 300) data sets. The first four columns report the root mean squared error (RMSE) associated with the estimation of β in each specification, averaged across the 25 data replicates. The results illustrate the relative strengths of each type of shrinkage prior. In specification (I) where β is purely dense, the hierarchical prior with ridge shrinkage across all levels of the tree fits best. Not surprisingly, a ridge prior is most appropriate when the true parameter is dense. In specification (II) where β appears dense but is sparse after subtracting off the prior mean, the hierarchical prior with horseshoe shrinkage for β and ridge shrinkage for 𝜃 is best. This shows how heavy horseshoe shrinkage can still be desirable for parameters that are sparse under some transformation of the data. In specification (III) where β is “group-wise” sparse, a hierarchical prior with horseshoe shrinkage for 𝜃 and ridge shrinkage for β is best. By forcing β to inherit its heaviness from 𝜃, the prior for β still exhibits heavy shrinkage—reaffirming some of the theory results in Section 3.4—and behaves like group-wise variable selection. In all three specifications, all hierarchical priors substantially outperform the standard shrinkage priors. In specification (III), unlike specifications (I) and (II), all 𝜃-Horseshoe priors outperform all 𝜃-Ridge priors. Finally, in specification (IV) where β is sparse in the traditional sense, then the standard horseshoe prior with fixed shrinkage at zero is best. However, either of the hierarchical priors with horseshoe shrinkage for β also offer competitive performance.

Table 2 Simulation results

The last four columns of Table 2 report the share of signs that are correctly estimated, averaging across data replicates. Producing incorrectly signed elasticity estimates—e.g., negative cross elasticity estimates for goods that are obviously substitutes—is one of the long-standing empirical problems with unrestricted log-linear models (Allenby, 1989; Blattberg & George, 1991; Boatwright et al., 1999). We find that hierarchical priors are largely able to mitigate this issue. For example, while the standard shrinkage priors correctly estimate 73–78% of signs in specifications (I) and (II), hierarchical priors correctly estimate 92–98%.

So far we have assumed that the product classification tree fit to the data matches that of the data generating process. In reality, we do not know whether there is a true hierarchical structure governing cross elasticities, let alone what that structure looks like. In this paper we take the view that category definitions of the retailer or data provider can be used as a reasonable proxy for boundaries in substitution, though this may ultimately be an empirical question (see, e.g., Smith et al., 2019). In Appendix B we provide additional simulations that explore robustness to tree misspecification. We conduct three sets of simulations that vary in the degree of tree misspecification. We find that hierarchical shrinkage can still provide gains (and is no-worse than standard shrinkage) in the presence of misspecification, although the magnitude of these gains vanishes as the degree of misspecification grows. This suggests that hierarchical priors are fairly robust to misspecification of the tree but performance gains over standard sparse approaches depends on the quality of the tree.

6 Empirical application

6.1 Data

We apply log-linear demand models with standard and hierarchical shrinkage priors to IRI store-level transaction data (Bronnenberg et al., 2008). We use data from the largest grocery retail store in Pittsfield, Massachusetts for the two-year period spanning 2011–2012. We use the first 78 weeks as training data and the last 26 weeks as holdout data to evaluate model fit. Although there is the potential to add data from other chains and markets, we take the perspective of the retailer who wants to estimate store-level elasticities to allow for more granular customization of marketing instruments (Montgomery, 1997).

The scope of products included in a large-scale demand analysis usually take one of two forms: (i) narrow and deep, where products only come from one category or subcategory but are defined at a very granular level like the UPC; or (ii) wide and shallow, where products span many categories but are defined at a higher level of aggregation. Here we take the latter approach, in part because a UPC-level analysis often creates challenges for log-linear models due to the potentially high incidence of zero quantities. Estimating demand for wider multi-category assortments also highlights the general flexibility of log-linear systems—e.g., the ability to accommodate a mix of substitutes and complements.

Our procedure for selecting products is as follows. We first choose nine product categories that cover a large portion of total expenditure. Within each category, we remove any subcategories that account for less than 2% of within category revenue, resulting in a total of 28 subcategories. We then aggregate UPCs to the category-subcategory-brand level using total volume (in ounces) and revenue-weighted prices (per ounce). We sort brands by their within-subcategory revenue and then keep top brands that together capture 85% of subcategory revenue and are also present in at least 95% of weeks in the data. This results in p = 275 total products, comprised of over 170,000 UPCs, that make up 81.5% of total revenue within the nine chosen categories. A list of the categories and subcategories used in our analysis is provided in Table 3.

Table 3 Summary of product categories

6.2 Models

We estimate log-linear demand models of the form in Eq. 1 assuming a diagonal error variance matrix Σ. In addition to the high-dimensional vector of prices, we also include product intercepts, summer and holiday dummy variables, and feature and display promotion variables as controls. We consider three different types of shrinkage priors for the price elasticity parameters: standard (where the prior mean is fixed to zero), hierarchical with ridge shrinkage at the upper levels, and hierarchical with horseshoe shrinkage at the upper levels. At the product level we consider ridge, lasso, and horseshoe shrinkage. Together, this results in a total of nine models.

Across all models, we allow the own elasticities to have a different prior than the cross elasticities to account for differences in their expected sign and magnitude. Specifically, in the sparse models we allow the own elasticities to have a separate global variance parameter. In the hierarchical models, we specify separate hierarchical priors for the own and cross elasticities. Each is based on a three-level tree (products at ℓ = 0, subcategories at ℓ = 1, categories at ℓ = 2) where shrinkage starts to propagate at the subcategory level. A complete list of prior and hyperparameter specifications is provided in Appendix C.1. All models are estimated using the MCMC algorithms outlined in Section 4 which are run for 100,000 iterations and thinned by keeping every 100th draw. The standard shrinkage models, hierarchical 𝜃-Ridge models, and hierarchical 𝜃-Horseshoe models take roughly two minutes, four minutes, and six minutes per 1,000 iterations, respectively. Mixing diagnostics are reported in Appendix C.

6.3 Results

6.3.1 Predictive fit

Table 4 reports the out-of-sample RMSEs associated with three sets of demand predictions. The first two columns in Table 4 report the mean and standard deviation of RMSEs across all 275 products. The middle two columns report RMSEs for a subset of 152 products with extrapolated price levels in the test sample. A product is included in this set if at least one price point in the test sample falls outside of its range of prices in the training sample. The final two columns report RMSEs for a subset of 69 products with limited price variation. A product j is included in this set if $\text {SD}_{j} = \text {SD}(\log p_{j1},\dotsc ,\log p_{jn})$ falls in the lower quartile of the distribution of $\text {SD}_{1},\dotsc ,\text {SD}_{275}$. Together, these three types of predictions allow us to examine model performance across a range of forecasting scenarios that retailers may face: predicting demand for an entire assortment, predicting demand at counterfactual price levels, and predicting demand for “low signal” goods.

Table 4 Out-of-sample fit statistics

We find that the (𝜃-Ridge, β-Ridge) hierarchical prior provides the best predictions across all three tasks. Relative to the best-performing standard shrinkage prior, the (𝜃-Ridge, β-Ridge) prior generates a 4.5% improvement in predictions across all products, a 5.7% improvement for products with extrapolated price levels, and a 6.8% improvement for products with limited price variation. We also find that horseshoe shrinkage at the product level tends to perform worst, regardless of if and how the prior mean is parameterized. One possible explanation is that the true elasticities are actually dense, rather than sparse, in which case ridge shrinkage should perform well (as shown in the simulations in Section 5). A second possibility is that the true magnitude of the elasticities may not be large enough to warrant a heavy-tailed prior like the horseshoe. In reality, it may be a combination of both; we will revisit this question as we analyze estimates from each model below.

6.3.2 Product-level elasticities

Next, we compare the estimated product-level elasticities from each model. Table 5 reports the overall average and the 10th, 50th, and 90th percentiles of the distribution of posterior means of β_ii and β_ij. We also report the share of own elasticities that are negative and the share of own elasticities that are significant at the 5% level. Complete distributions of price elasticity and promotion effect estimates are shown in Appendix C.3. Elasticity estimates are markedly different across prior specifications. Starting with own elasticities, we find that standard priors produce distributions of own elasticities where roughly 84% of estimates are negative, 21% of estimates are significant, and the average (median) own elasticity is around -1.2 (-0.9). In contrast, hierarchical priors produce distributions of own elasticity estimates where 93% are negative, 50% are significantly away from zero, and the average (median) own elasticity is around -1.5 (-1.4). We believe that being able to produce more economically reasonable and precise own elasticity estimates by simply shrinking to higher-level elasticities rather than zero is a strength of our approach.

Table 5 Summary of product-level price elasticity estimates

The distribution of cross elasticity estimates also differs across prior specifications. We are estimating 75,350 cross elasticities using less than 100 weeks of training data, and so it is not surprising that the prior imposes heavy regularization. Because typical sparse priors shrink estimates towards zero, the associated distribution of estimates is highly concentrated around zero. Hierarchical priors produce distributions of estimates that are also centered around zero, but spread mass more widely in the (-0.1, 0.1) interval. The exact shape of the distribution depends on the type of shrinkage imposed at each level of the tree. Interestingly, the (𝜃-Horseshoe, β-Horseshoe) prior generates a more widely dispersed distribution of elasticities than the (𝜃-Ridge, β-Ridge) prior. This is a consequence of hierarchical priors: endowing β_ij with a potentially non-zero prior mean leads to a build-up of mass away from zero when shrinkage in strong. Differences in the shape of cross-elasticity estimates can also be seen in the histograms reported in Appendix C.3.

6.3.3 Higher-level elasticities

In addition to product-level elasticities, we can also examine higher-level group elasticities in any of the hierarchical priors. For the sake of brevity, we focus our discussion on estimates from the (𝜃-Ridge, β-Ridge) prior. Figure 4 plots the distributions of higher-level elasticities at the category and subcategory level. The figure on the left plots own elasticities and the figure on the right plots cross elasticities, where the within-group elasticities (green lines) are separated from the across-group elasticities (red lines). Here, the within-group elasticities represent the diagonal elements of the category or subcategory-level elasticity matrix. For example, the BEER within-category elasticity represents the average cross-price elasticity of all products within the BEER category. Similarly, the Domestic Beer/Ale within-subcategory elasticity represents the average cross-price elasticity of all products within the Domestic Beer/Ale subcategory.

Fig. 4

Distributions of higher-level elasticities from the (𝜃-Ridge, β-Ridge) hierarchical prior

Figure 4 illustrates two economic properties of elasticities that are not imposed on the model but are a consequence of hierarchical shrinkage. First, own elasticities tend to be negative and are slightly more negative at the subcategory level than at the category level. The fact that product-level own elasticities are shrunk towards these negative values rather than zero is one reason why own elasticities tend to be more negative under hierarchical priors (as shown in Table 5). Second, cross elasticities within each category/subcategory are mostly positive and shifted to the right of the distribution of elasticities across categories/subcategories. This suggests that substitution and product competition tend to be strongest within each category/subcategory.

Table 6 provides further insight into the nature of category and subcategory-level substitution. For each category/subcategory, we report the associated largest (most positive) elasticity and smallest (most negative) elasticity. We find that for six of the nine categories, demand changes most in response to price changes within the same category (i.e., the within elasticities shown in Fig. 4). For example, the largest elasticity associated with the demand of BEER/ALE is the price of BEER/ALE. This is to be expected if the competition is stronger within categories than across categories. Many of the cross-category relationships also appear reasonable. For example, BEER/ALE and SALTY SNACKS, CARBONATED BEVERAGES and SALTY SNACKS, and MILK and CEREAL are all pairs of strong complements. Results at the subcategory level are similar. For 15 of the 28 subcategories, the largest elasticity corresponds to the either the within subcategory elasticity or the across elasticity within the category (e.g., Domestic vs. Imported Beer/Ale). Many of the strong cross-subcategory complements such as Imported Beer/Ale and Tortilla/Tostada Chips or Rfg Skim/Lowfat Milk and Ready-to-Eat Cereal appear to be inherited from their respective cross-category parent elasticities.

Table 6 Summaries of higher-level cross-price elasticities from the (𝜃-Ridge, β-Ridge) Hierarchical Prior

6.3.4 Shrinkage factors

In addition to the summary of elasticity parameters presented above, we can also summarize the variance parameters to learn about the strength of shrinkage imposed by the prior. To this end, we explore the posterior distribution of product-level shrinkage factors, which are common summary measures used to convey the strength of shrinkage in global-local models (Carvalho et al., 2010; Bhadra et al., 2019). Shrinkage factors measure the extent to which the posterior mean is pulled towards the prior. Formally, the posterior mean of the regression coefficient β takes the form:

$$ \mathbb{E}(\beta|\text{data})= (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\tilde{\text{X}}^{\prime}\tilde{\text{X}}\hat{\beta}+(\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}{\Lambda}_{*}^{-1}\bar{\beta}(\theta) $$

(24)

which is a weighted average of the maximum likelihood estimator $\hat {\beta }$ and the prior mean $\bar {\beta }(\theta )$. The weight on the prior mean, $(\tilde {\text {X}}^{\prime }\tilde {\text {X}}+{\Lambda }_{*}^{-1})^{-1}{\Lambda }_{*}^{-1}$, defines the matrix of shrinkage factors. For simplicity, we use the component-wise approximation:

$$ \mathbb{E}(\beta_{ij}|\text{data}) \approx (1-\kappa_{ij})\hat{\beta}_{ij}+\kappa_{ij}\bar{\beta}(\theta)_{ij} $$

(25)

where

$$ \kappa_{ij}=\frac{1}{1+n{s_{j}^{2}}\sigma_{i}^{-2}\tau_{\beta}^{2}{\Psi}_{ij}} $$

(26)

and ${s_{j}^{2}}=\text {Var}(\log p_{j})$. Notice that $n{s_{j}^{2}}/{\sigma _{i}^{2}}$ can be interpreted as a signal-to-noise ratio. When the signal dominates the noise, κ_ij → 0 and the posterior mean of β_ij converges to $\hat {\beta }_{ij}$; when the noise dominates, then κ_ij → 1 and the posterior mean of β_ij converges to the prior mean.

Table 7 reports summary statistics of global variances and product-level price elasticity shrinkage factors across model specifications. We first compute the posterior median of each κ_ij and then report summary statistics across the distribution of estimates. The first finding is that there is a sizable difference in the strength of shrinkage between own and cross-price elasticities. We find that estimates of $\tau _{\beta \text {cross}}^{2}$ tend to be four to five orders of magnitude smaller than $\tau _{\beta \text {own}}^{2}$. Consequently, estimates of κ_ij (for i≠j) tend to be bunched at one while estimates of κ_ii are more dispersed throughout the unit interval. One explanation for this difference in shrinkage is that retail scanner data tends to exhibit a stronger signal for estimating own elasticities than cross elasticities (Hitsch et al., 2021). Our estimation problem is also high-dimensional as we are estimating 75,350 cross elasticity parameters from 78 weeks of training data.

Table 7 Global variances and shrinkage factors

Across models, we find that hierarchical priors impose heavier shrinkage, on average, than standard global-local priors—especially for own elasticities. For example, the average shrinkage factor κ_ii is 0.19 for the β-Horseshoe model but 0.76 for the (β-Ridge, β-Horseshoe) model. If the shrinkage points are misspecified (as appears to be the case for standard priors with a mean fixed at zero), then the prior variances will need to get larger to accommodate deviations from zero. Since the hierarchical priors center the product-level elasticities around more reasonable values, then the prior variance can get smaller and shrinkage will “kick in” for noisy estimates. For differences in shrinkage factors across product categories, see Appendix C.4 where we plot the empirical CDF of posterior medians of κ_ii across both categories and models. We find appreciable variation in the strength of category-level shrinkage. While there is variation across models, we find that shrinkage tends to be heaviest in categories like BEER/ALE and CARBONATED BEVERAGES, and lightest in FZ PIZZA and SALTY SNACKS.

6.4 Discussion

So far, we have provided evidence that hierarchical shrinkage priors can lead to more negative and precisely estimated own elasticities, larger and more dispersed cross elasticities, and improvements in out-of-sample demand predictions. We close this section with a discussion of implications for analysts and managers. We first discuss the nature of price variation in retail markets, and show how judicious prior choices can help mitigate challenges of estimating price elasticities with weakly informative data. We then discuss the benefits of imposing hierarchical shrinkage when producing competitive maps used for market structure analysis.

6.4.1 Retail prices and prior regularization

In the era of big data it may be tempting to believe that prior specification is less of a concern as the data will simply overwhelm the prior with a sufficiently large sample size. We argue that this view is misguided in a demand estimation context because more data does not necessarily imply more variation in key demand shifters.⁴ In many retail markets, for example, prices are notoriously “sticky” (Bils & Klenow, 2004) and exhibit limited variation over time—a feature that need not dissipate as more data are collected. With limited variation in prices, price coefficients will in turn be subject to heavy regularization. Analysts interested in using observational data to estimate price elasticities will almost always face a problem of weakly informative data, calling for more judicious prior choices.

We illustrate the interplay between weakly informative data and regularization in Fig. 5. Each scatter plot compares the own elasticities from a sparse prior (x-axis) to the own elasticities from a hierarchical prior (y-axis). For example, the top left corner compares estimates from the sparse β-Ridge prior to estimates from the hierarchical (𝜃-Ridge, β-Ridge) prior. Each point is one of 275 products colored according to the strength of the signal provided its price vector. Our specific measure of signal strength for product j is the standard deviation of log prices across weeks in the training data: $\text {SD}_{j}=\text {SD}(\log p_{j1},\dotsc ,\log p_{jn})$. Red triangles represent products in the bottom quartile of this distribution (i.e., products with relatively limited price variation), green squares represent products in the top quartile of this distribution, and grey circles represent products in the second and third quartiles.

Fig. 5

The effects of non-sparse shrinkage on own-price elasticities

We find that most of green squares fall along the diagonal line, implying that the own elasticity estimates produced by sparse and hierarchical priors are similar for goods with relatively high price variation. In contrast, most of the red triangles fall below the diagonal line where estimates from the sparse prior estimates are greater than estimates from the hierarchical prior. This set of products illustrates the value of hierarchical shrinkage: in the absence of a strong signal in the data, we can produce more economically reasonable estimates by imposing shrinkage towards higher-level elasticities rather than zero.

6.4.2 Interpretable market structure

A second implication of hierarchical, non-sparse shrinkage is that it can allow for more interpretable market structure analysis. Marketing researchers have a long history of using competitive maps—i.e., visual representations of product or brand competition—for understanding customer preferences and guiding managerial decisions related to brand positioning (Elrod, 1988; Allenby, 1989; Rutz & Sonnier, 2011), product line management (Chintagunta, 1998), and assortment planning (Sinha et al., 2013). One challenge in producing competitive maps for large assortments is that it is hard to flexibly estimate demand at scale.⁵ As we have shown, log-linear demand models with appropriate forms of regularization can produce estimates of large elasticity matrices. Do different priors lead to appreciably different inferences about competition and market structure?

Figure 6 plots elasticity-based competitive maps across all nine prior specifications. Each map is made by using a two-dimensional t-SNE projection (van der Maaten & Hinton, 2008) of the estimated price elasticity matrix. Each point on the map is one of 275 products and distances between products reflect degrees of substitution, with more related products appearing closer together. Points are colored based on category labels to help interpret competitive boundaries. We find substantial differences in the interpretability of competitive maps across sparse and hierarchical prior specifications. The maps produced by standard shrinkage priors do not, at first glance, reflect any deeper structure of demand. In contrast, the maps produced by hierarchical shrinkage priors feature a co-clustering of goods belonging to the same or similar categories. For example, in the (𝜃-Ridge, β-Ridge) map, most beverages appear on the right-hand side and many beers and carbonated beverages are located near clusters of salty snacks, frozen dinners, and frozen pizza.

Fig. 6

Competitive maps based on t-SNE projections of each model’s estimated 275 × 275 price elasticity matrix. Each point represents a product and is colored by its category label

In Appendix C5, we show a subcategory-level version of Fig. 6 for two selected models to show how hierarchical shrinkage leads to more coherent subcategory clustering behavior. We also provide zoomed-in plots for the SALTY SNACK category to examine the ways in which brands co-cluster. In the hierarchical shrinkage map, we find that category and subcategory labels tend have more influence over clustering outcomes than brand labels. For instance, we do not find that brands co-cluster across subcategories (as would be expected if umbrella branding or quality tiers induced strong cross-subcategory substitution, for example). Instead, we find that clusters tend to include all brands within the same subcategory. Relative to hierarchical shrinkage maps, standard shrinkage maps exhibit no discernible clustering behavior across brands or subcategories. Overall, we believe that improvements in map interpretability can lead to better inferences about product competition and more valuable insights for for decision-making.

7 Conclusion

This paper studies shrinkage priors for high-dimensional demand systems. We propose a hierarchical extension to the class of global-local priors where prior means and variances are parameterized by product classification trees that commonly accompany retail scanner data sets. The principal benefit is that the price elasticity between two goods will be shrunk towards higher-level category elasticities rather than zero. We also formally examine the shrinkage properties of hierarchical global-local priors and show that including a heavy tailed mixing distribution at any level of the tree is sufficient for imposing heavy shrinkage for product-level elasticities.

We apply our hierarchical priors to the elasticity parameters of a log-linear demand model in which store-level sales are regressed on a high-dimensional vector of prices as well as seasonal trends and other product controls. We propose a simple modified version of the fast sampling algorithm in Bhattacharya et al. (2016) to help alleviate the typical computational bottleneck that arises when inverting the posterior precision matrix. We then use both simulated data and retail scanner data to show the value of non-sparse shrinkage. Our simulation experiments shed light on the situations in which different types of shrinkage are most/least appropriate. Hierarchical priors can offer significant gains when the true elasticity matrix is dense and inherits its structure from a product classification tree. Moreover, hierarchical priors are fairly robust to tree misspecification and are still competitive with standard sparsity priors when the parameters are actually sparse.

Our empirical application uses two years of data to estimate 75,625 price elasticities associated with an assortment of 275 goods that span 28 subcategories and nine categories. We find that the hierarchical prior with ridge shrinkage throughout the tree provides the best predictive performance. We also find that hierarchical priors provide much more reasonable estimates of own elasticities than the standard shrinkage priors which impose a fixed shrinkage point at zero. The hierarchical global-local structure also allows us to learn about within and cross-subcategory and category elasticities, which is useful for identifying boundaries of competition. Our results provide evidence that, in the absence of a strong signal in the data, hierarchical shrinkage can lead to improvements in different aspects of demand estimation relative to “off-the-shelf” regularization. More generally, we believe our work highlights the importance of judicious priors in high-dimensional estimation problems.

Appendices

Appendix A: Posterior computation with hierarchical global-local priors

1.1 A.1: Full Conditionals

Means

The higher-level elasticity parameters 𝜃_π(ij|ℓ) are assumed to follow a normal prior and therefore have a normal full conditional distribution: $\theta _{\pi (ij|\ell )}|\text {else} \sim \text {N}(\tilde {\theta }_{\pi (ij|\ell )},V_{\pi (ij|\ell )})$, where

$$ \begin{array}{@{}rcl@{}} \tilde{\theta}_{\pi(ij|\ell)} &=& V_{\pi(ij|\ell)}\left( {\sum}_{a\in\mathcal{C}_{i}^{\ell}} {\sum}_{b\in\mathcal{C}_{j}^{\ell}}\frac{\theta_{\pi(ab|\ell-1)}}{\tau_{\ell-1}^{2}{\Psi}_{\pi(ab|\ell-1)} } + \frac{\theta_{\pi(ij|\ell+1)}}{\tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell)} }\right),\\ V_{\pi(ij|\ell)}&=&\left( {\sum}_{a\in\mathcal{C}_{i}^{\ell}}{\sum}_{b\in\mathcal{C}_{j}^{\ell}} \frac{1}{\tau_{\ell-1}^{2}{\Psi}_{\pi(ab|\ell-1)}} + \frac{1}{\tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell)}}\right)^{-1}. \end{array} $$

Here $\mathcal {C}_{i}^{\ell }=\left \{i^{\prime }\in \{1,\dotsc ,n_{\ell }\}:\pi (i^{\prime }j|\ell )=\pi (ij|\ell )\right \}$ and $\mathcal {C}_{j}^{\ell }=\left \{j^{\prime }\in \{1,\dotsc ,n_{\ell }\}:\pi (ij^{\prime }|\ell )=\pi (ij|\ell )\right \}$ each represent sets of group indices that share a common ancestry with group i or j at level ℓ.

Local variances

First rewrite Eq. 6 as ${\Psi }_{\pi (ij|\ell )}=\lambda _{\pi (ij|\ell )}^{2} {\prod }_{s=\ell +1}^{L-1} \lambda _{\pi (ij|s)}^{2}=\lambda _{\pi (ij|\ell )}^{2} {\Psi }_{\pi (ij|\ell +1)}$ and so at level ℓ, all $\lambda _{\pi (ij|\ell )}^{2}$ terms need to be sampled from their full conditional distribution given Ψ_{π(ij|ℓ+ 1)}. Here we focus on the case where $\lambda _{\pi (ij|\ell )}\sim \text {C}^{+}(0,1)$, which corresponds to horseshoe shrinkage. We exploit the following scale mixture representation of the half-Cauchy prior (Makalic and Schmidt, 2015): if $\lambda ^{2}|\zeta \sim \text {IG}(1/2,1/\zeta )$ and $\zeta \sim \text {IG}(1/2,1)$, then $\lambda \sim \text {C}^{+}(0,1)$.

$$ \begin{array}{@{}rcl@{}} \lambda_{\pi(ij|\ell)}^{2}|\zeta_{\pi(ij|\ell)},\text{else} &\sim& \text{IG}\left( \frac{1}{2} + \frac{1}{2}{\sum}_{s\leq\ell} {n_{s}^{2}},\frac{1}{\zeta_{\pi(ij|\ell)}}+ \frac{(\theta_{\pi(ij|\ell)}-\theta_{\pi(ij|\ell+1)})^{2}}{2\tau_{\ell}^{2}{\Psi}_{\pi(ij|\ell+1)}}\right.\\ &&\left.+\frac{1}{2} {\sum}_{s<\ell} {\sum}_{a\in\mathcal{C}_{i}^{s}} {\sum}_{b\in\mathcal{C}_{j}^{s}} \frac{(\theta_{\pi(ab|s)}-\theta_{\pi(ab|s+1)})^{2}}{\tau_{s}^{2}{\Psi}_{\pi(ab|s+1)}} \right)\\ \zeta_{\pi(ij|\ell)}|\lambda_{\pi(ij|\ell)}^{2} &\sim& \text{IG}\left( 1,1+\frac{1}{\lambda_{\pi(ij|\ell)}^{2}} \right) \end{array} $$

Global variances

We place a half-Cauchy prior on τ and use the same scale mixture representation outlined above for the local variances.

$$ \begin{array}{@{}rcl@{}} \tau_{\ell}^{2}|\zeta_{\ell},\text{else} &\sim&\text{IG}\left( \frac{n_{\ell}^{2}+1}{2},\frac{1}{\zeta_{\ell}}+\frac{1}{2}{\sum}_{a=1}^{n_{\ell}^{2}}{\sum}_{b=1}^{n_{\ell}^{2}}\frac{\big(\theta_{\pi(ab|\ell)}-\theta_{\pi(ab|\ell+1)}\big)^{2}}{{\Psi}_{\pi(ab|\ell)}} \right)\\ \zeta_{\ell}|\tau_{\ell}^{2} &\sim& \text{IG}\left( 1,1+\frac{1}{\tau_{\ell}^{2}} \right)\\ \end{array} $$

1.2 A.2: Fast sampling algorithm

We show that our version of the Bhattacharya et al. (2016) fast sampling algorithm, as outlined in Section 4.2, produces a draw of β with the correct posterior mean and covariance matrix:

$$ \begin{array}{@{}rcl@{}} \mathbb{E}(\beta|\text{data}) &=&(\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}(\tilde{\text{X}}^{\prime}\tilde{y}+{\Lambda}_{*}^{-1}\bar{\beta}(\theta))\\\text{Cov}(\beta|\text{data}) &=&(\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1} \end{array} $$

where $\bar {\beta }(\theta )$ denotes the prior mean of β which depends on higher-level elasticity parameters 𝜃. Note that our proofs below rely on the Woodbury matrix identity: (A + UCV )^− 1 = A^− 1 − A^− 1U(C^− 1 + V A^− 1U)^− 1V A^− 1.

$$ \begin{array}{@{}rcl@{}} \mathbb{E}(\beta|\text{data}) &=& \mathbb{E}(u) + {\Lambda}_{*} \tilde{\text{X}}^{\prime}\mathbb{E}(w)\\ &=& \mathbb{E}(u) + {\Lambda}_{*} \tilde{\text{X}}^{\prime}\mathbb{E}\left( (\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}(\tilde{y}-v)\right)\\ &=& \mathbb{E}(u) + {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}(\tilde{y}-\mathbb{E}(v))\\ &=& \mathbb{E}(u) + {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}(\tilde{y}-\tilde{\text{X}}\mathbb{E}(u)-\mathbb{E}(\delta))\\ &=& {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{y} + \bar{\beta}(\theta) - {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{\text{X}}\bar{\beta}(\theta) \\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\tilde{\text{X}}^{\prime}\tilde{y}\\ &&+ \left( I - {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{\text{X}}\right)\bar{\beta}(\theta) \ \text{ by Woodbury}\\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\tilde{\text{X}}^{\prime}\tilde{y} + \left( I - {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{\text{X}}\right){\Lambda}_{*}{\Lambda}_{*}^{-1}\bar{\beta}(\theta) \\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\tilde{\text{X}}^{\prime}\tilde{y} + \left( {\Lambda}_{*} - {\Lambda}_{*} \tilde{\text{X}}^{\prime}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{\text{X}}{\Lambda}_{*}\right){\Lambda}_{*}^{-1}\bar{\beta}(\theta)\\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}\tilde{\text{X}}^{\prime}\tilde{y} + (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1}){\Lambda}_{*}^{-1}\bar{\beta}(\theta) \ \text{ by Woodbury}\\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1}(\tilde{\text{X}}^{\prime}\tilde{y}+{\Lambda}_{*}^{-1}\bar{\beta}(\theta))\\ \text{Cov}(\beta|\text{data}) &=& \text{Cov}(u + {\Lambda}_{*}^{\prime}\tilde{\text{X}}w)\\ &=& \text{Cov}(u + {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma}(\tilde{y}-v))\\ &=& \text{Cov}(u - {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} v)\\ &=& \text{Var}(u) + \text{Var}({\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} v) - \text{Cov}(u,{\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} v) - \text{Cov}({\Lambda}_{*} ^{\prime}\tilde{\text{X}}{\Sigma} v, u)\\ &=& \text{Var}(u) + {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} \text{Var}(v){\Sigma} \tilde{\text{X}}^{\prime}{\Lambda}_{*}\\ &&- \text{Cov}(u,v){\Sigma} \tilde{\text{X}}^{\prime}{\Lambda}_{*} - {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} \text{Cov}(v, u)\\ &=& {\Lambda}_{*} + {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} {\Sigma}^{-1}{\Sigma} \tilde{\text{X}}^{\prime}{\Lambda}_{*} - {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} \tilde{\text{X}}^{\prime}{\Lambda}_{*} - {\Lambda}_{*}^{\prime}\tilde{\text{X}}{\Sigma} \tilde{\text{X}}^{\prime}{\Lambda}_{*} \\ &=& {\Lambda}_{*} - {\Lambda}_{*}^{\prime}\tilde{\text{X}}(\tilde{\text{X}}{\Lambda}_{*} \tilde{\text{X}}^{\prime}+I)^{-1}\tilde{\text{X}}^{\prime}{\Lambda}_{*} \\ &=& (\tilde{\text{X}}^{\prime}\tilde{\text{X}}+{\Lambda}_{*}^{-1})^{-1} \ \text{ by Woodbury} \\ \end{array} $$

Appendix B: Additional simulation experiments

1.1 B.1: Parameter recovery

The goal of this section is to show that the MCMC algorithms outlined in Section 4 can accurately recover model parameters at each level of the tree. We focus on one of the 25 data sets generated by specification (I) with n = 50 and p = 100 (for details, see the discussion in Section 5). The tree corresponding to this data set has 5 categories, 10 subcategories, and 100 products. There are then 5² = 25 category elasticities 𝜃_π(ij|2), 10² = 100 subcategory elasticities 𝜃_π(ij|1), and 100² = 10, 000 product elasticities β_ij.

For simplicity, we report estimates from two models: the (𝜃-Ridge, β-Ridge) hierarchical prior and the standard (β-Ridge) prior. Figure 7 plots the posterior mean of each elasticity parameter against its true value. The vertical lines correspond to 95% credible intervals. The first three figures report estimates from the hierarchical shrinkage prior and the last figure reports estimates from the standard shrinkage prior. We find that all 95% credible intervals cover true values for the category and subcategory-level elasticities, and nearly all credible intervals cover true values for product-level elasticities.

Fig. 7

Posterior means and 95% credible intervals of elasticity parameters are plotted against true values. The first three figures report estimates from the hierarchical (𝜃-Ridge, β-Ridge) prior and the last figure reports estimates from the standard (β-Ridge) model. The data are generated from specification (I) as described in Section 5 with n = 50 and p = 100

The benefits of hierarchical shrinkage can be seen by comparing the estimates of product-level elasticities β_ij in the last two figures. With high-dimensional p > n data, the design matrix will be rank deficient and the regularization imposed by the prior will bite. The last figure on the right shows that default prior assumptions can produce very noisy and biased estimates, especially for elasticities that are larger in magnitude. In comparison, our hierarchical priors shrink noisy estimates towards more reasonable values by pooling information across products. Overall, this further emphasizes the importances of judicious prior choices in high-dimensional settings.

1.2 B.2: Tree misspecification

The simulation experiments in Section 5 assume that the tree used to construct the hierarchical shrinkage prior matches the “true” tree used to generate the data. When working with observational data, the existence or structure of a true tree is not known so there may be a concern of tree misspecification. In the context of scanner data, the reported product classification tree could be misspecified if it does not reflect consumers’ true boundaries of substitution across product groups. For example, in the IRI scanner data set “Ready-to-Eat Cereal” is the only subcategory within the CEREAL category. This part of the tree may be too coarse if there is a more granular partitioning of cereal brands, flavors, and qualities that better aligns with consumer cross-product substitution.

In this section we use the same 25 (n = 50, p = 100) simulated data sets from specification (I) in Section 5 to explore consequences of tree misspecification. Let T_true denote the tree used to simulate the data. T_true has five equal-sized categories on the top level (each having two child subcategories), 10 equal-sized subcategories on the middle level (each having 10 child products), and 100 products on the bottom level. In addition to standard shrinkage priors and hierarchical priors based on T_true, we also fit hierarchical priors based on the following three misspecified trees.

• In $T_{A}^{\prime }$, the ordering of group nodes on the top and middle levels are kept the same, but the bottom-level nodes (the “products”) are permuted. In T_true, products fill up one subcategory at a time—i.e., goods $1,\dotsc ,10$ are assigned to subcategory 1, goods $11, \dotsc ,20$ are assigned to subcategory 2, and so on. We generate $T_{A}^{\prime }$ by assigning the first product to subcategory 1, the second product to subcategory 2, and so on until each subcategory has one product. This process repeats until all products have been assigned into a subcategory. The resulting tree shares no common structure with T_true.

• In $T_{B}^{\prime }$, half of the tree is misspecified (in the same way as $T_{A}^{\prime }$) while the other half matches T_true.

• In $T_{C}^{\prime }$, half of the tree is misspecified as an overly granular version of T_true (each group is split into two) while the other half matches T_true.

Examples of each form of misspecification are provided in Fig. 8 and simulation results are reported in Table 8. For each misspecified tree, we also report the distance between $T^{\prime }$ and T_true using the adjusted Rand index (ARI). Similarity is maximized when $ARI(T^{\prime },T_{true})=1$. Our results indicate that hierarchical shrinkage can still provide improved estimates over standard shrinkage methods—and is never worse than standard shrinkage methods—even when the tree is misspecified. However, the magnitude of these gains vanishes as the degree of misspecification grows. If an analyst is concerned with the threat of misspecification, then different tree structures could be fit to the data and compared based on out-of-sample fit metrics.

Fig. 8

A minimal example with p = 16 highlighting the three forms of misspecification considered in our simulation experiments. Shaded circles indicate misspecification relative to T_true

Table 8 Effects of tree misspecification

Appendix C: Additional empirical details and results

1.1 C.1: Summary of Priors and Hyperparameter Specifications

Standard shrinkage priors

• Cross elasticities

  $$ {\beta}_{ij} \sim \text{N}\left( 0,{\lambda}_{ij}^{2}{\tau}_{\text{cross}}^{2}\right),\quad {\tau}_{\text{cross}}\sim{\text{C}}^{+}(0,1) $$

• Own elasticities

  $$ {\beta}_{ii} \sim \text{N}\left( 0,{\lambda}_{ii}^{2}{\tau}_{\text{own}}^{2}\right), \quad {\tau}_{\text{own}}\sim{\text{C}}^{+}(0,1) $$

• Control coefficient vector (product intercepts, seasonal variables, promotional variables)

  $$ {\phi}_{i} \sim \text{N}(0,{10}^{2}I_{d}) $$

• Observational error variance

  $$ {{\sigma}_{i}^{2}} \sim \text{IG}(5,5) $$

Hierarchical shrinkage priors

• Cross elasticities

  $$ \begin{array}{@{}rcl@{}} {\beta}_{ij} \sim \text{N}\left( {\theta}_{\pi(ij|1)},{\Psi}_{ij}{\tau}_{\beta\text{cross}}^{2}\right), &\quad& {\tau}_{\beta\text{cross}^{\text{C}}}^{+}(0,1)\\ {\theta}_{\pi(ij|1)} \text{N}\left( {\theta}_{\pi(ij|2)},{\Psi}_{\pi(ij|1)}{\tau}_{1\text{cross}}^{2}\right), &\quad& {\tau}_{1\text{cross}\text{C}}^{+}(0,1)\\ {\theta}_{\pi(ij|2)} \text{N}\left( {\bar{\theta}}_{\text{own}},{\Psi}_{\pi(ij|2)}{\tau}_{2\text{cross}}^{2}\right), &\quad& \tau{\text{cross}}^{2}{\text{C}}^{+}(0,1)\\ {\bar{\theta}}_{\text{cross}} \text{N}(0,1)&& \end{array} $$

• Own elasticities

  $$ \begin{array}{@{}rcl@{}} {\beta}_{ii} \text{N}\left( {\theta}_{\pi(ii|1)},{\Psi}_{ii}{\tau}_{\beta\text{own}}^{2}\right), &\quad& {{\tau}_{\beta\text{own}}^{\text{C}}}^{+}(0,1)\\ {\theta}_{\pi(ii|1)}\text{N}\left( {\theta}_{\pi(ii|2)},{\Psi}_{\pi(ii|1)}{\tau}_{1\text{own}}^{2}\right), &\quad& {{\tau}_{1\text{own}}^{\text{C}}}^{+}(0,1)\\ {\theta}_{\pi(ii|2)}\text{N}\left( {\bar{\theta}}_{\text{cross}},{\Psi}_{\pi(ii|2)}{\tau}_{2\text{own}}^{2}\right), &\quad& {\tau}_{2\text{own}}\text{C}^{+}(0,1)\\ \bar{\theta}_{\text{own}}\text{N}(0,1)&& \end{array} $$

• Control coefficient vector (product intercepts, seasonal variables, promotional variables)

  $${\phi}_{i}\text{N}(0,10^{2}I_{d})$$

• Observational error variance

  $${{\sigma}_{i}^{2}}\text{IG}(5,5)$$

1.2 C.2: Mixing diagnostics

Fig. 9

Percentiles of the autocorrelation function across own-price elasticity parameters

Fig. 10

Percentiles of the autocorrelation function across cross-price elasticity parameters. In panel (c), we randomly sample 1,000 of the 75,625 total elasticity parameters

1.3 C.3: Distributions of Price Elasticity and Promotional Effect Estimates

Fig. 11

Distributions of product-level price elasticity estimates

Fig. 12

Distributions of product-level own-promotion effect estimates

1.4 C.4: Shrinkage Factors by Category

Fig. 13

Empirical CDFs of own-price elasticity shrinkage factor estimates median(κ_ii|data) plotted across models and product categories. There is maximum shrinkage when κ_ii = 1 and no shrinkage when κ_ii = 0

1.5 C.5: Competitive maps by category

Fig. 14

Competitive maps based on t-SNE projections of the 275 × 275 price elasticity matrix separated by category for two selected models. Points are assigned the same colors as in Fig. 6 and are also assigned separate shapes based on subcategory labels (see Table 3). The number of subcategories within a category is listed in parentheses next to the category name

Fig. 15

Competitive maps for the SALTY SNACK category from two selected models. This is a zoomed-in, product-level view of Fig. 6. Each point is a product (brand) and is colored by its subcategory label