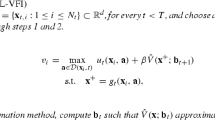Adaptive grids for the estimation of dynamic models

Abstract

This paper develops a method to flexibly adapt interpolation grids of value function approximations in the estimation of dynamic models using either NFXP (Rust, Econometrica: Journal of the Econometric Society, 55, 999–1033, 1987) or MPEC (Su & Judd, Econometrica: Journal of the Econometric Society, 80, 2213–2230, 2012). Since MPEC requires the grid structure for the value function approximation to be hard-coded into the constraints, one cannot apply iterative node insertion for grid refinement; for NFXP, grid adaption by (iteratively) inserting new grid nodes will generally lead to discontinuous likelihood functions. Therefore, we show how to continuously adapt the grid by moving the nodes, a technique referred to as r-adaption. We demonstrate how to obtain optimal grids based on the balanced error principle, and implement this approach by including additional constraints to the likelihood maximization problem. The method is applied to two models: (i) the bus engine replacement model (Rust, 1987), modified to feature a continuous mileage state, and (ii) to a dynamic model of content consumption using original data from one of the world’s leading user-generated content networks in the domain of music.

1 Introduction

This paper develops a method to flexibly adapt interpolation grids of value function approximation in dynamic programming models, such as dynamic discrete choice models, when the estimation is either carried out using the nested fixed point algorithm of Rust (1987), or using constrained optimization—namely, the MPEC approach of Su and Judd (2012). Introducing grid adaption by (iterative) node insertion into NFXP will generally produce discontinuous likelihood functions and thus make their maximization potentially very difficult. On the other hand, the MPEC approach needs the structure of the value function approximation to be hard-coded into the constraints of the likelihood optimization problem; as a consequence, one cannot use iteratively adaptive procedures for grid refinement in every iteration of the optimization. In this paper, we show how to adapt the interpolation grid by moving the nodes, a technique referred to as r-adaptive refinement. We demonstrate how to obtain optimal grids (given a fixed number of nodes), and show how to integrate this approach into the likelihood maximization problem using the equioscillation principle. The method is applied to the bus engine replacement model of Rust (1987), modified to feature a continuous mileage state as well as a serially correlated, unobserved utility component.

Many models in modern applications of structural estimation assume the agents to behave in a dynamically optimal manner. A popular example is the literature on dynamic discrete choice models (DDCM), pioneered by the seminal work of Rust (1987) and Rust (1988); for recent surveys on the estimation of DDCMs, see Aguirregabiria and Mira (2010), Keane et al. (2011), and Arcidiacono and Ellickson (2011). In these applications, data on the decisions of an agent in a particular dynamic problem are observed, along with other state variables that enter the agent’s optimization. Using this data, the structural parameters of the model—such as the parameters of the utility functions or of the law of motion of the state variables—are estimated, for example by the method of maximum likelihood or Bayesian approaches.

The estimation of dynamic programming models is challenging both methodologically and computationally, as—in principle—the dynamic optimization problem and the likelihood maximization problem have to be solved simultaneously. While there exist methods that avoid solving the model by estimating the conditional choice probabilities directly from the data and go back to the work of Hotz and Miller (1993), and methods that avoid explicitly maximizing the likelihood by using Bayesian approaches with Markov chain Monte Carlo simulation (Imai et al., 2009; Norets, 2009), many of the widely used workhorse algorithms still rely on solving both problems simultaneously, thus showing excellent numerical and statistical efficiency.

In particular, the nested fixed point (NFXP) algorithm of Rust (1987) and the constrained optimization approach (mathematical programming with equilibrium constraints (MPEC)) of Su and Judd (2012) are among the most used algorithms. In NFXP, the dynamic problem is solved iteratively within an “inner loop”, and its solution is used to obtain the choice probability to compute the likelihood function for a particular parameter value, which is itself maximized in an “outer loop”. The methodological separation of the two steps makes this algorithm a robust and efficient choice for many applications, as the very special structure of the two problems can be exploited; in particular, this includes the contraction mapping property of the underlying dynamic problem, and structure of likelihood maximization problems, where the Hessian can be computed as the outer product of the gradients. On the other hand, the MPEC approach tries to avoid computing the full solution of the dynamic problem throughout the likelihood optimization, except at the optimal parameter vector itself. This can potentially be achieved by inserting the optimality conditions of the underlying dynamic problem as nonlinear constraints into the likelihood maximization, and solving the resulting problem using constrained optimization techniques. The fact that the solution of the model is not computed at every iteration of the optimization is conceptually very attractive as such computation often accounts for most of the computation time, but solutions other than at the optimal parameter vector rarely have any relevance. Therefore, MPEC has shown excellent numerical efficiency in many applications.

When solving dynamic programming models with continuous state spaces, most methods for approximating the value function require the researcher to specify a grid over the domain of approximation. Depending on the approximation scheme in use, the nodes of this grid serve as interpolation or collocation points, and potentially as breakpoints if the approximation is assembled from piecewise basis functions. Popular grids include the uniform grid and the Chebyshev grid. While these choices might be good “ex ante” without much knowledge about the approximated function, they are generally suboptimal once the function—or an approximation thereof—is known. Consequently, a popular approach to grid creation is iterative refinement: given the grid from the last iteration (or starting from a uniform grid), the unknown function is approximated, and—based on some approximation error criterion—a new grid is created by inserting additional nodes in regions of high approximation error; this procedure is repeated until the maximum approximation error is below some threshold. Iterative grid refinement methods have successfully been applied to dynamic programming problems with continuous state variables in economics; see, for example, Grüne and Semmler (2004), Brumm and Scheidegger (2017), and Reich (2018).

As we will demonstrate, the integration of iterative grid adaption into both NFXP and MPEC is a delicate task. First, while iterative refinement can formally be integrated into NFXP, as it is agnostic about the function approximation algorithm used in the model solution step, it will create a discontinuous likelihood function;¹ since the likelihood function optimization process is generally a non-trivial task anyway, introducing such a difficulty on top of this non-triviality is definitely undesirable. Second, the integration of iterative refinement into MPEC is not obvious for two reasons: One the one hand, inserting an interpolation or collocation node into the grid corresponds to inserting a constraint into the likelihood optimization problem while the optimizer runs, which generally leads to instability. On the other hand, since MPEC gives no guarantee that the dynamic problem is solved at any point of the optimization except for the solution, no valid value function approximation exists on which a criterion governing the choice of where to actually insert the nodes can be based. Therefore, the integration of MPEC with flexible grids calls for a different methodology.

An alternative to grid refinement by node insertion is adaption by node movement: instead of inserting a new node in a region of high approximation error, an existing node is moved there from a region of low approximation error, keeping the total number of nodes in the grid fixed. Obviously, finding a good (or optimal) grid is more difficult, as moving a node does not only affect the approximation in the region where the node is moved to, but also does so where that node has been moved from. While not being as popular as the iterative schemes, grid adaption by node movement has attracted attention for example in the literature on free-knot splines for curve fitting (see, for example, Schumaker, 2007 and the literature cited therein), and in the solution of partial differential equations with moving meshes (see, for example, Huang & Russell, 2011 and the literature cited therein).

A particular difference between node insertion and node movement is the adaption criterion. In the case of insertion, this criterion is usually binary, as nodes are inserted at pre-specified locations if the approximation error locally exceeds some threshold, otherwise not. In contrast, node movement is a continuous operation, as—for each node—the position on the refined grid (or the direction of movement) must be specified; this information is either obtained from conditions on the node positions based on the approximated function (for example, equidistributed over the function’s values or over its arc length), or from the solution of a minimization problem over the approximation error; see Baines (1998) for a comparison of these two criteria.

The method we develop in this paper is based on approximation error minimization. However, directly integrating this optimization problem into an estimation procedure results in a bi-level optimization problem, where the likelihood maximization is “wrapped around” the approximation error minimization, which makes the resulting combined problem difficult to solve. A common approach to bi-level optimization is to replace the lower-level problem by its first-order optimality constraints—in the case of inequality constraint lower-level problems the Karush–Kuhn–Tucker (KKT) conditions—and solve the resulting problem using constrained optimization techniques. However, solving bi-level problems using first-order necessary conditions is known to cause numerical issues, such as difficult to handle complementarity constraints that violate the constraint qualifications of the first-order conditions of the combined problem; for a discussion of this issue, see, for example, Colson et al. (2007) and Fletcher et al. (2006).

Nevertheless, our method also replaces the lower-level approximation minimization problem by a set of optimality constraints using (in)equalities only, and thus allows the problem to be solved by standard constrained optimization solvers. However, instead of relying on generic conditions such as KKT, the structure of our problem makes it possible to use a classical result from numerical analysis to derive an alternative set of conditions, which is actually even sufficient for optimality. The “equioscillation” theorem for polynomial approximation and its generalizations to other functional forms state that if an approximation of a continuous function has “balanced and alternating errors”, it is uniform (best approximation in the $L_{\infty }$ norm). Geometrically speaking, best polynomial approximations have errors that (i) oscillate—and therefore have “alternating” signs—, and (ii) their amplitude is equal to the maximum absolute error, i.e. they “balance the error” over the whole domain. Conversely, it has been shown that “balanced errors” (BE) alone form a sufficient condition for a (locally) optimal node placement under quite general conditions (see, e.g., Lawson, 1964): If the approximation errors between two neighboring nodes are pairwise equal, then the overall approximation error, i.e. the maximum of the errors over the individual intervals, is (locally) minimal.

Using the balanced error principle, we show that it is straightforward to derive a set of (in)equalities that form optimality conditions for the approximation error minimization, which we finally integrate into the estimation procedures. In the case of NFXP, this resolves the continuity issue of iterative grid adaption if (i) the optimal grid continuously depends on the value function and if (ii) the value function itself continuously depends on the model parameters.² In the MPEC case, we demonstrate how to simultaneously solve the grid optimization and the likelihood maximization problems using standard constrained optimization. In summary, we derive a procedure for integrating grid adaption by node movement into the estimation of dynamic programming models, resulting in value function approximations that are optimal in the $L_{\infty }$ norm, given their functional form and the total number of grid nodes. To the best of our knowledge, we are the first to solve dynamic programming models and the grid adaption problem simultaneously by using node movement based on error balancing; this allows us to incorporate our method into MPEC-type estimation algorithms, where—additionally—the estimation problem is solved at the same time.

In the second part of this paper, we present a series of examples and applications in order to verify our method, and demonstrate its mechanics and performance advantages.

In Section 3.1, we apply approximation with BE conditions to a standard function interpolation example, leaving aside the estimation of any model parameters. We do this in order to further illustrate the principle of equioscillation and its application to grid adaption, and—moreover—to verify our method by situating it in relation to other approaches and theoretical results: First, the function approximation example is computed both using BE conditions and by direct minimization of the approximation error measured by the $L_{\infty }$ norm; in this way, we also experimentally confirm the equivalence of the two problems. Interestingly, while we find the solutions to be identical as expected, the BE variant appears to be numerically much more efficient than direct minimization.³

In our experiments (some of which are deferred to the appendix), we approximate different polynomials and the exponential function, using polynomial interpolation on Chebyshev nodes, and piecewise linear and piecewise quadratic interpolation on uniform grids, and compare their accuracy to the respective approximations over flexible grids obtained from BE conditions. We find that in all cases the flexible grid allows for more accurate approximation given the same number of interpolation nodes (except for the closed-form benchmark, which has identical accuracy).

In Section 3.2 we apply our method to two versions of the bus engine replacement model of Rust (1987), both of which we modify to feature a continuous mileage state.⁴ While the first version is identical to the original except for the continuous nature of the state variable, the second version features a serially correlated, unobserved utility component, thus resulting in a two-dimensional value function approximation problem.

Apart from the fact that we have to specify a continuous mileage transition process, the computation deviates from the original model in two ways: first, the expectation over the one-period ahead values in the Bellman equation is continuous and thus has to be approximated using numerical quadrature. second, the expected value function becomes two-dimensional in the serial correlation case, which raises the need to adapt the balanced error criterion. Similar to the function approximation examples, we first approximate the expected value function for a fixed parameter vector; we do this in order to verify the method by comparing it to a benchmark solution, which is computed using a very fine grid, as well as to demonstrate the potential efficiency gains from node movement in a particular application. We find that even in this simplified problem our method uses significantly fewer nodes to attain a pre-specified level of accuracy, compared to a uniform grid.

In Section 3.2.3 we estimate the cost parameters of the model using both nested fixed point (NFXP) and constrained optimization (MPEC) with grid adaption by node movement. In order to obtain a measure of the variation of the estimates and the corresponding errors, we carry out a Monte Carlo study with 100 artificial datasets. In the case of the original model, we find that the comparative advantage compared to a uniform grid in terms of accuracy and computational efficiency is substantial, even in this simple one-dimensional application: the mean squared error of a uniform grid is an order of magnitude higher compared to a grid of equally many flexible nodes; conversely, estimating the model using a uniform grid that is fine enough to achieve the same accuracy as its flexible counterpart results in roughly 1.5 times longer computation times. The case of the model with a serially correlated, unobserved utility component requires us (i) to approximate the expected value as a function of a two-dimensional state variable, and (ii) to integrate out the random shock when computing the likelihood function; we do the latter by applying the recursive likelihood integration method (RLI; Reich, 2018; Lanz, 2021). Our findings regarding the efficiency of the balanced error approach compared to fixed and uniform grids in the two-dimensional case are comparable, but given the longer absolute computing times, the absolute gains are even more significant.

Finally, in Section 4 we demonstrate the applicability of the proposed method by utilizing data from one of the world’s leading user-generated content networks in the domain of music. More specifically, we apply the proposed method to a dynamic model of content consumption and consider the consumers’ inherent trade-off between exploration and exploitation in their decisions: To counter the gradual decrease of satisfaction while listening to the same artists over and over again, the consumer has to search for a new artist but, at the same time, is faced with uncertainty regarding the degree of positive spillovers from this new artist on the current stock. Hence, while exploring, the potential increase in satisfaction is contrasted with the search costs of finding a new artist. The estimated model—covering 1,171 consumers who altogether played 3,094,418 songs—allows us to understand whether consumers enjoy the process of searching for new artists itself, or if consumers attach costs to the search process and obtain utility from consuming their current stock of artists. This question is inherently linked to the efficiency of the platform’s recommender system for which we find supportive evidence that additional features do not create significant additional value in terms of search cost reduction potential. In our analysis we do not find supportive evidence that recommender systems—beyond the features that have been in place when the data collection took place—do create significant additional value in terms of search cost reduction potential.

The remainder of this paper is structured as follows: Section 2 will motivate the problem of estimating dynamic programming models and present solution algorithms, motivate the use of grid adaption and introduce different approaches, derive sufficient conditions for uniform approximation, and finally integrate the conditions with the NFXP and MPEC estimation procedures. In order to both verify and illustrate our method, Section 3 first applies the uniform approximation conditions to standard interpolation problems and to the solution of the model of Rust (1987) for fixed parameter vectors, and then applies the method to the cost parameter estimation problem. Section 4 demonstrates the applicability of the proposed method and Section 5 concludes and states the agenda for future research. Appendix A.1 gives a very short introduction to function approximation using polynomial approximation, piecewise polynomial approximation, and splines, mainly to ensure precise nomenclature throughout the paper, and states an interesting benchmark case for the grid adaption problem using Chebyshev polynomials; moreover, different grid structures for the two-dimensional case are discussed.

2 Parameter estimation with flexible grids

This part of the paper develops a method for the use of flexible grids within the maximum likelihood estimation of dynamic programming models. To keep the discussion of our method generic, we will not specify a concrete type of model or application in this part of the paper; in the second part, we will demonstrate the method by applying it to the bus engine replacement model of Rust (1987), which is a well-known model from the dynamic discrete choice literature.

2.1 Estimation of dynamic programming models

In this subsection, we will state the formal problem of estimating dynamic programming models by maximum likelihood, and will present methods for solving the dynamic problem and the likelihood maximization, and the motivation for using adaptive grid methods in this context.

2.1.1 Problem statement

We begin with the formal statement of the problem we attempt to solve. Consider the following discrete time, continuous (or mixed discrete-continuous) state dynamic optimization problem:

$$V_{\theta}(x_{0})=\underset{\{U_{t}(x_{t})\}_{t=0}^{H}}{\max} \mathbb{E}\left[ \sum\limits_{t=0}^{H} \beta^{t} \pi(x_{t},y_{t};\theta) \right] \quad\text{s.t. } y_{t} \in {D}(x_{t}), t=0,\dots,H,$$

(DP)

where y is the control variable, which is at all times required to be in the feasible set of controls ${D}\subseteq \mathcal {D}$, given state $x\in \mathcal {S}$; U is a policy function that maps each state x to a dynamically optimal response y; π is the instantaneous payoff function; β < 1 is the discount factor; $H\leq \infty$ is the time horizon; the distribution over future values of the state $x^{\prime }$ conditional on current values of state and control is given by $Pr(x^{\prime } \vert x,y;\theta )$, which we also call the law of motion of the state variables; 𝜃 is an m-dimensional, real-valued parameter vector acting on the payoff function π ∈ and the law of motion, $Pr(x^{\prime } \vert x,y;\theta )$. (W.l.o.g., we assume the problem to be of an infinite time horizon and to be time stationary, and thus can drop all time indices.)

As shown by Bellman (1952), the following functional equation constitutes a necessary optimality condition to problem Eq. DP:

$$V_{\theta}(x)=\max_{y\in {D}(x)}\{ \pi(x,y) + \beta\mathbb{E}[V_{\theta}(x{'})\vert x,y] \} \equiv T[V](x)$$

(1)

where $V_{\theta }:\mathcal {S}\rightarrow \mathbb {R}$ is referred to as the value function, which implicitly depends on 𝜃 through the payoff function and the law of motion. In the following, we will address the dynamic problem solely in terms of its Bellman Eq. 1.

Suppose we do not only want to solve Eq. DP, but rather, given a dataset consisting of (partial) data on state and control realizations $\boldsymbol {D} = \{\tilde {x}_{t},{y}_{t}\}_{t=1}^{T}$, $\tilde {x}\in \tilde {\mathcal {S}}$⁵, we want to identify the parameter, 𝜃, of the payoff function π and the law of motion of states $Pr(x^{\prime } \vert x,y;\theta )$ that maximizes the likelihood of the data, given the dynamic problem is solved at the solution of the maximum likelihood estimation (MLE) problem. This problem frequently arises in different fields of econometrics, for example in dynamic discrete choice modelling (DDCM); see, for example, Aguirregabiria and Mira (2010), Keane et al. (2011), and Arcidiacono and Ellickson (2011) for surveys on DDCMs and their estimation. Formally, we attempt to solve the following two problems simultaneously:

$$\left.\begin{array}{ccc} \theta^{*} &=& \arg \underset{\theta}{\max} L(\theta;V_{\theta},\boldsymbol{D})\equiv Pr\left( \boldsymbol{D};\theta,V_{\theta}\right)\\ V_{\theta}(x) &=& \underset{y\in {D}(x)}{\max}\{ \pi(x,y;\theta) + \beta\mathbb{E}[V_{\theta}(x{^{\prime}})\vert x,y;\theta] \}|_{\theta=\theta^{*}} \end{array}\right\}$$

(MLDP)

The two problems are connected in the following way: The link between likelihood function and the model is through the parameter vector, which enters the payoff and the law of motion of the states. In the other direction, the value function for a given parameter value enters the likelihood function through the probabilities or density functions for the choice variables and the observable states in the data, $Pr\left (\boldsymbol {D};\theta ,V_{\theta }\right )$, out of which the likelihood function is composed. Variables of the model for which no data is observed will be integrated out in the likelihood computation.

2.1.2 The projection method for solving Eq. DP

We now turn to the description of solution techniques for the stand-alone dynamic problem in terms of its Bellman Eq. 1, which is a topic well covered by the literature (see, for example, Cai & Judd, 2013; Judd, 1998; Rust, 1996). Projection methods are a popular family of solution methods, out of which we choose the collocation method; see (Judd, 1992; 1998).⁶ The reason for this particular choice will become apparent at a later stage, when deriving a set of optimality conditions for the value function approximation. We now briefly describe the collocation method and some technical details, but only to the extent necessary for the derivation of our adaptive grid method.

Finding a function V (⋅) that solves the functional Eq. 1 is an infinite-dimensional problem, as functions are generally infinite-dimensional objects (even if the domain of the function is finite-dimensional). However, many functions can be approximated well by (sums of) basis functions with finite-dimensional representations.⁷ For example, approximations using polynomials of finite degree can be represented by a finite-dimensional vector of coefficients. Projection methods replace the true function V (⋅) in Eq. 1 by its approximation $\hat {V}(\cdot ;\mathbf {a})$ parametrized by a vector a. Obviously, the Bellman equation will only be approximately satisfied, and the different kinds of projection methods are all ways to “make this error small”. Formally, we define the residual as

$$R_{\hat{V}}(x;\mathbf{a})\equiv \hat{V}(x;\mathbf{a})-T[\hat{V}](x;\mathbf{a}).$$

(2)

The projection methods differ in the way they project the residual function against different test functions (including the residual itself, which results in a least squares approximation); these projections are then minimized or set equal to zero. The collocation method ensures that the residual function is zero at a chosen vector of n collocation nodes, $\mathbf {x} \in \mathcal {S}^{n}$. Note that this is equivalent to interpolation if the function to be approximated can be evaluated directly. In order to solve the dynamic problem using collocation together with polynomial approximation of degree n − 1, we need n nodes to identify the coefficients of the polynomial (or the “degrees of freedom”, as they are often referred to in the literature), and solve a (generally nonlinear) system of equations with the coefficients being the variables, and one equation for each collocation node (using more/fewer collocation nodes will result in an over-/under-identified system of equations, with generally no/infinitely many solutions, respectively)

$$R_{\hat{V}}(x_{i};\mathbf{a}) =0, \forall x_{i} \in \mathbf{x}.$$

(CO)

If the value function is approximated using piecewise polynomial approximation or splines, a vector of breakpoints has to be chosen as well. In the case of piecewise linear approximation, or splines of any order, the number of breakpoints equals the number of collocation nodes, and it is natural to choose them such that they are identical. However, if higher-order piecewise polynomial approximation is used without imposing additional smoothness constraints, more collocation nodes are needed in order to identify the degrees of freedom. In the remainder of this paper, we either use approximation methods that allow us to treat the collocation nodes and the breakpoints as one single set of nodes, or we simply distribute the additional collocation nodes uniformly between the breakpoints without making it explicit in the collocation Eq. CO, to not complicate the notation without adding any more insight to our approach.

2.1.3 Maximum likelihood estimation of dynamic programming models

Having argued that the continuous state dynamic program Eq. DP can be represented and solved approximately as a nonlinear system of equations CO, we now turn to the solution of the full estimation problem Eq. MLDP. We will describe the two most popular approaches to the estimation of dynamic programming models: the nested fixed point (NFXP) approach of Rust (1987), and the constrained optimization approach (or mathematical programming with equilibrium constraints (MPEC)) approach of Su and Judd (2012); we proceed in chronological order.

The nested fixed point algorithm of Rust (1987) addresses problem Eq. MLDP by completely solving the dynamic problem not only at the maximum of the likelihood function, but for every guess of the parameter vector 𝜃; see Algorithm 1.

It is important to note that the evaluation of the likelihood function is completely agnostic about the value function approximation step, as long as it is provided a function that can be evaluated over the whole state space. This not only allows for a wide variety of algorithms (and combinations thereof) for solving the dynamic problem, it also also allows us to make use of important properties of the problem, such as the contraction mapping property; moreover, the fact that the function to be maximized is a likelihood function can be exploited, for example when computing its Hessian matrix.

In contrast, the MPEC approach of Su and Judd (2012) interprets problem Eq. MLDP as a bi-level optimization problem, where the lower-level problem is replaced by some optimality (or equilibrium) constraints, in our case the Bellman Eq. 1, hence its name. As argued above, the Bellman equation has to be replaced by a finite-dimensional approximation, in our case the collocation system Eq. CO, yielding

$$\begin{array}{@{}rcl@{}} \underset{\theta,\mathbf{a}}{\max} L(\theta;\hat{V}_{\theta}(\cdot{,\mathbf{a}}),\boldsymbol{D}) \end{array}$$

(3a)

$$\begin{array}{@{}rcl@{}} \text{s.t. } R_{\hat{V}_{\theta}}(x_{i};\mathbf{a}) =0, \forall x_{i} \in \mathbf{x}. \end{array}$$

(CO)

Conceptually, the motivation for MPEC is to avoid solving the dynamic problem for every parameter value on the trajectory of the likelihood maximization, but rather to increase feasibility (here: accuracy of the solution to the dynamic problem) and optimality (here: the likelihood function value) simultaneously. Of course, since the solution of the dynamic problem depends on the actual value of the parameter vector, this is a potentially difficult nonlinear constrained optimization problem.

Whether to use NFXP or MPEC to estimate the parameters of dynamic programming models using MLE is an active field of research, and might turn out to be highly problem dependent. While it is argued that MPEC might be more efficient because it does not require solving the dynamic programming model in each iteration, it clearly cannot—in contrast to NXFP—make use of the contraction mapping property, which might cause MPEC to use more iterations to solve the likelihood problem (or even to fail to converge). Also, the memory needs are very different, as both algorithms can use the sparsity of the problem in the Jacobian of the collocation system (if present), but the Hessian of the MPEC problem is much larger than that in NFXP, and is—moreover—generally not sparse. In this paper, we make no attempt to contribute any evidence in favour of either MPEC or NFXP. Rather, we assume that the researcher we address has made his or her choice of one of the two, and is looking for a way to make the grid creation more efficient.

We now turn to the discussion of the core issues of the integration of grid adaption in estimation procedures.

A particular difference between MPEC and NFXP is the way approximations of continuous value functions are handled: In NFXP as defined in Algorithm 1, the procedure for obtaining an approximation to the value function is technically independent of the likelihood maximization, as long as the optimizer is fed with a valid approximation of the value function (given a particular value for the parameter vector) in order to evaluate the likelihood. In particular, this algorithm is formally suitable for the application of any iterative refinement scheme for the grid over state variables of the dynamic problem. Algorithm 2 conceptually extends NFXP with iterative grid updating (for every parameter value), as proposed by Reich (2018). However, if the refinement step in line 6 of Algorithm 2 is discrete (as it is in grid adaption by node insertion), the likelihood function L, which itself depends on the approximation of the value function—and thus on its grid, will generally become discontinuous, as the change of the underlying value function grid is discontinuous itself. Since many optimization algorithms require the objective function to be at least continuous (if not smooth), avoiding this artificially introduced discontinuity is highly desirable.

In contrast to NFXP, the application of grid adaption techniques is not obvious in the MPEC approach: if, for example, the value function is obtained by projection using collocation, for each collocation node the corresponding equality constraint has to be specified in the MPEC problem. Iterative refinement by insertion (or deletion) of nodes in the way it is done in Algorithm 2 is not directly applicable for two reasons: first, inserting a collocation node corresponds to inserting a constraint, which generally cannot be done while the optimization runs;⁸ second, since MPEC gives no guarantee that the dynamic problem is solved at any point of the optimization except for the solution to the MLE problem, no straightforward criterion of where to actually insert or delete nodes can be derived. Consequently, the application of grid adaption to MPEC raises the need for grid adaption schemes other than the popular iterative methods, as the structure of the function approximation problem is “hard-coded” into the optimization problem.

2.1.4 Types of grid adaption

As we have pointed out, integrating grid adaption with the estimation of dynamic programming models is not straightforward, because there are continuity issues with NFXP, and because MPEC requires the function approximation structure to be hard-coded into the constraints, both of which points rule out adaption by node insertion. To better motivate our approach, we first give an overview over the two main concepts of grid adaption, and argue why they might be suited to our purpose, or why they are not.

The refinement of function approximations has been studied widely in the literature, and has been successfully applied to the solution of dynamic problems with continuous state variables in economics (see, for example, Grüne & Semmler, 2004, Brumm & Scheidegger, 2017; Reich, 2018). Following (Huang and Russell, 2011), we classify these methods as follows—⁹

h -adaptive refinement: :

The most popular refinement method is adaption by node insertion. Based on some criterion such as the residual function, additional nodes are inserted at places where the approximation quality is “poor” (or deleted at locations where they are not needed), and the approximation problem is re-solved using the refined grid, with the interpolation or collocation conditions Eq. CO being enforced also at the new nodes. The resulting grid data structure usually forms a hierarchy of grids of different refinement levels. While this approach is intuitive and relatively easy to implement, it is intrinsically iterative in the sense that it needs a temporary solution of the problem in order the compute the next, refined solution; as already pointed out, this rules out its integration into MPEC, and causes continuity issues with NFXP.

r -adaptive refinement: :

In contrast to h-adaption, r-adaption does not change the structure of a particular grid, but rather moves its nodes such that local features of the approximated function are well covered. Consequently, the total number of nodes and their (dimension-wise) ordering is preserved.

More formally, r-adaptive grid adaption can be seen as a continuous, monotone and usually smooth function, mapping between the original, more structured (maybe even uniform) grid over the unit hypercube—often referred to as the “computational domain”—to the adapted grid defined over the domain of approximation, often referred to as the “physical domain”. Depending on the problem, this mapping function takes into account various properties of the original function to be approximated, such as the size of its gradients, the curvature, or the approximation error induced by a specific approximation method. Moreover, the mapping function (or a proxy thereof) is either explicitly known from the physical problem, or it is solved for simultaneously with the function approximation problem itself. The later case further distinguishes between an explicit approximation of the mapping function, which continuously maps every point in the “computational domain” to a point in the “physical domain” (even if there is no grid node at this point), and the implicit representation which implies (in-)equality conditions on the node locations. As we will employ the very last approach only in a very self-contained manner below, we refer the reader interested in more background to Baines (1998). In all cases, a popular criterion of where to actually place the nodes is equidistribution, which uniformly distributes nodes for example according to the gradient of the approximated function, or on its arc length. Alternatively, if the function of interest (or an approximation thereof) can be evaluated, a direct minimization problem over the approximation error can be solved; see again Baines (1998) for an in-depth comparison of the different criteria.¹⁰

Since the r-adaption of a grid is done without changing the functional form of the approximation, this idea can potentially be integrated with MPEC; similarly, since the grid adaption is continuous for many types of functions, this approach is well suited for integration with NFXP.

In this paper, we develop a method with r-adaptive grids that is based on approximation errors rather than equidistribution; the reason for this choice of foundation is twofold: first, equidistribution generally requires either that the gradient of the approximated function can be evaluated as well, or that its arc length can be computed, which is not always possible in value function approximation; second, depending on the type of interpolation, placing nodes at regions of high curvature might be even more accurate than placing them in regions of steep gradients.

In summary, we have stated the problem of estimating dynamic programming models using maximum likelihood, presented the collocation method for solving the stand-alone dynamic problem, and shown how two popular approaches—namely NFXP and MPEC, integrate collocation to estimate the model. Furthermore, we have argued it is not obvious how to rigorously integrate grid adaption with either NFXP or MPEC, as node insertion can cause the likelihood function to be discontinuous, and the structure of the function approximation has to be hard-coded into the optimization problem in the MPEC case. In the next section, we turn to uniform function approximation as well as optimal breakpoint and collocation node distribution, which we finally show how to integrate with each estimation algorithm.

2.2 Uniform approximation and the balanced error property

In this section, we briefly introduce the concepts of uniform approximation, equioscillation, and “balanced errors”, which are then applied to form a criterion for node placement in r-adaption within NFXP and MPEC in the subsequent section.

2.2.1 Uniform approximation and node placement

Recall that we defined the residual function Eq. 2 as the difference between the unknown function and its approximation; the closer the residual approaches zero over the whole domain, the better our approximation will be. A formalization of this is the uniform approximation problem, which minimizes the maximum absolute error between the unknown function and its finite-dimensional approximation with generic parameter vector p:

$$\underset{\mathbf{p}}{\min} \Vert R_{\hat{V}}(x;\mathbf{p}) \Vert_{\infty}\equiv \underset{x \in \mathcal{S}}{\max} \vert R_{\hat{V}}(x;\mathbf{p}) \vert.$$

(4)

It is important to note that there is no explicit notion of nodes in problem Eq. 4 yet. (Consequently, there are no collocation constraints either.)

As we pointed out earlier, we assume the breakpoints of a piecewise polynomial approximation and the collocation nodes to coincide. Suppose we approximate the solution to the Bellman equation using one of these methods, and further suppose we interpret one part of vector p ≡ (x,a) as nodes x that serve as both collocation and breakpoints, and the other part as the corresponding coefficients a. While most approaches to function approximation assume the nodes to be fixed, we treat them as variables of the following uniform approximation problem:

$$\begin{array}{@{}rcl@{}} \underset{\mathbf{a},\mathbf{x}}{\min} \Vert R_{\hat{V}}(x;\mathbf{a},\mathbf{x}) \Vert_{\infty}\equiv \underset{i\in I}{\min} \underset{x_{i} \leq x < x_{i+1}}{\max} \vert R_{\hat{V}}(x;\mathbf{a},\mathbf{x}) \end{array}$$

(5a)

$$\begin{array}{@{}rcl@{}} \text{s.t. } R_{\hat{V}}(x_{i};\mathbf{a},\mathbf{x})=0, \forall x_{i} \in \mathbf{x} \end{array}$$

(CO)

$$\begin{array}{@{}rcl@{}} \qquad\mathbf{x} \in \mathcal{X}^{n}, \end{array}$$

(5b)

where $I=\{1,\dots , n+1\}$ is the set of grid cell indices in one dimension.¹¹ Besides adding the node variables, we also added two sets of constraints: First, the grid validity conditions Eq. 5b ensure that the structure of the grid, including neighborship relations, is preserved; in the one-dimensional case, the set of all valid grids over the state space is defined by $\mathcal {X}^{n}\equiv \{\mathbf {x}\in \mathcal {S}^{n}:x_{i}\leq x_{i+1}\}$. Second, the collocation constraints Eq. CO are added. Note that none of these constraints is conceptually necessary at this point. However, we include them for a reason: the grid validity constraints rule out a great number of local solutions to the approximation problem with different orderings of nodes; adding the collocation constraint cannot improve the quality of the approximation problem, but it is mandatory for our optimality criterion, which we will shortly derive as applicable.

If the vector of breakpoints and collocation nodes is fixed, the coefficients of the approximation problem are identified solely by the constraints, and thus no explicit minimization is necessary (or possible). While we treat the nodes as variables in this paper, we still want to mention a popular approach to static node choice in the case of (non-piecewise) polynomial approximation—the Chebyshev nodes. Suppose that the function f we approximate is k ≥ 1 times continuously differentiable. Suppose q_n− 1 is a polynomial interpolant of degree n − 1 that interpolates f at the n roots of the degree n Chebyshev polynomial. Then, q_n− 1 minimizes the tightest known error bound for polynomial interpolation that can be minimized over the nodes independently of f: The idea behind this error bound is to split it up into a contribution from the function itself—which cannot be reduced by any choice of nodes interpolation nodes (n fixed) and which is usually expressed as the variation in some higher order derivative—, and a contribution solely from node choice, but independent of the concrete function to be approximated. For a detailed description of Chebyshev nodes and the optimization problem they solve, we refer the reader to Appendix A.1.2. While this is unquestionably a strong result with significant practical implications, we show in numerical examples below that Chebyshev nodes are generally not optimal given a specific f. Also, Chebyshev nodes have no direct application in the context of breakpoint choice for the piecewise interpolation schemes, which are our methods of choice.

2.2.2 Equioscillation and balanced errors

While problem Eq. (5) can, in principle, be solved directly using nonlinear constrained optimization techniques, we now reformulate it as a set of optimality conditions, in order to easily integrate it as constraints with the original estimation problem using MPEC. (Moreover, as we demonstrate in the numerical part of the paper, the direct minimization approach is much less efficient in practice compared to directly solving the optimality conditions derived below.)

To derive our approach to optimal node placement, we restate an important result from polynomial approximation theory, the equioscillation theorem (restated from Judd, 1998, p. 212): define the $L_{\infty }$ error of the best approximation of a (one-dimensional) function $f\in \mathcal {C}^{k}, k\geq 0$ by a polynomial of degree n − 1 or less, $q^{*}\in \mathcal {P}^{n-1}$, as

$${\varrho}_{n-1}(f)\equiv \underset{\{q\in\mathcal{P}^{n-1} : deg(q)\leq {n-1}\}}{\inf} \Vert f-q \Vert_{\infty}.$$

(6)

Then, we can state the following theorem:

Theorem 1 (equioscillation)

If $f \in \mathcal {C}[a, b]$, then there is a unique polynomial of degree n − 1, $q^{*}_{n-1}(x)$, such that $\Vert f - q^{*}_{n-1} \Vert _{\infty } = {\varrho }_{n-1}(f)$. The polynomial $q^{*}_{n-1}$ is also the unique polynomial for which there are at least n + 1 points $a \leq y_{0} <\dots <y_{n} \leq b$ such that for m = 1 or m = − 1,

$$f(y_{j})-q^{*}_{n-1}(y_{j})=m(-1)^{j} {\varrho}_{n-1}(f), j=0,\dots,n.$$

(7)

From the equioscillation theorem we know that the best polynomial approximation of the continuous function f will have “balanced and alternating errors”. More precisely, if $x_{i}, i \in \{1,\dots ,k\}$ are the k ≥ n zeros of f(x) − q(x), and x₀ = a, x_k+ 1 = b, we refer to the errors as balanced if

$$\underset{x_{i} \leq x \leq x_{i+1}}{\max}\vert f(x)-q(x)\vert=c, i=0,\dots,k,$$

(BE)

where c is a constant, and as alternating if, for m = 1 or m = − 1,

$$\text{sign} (f(x)-q(x)) = m(-1)^{i}, x_{i} < x < x_{i+1}, i=0,\dots,k.$$

(8)

As an illustration, we include Fig. 1 where the absolute value function is uniformly approximated by a polynomial, depicting both the function and its approximation in the left panel, and the approximation error in the right panel; as predicted by the equioscillation theorem, the errors of the $L_{\infty }$-minimizing polynomial approximation are balanced and n times alternating.

Fig. 1

Approximation of f(x) = |x − 0.5| Using the Best Degree 10 Polynomial Approximation. Approximation of f(x) = |x − 0.5| using the best degree 10 polynomial on the interval [− 1,1]. Left—the blue line shows the true function f(x) and the green line shows the best polynomial approximation $\hat {f}(x)$. Right—the black line shows the approximation error $f(x) - \hat {f}(x)$

It is important to note that Theorem 1 states a sufficient condition for optimality: since the unique best approximating polynomial of degree n − 1 or less exists for every continuous function, and since it is also the unique polynomial with n times equioscillating errors, we can conclude that a polynomial with n times equioscillating errors is the best approximation of f (of degree n − 1 or less) in the sense of definition Eq. 6. An iterative procedure for obtaining best polynomial approximations of functions of one variable based on equioscillation is the Remez algorithm (see, for example, Fraser, 1965).

So far, we have only considered polynomial approximation, where the interpolation or collocation nodes are determined implicitly by the zeros of f(x) − q(x). However, when using piecewise polynomial approximation or splines, the choice of breakpoints (and possibly also of interpolation nodes if not identical) is explicitly required from the user.

Therefore, sufficient optimality conditions based on balanced errors have been derived for the specific piecewise schemes as well. The idea behind these proves is to show that if the single segments of a piecewise polynomial interpolant are locally error minimizing (implying that they are equioscillating within the segment by Theorem 1), balancing the error among the segments through breakpoint movement will serve as a sufficient optimality condition: Suppose two neighboring segments do not have the same local approximation error; then, moving the breakpoint towards the segment with the higher local approximation error will reduce the higher error, while increasing the smaller one, until they equate (always assuming that both errors are minimized within the segment, in particular after they have been “moved”); consequently, the overall error after balancing the local errors must be lower than before.

This procedure can be formalized and extended to more than two segments by induction. In particular, Lawson (1964) proves for piecewise polynomials that if all segments are locally minimizing the maximum approximation error, then a set of breakpoints balancing these “min-max” errors over all segments exists and is, moreover, a sufficient condition for optimal breakpoint choice. (For the formal results, which require a substantially more general notation that is, however, not necessary for algorithm construction, we refer the reader to Lawson (1964) in particular Theorem 2 and Lemma 6 for details). An important difference between the equioscillation as in Theorem 1 and the results of Lawson (1964) is that optimal piecewise interpolants—while having balanced errors and being optimal—do not generally have alternating errors at the breakpoints. In fact, only for special cases are these interpolants continuous at all. Therefore, we impose continuity by requiring the breakpoints to be interpolation points at the same time (also see Appendix A.1.4 for the relation between breakpoints and interpolation nodes).¹²¹³

2.2.3 Imposing balanced error and collocation constraints

In this paper, we present an approach to optimal node placement based on balancing the maximum approximation errors of the segments, which is partially motivated by the optimality criterion of Lawson (1964). However, instead of identifying the coefficients by explicit segment-wise error minimization, we impose the collocation constraints Eq. CO at the breakpoints, which is—together with continuity—sufficient to identify the parameters of a piecewise linear approximation; if higher-order piecewise polynomials are fitted, additional collocation nodes have to be inserted in the interior of the segments. Consequently, in order to find a solution to the uniform approximation and collocation problem with explicit node choice, Eq. (5), we need to find a vector of nodes and coefficients such that the constraints of Eq. (5) are satisfied, and the errors of the approximation are balanced.

In particular, let us introduce a slack variable for the cell-wise error

$$z_{i} = \underset{x_{i} \leq x < x_{i+1}}{\max} \vert R_{\hat{V}}(x;\mathbf{a},\mathbf{x}) \vert \quad \forall i \in I.$$

(9)

Then, (approximate) BE with tolerance 𝜖_z can either be imposed by the n + 1 Eq. BE, or—as we found it to be numerically more efficient—by pairwise comparison of all cell-wise errors

$$\frac{\vert z_{i} - z_{j} \vert}{z_{i}} \leq \epsilon_{\mathbf{z}} \quad \forall (i,j) \in I\times I, i\neq j.$$

(10)

Note that Eq. 10 can be reformulated as a linear constraint (see below). Thus, imposing BE yields a system of n + 1 nonlinear equality constraints for the slack variables z_i, and 2n(n + 1) linear inequality constraints for the actual comparisons.

Combining the BE constraints for optimal node placement, Eqs. 9 and 10, with the constraints of Eq. (5), the following system of equations in the variables (a,x,z) identifies a solution to Eq. (5):

$$\begin{array}{@{}rcl@{}} &&R_{\hat{V}}(x_{i};\mathbf{a},\mathbf{x})=0, \quad\forall x_{i} \in \mathbf{x} \end{array}$$

(11a)

$$\begin{array}{@{}rcl@{}} && z_{i} = \max_{x_{i} \leq x < x_{i+1}} \vert R_{\hat{V}}(x;\mathbf{a},\mathbf{x}) \vert \quad \forall i \in I \end{array}$$

(11b)

$$\begin{array}{@{}rcl@{}} &&(1-\epsilon_{\mathbf{z}})z_{i} - z_{j} \leq 0 \quad \forall (i,j) \in I \times I, i\neq j \end{array}$$

(11c)

$$\begin{array}{@{}rcl@{}} &&(-1-\epsilon_{\mathbf{z}})z_{i} + z_{j} \leq 0 \quad \forall (i,j) \in I \times I, i\neq j \end{array}$$

(11d)

$$\begin{array}{@{}rcl@{}} && x_{i} + \epsilon_{\mathbf{x}} \leq x_{i+1}\quad\forall x_{i},x_{i+1} \in \mathbf{x}, \end{array}$$

(11e)

where Eqs. 11c and 11d are the reformulated linear BE conditions, and Eq. 11e is the grid validity constraint, which additionally enforces some minimum distance 𝜖_x between grid nodes.

In summary, this section derived a sufficient optimality criterion of the distribution of breakpoints and collocation nodes, which will be integrated with both the NFXP and the MPEC algorithms in the next section. We conclude this section on balanced errors and its application of uniform approximation and collocation problems with a remark: In the context of node choice, the mechanics behind equioscillation as an optimality criterion are actually very intuitive. Suppose the global maximum approximation error lies in the interval [x_i,x_i+ 1]. Then, slightly shifting the interpolation node x_i to the right (assuming that f and q are not intersecting in the interior of (x_i,x_i+ 1)) will decrease the maximum error, while increasing the error of the cell to the left of x_i; thus the $L_{\infty }$ norm of the approximation will decrease. Thus, q cannot be optimal until the errors in all cells are balanced.

2.3 Parameter estimation with flexible grids

In this section, we will demonstrate how to integrate grid adaption by node movement into parameter estimation for dynamic programming models, using both NFXP and MPEC.

2.3.1 NFXP with flexible grids

As we have argued above, the integration of grid adaption into NFXP is—formally—straightforward, as the algorithm is agnostic about the value function approximation step. Therefore, since we modelled the value function approximation and the adaption of its grid as a simultaneous problem in Eq. (5), we can state the NFXP algorithm with grid adaption by node movement by Algorithm 3.

We have two important remarks. First, note that in contrast to Algorithm 2, the continuity of the likelihood function is not affected by the application of grid adaption if two conditions hold: (i) the optimal grid depends continuously on the value function, and (ii) the value function itself depends continuously on the model parameters.¹⁴ Second, while Algorithm 3 is in principle agnostic about how to solve problem Eq. (5), we found that—in our examples—it was most efficient and stable to solve the set of sufficient optimality conditions Eq. (11) (examples are given below).

2.3.2 MPEC with flexible grids

We now turn to the question of how to integrate (optimal) node placement with the MPEC approach of estimation of dynamic programming models. First, note that if $R_{\hat {V}}$ is the residual of the functional equation determining the value function of interest, the optimization problem Eq. (5) fully determines our function approximation, with degrees of freedom being the coefficients of the polynomials and the nodes themselves. Thus, we replace the collocation constraints in the original MPEC problem Eq. (3) with problem Eq. (5) to obtain our new bi-level optimization problem

$$\begin{array}{@{}rcl@{}} \underset{\theta,\mathbf{a},\mathbf{x}}{\max} && L(\theta;\hat{V}_{\theta}(\cdot{,\mathbf{a}}),\boldsymbol{D}) \end{array}$$

(12a)

$$\begin{array}{@{}rcl@{}} && \text{s.t. } (\mathbf{a},\mathbf{x})=\arg \underset{\mathbf{b},\mathbf{y}}{\min} \Vert R_{\hat{V}_{\theta}}(y;\mathbf{b},\mathbf{y}) \Vert_{\infty} \end{array}$$

(12b)

$$\begin{array}{@{}rcl@{}} && \qquad\qquad\qquad\text{s.t. (CO), (5b) hold.} \end{array}$$

(12c)

However, it is not obvious how to obtain a solution to Eq. (12). While there is a large literature on how to solve this kind of bi-level optimization problem (see, for example, Colson et al. (2007) and Fletcher et al. (2006)), they remain “notoriously difficult” to solve for the following reason: if we want to avoid solving the system of constraints in every iteration of the solution process (which would then constitute an NFXP approach with an r-adaptive grid using direct minimization), the lower-level minimization problem Eqs. 12b, 12c has to be replaced by something that can be handled by a constrained optimization solver, which is usually systems of equalities and inequalities. One approach is to replace the lower-level optimization problem by its first-order constraints, which are the KKT conditions in the case of inequality constrained lower-level problems. However, this procedure will establish complementarity constraints in the new single-level problem, which cause severe problems for most algorithms currently available for constrained optimization (see, for example, Colson et al. (2007) and Fletcher et al. (2006)), thus giving rise to a very active field of research in optimization. Instead, in the following we will use the system of (in-) equalities that constitutes a set of sufficient optimality conditions for our node placement problem based on balanced errors, Eq. (11), without introducing complementarity constraints into the estimation problem.

Replacing the lower-level optimization problem in Eq. (12) by the set of sufficient conditions Eq. (11), we finally solve the following optimization problem in order to obtain a maximum likelihood estimate of the parameter vector 𝜃 using MPEC:

$$\begin{array}{cc} \underset{\theta,\mathbf{a},\mathbf{x},\mathbf{z}}{\max} & L(\theta;\hat{V}_{\theta}(\cdot,\mathbf{a},\mathbf{x}),\boldsymbol{D})\\ &\text{s.t. (11) holds}. \end{array}$$

(13)

The statement of problem Eq. 13 concludes the general description of the method. In the next section, we turn to numerical examples and applications.

3 Numerical examples and applications

In this section, we first present a concrete numerical example to demonstrate the idea of flexible grids and show the equivalence of minimizing the $L_{\infty }$ norm and imposing the balanced error (BE) constraints. Second, we apply the adaptive grid method to the estimation of the well-known bus engine replacement model of Rust (1987), which is modified to feature a continuous mileage state; furthermore, we solve and estimate a version of the Rust (1987) model that features a serially correlated, unobserved utility component.

3.1 Function interpolation with flexible grids—A numerical example

In the following example, we assume that the function we are approximating is known and can be evaluated directly. Consequently, we can write the residual function Eq. 2 as

$$R_{\hat{f}}(x;\mathbf{a},\mathbf{x}) = f(x) - \hat{f}(x;\mathbf{a},\mathbf{x})$$

and hence we are facing a standard function approximation problem (see Appendix A.1 for a short introduction to function approximation).

For the function approximation problem in this section, we will compare three cases: First, we consider the case of standard interpolation where the residual function is set equal to zero at all the nodes of a fixed grid; this corresponds to solving the system of equations given by Eq. CO, which is linear for standard function interpolation problems. Second, we directly minimize the $L_{\infty }$ norm of the residual function, but at the same time impose the interpolation property as constraints; the corresponding constrained optimization problem is described by problem Eq. (5). Last, we impose the BE constraints on the residual function to obtain the optimal grid by solving the nonlinear system Eq. (11). This procedure allows us to (i) compare the results of the flexible-grid method to standard interpolation over fixed grids, (ii) demonstrate the equivalence of direct minimization and balanced error conditions, and (iii) compare the different approaches with regard to accuracy and computation time.

To assess the quantitative aspects, our example demonstrates the advantages of balanced errors using piecewise linear approximations. We show that optimal grids produce significantly smaller approximation errors compared to uniform grids with the same number of nodes. This example is of particular interest as we are going to use piecewise linear approximations for the full parameter estimation problem in Section 3.2.

In the appendix, we also argue how Chebyshev polynomials (using the well-known Chebyshev nodes as interpolation locations) relate to our approach; see Appendix A.1.3. Moreover, we demonstrate the use of higher order piecewise polynomials, which works essentially the same as piecewise linear approximations; see Appendix A.

For the example in this subsection, we use the following parametrizations: The minimum difference between the flexible nodes it set to 𝜖_x = 0.01 (none of the grid validity constraints are binding though). For the error tolerance of the BE constraints we use 𝜖_z = 0, which proves to be the most stable from a computational point of view; we conjecture that this is because otherwise a continuum of solutions would exist. In order to compute the cell-wise maximum error, we use a grid search with 100 uniformly distributed nodes. To initialize the algorithm, we first compute an optimal solution with regard to the L₁ norm, which we then use as an initial guess for the solution in the $L_{\infty }$ norm; this approach increases both numerical efficiency and stability. All computation times are reported including the initialization phase. We use Gauss–Legendre quadrature with 10 nodes in each interval to compute the corresponding integrals for the L₁ norm (see Judd, 1998, for a detailed description of different quadrature methods). All examples are computed in Matlab 2017a (Version 9.2) using the “fmincon” solver with the “sqp” and “interior point” algorithms, and default settings otherwise. In those examples where we approximate polynomials, their coefficients are randomly generated and reported along with the results. We use AMD Opteron 6380 (“Abu Dhabi”) hardware clocked at 2.5GHz, and all reported runtimes are serialized (i.e. core time, not wall clock time).

The function we approximate is a degree 9 ordinary polynomial by a piecewise linear approximation with six nodes, of which four are potentially flexible.¹⁵ We use a uniform grid for the fixed grid piecewise linear approximation.

Figure 2 plots the results; the corresponding approximation errors and computation times are stated in Table 1. We find that the standard piecewise linear interpolation over a fixed uniform grid produces large approximation errors, especially in the areas where the approximated function has high curvature, as is the case between the first and second node for example. Consequently, the flexible-grid solutions demonstrate how the approximation error can be reduced by shifting the nodes toward this area. Looking at the residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$ we find that for both the direct minimization and the BE solution the errors are balanced, while the error for the uniform-grid interpolation strongly varies among the intervals. Note that this example demonstrates the difference between balanced errors, alternating errors, and equioscillation: while the errors of the optimal solutions are obviously balanced—the maximum absolute error is the same for each interval [x_i,x_i+ 1]—they are not alternating (and hence not equioscillating) as the residual does not change sign at all its zeros (including the breakpoints).

Fig. 2

Approximation of a Degree 9 Polynomial Using Piecewise Linear Approximation. Approximation of a degree 9 ordinary polynomial on the interval [− 1,1] by a piecewise linear approximation with six nodes, of which four are potentially flexible. The blue line corresponds to the true function, whereas the green line represents the fitted piecewise linear approximation. Turquoise diamonds and red circles depict the fixed uniform nodes, and the optimized approximation nodes obtained from imposing the BE conditions or direct minimization, respectively. The plots in the right panel show corresponding residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$. From the top to the bottom, the figure shows piecewise linear interpolation using uniformly distributed nodes, flexible nodes with direct minimization of the $L_{\infty }$ norm, and flexible nodes with BE constraints. The coefficients of the true polynomial function f are given by α = [4.1239,2.7956,5.0862,− 1.2933,7.8788,− 7.8582,9.9192,− 2.8339,3.4032,− 9.9500]

Table 1 Comparison of Approximation Errors—Piecewise Linear Approximation

Table 1 further confirms these findings: the $L_{\infty }$ norm decreases by an order of magnitude from 11.8250 to 1.5649 for the optimal flexible grid compared to the uniform-grid approximation. Again, we find that imposing the BE constraints yields the same solution as direct minimization, but computation times and the number of iterations are significantly lower for the BE approach.

3.2 Parameter estimation with flexible grids—numerical results

In this section, we apply our balanced error grid adaption method to the estimation of the well-known bus engine replacement model of Rust (1987), first with a continuous mileage state variable, but in its original for otherwise, and second extended to feature a serially correlated, unobserved utility component, thus resulting in a two-dimensional value function approximation problem.

In both cases, we begin with a brief description of the model, and then compare the fixed- and flexible-grid approaches in two steps: First, we present results for fixed model parameters in order to demonstrate the potential advantages of flexible grids for solving dynamic programming models; this is similar to the interpolation examples in Section 3.1, except that the function to be approximated can not be evaluated directly. Second, we solve the complete maximum likelihood estimation problem for the cost parameters of the model, using MPEC and NFXP (as we obtain qualitatively similar results for NFXP and MPEC, we only report results for both algorithms for the original specification and focus on MPEC thereafter); therefore, we set up a Monte Carlo experiment with 100 artificial datasets to study and compare the results of the fixed- and flexible-grid solutions with regards to accuracy and efficiency.

3.2.1 The bus engine replacement model of Rust (1987)

In the bus engine replacement model of Rust (1987), a manager of a fleet of buses repeatedly decides whether or not to replace the engine of each of the buses. The manager’s decision is based on the observation of the current mileage state, and on choice of bus and the consequent bus-specific utility shock. The manager’s per-period utility function for one single bus is given by

$$u_{\theta}(i,x_{t}) + \varepsilon_{t}(i) ,\quad u_{\theta}(i,x_{t}) = \begin{cases} -RC & \text{if } i=1\\ -c(x_{t},\theta_{1}) & \text{if } i=0. \end{cases}$$

(14)

Hence, the manager faces the decision trade-off of replacing the engine at a high fixed cost of RC (decision i = 1), or just paying the maintenance costs c(x_t,𝜃₁) (decision i = 0), which increase with the mileage state x_t and depend on the maintenance cost parameter 𝜃₁. ε_t(i) is the choice-specific shock to utility that is observed by the manager, but not by the econometrician. Assuming that the manager behaves in a dynamically optimal manner, his or her value function is given by

$$V_{\theta}(x_{t},\varepsilon_{t}) = \underset{i \in\{0,1\}}{\max} \{u(i,x_{t},\theta_{1}) + \varepsilon_{t}(i)+ \beta E [V_{\theta}(x_{t+1},\varepsilon_{t+1})| i,x_{t},\varepsilon_{t}]\},$$

(15)

where β is the time discount factor and the subscript 𝜃 denotes the dependence of the value function on the parameters RC and 𝜃₁. The conditional expected continuation value in Eq. 15 is given by

$$\begin{array}{@{}rcl@{}} EV_{\theta}(i ,x_{t}, \varepsilon_{t}) &\equiv& E [V_{\theta}(x_{t+1},\varepsilon_{t+1})| i ,x_{t}, \varepsilon_{t}] \\ &=& \int V_{\theta}(x_{t+1},\varepsilon_{t+1}) Pr(x_{t+1},\varepsilon_{t+1} | i, x_{t}, \varepsilon_{t}, \theta) \mathrm{d}(x_{t+1},\varepsilon_{t+1}). \end{array}$$

(16)

Even though the observed mileage state x_t has a continuous support in reality, it is a common approach to discretize the state space into a finite number of “bins” (see, for example, (Su and Judd, 2012; Rust, 1987). We, however, do not make this assumption as our solution method is designed for continuous state spaces. Consequently, while the law of motion for discrete Markov states is a matrix, we need a probability density function for the continuous model. As proposed in (Rust, 1987) we use the exponential function, so ${\Delta }_{x_{t+1}} = x_{t+1} - x_{t}$ is exponentially distributed with the rate parameter 𝜃₂. We follow (Rust, 1987) by assuming that (i) the utility shock ε_t(i) is extreme value type I iid. distributed, $\varepsilon _{t}(i) \sim EV1 \text { iid}$, and (ii) x and ε are conditionally independent. Under this assumption, closed form solutions for the integral over the unobserved state variables exist, and the EV function for the continuous problem is given by

$$EV_{\theta}(i,x) = {\int}_{0}^{\infty} \log \left( \sum\limits_{i^{\prime} \in \{0,1\}} \exp\left( u_{\theta}(i^{\prime},(1-i)x + {\Delta}_{x}) + \beta EV_{\theta}(i^{\prime},(1-i)x + {\Delta}_{x}) \right) \right)h_{\theta_{2}}({\Delta}_{x} ) \mathrm{d} {\Delta}_{x},$$

(17)

where $i^{\prime }$ denotes the decision in the next period and $h_{\theta _{2}}({\Delta }_{x} )$ is the probability density function of the exponential distribution with the rate parameter 𝜃₂. We approximate the integral over the observed state by Gauss–Laguerre quadrature, which is a natural choice as it is optimized for the integration over exponential kernels (see Judd 1998). Finally the log-likelihood function for the full sample of M buses reads

$$\begin{array}{@{}rcl@{}} L(\theta;EV_{\theta}(\cdot),\{{x_{t}^{j}},{i_{t}^{j}}\}_{t=1,j=1}^{T,M}) &=& \sum\limits_{j=1}^{M} \sum\limits_{t=1}^{T} \log \left( \frac{\exp \left( u_{\theta}({i_{t}^{j}},{x_{t}^{j}}) + \beta EV_{\theta}({i_{t}^{j}},{x_{t}^{j}})\right)}{{\sum}_{i \in\{0,1\}} \exp \left( u_{\theta}(i,{x_{t}^{j}}) + \beta EV_{\theta}(i,{x_{t}^{j}})\right)}\right) \\ &&\quad+ \sum\limits_{j=1}^{M} \sum\limits_{t=1}^{T} \log h_{\theta_{2}}({\Delta}_{{x_{t}^{j}}}). \end{array}$$

(18)

3.2.2 Approximating the EV function for fixed 𝜃

In this subsection, we assume that the model parameters 𝜃 are fixed; consequently, we only have to solve the dynamic problem Eq. 17. This allows us to compare the solutions for a fixed uniform grid and the flexible grid with BE constraints in a simple and demonstrative context.

In particular, we use the following parametrisations of the model and the algorithm: For the model parameter vector 𝜃, we use the original estimates from Rust (1987), given by RC = 11.7257, 𝜃₁ = 2.4569, and β = 0.99, and assume 𝜃₂ = 1.5. For the utility function, we use the standard linear costs given by

$$c(x_{t},\theta_{1}) = 10^{-3}\cdot \theta_{1} x_{t}.$$

(19)

Additionally, we also consider a cubic cost function to introduce more nonlinearities into the problem, and hence make the approximation problem of the EV function more interesting

$$c(x_{t},\theta_{1}) = 10^{-5} \cdot \theta_{1} {x_{t}^{3}}.$$

(20)

For the mileage state, we assume that the maximum mileage is given by x_max = 400 (similar to Rust 1987). For the EV function, we use a piecewise linear approximation. We use the same algorithm parametrisation as in Section 3.1.

In our analysis, we consider four different approximations for each of the cost functions: a benchmark case using 400 uniformly distributed nodes; the BE solution with five nodes, of which three are flexible; a uniform fixed grid with as many nodes as the flexible grid; and a uniform grid where the number of nodes is chosen such that the two grids have roughly the same accuracy in terms of the $L_{\infty }$ norm.

Table 2 lists approximation errors, computation times, and iteration counts for all approximations. The upper panel shows the results for the linear cost function Eq. 19. We find that for the benchmark case with 400 nodes the approximation errors are small with a $L_{\infty }$ error of 1.7e − 4. The BE solution with five nodes has an error of 0.0441, while the error with a uniform grid with equally many nodes is more than twice as large. To obtain the same accuracy with the uniform grid, 10 nodes are needed in this example. Comparing computation times, we find that the uniform-grid solution with 10 nodes is still significantly faster compared to the BE grid solution. Hence, in this example it appears to be more efficient to simply increase the number of nodes of the uniform grid instead of using the flexible-grid method.

Table 2 Approximation of the EV Function of the (Rust, 1987) Model

The results turn in favour of the BE solutions when we solve the model with the cubic cost function Eq. 20: In this case, 40 uniformly distributed nodes are needed to obtain the same accuracy as with the BE grid with five nodes. Comparing computation times, we find that it actually takes longer to compute the fixed-grid solution (0.5201 seconds) compared to the flexible grid (0.4391 seconds). Figures 3 and 4 depict the four different approximations of the EV functions for the linear and the cubic cost functions, respectively, and illustrate why this is the case: Using the cubic cost function, we find that most curvature is massed at the low mileage states, while it is almost linear or even constant otherwise. This makes the approximation of the EV function by piecewise linear segments over a uniform grid very inefficient, as the nodes should be placed in regions of high curvature. Conversely, the BE grid efficiently moves the nodes to the critical area of high curvature, and therefore achieves much higher accuracy using an equal amount of nodes. Hence, even in such a simple example, and in particular isolated from the full estimation problem, the flexible-grid solution can be more efficient compared to approximation over uniform grids.

Fig. 3

EV as a Function of x for the Linear Cost Function Eq. 19. EV as a function of mileage state x for fixed 𝜃 and linear cost function Eq. 19

Fig. 4

EV as a Function x for the Cubic Cost Function Eq. 20. EV as a function of mileage state x for fixed 𝜃 and cubic cost function Eq. 20

So far, we have assumed that the parameter vector 𝜃 is fixed, and thus only the dynamic programming model needs to be solved. The next subsection addresses the complete parameter estimation problem using simulated data.

We conclude this example with a note on approximation errors and their potential implications on the estimation error in the maximum likelihood process: Figures 3 and 4 imply that much of the error from approximation over coarser grids comes from a wrong level of value. This is actually very natural: Recall that in contrast to the interpolation examples above, the true level of the value function is not explicitly given; rather, the value function as defined in Eq. DP is the discounted sum of future expected values, forming the fixed-point Eq. 1. Therefore, if future value is overestimated, the present value will be overestimated, too. Since the value function in this example is convex, every linear interpolation will overestimate the value, which becomes particularly apparent if the grid is coarse, such as in the example with the uniform grid with 5 nodes. (Of course, this effect cannot be corrected by shifting the value function downwards, as in general the true level of the value function is unknown.)

With regard to the maximum likelihood estimation and in particular the parameter estimation error, it is important to note that the error in the level of the value function—which serves as a natural quality measure in the present context of function approximation—does not matter anymore. Rather, the likelihood function computes the probability (or density function value) of value differences for different choices, which is more related to the gradient of the value function. While we can see from the pictures that these differences will also be dampened by linear approximations (i.e. underestimated when comparing high- to low-mileage states), their quantitative effect cannot be easily anticipated given (i) the non-linearities induced by the density functions of the random variables forming the likelihood function, (ii) and the potentially highly non-uniform “weighting” induced by the data. Therefore, the fact that approximation over balanced error grid roughly produces the same approximation error as the uniform grid with 10 nodes does not imply that the two configurations will also result in similar estimation errors. As a consequence, the fact that the balanced error grid is less efficient in approximating the value function implied by a linear cost function compared to a uniform grid with more nodes, does not imply that it is also less efficient when assessing the parameter estimation error; actually, as we will show shortly, the opposite is true in this model.

3.2.3 Monte Carlo study for the parameter estimation problem

In this subsection, we estimate the parameters of the bus engine replacement model of Rust (1987) using the flexible-grid approach and compare it to the standard fixed-grid solution by solving problem Eq. (3). In the first example with a linear cost function, we demonstrate the applicability and efficiency of the flexible-grid approach for both MPEC and NFXP. To limit the number of examples, we concentrate on the MPEC implementations for the additional examples thereafter.

In order to obtain a measurement of variation, we simulate 100 datasets with 500 buses each running for 150 periods. For the simulation of the data, we use the same parameters as in the previous example, given by β = 0.99, RC = 11.7257, 𝜃₁ = 2.4569, and 𝜃₂ = 1.5; furthermore, we use a linear cost function as in Eq. 19 as well as a cubic cost function as in Eq. 20. For each dataset, we use three starting points for 𝜃, given by $(RC,\theta _{1})\in \left \{(2,1),(10,3),(17,5)\right \}$ (one significantly smaller, one close to, and one significantly larger than the true parameters). Also, as in the original model, the parameter of the mileage state transition, 𝜃₂ = 1.5, can be estimated independently, which is why we focus on the estimation of the cost parameters RC and 𝜃₁.¹⁶ To compute the one-period-ahead value expectations in Eq. 17, we use 10-node Gauss–Laguerre quadrature rules. For the maximum value of the approximation interval we use 1.5 times the maximum value of the mileage state obtained from the simulated data.

As in the previous section, we use four different approximations of the expected value function: a benchmark solution using 400 uniformly distributed nodes; the BE solution with five nodes, of which three are flexible; a uniform fixed grid with as many nodes as the flexible grid; and a uniform grid where the number of nodes is chosen to roughly match the relative root mean squared error (rRMSE)¹⁷ of the BE grid.

Table 3 lists parameter estimates, errors with respect to the benchmark solution (rRMSE) and computation times for all approximations for the estimation using MPEC. We find that for the 5-node uniform grid, the estimates dramatically differ from the benchmark solution, and are not even within four standard deviations; the error of the 5-node uniform grid is large given an rRMSE of 0.1101. The BE solution with five nodes, of which three are flexible, produces much more accurate results, with an rRMSE of 0.0264. To obtain the same level of accuracy, a uniform grid with 17 nodes is needed. Comparing efficiency, we find that the BE solution is about 1.6 times faster than the uniform solution with the same accuracy. Also, we find that for all approximation methods all runs converged, which indicates that the BE method is also sufficiently stable. The results for the estimations using NFXP are reported in Table 4; we find them to be very similar to the MPEC case, and draw the same qualitative conclusions.¹⁸

Table 3 Results for the MPEC Estimation of the (Rust, 1987) Model with a Linear Cost Function

Table 4 Results for the NFXP Estimation of the (Rust, 1987) Model with a Linear Cost Function

In Table 5 we show the corresponding results for the cubic cost function Eq. 20. For this, we slightly recalibrate the model and use 𝜃₂ = 0.075 instead of 𝜃₂ = 1.5. For 𝜃₂ = 1.5, the realizations of the mileage state of the Monte Carlo runs are not in the area of the EV function with a significant amount of curvature (see left panel of Fig. 5). Hence, a flexible grid method can not show its full potential. For 𝜃₂ = 0.075, the situation changes and more realizations of the mileage state are within the part of the EV function with high curvature. Therefore, we use this calibration to show the methods potential instead.

Table 5 Results for the MPEC Estimation of the (Rust, 1987) Model with a Cubic Cost Function

Fig. 5

Comparison of EV Functions for Different Values of 𝜃₂. The figure shows the true EV function for the 1D bus replacement problem with a cubic cost function. The left panel depicts the case with 𝜃₂ = 1.5 and the right panel with 𝜃₂ = 0.075. All other model parameters are choosen as described in the beginning of Section 3.2.3. The figures also show the histrograms for the mileage state from the 300 Monte Carlo runs (right y-axis)

Table 5 shows that a uniform grid with 26 nodes is required to match the accuracy of the BE solution with 5 nodes. This in turn requires a computation time 1.7 times as long as for the BE method. Hence, the efficiency gain is even larger than for the linear cost function.

We conclude the discussion of the results by noting that by using flexible grids with BE constraints in the context of both NFXP and MPEC estimation of dynamic programming models, one can potentially harvest significant gains in efficiency, compared to standard uniform-grid approximations.

3.2.4 Discontinuities in the likelihood functions caused by node insertion

In the previous section, we have demonstrated that the balanced error approach for grid adaption enables the use of flexible interpolation grids in MPEC type estimation algorithms, which can be highly beneficial in terms of computational efficiency. However, we also argued that its application in the context of NFXP type methods can be beneficial, too, because it avoids the discontinuities induced by node insertion type grid adaption. In the next few paragraphs, we illustrate how these discontinuities can arise and what trouble they can cause for optimizers, using the bus engine replacement example from the previous section.

An important difference to the analysis above is that the effect of discontinuities caused by node insertion is extremely difficult to quantify. This is because we would need to interpret actual solver behavior, which can only be observed through a set of possible symptoms, such as early termination (throwing an error), wrong convergence (without error), very slow or even no convergence at all, etc. However, linking these effects causally to the discontinuities is very hard, if not impossible, and highly speculative, too. Moreover, the presence and severeness of problems caused by these discontinuities depends on many factors (and their interactions), such as the solver’s algorithm and its implementation, the concrete grid node insertion and deletion mechanism (of which many fundamentally different variants exist), the concrete model, and even the starting points of the likelihood optimization.

Hence, our approach to addressing this issue is purely qualitative. In the following, we work with two fixed grids: a uniform “original” grid, and the “adapted” grid, where one node has been deleted in a region with low curvature, and inserted in a region with high curvature; Figure 6 depicts the EV function approximation over both grids for two different parameters RC; for expositional purposes, we ignore all other parameters in this section. One can think of these two grids as one step within an algorithm for grid adaption by node insertion.

Fig. 6

Comparison of EV Function Approximations over Two Different Grids for Different Values of RC. The figure shows the true EV function as well as two approximations over different grids for the 1D bus engine replacement model with a linear cost function. The left panel depicts the case with RC = 10.2257 and the right panel with RC = 11.7257. The true EV function is depicted by the thin black dashed line; the red and the blue lines depict the two approximations over different grids (red: uniform grid, blue: one node inserted, one node deleted to/from uniform grid)

Most node insertion algorithms have an approximation error threshold, which—once reached—triggers the insertion (and possibly deletion) of one or several nodes. In this example, we assume that somewhere between RC = 10.2257 and RC = 11.7257, say at RC₀, some criterion triggers the insertion of one node (for example a function estimating the relative improvement in approximation error from adding a particular node). Consequently, if we approximate the EV function for a sequence of values of RC—which is what the likelihood maximization process will eventually do—, the sequence of corresponding EV approximations is discontinuous at RC₀, because of the change of the underlying grid.

Consider the two likelihood functions for the Rust (1987) model as in the previous sections depicted in Fig. 7; note that both likelihood functions represent the same model and data set, but use choice probabilities based on approximations of the EV functions over the two different grids. We choose an arbitrary value of RC₀, and denote the intersection of the two likelihood functions by RC^∗. Then, it becomes apparent that of for every potential solver step from RC_i to RC_i+ 1, where RC_i < RC₀ and RC₀ < RC_i+ 1 < RC^∗, the active grid for the EV approximations changes from the “original” to the “adapted” grid (by definition of RC₀), and therefore the “relevant” likelihood function switches discontinuously, too. Consequently, the solver might find that the objective function value has decreased (while maximizing), which is, however, and artifact of changing the underlying grid adaption. As a consequence, many solvers will reduce the step or trust region size and try until they find a search direction and step size which yields an improvement. If in this process, the solver iterates to a point where RC_i ≈ RC₀, it might stop prematurely because no local improvement is possible from this point.

Fig. 7

Comparison of the Likelihood Function using Two Different Grids to Compute Choice Probabilities. The left figure shows the likelihood functions for the 1D bus engine replacement model with a linear cost function, for the true EV function as well as approximations thereof over two different grids. The likelihood function using the true EV function is depicted by the thin black dashed line; the red and the blue lines depict the likelihood functions using the two approximations on different grids (red: uniform grid, blue: one node inserted, one node deleted to/from uniform grid). The right figure depicts the single likelihood function as a solver can evaluate it, given it switches the active grid at RC₀

We conclude this analysis by noting again that it is neither complete nor able to capture any of the effects quantitatively; however, it still gives an idea of the numerical problems that might cause trouble even for high-quality solvers. Therefore, we argue that also when using NFXP for estimating dynamic programming models, where the implementation of grid adaption by node insertion is technically possible, one might want to adapt our approach of continuous grid adaption by node movement, solely to avoid the artificial discontinuities node insertion creates even for smooth and well-defined problems.

3.2.5 The Rust (1987) model with a serially correlated unobserved utility component

In this section we show, that our grid adaption approach can also lead to large efficiency gains for higher dimensional models. For this, we extend the bus engine replacement model of Rust (1987) to feature a serially correlated error component, similar to Reich (2018), but keeping the usual EV1 iid. error component intact. We assume that the additional utility shock η_t follows an AR(1) process; the modified utility function becomes

$$u_{\theta}(i,x_{t},\eta_{t}) + \varepsilon_{t}(i) ,\quad u_{\theta}(i,x_{t}) = \begin{cases} -RC & \text{if } i=1\\ -c(x_{t},\theta_{1}) + \eta_{t} & \text{if } i=0. \end{cases}$$

(22)

where $\eta _{t} = \rho \eta _{t-1} + {\Delta }_{\eta _{t}}$ with ${\Delta }_{\eta _{t}} \sim N(0,\sigma )$. The serially correlated utility shock can be thought of as a persistent damage or problem with a particular bus.

Due to the serial dependence of the utility shock, the EV function features an additional state and thus re-writes as

$$\begin{array}{@{}rcl@{}} EV_{\theta}(i,x,\eta) &=& {\int}_{-\infty}^{\infty} {\int}_{0}^{\infty} \log \Bigg(\sum\limits_{i^{\prime} \in \{0,1\}} \exp\Big(u_{\theta}(i^{\prime},(1-i)x + {\Delta}_{x}, (1-i)(\rho \eta + {\Delta}_{\eta}))\\ && +\beta EV_{\theta}(i^{\prime},(1-i)x + {\Delta}_{x}, (1-i)(\rho \eta + {\Delta}_{\eta}) \Big) \Bigg) h_{\theta_{2}}({\Delta}_{x} ) \phi_{\sigma}({\Delta}_{\eta}) \mathrm{d} {\Delta}_{x} \mathrm{d} {\Delta}_{\eta} \end{array}$$

(23)

where ϕ_σ(Δ_η) is the probability density function of the normal distribution with mean zero and standard deviation σ. Note that the main difficulty arising from a utility specification with serially correlated unobserved states as in Eq. 22 is not the approximation of the EV function Eq. 23 which increases in dimensionality by the dimension of the state variable, but rather the computation of the corresponding likelihood function, as the serially correlated unobserved states have to be integrated out. This leads to a numerical integration problem of dimensionality proportional to the time horizon, which can be very large. Therefore, we apply the recursive likelihood function integration method of Reich (2018) in the maximum likelihood estimation of the extended model in the next two sections.

3.2.6 Approximating the EV function for fixed 𝜃

Analogously to the analysis of the one-dimensional model, we first demonstrate the approximation of the expected value function Eq. 23 for a fixed parameter value 𝜃, whereas the estimation of the model is deferred to the next subsection.

As mentioned in the previous section, the key difference between the expected value function of the model with a serially correlated unobserved utility component, in contrast to the one without it, is that EV is now a function of two continuous variables, x and η (leaving aside the binary choice variable i for readability), since both values are observed by the agent and thus influence his decisions. However, the application of balanced errors and grid adaption by node movement is not a direct extension of our results from the previous sections: As we argue in detail in Appendix A.2, going to dimensions higher than one, there is generally a mismatch between the number of grid cells on which error comparisons can be carried out (serving as a basis for error balancing), and the number of degrees of freedom to actually move the nodes; as a consequence, the set of equations from balanced errors will be non-square, potentially causing several sorts of numerical issues of under- or over-determination.

Consequently, we will limit our attention to an extension of our method which performs grid adaption in one dimension only: If one thinks about each node as a vector of two components each and thus the whole grid as a matrix of vectors (i.e. an (m,n,2)-tensor), $\mathbf {x}\equiv (x_{i}, \eta _{j})_{i=1, j=1}^{m,n}$, we allow only one of the two components to be adapted. At the same time, the maximum error within each “cell block” (i.e. all cells for which the adapted component’s indices are either i or i + 1) is computed, and balanced across cell blocks; more formally, if for example the grid is flexible in the x dimension, the maximum error within each cell block is—analogously to Eq. 11b—given by:

$$z_{i} = \underset{x_{i} \leq x < x_{i+1}, \eta}{\max} \vert R_{\hat{V}}(x, \eta;\mathbf{a},\mathbf{x}) \vert \quad \forall i \in I$$

where the error maximization now explicitly involves η. Otherwise, the balanced error system is identical to the one-dimensional system Eq. (11).

In Fig. 8, we plot the expected value function Eq. 23 and the corresponding two-dimensional grid for a particular parametrization; in particular, we set 𝜃, we use RC = 30, 𝜃₁ = 7, β = 0.99, ρ = 0.65, σ = 2 and 𝜃₂ = 0.05.¹⁹ For the utility function, we use the standard linear function Eq. 19. For the mileage state, we assume that the maximum mileage is given by x_max = 2000 and for η_t we use an approximation interval of ± 4 standard deviations around its unconditional mean.

Fig. 8

Balanced Error Grid and EV Function for the Rust (1987) Model with a Serially Correlated Unobserved Utility Component. The figure shows the balanced error grid (left) as well as the corresponding EV function (right) for the Rust (1987) model with a serially correlated unobserved utility component, obtained from the approximation of the two-dimensional EV function Eq. 23 for a fixed parameter vector 𝜃

For the algorithm, we use the same parametrization, software and hardware as in Section 3.1 (except that the “fmincon” algorithm option is “interior point”). Analogously to Section 3.2.2, we consider four different approximations for each of the cost functions: a benchmark case using 900 uniformly distributed nodes (30 in each dimension); the BE solution with four nodes in the mileage dimension, of which two are flexible; a uniform fixed grid with as many nodes as the flexible grid; and a uniform grid where the number of nodes is chosen such that the two grids have roughly the same accuracy in terms of the $L_{\infty }$ norm. For the η-dimension, we use eight nodes.

Table 6 lists the quantitative results; similar to the one-dimensional case (cf. Table 2), we see that for the EV problem alone with linear cost functions, the overhead of the larger system involving error balancing dominates the efficiency gains from having less grid nodes. As we will see in the next section, the efficiency gais for the estimation of the full problem are nevertheless large and significant. Figure 9 depicts “cuts” through the EV function for three different values of η in order to allow for visual comparison of the various configurations and their approximation errors, which qualitatively yield the same result as in the one-dimensional case.

Table 6 Approximation of the EV Function of the (Rust, 1987) Model with a Serially Correlated Unobserved Utility Component and Linear Cost Function

Fig. 9

EV as a Function of x for the Rust (1987) Model with a Serially Correlated Unobserved Utility Component. EV as a function of mileage state x and a linear cost function Eq. 19 obtained from the approximation of the 2 dimensional EV function Eq. 23 for a fixed parameter vector 𝜃. The three panels show the cases where η_t is 4 standard deviations below its unconditional mean (left), at its unconditional mean (center) and 4 standard deviations above its unconditional mean (right)

3.2.7 Monte Carlo study for the parameter estimation problem

In this subsection, we estimate the parameters of the bus engine replacement model of Rust (1987) with a serially correlated unobserved utility component. For this, we simulate 30 datasets each containing 3000 engine replacements. For the simulation of the data, we use the same parameters as in the previous subsection, given by RC = 30, 𝜃₁ = 7, β = 0.99, ρ = 0.65, σ = 2 and 𝜃₂ = 0.05, together with the linear cost function Eq. 19. For each dataset, we start the estimation procedure from three different starting points for 𝜃, given by $(RC,\theta _{1})\in \left \{(25,5),(30,7),(35,9)\right \}$ (one larger, one equal to, and one smaller than the true parameters). Also, as in the original model, the parameter of the mileage state transition, 𝜃₂ = 0.05, can be estimated independently, which is why we focus on the estimation of the cost parameters RC and 𝜃₁. We use 3-node Gauss–Laguerre quadrature rules to compute the one-period-ahead value expectations in Eq. 23 for the mileage state and 3-node Gauss–Hermite quadrature rules to compute the one-period-ahead value expectations for the η-state. For the maximum value of the approximation interval of the mileage state, we use 1.5 times the maximum value obtained from the simulated data. For the η-state we use ± 4 standard deviations around its unconditional mean.

Table 7 lists parameter estimates, errors with respect to the benchmark solution (rRMSE) and computation times for the estimation using MPEC. We find that the uniform solution with only 4 x-nodes produces a large rRMSE and the parameter estimates significantly differ from the benchmark solution. By allowing two out of the four nodes to be flexible, the RMSE can be improved significantly (from 0.5139 to 0.1448) and the parameter estimates become much closer to the benchmark values. To achieve about the same accuracy in terms of the rRMSE, a fixed grid solution with 8 nodes in the x-dimension is required.²⁰ This in turn significantly increases computation times. We observe that the BE solution that matches the accuracy of the fixed grid solution is 1.74 times faster. In absolute values the computation time can be reduced from 7595 to 4365 minutes—a reduction by more than 53 hours. Also, we find that for all approximation methods all runs converged, which indicates that the BE method is also sufficiently stable.

Table 7 Results for the MPEC Estimation of the Rust (1987) Model with a Serially Correlated Unobserved Utility Component

4 Empirical application

To demonstrate the applicability of the proposed method, we utilize data from one of the world’s leading user-generated content networks in the domain of music. Inspired by the pioneering work by Erdem and Keane (1996), in our demonstration we consider the consumers’ inherent trade-off between exploration and exploitation in their consumption decisions: When consumers enter a market, they sample products to gather information, an activity that eventually becomes somewhat routinized. However, since products evolve over time and new ones are introduced, this routine is continuously disrupted forcing consumers to resume their sampling activity.

We postulate that platform users face a similar trade-off: When signing up, consumers are exposed to a variety of music artists in the form of ”trending playlists” from each genre. This allows the consumers to explore new music artists and their songs. Following this initial sampling activity, they may listen to the same artists again (exploitation) or explore new ones (exploration).

In this section, our objective is to specify a model to understand this trade-off between exploration and exploitation. We assume that there is an inherent satisfaction with the consumed content, i.e., the previously listened artists on the platform. The satisfaction with this ”stock of artists,” however, is subject to depreciation: If a consumer engages in exploitation by listening to the same artists over and over again, then satisfaction decreases gradually. To counter, one can engage in exploration, which involves risk: The consumer has to search for a new artist but, at the same time, is faced with uncertainty regarding the degree of positive spillovers from this new artist on the current stock. Hence, while exploring, the potential increase in satisfaction is contrasted with the search costs of finding a new artist.

We estimate this model, which allows us to understand the trade-off between exploration and exploitation, with MPEC (Su & Judd, 2012) including grid adaption as proposed in the previous section. The estimated model allows us to understand whether consumers enjoy the process of searching for new artists itself, or if consumers attach costs to the search process and obtain utility from consuming their current stock of artists. This question is inherently linked to the efficiency of the platform’s recommender system. The main premise of such a system is to facilitate the exploration of new content and therefore decrease search costs (see Ricci et al., 2011 for an overview). Along these lines, our objective is to uncover the sign as well as magnitude of these search costs of a set of active platform users.

In the following we introduce the model specification, followed by the description of the data as well as the model estimation and results.

4.1 Model

We refer to exploration as listening to a song from a new music artist, i.e., from someone who a given consumer has never played a song during his or her tenure on the platform. Correspondingly, exploitation is the instance in which a given consumer listens to a song from a familiar artist. Once a consumer signs up to the platform, s/he has not played any song yet and therefore the continuous satisfaction state x is zero, and can reach at maximum one once this consumer starts browsing the platform. Hence, zero reflects a totally unsatisfied and one a totally satisfied consumer.

The choice between exploration and exploitation yields the following instantaneous pay-offs: On the one hand, discovering an appealing new artist is associated with exploring and then finding this artist. We assume that searching for new artists induces costs (i.e., time) which—net of an average utility obtained from listening to a song from a new artist²¹—is denoted 𝜃_NSC, where NSC stands for net search costs. Note that this utility is independent of the satisfaction state with the current stock of artists.

On the other hand, exploitation delivers a utility that depends on the satisfaction state with current stock of artists, formally modelled by a function of the satisfaction state U(x;𝜃_U), which is parametrized by 𝜃_U. Note that we impose U(0;𝜃_U) = 0 to give the sign of utility and the net search costs a natural interpretation. Adding extreme value type 1 random utility component to both choices, i.e., exploration and exploitation, we can summarize the instantaneous pay-offs as follows:

$$\pi(x, i; \theta) + \epsilon(i) =\begin{cases} \theta_{NSC} + \epsilon (1) & \text{ if explore, } \\ U(x; \theta_{U}) + \epsilon (0) & \text{ if exploit. } \end{cases}$$

(24)

Exploitation results in depreciation of the satisfaction state with the current stock of artists, i.e., x_t = x_t− 1 ∗ 𝜃_exploit, whereas exploration follows a continuous probability density distribution with the following properties (see Appendix A.3 for details): Given x_t, all higher satisfaction states have positive density—with a shape parametrized by (a vector) 𝜃_explore—, except at the satisfaction maximum 1, which has zero density.

If we assume that consumers behave dynamically optimal—i.e., they maximize their expected discounted utility from future content consumption—the specification of the model gives rise to a standard Bellman equation, where the decision probabilities are the well-known logit decision probabilities. Denoting the discount factor of the dynamic optimization problem by β, the vector of structural parameters consists of 𝜃 ≡ (𝜃_NSC,𝜃_U,β,𝜃_explore,𝜃_exploit).

4.2 Data

We utilize data from one of the world’s leading user-generated content networks in the domain of music, where music artists can build their career by interacting with their fans (see, e.g. Lanz 2019). Hence, this platform consists of two types of users: music artists and fans. We focus on the latter type as our goal is to understand the trade-off between exploration and exploitation from a consumer perspective.

On the platform, consumers can listen to songs from music artists uploaded on the artists’ profiles, where some of these songs also get featured in the trending playlists published on the front page. Therefore, for new sign-ups, these playlists provide the first opportunity to explore new music artists. Following the initial sampling activity, they may listen to further songs by the same artist when browsing the respective profile.

Within the scope of our research collaboration with the platform, we received a data sample on sign-ups covering their listening activity on a consumer level over four years. This individual-level panel reveals for each consumer what song by which music artist s/he played at which moment in time. This allows us to determine whether, over time, a consumer engaged in exploration or exploitation, i.e., listened to the same artists again or explored a new one.

For our analysis we rely on a set of sufficiently active platform users and therefore consider consumers in the top 20% in terms of song plays. The resulting sample consists of a total of 1,171 consumers who altogether played 3,094,418 songs (mean= 2,642.54; sd= 4,316.98). On average, they explored in every fourth song play a new artist (mean=.28; sd=.13). Since there is considerable heterogeneity in the exploration activity, for the estimation we form 20 dataset-buckets, each capturing five percents along the distribution, which we then compare. Table 8 shows further summary statistics on our sample, including the distribution of the consumers’ song plays and proportion of exploration as well as exploitation. It also contains the distribution concerning the longest sequence of exploration as well as exploitation on the consumer level.

Table 8 Summary Statistics on Consumer Sample

4.3 Estimation with unobserved states

To estimate this model we apply—utilizing the platform data—maximum likelihood estimation using MPEC (Su & Judd, 2012) including grid adaption. In our context in which the consumer’s satisfaction with the consumed content is unobserved, the likelihood is not straightforward to compute, because it forms an integral over the unobserved states. To cope with this condition, we apply recursive likelihood integration (RLI; Reich 2018; Lanz et al., 2021). The model and the estimation method are implemented in MATLAB using CasADi (Andersson et al., 2019); the MPEC problem is solved using the KNITRO constrained optimization solver.

4.4 Results

Table 9 exhibits the estimation results of all parameters across all dataset-buckets, where each bucket captures five percents along the distribution of exploration activity. First and foremost, we find that the net search costs 𝜃_NSC are always negative. Recall that negative search costs mean, in fact, positive utility obtained from listening to a song from a new artist. Considering the estimate, it seems that consumers associate a positive attitude towards exploring and finding new artists—even in those buckets pooling consumers with a low exploration activity.

Table 9 Summary Statistics on Estimates

Furthermore, we find not only the net search costs 𝜃_NSC to be quite stable across dataset-buckets, but also all other utility parameters. Regarding the discount factor β, we find considerable variation in the estimates across all dataset-buckets, and thus the degree of dynamic behavior underlying the observed decisions, ranging from zero to significant, though rather low values. This is consistent with the finding that consumers obtain utility from searching itself, hence they are not necessarily as forward-looking to achieve reasonable utility levels.

Note that since of the formed 20 dataset-buckets 18 converged, we excluded two buckets in the summary statistics in Table 9, i.e., the two covering the bottom ten percents of the exploration activity distribution. Also note that we report estimates for linear exploration utility; other functional forms yielded qualitative similar results.

We conclude that we do not find supportive evidence that recommender systems—beyond the features that have been in place when the data collection took place—do create significant additional value in terms of search cost reduction potential. This is in line with the conjecture that platform users tend to like exploring new music artists and therefore self-select into our sample by signing up to the platform.

5 Conclusion

In this paper we show how to integrate flexible interpolation grids with the estimation of dynamic programming models using both the NFXP of Rust (1987) and the MPEC approach of Su and Judd (2012). We derive a set of conditions to enforce balanced errors (BE), which we argue to be sufficient for optimality for functions in one dimension. In particular we make use of the equioscillation theorem to obtain value function approximations that are optimal in the $L_{\infty }$ norm, given their functional form and the total number of grid nodes.

We demonstrate the equivalence of minimizing the $L_{\infty }$ norm directly using nonlinear optimization and imposing BE constraints in several numerical experiments. We observe that in all cases considered, computations using the BE constraints are significantly faster than direct minimization. This finding suggests that our approach, integrated with NFXP or MPEC might be a fast and efficient way of obtaining precise parameter estimates using optimal grids.

We apply our method to the well-known bus engine replacement model of Rust (1987)—modified to feature a continuous mileage state—and compare our results to standard uniform-grid approximations with regard to accuracy and efficiency: first, using fixed model parameters we find that the BE grid can significantly reduce approximation errors compared to a uniform grid with equally many nodes. Furthermore, we show that if the approximated function is of sufficient complexity, our solution method also has better efficiency; conversely, a fixed-grid solution that achieves the same level of accuracy as the flexible grid requires considerably longer computation time.

Second, we compute solutions for the full maximum likelihood estimation problem for the cost parameters of the bus engine replacement model on simulated data using NFXP and MPEC with flexible grids. We find that the parameter estimates of the BE grid approach are significantly closer to the true parameter estimates compared to those of the fixed-grid solution with equally many approximation nodes. Moreover, a uniform-grid solution where the number of nodes is chosen to match the accuracy of the flexible grid requires considerably longer computation time. Consequently, we conclude that using the BE grid approach developed in this paper to estimate dynamic programming models using NFXP or MPEC with flexible grids can lead to significant gains in efficiency and accuracy compared to the commonly used fixed-grid approaches.

Lastly, we extend the model of Rust (1987) to feature a serially correlated, unobserved utility component, thus resulting in a two-dimensional value function approximation problem. We show how the balanced error criterion can be applied in multi-dimensional setups, and find that the corresponding relative efficiency gains are as substantial as in the one-dimensional case; since the absolute timings are much higher in the two-dimensional case, the absolute gains from grid adaption are even more significant. The development of a generic approach to adjust node positions by a single system of equations to augment the constraint optimization approach is subject to ongoing research.

We conclude this section with a discussion of the limitations of our approach: We have demonstrated the efficiency gains in examples of one-dimensional state spaces, as well as two-dimensional state spaces where nodes are only adapted along one dimensions. In Appendix A.2, we argue that freeing up nodes in two dimensions comes with problems, as the degrees of freedom do no longer match the number of BE constraints and thus induce potential problems with over- or under-specification of the constraint system. While full adaptability of the nodes would be desirable, the development of more general grid topologies with well-specified BE constraints under full node flexibility is subject to further research. Meanwhile, we argue (and demonstrate) that partial adaption of grid nodes, i.e., the movement of nodes along one dimension only, can still be a valuable improvement in terms of computational efficiency—at least in low- to moderate-dimensional state spaces, and in particular if some of the dimensions are discrete (and thus have, in some sense, fixed “nodes” anyway). To which extent these gains persist in even higher-dimensional setups is also still an open question. Finally, the adoption of our approach of course comes at increased complexity for the researcher, who has to set up a more complex MPEC estimation problem. We try to alleviate this by providing an exemplary implementation for the main model of this paper, and encourage researchers to try our method in particular in situations with little or no prior knowledge about the shape and the complexity of the (expected) value function as well as its sensitivity to the model parameters.

Appendix: A

1.1 A.1 Function Approximation

Suppose an unknown function $f:\mathbb {R}\supseteq D \rightarrow \mathbb {R}$ is to be represented on a computer. While there are many functions for which a finite-dimensional representation exists, this is generally an infinite-dimensional problem; also, even if such a representation exists, it might be unknown, and thus one might need to approximate the function from a finite number of evaluations. There are several popular approaches to function approximation, of which we will briefly introduce polynomial approximation, piecewise polynomial approximation, and splines, mainly to define the nomenclature used in the paper.

1.1.1 A.1.1: Polynomial Approximation

In many function approximation schemes, the approximating function $\hat {f}(\cdot ;\mathbf {a})$ is composed as a weighted sum of basis functions ${\Phi }^{n}\equiv \{\varphi _{i}\}_{i=0}^{n}$, with weight vector $\mathbf {a}\equiv (a_{i})_{i=1}^{n}$

$$\hat{f}(x;\mathbf{a})\equiv \sum\limits_{i=0}^{n} a_{i} \varphi_{i}(x).$$

(25)

The task of approximating f is thus twofold: first, a suitable set of basis function has to be identified, and second, the parameters of the function approximation—in our case the weights on the basis functions—have to be identified, such that the approximation is “as close as possible” to the approximated function.

In polynomial approximation, the basis functions used to form $\hat {f}$ are polynomials of degree n or less, and thus the approximation is itself an element of the space of all polynomials of degree n or less, $\hat {f}\in \mathcal {P}^{n}$. Consequently, the set of basis functions used to form Eq. 25 is often chosen to form an orthogonal basis of $\mathcal {P}^{n}$; popular choices are the Chebyshev, the Hermite, or the Laguerre polynomials (see, for example, Judd, 1998 p. 204). Of course, a naive approach is to set Φⁿ equal to the set of all monomials of degree n or less; however, this can lead to serious numerical problems when computing the weights a.

The second problem is to find parameters such that the quality of approximation is “good”. The most widely used approaches are based on one of two concepts—least squares minimization or interpolation.

Define the residual

$$R_{\hat{f}}(x;\mathbf{a})\equiv f(x) - \hat{f}(x;\mathbf{a}).$$

(26)

The least squares approach minimizes the weighted squared errors over the domain of approximation

$$\underset{\mathbf{a}}{\min} {\int}_{D} R_{\hat{f}}(x;\mathbf{a})^{2} w(x) dx,$$

(27)

where w is a non-negative weighting function, imposing “priorities” on the domain of approximation. Depending on the algorithm in use, different variants of computing the integral in Eq. 27, and different weighting functions w, can be applied.

On the other hand, interpolation ensures that the approximation equals the function at a specific set of interpolation nodes $\mathbf {x}\equiv (x_{i})_{i=1}^{n}$

$$\hat{f}(x_{i};\mathbf{a})=f(x_{i}), \forall x_{i} \in\mathbf{x}.$$

(28)

Here, the parameters a are the solution to the linear system of 28, which is square if |a| = |x| = n. While the interpolation approach is easy and intuitive, its result is not as rigorous as the least squares approximation error minimization; a way to combine the two is the Chebyshev regression approach (see Judd, 1998, p. 223).

1.1.2 A.1.2: Chebyshev Nodes

An important special case of interpolation node choice for polynomial approximation is the Chebyshev nodes. Suppose a function f on [− 1, 1] is interpolated at n nodes $\mathbf {x}\equiv (x_{i})_{i=1}^{n}$ by $\hat {f}\in \mathcal {P}^{n-1}$ such that Eq. 28 holds. Then, one can show that the residual as defined by Eq. 26 is (see, for example, Judd, 1998, Theorem 6.7.1)

$$R_{\hat{f}}(x;\mathbf{a}) = \frac{f^{(n)}(\xi(x))}{n!} {\Psi}(x;\mathbf{x})$$

(29)

for some ξ(x) ∈ [− 1, 1], and where ${\Psi }(x;\mathbf {x})\equiv {\prod }_{i=1}^{n}(x-x_{i})$.

Consequently, a natural approach to (static) node choice is

$$\mathbf{x^{*}} = \arg\underset{\mathbf{x}} {\min}\Vert {\Psi}(x;\mathbf{x}) \Vert_{\infty},$$

(30)

since it is independent of the function f to be approximated. Note that Ψ(x; x) is monic. If we choose the x_is to be the roots of the degree n Chebyshev polynomial,

$$\tilde{x}_{i}\equiv\cos\left( \frac{(2i-1)\pi}{2n}\right),$$

(31)

${\Psi }(x;\tilde {\mathbf {{x}}})$ can be shown to be the $L_{\infty }$ minimizing polynomial among all monic polynomials of degree n, and therefore constitutes a solution to problem Eq. 30; thus, $\mathbf {x^{*}} = \tilde {\mathbf {{x}}}$. Moreover (see, for example, Judd, 1998, Theorem 6.7.2)

$$\Vert {\Psi}(x;\tilde{\mathbf{{x}}})\Vert_{\infty} = 2^{1-n}.$$

(32)

Consequently, using Chebyshev nodes bounds the interpolation error from above by²²

$$\Vert R_{\hat{f}} \Vert_{\infty} \leq \frac{\Vert f^{(n)}\Vert_{\infty}}{n!} 2^{1-n}.$$

(33)

This result has great practical implications, as the interpolation nodes can be computed independently of f. Furthermore, if f is sufficiently smooth, one can show that the approximation $\hat {f}$ converges as the number of Chebyshev interpolation nodes is increased (see, for example, Judd, 1998, Theorem 6.7.3), which is not necessarily true for general grid choices (such as uniform grids) in conjunction with polynomial approximation.

It is important to note that Chebyshev nodes do not necessarily minimize the actual interpolation error; rather, they minimize the portion of the error that is independent of the function to be approximated. However, we would like to highlight two interesting special cases: First, suppose the f is such that its n th derivative is constant. Then, the residual Eq. 29 is constant in ξ, and thus x^∗ minimizes the total maximum absolute interpolation error. For example, if ${f}\in \mathcal {P}^{n}$ and $\hat {f}\in \mathcal {P}^{n-1}$, and thus if we approximate a degree n polynomial by a degree n − 1 interpolating polynomial, using Chebyshev nodes minimizes the $L_{\infty }$ norm of the residual and thus results in a uniform approximation. Second, for any function with f⁽ⁿ⁾ = 0, the approximation is exact, independent of the node choice; this includes, for example, any ${f}\in \mathcal {P}^{k}, k\leq n-1$.

In the next section, we will present a concrete numerical example.

1.1.3 A.1.3: Numerical Example—Function Approximation with Chebyshev Polynomials

In this example, we approximate three different functions using polynomial approximation on Chebyshev grids and on optimal flexible grids. In particular, we verify our grid adaption by ensuring that the solutions are compatible with properties we can derive from theory: first, the BE solution must always be at least as good or better than that obtained using a fixed Chebyshev grid; second, there are special cases where the Chebyshev grid actually produces a uniform approximation—for a detailed discussion of these properties, see Appendix A.1.2. Consequently, the results from this example are of a qualitative nature, as they serve as benchmarks for our verification analysis.

In this example, we approximate degree 5 and 6 ordinary polynomials and the function $f(x) = \exp (x^{2})$ by a degree 4 Chebyshev polynomial. The purpose of this example is to show that the method produces results that are in line with results from interpolation theory: As stated in Section 2.2.1 and Appendix A.1.2, using Chebyshev nodes for polynomial approximation minimizes the tightest known error bound that can be optimized over the nodes independently of f. This is a very strong result as it holds for any continuous function. However, Chebyshev nodes only put an upper bound on the $L_{\infty }$ norm of the residual, and they are not generally optimal. Hence, we demonstrate that the BE grid yields approximations that are at least as good as, and in many cases better than, the polynomial interpolation using Chebyshev nodes. As a special case, we present one example for which we know the Chebyshev nodes to be optimal; this example serves as an important benchmark, as it provides a non-trivial closed form solution for our method to replicate.

Figures 10 and 11 show the results for the degree 5 and degree 6 polynomial approximations, respectively, and Fig. 12 shows the results for $f(x) = \exp (x^{2})$; Table 10 lists the corresponding error measures and computation times. First, note that for all three functions, imposing the BE constraints and directly minimizing the $L_{\infty }$ norm yield the same solution. However, comparing computation times and the number of iterations, we find that the BE solution converges significantly faster. We conjecture that this is because by imposing the BE constraints, the solver accommodates for the approximation error in each individual cell of the grid, and thus has more detailed information about how the approximation error over the whole domain is composed, and how it is affected by a potential node movement. On the other hand, this information is mostly lost when minimizing the aggregate value (the maximum over all cell-wise errors) as in the direct minimization. This observation will be confirmed in the following examples and suggests that imposing the BE constraints might be a fast and efficient approach to obtaining optimal grids.

Fig. 10

Approximation of a Degree 5 Polynomial Using a Degree 4 Polynomial. Approximation of a degree 5 ordinary polynomial using a degree 4 Chebyshev polynomial on the interval [− 1,1]. The blue line corresponds to the true function, whereas the green line represents the fitted polynomial approximation. Turquoise diamonds and red circles depict the Chebyshev nodes on the interval [− 1,1], and the optimized approximation nodes obtained from imposing the BE conditions or direct minimization, respectively. The plots in the right panel show corresponding residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$. From the top to the bottom, the figure shows interpolation using Chebyshev nodes, a flexible grid with direct minimization of the $L_{\infty }$ norm, and a flexible grid with BE constraints. The coefficients of the true polynomial function f are given by α = [0.2164,− 5.9189,− 7.1890,− 5.9051,0.5161,− 6.9019]

Fig. 11

Approximation of a Degree 6 Polynomial Using a Degree 4 Polynomial. Approximation of a degree 6 ordinary polynomial using a degree 4 Chebyshev polynomial on the interval [− 1,1]. The blue line corresponds to the true function, whereas the green line represents the fitted polynomial approximation. Turquoise diamonds and red circles depict the Chebyshev nodes on the interval [− 1,1], and the optimized approximation nodes obtained from imposing the equioscillation conditions or direct minimization, respectively. The plots in the right panel show corresponding residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$. From the top to the bottom, the figure shows interpolation using Chebyshev nodes, a flexible grid with direct minimization of the $L_{\infty }$ norm, and a flexible grid with BE constraints. The coefficients of the true polynomial function f are given by α = [6.2356,9.2929,− 9.2861,3.3064,− 0.9446,− 5.5323,1.8073]

Fig. 12

Approximation of $f(x) = \exp (x^{2})$ Using a Degree 4 Polynomial. Approximation of $f(x) = \exp (x^{2})$ using a degree 4 Chebyshev polynomial on the interval [0,2]. The blue line corresponds to the true function, whereas the green line represents the fitted polynomial approximation. Turquoise diamonds and red circles depict the Chebyshev nodes on the interval [− 1,1], and the optimized approximation nodes obtained from imposing the equioscillation conditions or direct minimization, respectively. The plots in the right panel show corresponding residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$. From the top to the bottom, the figure shows interpolation using Chebyshev nodes, a flexible grid with direct minimization of the $L_{\infty }$ norm, and a flexible grid with BE constraints

Table 10 Comparison of Approximation Errors—Polynomial Approximation

For the degree 5 polynomial (Fig. 11), we find that the flexible-grid solutions exactly replicate the Chebyshev nodes (the red optimized nodes coincide with the turquoise Chebyshev nodes). In Appendix A.1.2, we argue why Chebyshev nodes are optimal in the $L_{\infty }$ norm for any degree n polynomial interpolated by a degree n − 1 polynomial. Consequently, this result implies that the optimal grid solution (obtained either by direct minimization or by imposing the BE constraints) is correct.

In the case of the degree 6 polynomial (Fig. 11), we observe that the nodes of the optimal grid do not coincide with the Chebyshev nodes in this particular example; conversely, the interpolation over the Chebyshev grid does not exhibit the BE property. And indeed, the maximum absolute approximation error is significantly smaller for the optimal grid compared to the Chebyshev grid. As mentioned above, this result is in line with the theory, as Chebyshev nodes only put an upper bound on the approximation error.

Similarly, Fig. 12 confirms the findings for the approximation of $f(x) = \exp (x^{2})$.

1.1.4 A.1.4: Piecewise Polynomial Approximation and Splines

If the approximating polynomial has full support over D, features of the approximated function in one region can have a substantial impact on the approximation quality also in other regions. A well-known example is the fact that regions of steep gradients can cause polynomial approximations to oscillate more in all parts of the approximated function.

A popular way of addressing this issue is piecewise polynomial approximation: instead of a polynomial with full support, the domain of approximation is subdivided by a grid $\mathbf {y}\equiv (y_{i})_{i=1}^{m}$, and lower-degree polynomials with support only over the respective grid cell (and sometimes its neighbors) are fitted, using interpolation for example. Formally, the interpolant is composed as

$$\hat{f}(x;\mathbf{a},\mathbf{y})\equiv \sum\limits_{i=0}^{n} a_{ij} \varphi_{i}(x), x\in[y_{j},y_{j+1}).$$

(34)

Note that if the breakpoints of the approximation are used as interpolation nodes—thus if x = y—the approximation will automatically be continuous, but not smooth in general.

As with polynomial approximation, the user is faced with two problems—namely, what degree of basis function polynomial to use, and how to identify the degrees of freedom (the coefficients). However, with piecewise methods these problems are slightly more interconnected: if only the breakpoints are used as interpolation nodes, only |y| = m equations exist to identify the coefficients in Eq. 34. However, this limits the degree of the local polynomials to one if no additional constraints are imposed. Thus, the approximation is a combination of piecewise linear segments. While this is straightforward to handle and does not add any additional complications to the identification of a, one usually needs a large number of break and interpolation points even for smooth functions.

Two popular approaches exist for applying higher-order polynomials: First, additional interpolation nodes can be inserted in the interior of the cells. This procedure generates additional equations for the approximation problem, which in turn identify the coefficients of the higher-order polynomial terms in Eq. 34. For simplicity, we distribute the additional interpolation nodes uniformly between the breakpoints of the piecewise polynomial, without making this explicit in the collocation Eq. CO in order not to overload the notation. Thus, the set of breakpoints is a strict subset of the set of interpolation nodes.

Second, additional constraints can be imposed on the derivatives of the approximation, since its functional form (and thus its derivatives) is known. Usually, the constraints impose equality of the derivatives at the breakpoints, in order to ensure smooth approximating functions. This form of approximation is called splines. Formally, the parameters of a polynomial spline of order k are obtained by solving the following linear system of equations:

$$\begin{array}{@{}rcl@{}} f(x_{i}) &=& \hat{f}(x_{i};\mathbf{a},\mathbf{y}), \forall x_{i} \in \mathbf{x}\equiv\mathbf{y} \end{array}$$

(35a)

$$\begin{array}{@{}rcl@{}} \hat{f}^{(h)}_{i}(x_{i+1};\mathbf{a},\mathbf{y}) &=& \hat{f}^{(h)}_{i+1}(x_{i+1};\mathbf{a},\mathbf{y}), h=1,\dots,k-2, i=1,\dots,n-2 \end{array}$$

(35b)

$$\begin{array}{@{}rcl@{}} \hat{f}^{(\cdot)} &=& 0 |_{\partial D}, \end{array}$$

(35c)

where $\hat {f}_{j}(x;\mathbf {a},\mathbf {y})= {\sum }_{i=0}^{n} a_{ij} \varphi _{i}(x)$ is the j th segment of the spline, and Eq. 35c is a generic boundary condition necessary for identifying all degrees of freedom. Note that

$$\hat{f}(\cdot;\mathbf{a},\mathbf{y})\in\mathcal{C}^{k-2}$$

(36)

and thus that a spline of order k is k − 2 times continuously differentiable. A different approach to spline approximations, which relates to the idea of composing an approximation from an orthogonal basis, is that of B-splines, which form a basis of the space of all order k splines; for details, see de Boor (2001).

1.1.5 A.1.5: Numerical Example—Higher Order Piecewise Polynomial Approximation

In this example, we show that the previously obtained results also hold for higher order piecewise polynomial approximations. For this purpose, we approximate the same function as in Example 2, but by a piecewise quadratic polynomial approximation with four nodes, two of which are flexible. Note, that for simplicity, we distribute the additional interpolation nodes necessary to identify all degrees of freedom uniformly between the breakpoints (see Appendix A.1.4 for details).

Figure 13 plots the corresponding results; the corresponding approximation errors and computation times are stated in Table 11. We find that in this example, the uniform-grid piecewise polynomial approximation shows large approximation errors between the first two nodes. By allocating the nodes more efficiently, the approximation errors can be decreased significantly. In particular, the maximum absolute error decreases from 5.3260 for the standard interpolation to 1.2731 for the flexible grid. Again, we find that imposing the BE constraints yields the same solution as direct minimization, but computation times and the number of iterations are significantly lower for the BE approach.

Fig. 13

Approximation of a Degree 9 Polynomial Using Piecewise Quadric Approximation. Approximation of a degree 9 ordinary polynomial on the interval [− 1,1] by a piecewise quadratic polynomial approximation with 4 nodes, out of which 2 nodes are potentially flexible. The blue line corresponds to the true function, whereas the green line represents the fitted piecewise polynomial approximation. Turquoise diamonds and red circles depict the fixed uniform nodes, and the optimized approximation nodes obtained from imposing the BE conditions or direct minimization, respectively. The plots in the right panel show corresponding residuals $f(x) - \hat {f}(x;\mathbf {a},\mathbf {x})$. From the top to the bottom, the figure shows piecewise polynomial approximation using uniformly distributed nodes, flexible nodes with direct minimization of the $L_{\infty }$ norm, and flexible nodes with BE constraints. The coefficients of the true polynomial function f are given by α = [4.1239,2.7956,5.0862,− 1.2933,7.8788,− 7.8582,9.9192,− 2.8339,3.4032,− 9.9500]

Table 11 Comparison of Approximation Errors—Piecewise Quadratic Approximation

1.2 A.2: Grid Creation and Balanced Errors in Two Dimensions

While grid creation is trivial in one dimension — a set of grid nodes $a = x_{0} < x_{1} <{\dots } < x_{n+1}=b$ suffices to uniquely define a grid over a domain [a,b] — grid creation the two dimensions is generally non-unique, even if the same set of nodes $\mathbf {x}=(x_{i})_{i=0}^{(n+1)^{2}}, x_{i}\in \mathbb {R}^{2}$ is used. One reason is that a grid cell in one dimension, an interval, can be thought of as a 1-hypercube, which would generalize to a quadrilateral grid in two dimensions, or it can be though of as a 1-simplex, which would generalize to a triangulation in two dimensions. Figure 14 depicts different grid variants in two dimensions; in particular, Fig. 14a and b demonstrate how an identical set of grid nodes can be interpreted differently, depending on the imposed grid cell geometry.

Fig. 14

Different Types of Grids in Two Dimensions. The figure shows different types of two-dimensional grids: Panel (a) shows a regular quadrilateral grid with 16 cells; Panel (b) shows a regular simplex grid with 32 cells; Panel (c) shows another regular simplex grid with 64 cells; Panel (d) shows an unstructured simplex grid with 32 cells

Closely related, and highly relevant to the implementation of balanced errors over a two-dimensional grid, is the relation between number of degrees of freedom (the coordinates of the variable grid nodes in the balanced error system) and the number of BE conditions: While in the one-dimensional case, the number of variable grid nodes matches the number of error comparisons across intervals exactly (n flexible nodes yield n + 1 intervals and thus n error comparisons), these numbers are generally not matching in higher dimensions. In fact, we were not able to construct any grid with equally many degrees of freedom as balanced error constraints;²³ Table 12 summarizes this mismatch for the grid depicted in Fig. 14. Consequently, imposing balanced errors leads either to an over- or an underspecified system, depending on the grid topology. As the former will generally have no solution, we opt for underspecification, either by choosing a topology with less BE constraints than degrees of freedom, or by reducing the number of BE constraints.

Table 12 Properties of Different Types of Grids in Two Dimensions

Moreover, not all the grid topologies and the corresponding interpolation formats allow for continuous interpolant on grids with moving nodes. For example, moving grid nodes of a quadrilateral grid as in Fig. 14a, together with bilinear interpolation or tensor product splines, will generally lead to a discontinuous interpolant. Therefore, we restrict ourselves to piecewise linear interpolation over each simplex — and therefore to simplicial grids —, which is guaranteed to be continuous under mild regularity conditions. Since all simplicial grids in Fig. 14 lead to overspecified BE systems, we use a grid as in Fig. 14b, but impose BE constraints on the pairwise maximum of each cell neighbors forming a quadrilateral only, yielding an underspecified BE system, where — technically speaking — half of the BE conditions are turned into implicitly enforced inequality constraints.

We conclude this short discussion on grid creation and balanced errors in two dimensions by adding two remarks: First, due to the underspecification of the BE system, we cannot expect the solution to be unique. Moreover, not only can we expect several isolated solutions for optimal grids with potentially different (but always balanced) errors, but there might even be continua of solutions; obviously, the appearance of the later would annihilate the BE criterion as a sufficient optimality condition. Second, and closely related, the numerical solution of the non-square BE system turns out to be much more difficult; the reasons for this are manifold, such as non-square nature of the BE system and the potential existence of continua of solutions (yielding rank deficient Jacobian matrices), or the reduction of the over-specified BE system which implicitly imposes additional inequality constraints.

1.3 An Easy-to-Integrate Distribution With Compact Support and Special Properties

In the following we define a distribution density over the interval [0, 1]—-or any interval [a,b]—-which has the following features:

• The right end point of the support interval can never be reached;

• The expecrtation of a function of the corresponding random variable can be easily integrated numerically.

For example, this allows us to model a “shooting” process where one stands at a and shoots towars b without ever reaching it.

Formally, let us consider a random variable X with the parametrized probability density function $\tilde {q}(\cdot ;\lambda )$ that has compact support, where the expected value of the continuous function f of the random variable is defined as

$$\begin{array}{@{}rcl@{}} E(f(x))&=&{{\int}_{a}^{b}}f(x)\tilde{q}(x;\lambda)dx \end{array}$$

(37)

$$\begin{array}{@{}rcl@{}} &=&(b-a){{\int}_{0}^{1}}f(s(b-a)+a)\tilde{q}(s(b-a)+a;\lambda)ds, \end{array}$$

(38)

where the second equation is a simple, linear change of variables, x = s(b − a) + a, to normalize the domain.

Applying a change of variable $\phi : [0,\infty ]\rightarrow [0,1]$, we can rewrite Eq. 37 as

$$E(f(x))=(b-a){\int}_{\phi^{-1}(0)=0}^{\phi^{-1}(1)=\infty}f(\phi(t)(b-a)+a)\tilde{q}(\phi(t)(b-a)+a;\lambda)\phi^{\prime}(t)dt.$$

(39)

We assume $T\sim \exp (\lambda )$ and $x=\phi (t)=\frac {t}{t+1}$. Denoting by q(⋅; λ) the density of the exponential distribution with parameter λ, $\tilde {q}(\cdot ;\lambda )$ is implicitly defined by the equation

$$(b-a)\tilde{q}(\phi(t)(b-a)+a;\lambda)\phi^{\prime}(t)=q(t;\lambda)$$

(40)

as

$$\tilde{q}(x;\lambda)= \frac{q\left( \phi^{-1}\left( \frac{x-a}{b-a}\right);\lambda\right)} {(b-a)\phi^{\prime}\left( \phi^{-1}\left( \frac{x-a}{b-a}\right)\right)}.$$

(41)

This set-up allows us to apply Gauss–Laguerre quadrature to approximate the expectation

$$\begin{array}{@{}rcl@{}} E(f(x))&=&{\int}_{0}^{\infty}f(\phi(t)(b-a)+a)q(t;\lambda)dt \end{array}$$

(42)

$$\begin{array}{@{}rcl@{}} &&\approx \sum\limits_{i=1}^{N} f(\phi(t_{i}/\lambda)(b-a)+a)\omega_{i}, \end{array}$$

(43)

where N is the degree of the quadrature rule, and (t_i,ω_i) are the respective nodes and weights, which are readily tabulated or can be precomputed.

For example, using 21 nodes (λ = 1), the expectation of X can be computed up to 6 digits of precision. Figure 15 depicts the distribution for various levels of λ, including λ = 1 (violet curve).

Fig. 15

Distributions Given λ