Logical qubit behavior model and fast simulation for surface code

Abstract

This study proposes a logical qubit behavior model (LQBM) that calculates the state of the logical qubit based on a surface code after a logical qubit operation. LQBM can simulate the surface code whose distance exceeds 5, which is impossible with conventional quantum simulators. A complex error syndrome measurement must not be executed in this model. LQBM works at the mixed level of a logical and physical qubit. Probability amplitudes and the number of state vectors are designed at the physical qubit level. The state vectors of physical qubits constituting a logical qubit are abstracted to the value of the logical qubit level. LQBM converts all logical qubit operations, which include an initialization, a state injection, universal gates, and lattice surgery operations (e.g., a merge and a split) to simple calculations. LQBM provides a better computational complexity of O(log(distance)) than O(distance$^2$). Through simulation experiments, it was found that LQBM performs logical qubit operations up to 24 million times faster than existing quantum simulators in the case of distance = 5.

1 Introduction

Quantum computers are attracting much attention because of their performance beyond the limits of conventional computers [1, 2]. Recently, large IT companies (e.g., IBM and Google) have been conducting more research with the goal of commercialization, but one of the main obstacles to the development and operation of quantum computers is errors occurring in qubits. Quantum computer qubits can be implemented in various ways, including superconductors [3, 4], trapped ions [5], and photons [6]. However, these qubits have a fundamental limitation in those errors that occur. To solve this problem, Quantum Error Correction (QEC) [7,8,9] is used to reduce the error. QEC is a technology that generates a syndrome of qubit error and corrects it by decoding the syndrome.

Until now, various error correction technologies, such as a repetition code [10], a toric code [11, 12], and a surface code [13,14,15,16], have been developed, and the surface code is currently the most active and studied one. The surface code is divided into a defect-based surface code [14] and a planar surface code [16]. Now, among the variants of the planar surface code, the rotated surface code [16, 17] using a smaller number of physical qubits has been studied a lot.

The most basic operation in the surface code is error syndrome measurement (ESM), which is used to correct qubit errors by generating error syndromes. ESM is also used to perform logical qubit initialization and operations based on lattice surgery [16, 18,19,20]. When a logical qubit based on the surface code is simulated using conventional quantum simulators, the actual states of the physical qubits constituting the logical qubit are derived, which are the probability amplitudes of the physical qubits, the state vectors of the physical qubits, and the number of state vectors. However, since ESM is performed through complex physical qubit operations of O($d^2$) that depend on the distance d of the logical qubit, the complexity of an ESM execution increases exponentially as d increases, making the simulation difficult. Currently, quantum simulators can simulate up to 49 qubits when using a supercomputer [21], and QPlayer supports up to 85 physical qubits for a surface code simulation [22]. Therefore, a distance of 3 or 5 is the simulation limit for the rotated surface code.

We analyzed the input and output qubit states of logical qubit operations from the behavioral perspective of ESM. We developed a model that can calculate the output state of the logical qubit after the logical operation without performing a complex process of ESM. We propose it as logical qubit behavior model (LQBM). LQBM is the model working at the mixed level of the logical and physical qubit. At the physical qubit level, it can simply calculate the probability amplitudes and the number of state vectors of physical qubits constituting a logical qubit. At the logical qubit level, the state vector composed of the physical qubits is abstracted to the value of the logical level. These calculations are performed without the complex physical qubit operations. Based on this model, it is possible to calculate the state of logical qubits with high distance, which cannot be implemented with current quantum simulators. It also provides up to 24.75 million times faster execution than existing quantum simulators. The contribution of LQBM proposed in this paper is as follows.

• State representation of the logical qubit: A state of a logical qubit after an initialization or state injection can be quickly calculated without the complicated ESM process.

• Lattice surgery-based logical operation: Quantum operations on two logical qubits are performed using the lattice surgery technique. A state of the logical qubits after performing the lattice surgery operation is calculated mathematically.

• Mixed model and low computational complexity: ESM has an O($d^2$) computational complexity. However, LQBM provides the complexity of O($log \; d$) using the mixed model of the physical and logical qubit.

• Performance of an LQBM simulator: A simple simulator based on LQBM was created, and higher performance was verified. The $\vert 0\rangle _L$ initialization of the logical qubit with distance 5 shows that LQBM is 24.75 million times faster than the conventional quantum simulators.

The rest of the paper is organized as follows. Section 2 describes the related studies for this paper. Section 3 proposes a concept of LQBM proposed in this paper. Sections 4 through 6 describe the state representation of logical qubits, the logical operations for a single logical qubit, and the lattice surgery-based logical operations of LQBM. Section 7 defines logical operation matrices for LQBM based on the descriptions in Sects. 4 to 6. Section 8 compares the performance of a simple simulator based on LQBM with that of a conventional quantum simulator. Finally, Sect. 9 presents the main conclusions of this study.

2 Related works

Surface code: A surface code [23,24,25,26,27] is the most actively studied QEC method. The surface code arranges data qubits and X/Z stabilizer qubits on a two-dimensional qubit array. The data qubits represent the state of the logical qubit using an entanglement, and the X/Z stabilizers are used to detect and correct errors in the data qubits. The most critical process in the surface code is ESM, which marks the error symptoms of the data qubits in the X/Z stabilizer. The error syndrome generated by ESM goes through the decoding process to find the location of the physical qubit where the error occurs and the type of error (X or Z error).

ESM is not only used to correct errors but is also used to perform quantum operations on logical qubits. Initializing a logical qubit to a specific state such as $\vert 0\rangle$ or $\vert +\rangle$ uses ESM, and a state injection to set an arbitrary quantum state into a logical qubit also uses ESM. In addition, the lattice surgery technique is used to perform the logical qubit operations targeting multiple logical qubits, and the basis of this technique is to use ESM. The most basic operations of the lattice surgery are a merge and a split. The merge is the method of merging two logical qubits into one logical qubit. The split operation is to split one logical qubit into two logical qubits. The merge and the split operate based on an X or Z boundary. If the merge and the split are combined, logical qubit operations (e.g., CNOT, MOVE, and SWAP) can be performed, and Z phase shit operations (e.g., S gate and T gate) can also be performed [16, 18, 28,29,30,31].

There is the rotated surface code using fewer physical qubits [16]. The rotated surface code is created by rotating the planar surface code by 45$^{\circ }$ and removing some qubits. The rotated surface code with the smallest distance 3 consists of 9 data qubits and eight stabilizer qubits. The eight stabilizer qubits comprise 4 X stabilizers and 4 Z stabilizers. The X and Z stabilizers detect the Z and X errors of the data qubits, respectively.

Quantum Simulator: Quantum simulators utilize classical computers to simulate qubits. Since these simulators require a memory size of $2^N$ (N: the number of qubits) to express the entanglement of qubits, the memory consumption increases exponentially as the number of qubits increases [21, 32,33,34,35]. If there are 36 or 50 qubits, approximately 1TB or 16PB of memory is required, respectively [32]. Therefore, if the number of qubits increases, the memory requirement cannot be satisfied even when a large-scale system is used. This is a limitation of the quantum simulators.

The quantum simulator of ETH Zurich simulated a 45-qubit circuit on the Cori II supercomputing system with 0.5 petabytes of memory and 8192 nodes [34]. QuEST showed the capability of simulating a 38 qubits circuit on the ARCUS supercomputer with 2048 nodes [35]. At Tsinghua University, the quantum supremacy circuit simulation on Sunway TaihuLight with 16K nodes showed that a 49-qubit circuit with a depth of 39 could be simulated [21]. QPlayer simulated an 85-qubit circuit for the surface code on 512 GB memory by removing unnecessary state vectors of qubits instead of increasing the memory capacity [22].

3 Logical qubit behavior model

LQBM can derive the state changes after performing the logical qubit operations through simple calculations instead of a complex ESM on physical qubits. LQBM consists of two elements: a state representation of a logical qubit and a logical qubit operation.

State representation of a logical qubit: The state representation of a logical qubit describes the quantum state when an initialization or a state injection is applied to the logical qubit. The state $\vert \psi \rangle _L$ of the logical qubit consists of three elements which are S, pa, and m, and the relationship between them is as in (1). $\vert \psi \rangle _L$ is composed of logical values (S) of state vectors constituting the logical qubit and probability amplitudes (pa) corresponding to each logical value. Also, each S is expressed as an entanglement of m state vectors of physical qubits. pa and m are elements based on the physical qubit level, and S is based on the logical qubit level.

$$\begin{aligned} \begin{aligned} \vert \psi \rangle _L&= \alpha \vert 0 \rangle _L + \beta \vert 1 \rangle _L = \alpha \vert S_0 \rangle _L + \beta \vert S_1 \rangle _L \\&= pa_0(\vert S_0 \rangle _{L\_1} + \ldots + \vert S_0 \rangle _{L\_m}) +pa_1(\vert S_1 \rangle _{L\_1} + \ldots + \vert S_1 \rangle _{L\_m}) \end{aligned} \end{aligned}$$

(1)

• S: S is the logical value of state vectors constituting a logical qubit. S for a logical qubit consists of $S_0$ (=0) and $S_1$ (=1).

• m: One $\vert S_j \rangle _L$ is expressed as an entanglement of m state vectors $\vert S_j \rangle _{L\_i}$. Also, if one logical qubit consists of k physical data qubits, it is expressed as $\vert S_j \rangle _{L\_i} = \vert d_1 \ldots d_k \rangle$. A logical value of $\vert S_j \rangle _{L\_i}$ is determined by combining the physical data qubits.

• pa: pa is the probability amplitude in units of the physical data qubits constituting the logical qubit. $pa_j$ is the value for $\vert S_j \rangle _{L\_i}$. If m probability amplitudes for $\vert S_j \rangle _{L\_i}$ are gathered, they behave like the logical probability amplitude for $\vert S_j \rangle _L$.

The state of one logical qubit is also expressed as a function of the quantum state $\alpha \vert 0 \rangle + \beta \vert 1 \rangle$ to be initialized and the number of X stabilizers constituting the logical qubit, as follows. Details will be explained in Sect. 4.

$$\begin{aligned} \begin{aligned} \vert \psi \rangle _L&= F_{Init} (\alpha , \beta , the\, number\, of\, X\, stabilizers) \\ F_{Init}&= \{Initialization, State\, Injection\} \end{aligned} \end{aligned}$$

Logical qubit operation: When a logical qubit operation is applied on the state $\vert \psi \rangle _{L\_input}$ of logical input qubit, an output logical qubit state $\vert \psi \rangle _{L\_output}$ is generated. $F_{OP}$ represents various logical qubit operations. In addition to the existing universal gate set, $F_{OP}$ supports the merge and the split with X and Z boundaries for the lattice surgery. Details will be explained in Sects. 5 to 6.

$$\begin{aligned} \begin{aligned} \vert \psi \rangle _{L\_output}&= F_{OP} (\vert \psi \rangle _{L\_input}, the\, number\, of X\, stabilizers)\\ F_{OP}&=\{X, Z, H, XMerge, XSplit, ZMerge, ZSplit, CNOT, S, T\} \end{aligned} \end{aligned}$$

4 State representation of logical qubit

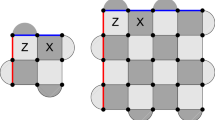
The initialization and the state injection define the state of logical qubits based on the rotated surface code. The initialization is to set the state of a logical qubit to a specific quantum state, such as $\vert 0\rangle _L$ or $\vert +\rangle _L$. The state injection sets a logical qubit to an arbitrary quantum state of $\vert \psi \rangle _L = \alpha \vert 0\rangle _L + \beta \vert 1\rangle _L$. Figure 1 shows the structure of the logical qubit based on the rotated surface code [16] targeted in this paper, and the ESM circuit is in Fig. 2. The logical qubit generally uses dx and dz of the same value, which are usually expressed as distance d. In this paper, they are marked differently to distinguish the effects of dx and dz during the ESM process.

Fig. 1

This figure shows the structure of the rotated surface code. The hollow, black, and gray circles represent the data qubit, X stabilizer, and Z stabilizer, respectively. dx and dz denote the number of data qubits on the X and Z boundaries, which are typically positive odd. $nx(=(dx-1)(dz+1)/2)$ and $nz(=(dx+1)(dz-1)/2)$ represent the number of X and Z stabilizers, respectively. $X_L$ and $Z_L$ define the logical X and Z operators for the logical qubit

Fig. 2

a, b are ESM circuits that generate an X/Z stabilizer to detect errors in data qubits. The X and Z stabilizers are used to detect Z and X errors in the data qubits, respectively. One X or Z stabilizer is associated with four neighboring data qubits. D0 through D5 in the circuit are the data qubits in Fig. 1

4.1 $\vert 0\rangle _L$ initialization

A $\vert 0\rangle _L$ initialization sets all data qubits constituting a logical qubit to $\vert 0\rangle$ and performs an ESM process to generate all X and Z stabilizers. After that, the error syndromes composed of X and Z stabilizers are decoded, and the errors are corrected. Only X syndrome errors arise randomly in the $\vert 0\rangle _L$ initialization. A $\vert +\rangle _L$ initialization is similar to the $\vert 0\rangle _L$ initialization except that all data qubits are initialized to $\vert +\rangle$ and that only Z syndrome errors occur randomly.

First, to initialize a logical qubit to $\vert 0\rangle _L$, all data qubits and X/Z stabilizers of the logical qubit are initialized to $\vert 0\rangle$. The initial state $\vert \psi \rangle _L$ of the logical qubit is described as the tensor product of the X stabilizers, the Z stabilizers, and the data qubits as follows. XS, ZS, and D represent the X stabilizers, the Z stabilizers, and the data qubits, respectively, and the states of all qubits are $\vert 0\rangle$.

$$\begin{aligned} \vert \psi \rangle _L = \vert 0_1 \ldots 0_{nx}\rangle _{XS} \, \vert 0_1 \ldots 0_{nz}\rangle _{ZS} \, \vert 0_1 \ldots 0_{dx \, \times \, dz}\rangle _{D} \end{aligned}$$

The X and Z stabilizers produce the same result even if they are performed simultaneously or in sequence because they commute. Assuming that the Z stabilizers are generated before the X stabilizers, look at Fig. 2b. Since all data qubits, the control of the CNOT operations, are $\vert 0\rangle$, the Z stabilizer generation does not change the state $\vert \psi \rangle _L$. Therefore, in the $\vert 0\rangle _L$ initialization, only the generation of the X stabilizers plays an important role, and we will look into this in detail.

nx X stabilizers can be generated in order from X stabilizer 1 to nx because all X stabilizers commute each other. So let’s assume that X stabilizer 1 is generated for the first time. In Fig. 2a, the first step of generating the X stabilizer is to perform an H gate on the X stabilizer, and the result is expressed as (2). In (2), the state of the Z stabilizer, which always has a value of $\vert 0\rangle$, is deleted for convenience of explanation, and the data qubit is displayed immediately after the first X stabilizer.

$$\begin{aligned} \begin{aligned} \vert \psi \rangle _L =\frac{1}{\sqrt{2}} (\vert 0_1\rangle _{XS} + \vert 1_1\rangle _{XS}) \vert 0_1 \ldots 0_{dx \times dz}\rangle _{D} \vert 0_2 \ldots 0_{nx}\rangle _{XS} \end{aligned} \end{aligned}$$

(2)

In the second step, CNOT gates are performed with the X stabilizers as a control and the data qubits as a target. Depending on whether the state of the $Z_L$ operator on a logical qubit has even or odd parity, the state of the logical qubit is either $\vert 0\rangle _L$ or $\vert 1\rangle _L$. When the $Z_L$ operator is defined as shown in Fig. 1, the current state of the $Z_L$ operator has even parity because the eigenvalue of all data qubits constituting the $Z_L$ operator is +1. Therefore, $\vert 0_1 \ldots 0_{dx \times dz}\rangle _{D}$ can be abstracted as the logical state $\vert 0\rangle _L$. There are $(dx-1)$ X stabilizers above and below the $Z_L$ operator, and each X stabilizer can affect two data qubits involved in the $Z_L$ operator. From (2), the state of the $Z_L$ operator remains even parity because the CNOT using $\vert 0_1\rangle _{XS}$ as the control and the data qubit as the target does not change the data qubits constituting the $Z_L$ operator. Since CNOT using $\vert 1_1\rangle _{XS}$ as the control performs X operations on two data qubits in the $Z_L$ operator, the state of the $Z_L$ operator remains even parity. Therefore, the state of the logical qubit after executing the CNOT gates remains $\vert 0\rangle _L$. The result of performing the CNOT operations in (2) is summarized in (3). Although the logical qubit state remains $\vert 0\rangle _L$, the combinations of the data qubits constituting it are different, and this is expressed as $\vert 0\rangle _{L\_1\_0}$ and $\vert 0\rangle _{L\_1\_1}$ in (3). $\vert 0\rangle _{L\_1\_0}$ or $\vert 0\rangle _{L\_1\_1}$ is the state of the data qubits generated by CNOT operations using the $\vert 0_1\rangle _{XS}$ or $\vert 1_1\rangle _{XS}$ value of the X stabilizer as the control when the first X stabilizer is generated.

$$\begin{aligned} \begin{aligned} \vert \psi \rangle _L =\frac{1}{\sqrt{2}} (\vert 0_1\rangle _{XS}\vert 0\rangle _{L\_1\_0} + \vert 1_1\rangle _{XS}\vert 0\rangle _{L\_1\_1}) \vert 0_2 \ldots 0_{nx}\rangle _{XS} \end{aligned} \end{aligned}$$

(3)

The third step of generating the X stabilizer is to perform the second H gate on the X stabilizer, which is expressed by (4). The phases ($P_{1\_ji}$) are separated from the entanglement of the first X stabilizer and the data qubits.

$$\begin{aligned} \begin{aligned} \vert \psi { \rangle _L}&= \frac{1}{{{{\sqrt{2} }^2}}}(\vert {0_1}{ \rangle _{XS}}\,\vert 0{ \rangle _{L\_1\_0}} + \vert {1_1}{ \rangle _{XS}}\,\vert 0{ \rangle _{L\_1\_0}}&\\&\qquad \qquad + \,\vert {0_1}{ \rangle _{XS}}\,\vert 0{ \rangle _{L\_1\_1}} - \vert {1_1}{ \rangle _{XS}}\,\vert 0{ \rangle _{L\_1\_1}})\vert {0_2}\,\ldots \,\,{0_{nx}}{ \rangle _{XS}}&\\&= \frac{1}{{\sqrt{2} }^2} (\sum \limits _{j = 0}^{2 - 1} {\sum \limits _{i = 0}^{2 - 1} {{{( - 1)}^{{P_{1\_ji}}}}\vert {XS_1}_{\_j}{ \rangle _{XS}}\vert 0{ \rangle _{L\_1\_i}}} } )\vert {0_2}\,\ldots \,\,{0_{nx}}{ \rangle _{XS}}&\\&\qquad \qquad \vert {XS_1}_{\_j}{ \rangle _{XS}}\, = \left\{ {\begin{array}{*{20}{c}} {\vert {0_1}{ \rangle _{XS}}\,\,\,if\,\,j = 0}\\ {\vert {1_1}{ \rangle _{XS}}\,\,if\,\,j = 1} \end{array}} \right. \,\,&\\&\qquad \qquad \qquad {P_{1\_00}} = {P_{1\_01}} = {P_{1\_10}} = 0,\,\,{P_{1\_11}} = 1&\end{aligned} \end{aligned}$$

(4)

From (4), the state when all nx X stabilizers are generated is derived as (5). The X stabilizer expression, which is separated until (4), is combined into one since all X stabilizers are generated. Because nx is a fixed constant, it can be omitted for convenience of notation.

$$\begin{aligned} \begin{aligned} \vert \psi { \rangle _L}&= \frac{1}{{{{\sqrt{2} }^{2nx}}}}\sum \limits _{j = 0}^{{2^{nx}} - 1} {\sum \limits _{i = 0}^{{2^{nx}} - 1} {{{( - 1)}^{P{}_{nx\_ji}}}\vert {XS_{nx\_j}}{ \rangle _{XS}}\vert 0{ \rangle _{L\_nx\_i}}} }&\\&= \frac{1}{{{{\sqrt{2} }^{2nx}}}}\sum \limits _{j = 0}^{{2^{nx}} - 1} {\sum \limits _{i = 0}^{{2^{nx}} - 1} {{{( - 1)}^{{P_{ji}}}}\vert {XS_j}{ \rangle _{XS}}\vert 0{ \rangle _{L\_i}}} }&\end{aligned} \end{aligned}$$

(5)

• $\vert XS_j\rangle _{XS}$: The X stabilizers are represented by $2^{nx}$ entangled state vectors, and $\vert XS_j\rangle _{XS}$ is the j-th state vector among the entangled states.

• $\vert 0\rangle _{L\_i}$: The data qubit $\vert 0\rangle _L$ is represented by $2^{nx}$ entangled state vectors, and $\vert 0\rangle _{L\_i}$ is the i-th state vector among the entangled states.

• $P_{ji} \in \{0, 1\}$: the phase value for the tensor product of $\vert XS_j\rangle _{XS}$ and $\vert 0\rangle _{L\_i}$.

The state of the logical qubit after generating all nx X stabilizers is a form in which phases are added to the tensor product of the X stabilizers with the $2^{nx}$ entangled state vectors and the $\vert 0\rangle _L$ data qubits with the $2^{nx}$ entangled state vectors. The total number of state vectors of one logical qubit becomes $2^{2nx}$, and the probability amplitude of each state vector becomes $1/\sqrt{2}^{2nx}$.

The fourth step is to measure all the generated X stabilizers. The q-th X stabilizer value is randomly selected among the entanglement of $2^{nx}$ X stabilizers. This is expressed as (6).

$$\begin{aligned} \begin{aligned} \vert \psi { \rangle _L} = \frac{1}{{{{\sqrt{2} }^{nx}}}}\sum \limits _{i = 0}^{{2^{nx}} - 1} {{{( - 1)}^{{P_{qi}}}}\vert {XS_q}{ \rangle _{XS}}\vert 0{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(6)

Here, the Z errors of the data qubits are corrected according to the $\vert XS_q\rangle _{XS}$ syndrome, and all $(-1)^{P_{qi}}$ values become +1. The final $\vert 0\rangle _{L}$ initialization state is described as (7). The X stabilizers are deleted when the initialization is completed because they are no longer needed. Also, for convenience of notation, i is changed to start from 1 instead of 0. From (7), it can be seen that the $\vert 0\rangle _{L}$ logical qubit is expressed as the entanglement of $2^{nx}$ state vectors of the data qubits representing $\vert 0\rangle _{L}$ and the probability amplitude of each state vector is equal to $1/\sqrt{m}$. Also, the $\vert 0\rangle _{L}$ initialization depends on nx, the number of X stabilizers.

$$\begin{aligned} \begin{aligned} \vert 0{ \rangle _L} = \frac{1}{{{{\sqrt{2} }^{nx}}}}\sum \limits _{i = 0}^{{2^{nx}} - 1} {\vert 0{ \rangle _{L\_i}}} = \frac{1}{{{{\sqrt{2} }^{nx}}}}\sum \limits _{i = 1}^{{2^{nx}}} {\vert 0{ \rangle _{L\_i}}} = \frac{1}{{\sqrt{m} }}\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} \,\,\,(m = {2^{nx}}) \end{aligned} \end{aligned}$$

(7)

From now on, we can use (7) to obtain the state of the $\vert 0\rangle _{L}$ logical qubit by a simple calculation instead of the complex ESM. The logical qubit initialization using the quantum simulators requires $nx \times (4 \, CNOTs + 2 \, H gates) + nz \times 4 \, CNOTs$ quantum operations, to calculate the entangled states of the data qubits constituting a logical qubit. It has the complexity of O($d^2$) (=O$(dx \times dz)$). The distances dx and dz are unified by d to simplify the complexity expression.

In LQBM, the $\vert 0\rangle _{L}$ initialization consists of computing $m (=2^{(d^2-1)/2})$, $1 / \sqrt{m} \, (=pa)$, and $\vert 0\rangle _{L\_i}$ in (7). m and $1 / \sqrt{m}$ are derived by computing the power of two. Since the complexity of computing $2^n$ is O$(log \; n)$, the computation of m has O$(log \; d)$ complexity. $1 / \sqrt{m}$ also has O$(log \; d)$ complexity. Instead of computing the entangled state vectors of the data qubits, which increases complexity, LQBM abstracts the state vectors as logical values, such as $\vert 0\rangle _{L\_i}$. The logical values of all $\vert 0\rangle _{L\_i}$ are equal to each other. Therefore, LQBM does not need to maintain the logical values of all $\vert 0\rangle _{L\_i}$, but only one logical value. And it manages m, the number of state vectors, together. Thus, the superposition in (7) does not affect the complexity of LQBM, and we can see that the complexity of LQBM is O($log \; d$). In addition, it is easy to find the $\vert 0\rangle _{L}$ initialization state of the logical qubit with a high distance, which is impossible in conventional simulators.

4.2 State injection

The state injection sets a logical qubit to an arbitrary quantum state of $\vert \psi \rangle _{L} = \alpha \vert 0\rangle _{L} + \beta \vert 1\rangle _{L}$. The $\vert 1\rangle _{L}$ state representation of the logical qubit can be derived by performing a logical X operation on the $\vert 0\rangle _{L}$ logical qubit, as shown in (8). The quantum state of the logical qubit after the state injection is described as (9). c and d correspond to pa0 and pa1 in (1).

A logical qubit is described as an entanglement of 2m state vectors. Of the 2m state vectors, m state vectors are for $\vert 0\rangle _{L\_i}$, and the other m state vectors are for $\vert 1\rangle _{L\_i}$. The probability amplitudes for $\vert 0\rangle _{L\_i}$ are all $\alpha / \sqrt{m}$. If those m probability amplitudes are gathered, they behave like the logical probability amplitude for $\vert 0\rangle _{L}$. This is the same for $\vert 1\rangle _{L}$. Using (9), $\vert +\rangle _{L}$ initialization state is also expressed as (10).

$$\begin{aligned}{} & {} \begin{aligned} \vert 1{ \rangle _L} = X(\vert 0{ \rangle _L}) = \frac{1}{{\sqrt{m} }}\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} \begin{aligned} \vert \psi { \rangle _L}&= \alpha \vert 0{ \rangle _L} + \beta \vert 1{ \rangle _L} = \frac{\alpha }{{\sqrt{m} }}\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + \frac{\beta }{{\sqrt{m}}}\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}}&\\&= c\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + d\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}}&\\&\quad \left( \frac{\alpha }{{\sqrt{m} }} = c, \frac{\beta }{{\sqrt{m}}} = d, ({c^2} + {d^2}) \times m = {\alpha ^2} + {\beta ^2} = 1\right)&\end{aligned} \end{aligned}$$

(9)

$$\begin{aligned}{} & {} \begin{aligned} \,\vert + { \rangle _L} = \frac{1}{{\sqrt{2} }}\vert 0{ \rangle _L} + \frac{1}{{\sqrt{2}}}\vert 1{ \rangle _L} = \frac{1}{{\sqrt{2m} }}\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + \frac{1}{{\sqrt{2m}}}\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(10)

5 Operators for single logical qubit

The quantum operations for the single logical qubit are X, Z, and H. Based on the lattice surgery, since S and T use an ancilla qubit, they are not included in this section.

After applying logical X or Z operation, the state of the logical qubit is expressed as (11). Multiple logical X operators can be defined for the single logical qubit and have the same result. Any valid logical X operator changes $\vert 0\rangle _{L}$ to $\vert 1\rangle _{L}$ and $\vert 1\rangle _{L}$ to $\vert 0\rangle _{L}$. Multiple logical Z operators are also defined, and a phase of $\vert 1\rangle _{L}$ changes from $+$ to − and − to $+$. The logical X and Z operators do not change the number of state vectors of data qubits.

A logical H operator is as shown in (12). The logical H operator is achieved by performing transversal H gates on all data qubits constituting a logical qubit, and it changes $\vert 0\rangle _{L}$ to $\vert +\rangle _{L}$ and $\vert 1\rangle _{L}$ to $\vert -\rangle _{L}$.

$$\begin{aligned}{} & {} \begin{aligned} X(\vert \psi {\rangle _L}) = d\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + c\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} \\ Z(\vert \psi {\rangle _L}) = c\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} - d\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \begin{aligned} H(\vert \psi { \rangle _L})&= c\sum \limits _{i = 1}^m {\vert + { \rangle _{L\_i}}} + d\sum \limits _{i = 1}^m {\vert - { \rangle _{L\_i}}}&\\&= \frac{{(c + d)}}{{\sqrt{2} }}\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + \frac{{(c - d)}}{{\sqrt{2}}}\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}}&\end{aligned} \end{aligned}$$

(12)

6 Operators using lattice surgery

6.1 Logical tensor product

Before expressing logical operators using the lattice surgery, let’s first look at how to describe a tensor product of logical qubits. Suppose that there are N logical qubits $\vert \psi _1\rangle _{L}, \ldots \,, \vert \psi _N\rangle _{L}$. The logical tensor product is expressed as (13) using $2^N$ logical state vectors. $C_i$ represents a complex number.Each logical state vector from $\vert 0_1 0_2 \ldots 0_N\rangle _{L}$ to $\vert 1_1 1_2 \ldots 1_N\rangle _{L}$ is expressed as shown in (14), and $\vert S_j\rangle _{L_\_i}$ is a combination of the physical data qubits as described in (1). This indicates that $\vert S_1 S_2 \ldots S_N\rangle _{L}$ equals the tensor product of the state vectors of the physical data qubits constituting $\vert S_i\rangle _{L}$. So, $\vert S_1 S_2 \ldots S_N\rangle _{L}$ has $m_{tp}$ physical state vectors corresponding to the product of $m_1$ to $m_N$. Also, the probability amplitude (=$1/\sqrt{m_{tp}}$ ) is defined as the product of $1 / \sqrt{m_1}$ to $1 / \sqrt{m_N}$.

$$\begin{aligned}{} & {} \begin{aligned} \vert {\psi _1}\,{\psi _2}\,\ldots \,\,{\psi _N}{ \rangle _L} = {C_1}\,\vert {0_1}{0_2}\ldots {0_N}{ \rangle _L} + {C_2}\,\vert {0_1}{0_2}..\,{.1_N}{ \rangle _L} + \,\,\ldots \,\, \\ + {C_{{2^N}}}\,\vert {1_1}{1_2}\ldots {1_N}{ \rangle _L} \end{aligned} \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \begin{aligned} \vert {S_1}\,{S_2}\ldots {S_N}{ \rangle _L}\,\,\,&= \frac{1}{{\sqrt{{m_1}} }}\sum \limits _{i = 1}^{{m_{1\,}}} {\vert {S_1}{ \rangle _{L\_i}}} \,\, \otimes \cdots \,\, \otimes \,\frac{1}{{\sqrt{{m_N}} }}\sum \limits _{i = 1}^{{m_N}} {\vert {S_N}{ \rangle _{L\_i}}}&\\&= \frac{1}{{\sqrt{{m_{tp}}} }}\,\sum \limits _{i = 1}^{{m_{tp}}} {\vert {S_1}\,{S_2} \ldots {S_N}{ \rangle _{L\_i}}}&\\&({S_j} \in \{ 0,1\}, {m_{tp}} = \prod \limits _{j = 1}^N {{m_j}} )&\end{aligned} \end{aligned}$$

(14)

Therefore, it can be seen that the tensor product of the N logical qubits is the same as the tensor product of the physical state vectors constituting each logical qubit, as shown in (15)

$$\begin{aligned} \begin{aligned} \vert {\psi _1}\,{\psi _2}\,\ldots \,\,{\psi _N}{ \rangle _L} = \frac{{{C_1}}}{{\sqrt{{m_{tp}}} }}\,\sum \limits _{i = 1}^{{m_{tp}}} {\vert 00\ldots 0{ \rangle _{L\_i}}} + \frac{{{C_2}}}{{\sqrt{{m_{tp}}} }}\,\sum \limits _{i = 1}^{{m_{tp}}} {\vert 00\ldots 1{ \rangle _{L\_i}}}\\ + \,\,\ldots \,\, + \frac{{{C_{{2^N}}}}}{{\sqrt{{m_{tp}}} }}\,\sum \limits _{i = 1}^{{m_{tp}}} {\vert 11\ldots 1{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(15)

6.2 Merge and split

Logical qubit operations for two logical qubits in the rotated surface code are performed using the lattice surgery technique. The most basic lattice surgery operations are a merge and a split. The merge is the method of merging two logical qubits facing the same boundary into one logical qubit, and there are X and Z merges according to a boundary type. The split is to divide one logical qubit into two logical qubits. There are also X and Z boundary splits. Figure 3 is the diagram explaining the merge and the split.

Fig. 3

a the Z boundary merge is the method of merging two logical qubits facing the Z boundary into one logical qubit. New X stabilizers are added to the merged Z boundary, and the product of the measurements of the new X stabilizers is used as the M value for the Z boundary merge. The Z boundary split is to split one merged logical qubit into two logical qubits based on the Z boundary. When the Z boundary split is performed, the new X stabilizers added at the time of merging disappear. b the X boundary merge/split performs the merge and split based on the X boundary. The merge adds new Z stabilizers, and the split removes the new Z stabilizers. The product of the measurements of the new Z stabilizers is used as the M value for the X boundary merge

For the Z boundary merge, the number of data qubits in the Z boundary must be the same ($dz=dz'$). The Z boundary merge of two logical qubits $\vert \psi \rangle _{L}$ and $\vert \psi '\rangle _{L}$ is expressed as (16) [16].

$$\begin{aligned} \begin{aligned} \vert \psi { \rangle _L} = \,\alpha \vert 0{ \rangle _L} + \beta \vert 1{ \rangle _L}\,\,\,(dx,\,\,dz), \vert \psi '{ \rangle _L} = \,\alpha '\vert 0{ \rangle _L} + \beta '\vert 1{ \rangle _L}\,\,\,(dx',\,\,dz')\\ ZMerge(\vert \psi { \rangle _L},\,\,\vert \psi '{ \rangle _L}) = \frac{1}{{\sqrt{2} }}((\alpha \alpha ' + {( - 1)^M}\beta \beta ')(\vert 00{ \rangle _L} + {( - 1)^M}\vert 11{ \rangle _L}) \\ + (\alpha \beta ' + {( - 1)^M}\beta \alpha ')(\vert 01{ \rangle _L} + {( - 1)^M}\vert 10{ \rangle _L})) \end{aligned} \end{aligned}$$

(16)

The state of a merged logical qubit is an entanglement of two logical qubits. $\vert 00\rangle _{L} + (-1)^M \vert 11\rangle _{L}$ and $\vert 01\rangle _{L} + (-1)^M \vert 10\rangle _{L}$ are interpreted as $\vert 0\rangle _{L}$ and $\vert 1\rangle _{L}$, respectively, in terms of the merged logical qubit. One logical qubit has one probability amplitude value for $\vert 0\rangle _{L}$ and $\vert 1\rangle _{L}$, respectively. The merged logical qubit follows this rule when $M=0$. However, two probability amplitudes for $\vert 00\rangle _{L}$ and $\vert 11\rangle _{L}$ have opposite phases in terms of the merged logical state $\vert 0\rangle _{L}$, when $M=1$. The two probability amplitudes for $\vert 01\rangle _{L}$ and $\vert 10\rangle _{L}$ also have opposite phases in the merged logical state $\vert 1\rangle _{L}$. Therefore, one merged logical qubit with $M=1$ has four probability amplitudes for $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$, which are based on two logical qubits before merging. Because LQBM uses the state vectors and their probability amplitudes, we determine to express the state of the merged logical qubit based on $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$. Suppose you want to express the Z boundary merge in terms of the merged logical qubit, adding the value of M together like $\vert 0\rangle _L^M = \vert 00\rangle _{L} + (-1)^M \vert 11\rangle _{L}$ and $\vert 1\rangle _L^M = \vert 01\rangle _{L} + (-1)^M \vert 10\rangle _{L}$ is necessary. Also, a complex model that considers the opposite phase is required for logical operations.

If we calculate the sum of the squares of the probability amplitudes of the merged logical qubit in (16), it is seen that the sum is not always 1. Therefore, normalization must be performed so that the sum of the squares of the probability amplitudes becomes 1. After that, the merge operation can be applied to LQBM. The normalization operation is performed by dividing each probability amplitude in (16) by the sum of the squares of the probability amplitudes as in (17).

$$\begin{aligned} \begin{aligned}&ZMerge(\vert \psi { \rangle _L},\,\,\vert \psi '{ \rangle _L})&\\&\quad = \frac{1}{{\sqrt{2K} }}(A(\vert 00{ \rangle _L} + {( - 1)^M}\vert 11{ \rangle _L}) + B(\vert 01{ \rangle _L} + {( - 1)^M}\vert 10{ \rangle _L}))&\\&(\,A = \alpha \alpha ' + {( - 1)^M}\beta \beta ',\,\,\,\,B = \alpha \beta ' + {( - 1)^M}\beta \alpha ',&\\&K = 2{\left| {\frac{A}{{\sqrt{2} }}} \right| ^2} + 2{\left| {\frac{B}{{\sqrt{2} }}} \right| ^2} = \vert {A\vert ^2} + \vert {B\vert ^2}\,\,)&\end{aligned} \end{aligned}$$

(17)

The number of X stabilizers in the merged logical qubit is $nx+nx'+(dz+1)/2$. The number of X stabilizers added to the facing Z boundary is $(dz+1)/2$. Therefore, the number of state vectors for $\vert 0\rangle _{L}$ or $\vert 1\rangle _{L}$ in the merged logical qubit becomes (18). The merged logical state $\vert 0\rangle _{L}$ is expressed as a combination of $\vert 00\rangle _{L}$ and $\vert 11\rangle _{L}$, and $\vert 1\rangle _{L}$ is described as a combination of $\vert 01\rangle _{L}$ and $\vert 10\rangle _{L}$. Thus, each of $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$ has the number of state vectors shown in (19).

$$\begin{aligned}{} & {} m \times m' \times {2^{\frac{{dz + 1}}{2}}}( = {2^{(nx + nx' + \frac{{dz + 1}}{2})}}) \end{aligned}$$

(18)

$$\begin{aligned}{} & {} (m \times m' \times {2^{\frac{{dz + 1}}{2}}}) \div 2 = m \times m' \times r\,\,\,(r = {2^{\frac{{dz - 1}}{2}}}) \end{aligned}$$

(19)

We describe the output state of the Z boundary merge as (20) by reflecting the number of state vectors.

$$\begin{aligned} \begin{aligned} \frac{1}{{\sqrt{2Krmm'} }}(A(\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} + {( - 1)^M}\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} )\\ +\quad B(\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}} + {( - 1)^M}\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}})) \end{aligned} \end{aligned}$$

(20)

If A, B, and K are changed to $A_L$, $B_L$, and $K_L$ using c, d, and m of (9), the final Z boundary merge is described as shown in (21).

$$\begin{aligned} \begin{aligned}&\frac{1}{{\sqrt{2{K_L}rmm'} }}({A_L}\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} \,\, + \,\,\,{B_L}\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}}&\\&\qquad \qquad + {B_L}{( - 1)^M}\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}} + {A_L}{( - 1)^M}\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} )&\\&({A_L} = cc' + {( - 1)^M}dd' = A/\sqrt{m \times m'}&\\&{B_L} = cd' + {( - 1)^M}dc' = B/\sqrt{m \times m'}&\\&\qquad {K_L} = \vert {A_L}{\vert ^2} + \vert {B_L}{\vert ^2} = K/mm')&\end{aligned} \end{aligned}$$

(21)

In addition, the Z boundary merge is expressed as (22) using the tensor product of two logical qubits as an input. This will be used when defining an operation matrix in Sect. 7.

$$\begin{aligned} \begin{aligned}&ZMerge({C_1}\sum \limits _{i = 1}^{mm'} {\vert 00{ \rangle _{L\_i}}} + \,{C_2}\sum \limits _{i = 1}^{mm'} {\vert 01{ \rangle _{L\_i}}} + {C_3}\sum \limits _{i = 1}^{mm'} {\vert 10{ \rangle _{L\_i}}} + {C_4}\sum \limits _{i = 1}^{mm'} {\vert 11{ \rangle _{L\_i}}} )&\\&\quad = \frac{1}{{\sqrt{2{K_L}rmm'} }}(({C_1} + {( - 1)^M}{C_4})\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} \\ {}&\quad + \,\,({C_2} + {( - 1)^M}{C_3})\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}}&\\&\quad +{( - 1)^M}({C_2} + {( - 1)^M}{C_3})\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}} + {( - 1)^M}({C_1} + {( - 1)^M}{C_4})\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} )&\\&({K_L} = \vert {C_1} + {( - 1)^M}{C_4}{\vert ^2} + \vert {C_2} + {( - 1)^M}{C_3}{\vert ^2})&\end{aligned} \end{aligned}$$

(22)

The Z boundary split is to split one merged logical qubit into two logical qubits based on the Z boundary. The Z boundary split is expressed as $ZSplit(\alpha \vert 0\rangle _{L}+\beta \vert 1\rangle _{L})=\alpha \vert ++\rangle _{L}+\beta \vert --\rangle _{L}$ based on an X basis. Since the expression of LQBM is based on a Z basis, the expression of the Z boundary split is converted to the Z basis as shown in (23). The probability amplitudes for $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$ of the merged result in (21) are expressed briefly using $C_1$, $C_2$, $C_3$, and $C_4$, and they are used as inputs for the X boundary split. When the Z boundary split is performed, the X stabilizers added at the time of merging disappear, and the number of state vectors for $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$ is reduced from $r \times m \times m'$ to $m \times m'$. The ratio of the probability amplitudes is maintained as it is.

$$\begin{aligned} \begin{aligned}&ZSplit\big ({C_1}\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} + \,{C_2}\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}} + {C_3}\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}} + {C_4}\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} \big )\\&\quad = \sqrt{r} \big ({C_1}\sum \limits _{i = 1}^{mm'} {\vert 00{ \rangle _{L\_i}}} + \,{C_2}\sum \limits _{i = 1}^{mm'} {\vert 01{ \rangle _{L\_i}}} + {C_3}\sum \limits _{i = 1}^{mm'} {\vert 10{ \rangle _{L\_i}}} + {C_4}\sum \limits _{i = 1}^{mm'} {\vert 11{ \rangle _{L\_i}}}\big ) \end{aligned}\nonumber \\ \end{aligned}$$

(23)

The X boundary merge and split can also be derived through a process similar to the Z boundary merge and split. For the X boundary merge, the number of data qubits in the X boundary must be the same ($dx=dx'$). The result of the X boundary merge is as (24). The X boundary merge is performed using the X basis, so the logical qubit expressed as the Z basis is converted to the X basis, merged, and then transformed back to the Z basis for LQBM. The difference between the X and Z boundary merge is that in the X boundary merge, overlapping X stabilizers at the facing X boundary of two logical qubits are deleted. It means that r is less than 1. Therefore, after the completion of the X boundary merge, the number of state vectors of the merged logical qubits is less than the tensor product of two logical qubits before the merge.

$$\begin{aligned} \begin{aligned}&M = 0{{: }}\sqrt{\frac{2}{{{K_L}rmm'}}} (cc'\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} + \,\,\,dd'\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} ) (r = {2^{\frac{{ - dx - 1}}{2}}})\\&M = 1{{: }}\sqrt{\frac{2}{{{K_L}rmm'}}} (cd'\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}} + \,\,\,dc'\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}} )\\&({A_L} = \frac{{(c + d)}}{{\sqrt{2} }}\frac{{(c' + d')}}{{\sqrt{2} }} + {( - 1)^M}\frac{{(c - d)}}{{\sqrt{2} }}\frac{{(c' - d')}}{{\sqrt{2} }}\\&{B_L} = \frac{{(c + d)}}{{\sqrt{2} }}\frac{{(c' - d')}}{{\sqrt{2} }} + {( - 1)^M}\frac{{(c - d)}}{{\sqrt{2} }}\frac{{(c' + d')}}{{\sqrt{2} }}\\&{K_L} = \vert {A_L}{\vert ^2} + \vert {B_L}{\vert ^2}) \end{aligned} \end{aligned}$$

(24)

The X boundary merge is also expressed as (25) using the tensor product state of two logical qubits as an input. This will be used when defining an operation matrix in Sect. 7.

$$\begin{aligned} \begin{aligned} \begin{array}{l} XMerge({C_1}\sum \limits _{i = 1}^{mm'} {\vert 00{ \rangle _{L\_i}}} + \,{C_2}\sum \limits _{i = 1}^{mm'} {\vert 01{ \rangle _{L\_i}}} + {C_3}\sum \limits _{i = 1}^{mm'} {\vert 10{ \rangle _{L\_i}}} + {C_4}\sum \limits _{i = 1}^{mm'} {\vert 11{ \rangle _{L\_i}}} )\\ = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} if M = 0:\sqrt{\frac{2}{{{K_L}rmm'}}} ({C_1}\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} \, + {C_4}\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} ){{ }}\\ \qquad ({K_L} = \vert {C_1} + {C_4}{\vert ^2} + \vert {C_1} - {C_4}{\vert ^2}) \end{array}\\ \begin{array}{l} if M = 1:\sqrt{\frac{2}{{{K_L}rmm'}}} ({C_2}\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}} \,\, + {C_3}\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}}} )\\ \qquad ({K_L} = \vert {C_2} + {C_3}{\vert ^2} + \vert - {C_2} + {C_3}{\vert ^2}) \end{array} \end{array}} \right. \end{array} \end{aligned} \end{aligned}$$

(25)

The X boundary split divides one merged logical qubit into two logical qubits based on the X boundary. The X boundary split is expressed using the Z basis as (26). Like the Z boundary split, the input probability amplitudes of the X boundary split are also described as $C_1$, $C_2$, $C_3$, and $C_4$. When the X boundary split is performed, the X stabilizers that were deleted at the time of merging are added again, and the number of state vectors representing $\vert 00\rangle _{L}$, $\vert 01\rangle _{L}$, $\vert 10\rangle _{L}$, and $\vert 11\rangle _{L}$ changes from $r \times m \times m'$ to $m \times m'$. Since r is less than 1, the X boundary split increases the number of state vectors.

$$\begin{aligned} \begin{aligned} \begin{array}{l} M = 0:XSplit({C_1}\sum \limits _{i = 1}^{rmm'} {\vert 00{ \rangle _{L\_i}}} + \,\,\,{C_4}\sum \limits _{i = 1}^{rmm'} {\vert 11{ \rangle _{L\_i}}} )\,\,\\ \qquad \qquad = \sqrt{r} ({C_1}\sum \limits _{i = 1}^{mm'} {\vert 00{ \rangle _{Li}}} + {C_4}\sum \limits _{i = 1}^{mm'} {\vert 11{ \rangle _{Li}}} )\,\\ M = 1:XSplit({C_2}\sum \limits _{i = 1}^{rmm'} {\vert 01{ \rangle _{L\_i}}} + \,\,\,{C_3}\sum \limits _{i = 1}^{rmm'} {\vert 10{ \rangle _{L\_i}})} \\ \qquad \qquad = \sqrt{r} ({C_2}\sum \limits _{i = 1}^{mm'} {\vert 01{ \rangle _{Li}}} + {C_3}\sum \limits _{i = 1}^{mm'} {\vert 10{ \rangle _{Li}}} )\, \end{array} \end{aligned} \end{aligned}$$

(26)

6.3 CNOT, S, and T operator

In the rotated surface code, CNOT, S, and T operators are decomposed into the merge and split operators based on the lattice surgery as shown in Fig. 4 [16, 18, 28, 29]. LQBM also implements these operators as a combination of the merge and the split. For the convenience of understanding, this chapter summarizes only the final execution results, not the intermediate process, of the CNOT, S, and T operators, as shown in (27, 28).

Fig. 4

a–c show circuits that perform logical CNOT, S, and T gates based on the lattice surgery. Mxx means that the Z boundary merge and split are continuously performed, and Mzz is the sequence of the X boundary merge and split. The M value is obtained by performing Mxx and Mzz. The Mxx, Mzz, and Mx measurements determine a, b, and c. In addition to the control qubit $\vert C \rangle$ and target qubit $\vert T \rangle$, CNOT requires an ancilla qubit $\vert 0 \rangle$. The S and T gates require magic states $\vert Y \rangle$ and $\vert A \rangle$, respectively

After executing CNOT with $\vert \psi \rangle _{L}$ as a control and $\vert \psi '\rangle _{L}$ as a target, the result is shown in (27).

$$\begin{aligned} \begin{aligned} cc'\sum \limits _{i=1}^{mm'} {\vert 00{ \rangle _{L\_i}}} + cd'\sum \limits _{i=1}^{mm'} {\vert 01{ \rangle _{L\_i}}} + dd'\sum \limits _{i=1}^{mm'} {\vert 10{ \rangle _{L\_i}}} + dc\sum \limits _{i=1}^{mm'} {\vert 11{ \rangle _{L\_i}}} \end{aligned} \end{aligned}$$

(27)

The final execution results of the S and T operations are in (28). The S and T operators for the logical qubit are implemented using the X boundary merge and split. When an Mzz measurement is $-1$, a global phase is added and expressed as $e^{i\theta }$ in (28). The exact value of $\theta$ is determined based on the combination of the Mzz measurement, an ancilla’s Mx measurement, and an execution result of an additional S gate. $\theta$ values for S gate are 0, $\pi /2$, and $3\pi /2$, and $\theta$ values for T gate are 0, $\pi /4$, $3\pi /4$, $5\pi /4$, and $7\pi /4$.

$$\begin{aligned} \begin{aligned} \begin{array}{l} S(\vert \psi { \rangle _L}) = {e^{i\theta }}(c\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + di\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} )\\ T(\vert \psi { \rangle _L}) = {e^{i\theta }}(c\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + d{e^{i\pi /4}}\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} ) \end{array} \end{aligned} \end{aligned}$$

(28)

7 Operation matrix

This section defines operation matrices for the logical operations described in Sects. 4 to 6. The operation matrices will help improve our understanding of LQBM as matrices for physical qubit operations have been useful. In addition, these matrices are expected to be helpful when performing logical qubit operations or simulations based on LQBM. For the operation matrices, the number m of state vectors constituting logical qubits is added to the upper right of the state vector, as shown in (29). The number m of state vectors in N logical qubits is equal to $m_{tp}$ defined in (15).

$$\begin{aligned} \begin{aligned} \begin{array}{l} Single \, logical \, qubit: \vert \psi { \rangle _L} = c\sum \limits _{i = 1}^m {\vert 0{ \rangle _{L\_i}}} + d\sum \limits _{i = 1}^m {\vert 1{ \rangle _{L\_i}}} = \left( {\begin{array}{*{20}{c}} c\\ d \end{array}} \right) _L^m\\ N \, logical \, qubits:\\ \vert {\psi _1} \cdots {\psi _N}{ \rangle _L} = {C_1}\sum \limits _{i = 1}^m {\vert 0 \cdots 0{ \rangle _{L\_i}}} + \cdots + {C_{2^N}}\sum \limits _{i = 1}^m {\vert 1 \cdots 1{ \rangle _{L\_i}}} = \left( {\begin{array}{*{20}{c}} {{C_1}}\\ \vdots \\ {{C_{2^N}}} \end{array}} \right) _L^m\\ \qquad \qquad \qquad \qquad \left( \sum \limits _{i = 1}^{2^N} {\vert {C_i}{\vert ^2}} \times m = 1\right) \end{array} \end{aligned} \end{aligned}$$

(29)

The operation matrix for a logical qubit is similar to the operation matrix for a physical qubit, and w is added for the matrix, as shown in (30). w specifies the multiplier of increasing the number of state vectors after completing a logical qubit operation. w actually has meaning in the initialization, the state injection, the merge, and the split, and is always 1 in other operations. When a logical qubit operation is executed on a logical qubit composed of m state vectors, the result of the operation has $w \times m$ state vectors. $CR_1$ to $CR_n$ is the probability amplitudes of the output derived from the logical qubit operation.

$$\begin{aligned} \begin{aligned} {\left( {\begin{array}{*{20}{c}} {{S_{11}}}&{} \cdots &{}{{S_{1n}}}\\ \vdots &{} \ddots &{} \vdots \\ {{S_{n1}}}&{} \cdots &{}{{S_{nn}}} \end{array}} \right) ^w}\left( {\begin{array}{*{20}{c}} {{C_1}}\\ \vdots \\ {{C_n}} \end{array}} \right) _L^m = \left( {\begin{array}{*{20}{c}} {C{R_1}}\\ \vdots \\ {C{R_n}} \end{array}} \right) _L^{w \times m} \end{aligned} \end{aligned}$$

(30)

LQBM defines the operation matrix and usage for the initialization and the state injection as (31). Since the state representation of the initialization is a subset of the state representation of the state injection, the state injection and the initialization use the same operation matrix. An input vector of the state injection is expressed as $\alpha$ and $\beta$ of the desired qubit state to be injected, and it has only one state vector. The w value of the operation matrix for the state injection becomes m dependent on the distance d. Therefore, the input vector with one state vector has m state vectors after the state injection, and the probability amplitudes become $\alpha / \sqrt{m}$ and $\beta / \sqrt{m}$. The initializations for $\vert 0\rangle _{L}$ and $\vert +\rangle _{L}$ are performed by specifying $\alpha$ and $\beta$ for $\vert 0\rangle$ and $\vert 1\rangle$, respectively.

$$\begin{aligned} \begin{aligned} \frac{1}{{\sqrt{m} }}{\left( {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right) ^m}\left( {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right) _L^1 = \frac{1}{{\sqrt{m}}}\left( {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right) _L^m \end{aligned} \end{aligned}$$

(31)

The operation matrices for the X, Z, and H operators are presented in (32). The X operator part contains an example of using these operators. The X, Z, and H operations have the advantage of utilizing the existing operation matrix for the physical qubits as they are. w of the operations is set to 1. The matrices for the final outputs of CNOT, S, and T are also defined similarly.

$$\begin{aligned} \begin{aligned}&X: {\left( {\begin{array}{*{20}{c}} 0&{}1\\ 1&{}0 \end{array}} \right) ^1}\left( {\begin{array}{*{20}{c}} {{C_1}}\\ {{C_2}} \end{array}} \right) _L^m = \left( {\begin{array}{*{20}{c}} {{C_2}}\\ {{C_1}} \end{array}} \right) _L^m \qquad Z = {\left( {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}{ - 1} \end{array}} \right) ^1} \qquad H = \frac{1}{{\sqrt{2} }}{\left( {\begin{array}{*{20}{c}} 1&{}1\\ 1&{}{ - 1} \end{array}} \right) ^1}&\\ \\&CNOT = {\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{array}} \right) ^1} \qquad S = {e^{i\theta }}{\left( {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}i \end{array}} \right) ^1}\qquad T = {e^{i\theta }}{\left( {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}{{e^{i\pi /4}}} \end{array}} \right) ^1}&\end{aligned} \end{aligned}$$

(32)

Based on (22), an operation matrix for the Z boundary merge and its usage is defined as (33). w for the matrix is r in (19). From (23), an operation matrix for the Z boundary split is defined as (34), and w for the matrix is 1/r.

$$\begin{aligned}{} & {} \begin{aligned}&\frac{1}{{\sqrt{2{K_L}rmm'} }}{\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad {{{( - 1)}^M}}\\ 0&{}\quad 1&{}\quad {{{( - 1)}^M}}&{}\quad 0\\ 0&{}\quad {{{( - 1)}^M}}&{}\quad 1&{}\quad 0\\ {{{( - 1)}^M}}&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right) ^r}\left( {\begin{array}{*{20}{c}} {{C_1}}\\ {{C_2}}\\ {{C_3}}\\ {{C_4}} \end{array}} \right) _L^{mm'}&\\&\quad = \frac{1}{{\sqrt{2{K_L}rmm'} }}\left( {\begin{array}{*{20}{c}} {{C_1} + {{( - 1)}^M}{C_4}}\\ {{C_2} + {{( - 1)}^M}{C_3}}\\ {{{( - 1)}^M}{C_2} + {C_3}}\\ {{{( - 1)}^M}{C_1} + {C_4}} \end{array}} \right) _L^{rmm'}&\end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \begin{aligned} \sqrt{r} {\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right) ^{\frac{1}{r}}}\left( {\begin{array}{*{20}{c}} {{C_1}}\\ {{C_2}}\\ {{C_3}}\\ {{C_4}} \end{array}} \right) _L^{rmm'} = \sqrt{r} \left( {\begin{array}{*{20}{c}} {{C_1}}\\ {{C_2}}\\ {{C_3}}\\ {{C_4}} \end{array}} \right) _L^{mm'} \end{aligned} \end{aligned}$$

(34)

A matrix for the X boundary merge is derived as (35) using (25), where w is r in (24).

$$\begin{aligned} \begin{aligned}&M = 0\,\,:\,\,\,\sqrt{\frac{2}{{{K_L}rmm'}}} {\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right) ^r}&\\ \\&M = 1\,\,:\,\,\,\sqrt{\frac{2}{{{K_L}rmm'}}} {\left( {\begin{array}{*{20}{c}} 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}} \right) ^r}&\end{aligned} \end{aligned}$$

(35)

The X boundary split based on (26) can utilize the same operation matrix as the Z boundary split. An input state of the X boundary split uses an output state of the X boundary merge. In the output state of the X boundary merge with $M=0$, $C_2$ and $C_3$ are 0. In the output state of the X boundary merge with $M=1$, $C_1$ and $C_4$ are 0. Utilizing this, the X boundary split can use the same matrix as the Z boundary split, as shown in (36).

$$\begin{aligned} \begin{aligned} M = 0:\sqrt{r} {\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right) ^{\frac{1}{r}}}\left( {\begin{array}{*{20}{c}} {{C_1}}\\ 0\\ 0\\ {{C_4}} \end{array}} \right) _L^{rmm'} = \sqrt{r} \left( {\begin{array}{*{20}{c}} {{C_1}}\\ 0\\ 0\\ {{C_4}} \end{array}} \right) _L^{mm'}\\ \\ M = 1:\sqrt{r} {\left( {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right) ^{\frac{1}{r}}}\left( {\begin{array}{*{20}{c}} 0\\ {{C_2}}\\ {{C_3}}\\ 0 \end{array}} \right) _L^{rmm'} = \sqrt{r} \left( {\begin{array}{*{20}{c}} 0\\ {{C_2}}\\ {{C_3}}\\ 0 \end{array}} \right) _L^{mm'} \end{aligned} \end{aligned}$$

(36)

8 Experimental results

We wrote a simple simulator for LQBM by utilizing the GMP library supporting high-precision arithmetic calculation [36]. For comparison, we also implemented the logical qubit operations on the popular QuEST simulator [35]. Intel Xeon Gold 6132 CPU (2.6G) and 1TB memory were used for experiments. Both simulators did not use a GPU acceleration option. The experiments were performed using a single process and thread although the experimental environment supports the multicore environment.

8.1 $\vert 0\rangle _L$ initialization with various distances

Conventional quantum simulators cannot perform the $\vert 0\rangle _L$ initialization if the distance exceeds 5. However, this experiment shows that LQBM can initialize a logical qubit to $\vert 0\rangle _L$ state regardless of the distance size. Figure 5 and Table 1 show the change in the number of state vectors and the probability amplitude according to the distance when a logical qubit is initialized to $\vert 0\rangle _L$. This experiment was performed only on LQBM. In this experiment, dx and dz are set equal, and they are the same as the distance d of the logical qubit.

Figure 5a and Table 1 show the change in the number of state vectors constituting the $\vert 0\rangle _L$ state as the distance increases. The vertical axis is the value obtained by taking $log_{10}$ on the number of state vectors. The number m of state vectors is 2 to the power of $(d^2-1)/2$ according to (7). So as the distance d increases, the number m of state vectors increases exponentially. The logical qubit of distance 3 has $0.16 \times 10^2$ state vectors, and the logical qubit of distance 9999 has $0.3042 \times 10^{15048490}$ state vectors.

When $d = 3$, 17 physical qubits are required for one logical qubit, and $2^{17}$ state vectors are necessary to express the 17 physical qubits. However, after the $\vert 0\rangle _L$ initialization, only $0.16 \times 10^2$ of $2^{17}$ state vectors are valid to describe the $\vert 0\rangle _L$ state. In $d=203$, $0.2642 \times 10^{6203}$ of $2^{82417}$ state vectors are used for the $\vert 0\rangle _L$ state representation.

Fig. 5

a, b show the change in the number of state vectors and the probability amplitude according to a distance when a logical qubit is initialized to $\vert 0\rangle _L$. The vertical axes of (a) and (b) are the values obtained by taking $log_{10}$ on the number of state vectors and the probability amplitude of each state vector, respectively. As the distance d increases, the number m of state vectors increases exponentially, and the probability amplitude decreases exponentially

Table 1 The state of a logical qubit after $\vert 0\rangle _L$ initialization

Figure 5b shows the probability amplitude of each state vector as the distance increases. The vertical axis is the value obtained by taking $log_{10}$ on the probability amplitude of each state vector. The probability amplitude in the $\vert 0\rangle _L$ state is $1/\sqrt{m}$. As the distance of the logical qubit increases, the probability amplitude also decreases exponentially. The logical qubit of distance 3 has a probability amplitude of $0.25 \times 10^{0}$, and the logical qubit of distance 9999 has a probability amplitude of $0.1812 \times 10^{-7524244}$.

From the experiments of this section, it can be seen that LQBM can perform the $\vert 0\rangle _L$ initialization regardless of the distance size using the simple formula in (7).

8.2 Execution times of LQBM according to distance

The execution times of logical qubit operations were measured while increasing the distance from 3 to 33333 in LQBM. The time unit of the experiment is nanosecond. Table 2 shows that as the distance increases 11111 times from 3 to 33333, the execution time of each logical qubit operation increases from 1.00 to 3.89 times. The initialization and the state injection show a time increase of 3.89 and 2.14 times, respectively. This is because they perform power-of-two calculations with the O($log \; d$) complexity to compute m and pa. The values of m and pa computed in the initialization and the state injection are reused in subsequent logical qubit operations. The X, Z, and H operations have no complex computations, so there is little increase in the execution time. The merge and split operations perform mainly multiplicative computations based on m and pa derived from the initialization and the state injection, which show the 1.x time increase.

The execution time increases up to 3.89 times as the distance increases. However, it can be seen that the absolute execution time of the logical qubit operations is still fast within several thousand nanoseconds.

Table 2 Execution time of logical qubit operations according to distance in LQBM (time unit: ns)

8.3 Operators for single logical qubit

The execution times of the initialization, the state injection, and the logical X, Z, and H operations, which are performed on a single logical qubit, were measured. Since the QuEST simulator does not model qubit errors, the $\vert 0\rangle _L$ initialization was run in one round of ESM, not the d rounds. The ESM and error corrections were also not executed after the logical X, Z, and H operations. This experiment was performed on the logical qubit with distances of 3 and 5. The logical qubit with distance 5 requires 49 physical qubits, but QuEST cannot simulate 49 qubits. So, only 25 physical data qubits and one stabilizer qubit were used for QuEST. Using one stabilizer qubit, one X or Z stabilizer was generated and measured at a time, and this process was repeated for a total of 24 X/Z stabilizers. In Table 3, the time unit of the QuEST experiment result is second, and the time unit of LQBM is nanosecond. In QuEST, the state injection with $d=5$ consists of complex operations such as the state injection with $d=3$ and two additional ESMs, which increase the distance to 5. Therefore, this result was estimated by summing the three execution times, which are the state injection time (9.49 ns) with the distance 3 and two $\vert 0\rangle _L$ initialization (ESM) times (17.44 and 27.67 ns) with the distance 4 and 5. The execution time, 17.44 ns, of ESM with the distance 4 was approximated by interpolating the execution times, which are two $\vert 0\rangle _L$ initialization times (9.49 and 27.67 ns) with the distance 3 and 5.

According to Table 3 with the distance of 3 and 5, first, LQBM operates at least 0.61 million times faster than QuEST and up to 24.75 million times faster. The performance improvement of 24.75 million times is achieved in the $\vert 0\rangle _L$ initializationn with $d=5$. Second, as the distance increases, the improvement of LQBM over QuEST becomes greater. In the case of state injection, when the distance increases from 3 to 5, the improvement of LQBM increases from 4.03 to 20.24 million times.

Table 3 Execution time of operations for single logical qubit

8.4 Operations based on lattice surgery

The execution times of the merge and the split are shown in Table 4. Since it is impossible to perform the merge and split operations when $d=5$ in QuEST, the experiments for QuEST were performed only when $d=3$. Table 4 also shows that LQBM outperforms QuEST distinctly. The Z boundary split is performed 5.87 million times faster by LQBM than by QuEST.

Table 4 Execution time of merge and split

Table 5 shows the execution times for the logical CNOT, S, and T using the merge and the split, as shown in Fig. 4. The T operation shows two cases depending on whether an additional S operation is executed or not according to an Mzz value. The results of LQBM are derived from Table 4, not actual experiments. For example, the CNOT result of LQBM is the sum of the execution times of XMerge, XSplit, ZMerge and ZSplit. Table 5 indicates that LQBM offers approximately 3 to 4 million times higher performance than QuEST.

From the experimental results of Sect. 8, we can summarize three advantages of LQBM. First, LQBM can perform logical operations with high distances, which are impossible in conventional quantum simulators. Second, even though the distance increases 11111 times from 3 to 33333, the execution time of LQBM only increases by a maximum of 3.89 times. Third, LQBM is 0.61 to 24.75 million times faster than QuEST at distances of 3 and 5. In particular, the $\vert 0\rangle _L$ initialization of $d=5$ shows up to 24.75 million times faster performance.

Table 5 Execution time of CNOT, S, and T operation

9 Conclusions

We proposed LQBM that calculates the output state of a logical qubit after the logical qubit operation without performing a complex process of ESM. LQBM is the model working at the mixed level of the logical and physical qubit. At the physical qubit level, it can simply calculate the probability amplitudes and the number of state vectors of physical qubits constituting a logical qubit. At the logical qubit level, the state vector composed of the physical qubits is abstracted to the value of the logical level. These calculations are performed without the complex ESM operations. LQBM consists of the state representation of the logical qubits and the operations. The state representation of the logical qubits converts the initialization and state injection processes into simple arithmetic calculations. The logical qubit operation of LQBM can calculate the output states of the universal gates, the merge, and the split for the logical qubits.

In addition, the execution of the logical qubit operation using LQBM is more simplified by expressing all the logical qubit operations of LQBM in the form of the operation matrix. The ESM operation of the rotated surface code has the operation complexity of O($d^2$). However, LQBM provides the operation complexity of O($log \; d$), so it has high performance. Through the comparative experiments of LQBM and QuEST, we found three advantages of LQBM over QuEST. First, LQBM can simulate the surface code whose distance exceeds 5, which is impossible with conventional quantum simulators. Second, even though the distance increases 11111 times from 3 to 33333, the execution time of LQBM only increases by a maximum of 3.89 times. And the absolute execution time of LQBM is still fast within several thousand nanoseconds. Third, LQBM is 0.61 to 24.75 million times faster than QuEST at distances of 3 and 5. In particular, LQBM provided up to 24.75 million times faster performance in the $\vert 0\rangle _L$ initialization of $d=5$. In future works, we would like to develop a model that computes an exact combination of the physical qubits for the logical qubit instead of the value of the logical qubit level and add an error correction model.