Quantifying the information distribution of quantum information masking

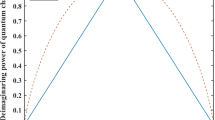
Abstract

Quantum information masking encodes an arbitrary quantum state into a multipartite system such that the original information of input states is completely unknown to local subsystems. In this work, we investigate the quantitative distribution of quantum information masking. We regard quantum information maskers as quantum broadcasting channels and propose the Holevo’s quantity as a measure of the information carried by local subsystems. Based on the theory of quantum channels, we first give necessary and sufficient conditions for the existence of perfect quantum information masking. Then, we investigate information recovery from the union of local subsystems. We find a close connection between quantum information masking and codes for quantum erasing channels, by which the no-masking theorem is rediscovered from the point of view of information transmission. Finally, we discuss the storage behavior of quantum information and propose that quantum information can reside in the correlations of subsystems in a redundant way. Our work deepens the understanding of the way that quantum information resides.

Appendices

Appendix A: Proof for the monotonicity of the Holevo’s quantity

Proof

Let us consider a quantum state of system Q denoted by $\rho ^{Q}=\sum _i p_i \rho _i^{Q}$ and quantum channel $\varepsilon : {\mathcal {B}}(\mathcal {H_Q})\rightarrow {\mathcal {B}}(\mathcal {H_{Q}})$ applied on $\rho ^Q$, that is,

$$\begin{aligned} \sigma ^{Q}\equiv \varepsilon (\rho ^{Q})= \sum _{k} E_k \rho ^{Q} E_k^{\dagger }, \end{aligned}$$

(A1)

where $E_{k}$ are Kraus operators of $\varepsilon$. Let us introduce an environment system labeled E. By Stinespring’s theorem [1, 2], the channel $\varepsilon$ can also be represented as

$$\begin{aligned} \varepsilon (\rho ^{Q})=Tr_E\left( U (\rho ^{Q} \otimes (\vert {0}\rangle \langle {0}\vert )^{E})U^{\dagger }\right) =Tr_E[\sum _{mn} E_m \rho ^Q E_n^{\dagger } \otimes (\vert {m}\rangle \langle {n}\vert )^E], \nonumber \\ \end{aligned}$$

(A2)

where $\{\vert {m}\rangle ^E\}$ forms a set of orthonormal bases of E. We also introduce a reference system labeled R and initialize the whole state as follows:

$$\begin{aligned} \rho ^{R Q E } = \sum _{i} p_i (\vert {i}\rangle \langle {i}\vert )^{R} \otimes \rho _i^{Q} \otimes (\vert {0}\rangle \langle {0}\vert )^{E}, \end{aligned}$$

(A3)

where $\{\vert {i}\rangle ^R\}$ forms a set of orthonormal bases of R. The superscript is omitted if there is no ambiguity. Applying U on systems Q and E, we obtain

$$\begin{aligned} \sigma ^{R Q E } = \sum _{imn}p_i \vert {i}\rangle \langle {i}\vert \otimes E_{m}\rho _i E_{n}^{\dagger }\otimes \vert {m}\rangle \langle {n}\vert . \end{aligned}$$

(A4)

By the monotonicity of quantum relative entropy [53, 54], the following inequality holds:

$$\begin{aligned} \begin{aligned} S(\sigma ^{R Q}\Vert \sigma ^{R}\otimes \sigma ^{Q}) =&S(id\otimes \varepsilon (\rho ^{R Q})\Vert id\otimes \varepsilon (\rho ^{R}\otimes \rho ^{Q})\\ \le&S(\rho ^{R Q}\Vert \rho ^{R}\otimes \rho ^{Q}), \end{aligned} \end{aligned}$$

(A5)

where $S(\rho \Vert \sigma )\equiv Tr (\rho \log (\rho -\sigma ))$ is the quantum relative entropy of $\rho$ and $\sigma$. Therefore,

$$\begin{aligned} \begin{aligned}&S(\sigma ^{R Q}\Vert \sigma ^{R}\otimes \sigma ^{Q})- S(\rho ^{R Q }\Vert \rho ^{R }\otimes \rho ^{ Q})\\ =&S(\rho ^{R Q})+S(\sigma ^{Q})-S(\sigma ^{R Q})-S(\rho ^{Q})\le 0. \end{aligned} \end{aligned}$$

(A6)

Since

$$\begin{aligned}&S(\rho ^{R Q})=H(p_i)+\sum _i p_i S(\rho _i), \end{aligned}$$

(A7)

$$\begin{aligned}&S(\sigma ^{Q})=S(\varepsilon (\rho )), \end{aligned}$$

(A8)

$$\begin{aligned}&S(\sigma ^{R Q})=H(p_i) + \sum _{i}p_i S(\varepsilon (\rho _i)), \end{aligned}$$

(A9)

$$\begin{aligned}&S(\rho ^{Q})=S(\rho ), \end{aligned}$$

(A10)

we obtain

$$\begin{aligned} S(\varepsilon (\rho ))- \sum _{i}p_i S(\varepsilon (\rho _i)) \le S(\rho )-\sum _i p_i S(\rho _i), \end{aligned}$$

(A11)

which is the monotonicity of the Holevo’s quantity. $\square$

We note that if $\rho = \sum _i p_i \vert {\psi _i}\rangle \langle {\psi _i}\vert$, then Eq. (A11) is simplified as

$$\begin{aligned} S(\varepsilon (\rho ))- \sum _{i}p_i S(\varepsilon (\vert {\psi _i}\rangle \langle {\psi _i}\vert )) \le S(\rho ). \end{aligned}$$

(A12)

Appendix B: Proof for Proposition 1

Proof

Sufficiency. Let us suppose the channel $\varepsilon$ is reversible on $\mathcal{Q}\mathcal{S}$; that is, there exists a reversal channel denoted by $\varepsilon ^{-1}$ such that for any $\rho _i$, the following equation holds:

$$\begin{aligned} \varepsilon ^{-1}\circ \varepsilon (\rho _i)=\rho _i. \end{aligned}$$

(B13)

By the monotonicity of the Holevo’s quantity, it holds that

$$\begin{aligned} \begin{aligned}&S(\sum _i p_i\rho _i)-\sum _i p_i S(\rho _i)\\ \ge&S(\varepsilon (\sum _i p_i\rho _i))-\sum _i p_i S(\varepsilon (\rho _i))\\ \ge&S(\varepsilon ^{-1}\circ \varepsilon (\sum _i p_i\rho _i))- \sum _i p_i S(\varepsilon ^{-1}\circ \varepsilon (\rho _i))\\ =&S(\sum _i p_i\rho _i)-\sum _i p_i S(\rho _i). \end{aligned} \end{aligned}$$

(B14)

Thus, we obtain $S(\varepsilon (\sum _i p_i\rho _i))-\sum _i p_i S(\varepsilon (\rho _i))=S(\sum _i p_i\rho _i)-\sum _i p_iS(\rho _i)$.

Necessity. We suppose Eq. (10) is true. Let us consider the following formula:

$$\begin{aligned} \begin{aligned} \Delta _i \equiv&S(\rho _i \Vert \rho _s) - S\left( \varepsilon (\rho _i) \Vert \varepsilon (\rho _s)\right) \\ =&S(\varepsilon (\rho _i))+\text {Tr} (\varepsilon (\rho _i)\log _2 \varepsilon (\rho _s))-S(\rho _i)-\text {Tr}(\rho _i\log _2 \rho _s)\\ \ge&0. \end{aligned} \end{aligned}$$

(B15)

For any $p_i>0$ and $\sum _i p_i =1$, we have

$$\begin{aligned} \begin{aligned}&\sum _i p_i \Delta _i \\&\quad =\sum _i p_i \left( S(\varepsilon (\rho _i))+\text {Tr}(\varepsilon (\rho _i)\log _2 \varepsilon (\rho _s))-S(\rho _i)-\text {Tr}(\rho _i\log _2 \rho _s)\right) \\&\quad = \sum _i p_i S(\varepsilon (\rho _i))+\text {Tr}(\sum _i \varepsilon (p_i\rho _i)\log _2 \varepsilon (\rho _s))-\sum _i p_i S(\rho _i)-\text {Tr}(\sum _i p_i\rho _i\log _2 \rho _s)\\&\quad = \sum _i p_i S(\varepsilon (\rho _i))-S(\varepsilon (\rho _s))-\sum _i p_iS(\rho _i)+S(\rho _s)\\&\quad = \chi (\mathcal{Q}\mathcal{S}, id)-\chi (\mathcal{Q}\mathcal{S},\varepsilon )\\&\quad = 0. \end{aligned} \nonumber \\ \end{aligned}$$

(B16)

This results in $\Delta _i =S(\rho _i \Vert \rho _s) - S(\varepsilon (\rho _i) \Vert \varepsilon (\rho _s))=0$ for all $\rho _i$. By the recoverability theorem [55, 56], there exists a perfect recovery channel $\varepsilon ^{-1}$ (depends on $\rho _s$ and $\varepsilon$) such that for any $\rho _i$,

$$\begin{aligned} \varepsilon ^{-1}\circ \varepsilon (\rho _i)=\rho _i. \end{aligned}$$

(B17)

$\square$

Appendix C: Proof for Proposition 2

Proof

For any mixed state $\rho$, there exists a set of orthonormal basis $\{\vert {e_i}\rangle \}$ such that

$$\begin{aligned} \rho =\sum _{i}\rho _{i}\vert {e_i}\rangle \langle {e_i}\vert . \end{aligned}$$

(C18)

Let us suppose $\varepsilon$ is a universal bleaching channel that transforms any pure input state $\vert {\psi _i}\rangle$ into a constant state $\sigma$, then we obtain

$$\begin{aligned} \varepsilon (\rho )=\varepsilon (\sum _{i}\rho _{i} \vert {e_i}\rangle \langle {e_i}\vert )=\sum _{i}\rho _{i}\varepsilon ( \vert {e_i}\rangle \langle {e_i}\vert )=\sigma , \end{aligned}$$

(C19)

that is to say, the channel $\varepsilon$ also transforms any mixed state into $\sigma$. The $\rho$ can also been represented by another set of orthonormal basis $\{\vert {f_i}\rangle \}$ as $\rho =\sum _{ij}\rho _{ij} \vert {f_i}\rangle \langle {f_j}\vert$. Therefore, we have

$$\begin{aligned} \begin{aligned} \sigma =&\, \varepsilon (\sum _{ij}\rho _{ij} \vert {f_i}\rangle \langle {f_j}\vert )\\ =&\, \sum _{i}\rho _{ii} \varepsilon (\vert {f_i}\rangle \langle {f_i}\vert )+\sum _{i\ne j}\rho _{ij}\varepsilon ( \vert {f_i}\rangle \langle {f_j}\vert )\\ =&\, \sigma +\sum _{i\ne j}\rho _{ij}\varepsilon ( \vert {f_i}\rangle \langle {f_j}\vert ). \end{aligned} \end{aligned}$$

(C20)

Thus, we obtain $\varepsilon ( \vert {f_i}\rangle \langle {f_j}\vert )=\delta _{ij}\sigma$, where $\delta _{ij}$ is the Kronecker delta. Here, $\{\vert {f_i}\rangle \}$ can be any orthogonal basis.

Let $\vert {\Psi }\rangle ^{RQ}$ be an arbitrary pure state of systems R and Q described by

$$\begin{aligned} \vert {\Psi }\rangle ^{RQ} = \sum _i \sqrt{p_i}\vert {\psi _i}\rangle ^R\vert {i}\rangle ^Q, \end{aligned}$$

(C21)

where $\{\vert {i}\rangle ^Q\}$ is the set of orthonormal basis of system Q. Applying the channel $\varepsilon$ to the system Q, we obtain

$$\begin{aligned} \begin{aligned} \sigma ^{RQ'}=&\, id \otimes \varepsilon ((\vert {\Psi }\rangle \langle {\Psi }\vert )^{RQ})\\ =&\, \sum _{ij} \sqrt{p_i p_j}(\vert {\psi _i}\rangle \langle {\psi _j}\vert )^R\otimes \varepsilon ((\vert {i}\rangle \langle {j}\vert )^Q)\\ =&\, \sum _{ij} \sqrt{p_i p_j}(\vert {\psi _i}\rangle \langle {\psi _j}\vert )^R \otimes \sigma ^{Q'}\delta _{ij}\\ =&\, \sigma ^R \otimes \sigma ^{Q'}, \end{aligned} \end{aligned}$$

(C22)

where $\sigma ^R=\sum _{i} p_i \vert {\psi _i}\rangle \langle {\psi _i}\vert$. This shows that the bleaching channel completely erases the information of the input system, not only the information it carries, but also all its correlations to the systems that initially entangle it. $\square$