Introduction

Yield prediction has been recognized as a key subject in agriculture (Klompenburg et al., 2020), and particularly in the grape and wine industry (Carrillo et al., 2016; Clingeleffer et al., 2001; Dunn & Martin, 2003; Laurent et al., 2021; Taylor et al., 2019). Vineyard yield prediction is crucial to achieve the desired fruit quantity and quality (Krstic et al., 1998; Taylor et al., 2019), therefore, the objective and fast estimation of vine yield would be very valuable for grapegrowers (Dunn & Martin, 2000; Laurent et al., 2021; Martin et al., 2003). Several works on yield estimation and forecasting in vineyards have been published in the last decades. An interesting review of the approaches, methods and challenges for vineyard yield estimation, prediction and forecasting was recently published by Laurent et al. (2021). In this review, the most relevant features regarding yield development in an operational scenario that have to be considered by yield assessment methods are summarized and discussed. Moreover, the yield assessment methods reported in the literature are classified and compared in light of the measurement, estimation and modelling approaches. Conventional methods for assessing yield are destructive, labour-demanding and time-consuming (Clingeleffer et al., 2001; Martin et al., 2003), thus accurate, objective and rapid approaches are needed for improving yield assessment in operational contexts (Dunn & Martin, 2004; Laurent et al., 2021; Taylor et al., 2019). Moreover, the new methods should consider the high spatial and temporal variability of yield components (Bramley et al., 2019; Carrillo et al., 2016; Li et al., 2017; Oger et al., 2021a, 2021b; Taylor et al., 2005).

Yield components including the number of clusters per vine, cluster weight, berry number per cluster and berry weight are important in vineyard yield estimation. High annual variation (60 to 70%) of final yield is explained by the number of clusters per vine (Clingeleffer et al., 2001). However, recent trials in several vineyards in southern France (involving different training system, age of vines and grapevine variety) across different seasons revealed that the role of the number of clusters per vine was more variable, explaining from 39 to 99% of the temporal yield variance (Carrillo et al., 2016). Clingeleffer et al. (2001) also reported that the number of berries per bunch, the berry weight and the interaction between the number of clusters per vine and the number of berries per cluster respectively explained 11%, 4% and 20% of the spatial yield variability. Laurent et al. (2021) suggested that the classical values of vineyard yield components variability (60%, 30% and 10% for number of clusters per vine, number of berries per cluster and berry weight, respectively) should not be established for all situations in yield assessment.

Novel sensing technologies enable an efficient acquisition of data and precise forecasts in agriculture. Optical sensors are widely proposed for assessing vineyard spatial variability in precision viticulture (Ballesteros et al., 2020; Hall et al., 2011). Spectral sensors are applied to detect vegetation features, yield and canopy characteristics. A high correlation value was found between vegetation indices and yield using both remote (Hall et al., 2011) and proximal sensing technologies (Sozzi et al., 2019). Moreover, crop models can be used for yield prediction of different vineyard zones (Laurent et al., 2021). Vineyard yield was predicted by combining vegetation indices (using a spectral sensor mounted in UAV) and computer vision to obtain the vegetated fraction cover as an indicator of vine vigour (Ballesteros et al., 2020).

Computer vision systems are powerful tools to automate inspection tasks in agriculture and food processing (Cubero et al., 2011; Tian et al., 2020). Typical target applications of such systems include grading, yield component monitoring (Cubero et al., 2011; Liu et al., 2018; Nuske et al., 2014a, 2014b). With computer vision techniques, a large set of samples can be evaluated to provide more objective information (Cubero et al., 2011; Grimm et al., 2019; Liu & Whitty, 2015).

Grapevine yield estimation has been widely addressed using computer vision at different phenological stages, such as budbreak (Liu et al., 2017), flowering (Liu et al., 2018; Palacios et al., 2020), pea-size (Aquino et al., 2018; Liu et al., 2020; Palacios et al., 2021, 2022), and harvest (Dunn & Martin, 2004; Liu et al., 2013, 2015; Nuske et al., 2014b; Xin et al., 2020). A recent work (Hacking et al., 2020), concluded that the final stage of berry ripening was the ideal phenological stage for grapevine yield estimation. Information about the number of berries can lead to an adequate and early estimation of the yield in grapevine. Most of the previous works have focused on the detection of visible fruits. Some authors have developed algorithms capable of quantifying the number of visible berries in RGB images acquired under natural conditions, using traditional image analysis methods (Aquino et al., 2018; Nuske et al., 2014b) or newer deep learning techniques (Buayai et al., 2021; Grimm et al., 2019; Klompenburg et al., 2020). These works have suggested a procedure on yield forecasting for defoliated vineyards where the number of visible berries in the images was proportional to the total number of berries. However, the number of visible berries was only a fraction of the actual number of berries in the vine, as the percentage of exposed berries may vary beyond lineal relationships according to canopy conditions in the fruiting zone (Iñiguez et al., 2021). Leaf and berry occlusions are the main challenges for yield forecasting using computer vision based methods in commercial vineyards (Iñiguez et al., 2021; Victorino et al., 2020). As leaf occlusion rate (cluster occlusion by leaves) increased, the relationship between fruit pixels and yield was gradually reduced (Iñiguez et al., 2021). Yield prediction based on computer vision can also be benefited by leaf removal (a common practice in many winegrape regions) in the fruiting zone to decrease the berry occlusion affected by leaves (Iñiguez et al., 2021). Additionally, different grapevine varieties develop canopies of variable vigour, leading to occlusion situations of different extent (Diago et al., 2016; Nuske et al., 2014b), so new algorithms for yield prediction using vine images in different grapevine varieties need to be investigated.

The yield spatial variability within a commercial vineyard is a well-known fact (Bramley et al., 2019; Taylor et al., 2005). For this reason, understanding and monitoring the spatial distribution of yield variation is essential. This cannot be achieved using classical, destructive methods, as a large number of measurements are required for adequate representativeness and yield estimation. Indeed, it is a highly relevant task to perform and to obtain more precise early yield predictions in commercial vineyards. The image acquisition for monitoring commercial vineyards could be carried out using mobile sensing platforms. These moving platforms (e.g. All-terrain vehicles, tractors, agricultural machinery) can be used to improve yield estimation following the suggestions of several authors (Arnó et al., 2017; Oger et al., 2021b; Tisseyre et al., 2018).

Machine learning is an important element of a decision support tool for crop yield prediction in agriculture (Klompenburg et al., 2020). Several machine learning algorithms have been applied for predicting the number of actual berries and final yield at harvest (Zabawa et al., 2020) under different levels of leaf and berry occlusions in grapevines. Similarly, Monga et al. (2018) used convolution neural networks to develop models that can estimate yield using RGB images. A new approach for vineyard yield estimation was recently suggested by Ballesteros et al. (2020) combining remote sensing, computer vision and artificial neural network techniques.

The research idea was guided by a heuristic engineering method proposed by Koen (1988), which involves defining a problem, proposing a solution and testing that solution. Aiming at the task of early yield prediction in commercial vineyards, a method based on computer vision and machine learning using RGB images acquired on-the-go was developed. To test the solution, the evaluation results were also compared with the reference method and the limitations of the method proposed were analysed. Moreover, the differences in the method performance when prediction modelling was conducted individually for each grapevine variety versus a general model were evaluated.

Materials and methods

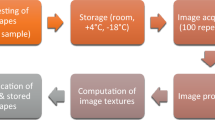
The experimental procedure comprised several steps (Fig. 1). It started from on-the-go image acquisition of six grapevine varieties under field conditions at night time. The clusters were then segmented in the vine images, and the output was used for berries’ and canopy elements’ segmentation. The number of berries, obtained after a second segmentation step, and several features related to elements of the canopy, obtained after canopy elements’ segmentation, were then combined into a dataset, and used in regression models to obtain an estimation of the number of actual berries and the yield per vine. Two possible scenarios of applicability were considered for these models: global models, where the training set contained multiple varieties, and local models, where a different model was trained and tested on each variety individually. For global models, three cross validation methods were considered: leave-one-out (LOOCV) and eightfold, where test sets contained varieties already included in the training set (to analyse the behaviour on varieties previously known by the model), and leave-one-variety-out (LOVOCV), where the test sets included a variety not included in the training set (to analyse the behaviour on varieties unknown by the model). In the case of local models, only LOOCV was performed on each variety individually to test the performance of a model trained only with the variety on which it will be applied.

Fig. 1
figure 1

Flow-chart of the full process for the estimation of the number of actual berries and yield in commercial vineyards

Full size image

Experimental layout

A set of six grapevine (Vitis vinifera L.) varieties were selected for the experiment in a commercial vineyard during season 2018.Three red (Cabernet Sauvignon, Syrah and Tempranillo) and three white (Malvasia, Muscat of Alexandria and Verdejo) varieties were used in this work (Fig. 2). The vineyard was located in Vergalijo (lat. 42°27′46.0″ N; long. 1°48′13.1″ W; Navarra, Spain). A set of 96 vines (16 per grape variety) were selected and vertically delimited using a plastic strip. Each grapevine variety was planted in a single row. In total six rows were monitored (one per variety). A vertical shoot positioned (VSP) trellis system was used for training the vines, with 2 m row spacing and 1 m vine spacing. Partial defoliation, a common viticultural practice in northern Spain, consisting of removal of three leaves per shoot around the fruiting zone was applied to the vines at fruit-set stage (Fig. 2). Partial defoliation in this work was manually applied in order to remove precisely the same number of main basal leaves per each shoot (only three leaves per shoot were removed).

Fig. 2
figure 2

Examples of vine canopy images of each grapevine variety: a Cabernet Sauvignon, b Malvasia, c Muscat of Alexandria, d Syrah, e Tempranillo and f Verdejo

Full size image

At harvest, for each tagged vine their clusters were collected, weighted and transported to the laboratory for destemming and manual counting of their berries. Yield, berry number and berry weight were determined for each vine.

Image acquisition

The acquisition of RGB images was performed the 3rd July 2018 (66 days before harvest), at the phenological stage of pea size (green berries of around 7 mm diameter, according to Coombe, 1995). A mobile sensing platform developed at the University of La Rioja (Fig. 3a) was used for the night-time image acquisition. The main component of this platform was an all-terrain-vehicle (ATV (Trail Boss 330, Polaris Industries, Minnesota, USA) customized to incorporate a custom-made aluminium structure. This structure included a RGB Canon EOS 5D Mark IV (Canon Inc. Tokyo, Japan) camera, mounting a full-frame CMOS (ccomplementary metal–oxide–semiconductor) sensor (35 mm and 30.4 MP) and equipped with a Canon EF 35 mm F/2 IS USM lens. The camera was positioned at a distance of 1.80 m, perpendicular to the canopy and at a 1 m of height from the ground. The camera settings were manually fixed at the beginning of the trials with the following values: exposure time of 1/1600 s, ISO speed of 2000 and f-number of f/5.6. This camera enabled the acquisition of images with a resolution of 6720 × 4480 pixels. The structure also included a triggering system for automating the RGB image capture and an artificial illumination system for the night-time image acquisition, necessary to obtain vine images with homogeneous illumination, and to differentiate the vine under evaluation from the vines of the opposite row. This illumination system consisted of a 1200 LEDs NanGuang CN-1200CHS panel (72 W, 3681.5 lm) and a 900 LEDs Bestlight panel (54 W, 6480 lm). The mobile platform was described and used in previous works (Diago et al., 2019; Palacios et al., 2020).

Fig. 3
figure 3

Mobile imaging platform and image processing stages: a an all-terrain-vehicle (ATV) modified to incorporate a RGB camera for on-the-go image acquisition, b original vine image, c berries’ segmentation and d canopy features’ segmentation

Full size image

Image processing

Deep learning (Deng & Yu, 2014) was used in this work to perform the semantic segmentation of the elements presented in the images (Fig. 3b). Each image pixel was assigned to a predefined class using the SegNet DL architecture (Badrinarayanan et al., 2017). This architecture was designed with an encoder, that performs down-sampling operations in order to extract feature maps from the images, and a decoder, that produces the final pixel-wise labelling by reversing the operations performed by the encoder. The encoder was formed by the layers of a convolutional neural network (CNN) pre-trained model, and the decoder mirrored the encoder. The layers for the encoder used in this work were the ones from VGG16, introduced by Simonyan and Zisserman (2015).

The segmentation of the berries and canopy elements was previously described in Palacios et al. (2022). The first step was to segment the clusters, in order to identify the image regions that contained berries, and to reduce false positives at segmenting them. Also, the segmented clusters were used in canopy segmentation. SegNet was trained with a set of 1646 image patches randomly extracted from 18 full-resolution images from different vines than the 96 presented in the experimental layout section, but from the same vineyard and varieties. Two image scales were considered for these images: the original full-resolution image scale, of which half of them (823 image patches) contained clusters while the remaining ones contained other objects (usually canopy elements). Each pixel of these patches was labelled as “cluster” class or “background” class. The size of the image patches was 1120 × 1120 but they were resized to 560 × 560 pixels in order to reduce the training time.

After performing the segmentation of the clusters, SegNet was trained to segment berries (Fig. 3c) using the same image patches with a new pixel labelling. In this step pixels were labelled as “background”, representing non-berry pixels, “contour” and “center”, representing the contour and the center of the berries, defined as berry pixels completely surrounded by “contour” pixels (Fig. 3c).

Finally, the canopy elements were segmented using six canopy classes (Fig. 3d). These were “gap”, “leaf abaxial” (lower side of the leaf), “leaf adaxial” (upper side of the leaf), “shoot”, “trunk” and “cluster” (segmented previously in the first step). The labelling of these classes was achieved using a semi-automatic approach. Six colour features, corresponding to the red–green–blue from RGB colour space, and L-a-b from CIELAB, were extracted from the images and a different multinomial logistic regression (MLR) model was trained for each variety using these features. Each training dataset contained 300 pixels (50 per class). Then, these models were used to segment the images of its corresponding variety and the outputs were used as training masks for SegNet, which enabled performing the semantic segmentation of the canopy elements for all varieties (Fig. 3d).

Models for number of actual berries and yield estimation

The canopy features calculated per vine after the canopy segmentation for the number of actual berries estimation were the following:

  • F1: Number of estimated visible berries (calculated as the number of adjacent pixel groups from berry “center” class).

  • F2: The average of the ratios between the number of “leaf abaxial” pixels and the total area for each bounding box (rectangular regions of the image) containing a cluster.

  • F3: The number of “shoot” class pixels in the fruiting zone.

  • F4: The number of “leaf adaxial” class pixels in the fruiting zone.

  • F5: The ratio between F4 and the area of the fruiting zone.

  • F6: The area of the fruiting zone, expressed in pixels.

These features were included in a regression model to estimate the number of actual berries (Palacios et al., 2022). For yield estimation, in addition to these features, the average berry weight determined at harvest for each grapevine variety was also included in the model. This was done in order to study the hypothetical improvement that could be obtained when the average berry weight per variety (which could be calculated from previous seasons) is included in the model. Descriptive statistics for each feature included in the models and possible outcomes are shown in Tables 1 and 2.

Table 1 Average and standard deviation of each feature included in the model and output parameter, calculated per variety and combining all varieties in the full set
Full size table
Table 2 Coefficient of variation for each feature included in the model and output parameter, calculated per variety and combining all varieties in the full set
Full size table

The regression method used in this work for both estimation tasks (number of actual berries and yield) was a support vector regression (Bishop, 2006).

Evaluation metrics

The metrics used in this work to test the performance of the algorithm at detecting individual berries were the following:

$$Precision= \frac{TP}{TP+FP}$$
(1)
$$Recall=\frac{TP}{TP+FN}$$
(2)
$${F}_{1} \, score=2\times \frac{Precision\times Recall}{Precision+Recall}$$
(3)

Being TP the true positives (number of correctly detected berries), FP the false positives (number of detected berries that were not actually berries) and FN the false negatives (number of actual berries that were not detected). In the context of this work, precision (Eq. 1) represents the proportion of correctly detected berries from the whole set of objects identified as berries by the algorithm. Recall (Eq. 2) is the proportion of actual berries detected by the algorithm from the whole set of berries visible in the images. A perfect performance of the algorithm would be achieved with a precision and recall of 1.0. The balance between both metrics is represented by the F1-score (Eq. 3), that is defined as the harmonic mean of precision and recall (Chinchor, 1992).

For the estimation of the number of actual berries and yield, three regression metrics were selected. These include the coefficient of determination (R2), the root-mean-squared error (RMSE) and the normalized root-mean-squared error (NRMSE), calculated as the ratio of RMSE over the average of the number of actual berries. The RMSE and NRMSE are mathematically defined as:

$$RMSE= \sqrt{\frac{\sum_{i=1}^{n}{({y{^{\prime}}}_{i}-{y}_{i})}^{2}}{n}}$$
(4)
$$NRMSE=\frac{RMSE}{\frac{\sum_{i=1}^{n}{y}_{i}}{n}}\times 100 \%$$
(5)

where \({y}_{i}\) is the observed value from the i-th vine (the number of actual berries or yield weighted), \({y{^{\prime}}}_{i}\) is the estimation performed on the i-th vine and \(n\) is the number of vines.

Support vector regression hyperparameters’ tuning

The support vector regression hyperparameter’s tuning was performed using a Bayesian Optimization algorithm (Mockus et al., 2014), which aims to minimize an objective function (a performance metric for the model trained with a set of hyperparameters) using a gaussian process model, a bayesian procedure that modifies the Gaussian process model at each new evaluation of the objective function, and an acquisition function that is maximized to find the next point to be evaluated by the objective function (i.e. the next set of hyperparameters). The Bayesian optimization algorithm has probed to outperform other optimization algorithms (Jones, 2001).

The function fitrsvm implemented in Matlab 2018b was used to train the support vector regression and optimize the hyperparameters using the bayesian optimization algorithm. In this algorithm a gaussian process with ARD Matérn 5/2 kernel model and the “expected-improvement-plus” acquisition function were employed, along with the mean-squared-error (MSE) metric as the objective function (calculated using leave-one-out cross validation performed on the full set of 95 vines).

Two sets of hyperparameters for support vector regression were obtained: one for the actual berry number estimation, and another one for yield estimation. These hyperparameters are shown in Table 3 and remained fixed for all cross-validation methods within each estimation task. In addition, these features were standardized before training.

Table 3 Support vector regression hyperparameters sets employed for number of actual berries and yield estimation
Full size table

Models’ validation

The validation set for the individual berries’ segmentation step was formed by a set of 60 full-resolution (6720 × 4480 pixels) images (ten per grapevine variety). The validation was focused on testing the accuracy of the method at counting the visible berries, rather than testing the quality of the segmentation. Therefore, the centres of the berries were manually checked in the images.

For the estimation model, three cross-validation methods were applied on the 96 vines. These methods were considered to test the applicability and the performance of the support vector regression model as a global model (involving all grapevine varieties) and as a local model (separate models for the different varieties). As a global model, two possible cases of application were considered. In the first one, the model was trained with data acquired from of all varieties and tested on other vines from the same varieties. For this, leave one out cross validation (LOOCV) and eightfold cross validation were tested. In LOOCV, in each iteration the model was trained with 95 vines and tested on one vine, while in the eightfold cross validation, the model was trained with 84 vines and tested with 12 in each iteration, randomly selecting the vines included in the training and test sets. In order to avoid bias in the partitioning of the data into both sets, eightfold was repeated 30 times, and the average of the values obtained for the regression metrics (RMSE, NRMSE and R2) in the 30 repetitions was selected as the final result for eightfold. In the second case of application as a global model, this was trained with data acquired from five of the six varieties and tested on the remaining variety, in order to verify the generalization capability of the model to estimate the number of actual berries and yield in new varieties previously unknown to the model. Hence, a leave-one-variety-out cross validation was applied, were in each iteration the model was trained with 80 vines from five varieties (all 16 vines from five varieties) and tested in the 16 vines of the remaining variety. As a local model, each variety was considered a different dataset and the model was trained in each variety independently. As the number of vines per variety was low (16 vines), LOOCV was carried out. Likewise, for each iteration the model was trained in 15 vines and tested in the remaining one.

The average berry weight feature for yield estimation was calculated considering only the vines in the training fold for each cross validation method.

Results and discussion

Individual berries’ detection

The performance metrics of the individual berries’ detection step are shown in Table 4. It can be observed that the algorithm achieved a precision higher than 0.60 for most of the varieties, except for Verdejo (precision = 0.52), indicating a higher false positive rate for this variety. In terms of recall, similar results, all of them above 0.84, were obtained for all varieties. The balance between both metrics is expressed by the F1-Score which shows values over 0.70 for all varieties except for Verdejo (with a F1-Score of 0.65). The poorer results observed for this white variety could be related to the higher size of its clusters, as compared to the other five varieties. Likewise, Verdejo clusters, with a bigger number of berries, may have led the algorithm to detect wrong artefacts in the images and identify them as berries. This could be improved by training SegNet with a higher number of images from Verdejo and other varieties with clusters similar to the ones of Verdejo.

Table 4 Performance results of the detection of the number of visible berries
Full size table

The correlation between the number of estimated visible berries (using the detection algorithm) and the actual visible berries per image is shown in Fig. 4. A strong correlation was found for all varieties, with coefficient of determination (R2) above 0.92, suggesting that the error made by the algorithm is proportional to the number of visible berries, while a fixed deviation still existed for all varieties. Generally speaking, the algorithm overestimated the number of visible berries, but this was more pronounced in Cabernet Sauvignon (Fig. 4a), Malvasia (Fig. 4b) and Verdejo (Fig. 4f).

Fig. 4
figure 4

Correlation between the number of estimated visible berries (F1 feature) and the number of visible berries per image, for each grapevine variety (10 images per variety): a Cabernet Sauvignon, b Malvasia, c Muscat of Alexandria, d Syrah, e Tempranillo and f Verdejo. Determination coefficients (R2) were significant at p = 0.001 (***). The solid line represents the correlation line and the dotted line represents the 1:1 line

Full size image

In the work of Nuske et al. (2014b), the berries’ detection algorithm presented by these authors obtained different recall values depending on the illumination conditions and the variety. These values ranged from 0.66 to 0.89. For some varieties the recall values were inferior to the ones presented in Table 4, while for the remaining ones (Traminette, Chardonnay, Flame Seedless and Petite Syrah) the recall values were similar. In good agreement with the present study, Aquino et al. (2018) reported recall values between 0.83 and 0.89 for Cabernet Sauvignon, Syrah and Tempranillo while the precision values ranged from 0.94 to 0.97. This means that Aquino et al. (2018) detected a similar rate of berries potentially due to the lower amount of canopy elements that can be mistaken for berries by the algorithm (mainly leaves), as the fruiting zone was fully defoliated. As in the case of the work of Aquino et al. (2018), the recall values (also the F1-scores) were higher in Grimm et al. (2019) while the precision achieved was very similar to that of the present study. In this case, the difference in colour of the ripe berries versus the canopy leaves (images were acquired after veraison and near harvest) made have played a significant role in the segmentation step, making the berries more distinguishable from the remaining canopy elements, leading to lower false positives’ rates. So, either occlusion phenomena (for instance by leaves) or similarities in the green colour of the berries at the pea-size phenological stage with that of leaves, shoots, or other elements of the canopy seem to difficult the proper identification and counting of berries, leading to a considerable number of false positives. In an interesting and recent work, Zabawa et al. (2020) reported high precision and recall values for Riesling berries detection. However, an artificial background was attached to the mobile phenotyping platform, which, from a practical perspective may have more limited application in an operational context.

Estimation of the number of actual berries

The correlations between the number of estimated visible berries and the number of actual berries per vine for each grapevine variety is shown in Fig. 5. These results show high R2 values for Muscat of Alexandria, Syrah, Tempranillo and Verdejo varieties, while for Cabernet Sauvignon and Malvasia lower R2 were obtained. These results proved that a linear relationship between the number of visible berries in the images and the number of actual berries in the vines existed for four of the six studied varieties. However, this linear relationship was only achieved within each variety independently, but not combining multiple varieties (global model). This can be inferred from the observation of the variability presented in the slopes of the linear functions for the different varieties, as these ranged from 1.19 (Syrah, Fig. 5d) to 2.18 (Muscat of Alexandria, Fig. 5c). Therefore, it was not possible to estimate the number of actual berries per vine using a global linear regression that included only the number of estimated visible berries from different varieties.

Fig. 5
figure 5

Linear correlation between the number of estimated visible berries (F1 feature) and the number of actual berries per vine (manually counted in the laboratory), for each grapevine variety: a Cabernet Sauvignon, b Malvasia, c Muscat of Alexandria, d Syrah, e Tempranillo and f Verdejo. Determination coefficients (R2) were significant at p = 0.05 (*) and p = 0.001 (***). The solid line represents the correlation line, and the dotted line represents the 1:1 line

Full size image

The performance of the estimation models that involved the number of estimated visible berries along canopy features is shown in Tables 5 and 6.

Table 5 Number of actual berries’ estimation performance using a support vector machine (SVM) global model
Full size table
Table 6 Number of actual berries estimation performance using a support vector machine (SVM) local model
Full size table

The results obtained for the application of a global model, where multiple varieties were used for training, are presented in Table 5. It can be observed that similar results were obtained between the two cross validation methods that used all varieties for training and the test set (leave-one-out and eightfold) either for each individual variety (R2 ranged between 0.59 to 0.86 and NRMSE ranged from 17.9 to 35.7%) and the average for all of them (R2 ~ 0.78; RMSE ~ 200; NRMSE ~ 24%). Regardless the use of LOOCV or eightfold, the estimation of the actual number of berries was more accurate for Syrah and Malvasia, while the poorest estimation was achieved for Muscat of Alexandria. When the LOVOCV was used (five varieties were used for training and the remaining one for testing) the performance metrics did not improve for any variety and particularly the NRMSE notably increased in Syrah (NRMSE = 55.96%) (Table 5).

Table 6 summarizes the performance metrics of the individual models, one per variety, involving the number of estimated visible berries and canopy features, using LOOCV. Overall, the individual or local models did not provide a more accurate estimation than the global models (when LOOCV and eightfold cross validation were used), and this was especially evident for Cabernet Sauvignon and Tempranillo, that showed R2 ~ 0.46 and NRMSE of 33.42% and 29.07%, respectively.

In general terms, the results obtained for all cross-validation methods (Tables 5 and 6) are similar for all varieties excepting for Cabernet Sauvignon, Tempranillo and Syrah. The fact that equally good results were obtained for Syrah in both LOOCV for global and local model (Tables 5 and 6) and eightfold (Table 5) but a poor performance was achieved in LOVOCV (Table 5) suggests that Syrah is highly different from the rest of varieties. In fact, the photographed vine canopies of this variety showed a higher canopy porosity or canopy gaps abundance in the fruiting zone that imaged canopies for all other five varieties (Fig. 2d). From this it can be inferred that the model trained without Syrah data is giving a higher relevance to the canopy features (due to the absence of vines with a high porosity in the training set) and increasing the training set size by including highly defoliated vines should help to improve the performance of the method on more porous vines. For Cabernet Sauvignon and Tempranillo, the results for the local models (Table 6) suggests that either the variability in the canopy conditions of the vines could not be properly captured by a model including only those varieties individually, or that the number of samples in the local models (16 vines) is not enough to estimate the number of actual berries in those varieties, and that a model that included also other varieties or a higher number of vines could improve the estimation on Cabernet Sauvignon and Tempranillo vines.

From a viticultural perspective, the most interesting results are presented in Table 5 for the LOVOCV, where the use of a global model trained with several varieties yielded promising results at estimating a new variety previously unknown for the model. Of the six studied varieties, only Syrah exhibited lower performance using the LOVOCV. This variety, together with Muscat of Alexandria showed the highest values of NRMSE. These results could be related to differential features of the canopy, clusters and berries in Syrah and Muscat as compared to those of the other varieties under study. The absence of Syrah or Muscat of Alexandria samples in the training set prevents to capture their singularity and, as a result, the estimation of the actual number of berries for these two varieties (when they are not included in the training set) is achieved with much higher uncertainty than for the other four cultivars.

The relevance of each feature in the dataset was evaluated (for all three cross validation methods) by testing the performance of the model when that particular feature had been removed. This is shown in Table 7 for leave-one-out cross validation, Table 8 for eightfold cross validation, and Table 9 for LOVOCV, where features were ordered by their relevance to the model, (in decreasing order of the RMSE/NRMSE obtained). As expected, regardless the cross-validation method, the number of estimated visible berries (F1) was the most relevant feature in the model. In fact, when F1 was not considered in the model the average R2 decreased from 0.77–0.79 to 0.49–0.51 and the NRMSE increased a 17.33% (for LOOCV, Table 7), 16.79% (eightfold, Table 8) and 14.08% (LOVOCV, Table 9). The relevance of the remaining features was found to be very similar for LOOCV (Table 7) and eightfold cross validation (Table 8). Likewise, two close groups of features could be identified in these global model validation methods. The first group formed by F2 and F3 features, whose removal led to models achieving NRMSE between 26 and 27%, and group two including F4, F5 and F6 features, whose removal led to models yielding NRMSE between 24 and 25%. This could imply that the model could be simplified (not including either F4, F5 or F6) with almost no increase in NRMSE and decrease of R2. For LOVOCV removal of a particular feature led to a greater variability in the NRMSE. Differently to the LOOCV and eightfold methods, when LOVOCV was used (Table 9) the most relevant feature after F1 was not F3 (number of “shoot” class pixels in the fruiting zone) but F2 (average of all cluster bounding boxes ratios between the number of “leaf abaxial” pixels and the total area of the corresponding bounding box). As a matter of fact, F3 was found to be the least relevant feature when LOVOCV was the cross validation method (on average of all varieties). However, when F3 was removed, the three performance metrics of Syrah substantially improved (Table 9), reducing the NRMSE from 55.72% to 25.03%. As observed in Fig. 2d, the presence of shoot pixels in the fruiting zone was noticeably higher for Syrah than for the remaining varieties (Fig. 2a–f), and this could explain these findings. Also, for Syrah in the LOVOCV, the most relevant features were “the average of all cluster bounding boxes ratios between the number of “leaf abaxial” pixels and the total area of the corresponding bounding box” (F2) and “the number of “leaf adaxial” class pixels in the fruiting zone” (F4), in first and second place, respectively, while “the number of estimated visible berries” (F1) was found to be the second least influential factor in the model (Table 9). These findings seem to confirm that the whole fruiting zone, rather than exclusively the number of estimated visible berries are particularly meaningful and determinant in the assessment of the actual number of berries in Syrah, as compared to the other five varieties. As mentioned, this could be explained by the differences in the conditions of the Syrah canopy, where a slight lower occlusion was found (Fig. 2d), compared to the conditions of the canopy for the rest of the varieties (Fig. 2a–f). The characterization of the different canopy elements in the fruiting zone has to do with the occlusion phenomena affecting the berries. Berry occlusion by leaves was recently studied by Iñiguez et al. (2021). In this work, the leaf occlusion rate (berry occlusion caused by leaves) was computed using a pixel segmentation approach. When this rate increased, from low to high, the determination coefficient between the number of cluster pixels and the yield decreased from 0.77 to 0.33.

Table 7 Results for the estimation of the number of actual berries performing leave-one-out cross validation after removing each feature
Full size table
Table 8 Results for the estimation of the number of actual berries performing eightfold cross validation after removing each feature
Full size table
Table 9 Results for the estimation of the number of actual berries performing leave-one-variety-out cross validation after removing each feature
Full size table

Victorino et al. (2020) evaluated the use of several canopy features for yield estimation and concluded that counting visible vine organs (as shoots, spurs, inflorescences and clusters) in non-defoliated vines could be used as auxiliary features but may not be sufficient individually for an accurate yield prediction. Their best result was achieved using the cluster projected area as a yield predictor. Moreover, the estimation of the number of bunches is a difficult task under high leaf occlusions conditions using image analysis. Sozzi et al. (2021) detected big bunches, which contribute the most to final grape yield. Other works have also addressed the problem of estimating the number of actual berries using several features extracted from RGB images. Buayai et al. (2021) estimated the number of actual berries using five features extracted from individual clusters’ images in which occlusion phenomena were only due to other berries, but not to leaves or other canopy elements. In this work, the authors achieved the best performance using a random forest regression that yielded a mean absolute error of estimation of 3.79 berries per cluster.

Yield prediction

The ultimate goal of identifying and counting the number of visible and actual berries per vine is to be able to predict the grapevine yield. Towards this end, the correlation between the yield, as estimated by the model, and the final yield (actual yield) at harvest, involving all six varieties altogether, is shown in Fig. 6. Significantly strong correlations, with determination coefficients above 0.82, were found for leave-one-out (Fig. 6a) and eightfold (Fig. 6c) cross-validation methods. For LOVOCV (Fig. 6e), a lower (R2 = 0.76), but still strong correlation was found. These correlations were similar to the one obtained between the number of actual berries and the actual yield (weight of the clusters) at harvest per vine, with a R2 of 0.81 (data not shown). In terms of accuracy, the RMSE per vine achieved was 0.45 kg for leave-one-out, 0.46 for eightfold, and 0.54 kg for leave-one-variety-out, which corresponded to NRMSE values of 30% (Fig. 6a, c) and 36% (Fig. 6e), respectively.

Fig. 6
figure 6

Linear correlation between the estimated yield and the actual yield per vine for a leave-one-out, c eightfold and e leave-one-variety-out cross-validation methods and b, d and f the same cross-validation methods without including the berry weight as a feature in the model. Determination coefficients (R2) were significant at p = 0.001 (***)

Full size image

The inclusion of berry weight in the yield estimation model proved to be highly valuable. Figure 6b, d and f shows the results of the yield estimation using leave-one-out, eightfold and LOVOCV without including the berry weight as a feature, respectively. As it can be observed, poorer results were obtained when the berry weight was removed from the model. For leave-one-out and eightfold results for R2 worsened from 0.83 and 0.82 (Fig. 6a, c) to 0.77 (Fig. 6b, d) and for RMSE and NRMSE the results worsened from 0.45 and 30% (Fig. 6a, c) to 0.52 and 30% (Fig. 6b, d). The most drastic worsening in the results occurred for LOVOCV (Fig. 6f), changing from previous results (Fig. 6c) for R2 of 0.76 to 0.54, RMSE of 0.54 to 0.75 and NRMSE of 35.89% to 49.75%. As regards the inclusion of berry weight (harvest values) in the prediction model, it could be argued that intrinsic variability of this yield component could affect yield prediction models. However, as pointed out by Clingeleffer et al. (2001) and Dunn (2010) berry weight (as a yield component) is not the most relevant factor influencing yield variation, which is mainly explained by the number of clusters (around 60–70% of yield variation), and berry number per cluster (Dunn, 2010), rather than by berry weight. Moreover, the work of Pagay and Cheng (2010) reported berry diameter variations smaller than 11% for two different cultivars at harvest time within given vineyards. Furthermore, the use of historical average values of berry weight (from longer periods of time, e.g. 10 years) would also contribute to mitigate inter seasonal fluctuations, providing a more robust indicator to be considered in yield prediction models based on computer vision and machine learning approaches.

For each individual variety, the correlation between the estimated yield and the actual yield at harvest using leave-one-out cross-validation is shown in Fig. 7. For most of the varieties, R2 values above 0.70 were achieved, except for Syrah (Fig. 7d) and Tempranillo (Fig. 7e), which showed R2 of 0.65 and 0.54, respectively. RSME values ranged from 0.27 kg (Tempranillo) to 0.72 kg (Malvasia). In terms of NRSME, values around 30% were yielded for four of the six varieties, while Muscat of Alexandria achieved 39.17% and Verdejo 16.47%.

Fig. 7
figure 7

Linear correlation between the estimated yield and the actual yield per vine including the berry weight as feature in the model and using leave-one-out cross validation for each grapevine variety: a Cabernet Sauvignon, b Malvasia, c Muscat of Alexandria, d Syrah, e Tempranillo and f Verdejo. Determination coefficients (R2) were significant at p = 0.01 (**) and p = 0.001 (***)

Full size image

These results prove that the image-based method developed in this work was useful to estimate the final yield in partially defoliated vines of several grapevine varieties in commercial vineyards, nearly two months before harvest. Dunn and Martin (2004) suggested a digital image analysis to predict vineyard yield. These authors observed that the ratio of fruit pixels to total image pixels explained 85% of the variation in yield in progressively de-fruited vines. Following a similar approach, Diago et al. (2012) employed a Mahalanobis colour segmentation method to extract cluster pixels and linear regressions to estimate the yield from the cluster pixels, achieving R2 values up to 0.73 in progressively de-fruited and defoliated vines, which are similar results to the ones presented in Fig. 6. Liu et al. (2017) attempted yield estimation based on shoot counting, very soon after budbreak, and reported absolute yield estimation errors ranging between 1.18% and 36.02%, which are results near to the NRMSE values presented in Fig. 6 (values near 30%). In another work, Font et al. (2015) using pixel-based segmentation approaches yielded a relative yield error of 16% for 25 non-occluded clusters on images from red grapes acquired using a vehicle and artificial illumination at night-time, these results were lower to the ones presented in this work but also their error metrics were calculated over individual clusters instead of full vines as in this work. On the other hand, Aquino et al. (2018) achieved similar results to the ones presented in this work, with R2 between the number of detected berries and the actual yield of 0.74 and a R2 between the predicted visible yield, calculated from the number of detected berries, and the actual yield of 0.78, although in this work the fruiting zone was fully defoliated, avoiding any occlusion phenomenon. Likewise, Nuske et al. (2014b) reported R2 values in the range between 0.60 and 0.73 (depending on the phenological stage and grapevine variety) for the correlation between the number of detected berries and actual harvest weight. The models in Nuske et al. (2014a, 2014b) were built individually for each variety while the yield estimation model in the present study was built from six different grapevine varieties overall. Nuske et al. (2014a, 2014b) acquired images from intensively defoliated vines in the fruiting zone, where occlusions were mostly due to other berries, but not to leaves or shoots. In the work of Nuske et al. (2014a) overall yield-per vine prediction errors based on imaged-based berry counting in Traminette and Riesling varieties ten days prior to harvest varied between 15 and 20%. In a more recent work, Victorino et al. (2020) achieved R2 values of 0.35, 0.64 and 0.55 (depending on grapevine variety) between the yield and the visible cluster area in non-defoliated vines but no yield estimation errors were provided, in contrast to the results presented in this work in Figs. 6 and 7.

Conventional methods for yield predicting used systematic, manual and labour-demanding procedures under field conditions (Dunn & Martin, 2003; Clingeleffer et al., 2001). Martin and Dunn (2003) described particular manual protocols to achieve a 15% tolerance in yield and yield components’ prediction, but its achievement required intensive manual counting and increased accuracy was expected when estimation was conducted closer to harvest time. In this regard, although prediction errors below 10–15% would be desirable, and certainly very useful for the wine industry, it is expected that the prediction metrics following the vision-approach of the present work would improve should a higher number of data be used to build and validate the models. Moreover, the inclusion of data coming for vineyards of increased canopy vigour variability, would enlarge the range of the data used for model building and validation. This factor could also lead to improved model performance. At this stage, it could be recognized that this study may be considered an initial approach that should deserve further development with substantially increased data from different cultivars and vigour conditions.

On the other hand, comparing the automated image-developed method in this work with conventional methods, it can be pointed out that the method developed in this work was non-destructive and applicable in an automated way to a very large number of vines o even to a whole vineyard using a mobile sensing platform. Thus, the image-based method described in the present study enables the increase of the representativeness of the sampled vines in commercial vineyards.

Finally, it is worth mentioning that the developed method was able to estimate yield near 60 days before harvest. It was applied in partially defoliated vines in commercial vineyards. The potential of addressing the spatial variability of berry number per vine, and its subsequent implication in grapevine yield is very informative and relevant, particularly within a precision viticulture framework. The automated image acquisition performed by a mobile sensing platform enables estimating the berry number and the yield on a large number of vines, which leads to a better modelling of the spatial variability of the vineyard and a more precise prediction of the total yield at harvest.

Conclusions

The results presented in this work prove the capability of the new method to estimate the number of actual berries and yield in different commercial grapevine varieties. The algorithm based on deep learning and computer vision was able to quantify the visible berries and extract canopy features. The cross validation methods proved that the model was able to predict the number of actual berries and yield on not only on varieties included in the model but also in other grapevine varieties.

The use of a mobile sensing platform eases the industrial applicability of this method in commercial vineyards. In addition, the new method allows an early yield estimation two months prior to harvest, which is highly valuable for wine industry, in order to understand and anticipate harvest logistics and pricing.