Abstract
Detailed knowledge of a soil’s lime requirement (LR) is a prerequisite for a demand-based lime fertilization to achieve the optimum soil pH and thus sustainably increasing soil fertility and crop yields. LR can be directly determined by the base neutralizing capacity (BNC) obtained by soil-base titration. For a site-specific soil acidity management, detailed information on the within-field variation of BNC is required. However, soil-base titrations for BNC determination are too laborious to be extensively applied in routine soil testing. In contrast, visible and near-infrared spectroscopy (visNIRS) is a time and cost-effective alternative that can analyze several soil characteristics within a single spectrum. VisNIRS was tested in the laboratory on 170 air-dried and sieved soil samples of nine agricultural fields of a quaternary landscape in North-east Germany predicting the soil’s BNC and the corresponding lime requirement (LRBNC) at a target pH of 6.5. Seven spectral pre-processing methods were tested including a new technique based on normalized differences (ND). Furthermore, six multivariate regression methods were conducted including a new method combining a forward stagewise subset selection algorithm with PLSR (FS-PLSR). The models were validated using an independent sample set. The best regression model for most target variables was FS-PLSR combined with the second Savitzky-Golay derivation as pre-processing method achieving R2s from 0.68 to 0.82. Finally, the performance of the direct prediction of LRBNC (R2 = 0.68) was compared with an indirect prediction that was calculated by the predicted BNC parameters. This resulted in slightly higher correlation coefficients for the indirect method with R2 = 0.75.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In recent years, visible and near-infrared (visNIR) spectroscopy has been increasingly applied to quantify a broad variety of chemical and physical soil constituents (e.g. Ben-Dor & Banin, 1995; Christy, 2008; Dalmolin et al., 2005; Kodaira & Shibusawa, 2013; Liu et al., 2017; Reeves et al., 2002; Viscarra Rossel et al., 2009). This technique has several methodological benefits for soil analysis such as time and cost saving, little sample preparation without environmentally harmful chemicals and a non-destructive sample analysis. Furthermore, it can address several soil characteristics with a single spectrum (Reeves, 2010; Viscarra Rossel et al., 2006a). However, the latter advantage entails a major challenge of visNIR soil spectroscopy, i.e. the complex nature of spectral data and the manifold and mostly overlapping interactions of molecules with radiation that are not fully understood. Disentangling these interactions requires sophisticated data pre-processing and chemometric analysis methods to correlate specific spectral features with a single soil parameter (Dotto et al., 2017; Viscarra Rossel et al., 2006b; Wight et al., 2016) as well as an appropriate amount of reference soil samples for calibration and validation (Pinheiro et al., 2017).
Lime fertilization is one of the most fundamental management strategies in agronomy to increase soil fertility and optimize crop yields. A precise lime application requires detailed knowledge about the field’s soil acidity and its pH buffer capacity to deduce its lime requirement (LR), i.e. the amount of lime needed to raise the soil pH to an optimum value. This information can be derived directly from conventional field or pot experiments (e.g. soil–lime incubations) or from laboratory analysis (e.g. soil-base titrations). The base neutralizing capacity (BNC) is a soil parameter, which is determined by a soil-base titration where the response of the soil to the addition of increasing concentrations of a basic solution (e.g. Ca(OH)2) is recorded. Subsequently, the soil’s LR can be derived by calculating the amount of Ca(OH)2 used to reach the optimum soil pH (target pH). However, this method is too laborious, time-consuming and expensive to be extensively applied in routine soil testing. In contrast, pedotransfer functions could be used to estimate the lime requirements using the statistical relationship with other soil properties which can be measured more effectively (Merry & Janik, 1999), such as visNIR spectra.
During the last decades, the potential of visNIR and mid-infrared (MIR) spectroscopy to predict soil pH and LR for digital soil mapping was discussed in several publications. Therein, diverse prediction methods such as Multivariate Regression (MVR), Partial Least Squares Regression (PLSR), or Support Vector Machines (SMV) were tested. Due to the complexity of soils and soil spectra, each of these methods had their advantages in certain environments and certain tasks and probably there is no ultimate best method. Viscarra Rossel and McBratney (2008) reviewed studies conducted between 1986 and 2006 that used visNIR spectroscopy to predict soil pH and LR. They averaged the coefficients of determination (R2) for pH and LR and concluded that soil spectra in the NIR region result in higher R2s (pH: Ø of R2 = 0.68; LR: Ø of R2 = 0.62) compared to soil spectra in the visible (vis) region (pH: Ø of R2 = 0.36; LR: Ø of R2 = 0.25). Pinheiro et al. (2017) evaluated the performance of visNIR spectral data for the prediction of soil properties in the Central Amazon (Brazil) using PLSR and a set of 41 pre-processing methods. For soil pH, they obtained a rather low R2 of 0.4, which, they state, corresponds with findings of Terra et al. (2015) where Brazilian soil reactive properties like pH could not be well predicted from the visNIR spectra using support vector machines (SVM). Merry and Janik (1999) analyzed the relationships between pH buffering capacity (pHBC) and related Australian soil acidity properties, such as pH, carbon content, clay content and LR using Fourier transform (FT)-NIR and FT-MIR spectrometers. They found MIR to be superior to NIR in most of the PLSR models. For soil pH and LR, they obtained R2 values of 0.45 and 0.77 for NIR spectra and 0.80 and 0.85 for MIR spectra, respectively. Viscarra Rossel et al. (2001) predicted pH and LR for Australian soil using MIR diffuse reflectance spectroscopy combined with PLSR and obtained an R2 of 0.85 for pH and 0.75 for LR. D’Acqui et al. (2010) used a FT infrared spectrometer in the near-to-mid-infrared spectral range to characterize soils typical for Italian Mediterranean offshore environments. Their best prediction of the soil pH using PLSR showed an R2 after validation of 0.72. Viscarra Rossel et al. (2006a) reviewed a large number of previous studies focusing on the prediction of various soil properties including pH and LR using vis, NIR and MIR spectroscopy. They reported R2s for soil pH ranging from 0.54 (Wijaya et al., 2001; using visNIR and stepwise multiple linear regression (SMLR)) to 0.74 (Reeves & McCarty, 2001; using NIR and PLSR). R2s for LR ranged from 0.73 (Janik et al., 1998; using FT-NIR and PLSR) to 0.86 (Janik et al., 1998; using MIR and PLSR). Their own predictions of LR were moderate using NIR (R2 = 0.50; PLSR) and improved using MIR (R2 = 0.75; PLSR). Leenen et al. (2019) predicted pH and LR using MIR and PLSR for six soil locations (pH: R2 = 0.63–0.93; LR: R2 = 0.47–0.92). Finally, Metzger et al. (2020) published R2s in the range of 0.41 to 0.86 for LR using MIR and PLSR. Additionally, they moved from laboratory to field analysis resulting in a promising R2 of 0.85 for LR using a handheld MIR spectrometer (Metzger et al., 2021). These results indicate that a higher precision and accuracy in predictions of soil pH and LR can be achieved with MIR spectroscopy and PLSR. This is because visNIR spectra show no distinct features that can be unambiguously related to molecules in the sample. Instead, absorption bands strongly overlap, especially in heterogeneous media like soils. Such absorption bands belong to molecular overtone and combination vibrations and occur in the NIR, while MIR spectra capture fundamental molecular vibrations, which are more intensive than overtone and combination vibrations (Sjaunja, 2005). However, MIR spectrometers are still more expensive rendering visNIR spectroscopy a more feasible and affordable alternative.
The main hypothesis (H1) of the present study states that visNIR spectroscopy has the capability to predict LR, for the first time based on lab-analysed BNC, for a target pH value of 6.5 (LRBNC) with particular regard to agricultural fields of a quaternary landscape of Central Europe (North-east Germany). In order to confirm the hypothesis, several data pre-processing techniques and multivariate calibration procedures including new chemometric techniques were applied searching for the best correlation with spectral reflectance signatures. In the few publications using optical spectroscopy to predict LR, except in Metzger et al., (2020, 2021), prediction models were not validated with a new and independent validation set, where R2 values are generally lower compared to the calibration set. Thus, the performances of the prediction models will be validated by an independent data set. Furthermore, it is hypothesized (H2) that important wavelength regions can be identified, which are most relevant for LRBNC prediction. In a novel approach, it is finally tested if the hypothesis (H3) is true that LRBNC can be determined more precisely by predicting LRBNC directly from the soil spectra than by predicting LRBNC indirectly using the predicted BNC parameters.
Materials and methods
Research area
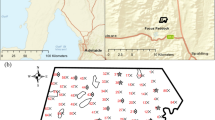
Nine agricultural fields on three farms were studied in a quaternary landscape of the North-east German Plain, which is part of the broader geomorphological region of the North European Plain (Fig. 1). The landscape is the result of repeated Pleistocene glaciations by the continental Scandinavian ice sheet as well as by subsequent periglacial and interglacial Holocene geomorphic processes. In the study area, the landforms and soils were particularly shaped by the advances of the Weichselian (115–12 ka BP) and the preceding Saalian glacial belt (150–130 ka BP; Krbetschek et al., 2008). Climatically, it is situated in a transitional zone between oceanic climate of Western and continental climate of Eastern Europe. Regional climatic differences are rather low due to a relatively low altitudinal range of the land surface of ~ 0 to 200 m a.s.l. Following the Koeppen–Geiger Climate Classification System, the climate of the study region can be classified as temperate oceanic with an increasing influence of continental circulations. The mean annual air temperature is around 9 °C. The coldest and warmest months are January and July with mean temperatures of − 1 and 18 °C, respectively. With a mean annual total precipitation of less than 550 mm, it is one of the driest regions in Germany.
The three farms are situated in the east and in the north of the federal state of Brandenburg (North-east Germany). They are mainly located in the Pleistocene young morainic landscape of the Weichselian glaciation as well as in the Holocene river valley of the Oderbruch showing a high within-field soil variability. Soil acidity of these soils often necessitates liming. However, at some places, the pH is naturally high due to the occurrence of carbonates from glacial till.
Soil samples were collected from the upper 30 cm of the soils’ Ap horizons. In accordance with the German soil classifcation system KA5, (Eckelmann et al., 2005), soil textures range from pure sand (class: Ss) to loamy clay (class: Tl) showing a dominance of sand and loam (classes: Sl, Su, St, Ls) (Vogel et al., 2022). The pH value of the soils range from 3.8 (extremely acidic) to 7.4 (slightly alkaline) with median values of 6.2 (slightly acidic). The soil organic matter content is rather low throughout the study region, having minima of 0.8%, maxima of 5.6% and median values around 1.4% (Vogel et al., 2020).
Analysis of the base neutralizing capacity (BNC)
A total of 170 soil samples were analyzed for the base neutralizing capacity (BNC), which are a partial set of BNC data previously published in Vogel et al. (2020). The BNC is defined as the amount of soil acidity that is neutralized by a base in a given time interval targeting a certain pH value (Meiwes et al., 1984; Vogel et al., 2020). To directly determine the LR of the studied soils from their base neutralizing capacity (LRBNC), the procedure of Meiwes et al. (1984) and Utermann et al. (2000) was followed. It is a laboratory analysis where a base of increasing concentration is added to a soil sample, the resulting pH change is recorded and a titration curve between pH development and the added base concentrations is generated. Then, the BNC of the analyzed soil sample for receiving a target pH value can be deduced from the parameters of the fitted titration curve and finally, the respective LR can be calculated.
In more detail, an air-dried and 2 mm-sieved soil sample is divided into 6 subsamples of 25 g. Afterwards, a control sample is added with 50 ml of deionized water. Furthermore, 25 ml of 2 N CaCl2 and 25 ml of 8 N NaOH solution are added in five concentrations to obtain Ca(OH)2 in the following 6 concentration levels: 0, 0.25, 0.5, 1.25, 2.5 and 5 mmolc (25 g soil)−1. By adding Ca2+ and Na+ ions to the soil solution, H+ and Al3+ ions are desorbed from the surface of soil colloids and neutralized by OH− (Meiwes et al., 1984). After 18 h of overhead shaking, the pH value is measured with a glass electrode (SenTix® 81; WTW) in the supernatant solution. For the quantification of the BNC, the pH values and concentrations of Ca(OH)2 added are displayed in a scatterplot and a titration curve is fitted to the six points by means of a non-linear regression model using the nls function implemented in the free software environment for statistical computing and graphics R (R Core Team, 2018). For the soils studied, Vogel et al. (2020) demonstrated that the non-linear reaction of the pH value on the application of increasing quantities of Ca(OH)2 is best described by an exponential model (Eq. 1):
where α, β and γ are the regression coefficients of the exponential function. The amount of Ca(OH)2 in mmolc (25 g soil)−1 needed to achieve a target pH of 6.5 was derived based on this model (Eq. 2) and the LR, expressed in kg CaCO3 (ha × dm)−1 (dm: decimeter), was calculated by multiplying BNC with the factor 2 000 (Meiwes et al., 1984; Utermann et al., 2000). A pH of 6.5 was chosen as the target pH value because fertilization guidelines, e.g. for the UK (Devra, 2010) and many other countries advice to maintain a soil pH of 6.5 for arable lands to bring most of the nutrients to their optimal availability for plants (Goulding, 2016). Of course, this does not reflect the fact that arable crops differ in their sensitivity to soil acidity. For more detailed information on BNC parameters and how to determine lime requirement by using the BNC, the reader is referred to Vogel et al. (2020).
Spectral analysis
Spectral measurements were conducted with an ultra-broadband UV–Vis-NIR spectrometer system by ArcOptix (Arcspectro UV–Vis-NIR fibered, ArcOptix S.A., Neuchatel, Switzerland). The device is equipped with a dispersive spectrometer using a silicon array detector for the ultra violet (UV) and visual (vis) range (200 to 1000 nm) and a Fourier-Transform spectrometer for the near-infrared region (FT-NIR; 900 to 2500 nm) with an extended range InGaAs photo diode. The spectral resolution is < 5 nm in the UV and Vis and < 8 nm in the NIR region with a reporting interval of 1 nm. Samples were irradiated by four halogen lamps at 45° inside a box which excluded ambient light. The diffuse reflected light was transmitted to the spectrometer via two glass fibres: one high OH fibre for the vis range and another one with low OH bindings specialized for the NIR region. For sample preparation, each soil sample was sieved to < 2 mm, air dried, filled in a petri dish and flattened with a spatula. Measurements were repeated three times in different positions by rotating the sample by about 90 degrees. Each spectrum reported by the spectrometer was the average of 10 internal replicates in the vis range with an integration time of 1100 to 1700 ms and 16 replicates in the NIR using the high gain factor setting. After about every 60 min, the spectrum of a 20% reflection standard (Lake Photonics, Uhldingen-Mühlhofen, Germany) with certified reflection grades was recorded. Furthermore, a dark current measurement was carried out twice a day.
Data modelling
Raw reflection spectra (I) of the soil samples, the reflection standard (I0) with its reference correction values for each wavelength (zλ) and the dark current (Id) were converted into reflectance spectra (R) using Eq. 3:
Reflection values from 250 to 359 nm were removed due to detector noise. The spectra were then smoothed by a Savitzky–Golay filter with a polynomial first order combined with 11 or 36 windows (Savitzky & Golay, 1964). Afterwards, several pre-processing techniques were tested for optimizing the prediction of the BNC properties. These included:
(i)Pseudo-absorbance transformation (pA; Eq. 4; analogous to Lambert-Beer’s law for transmitted light from 1852),
(ii)Kubelka-Munk transformation (KM; Eq. 5; Kubelka & Munk, 1931),
(iii)Standard normal variate transformation (SNV; Eq. 6; Barnes et al., 1989),
(iv)Multiple scatter correction (MSC; Eq. 7; Martens et al., 1983; Geladi et al., 1985),
(v-vi)Savitzky-Golay first and second derivative (SG1, SG2; Savitzky & Golay, 1964),
(vii)Orthogonal signal correction (OSC; Wold et al., 1998) and
(viii)A technique based on normalized differences (ND) using dual wavelengths indices (DWI; Eq. 8; Schirrmann et al., 2013), where all possible normalized differences of each wavelength are calculated requiring considerable processing power.
Details for SNV, MSC and the Savitzky-Golay derivatives can be found in (Rinnan et al., 2009).
where R is the reflectance spectrum, yw the reflectance at a specific wavelength, ӯ the mean value of all measured values of one spectrum, ai the additive effect calculated by ordinary-least-square-regression (OLS) for each spectrum on the mean spectrum of all spectra, bi the multiplicative effect calculated by ordinary-least-square-regression (OLS) for each spectrum on the mean spectrum of all spectra, and Ri and Rj the reflectance values at the ith and jth wavelength of a spectrum. The LRBNC (BNC-based LR determined for a target pH value of 6.5) and the following five parameters were used as dependent variables:
(i) pH0: initial pH value of the soil sample measured in deionized water before base addition,
(ii) δpHtotal: total pH increase over all five base additions, and
(iii-v) α, β and γ: regression coefficients of the exponential model.
To find the best correlation between spectral reflectance signatures and the six dependent variables, six regression methods were applied and the results compared:
-
(i)
partial least squares regression (PLSR; Wold, 1975) with a tenfold cross validation using the non-linear iterative partial least squares (NIPALS) algorithm,
-
(ii)
canonical powered PLSR (CPPLSR; Indahl et al., 2009),
-
(iii)
least absolute shrinkage and selection operator regression (LASSO; Tibshirani, 1996),
-
(iv)
least angle regression (LARS; Efron et al., 2004),
- (v)
-
(vi)
forward stagewise subset selection combined with PLSR (FS-PLSR).
The FS-PLSR preselects wavelengths by an algorithm that belongs to the family of forward stagewise regressions (Sen & Srivastava, 1990) before using PLSR. The algorithm is inspired by sure independence screening (SIS) from Fan and Lv (2014) and it involves the following data processing steps: Firstly, the predictor variable (wavelength) with the absolute maximum of Kendall τ correlation to the response variable is selected (Kendalls τ is supposed to be a robust variant for correlations of nonparametric variables; Fan & Lv, 2014). Secondly, a robust linear model is built between the selected predictor variable and the response variable. Thirdly, the residues of this model are taken as new response variable and the complete procedure is started again until the same predictor is selected twice consecutively. Finally, the set of selected predictor variables is used to build a PLSR model.
All 170 spectra were randomly separated into a training dataset for calibration including a tenfold cross-validation (repeated for 20 times) and an independent test set for validating the model algorithms in a ratio of 3:1. This resulted in 127 samples for calibration and 43 samples for validation. The prediction models were evaluated by the following diagnostic variables: coefficient of determination (R2; Eq. 9), root mean square error of prediction (RMSEP; Eq. 10), (RPIQ; Bellon-Maurel et al., 2010; Eq. 11) and the number of used components.
where N is the number of samples, \(\overline{y }\) is the mean of all reference values, \(\overline{\widehat{y} }\) is the mean of all predicted values, yi is the ith reference value, \({\widehat{y}}_{i}\) is the ith predicted value, Q1 the first quartile of all reference values, and Q3 the third quartile of all reference values.
The ratio of performance to interquartile range was displayed to describe the relationship between the spread of the data and error of prediction, e.g. an RPIQ of 2 means that the spread of 50% of the data around the median is twice the root mean square error of prediction, thus the higher RPIQ the better the prediction performance (Bellon-Maurel et al., 2010).
Results and discussion
The descriptive statistics of BNC parameters for all studied soil samples are shown in Table 1. The initial soil pH values in deionized water (pH0) varies from 4.5 to 8.0 with a mean value of 6.6 and a strong skewness of − 0.80 towards higher pH values. pH0 is strongly negatively correlated with BNC-based lime requirement (LRBNC) as given by a Pearson’s correlation coefficient of r = − 0.95 (Table 2). When pH0 is higher than the target pH value of 6.5, LRBNC becomes negative implicating that there is no need for lime treatment. With higher pH values it might even be considered to use acid fertilizers or other soil amendments to lower the pH value (Vogel et al., 2020). As the mean value of pH0 of 6.6 is close to the target pH, the mean value of LRBNC for all samples is close to zero. Moreover, the number of negative LRBNC values are higher than the positive ones because of a skewness of over 0.6. This means that there are less acidic soil samples than basic soil samples in the present dataset, i.e. 60 soil samples (35%) are below the target pH value and 110 (65%) are above.
The regression coefficient α represents the maximum pH value at the endpoint of the soil-base titration (pH5) having a mean value of 12.4. It varies less than all other parameters showing a coefficient of variation (CV) of only 2.6%. In contrast, β, which is the difference from the starting point (pH0) to the end point (pH5) of the titration curve, has a mean value of 5.4. Thus, pH0 should be equal to α–β. However, small differences between experimentally determined titration points and the fitted exponential function can occur (Vogel et al., 2020). There is strongly negative correlation of r = − 0.95 between pH0 and β (Table 2). The third regression coefficient γ varies between 0 and 1 and refers to the curvature of the titration curve, whereas 1 results in a linear and near 0 in an almost right-angled curve. In this sample set, γ varies more than all other BNC parameters showing a coefficient of variation of almost 25% (Table 1). This indicates a high variability in the pH buffer capacity of the investigated soils (Vogel et al., 2020).
The BNC parameters pH0, δpHtotal, β and LRBNC are strongly correlated with absolute Pearson’s r coefficients between 0.82 and 0.95 (Table 2). Although the correlation of γ to pH0, δpHtotal, α, β and LRBNC is less pronounced, a higher correlation to single titration points (pH0.5, pH1.25 and pH2.5) exists. Parameter α shows the lowest correlations. It only exhibits closer relationship with β (r = 0.79).
The descriptive statistics of the 170 reflectance spectra used in this study are presented in Fig. 2. The samples show a classical spectral signature of mineral soils in the visNIR region from 360 to 2450 nm with reflectances up to 50%. Three absorption bands can be recognized in the region of 1400, 1900 and 2200 nm. According to Bishop et al. (1994), the absorptions around 1400 and 1900 nm belong to combination vibrations of water bound as hydrated cations in the interlayer lattices or water adsorbed on particle surfaces. Moreover, the absorption at around 1400 nm can also occur due to overtone O–H stretch vibrations, as they exist in e.g. octahedral lattices of clay minerals. Absorptions near 2 200 nm result from O–H stretch combination vibrations or overtone bending vibrations of aluminium hydroxides (Al–OH) as they occur in kaolinite, illite and montmorillonite (Stenberg et al., 2010).
Descriptive statistics of 170 soil reflectance spectra from 360 to 2450 nm. Min and Max: minimum and maximum of all reflectance spectra; Q1 and Q3: first and third quartile of all reflectance spectra; LR-Min: spectrum of the sample with the lowest LR; LR-Max: spectrum of the sample with the highest LR
In Fig. 2, a relationship between the original reflectance spectra and LR is not visible. In contrast minimum and maximum LR show only a small difference in reflectance. However, from the concavity of the spectral curves (Fig. 3) highlighted by the 2nd derivative, an inverse correlation at around 1914 nm can be recognized showing a more pronounced concavity of low LRs compared to high LRs. This is mathematically confirmed, because the 2nd derivative was the best performing pre-processing method for predicting LR with 1914 nm being the most important wavelength (Tables 3 and 4).
The model performances of all examined pre-processing and regression methods are shown in Appendix 1. Table 3 displays the best-performing prediction models for each soil parameter including the pre-processing methods and the evaluation parameters (R2, RMSEP, RPIQ and the number of components used). The frequently published ratio of performance to deviation (RPD) with its classifications for quality control of prediction models (Chang et al., 2001) was not calculated because of its equivalence with R2 (Minasny & McBratney, 2013) and its inappropriateness for skewed parameters (Bellon-Maurel et al., 2010). Best predictions for four out of six parameters (LRBNC, β, pH0, δpHtotal) were achieved by the regression model FS-PLSR. As pre-processing method, the second Savitzky-Golay derivation (SG2) produced best results for three out of six models (LRBNC, pH0, δpHtotal). PLSR achieved best prediction performances for α and γ. The best pre-processing method for the BNC curve parameter β was Kubelka–Munk (KM) transformation combined with normalized differences (ND) and for γ the standard normal variate (SNV) transformation. For α, no pre-processing method optimized prediction performance. However, the removal of two outliers out of 43 samples in the validation set improved R2 for α from 0.49 to 0.67. R2 in the validation set for all parameters were in the range of 0.67 (α) to 0.82 (δpHtotal) demonstrating the good model performances. Except for α and γ, the predictive power explained by RPIQ was good for of all models with RPIQs higher than 2.4. The reason, why α has the lowest R2 and RPIQ could be attributed to the generally poor correlations to the other BNC parameters. Although the R2 of γ is good with 0.72, the RPIQ is lower due to a centred distribution of the reference values which is responsible for a smaller interquartile range (Q3-Q1). The prediction models required a small number of PLSR-components from 5 (pH0, δpHtotal, α) to 8 (β) with one exception for γ, which needed 16 components. In general, a high number of components can include too much noise of the data set and thus might lead to overfitting when applying the model to independent data (Gowen et al., 2011). However, in this case, a reduction by e.g. 5 components to 11 components would decrease R2 from 0.73 to 0.62 and is thus not recommended.
From the current knowledge, the soil pH value, i.e. the soil’s proton concentration, does not seem to be directly spectrally active but it is suspected to correlate with other parameters that show spectral response such as soil organic matter (SOM) content or clay minerals (Chang et al., 2001). However, there could be a problem of predicting soil properties being only correlated to spectrally active components because the type and intensity of these correlations may differ from site to site (Stenberg et al., 2010). Nevertheless, comparing the prediction results for the initial pH value (pH0) of the examined nine study fields with previous studies, a validated R2 of 0.76 and an RMSEP of 0.28 can be considered quite good since the published R2 values for pH at an equal scale (country or state scale) vary from 0.55 to 0.77 with an RMSEP of a third to half a pH unit (Stenberg et al., 2010). Only at a smaller spatial scales like farm or field scale, literature results are sometimes better because of less variations in soil characteristics receiving R2s from 0.54 to 0.92 with RMSEPs from 0.17 to 0.31 (Stenberg et al., 2010).
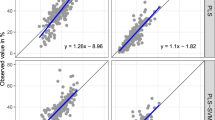
Figure 4 shows the plotted validation results for predicted and measured values of LR and the five BNC parameters. For the LRBNC, the two best direct modelling methods with two different prediction results are displayed (model A, Fig. 4A and model B, Fig. 4B). Although R2 is almost the same (0.67 vs. 0.68), the RMSEP of the predictions calculated with FS-PLSR and SNV pre-processing (model A) is with 144 kg CaCO3 (ha × dm)−1 much better than the other one calculated with FS-PLSR and SG 2nd derivation (model B) with 221 kg CaCO3 (ha × dm)−1. One reason is that the slope factor of model A is with 0.59 poorer than of model B having 0.91. This results in a smaller range of the predicted values of model A compared to model B. A comparison of the ratios of slope and RMSEP shows that they are the same for the two methods (0.65). This indicates that both models can be considered of equal quality if the prediction results of model A are corrected by the slope factor. Nevertheless, model B was regarded as best-performing prediction model because it avoids slope factor correction. Comparing the performance of direct prediction of LRBNC with the indirect prediction using the BNC parameters α, β and γ (Fig. 4C), the indirect method achieved slightly higher correlation coefficients of 0.75 versus 0.68, respectively. This is the opposite behaviour as one would expect, because the accumulated error of the three predicted variables α, β and γ was assumed to be higher than the error of the directly predicted variable LRBNC. Nevertheless, with the present data, it is not possible to give a general preference of either the direct or the indirect prediction method due to the relatively small number of samples in the validation set. This means that the two methods may just mathematically vary around the same expected value.
Validation results for predicted and measured values for A LRBNC (directly predicted, Model A); B LRBNC (directly predicted, Model B); C LRBNC (indirectly predicted by BNC parameters α, β, and γ); D initial pH value of the soil sample (pH0); E total pH increase (δpHtotal); F,G,H regression coefficients of the exponential model α, β and γ including 1:1-line (grey, regression line (black) as well as R.2, RMSEP, bias and slope of the regression model)
Figures 4D–H show the regression lines of the five BNC parameters. The reader should be aware that for alpha, two outliers, which were removed for modelling, are still displayed in the plot (Fig. 4F). The overall bias (intercept of the regression line and representative of the systematic error) for the best predictions of all BNC parameters is low and the slope factor is good with values close to 1 (0.79 to 0.95).
The influence of each individual wavelength by variable importance projection (VIP) scores on the PLSR prediction models, as well as the selected wavelengths by forward stagewise subset algorithm for each response variable are displayed in Table 4. VIP scores for wavelengths higher than 1 have a higher influence on the prediction results than the average. The prediction model for α mainly used wavelengths (i) < 500 nm, (ii) 1 000–1 200 nm and (iii) at the water band around 1900 nm, which were also important for δpHtotal, γ, and LRBNC. The model for γ mainly used wavelengths (i) 500–700 nm (ii) at the water band around 1400 nm, and between 2250 and 2450 nm, which were also particularly important for β. The region between 610 and 710 nm was important for all BNC parameters except α. Further less important wavelengths with VIP-scores can be seen in Appendix 2. The attempt to assign the important wavelengths to optically active components was not accomplished in this study as the potential compounds of soil organic matter or clay minerals have many different, wide and strongly overlapping vibrations, such as first, second, or third overtone vibrations as well as combination vibrations (e.g. of O–H, C–H, CH2, CH3, C = C, C-O, C = O, S–H, N–H etc.) including Fermi resonance shifts (Fang et al. (2018). Finding corresponding vibrations for the important wavelengths could be the scope of further research.
In the literature, LR predictions by spectroscopic methods are relatively rare. Reported R2 values are 0.73 (Janik et al., 1998), 0.77 (Merry & Janik, 1999), and 0.50 (Viscarra Rossel et al., 2006a, 2006b) using NIR as well as 0.75 (Viscarra Rossel et al., 2001 republished in Viscarra Rossel et al., 2006a, 2006b), 0.86 (Janik et al., 1998), 0.45 to 0.92 (Leenen et al., 2019), and 0.41 to 0.76 (Metzger et al., 2020) using MIR spectroscopy. However, in contrast to the present study, except for Metzger et al. (2020), they did not validate their models with a new and independent validation set, where R2 values are generally lower compared to the calibration set. In this regard, an R2 of 0.68 or 0.76 obtained in this study can be considered as good model performance.
An important aspect, which was neglected in this study, is the error of the laboratory method for determining BNC data. Janik et al. (1998) determined LR twice for 224 samples using a soil–lime incubation method based on a 14-day incubation (Richards, 1992) similar to this procedure. They found rather low replication R2 values of 0.73 for the slope and 0.85 for the intercept of the titration curves. Currently, it is unclear whether prediction errors of visNIR spectroscopy for LR are considerably different from laboratory errors. Hence, this topic needs further research.
Conclusions
VisNIR spectroscopy (visNIRS) was successfully used to predict the soil’s lime requirement and five parameters of the base neutralizing capacity by testing seven pre-processing techniques and six different multivariate regression methods on 170 soil spectra of nine agricultural fields, thus confirming the main hypothesis H1. The prediction performance in terms of a validated R2 ranged from 0.67 (α) to 0.82 (δpHtotal). In view of the presumption that the soil pH value does not seem to be directly spectrally active, this results indicate a good model performance. The good correlation seems to be attributed to other parameters that show spectral response such as soil organic matter (SOM) content or clay minerals. For four out of six response variables (LRBNC, β, pH0, δpHtotal), best predictions were obtained by a forward stagewise subset selection combined with PLSR as regression model whereas for three out of six models (LRBNC, pH0, δpHtotal) the second Savitzky-Golay derivation was the best pre-processing method. Important wavelength regions could be identified between 300 and 500 for α, between 610 and 710 nm for all BNC parameters except α, around 1400 for γ, around 1900 nm for δpHtotal, α, γ, and LRBNC, and between 2250 and 2450 nm for α and β. Hence, hypothesis H2 was confirmed. Even though the indirect prediction of LRBNC (by using the predicted BNC parameters α, β and γ) performed slightly better (R2 = 0.75) than the direct one (R2 = 0.68), it was not possible to generally prefer one of the two methods. Thus, hypothesis H3 could not be confirmed nor refuted. Field-dependent prediction models may improve the accuracy in comparison to field-independent models as presented in this study. However, practical agriculture demands rather general field-independent prediction models to reduce total soil mapping costs. The effect on the prediction performance of iteratively excluding one or more agricultural fields from the modelling data was not examined in this study due to a low number of samples. However, it is the subject of current research activities.
It can be concluded that visNIRS is a fast and cheap method for predicting lime requirements. Hence, much more field samples can be investigated compared to the standard lab method. This can make visNIR spectroscopy a very efficient method for soil acidity management particularly in combination with precision agriculture applications enabling a within field spatial analysis. Regarding its applicability for a site-specific soil acidity management, in a next step, visNIR spectroscopy will also be tested in the field on moist soils using an on-the-go sensing system. This transfer from lab to field is also encouraged by the promising results of Metzger et al. (2021) using a handheld MIR spectrometer to predict LR on field-moist samples.
Data availability
On request.
Code availability
On request.
References
Barnes, R. J., Dhanoa, M. S., & Lister, S. J. (1989). Standard normal variate transformation and De-trending of near-infrared diffuse reflectance spectra. Applied Spectroscopy, 43, 772–777. https://doi.org/10.1366/0003702894202201
Bellon-Maurel, V., Fernandez-Ahumada, E., Palagos, B., Roger, J. M., & McBratney, A. (2010). Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends in Analytical Chemistry, 29, 1073–1081. https://doi.org/10.1016/j.trac.2010.05.006
Ben-Dor, E., & Banin, A. (1995). Near-infrared analysis as a rapid method to simultaneously evaluate several soil properties. Soil Science Society of America Journal, 59, 364–372. https://doi.org/10.2136/sssaj1995.03615995005900020014x
Bishop, J. L., Pieters, C. M., & Edwards, J. O. (1994). Infrared spectroscopic analyses on the nature of water in montmorillonite. Clays and Clay Minerals, 42, 702–716. https://doi.org/10.1346/CCMN.1994.0420606
Breiman, L. (2001). Random forests. Machine Learning, 45, 5–32. https://doi.org/10.1023/A:1010933404324
Chang, C.-W., Laird, D., Mausbach, M., & Hurburgh, C. (2001). Near-infrared reflectance spectroscopy-principal components regression analyses of soil properties. Soil Science Society of America Journal, 65, 480–490. https://doi.org/10.2136/sssaj2001.652480x
Christy, C. D. (2008). Real-time measurement of soil attributes using on-the-go near infrared reflectance spectroscopy. Computers and Electronics in Agriculture, 61, 10–19. https://doi.org/10.1016/j.compag.2007.02.010
D’Acqui, L. P., Pucci, A., & Janik, L. J. (2010). Soil properties prediction of western Mediterranean islands with similar climatic environments by means of mid-infrared diffuse reflectance spectroscopy. European Journal of Soil Science, 61, 865–876. https://doi.org/10.1111/j.1365-2389.2010.01301.x
Dalmolin, R. S. D., Gonçalves, C. N., Klamt, E., & Dick, D. P. (2005). Relationship between the soil constituents and its spectral behavior. Ciência Rural, 35, 481–489.
Devra (2010). Devra’s Climate Change Plan 2010 (PB13358). www.defra.gov.uk.
Dotto, A. C., Dalmolin, R. S. D., Grunwald, S., ten Caten, A., & Filho, P. W. (2017). Two preprocessing techniques to reduce model covariables in soil property predictions by Vis-NIR spectroscopy. Soil and Tillage Research, 172, 59–68. https://doi.org/10.1016/j.still.2017.05.008
Eckelmann, W. (Eds). (2005). Bodenkundliche Kartieranleitung: Mit 103 Tabellen, 5th edn. Stuttgart: Schweizerbart‘sche Verlagsbuchhandlung
Efron, B., Hastie, T., Johnstone, I., & Tibshirani, R. (2004). Least angle regression. The Annals of Statistics, 32, 407–499. https://doi.org/10.1214/009053604000000067
Fan, J., & Lv, J. (2014). Sure independence screening. In N. Balakrishnan, T. Colton, B. Everitt, W. Piegorsch, F. Ruggeri, & J. L. Teugels (Eds.), Wiley StatsRef: Statistics Reference Online (Vol. 1, pp. 1–8). Chichester, UK: John Wiley & Sons Ltd.
Fang, Q., Hong, H., Zhao, L., Kukolich, S., Yin, K., & Wang, C. (2018). Visible and near-infrared reflectance spectroscopy for investigating soil mineralogy: A review. Journal of Spectroscopy, 2018, 1–14. https://doi.org/10.1155/2018/3168974
Geladi, P., MacDougall, D., & Martens, H. (1985). Linearization and scatter-correction for near-infrared reflectance spectra of meat. Applied Spectroscopy, 39(3), 491–500.
Goulding, K. W. T. (2016). Soil acidification and the importance of liming agricultural soils with particular reference to the United Kingdom. Soil Use and Management. https://doi.org/10.1111/sum.12270
Gowen, A. A., Downey, G., Esquerre, C., & O’Donnell, C. P. (2011). Preventing over-fitting in PLS calibration models of near-infrared (NIR) spectroscopy data using regression coefficients. Journal of Chemometrics, 25, 375–381. https://doi.org/10.1002/cem.1349
Ho, T. K. (1995). Random decision forests. In 3rd International Conference on Document Analysis and Recognition, Montreal, Que., Canada, 14–16 Aug. 1995 (pp. 278–282). IEEE Computer Society Press. doi:https://doi.org/10.1109/ICDAR.1995.598994.
Indahl, U. G., Liland, K. H., & Naes, T. (2009). Canonical partial least squares-a unified PLS approach to classification and regression problems. Journal of Chemometrics, 23, 495–504. https://doi.org/10.1002/cem.1243
Janik, L. J., Merry, R. H., & Skjemstad, J. O. (1998). Can mid infrared diffuse reflectance analysis replace soil extractions? Australian Journal of Experimental Agriculture, 38, 681–696. https://doi.org/10.1071/ea97144
Kodaira, M., & Shibusawa, S. (2013). Using a mobile real-time soil visible-near infrared sensor for high resolution soil property mapping. Geoderma, 199, 64–79. https://doi.org/10.1016/j.geoderma.2012.09.007
Koen, B. V. (1988). Toward a definition of the engineering method. European Journal of Engineering Education, 13, 307–315. https://doi.org/10.1080/03043798808939429
Krbetschek, M. R., Degering, D., & Alexowsky, W. (2008). Infrared radiofluorescence ages (IR-RF) of Lower Saalian sediments from Central and Eastern Germany. Zeitschrift Der Deutschen Gesellschaft Für Geowissenschaften, 159, 133–140. https://doi.org/10.1127/1860-1804/2008/0159-0133
Kubelka, P., & Munk, F. (1931). Ein Beitrag zur Optik der Farbanstriche (Contribution to the optic of paint). Zeitschrift Für Technische Physik, 12, 593–601.
Leenen, M., Welp, G., Gebbers, R., & Pätzold, S. (2019). Rapid determination of lime requirement by mid-infrared spectroscopy: A promising approach for precision agriculture. Journal of Plant Nutrition and Soil Science, 182, 953–963. https://doi.org/10.1002/jpln.201800670
Liu, L., Ji, M., & Buchroithner, M. (2017). Combining partial least squares and the gradient-boosting method for soil property retrieval using visible near-infrared shortwave infrared spectra. Remote Sensing, 9, 1299. https://doi.org/10.3390/rs9121299
Martens, H., Jensen, S. A., & Geladi, P. (Eds.). (1983) Proceedings of the Nordic symposium on applied statistics: Stokkand Forlag Publishers Stavanger, Norway.
Meiwes, K. J., König, N., Khana, P. K., Prenzel, J., & Ulrich, B. (1984). Chemische Untersuchungsverfahren für Mineralboden, Auflagehumus und Wurzeln zur Charakterisierung und Bewertung der Versauerung in Waldböden: Chemical test methods for mineral soils, litter layers and roots to characterize and evaluate acidification in forest soils.
Merry, R. H., & Janik, L. J. (1999). New methodology for lime requirements and use in decision support systems (RIRDC publication, no. 99/25). Barton: Rural Industries Research and Development Corporation (Australia).
Metzger, K., Zhang, C., & Daly, K. (2021). From benchtop to handheld MIR for soil analysis: Predicting lime requirement and organic matter in agricultural soils. Biosystems Engineering, 204, 257–269. https://doi.org/10.1016/j.biosystemseng.2021.01.025
Metzger, K., Zhang, C., Ward, M., & Daly, K. (2020). Mid-infrared spectroscopy as an alternative to laboratory extraction for the determination of lime requirement in tillage soils. Geoderma, 364, 114171. https://doi.org/10.1016/j.geoderma.2020.114171
Minasny, B., & McBratney, A. (2013). Why you don‘t need to use RPD. Pedometron, 33, 14–15.
Pinheiro, É., Ceddia, M., Clingensmith, C., Grunwald, S., & Vasques, G. (2017). Prediction of soil physical and chemical properties by visible and near-infrared diffuse reflectance spectroscopy in the central amazon. Remote Sensing, 9, 293. https://doi.org/10.3390/rs9040293
R Core Team. (2018). R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing.
Reeves, J. B. (2010). Near- versus mid-infrared diffuse reflectance spectroscopy for soil analysis emphasizing carbon and laboratory versus on-site analysis: Where are we and what needs to be done? Geoderma, 158, 3–14. https://doi.org/10.1016/j.geoderma.2009.04.005
Reeves, J. B., & McCarty, G. W. (2001). Quantitative analysis of agricultural soils using near infrared reflectance spectroscopy and a fibre-optic probe. Journal of near Infrared Spectroscopy, 9(1), 25–34.
Reeves, J. B., McCarty, G., & Mimmo, T. (2002). The potential of diffuse reflectance spectroscopy for the determination of carbon inventories in soils. Environmental Pollution, 116, S277–S284.
Richards, A. F. (1992). Improved Criteria for Predicting and Ameliorating Soil Acidity in the Higher Rainfall Areas of South Australia: Termination Report (Technical report (South Australia. Department of Agriculture)). Department of Agriculture, South Australia.
Rinnan, A., van den Berg, F., & Engelsen, S. B. (2009). Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trends in Analytical Chemistry, 28, 1201–1222. https://doi.org/10.1016/j.trac.2009.07.007
Savitzky, A., & Golay, M. J. E. (1964). Smoothing and differentiation of data by simplified least squares procedures. Analytical Chemistry, 36, 1627–1639. https://doi.org/10.1021/ac60214a047
Schirrmann, M., Gebbers, R., & Kramer, E. (2013). Performance of automated near-infrared reflectance spectrometry for continuous in situ mapping of soil fertility at field scale. Vadose Zone Journal, 12(vzj2012), 0199. https://doi.org/10.2136/vzj2012.0199
Sen, A., & Srivastava, M. (1990). Regression analysis: Theory, methods and applications. Springer Texts in Statistics. https://doi.org/10.1007/978-3-662-25092-1
Sjaunja, L.-O. (2005). A review of spectroscopic methods and their suitability as analytical techniques for farm testing. Precision Livestock Farming, 5, 25–32.
Stenberg, B., Viscarra Rossel, R. A., Mouazen, A. M., & Wetterlind, J. (2010). Visible and Near Infrared Spectroscopy in Soil Science. In B. Stenberg (Eds.), Advances in Agronomy. Vol 107. Elsevier. Amsterdam. pp. 163–215
Terra, F. S., Demattê, J. A. M., & Viscarra Rossel, R. A. (2015). Spectral libraries for quantitative analyses of tropical Brazilian soils: Comparing vis–NIR and mid-IR reflectance data. Geoderma, 255–256, 81–93. https://doi.org/10.1016/j.geoderma.2015.04.017
Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society. Series B (methodological), 58(1), 267–288.
Utermann, J., Gorny, A., & Hauenstein, M. (2000). Labormethoden-Dokumentation: Mit 5 Tabellen (Geologisches Jahrbuch Reihe G, Informationen aus den Bund/Länder-Arbeitsgruppen der Staatlichen Geologischen Dienste in der Bundesrepublik Deutschland, Vol. 8). Stuttgart: Schweizerbart.
Viscarra Rossel, R. A., Walvoort, D. J. J., McBratney, A. B., Janik, L., and Skjemstad, J. O. (2001). Proximal sensing of soil pH and lime requirement by mid infrared diffuse reflectance spectroscopy. In: 3 ECPA-EFITA Proceedings: Third European Conference on Precision Agriculture, Montpellier 2001/G. Grenier, S. Blackmore and J. Steffe. - Montpellier: Agro Montpellier, 2001.
Viscarra Rossel, R. A., Cattle, S. R., Ortega, A., & Fouad, Y. (2009). In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy. Geoderma, 150, 253–266. https://doi.org/10.1016/j.geoderma.2009.01.025
Viscarra Rossel, R. A., & McBratney, A. B. (2008). Diffuse reflectance spectroscopy as a tool for digital soil mapping. In A. E. Hartemink, A. McBratney, & M.-S. de Lourdes (Eds.), Digital soil mapping with limited data (pp. 165–172). Dordrecht: Springer.
Viscarra Rossel, R. A., McGlynn, R. N., & McBratney, A. B. (2006a). Determining the composition of mineral-organic mixes using UV–Vis–NIR diffuse reflectance spectroscopy. Geoderma, 137, 70–82. https://doi.org/10.1016/j.geoderma.2006.07.004
Viscarra Rossel, R. A., Walvoort, D. J. J., McBratney, A. B., Janik, L. J., & Skjemstad, J. O. (2006b). Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma, 131, 59–75. https://doi.org/10.1016/j.geoderma.2005.03.007
Vogel, S., Bönecke, E., Kling, C., Kramer, E., Lück, K., Nagel, A., et al. (2020). Base neutralizing capacity of agricultural soils in a quaternary landscape of North-East Germany and its relationship to best management practices in lime requirement determination. Agronomy, 10, 877. https://doi.org/10.3390/agronomy10060877
Vogel, S., Bönecke, E., Kling, C., Kramer, E., Lück, K., Philipp, G., et al. (2022). Direct prediction of site-specific lime requirement of arable fields using the base neutralizing capacity and a multi-sensor platform for on-the-go soil mapping. Precision Agriculture, 23, 127–149. https://doi.org/10.1007/s11119-021-09830-x
Wight, J. P., Ashworth, A. J., & Allen, F. L. (2016). Organic substrate, clay type, texture, and water influence on NIR carbon measurements. Geoderma, 261, 36–43.
Wijaya, I. A. S., Shibusawa, S., SASAO, A., & Hirako, S. (2001). Soil parameters maps in paddy field using the real time soil spectrophotometer. Journal of the Japanese Society of Agricultural Machinery, 63(3), 51–58.
Wold, H. (1975). Soft modelling by latent variables: The Non-Linear Iterative Partial Least Squares (NIPALS) approach. Journal of Applied Probability, 12, 117–142. https://doi.org/10.1017/S0021900200047604
Wold, S., Antti, H., Lindgren, F., & Öhman, J. (1998). Orthogonal signal correction of near-infrared spectra. Chemometrics and Intelligent Laboratory Systems, 44, 175–185. https://doi.org/10.1016/S0169-7439(98)00109-9
Acknowledgements
We would like to say special thanks to Jessica Pamela Hernández Duarte for laboratory and spectral analysis, but also to Leon Schade, Giovanna Rehde, and Markus Schleusener for their help with the laboratory analysis as well as Karl Josef Meiwes for his valuable advice. Furthermore, we thank the two anonymous reviewers for their helpful remarks.
Funding
Open Access funding enabled and organized by Projekt DEAL. This work was conducted within the project ‘pH-BB: precision liming in Brandenburg’ (http://ph-bb.com) which is part of the agricultural European Innovation Partnership program (EIP-AGRI) to improve agricultural productivity and sustainability (Project No.: 204016000014/80168341). The program is funded by the European Agricultural Fund for Rural Development of the European Commission and by the Ministry of Rural Development, Environment and Agriculture of the state Brandenburg in Germany.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
(see Tables
5 and
6).
Appendix 2
(see and Fig.
5 and Table
7).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Horf, M., Bönecke, E., Gebbers, R. et al. Utility of visible and near-infrared spectroscopy to predict base neutralizing capacity and lime requirement of quaternary soils. Precision Agric 24, 288–309 (2023). https://doi.org/10.1007/s11119-022-09945-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11119-022-09945-9