Introduction

Root system architecture (RSA) describes the morphology and topology of a root system, responsible for water and nutrient uptake, anchorage to soil and interacting with soil biota. Plant functions, such as water and nutrient uptake, are strongly affected by root system architecture (Hochholdinger 2016). The structure of root systems is usually different under different soil-environmental conditions (Fan et al. 2016; Gorim and Vandenberg 2017; de Moraes et al. 2018).

During the last few decades, plant-breeding programs have improved crop production significantly by introducing new varieties based on architectural root traits. Del Bianco and Kepinski (2018) showed the potential benefits of developing phenotypes such as crops with deep root systems to capture deep water and nutrients with high efficiency. In a study based on the hypothetical maize ideotypes, which adapt architectural root traits, Lynch (2013) demonstrated the possibility of extracting deep water and Nitrogen. Therefore, characterization of root system architectures is one of the highest interests in the root phenotyping community.

In comparison to field phenotyping, lab-based methods are widely used in root phenotyping due to a lack of accessibility and reliable methods to characterize the RSA of plants grown in field conditions (Atkinson et al. 2019; Meister et al. 2014). Imaging methods have been used successfully to recover RSA parameters of plants grown in soil (Bodner et al. 2018; Topp et al. 2013; van Dusschoten et al. 2016), which were subsequently used in RSA models that extrapolate RSA from the seedling to mature plant stage (Zhao et al. 2017). Methods for root sampling and for characterizing RSA traits and their limitations are summarized in Fang et al. (2012) and Judd et al. (2015).

However, the root traits of young plants grown in the controlled lab environment are not sufficient to determine traits of mature plants that grow in field soils subject to the real field soil and environmental conditions (Paez-Garcia et al. 2015). Therefore, field phenotyping methods are becoming increasingly popular to characterize RSA in real field conditions (Araus and Cairns 2014; Meister et al. 2014).

Root sampling methods are generally used to measure the root distribution with depth (as root length density) from soil cores (Wasson et al. 2014), root intersection counting in trench profiles (Vansteenkiste et al. 2014), root arrival curves (root length density varies with time in continuous measurement) using minirhizotron methods (Majdi 1996), and excavation methods (Böhm 1979), to determine the total root mass distribution of plants. All these methods have traditionally been used to obtain some limited information about the root distribution in the soil. Nevertheless, the data may contain information about the detailed root system architecture or architectural root traits, i.e., number of primary roots, the distance between lateral roots, branching angles. However, obtaining RSA parameters from field data remains a challenge as they represent more aggregated information about the root system. In addition to classical methods, innovative field sampling methods have been introduced to obtain more detailed information about the root system (Bucksch et al. 2014; Wu and Guo 2014). Although field sampling methods provide limited information, it is of utter interest to study the possibility of retrieving the hidden information (3-D RSA) in field sampling data.

Few studies were conducted to estimate the root architecture parameters inversely; a density-based model of root image data of individual root systems was investigated to determine the root growth parameters (Kalogiros et al. 2016). Although this study showed reasonable estimates with the measured root growth parameters, experiments were limited to short-lived root growth in filter papers that do not resemble real field conditions. Garre et al. (2012) used dynamic root growth data measured using minirhizotrons to calibrate a RSA model. The main limitation of this approach was that only a subset of the model parameters was estimated inversely, and the posterior distribution of the parameter estimates was not derived. Trench profiles and soil core data were used by Vansteenkiste et al. (2014) to estimate the trait information such as total root length and root distribution successfully from measured and simulated data, and this study did not consider the RSA parameters extensively. A study was conducted by Pagès et al. (2012) to show the possibility of retrieving some RSA parameters using field sampling methods. ‘CPU and memory consumption, especially for big root systems, as well as algorithmic and numerical problems due to the stochastic characteristics of the RSA model during inversion’ (Pagès et al. 2012) motivated them to develop a metamodel that was based on a global sensitivity analysis of the RSA model and that considered the main parameter effects as well as parameter interactions. The authors showed the possibility of estimating some RSA parameters that are directly linked to the RLD of specific depths. Furthermore, a recent study presented the use of the approximate Bayesian computation (ABC, e.g., Marjoram et al. 2003) framework to characterize root growth parameters from synthetic and experimental data that are limited to early stages of root system development and that use directly observed RSA instead of aggregated field sampling data (Ziegler et al. 2019).

To represent the fact that root systems of two plants of the same variety or even with the same genotype differ, random factors or stochasticity are built in RSA simulation models. Even though simulated RSA differ for different parameter sets, these differences may be averaged out in the aggregated sampling data so that different sets of RSA parameters may produce the same aggregated output. Therefore, when estimating parameters, care must be taken to prevent overfitting which is associated with parameter uncertainty. This randomness or stochasticity is averaged out in sampling data that aggregate information from different plants. Nevertheless, since sampling data contain information of a finite number of plants, the stochasticity or randomness of these individual plants is not averaged out completely but remains to some extent in the sampling data. This stochasticity or uncertainty in the sampling data is another source of parameter estimates uncertainty. Therefore, it is important to assess the uncertainty of the RSA parameters that are obtained from aggregated sampling data.

In previous work (Morandage et al. 2019), we identified the most sensitive parameters of root systems of wheat and maize with respect to aggregated data or root system measures derived from soil coring, trenching and minirhizotron root sampling methods. In that same study, we showed how the sensitivity of the model output to the different root architectural parameters varies with the sampling method and considered "root system measures" (such as root length density at different depths in the soil profile, maximal rooting depth, etc.). We indicated that the most sensitive parameters could be retrieved potentially by inverse estimation. Moreover, using a principal component analysis of parameter sensitivities, we identified parameter groups of which the effect of their changes on the simulated root system measures could be compensated by changes of other parameters in that group.

Bayesian inference can be identified as a potential approach for estimating RSA parameters from aggregated field sampling data and their uncertainty encoded within the so-called parameter posterior probability density function (pdf). The application of Bayesian methods has been tested successfully in many fields (Hines 2015; Vrugt et al. 2009) and has been shown to be a robust approach to estimate parameters and their uncertainty, also when the model outcome depends non-linearly on the parameters and non-linear parameter interactions exist. Previous sensitivity analyses (Garre et al. 2012; Morandage et al. 2019; Pagès et al. 2012) showed that this is the case for RSA models. In comparison to local and/or non-probabilistic optimization algorithms, the main disadvantage of Bayesian methods is that sampling the posterior distribution typically requires a large number of forward model runs. In addition, simulation of many root systems in the field and their sampling incurs large computational costs. Therefore, Bayesian inversion can take a considerable amount of time. Furthermore, an important problem that arises for RSA models that have a stochastic component is that the simulated observations themselves are stochastic. As mentioned before, this stochasticity can be reduced by increasing the number of plants that are simulated and used to calculate the aggregated root distribution. Unfortunately, this can incur prohibitively large computational costs. Therefore, approaches must be found to deal with this model stochasticity in a Bayesian inversion framework.

In this work, we present an approach to inversely estimate stochastic root architecture model parameters and their uncertainty from field sampling data using Bayesian inference. The rest of this paper is organized as follows. Section 2 presents our proposed inference method and how its performance is evaluated using plot-scale simulation of root density. In section 3, we study which RSA parameters can be successfully retrieved from the inversion of soil coring data. This is followed by section 4, which discusses the feasibility and remaining challenges associated with the application of our approach to real field conditions.

Materials and methods

Root architectural model and virtual root sampling data

The synthetic soil coring root sampling data analogous to real field sampling data were obtained from simulated root systems in a virtual field plot using known root architecture parameters. Using data from a virtual experiment instead of real data, we can evaluate how closely the inversely estimated RSA parameters match the known ‘true’ parameters. Based on this comparison, we can conclude which RSA parameters could be derived by inverse modeling.

We selected the stochastic root architecture model CRootBox (Schnepf et al. 2018a, b) for root system simulations and root sampling. CRootBox, the successor and C++ porting of the Matlab-based RootBox model (Leitner et al. 2010), is a generic root system architecture model used to simulate realistic root systems taking root architecture parameters as model input. CRootBox is primarily used for functional-structural root system modeling. Schnepf et al. (2018a, b) showed that the model could be used successfully for simulation of both individual root systems as well as field-grown root systems and performed a statistical characterization of CRootBox based on 18 characteristic root system measures including root tip density, root length density, root surface area density or convex hull volume. As an example use of the CRootBox model, Landl et al. (2018) showed that widely available 2D images of root systems can be used systematically and efficiently to parameterize 3D root architecture models. CRootBox is further developed as CPlantBox to simulate the whole plant structures and more complex plant functions (Zhou et al. 2020). Please refer to (Schnepf et al. 2018a, b) for detailed information about the root architecture model CRootBox. The detailed root system simulation, sampling, and the sensitivities of root system measures to parameters of each sampling scheme are discussed in (Morandage et al. 2019).

For the inversion, we selected the core sampling data obtained from winter wheat root sampling. Wheat plant root systems were simulated in a 72 cm*45 cm size plot that consists of seven rows with 16 plants in a row. The inter-row distance was 12 cm with 3 cm plant spacing within a row. Core sampling was performed with monthly time intervals for eight months. We adjusted the sampling size similar to real field sampling schemes. We chose 3 locations in-between rows for five different rows (15 core samples in a plot in total). To avoid boundary effects, zones of 20 cm from the borders of the plot were not considered for sampling (Fig. 1A). Cylindrical cores of 4.2 cm diameter and 160 cm long were sampled and subsequently sliced horizontally in 5 cm intervals to determine the RLD of each sampling volume (69.72 cm3). Thus, core root sampling data are written to a text file which consists of 15*8*32 values of root length densities (see below) as the output of the model. Fig. 1B indicates the RLD’s of 15 cores separately (black-dashed lines) and the mean RLD of those 15 cores (solid green line), while Fig. 1C shows the mean of 32 repetitions (solid blue line) of mean RLD of 15 core samples to understand the stochastic nature of sampling data of simulated root systems.

Fig. 1
figure 1

Top (A): Simulated winter wheat root systems in a virtual field plot until 240 days after sowing (color scale indicates the appearance time of the root segments and the vertical transparent cylinders represent the soil cores). Bottom: RLD profiles of simulated core sampling data. Black dashed lines show the RLD of each core sample separately. The green line shows the mean RLD of 15 core samples (B), the blue line in (C) indicates the mean of 32 sets of 15 soil cores and the red line indicates the average of 15 cores that was chosen and used as measured data for inverse estimation of RSA parameters (C)

Full size image

Root length density of 5 cm segments of 160 cm long core samples were taken at monthly time intervals up to 8 months (8-time step information for 32, 5 cm depth intervals). We sampled 15 cores from the plot and calculated the mean and standard deviations of those 15 core samples. Therefore, RLD root sampling data consists of 256 mean root length density values (MRLD (cm/cm3) (Eq. 1).

$$M_{{RLD}_{i,j}}=\frac1n\sum\limits_{k=1}^n{RLD}_{i,j,k}$$
(1)

where n is the number of samples per depth (15), i is sampling depth index, j the sampling time index, and k is the sampling number index. \({RLD}_{i,j,k}\) is a 3d matrix, which stores root length density (RLD) values obtained from 32 depth intervals (i), and 8 monthly intervals (j) in 15 core samples (k), n =15 (number of cores taken from the plot). Since the variability of the root length densities between the 15 soil samples that were collected at a certain depth and time also contains information about the root system architecture, we also calculated standard deviation values for each of the 256 time and depth observations (SRLD (cm/cm3) (Eq. 2).

$${S}_{{RLD}_{i,j}}=\sqrt{\frac{{\sum }_{k=1}^{n}{\left({RLD}_{i,j,k}-{M}_{{RLD}_{i,j}}\right)}^{2}}{n}}$$
(2)

Selection of the most sensitive parameters of root system architecture and their prior distribution

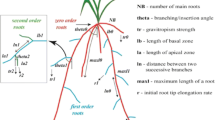
The CRootBox model was fitted against the synthetic soil coring data.”. We conducted a detailed analysis of sensitivities of 37 root architecture parameters in a previous study and found that the parameters of zeroth-order roots have higher sensitivities on root length densities obtained from soil cores (Morandage et al. 2019). Therefore, we selected numbers (NB), internodal distance (ln0 & ln0s) maximum length (maxl0 & maxl0s) elongation rate (r0 & r0s), tropism strength (tr0 & tr0s), insertion angle (theta0 & theta0s) of zero-order roots and length of apical zone (la1 & la1s), internodal distance (ln1 & ln1s), maximum length (maxl1 & maxl1s) of first-order laterals as inferred parameters. Primary roots, seminal roots, and crown roots are altogether referred to as "zero-order roots," and first-order laterals emerge from zero-order roots and second-order laterals emerge from first-order laterals (Fig. 2). All these parameters (except NB) are stochastic in the model and parameter names ending with “s” refer to the standard deviation of the parameter. The stochastic parameter distribution was assumed to be a Gaussian distribution. Since the literature data does not provide a proper estimation for desired limits and distribution of the field derived RSA parameters, we defined the 50% and 150% of true parameter values as the upper and lower bounds of the 17 inferred parameters and assumed that the priors are uniformly distributed within these limits. The true parameters were the same as the ones used in Morandage et al. (2019) to simulate RSA of wheat. The list of all RSA parameters of winter wheat and their bounds used in this study are listed in Table 1 and illustrates the meaning of the parameters in Fig. 2.

Fig. 2
figure 2

Description of wheat root system architecture and the terminology of root types (modified after Morandage et al. 2019; Tang et al. 2011). Embryonic and post embryonic roots (crown roots, seminal root, brace roots, and primary roots) are represented and termed collectively as “Zero order roots”

Full size image
Table 1 List of root architectural parameters of wheat used in root system simulations and the prior range of inferred parameters. Except for the number of zero-order roots NB, each parameter is a stochastic parameter with a mean and a standard deviation (values inside the brackets indicate the standard deviations of the parameters). Numbers in the parameter names refer to the root orders. Underlined values are the parameters used for inference and the others are fixed to true parameter values
Full size table

Selection of the synthetic measurements

To create the synthetic measurements, we ran the CRootBox model once using the reference or “true” parameters presented in Table 1. Since the CRootBox model is stochastic (see section 2.6), this creates just one realization of 256 MRLD and 256 SRLD values (see (Eq. 1) and (Eq. 2)) associated with the true parameters. However, such a single synthetic dataset would represent repeated root sampling data of the same plants and at the same locations. Since in real field experiments, soil core sampling is a destructive method; cores taken at different times come from different locations and sample roots of different plants. Therefore, the synthetic dataset was constructed from 15 virtual soil cores at 8 different times. For each of the 32 depths, and each time point, the virtual root length density data consist of a mean and a standard deviation, thus a total number of (32×8) + (32×8) = 512 values. In order to compute the standard deviations of the residual errors, σi, that are required by our likelihood function (Eq. 5), we generated this virtual data set 100 times and computed the standard deviation of each of the i=1, …, 512 simulated data points (i=1, …, 256: MRLD; i=257, .., 512: SRLD) across these 100 realizations.

Bayesian approach

In general, the output of a model F (\({\varvec{\upvartheta}}\)), where \({\varvec{\upvartheta}}\) = (\({\vartheta }_{1}\), \({\vartheta }_{2}\)…, \({\vartheta }_{d}\)) is a d- dimensional parameter vector, is compared with observations y to estimate the model parameters:

$$\mathbf{y}=F\left({\varvec{\upvartheta}}\right)+\mathbf{e}$$
(3)

where e is an error term that lumps measurement and model errors. When the process that is observed and the model that is used to describe the process is stochastic, i.e., when there is an unknown variability in the system that leads to different responses under the same external conditions, then e also comprises this stochasticity. Often, the parameters of the model are not known and are estimated by searching for the parameter values that minimize the norm of e. When using the Bayesian framework to acknowledge parameter uncertainty, the goal is to derive the posterior probability density function (pdf) of the model parameters of interest, \({\varvec{\upvartheta}}\), given the observations, y, as expressed by

$$p({\varvec{\upvartheta}}|\mathbf{y})=\frac{p(\mathbf{y}|{\varvec{\upvartheta}})p({\varvec{\upvartheta}})}{p(\mathbf{y})}$$
(4)

where p(\({\varvec{\upvartheta}}\)|y) is the posterior pdf of \({\varvec{\upvartheta}}\) given y, p(y|\({\varvec{\upvartheta}}\)) ≡ L(\({\varvec{\upvartheta}}\)|y) denotes the likelihood function of \({\varvec{\upvartheta}}\), p(\({\varvec{\upvartheta}}\)) is the prior pdf of \({\varvec{\upvartheta}}\), the normalization factor p(y) = ∫ p(y|\({\varvec{\upvartheta}}\))p(\({\varvec{\upvartheta}}\))d \({\varvec{\upvartheta}}\) is obtained from numerical integration over the parameter space so that p(\({\varvec{\upvartheta}}\)|y) scales to unity. The quantity p(y) is generally difficult to estimate in practice but is not required for parameter inference. In the remainder of this study, we will focus on the unnormalized posterior:

$$p\left({\varvec{\upvartheta}}|\mathbf{y}\right) \propto L\left({\varvec{\upvartheta}}|\mathbf{y}\right)p({\varvec{\upvartheta}})$$
(5)

Moreover, in case of a uniform prior, (Eq. 5) simplifies to p(\({\varvec{\upvartheta}}\)|y)∝ L(\({\varvec{\upvartheta}}\)|y). For numerical stability, it is often preferable to work with the log-likelihood function, \(\ell\) (\({\varvec{\upvartheta}}\)|y), instead of L(\({\varvec{\upvartheta}}\)|y). If we assume the error e to be normally distributed, uncorrelated and heteroscedastic, the log-likelihood function can be written as

$$\ell\left(\boldsymbol\vartheta\vert\mathbf y\right)=-\frac n2\log\left(2\pi\right)-\sum_{i=1}^nlog\left(\sigma_i\right)-\frac12\sum_{i=1}^n\frac{\left[y_i-F_i\left(\boldsymbol\vartheta\right)\right]^2}{\sigma_i^2}$$
(6)

where n is the number of measurement data and the \({\sigma }_{i}\) are the standard deviations of the residual errors \({e}_{i}\). Note that in our context, the subscript i refers to a combination of time and depth.

Markov chain Monte Carlo sampling

The inference aims to estimate the posterior distribution of the model parameters, \({\varvec{\upvartheta}}\), given the available measurements y: p(\({\varvec{\upvartheta}}\)|y). As an exact analytical solution of p(\({\varvec{\upvartheta}}\)|y) is not available, we resort to Markov chain Monte Carlo (MCMC) simulation to generate samples from this distribution. The basis of this technique is a Markov chain that generates a random walk through the search space and iteratively finds parameter sets with stable frequencies stemming from the posterior pdf of the model parameters (see, e.g., Robert and Casella 2004) for a comprehensive overview of MCMC simulation). The MCMC sampling efficiency largely depends on the proposal distribution used to generate candidate solutions in the Markov chain. In this study, the state-of-the-art DREAM(ZS) (Laloy and Vrugt 2012; ter Braak and Vrugt 2008; Vrugt 2016) algorithm is used to retrieve posterior samples. The DREAM(ZS) scheme evolves different interacting Markov chains in parallel. A detailed description of this sampling scheme, including convergence proof, can be found in the cited literature and is thus not reproduced here.

The convergence of the MCMC sampling to the posterior distribution was monitored by means of the potential scale reduction factor of Gelman and Rubin (Gelman and Rubin 1992), \(\widehat{R}\) a value of \(\widehat{R}\) smaller than 1.2 for every parameter was considered as indicating official convergence of the sampling to a stationary distribution.

The mean acceptance rate (AR %) of the proposed transitions in the Markov chains is an important sampling property and is thus also reported. A too small fraction of accepted moves points out poor mixing of the chains due to a too wide proposal distribution. In contrast, an overly large acceptance rate suggests a too narrow proposal distribution, causing the Markov chains to remain in the close vicinity of their current locations. The optimal AR value depends on the proposal and target posterior distributions, but a range of 10–40% generally indicates a good performance of DREAM(ZS) (Laloy and Vrugt 2012; Ter Braak 2006; Ter Braak and Vrugt 2008).

Dealing with model stochasticity and non-independent data errors

To represent the random nature of the root distribution in real field conditions, root architecture models internally draw realizations of some of their parameters from prescribed probability distributions (Tron et al. 2015). In other words, many of the parameters that are internally used in a given forward simulation by the model are randomly drawn from prespecified probability distributions. The parameters of these distributions (e.g., mean and standard deviation in case of a Gaussian distribution) are the actual RSA parameters and are to be set by the model user. Consequently, repeatedly using the same set of RSA parameter values leads to an ensemble of different outputs (such as RLD in soil core samples). With increasing size of the output (i.e., with an increasing number of soil cores that are taken), the variability of the ensemble in terms of MRLD and SRLD (see Eqs. 1, 2) will asymptotically converge to zero.

When using MCMC for Bayesian inference, the forward model is typically considered as deterministic and a given input parameter set thus always corresponds to the same log-likelihood. Hence, DREAM(ZS) requires the log-likelihood for a given parameter set not to vary. To deal with model stochasticity, we therefore averaged the simulated data corresponding to a given input parameter set over a certain number of realizations before computing the log-likelihood. Using the true model parameters, we studied how many realizations, i.e., sets of 15 soil cores, are needed to obtain a relatively stable log-likelihood estimate (red curve in Fig. 3). It is observed that from 150 realizations (or repetitions of 15 soil cores), the computed log-likelihood based on the true parameters given the used measurements becomes approximately stable (red curve in Fig. 3). Such averaging of the log-likelihood falls within the so-called likelihood ratio approximation method (Diggle and Graton 1984) which in a probabilistic setting is a form of ABC (Marjoram et al. 2003).

Fig. 3
figure 3

Evolution of the log-likelihood as a function of the number of repetitions, i.e., sets of 15 soil cores, used to average the simulated data before calculating the log-likelihood. The red line indicates changes in the classical log-likelihood while the blue line denotes changes in the inflated log-likelihood

Full size image

Nevertheless, a short preliminary MCMC trial using 150 simulated data realizations to calculate the log-likelihood led to a substantial overfitting of the measurement data, with the MCMC returning only log-likelihood values in the approximate 1030 - 1040 range after some 3000 iterations, whereas the true parameter set has a log-likelihood of about 950 for the simulated data (red curve in Fig. 3). We hypothesize that this overfitting is mainly due to unknown data error dependencies (correlations and higher-order dependencies) that are not accounted for by our classical uncorrelated Gaussian log-likelihood formulation that assumes independent data errors (Eq. 6). Models of data errors correlations could be included in the formulation of the log-likelihood functions. But these models require extra parameters that need to be estimated (e.g. parameters of spatial correlation functions) and these correlation functions may change over time and may also be dependent on the RSA parameters. We therefore used a simple and pragmatic approach to overcome this overfitting problem and ‘inflated’ the used log-likelihood function by multiplying the standard deviations of the data errors by a constant factor. We obtained the value of this inflation factor as follows. We computed two distributions of log-likelihoods, distributions I and II, always using the true parameter set and our classical uncorrelated Gaussian log-likelihood formulation:

  • Distribution I is the distribution of 200 log-likelihoods that are calculated from 200 white noise realizations used to corrupt the mean log-likelihood (over 150 simulated data realizations). The white noise distribution has a diagonal covariance matrix that contains the 512 variances of the data errors computed in section 2.1(for this calculation, the error term, \(\left[{y}_{i}-{F}_{i}\left({\varvec{\upvartheta}}\right)\right]\) was therefore randomly drawn from the assumed measurement error distribution). This distribution of log-likelihoods thus corresponds to the distribution that would be expected if the data errors were truly independent

  • Distribution II is the distribution of 200 log-likelihoods using each time a different realization as "observations" and the ensemble mean over 150 simulated realizations of RSA simulation model as the forward model simulation. This distribution of log-likelihoods thus somehow encodes the effect of dependencies between the data errors. In addition, this distribution is “wider”, i.e., has a larger 95% uncertainty interval and interquartile range (IQR).

Based on the comparison between distributions I and II (see Fig. 4), one can estimate what the effect of the unknown data error dependencies on our classical uncorrelated Gaussian log-likelihood function is. More specifically, it can be derived that for distribution I to have the same IQR as distribution II, the standard deviations of the data errors used to derive distribution I need to be multiplied by a value of 2. Therefore, in the remainder of this study, we inflated the log-likelihood function by multiplying the standard deviations of the data errors by 2.

Fig. 4
figure 4

Distributions I and II used to compute the used inflation factor (see main text for details)

Full size image

The inflation strategy described above was found to prevent overfitting, but the required averaging of the simulated data over 150 realizations makes it unfortunately too computationally-demanding for the MCMC to converge within a reasonable amount of time, given our available computational resources. In our case, each simulation model run takes about 1-12 minutes, depending on the parameter combinations. When using DREAM(ZS) with the required minimum of 3 interacting Markov chains together with parallelizing the 150 realizations per proposed parameter set over 32 CPUs, it still incurs a computational cost of about 9-10 days to perform 500 MCMC iterations (that is, to achieve 167 transitions in each of the used 3 Markov chains). To make the MCMC sampling affordable given our available 32 CPUs, we therefore decided to perform 32 realizations only. Averaging the simulated data over 32 realizations instead of 150 makes that the log-likelihood remains stochastic to some extent. To deal with this remaining stochasticity, we proceeded as follows.

The likelihood for a certain parameter set \({\varvec{\upvartheta}}\) for a given dataset y is calculated from [Eq. 6], where F(\({\varvec{\upvartheta}}\)) is the prediction by the model of the data. The problem now is that F(\({\varvec{\upvartheta}}\)) is stochastic and should be written as F(\({\varvec{\upvartheta}}\),\({\varvec{\epsilon}}\)) where \({\varvec{\epsilon}}\) represents a vector of zero-mean random numbers that varies from realization to realization. We can write F(\({\varvec{\upvartheta}}\),\({\varvec{\upepsilon}}\)) = <F(\({\varvec{\upvartheta}}\))> + δ where < > represents the expected value of F(\({\varvec{\upvartheta}}\),\({\varvec{\upepsilon}}\)) and δ is the deviation from the expected value for a certain set \({\varvec{\epsilon}}\). As we average F(\({\varvec{\upvartheta}}\),\({\varvec{\upepsilon}}\)) for a given \({\varvec{\upvartheta}}\) over an increasingly large number of \({\varvec{\epsilon}}\) realizations, F(\({\varvec{\upvartheta}}\),\({\varvec{\epsilon}}\)) converges to <F(\({\varvec{\upvartheta}}\))> and ||δ|| to 0. The problem is that it may require a prohibitively large number of F(\({\varvec{\upvartheta}}\),\({\varvec{\epsilon}}\)) simulations to reach a sufficiently small ||δ|| for the MCMC inference not to be disturbed. Let us define ε as the stochastic term that represents the random nature (or stochasticity) of the root growth after averaging over a number R of \({\varvec{\upepsilon}}\) realizations: F(\({\varvec{\upvartheta}}\),\({\varvec{\upepsilon}}\)) = \(\frac{1}{R}\sum_{i=1}^{R}F\left({\varvec{\upvartheta}},\boldsymbol{ }{{\varvec{\epsilon}}}_{i}\right)\) with \({\varvec{\upvarepsilon}}=\left[{{\varvec{\epsilon}}}_{1},\dots ,{{\varvec{\epsilon}}}_{R}\right]\). For a certain observation dataset \(\mathbf{y}\), we can define the log-likelihood of the combination of a given \({\varvec{\upvartheta}}\) and a certain realization ε as \(\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right).\)

In order to investigate the variation with \({\varvec{\upvarepsilon}}\) of the log-likelihood \(\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right)\) of a certain parameter set \({\varvec{\upvartheta}}\) and a limited set of \({\varvec{\upvarepsilon}}\) for a certain observation dataset y, the likelihood of the ‘true’ parameter set was evaluated for 20 observation datasets y and 15 sets of \({\varvec{\upvarepsilon}}\) where each \({\varvec{\upvarepsilon}}\) corresponded with stochastic forward simulations of 32 realizations of 15 soil cores. This was done for 9 different ‘true’ parameter sets (Table 2). The parameter sets were chosen by systematically increasing the parameter values from the lower bounds to the upper bounds of 17 selected parameters for the inference, i.e., P1 indicates the likelihoods of the lowest values (50% of the true parameter), while P9 indicates the highest values (150% of the true parameter) of each parameter. This means that for each considered parameter set, \(\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right)\) was evaluated for 15 different ε vectors and 20 y observation vectors. From this data set of 300 \(\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right)\) values we calculated the overall mean, the mean standard deviation of the \(\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right)\) values that were obtained for a given y but for different ε, stdev \(\ell\_\boldsymbol\varepsilon\), and the standard deviation of \(\ell\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\) values that were averaged over ε, stdev \(\ell\_\mathbf y\). The stdev \(\ell\_\mathbf y\) thus reflects the impact of the differences between different observation datasets on \(\ell\) due to the noise on the experimental data (which in turn is caused by the random nature of the root growth process). In contrast, stdev \(\ell\_\boldsymbol\varepsilon\) represents the impact on \(\ell\) of the stochastic noise associated with the simulation results due to the finite number of samples that are simulated. In Table 2, mean \(\ell\), stdev \(\ell\_\mathbf y\), and stdev \(\ell\_\boldsymbol\varepsilon\) are shown for 9 parameter sets \({\varvec{\upvartheta}}\).

Table 2 Mean of log-likelihoods \(\ell\) for the true parameter set that are obtained from a combination of 20 different observations and 15 sets of forward simulations (each consisting of 32 realizations of 15 soil cores), standard deviation of the log-likelihoods due to observation dataset noise stdev \(\ell\_y\), and due to stochastic simulation noise stdev \(\ell\_{\varvec{\varepsilon}}\) for 9 different parameter sets. See the main text for the calculation details of stdev \(\ell\_y\) and stdev \(\ell\_\boldsymbol\varepsilon\)
Full size table

Since the total number of RLD samples that is simulated for each log-likelihood evaluation is 32 times larger than the number of RLD samples in an observation dataset, stdev \(\ell\_{\varvec{\upvarepsilon}}\) is smaller than stdev \(\ell\_\mathbf{y}\). Table 2 also shows that the noise of the simulation results depends on the parameters. The parameter sets with a smaller log-likelihood have a larger standard deviation of the root growth parameters, which leads to more stochasticity and therefore to a larger variation in the log-likelihood.

As written above, the log-likelihood for a given observation dataset does not depend only on the parameter set \({\varvec{\upvartheta}}\) but also on the set of random numbers, ε. The combination of \({\varvec{\upvartheta}}\) and ε that jointly lead to the best match between the simulation results and observations will be selected by the MCMC. As sampling in the MCMC goes on, the algorithm always finds higher \(\ell\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\) for the same \({\varvec{\upvartheta}}\) due to the forward simulation model changing ε. The chance of finding a new (or the same) parameter set \({\varvec{\upvartheta}}\) for a new ε with sufficiently high \(\ell\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\) and accepting the new proposal decreases. This will cause the MCMC to get ‘stuck’ around a certain \({\varvec{\upvartheta}}\).

To avoid this problem, we propose to change the Metropolis acceptance rule of candidate parameter sets. The underlying idea is that we express the log-likelihood of the large ensemble \(\ell\left({\varvec{\upvartheta}}|\mathbf{y}\right)=\ell\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}\to \infty |\mathbf{y}\right)\) as the sum of the current log-likelihood \(\ell\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\) and a random number, κ, that is drawn from a distribution N(0, stdev \({\ell\_{\varvec{\upvarepsilon}}}^{2}\) ) (Eq. 7):

$$\ell\left(\boldsymbol\vartheta\vert\mathbf y\right)=\ell\left(\boldsymbol\vartheta,\boldsymbol\varepsilon\vert\mathbf y\right)+\kappa$$
(7)

For a deterministic model and a uniform prior distribution of \({\varvec{\upvartheta}}\), the Metropolis rule accepts a new parameter set \({{\varvec{\upvartheta}}}_{2}\) with probability

$$P=min\left(1,exp\left(\ell\left({{\varvec{\upvartheta}}}_{2}|\mathbf{y}\right)-\ell\left({{\varvec{\upvartheta}}}_{1}|\mathbf{y}\right)\right)\right)$$

For a stochastic model, our proposed probability of acceptance is thus:

$$P=min\left(1,exp\left(\ell\left({{\varvec{\upvartheta}}}_{2},{{\varvec{\varepsilon}}}_{2}|\mathbf{y}\right)-\ell\left({{\varvec{\upvartheta}}}_{1},{{\varvec{\varepsilon}}}_{1}|\mathbf{y}\right)+{\kappa }_{2}-{\kappa }_{1}\right)\right)$$

Based on the analyses reported in Table 2, we suggest to set stdev \(\ell\_{\varvec{\upvarepsilon}}\) = 4.

The pseudo-code of our modified MCMC approach for generating samples from \(p({\varvec{\upvartheta}}|\mathbf{y})\) in case of a stochastic likelihood, \(L\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\), reads as follows.

Algorithm A

A1. If now at \({{\varvec{\upvartheta}}}_{1}\), propose a move to \({{\varvec{\upvartheta}}}_{2}\) according to a transition kernel \(q\left({{\varvec{\upvartheta}}}_{1}\to {{\varvec{\upvartheta}}}_{2}\right)\)

A2. Calculate \(P=\mathrm{min}\left(1,\frac{L\left({{\varvec{\upvartheta}}}_{2},{{\varvec{\upvarepsilon}}}_{2}|\mathbf{y}\right)p\left({{\varvec{\upvartheta}}}_{2}\right)q\left({{{\varvec{\upvartheta}}}_{2\to }{\varvec{\upvartheta}}}_{1}\right)\mathrm{exp}\left({\kappa }_{2}\right)}{L\left({{\varvec{\upvartheta}}}_{1},{{\varvec{\upvarepsilon}}}_{1}|\mathbf{y}\right)p\left({{\varvec{\upvartheta}}}_{1}\right)q\left({{{\varvec{\upvartheta}}}_{1\to }{\varvec{\upvartheta}}}_{2}\right)\mathrm{exp}\left({\kappa }_{1}\right)}\right)\)

A3. Move to \({{\varvec{\upvartheta}}}_{2}\) with probability \(P\), else remain at \({{\varvec{\upvartheta}}}_{1}\); go to A1.

Under suitable regularity conditions and for a deterministic likelihood, \(L\left({\varvec{\upvartheta}},|\mathbf{y}\right)\), and \({\kappa }_{1}={\kappa }_{2}=0\), the so-derived \(p({\varvec{\upvartheta}}|\mathbf{y})\) is the stationary and limiting distribution of the chain. For a stochastic likelihood, \(L\left({\varvec{\upvartheta}},{\varvec{\upvarepsilon}}|\mathbf{y}\right)\), algorithm A will provide an approximation to \(p({\varvec{\upvartheta}}|\mathbf{y})\) of which the convergence properties still need to be studied. Yet we numerically show in section 2.7 that it can provide an unbiased estimate of the posterior mean and mode, with overestimated uncertainty.

Illustration of our approach for a simple toy problem

Before applying our method to our actual stochastic RSA model, this section illustrates the caveats associated with inference of stochastic models together with our proposed solution. For this toy problem, we consider a simple 2-dimensional linear stochastic forward model (toy model). This forward toy model, which has nothing to do with CRootBox simulation model except that both models are stochastic, is of the form:

$${\mathbf{y}}_{o}={\mathbf{w}}_{o}{\mathbf{X}}^{T}+{{\varvec{\upvarepsilon}}}_{o}$$
(8)
$${\mathbf{y}}_{m}={\mathbf{w}}_{m}{\mathbf{X}}^{T}+{{\varvec{\upvarepsilon}}}_{m}$$
(9)

where \({\mathbf{y}}_{o}\) is a vector of n observations (observed responses), \({\mathbf{w}}_{o}=\left[{w}_{0}^{o},{w}_{1}^{o}\right]\) contains a “true” intercept, \({w}_{0}^{o}\), and a “true” slope, \({w}_{1}^{o}\), \(\mathbf{X}\) is a matrix of input (or predictor) variables: \(\mathbf{X}=\left[\begin{array}{cc}1& {x}_{1}\\ \vdots & \vdots \\ 1& {x}_{n}\end{array}\right]\), \(T\) is the transpose operator, \({{\varvec{\upvarepsilon}}}_{o}\propto N(0,{\sigma }_{o}^{2}\mathbf{I})\) is the observational error with standard deviation \({\sigma }_{o}\), \({\mathbf{y}}_{m}\) is the n-dimensional vector of modelled variables, \({\mathbf{w}}_{m}=\left[{w}_{0}^{m},{w}_{1}^{m}\right]\) contains the two model parameters and \({{\varvec{\upvarepsilon}}}_{m}\propto N(0,{\sigma }_{m}^{2}\mathbf{I})\) is the stochastic component of the model with standard deviation \({\sigma }_{m}\). For such a linear problem with Gaussian errors, if the inferred model parameters, \({\mathbf{w}}_{m}\), are assigned a normal prior then the true posterior distribution of \({\mathbf{w}}_{m}\): \(p\left({\mathbf{w}}_{m}|{\mathbf{y}}_{o}\right)\), takes the closed form of a Gaussian density in \({\mathbf{w}}_{m}\). Using a zero-mean normal prior \({\mathbf{w}}_{m}\propto N(0,{{\varvec{\Sigma}}}_{w})\) with \({{\varvec{\Sigma}}}_{w}=\left[\begin{array}{cc}{\sigma }_{{w}_{0}}^{2}& 0\\ 0& {\sigma }_{{w}_{1}}^{2}\end{array}\right]\), \(p\left({\mathbf{w}}_{m}|{\mathbf{y}}_{o}\right)\) is given by

$$p\left({\mathbf{w}}_{m}|{\mathbf{y}}_{o}\right)=N\left({\mathbf{w}}_{m};{\mathbf{M}}^{-1}\mathbf{b},{\mathbf{M}}^{-1}\right)$$
(10)

with

$$\mathbf{M}=\frac{1}{{\sigma }_{p}^{2}}{\mathbf{X}}^{T}\mathbf{X}+{{{\varvec{\Sigma}}}_{w}}^{-1}$$
(11)
$$\mathbf{b}=\frac{{\mathbf{X}}^{T}{\mathbf{y}}_{o}}{{\sigma }_{p}^{2}}$$
(12)

where \({\sigma }_{{w}_{0}}^{2}\) and \({\sigma }_{{w}_{1}}^{2}\) are the prior variances of \({w}_{0}^{m}\) and \({w}_{1}^{m}\), \({\sigma }_{p}\) is the standard deviation of the measurement errors and the posterior mean vector is given by

$${\mathbf{M}}^{-1}\mathbf{b}={\left({\mathbf{X}}^{T}\mathbf{X}+{\sigma }_{p}^{2}{{{\varvec{\Sigma}}}_{w}}^{-1}\right)}^{-1}{\mathbf{X}}^{T}{\mathbf{y}}_{o}$$
(13)

Note that \({\sigma }_{p}={\sigma }_{o}\) in case of a deterministic model. For our stochastic model in (Eq. 9), \({\sigma }_{p}=\sqrt{{\sigma }_{o}^{2}+{\sigma }_{m}^{2}}\). In other words, the noise in the residual errors is the sum of the measurement noise with the forward model noise.

We used a 100-dimensional \(\mathbf{x}\) vector (given by the first feature from the well-known iris dataset: https://archive.ics.uci.edu/ml/datasets/iris) and created some synthetic measurements, \({\mathbf{y}}_{o}\), using \({w}_{0}^{o}=\) 2 (intercept) and \({w}_{1}^{o}=1\) (slope), and \({\sigma }_{o}= 0.5\). We set \({\sigma }_{{w}_{0}}={\sigma }_{{w}_{1}}=10\), \({\sigma }_{m}\)= 0.5 and performed two sampling-based inference of \(p\left({\mathbf{w}}_{m}|{\mathbf{y}}_{o}\right)\) with DREAM(ZS): a first one using regular MCMC and a second one using our proposed approach. In both cases, we allowed a total of 500,000 forward model evaluations of toy model, which we deem to be huge, given the fact that we only sample two parameters in a linear setup. Here the true posterior means, \({\mathbf{M}}^{-1}\mathbf{b}\) (Eqs.11 and 12), are \({\overline{w} }_{0}^{m}=0.959\) and \({\overline{w} }_{1}^{m}=1.174\).

Sampling results for the regular MCMC run are displayed in Fig. 5a, b as posterior (gray-colored) histograms, together with the true posterior distribution for \({\sigma }_{p}={\sigma }_{o}\) (red curve) and for \({\sigma }_{p}=\sqrt{{\sigma }_{o}^{2}+{\sigma }_{m}^{2}}\) (blue curve). Clearly, the MCMC-derived posterior distribution differs very much from the true one as it is quite erratic. It underestimates the true uncertainty a lot, it has completely wrong means and it does not encapsulate the true posterior means or modes (denoted by the red crosses). This pathological behavior of the MCMC is caused by the stochasticity in the forward toy model (\({{\varvec{\upvarepsilon}}}_{m}\) in (Eq. 9)).

Fig. 5
figure 5

True marginal posterior distributions (blue and red curves) and their MCMC-derived counterparts (gray histograms) for the two inferred parameters of our toy problem. Subfigures (a–b) display the results obtained by regular MCMC, while subfigures (c–d) and (e–f) depict the results of our proposed approach for two different values of \({\sigma }_{t}\). The red curves denote the true posterior distributions obtained for a deterministic (linear) model. The blue curves represent the true posterior distributions obtained if the (linear) model is stochastic (see Eq. 9 and associated text). The \(\widehat{m}\) symbol signifies the estimated posterior mean. The true posterior means are 0.959 and 1.174 for \({w}_{0}^{m}\) and \({w}_{1}^{m}\), respectively

Full size image

For our proposed approach, we take for this toy problem \(\kappa \propto N(0,{\sigma }_{t}^{2})\). Denoting by \({\mu }_{t}\) the mean of the log-likelihood of the true posterior means, \({\overline{w} }_{0}^{m}\) and \({\overline{w} }_{1}^{m}\), we test with coefficients of variation, \(\mathrm{CV}=\frac{{\sigma }_{t}}{{\mu }_{t}}\), of 10% (Fig. 5c, d) and 5% (Fig. 5e, f), respectively. It is seen that our approach estimates the true posterior means rather accurately. For the considered problem, this nevertheless comes with a substantial overestimation of the true posterior width for the case with CV = 10% (Fig. 5c, d). For CV = 5%, the derived posterior resembles the true posterior distribution (blue curves in Fig. 5e, f) a bit better, but some overestimation is still present. Yet \({\sigma }_{t}\) can of course not be decreased indefinitely. Still for this particular toy problem, our approach seems to keep providing accurate posterior means until CV becomes smaller than about 4% (not shown). As \({\sigma }_{t}\) is further decreased, the derived posterior becomes increasingly biased (not shown). Note that, unfortunately, the optimal value for \({\sigma }_{t}\) is very much problem-dependent, as it depends on the characteristics of both the stochasticity of the considered forward toy model and the used likelihood function. Overall, this toy problem demonstrates that our solution can dramatically improve MCMC sampling of a stochastic model, at the cost of overestimating uncertainty.

Results

MCMC sampling and convergence

We ran our Bayesian approach using a Python version of DREAM(ZS) (Laloy et al. 2017) in parallel over 32 CPUs for a total of 30,000 iterations (log-likelihood evaluations). The \(\widehat{R}\)-convergence was satisfied for every parameter from iteration 13620 on and we thus discarded the first 6810 samples as burn-in. Fig. 6 presents the evolution of the acceptance rate and variation of log-likelihoods throughout sampling. The final mean acceptance rate is about 14%. Moreover, the distribution of likelihoods after burn-in points to the mean value of 793 with a standard deviation of 7.

Fig. 6
figure 6

The trajectory of Log-likelihood and the MCMC acceptance rate throughout the sampling

Full size image

The number of zero-order roots (NB) parameter in the CRootBox model is considered as a plant parameter that determines how many primary roots emerge from the seed or next to the seed. This parameter is crucial in determining the total root length density of the sampling data. The tracer plot in Fig. 7a shows that the three chains equilibrated around the true NB value after some 3000 iterations. The posterior uncertainty associated with NB is however relatively large (Fig. 7b).

Fig. 7
figure 7

Sampling trajectory of the NB parameter in each of the 3 Markov chains (a). Each chain is coded with a different color (green, blue, orange) and the true value is denoted by the horizontal black dashed line. Corresponding marginal posterior density plot computed after discarding the first 6810 samples as burn-in (b)

Full size image

Fig. 8 shows the evolution of three Markov chains for the 16 remaining parameters (each chain coded with a different color). The black horizontal lines show the true parameter values. It is noticeable that the sampled maximum length of zero-order roots (maxl0) parameter values stabilize within the first 200 iterations and narrowly fluctuate around the true value. In addition, the sampled elongation rate of zero-order roots (r0) , insertion angle of zero-order roots (theta0), and standard deviation of elongation rate of zero-order roots (r0s) values also converge to their true counterparts, but with larger fluctuations. The other sampled parameters show higher posterior variations, especially the higher-order root parameters.

Fig. 8
figure 8

Tracer plots of MCMC sampling trajectories of inferred parameters of the three parallel Markov chains (panels: a to p). Each chain is coded by one different color. The dashed black lines show the true parameter values, and the y-axis indicates the lower and upper bounds of the uniform prior parameter distributions

Full size image

Fig. 9 shows the marginal posterior probability distribution. The blue markers represent true values. The probability distributions of the maximum length of zero-order roots (maxl0), elongation rate of zero-order roots (r0), standard deviation of elongation rate of zero-order roots (r0s), internodal distance of zero-order roots (ln0), and insertion angle of zero-order roots (theta0) parameters are normally distributed and approximately centered around the corresponding true values. Unlike the other zero-order parameters, standard deviation of internodal distance of zero-order roots (ln0s), standard deviation of maximum length of zero-order roots (maxl0s) , tropism strength of zero-order roots (tr0), and standard deviation of tropism strength of zero-order roots (tr0s) parameters are not resolved and display a wide posterior uncertainty. This is also the case for the higher-order parameters.

Fig. 9
figure 9

Marginal posterior probability density functions of sixteen parameters (panels a to p). The horizontal x indicates the prior range of parameter values, and the y-axes present the probability. The blue marker represents the true parameter value

Full size image

Parameter correlations

A principal component analysis of parameter sensitivities was conducted before the Bayesian inference to have insights of parameter combinations that interact and could produce problematic inversion results. According to that previous study (Morandage et al. 2019), the first two principal components explained 92.5 % of the total variability in the sensitivity of the soil coring data obtained at the end of the growth period (Fig. 10). The scatter plots in Fig. 11 highlight some important parameter correlations, while Appendix presents a detailed description of parameter correlations. The posterior correlations observed between the parameters (Fig. 11) are in agreement with the PCA analysis of sensitivities, especially with the first and second principal components. The parameters having high loadings in the PCA correspond with the parameters that were best resolved by the inversion (number of zero-order roots (NB), maximum length of zero-order roots (maxl0), insertion angle of zero-order roots (theta0)). Since measured data from different time intervals are used in the inversion while the performed PCA relied on the last observation time, elongation rate of zero-order roots (r0) parameter, which did not have a strong influence in the PCA, could also be inversely estimated with relatively high accuracy.

Fig. 10
figure 10

Biplot of principal component analysis of parameter loadings for the 1st and 2nd PCs of soil coring data (modified after (Morandage et al. 2019))

Full size image
Fig. 11
figure 11

Marginal probability distributions and joint distribution of strongly correlated parameter pairs with respective correlation factors (panels A, B, C and D)

Full size image

The internodal distance of the zero-order roots (ln0) parameter is related to the internodal distances of first-order roots on the zero-order roots and thus controls how many lateral roots (first-order laterals) emerge from the zero-order roots. An increasing number of zero-order roots (NB) and decreasing internodal distance of zero-order roots (ln0) both increase the root density. This implies that an increase in NB can be compensated by an increase in ln0 (Fig. 11A), which is reflected in a higher positive correlation of the parameter estimates of the number of zero-order roots (NB) and internodal distance of zero-order roots (ln0) as was also indicated by the PCA analysis (Fig. 10).

The insertion angle of zero-order roots (theta0) indicates the angle between the starting point of the root trajectory and the vertical (towards the gravity) direction. Wider insertion angles lead to a broader spreading of the root system, while narrower angles reduce the lateral spreading of roots. The insertion angle interacts with the tropism strength of zero-order roots (tr0), which determines how much the gravitational force influences root trajectory, i.e., higher values of tropism strength apply higher force on root tips to grow vertically towards the direction of the gravity. The higher gravitational force turns root tips towards the downward direction and reduces the lateral spreading of the root system. Consequently, insertion angle (theta0) and tropism strength of zero-order roots (tr0) show a relatively high positive linear correlation with R = 0.83 (Fig. 11B).

Fig. 11C shows a negative correlation between elongation rate of zero-order roots (r0) and standard deviation of elongation rate of zero-order roots (r0s). The negative correlation indicates the effect of the combination of parameter mean and its standard deviations. The correlation between insertion angle of zero-order roots (theta0) and standard deviation of insertion angle of zero-order roots (theta0s) shows the same effect (Fig. A. 1). The well resolved maximum length of zero-order roots (maxl0) parameter (Fig. 9c) determines the rooting depth of the entire root system. As shown in Figs. 11D and 1A, the maxl0 parameter is moderately correlated with the other parameters. As discussed previously, the tropism strength of zero-order roots (tr0), and maxl0 parameters influence the root distribution deeper in the soil profile. These two parameters show a moderate negative correlation in both the PCA analysis test and the joint correlation plots (Fig. 11D). Furthermore, the parameter pairs, elongation rate of zero-order roots (r0) - number of zero-order roots (NB) (R=-0-44), and elongation rate of zero-order roots (r0) - insertion angle of zero-order roots (theta0) (R=-0.41), show higher negative correlations, while maxl0-tr0s (R=0.51), number of zero-order roots (NB) - standard deviation of internodal distance of first-order laterals (ln1s) ((R=0.47), and internodal distance of first-order laterals (ln1)- standard deviation of internodal distance of first-order laterals (ln1s) (R=0.33) higher positive correlations (Fig. 1A).

Validation of inferred RSA parameters

We randomly selected hundred sets of parameters from the posterior and ran our simulation model with those parameters to compare the differences among RLD profiles that were derived from the true parameter set, measurement data, and estimated parameter sets. The left panel in Fig. 12 shows the simulated mean RLD profile (solid blue line) based on 32 realizations of 15 soil cores using the true parameter set. The shaded blue area represents the standard deviation of the RLD profiles among the different realizations. The solid black line and the gray shaded area represent the mean RLD profile and the standard deviation of RLDs for 100 randomly selected parameter sets from the posterior, respectively. For each selected parameter set, 32 realizations of 15 cores were simulated to obtain the RLD profile for that set. The right panel shows the profiles of simulated standard deviations of RLDs among the 15 soil cores. Note that the shaded areas here refer to standard deviations of standard deviations.

Fig. 12
figure 12

Root length density profiles (left: RLD-mean and right: RLD-std) simulated using the parameter sets of the posterior distribution (black), using the true parameter set (blue), and the measurement data (red). Shaded areas represent the standard deviations of the root length density profiles obtained from the true parameter set (blue and standard deviations of predictions using parameters sampled from the posterior distribution (gray). The lines with "+" markers represent the lowest (green) and the highest (Purple) RLD profiles derived by fixing higher-order root parameters to their lowest and highest extremes, respectively, without changing the true values of lower-order root parameters

Full size image

The red line indicates the measurement data used for this study. The posterior samples slightly overestimate the RLD predicted with the true parameter set between -10 cm and -60 cm depth, which is in agreement with the used measured data that also showed higher RLDs than predicted by the true parameter set in the largest part of this depth range. The widths of the shaded areas around the ‘true’ RLDs, which represent the variability or uncertainty of the measured RLDs that are derived from 15 soil cores, and around the mean posterior predictions, which represent the prediction uncertainty, are similar. The overlap of the shaded areas indicates that there is no overfitting and that the posterior parameter and prediction distributions do not underestimate the parameter and prediction uncertainty. For non-correlated measurement errors, one would expect a smaller posterior prediction uncertainty than the uncertainty of the observations or measurements. However, the analysis of likelihoods of different realizations demonstrated that errors were not independent (see Fig. 4) which we accounted for by ‘inflating’ the log-likelihood. Secondly, the stochasticity of the simulation model leads to wider posterior parameter distributions (see Fig. 4) which translates into larger prediction uncertainty. Since we could not obtain an estimate of the posterior parameter uncertainty for the deterministic simulation model, due to limitations in computational resources, we could not quantify the effect of the forward simulation model stochasticity of the RSA model on the posterior parameter distribution as we could for the simple toy model.

Next to fitting the mean RLD of 15 soil cores, also the standard deviation of root length densities among soil cores was used as information to estimate the RSA parameters. The right panel in Fig 12. demonstrates that the standard deviations predicted for the true parameter set (blue line) and for selections from the posterior parameter distribution (black line) match closely. They underestimated the measured standard deviation (red line) near -20 cm depth, but the uncertainty of the standard deviation that is obtained from 15 soil cores (shaded areas) is quite large. Similar to the mean root length densities, the uncertainty of the standard deviation ‘measurements’ (blue shaded areas) and of predictions of the standard error (gray shaded area) are similar. These results illustrate that also variability of root length densities can be predicted by RSA models and that RSA parameters that are estimated from RLD measurements consistently predict this variability. The information content of this variability was not analyzed in this study but this can be done in future studies by comparing posterior parameter distributions that are obtained from data sets that include and do not include the measured standard deviations.

Discussion

In this study, we identified potential challenges associated with the inference of RSA parameters from field sampling data using inverse modeling.

MCMC inversion run time for RSA parameter estimation

The requirement of higher computational demand and computing resources is one of the main drawbacks of the Bayesian approach (van de Schoot et al. 2014). Since the simulation of the root distribution in one virtual field plot requires simulating several root systems, our simulation model takes 1 to 12 minutes in total for one forward simulation model run. Additionally, we used 32 repetitions to reduce the stochasticity of the model and given our available computing resources, the inversion algorithm completed only about 500 iterations per day. Thus, the total sampling run time for 30000 iterations was approximately 60 days on our 32 computing nodes with 4 x AMD Opteron 6300 (Abu Dhabi) 2.3GHz CPU and 8.00 Gb RAM per each node. Although parallel implementation reduces the inversion time significantly, computing cost is still a limiting factor.

Fixing problematic and highly correlated parameters from field observations

We highlighted that one of the main obstacles in inference is that the correlation of parameters leads to difficulties in resolving parameters separately. Therefore, we propose to fix some parameters that can be measured directly in field experiments to improve the prediction uncertainty of the inferred parameters. Previous studies indicate that the number of zero-order roots (NB), can be estimated from field sampling techniques (Arifuzzaman et al. 2019; El Hassouni et al. 2018) and therefore can be used as a fixed parameter in inference. This will improve the accuracy of the other parameter estimates because NB parameter is one of the most sensitive parameters that determine the total root length density of soil core data. The influence of higher gravitropism strength compensates for the influence of a larger insertion angle. Therefore, it is difficult to estimate the parameters independently, and fixing one of these parameters would estimate the other with higher accuracy. The insertion angle and its variability can be measured directly from exposed root systems (Landl et al. 2018; Wu and Guo 2014). This indicates that improving field methods to extract information about parameters helps reduce the uncertainty of the inversely estimated parameters.

Fig 9 shows that some of the fitting parameters are well-constrained and close to their true values, these include lmax0, r0, r0s, ln0 and theta0, i.e., the primary root parameters. However, the remaining parameters were poorly constrained. There are two possible reasons that can explain the excellent agreement with the simulated data shown in Fig 12. One reason is that the poorly-constrained parameters “neutralize” each other because of parameter compensation, the other reason would be that they don’ t influence much the simulated RLD and thus aren’t really necessary. As our previous sensitivity analysis revealed all the parameters we fitted as at least moderately sensitive and without high nonlinear effects, neutralization is more likely. To double-check this, we included two scenarios in Fig 12, in which we simulated root systems architectures by fixing parameter values of higher-order roots to two extremes that produce the highest and lowest root length densities (only within the range of selected lower and upper bounds of the prior parameter distributions). The green curve corresponds to the lowest, and the purple curve indicates the highest RLDs, and both are well outside the grey shaded are. These two curves demonstrate that higher-order roots significantly affect RLDs. Therefore, using arbitrary parameter combinations leads to highly deviated RLDs compared to the RLD profile simulated based on the true parameter set. Parameters need to be drawn from the collected set of posterior samples, 100 of those are provided in the supplementary material.

An alternative approach to constrain better the higher-order root parameters could be to use early stages of root systems to retrieve parameters of lower orders and systematically add resolved parameters to the inversion. Another approach would be categorizing root orders based on diameters and including them in the likelihood function of the inversion algorithms to resolve root orders based on diameter classes

Possibility of application on real field root sampling data

Our approach was tested on synthetic root sampling data, derived from root architecture parameters and root system simulation model. The main advantage of a synthetic experiment is that the influence of soil environmental conditions is neglected and inversely estimated parameters and true parameters are independent of growth medium. Thus, we assumed that the soil is homogeneous, and the soil moisture, penetration resistance, and other chemical and biological conditions did not vary in the soil. Therefore, in our simulations, RSA of the plant and sampling data are independent of varying soil conditions. However, these assumptions are not valid for root growth in real field conditions. Therefore, root architecture models used in root simulations should account for the effects of spatial and temporal variations in soil conditions and weather influence on root growth. Current root system architecture models are capable of incorporating soil information. However, the models should be tested with experimental field data to implement the functions or effects, which are specific to both plant type and soil conditions. Notably, most commonly used root growth functions, i.e., linear or exponential growth, should be adjusted to account for C allocation and shoot-root communications.

In this study, we focused on root length density depth profiles regardless of root diameter classes or the relationship between diameter classes and root type. However, soil coring data provide additional information such as root diameter or number of root tips. Adding such information could improve the accuracy of estimated parameters. Moreover, the CRootBox simulation model is used to test the Bayesian inversion approach, which is independent of the specific simulation model. Therefore, similar models could also be used with this inversion approach

As indicated in the materials and methods section, selecting prior width and distribution of RSA parameters is challenging due to the scarcity of measured parameters. We considered uniform prior distributions and assumed that there was no prior information available about the parameter distribution within the defined parameter range. Setting this range is of course subjective and stating that parameter values outside this range are impossible presumes in fact strong prior knowledge about the parameter distribution. In order to set this range properly, a balance between the width of the parameter space in which the posterior distribution is determined and an improper exclusion of possible parameter values that fall outside of the range must be sought. As an alternative to bounded uniform distributions, unbounded prior distributions could be used. Selecting wider priors could result in a broad posterior distribution of non-sensitive parameters which is accompanied by a large computational cost. When strong parameter correlations exist, the algorithm needs to find a narrow region with high posterior probability density that stretches across the entire parameter space which may also lead to complications when prior parameter ranges are wide. Prior information about one of the correlated parameters that narrows the prior distribution of this parameter could constrain the width of the posterior distributions of other parameters and help to improve the accuracy of inferred parameters. Therefore, prior knowledge is highly influential when applying this approach for field-derived core sampling data.

Conclusions

In this study, we demonstrated using a synthetic experiment that soil core sampling data may contain enough information to inversely retrieve a few parameters (maximum length of zero-order roots (maxl0) , number of zero-order roots (NB), elongation rate of zero-order roots (r0) , insertion angle of zero-order roots (theta0)) of wheat root system architectures based on a RSA model that simulates root growth in a field plot. Although the inferred parameters of the higher-order roots show a large posterior uncertainty, we argue that our proposed approach is an important step towards retrieving RSA parameters by probabilistic inversion of field root sampling data. The Bayesian framework can extract information that is hidden in field observations and can be used to infer some parameters of RSA models. It also identifies parameters that cannot be extracted and for which information is lost in the field observations.

This work also provides useful insights about the challenges associated with the inverse estimation of RSA parameters by Markov chain Monte Carlo (MCMC) sampling, such as the mode stochasticity and high subsequent computational demand that requires to reduce the stochasticity. Challenges associated with the RSA model stochasticity were addressed by averaging the simulated data associated with each parameter set over multiple forward simulations. Since performing enough repetitions to get a fully stable likelihood was found intractable given our available computational resources, we proposed a modification of the Metropolis acceptance rule in the MCMC to account for the remaining likelihood stochasticity. Before using it for sampling the RSA model parameters, the impact of this modification is studied for a simple toy problem for which it is shown to allow for accurate recovery of the true posterior means, though at the cost of overestimating their uncertainty. Moreover, the observed overfitting problem could be solved by appropriately inflating the error variances in the likelihood. Importantly, we found that correlated parameters cannot be well resolved and therefore, care must be taken for selecting and fixing correlated parameters. Since our simulations assume that roots grow in a homogenous soil under optimal conditions, future work should investigate our inversion approach by considering site-specific soil and environmental conditions.