Introduction

Microbial decontamination remains a key challenge in the healthcare and food production sectors. Traditional approaches such as the use of UV radiation or the application of powerful chemical oxidizers are highly effective [1, 2], yet are often ill-suited for the decontamination of thermally liable substrates, such as delicate medical devices and food products [3]. A host of novel, non-thermal disinfection technologies are currently under active investigation and have shown great promise for efficient and effective microbial inactivation, without many of the drawbacks associated with conventional methods [4]. One such approach is the use of plasma activated water (PAW), where a non-equilibrium gas discharge is used to generate reactive chemical species directly within a liquid volume [5]. The ‘activated’ liquid can then be applied directly to disinfect contaminated surfaces or stored for some time prior to application [6].

A plethora of different plasma systems have been explored for their potential to activate water, with the most common being based on atmospheric pressure air. In all cases, high voltage electricity is used to ionise a gas which yields an abundance of highly reactive chemical states [7]. When humid air is used, typical reactive species created in the plasma include O, OH, NO, O3, \({\text{O}}_{2}^{ - }\) and H2O2, these are either dissolved on contact with a liquid or react at the interface to form secondary compounds such as HNO2, HNO3 and ONOOH [8]. The generation of these reactive compounds, using only air and electricity, has sparked enormous interest in PAW technology over the last decade. An interest that has driven PAW researchers to explore a wide variety of different decontamination applications, ranging from the inactivation of fungal spores on food products [9], right through to the inactivation of biofilms on medical devices [10].

A number of studies have considered the underpinning decontamination processes at play when PAW interacts with biological organisms. Such investigations are complex due to the constantly evolving composition of PAW, which changes throughout the plasma exposure and for many weeks afterwards [11]. During and immediately after plasma exposure, PAW contains a variety of short-lived chemical species such as ONOO− and ONOOH [12]. After a period of storage, such species are depleted, and the PAW solution typically exhibits a low pH (around 2–3) with a high concentration of \({\text{NO}}_{2}^{ - }\), \({\text{NO}}_{3}^{ - }\) and H2O2 [13]. Certainly, both freshly prepared and stored PAW are a source of highly oxidising chemical species that possess powerful antimicrobial properties. On contact with bacteria, the reactive species in PAW can induce oxidative stress and profoundly damage vital compounds such as DNA, RNA, membrane lipids and proteins [14]. To extend the effective lifetime of PAW, a number of studies have explored the use of low temperature storage; with such efforts demonstrating that the reactivity and therefore antimicrobial potential of a PAW solution can be maintained over an eighteen-month period if stored at −150 °C [15].

Despite the growing body of evidence demonstrating the benefits of PAW, its translation into a useable technology at the industrial scale remains fraught with difficulties. It is well-known that the choice of plasma reactor has a dramatic impact on the reactivity of the generated PAW [16], yet the most effective reactor is not necessarily the easiest to scale. Furthermore, the operating gas plays a crucial role in dictating the level of PAW reactivity, with several studies demonstrating the benefits of operating in a noble gas environment with small oxygen admixtures [17, 18]. Despite this, most real-world applications are inevitably restricted to operation in ambient air for economic reasons [19]. A third vital point, which is often overlooked in laboratory-based studies of PAW, is the quality of the initial water source. Most studies reported in the scientific literature employ purified water (e.g., distilled or reverse osmosis filtered) or local tap water for PAW generation, with little consideration as to how the composition of the water may influence the ability of plasma to activate it. Certainly, for widespread adoption of PAW technology the use of local potable water sources, with minimal additional filtration, will be of paramount importance for cost effective operation.

In this study, to investigate the impact of water origin on PAW generation, potable water samples were acquired from five countries including France, Norway, Palestine, Slovenia and the United-Kingdom. All water samples were subjected to an identical air plasma treatment and the formation kinetics of various aqueous phase species were probed. The buffer capacity of the plasma-exposed water samples was also investigated and compared to a chemical model. Finally, to highlight the impact of initial water composition on the effectiveness of PAW, water samples from the UK and Palestine were plasma activated and used to inactivate Staphylococcus aureus and Escherichia coli. A dramatic difference in microorganism inactivation efficacy was observed between the two samples, despite each having received an identical plasma exposure. These results not only demonstrate the sensitivity of PAW generation on the initial composition of water, but indicate pre-filtration steps may need to be taken to ensure the repeatability and efficacy of the generated PAW.

Materials and Methods

Plasma System and Exposure Conditions

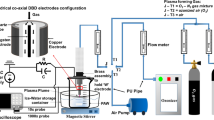
In this investigation, a surface barrier discharge (SBD) plasma system was used to activate liquid samples. In an SBD, the plasma forms as a thin layer on the surface of a dielectric material which is positioned several millimetres above the liquid layer. Mass transport of chemical species from the plasma layer to the liquid layer is driven by convection and diffusion. While such an approach is not necessarily the most efficient way to generate PAW, the physical separation between the plasma and liquid minimises their interaction, thus ensuring repeatability when exposing liquids with differing physicochemical parameters. The SBD electrode used in this study was constructed using a quartz glass dielectric with a surface area of 250 mm2. Thin film metallic electrodes were adhered either side of the quartz plate, as show in Fig. 1, with one electrode being connected to the electrical ground and the other to a high voltage power supply. A high voltage amplifier was used to create a variable voltage sinusoidal signal with a frequency of 27 kHz and a voltage up to 12 kVpp. On application of a sufficiently high voltage, breakdown occurred, and a luminous plasma discharge was observed to form on the liquid facing electrode, Fig. 1. The voltage and current waveforms were measured using a high voltage probe (TTP HVP 15HF) and a wide bandwidth current probe monitor (Pearson model 2877), and recorded using a digital storage oscilloscope (Keysight EDUX 1002A). To monitor the discharge power in real-time, the current and voltage signals were multiplied in the oscilloscope to obtain the instantaneous power which was averaged over multiple cycles to obtain the mean power. For all experiments, a constant operating power of 12 W was maintained for a maximum exposure of 25 min. During the plasma treatments, the SBD electrode was positioned 5 mm above a petri dish containing 20 mL of the water sample which was stirred at 200 rpm using a stir plate.

Fig. 1
figure 1

Experimental setup used for plasma activation of water samples; a experimental configuration showing surface barrier discharge, water sample and optical fibers for in-situ absorption measurements, b schematic of surface barrier discharge electrode, and c photograph of the discharge operating in ambient air at an average power of 12 W

Full size image

During plasma operation the density of Ozone within the reactor was monitored in real-time using UV absorption. An Ocean Optics Deuterium lamp (DH-2000-CAL) was used as the light source and two UV-transmitting optical fibers were used to guide light from the source to the detector via the reactor, as shown in Fig. 1. An Ocean Optics spectrometer (USB2000 +) was used to monitor the light intensity at 253.6 nm and the Beer-Lambert law was used to determine absolute O3 density using an absorption pathlength of 10 mm and an absorption cross-section of 1.1329 × 10−17 cm2.molecule−1.

Numerical Model of Reactive Species Transport

The numerical model used in the study is similar to that reported previously by Hasan and Walsh [20]. Briefly, a coupled set of 1D convection–diffusion-reaction equations were solved, in space and time, for the densities of 53 species. These include electrons, positive and negative ions, excited state neutral species and neutral reactive species, interacting through 624 reactions. A complete list of the species and reactions considered was reported by Sakiyama and co-workers [21]. The background air is assumed to consist of 79% N2, 20% O2 and 1% H2O. It was assumed that the discharge is driven by a Gaussian pulse of electric field with a duration of few nanoseconds, mimicking the lifetime of a filamentary discharge known to occur in a surface barrier discharge operating in ambient air. This field was converted to a mean electron energy through the local field approximation [22]. To calculate the density of reactive species as a function of distance away from the plasma generating electrode, the model was solved for all species, assuming the discharge is ignited in the first 40 µm of the computational domain, representing the plasma region of the discharge. At the end of each period of the applied waveform, the average power was calculated and the magnitude of the electric field was modified to adjust the average power in the next period to match that of the experiment. This procedure was repeated until the average power computed differed by less than 5% from that of experiments. If five consecutive periods of the applied waveform satisfied this condition, the generation and loss rates of neutral species were averaged over the last period of the waveform. In the second step, the model was solved only for the long-lived species until the species arrived to the surface of the water, adopting the time-averaged generation and loss rates obtained from the first step. This procedure allowed for the effect of short-lived species, such as electrons and ions, to influence the chemistry of the neutral species without needing to resolve every period of the applied waveform.

The model was run for an applied power of 12 W until the long-lived species filled the gap between the electrode and the surface of the water. All geometrical parameters of the model were set to match those used in the experiment.

Chemical Analysis of the PAW Samples

Spectrophotometric assays are widely used to assess water quality and were used in this investigation to provide a rapid indication of the impact of plasma exposure on the liquid [23, 24]. In all cases, a spectrophotometer (SPECTROstar Nano, BMG LABTECH) was employed. The calibration curves were created using filtered water generated with a Select Analyst water purification system (SUEZ Water Technologies & Solutions) including carbon pre-treatment, reverse osmosis, and deionisation. In all cases, the water obtained after purification had a low conductivity (2 ± 0.5 µS.m−1) and a pH of 6.0 ± 0.1. All experiments were conducted in triplicate and at different times and room temperature. In each case, filtered water was used as the blank for the analysis. The pH was measured using a pH monitor (Hanna Instruments 9813-6 with pH probe HI-1285-6), measurements were made immediately following plasma exposure. According to the manufacturers data, the pH monitor has an accuracy of ± 0.1. A K-type thermocouple (SIGNSTEK) was immersed in the water throughout plasma exposure to monitor the temperature of the liquid volume with an accuracy of ± 0.2 °C. Measurements were taken before plasma exposure and every 5 min during the exposure.

The concentration of H+ was directly calculated from the measurement of pH using the equation

$$\left[ {{\text{H}}^{ + } } \right] = 10^{{ - {\text{pH}}}}$$
(1)

HO− is typically calculated using the concentration of H+ and the ionic product of the water, Kw. However, in this investigation plasma exposure was found to induce a local elevation of the liquid temperature, thus affecting the calculation. To overcome this, the equation developed by Harned and Owen, which accounts for the thermal response of Kw was adopted:

$$\left[ {{\text{HO}}^{ - } } \right] = 10^{{{\text{pH}} + 0.0335T - 14.88}}$$
(2)

where pH is the measured pH, and T is the measured temperature [Kelvin] [25]. The concentration of \({\text{NO}}_{2}^{ - }\) was evaluated using a colorimetric assay based on the Griess reagent (Supelco Ltd, MFCD01866819) detected by spectrophotometry at 548 nm (detection range from 2 to 250 µM) [26]. The concentration of \({\text{NO}}_{3}^{ - }\) was also measured using a colorimetric assay based on the interaction of nitrate ions with sodium salicylate (Sigma-Aldrich Ltd, CAS 54–21-7) in a sulfuric acid medium after evaporation and quantified using spectrophotometry at 420 nm (detection range from 30 to 800 µM) [26]. The concentration of nitrous acid, \({\text{HNO}}_{2}\), was calculated using the acid–base relation and the value of the acidic constant (\({\text{pKa}}_{1} = 3.39\)):

$$\left[ {{\text{HNO}}_{2} } \right] = \frac{{\left[ {{\text{NO}}_{2}^{ - } } \right]}}{{10^{{{\text{pH}} - {\text{pKa}}_{1} }} }}$$
(3)

The acidic form of nitrate (HNO3) is completely dissociated in solution (pKa2 =  − 2) and cannot be determined due to the pH of the exposed water.

Carbonic compounds are present in most potable water sources in the form of bicarbonates, their concentration can be measured using the classic titration of water with a strong base (\(\left[ {{\text{NaOH}}} \right] = 0.1\) mM) or acid (\(\left[ {{\text{HCl}}} \right] = 0.1\) mM) depending on the pH of the solution. When plotting the first derivative of the titration curve, an equivalence point was obtained when the species reached equilibrium (acidic and basic conjugate). This equivalence point was then used to calculate the concentration of the total carbonic compounds (Ctotal) in the water using the equation

$$C_{{{\text{total}}}} = \frac{{C \cdot V_{{{\text{eq}}}} }}{{V_{{{\text{sample}}}} }}$$
(4)

where C is the concentration of the acid or base used in the titration, Veq the volume of acid at the equivalence point and Vsample the initial volume of the sample. The concentration of H2CO3, \({\text{HCO}}_{3}^{ - }\) and \({\text{CO}}_{3}^{2 - }\) was measured using acid–base equations in which appear the acid constant, pH of the solution analyzed and the concentration of total carbonic compounds (\({\text{pKa}}_{{{\text{H}}_{2} {\text{CO}}_{3} /{\text{HCO}}_{3}^{ - } }} = 6.37\) and \({\text{pKa}}_{{{\text{HCO}}_{3}^{ - } /{\text{CO}}_{3}^{2 - } }} = 10.32\)).

The concentration of H2O2 was quantified by spectrophotometry using TiOSO4 reagent in sulfuric acid solution (Sigma-Aldrich Ltd, CAS 123334-00-9) at 410 nm (detection range from 0.5 to 2 mM) [27].

Assessment of Microbial Inactivation Efficacy

Based on the liquid characterisation results, two water samples were selected that showed the greatest divergence in chemical composition following plasma exposure and their antimicrobial efficacy was explored. Water from the UK and Palestine, alongside a sample of filtered water, were plasma activated and tested against Escherichia coli BW25113 and Staphylococcus aureus USA300 JE2. To prepare the bacterial inoculum, single colonies of E. coli and S. aureus were inoculated, respectively, into 10 ml of either Luria–Bertani broth (LB, Sigma-Aldrich Company Ltd, Gillingham, United Kingdom) or Tryptone Soya broth (TSB, Sigma-Aldrich), and incubated for 24 h at 37 °C at 160 rpm (SI500; Stuart Equipment, Staffordshire, United Kingdom). 0.1 ml aliquots of the stationary-phase cultures were added to 10 ml of fresh culture media and incubated until the cell population reached 5.0 × 108 CFU.mL−1. 1 mL of the stationary-phase culture was centrifuged (C2500-230 V, Labnet International Inc, United States) for 10 min at 13,000 rpm at room temperature and the cell pellet was resuspended in freshly prepared PAW (created from UK, Palestinian, and filtered water samples and plasma exposure for 10 and 20 min) alongside an un-activated filtered water sample as a control. After 1 h of incubation at room temperature, the bacterial cells were recovered by centrifugation (13,000 rpm for 10 min at room temperature) and resuspended in Phosphate Buffered Saline (PBS, Sigma-Aldrich). Serial decimal dilutions were then prepared in PBS and 0.1 mL aliquots from appropriate dilutions were inoculated on LB agar and TSA plates (Sigma-Aldrich) for the determination of E. coli and S. aureus, respectively, and incubated for 24 h at 37 °C. A colony forming unit (CFU) count was performed and reported as log CFU.mL−1. Experiments were performed in triplicates across multiple days and room temperatures.

Potable Water Samples

To investigate the impact of plasma exposure on water sourced from different geological locations, potable water samples were obtained from five different countries, the characteristics of their origin are detailed in Table 1.

Table 1 Origin of the potable water samples
Full size table

All the potable water samples detailed in Table 1 are assumed to be processed in a similar fashion; following collection from the source they are subjected to different processing stages: pre-treatment, coagulation/flocculation/sedimentation, and filtration [33]. The pre-treatment removes the first traces of biological contamination (i.e., microorganisms, algae, etc.); coagulation/flocculation/sedimentation are used in conjunction, in which small particles are removed. The filtration stage consists of passing the water through different layers of sand, gravel, and charcoal to achieve chemical filtration. During this last stage, a small amount of chlorine (in a range of 0.2 to 1 mg.L−1) or ozone (maximum of 0.02 mg.min.L−1 at 5 °C, pH 6–7) is added to the water for microbial disinfection purposes [34, 35].

Despite the considerable efforts of potable water providers, it is inevitable that the final water chemistry is impacted by the soil characteristics of the source (e.g., porosity, minerals, etc.) and localised human activity (e.g., agriculture, industry). Consequently, a significant variation in the chemical composition of water samples collected from different geographical locations is inevitable. Table 2 shows the chemical composition (average and standard deviation in triplicates) of the five water samples used in this study.

Table 2 Initial chemical composition of tap water from the different countries included in this study
Full size table

No water samples were found to contain nitrites and the concentration of dissolved carbon dioxide and carbonates are not presented as they were found to be significantly lower than that of the bicarbonates due to the pH of the samples.

Results and Discussions

Plasma and Gas Phase Chemistry

In a low temperature plasma, ionisation, excitation, and dissociation reactions of O2, N2 and H2O, result in a plethora of both short- and long-lived reactive species, such as O, OH, NO, O3, H2O2. Specifically, in a surface barrier discharge, the powered and grounded electrode are separated by a thin dielectric material which changes the shape of the electric field. This characteristic reduces the breakdown voltage and promotes plasma formation along the edges of the electrode, where the electric field is the greatest.

Short-lived species are primarily created by electron driven reactions involving energetic electrons within the plasma, such as those highlight in R1–R5:

$${\text{H}}_{2} {\text{O}} + e^{ - } \to {\text{H}}^{ \cdot } + {\text{OH}}^{ \cdot } + e^{ - } \;\;\;\; \left( {{\text{R}}. 1.} \right)$$
$$e^{ - } + {\text{ O}}_{2} \to {\text{O}}^{ \cdot } + {\text{O}}^{ \cdot } \;\;\;\;\left( {{\text{R}}. 2.} \right)$$
$$e^{ - } + {\text{N}}_{2} \to {\text{N}}^{ \cdot } + {\text{N}}^{ \cdot } \;\;\;\;\left( {{\text{R}}. 3.} \right)$$
$${\text{O}}^{ \cdot } + {\text{N}}_{2} \to {\text{NO}} + {\text{N}}^{ \cdot } \;\;\;\;\left( {{\text{R}}. 4.} \right)$$
$${\text{N}}^{ \cdot } + {\text{O}}_{2} \to {\text{NO}} + {\text{O}}^{ \cdot } \;\;\;\;\left( {{\text{R}}. 5.} \right)$$

Beyond the discharge region, where the electric field is low, electrons rapidly cool below the energy threshold required for excitation, dissociation and ionisation reactions to occur. Consequently, many of the production pathways of short-lived species are inhibited and their density drops rapidly as they react to form long-lived species. As the SBD electrode used in this study was confined within a sealed volume, quantification of species densities was limited to the measurement of Ozone using optical absorption, a process that required no gas to be drawn from the enclosure. Figure 2a shows the temporal evolution of Ozone within the reactor as a function of plasma generation time. Notably, an increasing discharge power led to a higher ozone density peak followed by accelerated quenching. Ozone quenching in an air fed atmospheric pressure SBD has been widely studied [36], and it has been posited that the rapid formation of NO is attributed to the reaction between vibrationally excited N2 and O within the discharge region, which subsequently reacts with O3 to form NO2, R6–8 [37].

$${\text{O}} + {\text{O}}_{2} + {\text{M}} \to {\text{O}}_{3} + {\text{M}}\;\;\;\;\left( {{\text{R}}. 6.} \right)$$
$${\text{N}}_{2} \left( v \right) + {\text{O}} \to {\text{NO}} + {\text{N}}\;\;\;\;\left( {{\text{R}}. 7.} \right)$$
$${\text{O}}_{3} + {\text{NO}} \to {\text{NO}}_{2} + {\text{O}}_{2} \;\;\;\;\left( {{\text{R}}. 8.} \right)$$
Fig. 2
figure 2

a Evolution of Ozone concentration measured in-stiu at a constant dissipated plasma power of 6, 9, 12 and 18 W, and b calculated species densities as a function of distance downstream of the SBD electrode at a dissipated plasma power of 12 W

Full size image

Using the computational model described in “Numerical model of reactive species transport” section, the space resolved density of key RONS was calculated, Fig. 2b. As the model only captured the first few seconds of discharge operation, ozone quenching was not observed. It is clear from the figure that many of the short-lived RONS, including OH and HO2 were unable to reach the liquid surface, situated at a position 5 mm from the discharge. All charged species and various other short-lived species, such as O and N, were restricted to the discharge region (~ 40 µm) as they were rapidly converted into more stable long-lived species. Therefore, they played no direct role in activation of the liquid sample. Downstream of the SBD electrode, the calculated ozone density is overestimated by approximately 15% compared to the measured value; this is a likely result of the spatial averaging associated with the UV absorption measurement technique. Critically, these results indicate that the only plasma generated species able to reach the liquid surface are O3, N2O, NO, and NO2; therefore, it is these species that must act as precursors for liquid phase reactions.

Kinetic Evolution of the pH, Nitrite, Nitrate, and Nitrous Acid (HNO2)

It is well established that water exposed to air plasma experiences a drop in pH; in the case of purified water (i.e., distilled or deionized) the decrease can occur very rapidly and reach very low pH values (e.g., 1–2) [38]. Figure 3a shows the evolution of pH for the five samples with increasing plasma exposure time. From the figure it can be observed that the water samples did not respond equally to the plasma treatment. Water from the United Kingdom and Norway showed a significant drop in pH, decreasing from pH 8 ± 0.1 to below 3 ± 0.2. The pH of water sourced from France and Palestine was not affected by plasma exposure, remaining stable at 8 ± 0.1. Finally, water sourced from Slovenia initially had a pH of 8.1 ± 0.1 and was observed to linearly decrease to a pH of 7.5 ± 0.0 after 20 min of exposure. Subsequent plasma exposure resulted in a drop of pH to a final value of 6.7 ± 0.1.

Fig. 3
figure 3

Kinetic evolution of: a pH, b nitrite concentration, c nitrate concentration, and d nitrous acid concentration

Full size image

Figure 3b shows the kinetics of nitrite formation during plasma exposure. All water samples followed a similar trend, with an initial lag phase, followed by a sharp increase and, with the exception of the Norwegian water, a subsequent drop in concentration. Similar trends have been reported previously for nitrite formation in plasma-activated water [39]. Despite showing the same trend, the absolute values were found to differ, with water from Palestine showing the highest concentration (24.1 ± 4.8 µM), and water from the UK (10.2 ± 3.0 µM) showing the lowest peak concentration. The rapid rise in nitrite concentration can be attributed to the conversion of nitric oxide from the plasma into nitrogen dioxide through reactions 7 and 8. Nitrogen dioxide is readily dissolved into the aqueous phase, leading to the formation of nitrites, nitrates, and hydronium ions through the reaction [40].

$$2{\text{NO}}_{2\left( g \right)} + {\text{H}}_{2} {\text{O}} \to {\text{NO}}_{{2\left( {{\text{aq}}} \right)}}^{ - } + {\text{NO}}_{{3\left( {{\text{aq}}} \right)}}^{ - } + 2{\text{H}}_{{\left( {{\text{aq}}} \right)}}^{ + } \;\;\;\;\left( {{\text{R}}. 9.} \right)$$

The observed reduction in nitrite concentration has been linked to an oxidoreduction reaction that can occur leading to the conversion of nitrites into nitrates due to the presence of ozone:

$${\text{NO}}_{2}^{ - } + {\text{O}}_{3} \to {\text{NO}}_{3}^{ - } + {\text{O}}_{2} \;\;\;\;\left( {{\text{R}}. 10.} \right)$$

and the recombination of nitrites into nitrous acid with hydronium ions [41]

$${\text{NO}}_{2}^{ - } + {\text{H}}^{ + } \to {\text{HNO}}_{2} \;\;\;\;\left( {{\text{R}}. 11.} \right)$$

Figure 3c shows the kinetics of nitrate formation in the five water samples during plasma exposure. In all cases, nitrate concentration was observed to increases almost linearly, reaching a maximum after a plasma exposure of 25 min. Only minor differences were found in the final concentration, with the highest levels obtained for the French and Palestinian water, with both reaching 3.1 ± 0.3 mM. The evolution of nitrous acid formation is shown in Fig. 3d. From the figure it is clear that plasma exposure generates nitrous acid which increases in concentration with exposure time and coincides with the measured decrease in the pH. This is attributed to the accumulation of hydronium ions in the samples through reaction R. 9. and the conversion of nitrites into nitrous acid through reaction R. 11. Critically, the final concentration of nitrous acid was found to vary over four orders of magnitude depending on the origin of the water sample. As nitrous acid is known to be a major antimicrobial component of PAW [42], these results indicate that the five water samples may differ significantly in their antimicrobial properties.

Carbonic Acid (H2CO3), Bicarbonates (\({\text{HCO}}_{3}^{ - }\)) and Carbonate (\({\text{CO}}_{3}^{2 - }\))

In all untreated water samples, the dominant form of carbonic compounds was found to be \({\text{HCO}}_{3}^{ - }\) and was present in different concentrations; the Palestinian and UK tap water were found to contain, respectively, the highest (5.10 ± 0.06 mM) and lowest (0.55 ± 0.04 mM) concentrations. The kinetic evolution of bicarbonate, carbonic acid and carbonates is presented in Fig. 4a, b, c, respectively. The decrease of pH in the UK, Norwegian and Slovenian water is due to the conversion of the carbonates into bicarbonate and carbonic acid. Despite bicarbonates being the dominant form in the solution (\({\text{pKa}}_{{{\text{CO}}_{3}^{2 - } /{\text{HCO}}_{3}^{ - } }} = 10.32\)), there is however, a small concentration of carbonate present. The free hydrogen ions created through plasma exposure (R. 1.) and hydronium ions introduced by NO2 dissolution (R. 9.) shift the equilibrium of the carbonic compounds in the water. The carbonates are therefore converted into bicarbonate following the reaction:

$${\text{CO}}_{3}^{2 - } + {\text{H}}^{ + } \to {\text{HCO}}_{3}^{ - } \;\;\;\;\left( {{\text{R}}.12.} \right)$$

When the pH reaches the second value of the acidic constant (\({\text{pKa}}_{{{\text{HCO}}_{3}^{ - } /{\text{H}}_{2} {\text{CO}}_{3} }} = 6.37\)), the bicarbonates are transformed into carbonic acid (R. 13.). The remaining carbonate present in the water is converted into carbonic acid (R. 14.) as the solution becomes more acidic.

$${\text{HCO}}_{3}^{ - } + {\text{H}}^{ + } \to {\text{H}}_{2} {\text{CO}}_{3} \;\;\;\;\left( {{\text{R}}. 13.} \right)$$
$${\text{CO}}_{3}^{2 - } + 2{\text{H}}^{ + } \to {\text{H}}_{2} {\text{CO}}_{3} \;\;\;\;\left( {{\text{R}}. 14.} \right)$$

Reactions 13 and 14 can also be used to explain why water from France and Palestine were resistant to plasma induced acidification. Their initial concentration of carbonates and bicarbonates was significantly higher, thus enhancing their buffering capacity and explaining the reduction of nitrous acid through the scavenging of hydronium ions formed in reaction 9.

Fig. 4
figure 4

Kinetic evolution of: a bicarbonate, b carbonic acid, and c carbonate concentration

Full size image

Buffer Capacity of the Treated Waters

The buffer capacity or index is defined as the concentration of acid or base to add in order to modify the pH of an aqueous solution. In potable water, the buffer capacity is expressed as:

$$\beta = \left( {\ln 10} \right)K_{a1} \left[ {H^{ + } } \right]C_{T} \times \frac{{K_{a1} K_{a2} + 4K_{a2} \left[ {H^{ + } } \right] + \left[ {H^{ + } } \right]^{2} }}{{\left( {K_{a1} K_{a2} + K_{a1} \left[ {H^{ + } } \right] + \left[ {H^{ + } } \right]^{2} } \right)^{2} }}$$
(5)

With \(C_{T} = \left[ {{\text{H}}_{2} {\text{CO}}_{3} } \right] + \left[ {{\text{HCO}}_{3}^{ - } } \right] + \left[ {{\text{CO}}_{3}^{2 - } } \right]\) the concentration of dissolved inorganic carbon and, \(K_{a1} = {\text{Ka}}_{{\left[ {{\text{H}}_{2} {\text{CO}}_{3} } \right]/\left[ {{\text{HCO}}_{3}^{ - } } \right]}}\) and \(K_{a2} = {\text{Ka}}_{{\left[ {{\text{HCO}}_{3}^{ - } } \right]/\left[ {{\text{CO}}_{3}^{2 - } } \right]}}\) their respective acidic constant [43].

The contributions of the water dissociation (\(\beta_{W}\)) and carbonate buffer system \((\beta_{{\left[ {{\text{CO}}_{3} } \right]T}} )\) are shown in Fig. 5. The \(\beta\) coefficient obtained for the samples from the UK and Norway are also plotted for comparison with the chemical model. Waters from the UK and Norway were the most affected by the plasma acidification, as the dissolved carbonated species are converted in order to maintain the stability of the buffer system (R. 12–14). As shown in the figure, both waters follow the same trend as the chemical model reaching a maximum when \({\text{pH}} = {\text{pKa}}_{{\left[ {{\text{H}}_{2} {\text{CO}}_{3} } \right]/\left[ {{\text{HCO}}_{3}^{2 - } } \right]}}\); water from Norway has a lower maximum peak than the model which can be explained by the initial low concentration of carbonic compounds present in solution. When the pH decreases, the buffering system becomes unstable and β is dominated by the contribution brought by \(\beta_{W}\). Both samples from the UK and Norway showed a decrease in pH during plasma exposure and converge following \(\beta_{W}\). Consequently, the free hydrogen ions (R. 1.) and hydronium ions (R. 9.) introduced to the system are primarily responsible for the acidification of the water samples. Furthermore, the calculation of the buffer coefficient for those samples indicates clearly that the carbonic compounds are primarily responsible for the water buffering capacity to the plasma exposure. The possible contribution brought by the dissolved cations (e.g., \({\text{Ca}}^{ + } ,\;{\text{Mg}}^{2 + } ,\;{\text{Na}}^{ + }\)) is minimal.

Fig. 5
figure 5

Buffer capacity β for the waters from UK and Norway and comparison with \(\beta_{{\left[ {{\text{CO}}_{3} } \right]T}}\) and \(\beta_{W}\)

Full size image

The β coefficient for water samples obtained in France, Palestine and Slovenia were also compared to the chemical model (data non shown). In all cases, their β coefficient remained stable (β = 10–4, pH = 8 ± 0.1) with a slightly increase for the water from Slovenia in agreement with its pH (β = 10–3, pH = 6.7 ± 0.1).

Formation of Hydrogen Peroxide and Chlorine Oxide

The formation of hydrogen peroxide in PAW has been reported previously and is considered an important component that contributes significantly to the oxidative potential of the solution [44]. In previous studies of noble gas plasma interaction with water, H2O2 formation in the liquid phase has been attributed to the interaction of OH at the liquid interface [45]. In the air-fed SBD configuration used in this study, OH radicals cannot reach the liquid interface, as confirmed by the modelling results presented in Fig. 2b. Consequently, the primary H2O2 production pathway is inhibited; an alternate pathway follows the recombination of hydroxyl radicals created in the plasma phase,

$${\text{OH}}^{ \cdot } + {\text{OH}}^{ \cdot } \to {\text{H}}_{2} {\text{O}}_{2} ,\;\;\;\;\left( {{\text{R}}. 15.} \right)$$

and the subsequent diffusion of H2O2 to the liquid interface and its solvation following Henry’s law. Notably, in all treated samples in this investigation, no H2O2 was detected using the standard colorimetric detection method with a \({\text{TiOSO}}_{4}\) reagent.

From an application perspective, the interaction between plasma generated reactive species in PAW and chlorine added by some water suppliers remains a key question. The influence of plasma exposure on Chlorine was investigated by Haghigat et al. and it was observed that Cl− can scavenge OH· to form \({\text{ClOH}}^{ \cdot - }\); yet the product formed was unstable and rapidly decomposed (R. 17.). Under acidic conditions, the formation of \({\text{Cl}}_{2}^{ \cdot - }\) from \({\text{ClOH}}^{ \cdot - }\) (R. 18.) is favoured which recombines to form \({\text{Cl}}^{ - }\) and \({\text{HOCl}}\) (R. 19.):

$${\text{OH}}^{ \cdot } + {\text{Cl}}^{ - } \leftrightarrow {\text{ClOH}}^{ \cdot - } \;\;\;\;\left( {{\text{R}}. 16.} \right)$$
$${\text{ClOH}}^{ \cdot - } + {\text{Cl}}^{ - } \leftrightarrow {\text{Cl}}_{2}^{ \cdot - } + {\text{OH}}^{ - } \;\;\;\;\left( {{\text{R}}. 17.} \right)$$
$${\text{Cl}}_{2}^{ \cdot - } + {\text{OH}}^{ \cdot } \to {\text{HOCl}} + {\text{Cl}}^{ - } \;\;\;\;\left( {{\text{R}}. 18.} \right)$$

However, a significant concentration of chlorine is required (> 50 mg.L−1) to form HOCl, which is not typical in potable water. With the samples considered in this study estimated to contain between 0.2 to 1 mg.L−1, as described in “Potable water samples” section [46].

Impact of Water Origin on PAW Antimicrobial Efficacy

To determine the impact of water origin on the antimicrobial properties of PAW, water samples from the UK and Palestine were selected as they showed the largest discrepancy in initial composition. Two bacterial cultures were selected, E. coli and S. aureus, as representative Gram-negative and Gram-positive species. Several reports have shown Gram-positive species to be more resistant to plasma treatments [47, 48], which is mainly attributed to the presence of a thick peptidoglycan layer in their cell wall. The antibacterial efficacy of the various PAW samples is shown in Fig. 6. To underline the dependency of the water origin, filtered water was plasma activated for 10 and 20 min, reaching a pH of 3.5 ± 0.1 and 2.8 ± 0.2, [\({\text{NO}}_{2}^{ - }\)] of 18.8 ± 3.0 and 60.0 ± 4.2 µM, [HNO2] of 15.7 ± 4.6 and 298.7 ± 14.7 µM, respectively. As expected, plasma activated filtered water (FW) showed the greatest overall antibacterial activity, reaching the limit of detection (LOD: 2 × 102 CFU.mL−1; log10 = 2) for three out of four conditions tested. Water from the UK was less effective but was still capable of reaching the LOD for both bacterial species following a 20 min exposure. In contrast, the Palestinian water showed no significant inactivation for any condition tested.

Fig. 6
figure 6

Impact of water origin on PAW inactivation of: a E. coli, and b S. aureus

Full size image

Taking into account the chemistry of the plasma activated water samples (Figs. 3, 4), their antibacterial activity can be clearly linked by the dissolution of nitrogen oxide into the water (R. 9.), leading to the formation of nitrous acid by recombination of the nitrites with hydronium ions (R. 11.). After a plasma exposure of 10 and 20 min, both UK and Palestinian waters had a similar concentration of nitrites and nitrates, the main difference between them is their concentration of nitrous acid which, as explained in “Kinetic Evolution of the pH, Nitrite, Nitrate, and Nitrous Acid (HNO2)” section, is known to be a potent antibacterial compound in plasma activated water. These results demonstrate that the antimicrobial efficacy of PAW is extremely sensitive to the initial composition of the water source used, with potable water sources from different geographical locations showing vastly different levels of antimicrobial activity. This finding has significant ramifications for the scale up and industrial application of PAW technology, where additional monitoring and filtration steps may be required to ensure consistency, traceability and efficacy.

Conclusion

In this study, five potable water samples were obtained from different geographical locations. Their initial composition was analysed, and the evolution of pH, nitrate, nitrite, nitrous acid and carbonate compounds was evaluated during exposure to an identical air plasma treatment. It was found that water from the UK and Norway showed the most significant decrease in pH (from 8 to below 3) associated with the highest concentration of nitrous acid (respectively 14.5 ± 3.7 and 13.4 ± 2.0 µM), while the pH of water from Palestine and France remained relatively unchanged. The concentration of nitrates appeared to be independent of the pH and the initial concentration of bicarbonates present.

As PAW technology is currently under intensive investigation for use as a novel antimicrobial, the impact of water origin on the antimicrobial potential of PAW was investigated. Based on the chemical characterisation of the potable water samples, water sourced from the UK and Palestine was activated and assessed against both gram-positive and gram-negative bacterial species. It was demonstrated that PAW created from UK water was an extremely effective antimicrobial agent; whereas PAW created from Palestinian water showed very little antimicrobial activity. The implications of these results are significant for the future development of PAW technology. If the technology is to be widely adopted in areas such as food security and healthcare, then efficiency, repeatability and traceability are of paramount importance. This study demonstrates that the inevitable wide variation in the composition of potable water from different geographic locations has a dramatic impact on the overall effectiveness of PAW. Given this, it is essential that steps be taken to analyse and possibly adjust the composition of any water source prior to plasma activation in order to guarantee the repeatability and ultimately, the safety, of the process.