Abstract
Hydrocarbon exhaust gases containing residual amounts of oxygen may pose challenges for their conversion into value added chemicals downstream, because oxygen may affect the process. This could be avoided by plasma treating the exhaust to convert \(\hbox {O}_2\) in presence of hydrocarbons into CO or \(\hbox {CO}_2\) on demand. The underlying reaction mechanisms of plasma conversion of \(\hbox {O}_2\) in the presence of hydrocarbons are analysed in a model experiment using a radio frequency atmospheric pressure helium plasma in a plug flow design with admixtures of \(\hbox {O}_2\) and of \(\hbox {CH}_4\). The plasma process is analysed with infrared absorption spectroscopy to monitor \(\hbox {CH}_4\) as well as the reaction products CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O. It is shown that the plasma reaction for oxygen (or methane removal) is triggered by the formation of oxygen atoms from \(\hbox {O}_2\) by electron. Oxygen atoms are efficiently converted into CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O with CO being an intermediate in that reaction sequence. However, at very high oxygen admixtures to the gas stream, the conversion efficiency saturates because electron induced \(\hbox {O}_2\) dissociation in the plasma seems to be counterbalanced by a reduction of the efficiency of electron heating at high admixtures of \(\hbox {O}_2\). The impact of a typical industrial manganese oxide catalyst is evaluated for methane conversion. It is shown that the conversion efficiency is enhanced by 15–20% already at temperatures of 430 K.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Plasma oxidation of hydrocarbons is a well known process in the field of combustion or the removal of volatile organic compounds (VOC) [1, 2]. Plasma excitation of a gas accelerates the combustion speed and allows thereby a more efficient use of the fuel. Plasma-based removal of VOCs is a viable method to filter contaminated exhaust gas streams in industrial applications. Such VOC removal could also be performed using filter technologies or thermal treatment [3], but both technologies exhibit significant disadvantages such as limited lifetime of filters or installation and energy costs of a typical thermal treatment unit. VOC removal can also be performed by thermal catalysis in packed bed reactors. The catalyst and the operation window (surface temperature, residence time) of such reactors has to be carefully chosen, because different hydrocarbons exhibit different reactivities in thermal catalysis and such systems are prone to catalyst poisoning by coke formation. For example, the conversion of methane in the presence of oxygen into CO and \(\hbox {CO}_2\) requires catalyst temperatures of typically 1000 K, because methane chemisorption cannot easily compete with oxygen adsorption at lower catalyst temperatures [4]. The main disadvantage of catalytic processes is, however, their sensitivity to the gas composition. Impurities in small concentrations in the gas stream can easily poison the catalyst surface rendering the process very inefficient. Therefore, sensitive gas monitoring is required and to adjust and control the feed gas.
The on demand control of the gas composition that is fed to a catalytic process is a possible application of a plasma process, because plasmas react much faster to varying operation conditions in comparison to changing the temperature of a packed bed reactor filled with catalyst beads. In this paper, we explore the use of plasma conversion of hydrocarbons for the treatment of coke oven gas. This gas consists of \(\hbox {H}_2\) (55–60%), \(\hbox {CH}_4\) (23–27%), CO (5–8%), \(\hbox {N}_2\) (2–5%), \(\hbox {H}_2\)O (4%), \(\hbox {CO}_2\) (2%), less than 1% \(\hbox {O}_2\) and many trace compounds [5]. These exhaust gases are used in a second setup for recycling to for example separate and purify \(\hbox {H}_2\) in a pressure swing adsorption (PSA) stage [6]. However, these subsequent chemical processes can suffer from the presence of oxygen that may be present as an impurity in the incoming gas stream: (i) oxygen molecules may accumulate in the PSA, and together with \(\hbox {H}_2\) from the feed gas, the explosion limit for \(\hbox {H}_2\):\(\hbox {O}_2\) could be exceeded; (ii) oxygen may lead to corrosion in an industrial setup; (iii) oxygen may affect the process windows of a subsequent catalytic process. Currently, the impact of oxygen for these process technologies is being mitigated by regulating the allowed concentration of oxygen in natural gas to be below 10 ppm [7]. Such a solution by regulation cannot easily transferred to more complex processing environments such as blast furnaces or a coke ovens. The amount of \(\hbox {O}_2\) impurities in these gas streams mainly depends on the tightness of the coke oven itself that operates below atmospheric pressure. Given the complexity of these industrial installations and the aging of the facility, such a residual \(\hbox {O}_2\) level cannot completely be avoided and residual concentrations between 0.1 to 2% have to be expected. Therefore, a plasma process is explored to remove that oxygen from the gas stream before it enters the consecutive PSA stage. This goal is somewhat equivalent to VOC removal. Here, the focus is on oxygen removal (rather than VOC removal) and the abundance of VOC in the gas stream constitutes the reaction partner for that removal reaction.
The analysis of a plasma chemical system such as oxygen removal by reactions with hydrocarbons can be performed from an empirical perspective by evaluating a plasma process that is directly coupled to the final application. Due to the large size of a gas treatment facility connected to a coke oven, such an approach is not viable and more fundamental test experiments are required to understand the reaction mechanism in more detail to allow for a robust extrapolation prior to testing this on the actual industrial scale. This is achieved in a small model reactor, where the main reaction partners are also diluted in a helium gas stream to avoid the contribution of secondary reactions in a first step. Such a reduced system is also capable to analyse in more detail any plasma catalytic effects.
Recently, we devised a model experiment using a radio frequency atmospheric pressure helium or argon plasma in a plug flow design with admixtures of \(\hbox {CO}_2\) [8, 9]. The plasma conversion is analysed using infrared spectroscopy to monitor CO and \(\hbox {CO}_2\) as well as the species temperatures. It is shown that a non-equilibrium is created by rotational temperatures close to the gas temperature, but much higher vibrational temperatures. The high vibrational temperature originates from a balance between electron induced excitation and efficient quenching by collisions with noble gas atoms. The vibrational temperatures of CO and \(\hbox {CO}_2\) are higher when diluted in an argon plasma compared to a helium plasma due to the lower quenching efficiency of vibrational excitation by collisions with argon compared to helium, The conversion of \(\hbox {CO}_2\) is very efficient and is two times higher in the case of argon compared to helium.
This model experiment is now used to analyse the conversion of \(\hbox {O}_2\) in the presence of \(\hbox {CH}_4\) in a radio frequency atmospheric pressure helium plasma. The plasma conversion is analysed with infrared spectroscopy and \(\hbox {CH}_4\) as well as the reaction products CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O are monitored. Summarizing, the reaction scheme \(\hbox {CH}_4\)/\(\hbox {O}_2\) is on the one hand a model system for the plasma chemistry of VOC removal, but also a concrete reaction scheme for oxygen removal in hydrocarbon containing exhaust gases from a coke oven.
Experiment
Experimental Setup
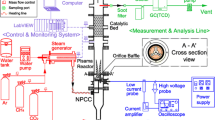
A scheme of the experimental setup is shown in Fig. 1: (a) shows the cross section of the plasma chamber along the gas flow direction, (b) shows the complete setup housing the plasma chamber in an evacuated compartment that is connected to the evacuated Fourier Transform Infrared (FTIR) spectrometer. The details of the setup including the various diagnostics are presented elsewhere [10] and only basic features are described in the following.
The plasma chamber consists of an aluminium body in which two temperature controlled electrode holders are inserted from the top and the bottom. The electrodes consist of a copper support, a macor insulation layer and a copper electrode. The 0.5 mm thick copper electrode (26 mm \(\times\) 13 mm) is protected by a 1 mm thin glass layer as a dielectric barrier to suppress arcing. The plasma volume is thereby 26 mm \(\times\) 13 mm \(\times\) 1 mm. The plasma volume is located in a central section within a rectangular gas channel with an extension of 54 mm \(\times\) 14 mm \(\times\) 1 mm. The copper electrodes can be temperature regulated by guiding a temperature controlled oil through internal compartments inside both electrodes.
The plasma gas is fed at the beginning of the rectangular gas channel and is guided to an exhaust at the end. The position along the gas channel is denoted as x. The plasma volume is observed in transmission at an angle of 30\(^{\circ }\) to the gas flow direction either at the centre (x = 13 mm) of the discharge using KBr side windows or at five positions along the gas channel (at x = 3 mm, 8 mm, 13 mm, 18 mm, 23 mm). This angle is required to avoid interferences in the optical windows [10]. The plasma forming gas consists of helium at a flow of 250 sccm with a variable admixture of \(\hbox {CH}_4\) and \(\hbox {O}_2\) at a flow between 0.3125 sccm and 2.5 sccm. The dilution in helium is not a desired process parameter in any efficient plasma application for methane oxidation. However, for the understanding of plasma reaction mechanisms, the dilution in helium suppresses the contribution of secondary reactions in the reaction schemes and simplifies the analysis of the plasma chemistry to a large extent. Thereby, the inherent ambiguities in plasma studies of the chemistry in pure mixtures containing oxygen and hydrocarbons involving hundreds of species and thousands of reactions can be avoided. Such a system consisting of a pure mixture of oxygen and hydrocarbons is realistic, but many reaction coefficients involving excited plasma species are not well known. Consequently, the isolation of a re-action mechanism in gas mixtures relevant for the application at the end is very difficult. Since the flow of helium is so much larger than the flow of \(\hbox {CH}_4\) or \(\hbox {O}_2\), an efficient and fast gas mixing is assured by injecting the helium directly in front of the molecular gas flow controllers. The flow of helium of 250 sccm leads to a gas flow velocity in the plasma channel of 0.3 m/s and residence times in the order of 100 ms.
The plasma is powered by a 13.56 MHz power supply connected to one of the electrodes via a matching network. The other electrode is grounded. The actual absorbed power in the plasma is measured using a VI probe in the RF power line. By measuring the phase shift between voltage and current, the actual absorbed power in the plasma is calculated by comparing the response of the setup with and without plasma. This yields values in the range of a few Watt, as being typical for atmospheric pressure non-equilibrium RF plasma jets [11].
a Cross section of the experimental setup along the gas flow. The plasma volume (26 mm \(\times\) 13 mm \(\times\) 1 mm) is confined by the two electrodes. The plasma is powered at 13.56 MHz by the RF generator attached to one electrode via a matching network. The IR beam path samples the plasma composition at the central position. b Sketch of the complete setup coupling the vacuum version of the FTIR spectrometer with the vacuum chamber housing the plasma chamber and the connection for gas, for temperature control, and for rf power and the corresponding VI probe
Catalyst Preparation
The plasma exposed glass surfaces that cover the copper electrodes can be coated with a catalyst. A typical catalyst for hydrocarbon oxidation is manganese oxide that has been prepared by a calcination procedure to form \(\alpha\)-\(\hbox {MnO}_2\) [12]. These catalyst particles are dissolved in a suspension of isopropanol and water, which is then pumped into a spray coating nozzle to deposit a quadratic pattern of dots on the glass surfaces. Finally, the glass layers are heated to 200 \(^\circ \text {C}\) to remove the solvent and are then mounted on the electrodes. Depending on the suspension/catalyst ratio, different catalyst loadings can be realized. More details of this spray coating system are presented elsewhere [13]. The loading of the catalyst is 0.75 mg/\(\hbox {cm}^{-2}\).
Infrared Analysis
The plasma chemistry is monitored by a Bruker Vertex 70v FTIR spectrometer using an external MCT detector. The parallel beam from the evacuated spectrometer is guided into an evacuated stainless steel housing and focused onto the plasma channel using off-axis parabolic mirrors with a focal length of 150 mm (see Fig. 1b). The complete beam path is evacuated besides a small section in front of the MCT detector that is purged with nitrogen gas. For each spectrum 100 scans at a wavenumber resolution of nominal 0.3 \(\hbox {cm}^{-1}\) are taken. Due to the 30\(^{\circ }\) tilt of the chamber, the optical path in the gas volume between the KBr windows increases from 14 mm to 16 mm. This implies also a gas sampling along the flow direction over approximately \(\Delta x \propto\) 3 mm. This can be converted into a finite temporal resolution of the measured gas densities in a plug flow approach of \(\Delta t \propto\) 10 ms.
Example Fit and residuum of a FTIR absorption spectrum for a 250 sccm He gas flow with 0.625 sccm \(\hbox {CH}_4\) and 0.625 sccm \(\hbox {O}_2\) admixture at 3.3 W plasma power. The density, rotational and vibrational (wagging mode) temperature are 2.7 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\), 352 K and 442 K
The excitation and dissociation of \(\hbox {CH}_4\), \(\hbox {CO}_2\), CO, and \(\hbox {H}_2\)O are monitored by evaluating the ro-vib transitions of the fundamentals of the stretching vibrations: the \(\hbox {CO}_2\) asymmetric stretching vibration at 2340 \(\hbox {cm}^{-1}\), the CO stretching vibration at 2149 \(\hbox {cm}^{-1}\), the \(\hbox {CH}_4\) stretching vibration at 3019 \(\hbox {cm}^{-1}\), and the second harmonic of the \(\hbox {H}_2\)O asymmetric stretching vibration at 3755 \(\hbox {cm}^{-1}\) ( see Fig. 2). The IR absorption spectra are modelled based on the fundamental data taken from the HiTRAN database [14,15,16]. The line strengths \(S_{ij}\) for \(\hbox {CO}_2\), CO and \(\hbox {CH}_4\) are calculated by invoking individual distribution functions for the population of each degree of freedom of the molecules such as vibrations and rotations. The calculation follows the same steps, as shown in detail by Klarenaar et al. [17]. The lines are then broadened by convoluting them with a normalized line width function f assuming pressure broadening, which is the dominant broadening mechanism in our experiment yielding Lorentzian line widths in the range of 0.1 \(\hbox {cm}^{-1}\). The wavenumber dependence of the absorption coefficient \(\alpha\) is calculated from the line strengths \(S_{ij}\) and the density of species n by the convolution with the line width function f. The wavenumber dependence of \(\alpha\) is used to calculate the transmission following Lambert-Beer’s law. Finally, the spectrum \(T(\nu )\) is convoluted with a Gaussian using a width of 0.22...0.3 \(\hbox {cm}^{-1}\) to account for the finite resolution of the FTIR spectrometer. The actual width is extracted directly from the spectra. This fitting is rather robust, because the Gaussian line width from the instrumental broadening and the Lorentzian line width from the pressure broadening lead to a very distinct line shape. The fitting is performed using a \(\chi ^2\)-Fit by varying the temperatures and concentrations of the species. The accuracy of this temperature determination is typically \(\Delta T_{vib} \pm\) 100 K and \(\Delta T_{rot} \pm\) 20 K. For the analysis of \(\hbox {H}_2\)O, the line strengths calculated by the HITRAN database at 300 K are being used. The accuracy of the FTIR modelling is tested by comparing the predicted line strengths \(S_{ij}\) with the tabulated values in the HITRAN database for a thermal equilibrium of 300 K. Excellent agreement is found. The simulated FTIR spectra are also directly compared to the simulations of Klarenaar et al. [17] for a specific concentration and temperatures. Both codes agree very well. An example for the fit of the \(\hbox {CH}_4\) absorption around 3019 \(\hbox {cm}^{-1}\) is shown in Fig. 3 for a plasma with 0.625 sccm \(\hbox {CH}_4\) and 0.625 sccm \(\hbox {O}_2\) at 3.3 W plasma power. The measurement and the model show a good agreement and provide a density of 2.7 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\), a rotational temperature of 352 K and a vibrational temperature for the wagging mode of 442 K.
Results
\(\hbox {CH}_4\) Oxidation Depending on Gas Mixture and Plasma Power
The oxygen removal in an \(\hbox {O}_2\):\(\hbox {CH}_4\) mixture diluted in a helium plasma is analyzed by using a flow of 0.625 sccm for \(\hbox {CH}_4\) and flows of 0.3125, 0.625, 1.25 and 2.5 sccm for \(\hbox {O}_2\). Thereby, the ratio of \(\hbox {CH}_4\) to \(\hbox {O}_2\) in the feed gas is changed from 0.5 to 4. The helium flow is set at 250 sccm and the measurements are taken in the middle position of the plasma volume (x= 13 mm). The power absorbed in the plasma is varied between 0.5 to 7 W
Rotational and Vibrational Temperatures
The dependence of the rotational temperatures of \(\hbox {CH}_4\) on the absorbed plasma power is shown in Fig. 4a. The rotational temperatures of CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O follow an almost identical trend (not shown). This rotational temperature is usually close to the gas temperature and indicates a heating of the gas stream at higher plasma powers. This is not surprising, given the fact that up to 7 W are being absorbed in the plasma mainly by helium ionization and excitation. The power is at first absorbed by the electrons in the plasma that cause excitation and ionization of helium and of the admixed molecular gases. This electronic excitation of the plasma species is eventually converted into other degrees of freedom of the molecules such as rotation, vibration and translation in super elastic collisions. The corresponding heating of the different degrees of freedom depends very much on the collision dynamics and on the different relaxation times in between these degrees of freedom. For example, electronic excitation of the molecules causes at first a vibrational excitation, which is then converted into rotational excitation and then into translational energy.
a Rotational temperature of \(\hbox {CH}_4\), b Vibrational temperature of the wagging mode at 1306 \(\hbox {cm}^{-1}\) of \(\hbox {CH}_4\) (the measured IR absorption around 3019 \(\hbox {cm}^{-1}\) also contains lines coupled with the excitation of the wagging mode that allow a determination of this temperature), c Vibrational Temperature of the asymmetric stretching mode at 2340 \(\hbox {cm}^{-1}\)of \(\hbox {CO}_2\), d Vibrational Temperature of the stretching mode at 2143 \(\hbox {cm}^{-1}\) of CO. The dashed line denote the expected increase in temperature based on the different heat capacities of the molecules due to the different degrees of freedom f for vibration (\(\hbox {CH}_4\) f=4, \(\hbox {CO}_2\) f=3, CO f=1) and an equal supply of excitation from the plasma
The dependence of the vibrational temperatures of \(\hbox {CH}_4\), \(\hbox {CO}_2\), and CO on the absorbed plasma power are shown in Fig. 4b–d, respectively. The temperatures of \(\hbox {H}_2\)O are not evaluated because the HITRAN fitting is based on using the line strengths at 300 K only. It can be seen that the vibrational temperatures are significantly higher than the rotational temperatures. This has already been observed previously and illustrates the non-equilibrium character of plasma excitation [8, 9]. The vibrational temperatures depend only weakly on the admixed concentration of \(\hbox {O}_2\) with the temperatures only a bit higher at very low admixture levels. Such higher vibrational temperatures at very low \(\hbox {O}_2\) admixtures can be clearly identified for CO. In general, such a relation between vibrational temperatures and \(\hbox {O}_2\) admixture seem reasonable, because less molecular gas in the channel allows the energy to be dissipated into fewer molecules that reach higher excitation temperatures.
In principle, the rotational and vibrational temperatures can also be deduced from the emission bands of CO, which requires a complete analysis of the excitation and emission processes. Such experiments are planned in the future. The advantage of the analysis of IR absorption spectra is their straightforward method of quantification that yields temperatures and densities at the same time.
As a simple estimate, the increase in vibrational temperatures \(\Delta T_{vib}\) of the different molecules is estimated based on their heat capacity \(C_V = \Delta U/\Delta T\) assuming the same energy input \(\Delta U\) from the plasma but different heat capacities due to the different number of degenerated vibrational modes of 1 for CO, 3 for \(\hbox {CO}_2\) and 4 for \(\hbox {CH}_4\). Therefore, the measured increase in vibrational temperature \(\Delta T_{vib}\) for CO can be re-scaled to an expected \(\Delta T_{vib}\) for \(\hbox {CO}_2\) and \(\hbox {CH}_4\). The experiments show an increase in vibrational temperature of CO from 300 to 1000 K indicated as a dashed line in Fig. 4d, which is extrapolated to the expected \(\Delta T_{vib}\) of \(\hbox {CO}_2\) and \(\hbox {CH}_4\) by dividing this temperature enhancement of 700 K by 3 for \(\hbox {CO}_2\) and by 4 for \(\hbox {CH}_4\), respectively. The resulting temperature estimates are shown as dashed lines in Fig. 4b, c. It can be seen that these estimates agree fairly well. It is striking that this very simple thermodynamic analysis reproduces the typical temperatures rather well and any more intricate excitation and de-excitation model is apparently not needed. Apparently, the frequent collisions among the species assure thermal equilibrium between the different degrees of freedom of the molecules.
\(\hbox {CH}_4\) Conversion and \(\hbox {O}_2\) Removal
Figure 5 shows the change in species densities for \(\hbox {CH}_4\), CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O for varying plasma power and oxygen admixture. It can be seen that \(\hbox {CH}_4\) depletion increases with plasma power and oxygen admixture. At the same time, the products CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O are created.
The CO production does not vary too much, although plasma power and oxygen admixture vary. This indicates that CO constitutes an intermediate product. At very high plasma powers, the density of CO decreases again. This could be explained by the fact that at high plasma powers, sufficient oxygen atoms are being produced so that the conversion of \(\hbox {CH}_4\) to CO can further proceed to also create \(\hbox {CO}_2\). This interpretation is supported by the data for very low oxygen admixture of 0.3125 sccm. Despite a high plasma power, no maximum in CO production is observed, because apparently the supply of oxygen atoms is insufficient to progress the reaction until the formation of \(\hbox {CO}_2\). This is also consistent with the observation that the densities of the final products \(\hbox {CO}_2\) and \(\hbox {H}_2\)O are also much lower for the lowest oxygen admixture.
The conversion rates for 1.25 sccm and 2.5 sccm \(\hbox {O}_2\) admixture are almost identical. This is striking, because the conversion of methane is not improved although more oxygen is admixed. Apparently, the oxygen atom production reaches an optimum with respect to oxygen admixture between 1.25 to 2.5 sccm. This constitutes a concentration between 0.5 and 1% in relation to helium. This observation is consistent with experiments performed on an equivalent radio frequency discharge in helium with varying admixture of oxygen [11, 18, 19]: in a so-called COST-jet an optimum oxygen atom production at an admixture level of 0.5–0.6% has been observed, because atomic oxygen production suffers from the larger loss due to vibrational excitation rather than dissociation at higher oxygen admixture levels. An optimum in atomic oxygen production could also be linked to the back reaction of O and \(\hbox {O}_2\) to \(\hbox {O}_3\). This reaction, however, is more evident in the afterglow of the plasma, since efficient ozone formation requires low electron temperatures [18].
The plasma chemistry is also analysed by regarding the mass balances of all atoms that are measured by FTIR in the system to identify the occurrence of other species invisible to our diagnostic. Figure 6 shows the carbon (a), hydrogen (b), and oxygen (c) balance of the atoms in the individually measured species. For example, the hydrogen balance results from adding the species densities times the stoichiometric factors \(H_{balance} = 4 \times n_{CH_4} + 2 \times n_{H_2O}\). It can be seen that the balances are almost fulfilled. A small decrease in all mass balances with increasing plasma power is observed that can be related to an increase in temperature with increasing plasma power and thus a lowering of the overall gas density. This hypothesis is tested by inspection of the measured rotational temperatures as a measure for the gas temperature and using the ideal gas law to describe the temperature induced decrease of the species density at constant atmospheric pressure, starting with a set density at T=300 K taken from the set gas mixture. The resulting extrapolation of the mass balances to higher plasma powers is shown as dotted lines in Fig. 6. Apparently, all atoms in the molecules fed into the plasma can be found in the plasma reaction products. This observation indicates that the chemistry in the system remains rather simple and despite a strong conversion of the feed gas methane, most of the species are properly accounted for by the products CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O only.
The mass balance concerning oxygen atoms, however, can only properly be extrapolated from the set gas mixture at higher plasma powers and small admixtures of 0.625 sccm and 0.3125 sccm. This is not surprising, since oxygen is only accounted for in our experiment, if measured in the infrared active molecules of CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O. Any atomic or molecular oxygen that is not consumed in the reaction is inherently missing in the oxygen mass balance. This is consistent with the data. At an admixture of 1.25 and 2.5 sccm, only a fraction between 0.1 and 0.7 of the oxygen is converted into the products CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O leading to a significant deviation of the measured oxygen balance and the expectation from the ideal gas law (dashed lines in Fig. 6c).
Conversion of \(\hbox {CH}_4\) depending on gas mixture and plasma power for 0.625 sccm of \(\hbox {CH}_4\) and varying oxygen admixture as indicated. The mass balance of the atoms in \(\hbox {CH}_4\), \(\hbox {CO}_2\), CO, and \(\hbox {H}_2\)O for carbon (a) hydrogen (b), and oxygen (c), respectively. The dashed lines denote the expected density variation based on the ideal gas law taking into account an increase in gas temperature according to measured rotational temperatures and thus a corresponding decrease of density at constant pressure
\(\hbox {CH}_4\) Conversion and \(\hbox {O}_2\) Removal Along the Plasma Channel
The plasma chemistry of \(\hbox {O}_2\):\(\hbox {CH}_4\) conversion is also analysed by measuring along the gas flow direction for varying plasma power, as shown in Fig. 7 for \(\hbox {CH}_4\) (a), CO (b), \(\hbox {CO}_2\) (c) and \(\hbox {H}_2\)O (d) for a mixture of 0.625 sccm \(\hbox {CH}_4\) and 1.25 sccm \(\hbox {O}_2\) that is expected to produce stoichiometrically correct \(\hbox {CO}_2\) and \(\hbox {H}_2\)O. The gas flow is in the direction of the increasing position coordinate.
Conversion of \(\hbox {CH}_4\) at 0.625 sccm of \(\hbox {CH}_4\) and 1.25 sccm of \(\hbox {O}_2\) measured along the gas flow at 5 positions for \(\hbox {CH}_4\) (a) CO (b), \(\hbox {CO}_2\) (c), and \(\hbox {H}_2\)O (d) at varying plasma power, as indicated. Open symbols in (a) denote the measured \(\hbox {CH}_4\) density without plasma as a reference
It can be seen that \(\hbox {CH}_4\) is being increasingly depleted with increasing position along the gas channel and thus longer reaction times. At the highest plasma power and almost at the end of the channel a depletion of 85% is reached. \(\hbox {CH}_4\) and \(\hbox {O}_2\) are converted mainly into \(\hbox {H}_2\)O and \(\hbox {CO}_2\) and a small amount of CO. The efficiency of depletion scales with the power absorbed in the plasma, although at the highest absorbed power of 6 W and 7 W no large differences can be found. The density of CO goes through a maximum in the center of the gas channel, before it decreases again. This confirms the intermediate character of CO in the reaction sequence, as already discussed above. Such an intermediate character seems also to be exhibited by the reaction product \(\hbox {H}_2\)O. The intermediate character of CO is rather easy to explain given the fact that the conversion is driven by O atoms and CO can be further oxidized to \(\hbox {CO}_2\). Nevertheless, when the oxygen atom driven conversion is completed and all \(\hbox {O}_2\) is consumed, the plasma dissociation by electrons may still proceed to dissociate also the end products \(\hbox {CO}_2\) and \(\hbox {H}_2\)O even further. That may lead to a maximum concentration along the gas flow for the products \(\hbox {CO}_2\) and \(\hbox {H}_2\)O. In any application, such reactions would be avoided by restricting the residence times so that the products leave the plasma volume when their maximum concentration is reached.
The variation of the different reaction channels for \(\hbox {CH}_4\) conversion along the gas flow are analyzed in Fig. 8 in more detail for three plasma powers of 0.55W, 4 W, and 7 W (solid lines and symbols) in combination with the mass balances of the atoms in the species (solid lines). All mass balances are re-scaled to be identical to the density of carbon atoms in methane of 6 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\).
-
(i)
at a small plasma power of 0.55 W (Fig. 8a), the mass balances for hydrogen and carbon are almost correct. Only the mass balance for oxygen is strongly varying, because most of oxygen is still present as O and \(\hbox {O}_2\) which is not accounted for by our IR detection.
-
(ii)
at a plasma power of 4 W (Fig. 8b), one can see that the carbon balance is somewhat smaller at the beginning and at the end of the plasma in comparison to the center of the discharge. Apparently, at the beginning and at the end of the plasma channel, the measured species \(\hbox {CH}_4\), \(\hbox {CO}_2\) and CO do not completely account for all species containing carbon atoms. This could be explained as follows: at the beginning of the plasma channel, the electron density is high, whereas the oxygen atom density is still low [20]. Consequently, electron impact reactions that cause the direct dissociation of methane might be more prevalent than reactions of methane with atomic oxygen. The electron impact reactions with methane may induce some hydrocarbon plasma polymerization leading to very different hydrocarbon species that are not measured or are at least not detectable given the sensitivity limit of our setup. Further downstream, however, these polymerized hydrocarbon species are eventually converted into CO and \(\hbox {CO}_2\) due to the abundance of oxygen atoms leading to a correct carbon balance, because the carbon species within CO and \(\hbox {CO}_2\) are now visible to the IR spectroscopy. The hydrogen balance is significantly lower than the scaling value, indicating that hydrogen atoms from the injected methane are not completely converted into \(\hbox {H}_2\)O, but other hydrogen containing species such as \(\hbox {H}_2\), \(\hbox {C}_x\hbox {H}_y\) or \(\hbox {C}_x\hbox {O}_y\hbox {H}_z\) may be formed. The complete and efficient conversion of \(\hbox {O}_2\) into CO and \(\hbox {CO}_2\) is indicated by the correct oxygen mass balance at a position of 15 mm. Therefore, the deficit in the hydrogen balance should correspond to \(\hbox {H}_2\) formation, which is not captured by our diagnostic. The carbon and hydrogen mass balances decrease also at the end of the plasma channel. This is reasonable, if we assume that the end products \(\hbox {CO}_2\) and \(\hbox {H}_2\)O originating from the chemical conversion of methane with dissociated oxygen upstream can still undergo further electron induced dissociation reactions downstream. These reactions may create \(\hbox {H}_2\), \(\hbox {C}_x\hbox {O}_y\) and \(\hbox {H}_x\hbox {O}_y\) species that are not detected and that induce this deficit in the balances. This behavior can also be interpreted as an optimum at 15 mm along the gas channel for \(\hbox {CH}_4\) and \(\hbox {O}_2\) conversion at these flows and plasma powers. If one converts the position of 15 mm into a residence time with the flow velocity of 0.3 m/s, one could also state that the optimum residence time for conversion is 50 ms.
-
(iii)
at a plasma power of 7 W (Fig. 8c), the trends of the mass balances with position along the plasma channel are similar to the trends observed at a plasma power of 4 W. The deviation of the balances from the scaling value of 6 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\) is only larger. This is consistent since these deviations have been explained by the influence of direct electron impact reactions on methane and oxygen leading to \(\hbox {H}_2\), \(\hbox {C}_x\hbox {O}_y\hbox {H}_z\) and \(\hbox {H}_x\hbox {O}_y\) species that are not tracked by the IR spectroscopy. This dependence can be used to define an optimum plasma power for a given flow and gas composition in the process. Apparently, \(\hbox {CH}_4\) and \(\hbox {O}_2\) conversion into CO and \(\hbox {CO}_2\) only works at a residence time of 50 ms and a plasma power of 4 W.
Conversion of \(\hbox {CH}_4\) at 0.625 sccm \(\hbox {CH}_4\) and 1.25 sccm \(\hbox {O}_2\) measured along the gas flow (same data as in Fig. 7). Mass balances for carbon (blue lines), oxygen (black lines), and hydrogen (red lines) for three plasma powers of 0.55 W (a), for 4 W (b), and for 7 W (c)
Plasma Catalytic Conversion of \(\hbox {CH}_4\):\(\hbox {O}_2\) Mixture Using a \(\hbox {MnO}_2\) Catalyst
The impact of a catalytic active surface is evaluated by regarding the conversion of 0.25% \(\hbox {CH}_4\) and 0.5% \(\hbox {O}_2\) admixed to helium into CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O at varying plasma power and three temperatures of 300 K, 378 K, and 423 K of the electrode surface covered with a \(\hbox {MnO}_2\) catalyst at a loading of 0.75 mg/\(\hbox {cm}^2\). Figure 9 shows the dependence of \(\hbox {CH}_4\) (a), of CO (b) and of \(\hbox {CO}_2\) (c) on plasma power and surface temperature. It can be seen that the overall trend of \(\hbox {CH}_4\) depletion and CO and \(\hbox {CO}_2\) formation with plasma power is reproduced at the different surface temperatures. For such a comparison, it is important to note that the reduction in species density at higher system temperature due to the ideal gas law has to be compensated for to allow a direct comparison of the experiments for different catalyst temperatures. Therefore, all species densities are re-scaled to the reference point of 6 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\) for the \(\hbox {CH}_4\) density at room temperature. It can be seen in Fig. 9 that the \(\hbox {CH}_4\) depletion is a bit larger at higher catalyst temperatures. More significantly, however, is the more efficient production of CO and \(\hbox {CO}_2\) at higher temperatures. The higher production of CO and of \(\hbox {CO}_2\) is consistent with the corresponding larger depletion of \(\hbox {CH}_4\) although this difference cannot so easily be identified in the \(\hbox {CH}_4\) signal due to a larger statistical error. Apparently, a plasma catalytic enhancement of 15–20% is observed. Here, the catalytic enhancement quantifies only the impact of the catalyst on the local conversion at the central position of the plasma channel. For any application at end, the net conversion after passing the gas stream through the plasma channel including also any back reaction would be needed to be measured by gas chromatography for example. Such an integral assessment is not yet in the focus of our analysis.
The catalyst effect is identified by comparing the reaction rates at 300 K and at 430 K. In principle, a comparison to the plasma conversion without a catalyst should be made (see for example data in Fig. 4). However, such a comparison is inherently based on two experimental campaigns using two electrode assemblies with a reproducibility in the wiring , accuracy of the catalyst coating etc. that is not better than 10–15%. This reproducibility is in the same range as the catalytic effect, which makes such a comparison not straightforward. Therefore, we decided to keep the experiment unaltered and only vary the temperature from room temperature, where any catalytic surface process can be excluded, to higher temperatures where for example CO2 desorption from the catalyst surface can occur.
Plasma catalytic conversion of \(\hbox {CH}_4\) in a plasma with 0.625 sccm \(\hbox {CH}_4\), 1.25 sccm \(\hbox {O}_2\) and 250 sccm He at room temperature and at 378 K and at 423 K for \(\hbox {CH}_4\) (a), CO (b) and \(\hbox {CO}_2\) (c), electrode surface covered with a \(\hbox {MnO}_2\) catalyst at a loading of 0.75 mg/\(\hbox {cm}^2\)
Discussion
A Simple Chemical Model for Plasma Oxidation of \(\hbox {CH}_4\) in He:\(\hbox {O}_2\):\(\hbox {CH}_4\) Mixtures
The plasma chemical conversion of methane in an oxygen containing helium plasma is usually analysed by a complex global model invoking hundreds of species and thousands of reactions that are combined with a Boltzmann solver to evaluate the electron energy distribution functions that is needed to calculate the rate coefficients for the electron induced reactions. The cross sections for the electron induced reactions can be found in the LXCat database [21], the neutral chemical reactions are from the chemical kinetics database of NIST. Such a model is prone to inaccuracies in the tabulated cross sections and rate coefficients. Therefore, we chose a data-driven approach to simulate the chemical reactions of methane oxidation based on a most simple chemical model that captures the reaction stoichiometry correctly, but covers only the major species and sums up sequences of detailed elementary reactions into a single representative reaction. Such an approach is especially suited for our experiment, because (i) the species are heavily diluted in helium so that secondary reactions leading to a multitude of species play a minor role and (ii) the mass balances of the individual atoms in our experiment are almost preserved by accounting only the main species, which indicates that the complexity of the plasma chemistry is very much reduced. This leads to a set of 10 chemical reactions shown in Table 1.
The position dependent data are modelled with scaled rate coefficients for a change in concentration per [mm] plasma channel, as shown in Fig. 10. For this, each density is normalized to the density of \(\hbox {CH}_4\) in the feed gas of 6 \(\times\) 10\(^{22}\) \(\hbox {m}^{-3}\). The helium flow of 250 sccm leads to a flow velocity of 0.3 \(\hbox {ms}^{-1}\) in the gas channel. With this flow velocity each position along the gas channel can be converted into a time coordinate. Thereby, a 2nd order rate coefficient in \(k_{literature, 2nd}\) [\(\hbox {m}^3/\hbox {s}\)] is converted into a scaled coefficient in the model \(k_{model, 2nd}\) per [mm] position along the flow path via \(k_{model, 2nd} \,[1/\hbox {mm}]= \frac{1}{v [\hbox {mm}/\hbox {s}]}\, k_{literature, 2nd} [\hbox {m}^3/\hbox {s}]\, 6 \times 10^{22}[1/\hbox {m}^3]\).
In addition, predictions of the rate coefficients from literature are given, for elementary reaction \(\hbox {k}_2\) to \(\hbox {k}_5\), \(\hbox {k}_7\) and \(\hbox {k}_{{10}}\). The input data from the literature are scaled in the same manner as the model rate coefficients for comparison. The following assumptions are being made for the rate coefficients from literature:
-
3-body reactions (\(\hbox {k}_2\), \(\hbox {k}_3\), \(\hbox {k}_5\), \(\hbox {k}_{{10}}\)): Three body collisions are necessary for most of the recombination reactions. For this, the density of \(2.4 \times 10^{25}[m^{-3}]\) for helium at atmospheric pressure is taken into account as a third body collision partner. Thereby, the rate coefficients from literature are converted into apparent 2nd order coefficients in the model via \(k_{model, 2nd} [mm^{-1}]= \frac{1}{v [mm/s]} k_{literature, 3rd} [m^6/s] 6 \times 10^{22}[1/m^3] 2.4 \times 10^{25}[1/m^3]\). The predictions from literature for three body collisions, usually assume a third reaction partner of the same kind instead of a light helium atom. Therefore, some differences between literature predictions and model values might be expected.
-
electron induced reactions (\(\hbox {k}_4\), \(\hbox {k}_7\), \(\hbox {k}_8\), \(\hbox {k}_9\)): The cross sections from the LXCat database are converted into rate coefficients assuming an Maxwellian distribution function with an electron temperature of 2 eV, which is very typical for helium plasma jets [19].
-
dissociative electron attachment and ionization (\(\hbox {k}_7\), \(\hbox {k}_8\), \(\hbox {k}_9\)): The rate coefficients for electron induced dissociative ionization and attachment are used as an estimate for the similar reactions \(\hbox {k}_7\), \(\hbox {k}_8\) and \(\hbox {k}_9\) of the simple model, where no direct rate coefficients could be found. This remains a crude assumption.
-
sum reaction (\(\hbox {k}_1\)): The sum reaction \(\hbox {k}_1\) describes the conversion \(\hbox {CH}_4\) + 2 O \(\rightarrow\) 2 \(\hbox {H}_2\)O + C and represents a real fitting parameter without any predictions from literature. The consecutive reactions of elemental carbon to CO and \(\hbox {CO}_2\) (\(k_2\) and \(k_3\)) can be compared with rate coefficients from literature. Reaction \(k_1\) is a simplification and it summarizes presumably a much more detailed elementary reaction sequence. Such a reaction sequence might not necessarily lead directly to elemental carbon but rather to more stable species such as CO and \(\hbox {CO}_2\). As an alternative, one could also combine reaction \(k_1\) with reactions \(k_2\) and \(k_3\) to create two stoichiometric reactions of \(\hbox {CH}_4\) + 4 O \(\rightarrow\) \(\hbox {CO}_2\) + 2 \(\hbox {H}_2\)O and of \(\hbox {CH}_4\) + 3 O \(\rightarrow\) CO + 2 \(\hbox {H}_2\)O. However, this would require two fitting values instead of only one as above.
-
unknown rate coefficients (\(\hbox {k}_6\)): no literature value is available, but the reaction should be similar to the reaction of carbon with atomic oxygen (\(\hbox {k}_2\)). Since the reaction partner in \(k_6\) is an oxygen molecule rather than an atom, a 10 times smaller value for \(k_6\) is chosen in comparison to \(k_2\). This is a crude estimate.
The model analysis is started by regarding the experiments at a plasma power of 4 W (b) and fixing the electron density to generate a specific oxygen dissociation rate consistent with a rate coefficient \(k_4\) close to the prediction by LXCat. This yields an electron density of \(n_e\) = 4 \(\times\) 10\(^{17}\) \(\hbox {m}^{-3}\). The depletion of methane is then quantified by the fitting parameter coefficient \(k_1\), but which is very much bound by the data, once the creation rate of oxygen atoms is set by \(k_4\) based on the LXCat predictions. Thereby, the creation rate of C atoms and of O atoms is set and the secondary reactions of CO formation and of CO oxidation are also very much defined. The comparison between the scaled rate coefficients from the model and literature predictions indicate good agreement (except for \(k_5\) and \(k_{10}\)) and apparently reproduces the main reaction pathways of the \(\hbox {CH}_4\)/\(\hbox {O}_2\) chemistry very well. This quantitative analysis of the chemistry works surprisingly well given the simplicity of the model, since almost all rate coefficients are within a factor 2 or less in agreement with literature values. Only the back reactions of oxygen atoms to create \(\hbox {O}_2\) (\(k_5\)) or \(\hbox {O}_3\) (\(k_{10}\)) seem to be much less dominant than predicted by literature.
The reliability of the fit is tested by extrapolating the reaction scheme at fixed rate coefficients to the experiments at lower and higher plasma powers of 0.55 W (a) and 7 W (c), respectively. For this, the electron density is adjusted and the position dependent variation of the species density is modelled. The correlation of the fitted electron density with plasma power is shown in Fig. 11 showing an almost linear dependence (red line for illustration). Such a linear dependence of the electron density on plasma power is consistent with a typical global plasma model. Nevertheless, the comparison of the model with the data at the highest plasma power (c), indicate larger deviations between model and data suggesting that the chemistry model may be too simple at very high electron densities.
The model is also extrapolated by comparing the modelled densities of \(\hbox {CH}_4\), CO, and \(\hbox {CO}_2\) for different mixtures of \(\hbox {CH}_4\) and \(\hbox {O}_2\) in the feed gas depending on plasma power, as shown in Fig. 12 with the model (left column) in comparison with the data (right column, same data as in Fig. 5). It can be seen that the model reproduces the major trends very well. For example, the observed independence of the CO concentration on the admixture of oxygen in the experiment is also shown in the model. Nevertheless, some trends are not reproduced by this model extrapolation: (i) at the lowest admixture of oxygen, the depletion in the model is too small in comparison to the measured data; (ii) at the highest admixture of oxygen, the depletion still changes with oxygen concentration in the model although the data indicate almost no variation. One may speculate that this deviation between data and model originates from the interplay between electron density and oxygen concentration in the gas stream [20]. At high admixture of oxygen, the power absorbed by the plasma is more and more dissipated by the excitation of molecules rather than dissociation reactions. The opposite occurs at very low admixture of oxygen. This non-linearity in the dependence of power and electron density is not yet covered by the model. A more detailed description of such data driven models comparing different formulations is being addressed elsewhere [29]. Most interesting would be a direct measurement of the atomic oxygen concentration in the plasma using for example laser spectroscopy such as TALIF.
In the current status, the model describes the measured data accurately below a maximum \(\hbox {CH}_4\):\(\hbox {O}_2\) ratio of two and at electron densities or plasma powers up to a specific maximum that is sufficient to trigger the complete chemical conversion of \(\hbox {CH}_4\) and \(\hbox {O}_2\) into \(\hbox {CO}_2\) and \(\hbox {H}_2\)O. Such a limit of the model validity is reasonable, because any higher values of plasma power may increase the contribution of electron induced secondary reactions that are not part of the simple chemical model.
Based on the observed trends in the data, one may develop a design recommendation for oxygen removal from exhaust gas streams. Apparently, the plasma power has to be adjusted accurately to trigger the complete stoichiometric conversion of \(\hbox {O}_2\). If the plasma power is too low, residual oxygen molecules may remain, if the plasma power is too high, the plasma process will be energy inefficient, but, even more important, secondary reactions may lead to many other \(\hbox {C}_x\hbox {H}_y\hbox {O}_z\) and \(\hbox {H}_x\hbox {O}_y\) species that could be harmful to a consecutive catalytic process.
Extrapolation of the model (left column) for different gas mixtures in comparison to the data (right column, same data as in Fig. 5). The electron density is normalized to 4 \(\times\) 10\(^{17}\) \(\hbox {m}^{-3}\)
Reaction Mechanisms for Plasma Catalytic Oxidation of \(\hbox {CH}_4\)
The occurrence of a plasma catalysis mechanism is discussed by using a typical Ni catalyst for thermal catalysis in a \(\hbox {CH}_4\):\(\hbox {O}_2\) mixtures as a reference case [4]. A more direct reference case for thermal catalysis would be a \(\hbox {MnO}_2\) catalyst for methane oxidation, as it is used in the experiment, but a detailed microscopic model for \(\hbox {MnO}_2\) is not available in the literature. We, therefore, used existing models for methane oxidation on a Ni catalyst to motivate the important temperature windows for the formation of CO and of \(\hbox {CO}_2\). These temperature windows are governed by the binding energies of CO and \(\hbox {CO}_2\) on these surfaces and are rather similar for many catalysts. In thermal catalysis for methane oxidation, the limiting step is the breaking of the first CH bond of the incident hydrocarbon upon impact at the catalyst surface. This is in competition with the blocking of surface sites by oxygen atoms, because oxygen molecules undergo dissociative chemisorption at the catalyst surface already at room temperature. This oxygen only desorbs at temperatures above 1000 K providing free sites for hydrocarbon chemisorption. Then, association reactions between adsorbed oxygen and adsorbed carbon take place creating adsorbed CO and \(\hbox {CO}_2\). \(\hbox {CO}_2\) may already desorb from the surface above 400 K, whereas the binding energy of CO is much higher implying a surface temperature above 700 K necessary for desorption. As a result, thermal catalysis of a \(\hbox {CH}_4\):\(\hbox {O}_2\) mixture leads preferably to CO at surface temperatures above 1000 K.
The experiments showed an 15% enhancement of the production of \(\hbox {CO}_2\) and CO due the presence of a catalytic surface at elevated temperatures of 400 K only, if compared to room temperature conversion. Apparently, feed gas molecules or their dissociation products in the plasma may adsorb at the catalyst surface and recombine to create adsorbed CO and \(\hbox {CO}_2\) species. Such an association at the surface may become visible as an enhanced production of \(\hbox {CO}_2\) in the gas phase, because \(\hbox {CO}_2\) is also able to desorb from the catalyst surface typically at temperatures above 400 K. In methane oxidation by thermal catalysis in \(\hbox {CH}_4\):\(\hbox {O}_2\) gas mixtures, however, the dissociative chemisorption of methane is the rate limiting step that competes with dissociative chemisorption of oxygen. As a result, \(\hbox {CO}_2\) formation at the very surface requires very high temperatures of typically 1000 K so that oxygen also desorbs leaving free sites for methane chemisorption. As a consequence, any \(\hbox {CO}_2\) production in such thermal catalysis systems at 450 K is not expected.
In case of plasma catalysis, however, the temperature windows for \(\hbox {CO}_2\) production may be different because dissociation products of \(\hbox {CH}_4\) such as \(\hbox {CH}_3\), \(\hbox {CH}_2\), CH or C may much more easily chemisorb in competition with dissociative chemisorption of oxygen. In addition, energetic particles from the plasma may also induce desorption of oxygen atoms from the surface that provides open sites for \(\hbox {CH}_x\) adsorption. As a consequence, \(\hbox {CO}_2\) formation may still be possible, if the plasma assists \(\hbox {CH}_x\) adsorption to compete with the inherent dissociative oxygen adsorption, followed by \(\hbox {CO}_2\) association and desorption above 400 K.
According to this sequence, the enhanced production of \(\hbox {CO}_2\) can be explained. However, also an enhanced production of CO is observed in the experiment, although it can only desorb from the surface at much higher temperatures of 700 K. CO may still be formed via association at the surface similar to \(\hbox {CO}_2\) above, but will not desorb at 400 K. Therefore, we speculate that the observed plasma catalytic effect may be linked to other effects: (i) it may be possible that the rate of oxygen atom creation is higher in the presence of the catalyst, which would lead to a higher CO and \(\hbox {CO}_2\) production at the same time. Such a surface assisted oxygen production could consist of the dissociative chemisorption of oxygen at the surface followed by a plasma particle induced desorption of oxygen atoms. Such a mechanism could also explain that the effect of the catalyst is more pronounced at higher plasma powers, which can most clearly be seen when inspecting the \(\hbox {CO}_2\) density data - above a plasma power of 3 W, the data for different temperatures start to deviate. Apparently, the plasma catalytic effect scales with the electron density in the plasma; (ii) it may also be possible that the plasma assists the desorption of CO from the surface at low substrate temperatures; (iii) the presence of the catalyst may affect the plasma generation and thus the plasma dissociation due to different secondary electron emission coefficients. However, such an effect should be almost independent on the surface temperature. In addition, all experiments are related to the absorbed power in the plasma, which would include any catalyst induced improvement of plasma generation. A direct experimental verification of the hypothesis of any surface assisted oxygen creation rate in the plasma is extremely difficult and we can provide here only possible mechanisms. Complete simulations and new experiments monitoring the surface coverages in real time are required to identify the exact mechanisms.
At the moment, the mechanisms that govern plasma catalytic oxidation cannot be identified from these data. These experiments nevertheless show that an enhancement of the conversion can be observed in a system where surface and species temperatures are controlled and well known. This removes the ambiguity in most plasma experiments, where the unintentional plasma heating of the surfaces may give the impression of a plasma catalytic effect although the enhancement can be explained by pure thermal catalysis where the catalyst is just heated by the plasma.
Conclusion
It is shown that the plasma reaction for oxygen (or methane removal) is triggered by the formation of oxygen atoms from \(\hbox {O}_2\) by electron impact since the threshold energy for electron induced dissociation of oxygen molecules is smaller than that for methane. Oxygen atoms are efficiently converted into CO, \(\hbox {CO}_2\) and \(\hbox {H}_2\)O with CO being an intermediate in that reaction sequence. At very high oxygen admixtures, however, the conversion efficiency is limited because the formation of oxygen atoms from \(\hbox {O}_2\) by electron impact saturates presumably at high oxygen admixtures. The impact of a typical manganese oxide catalyst is evaluated for methane conversion. It is shown that the conversion efficiency is enhanced by 15–20% at temperatures of 430 K. It is shown that the efficiency of oxygen removal from the gas stream is affected by the nonlinear interplay between plasma power and oxygen atom generation. Consequently, any industrial implementation of the plasma based removal of oxygen should invoke also a direct monitoring of the oxygen concentration in the gas stream to regulate the plasma operating parameters.
References
Chung W, Mei D, Tu X, Chang M (2019) Catal Rev Sci Eng 61:270
Bogaerts A, Neyts EC (2018) ACS Energy Lett 3:1013–1027
Choi B (2000) Chem Eng J 76:103–114
Maier L, Schädel B, Herrera Delgado K, Tischer S, Deutschmann O (2011) Topics Catal 54:845–858
Frey A, Goeke V, Voss C (2018) Chemie Ingenieur Technik 90:1384–1391
Wiesmann T, Hamel C, Kaluza S (2018) Chemie Ingenieur Technik 90:1446–1452
Ortloff F, Bohnau J, Graf F, Kolb T (2016) Appl Catal B Environ 182:375
Stewig C, Schüttler S, Urbanietz T, Böke M, von Keudell A (2020) J Phys D Appl Phys 53:125205
Urbanietz T, Böke M, Schul-von der Gzathen V, von Keudell A (2018) J Phys D Appl Phys 51:345202
Stewig C, Urbanietz T, Chauvet L, Böke M , von Keudell A (2020) (submitted)
Golda J, Held J, Redeker B, Konkowski M, Beijer P, Sobota A, Kroesen G, Braithwaite NSJ, Reuter S, Turner MM, Gans T, O’Connell D, Schulz-von der Gathen V (2016) J Phys D Appl Phys 49:084003
Ollegott K, Peters N, Antoni H, Muhler M (2019) Emission Control Sci Technol 5:378–391
Peters N, Schücke L, Ollegott K, Oberste-Beulmann, C, Awakowicz P , Muhler M (2020) (submitted)
Rothman L, Jacquemart D, Barbe A, Chris Benner D, Birk M, Brown L, Carleer M, Chackerian C, Chance K, Coudert L, Dana V, Devi V, Flaud JM, Gamache R, Goldman A, Hartmann JM, Jucks K, Maki A, Mandin JY, Massie S, Orphal J, Perrin A, Rinsland C, Smith M, Tennyson J, Tolchenov R, Toth R, Vander Auwera J, Varanasi P, Wagner G (2005) J Quant Spectr Radiat Transfer 96:139–204
Rothman L (1998) J Quant Spectrosc Radiat Transfer 60:665
Šimečková M, Jacquemart D, Rothman LS, Gamache RR, Goldman A (2006) J Quant Spectrosc Radiat Transfer 98:130–155
Klarenaar BLM, Engeln R, van den Bekerom DCM, van de Sanden MCM, Morillo-Candas AS, Guaitella O (2017) Plasma Sources Sci Technol 26:115008
Ellerweg D, Benedikt J, von Keudell A, Knake N, Schulz-von der Gathen V (2010) New J Phys 12:013021
Golda J, Held J, der Gathen VSv (2020) Plasma Sources Sci Technol 29:025014
Knake N, Schröder D, Winter J, Schulz-von der Gathen V (2010) J Phys Conf Ser 227:012020
Pitchford LC, Alves LL, Bartschat K, Biagi SF, Bordage MC, Bray I, Brion CE, Brunger MJ, Campbell L, Chachereau A, Chaudhury B, Christophorou LG, Carbone E, Dyatko NA, Franck CM, Fursa DV, Gangwar RK, Guerra V, Haefliger P, Hagelaar GJM, Hoesl A, Itikawa Y, Kochetov IV, McEachran RP, Morgan WL, Napartovich AP, Puech V, Rabie M, Sharma L, Srivastava R, Stauffer AD, Tennyson J, de Urquijo J, van Dijk J, Viehland LA, Zammit MC, Zatsarinny O, Pancheshnyi S (2017) Plasma Process Polym 14:1600098
Fairbarn A (1969) Proc R Soc A Math Phys Eng Sci 312:207
Tsang W , RF H (1986) J Phys Chem Ref Data 15
Itikawa Y (2009) J Phys Chem Ref Data 38:1
Itikawa Y (2002) J Phys Chem Ref Data 31:749–767
Itikawa Y, Mason N (2005) J Phys Chem Ref Data 34:1
Morgan W (1992) Plasma Chem Plasma Process 12:477
DeMOre W, Sander S, Golden S, Hampson D, Kurylo M, Howard C, Ravishankara A, Kolb C, Molina M (1997) JPL Public 97:1
Reiser D, Urbanietz T , von Keudell, A (2020) (submitted)
Acknowledgements
This project is supported by the BMBF in the framework of the L3 subproject of the Carbon2Chem consortium and by the DFG (German Science Foundation) within the framework of the Coordinated Research Centre SFB 1316 at Ruhr-University Bochum. We thank the Laboratory of Industrial Chemistry in Bochum for preparing and applying the catalyst and K. Ollegott and M. Muhler for helpful discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Urbanietz, T., Stewig, C., Böke, M. et al. Oxygen Removal from a Hydrocarbon Containing Gas Stream by Plasma Catalysis. Plasma Chem Plasma Process 41, 619–642 (2021). https://doi.org/10.1007/s11090-020-10151-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11090-020-10151-6