On the Possibilities of Straightforward Characterization of Plasma Activated Water

Abstract

Plasma activated deionized water from a hot arc 150 W PAW synthesizer has been analyzed for nitrite, nitrate and peroxide densities. Observed nitrite and nitrate levels are impressive, reaching several millimoles per liter at few hundred kiloJoules per liter energy input. Nitrate levels appear positively influenced by the applied energy density, together with a less pronounced increase in nitrite levels and limiting energy density for maximum peroxide levels. Active PAW cooling during synthesis appears to be essential for obtaining relevant peroxide levels and connected PAW activity. In addition to established laboratory diagnostics, alternative low access tools have been investigated for applicability of PAW characterization in off-lab situations. Although no unique parameter exists to properly represent PAW activity, pH, oxidizing-reduction potential and electrical conductivity provide important insight, together with aqueous phase nitrite absorption spectrometry. Finally, classic acid-base titration has been applied to find access to the complex mixture of acidic reactive nitrogen species.

Introduction

Plasma activated water (PAW) is a versatile medium for both biomedical and agricultural applications. Currently under investigation and promising are its applications e.g plant disease control, plant nutrition, surface disinfection, surgical equipment sterilization, skin disinfection, wound treatment, dental bleaching and root disinfection, bladder infection and cancer treatment [1,2,3,4,5,6]. PAW active ingredients comprise transient reactive oxygen and nitrogen species (ROS and RNS, combined abbreviation RONS).

The focus of this study has been on investigation of the possibilities of straightforward/low-access diagnostic tools for PAW characterization, as alternative to reference tools like ion chromatography and peroxotitanyl spectrometry. Simple diagnostic tools would be especially suitable for PAW synthesis process feedback control and also for PAW activity monitoring on locations, where only limited laboratory facilities are available. In comparison with the reference diagnostics, pH, oxidation reduction potential (ORP), electrical conductivity (EC), titrimetry, general UV absorption spectrometry and commercially available indicator strips have been studied.

PAW synthesis precedes by application of electric gas discharges in air or nitrogen-oxygen mixtures over a water volume [7]. Fundamental plasma phenomena, as will be discussed in  "Plasma Fundamental Considerations" section, explain the formation of simple atomic and molecular precursors to the observed liquid phase plasma chemistry, the key research of this study. Involved species are nitrogen oxides based RNS (NO, $\hbox {NO}_2$, $\hbox {NO}_3$,¹$\hbox {N}_2\hbox {O}_3$, $\hbox {N}_2\hbox {O}_4$, $\hbox {N}_2\hbox {O}_5$) nitrogen oxoacids based RNS ($\hbox {H}_a\hbox {N}_b\hbox {O}_c$²) and ROS ($\hbox {O}_3$, $^1\hbox {O}_2$, O, OH, $\hbox {HO}_2$, $\hbox {H}_2\hbox {O}_2$) [9,10,11,12,13]. PAW solutions typically comprise nitric ($\hbox {HNO}_3$) and nitrous ($\hbox {HNO}_2$) acid and low level transient RNS like e.g. peroxynitrous acid ONOOH / peroxynitrite $\hbox {ONOO}^-$ and accompanying ROS.

ONOO(H) is generally considered to account for major contribution to PAW activity due to powerful oxidizing and cytotoxic properties [11, 14,15,16,17,18], together with peroxynitric acid $\hbox {O}_2$NOOH / peroxynitrate ($\hbox {O}_2\hbox {NOO}^-$), a product from ONOOH and $\hbox {ONOO}^-$ at near neutral pH conditions [19]. Koppenol [19] and Kissner [20] propose ONOOH decomposition via the hydroxyl radical in a radical cage pair together with nitrogen dioxide [$\hbox {NO}_2\cdot \hbox {OH}\cdot$] to nitrate/nitric acid, or directly. The oxidizing potential of ONOOH may also be related to release of singlet oxygen ($^1\hbox {O}_2$) accompanied by nitroxyl (HNO) [21] upon decomposition.

Although the solubility of the higher nitrogen oxides in water is reasonable [22] and acidic conditions thus are easily reached, PAW normally is synthesized at about pH = 3.3. Then, PAW already features impressive disinfection performance, while material corrosion or etching damage in biochemical systems are minimized.

Experiments

Equipment and Settings

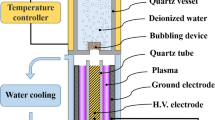
All experiments have been performed on PAW, obtained from a 150 W VitalFluid synthesizer. VitalFluid is a spin-off company from the Electrical Energy Systems Group at Eindhoven University of Technology, founded in 2014. The power system comprises a dual resonant power modulator switching at 1 MHz [23]. The power (J/s) is modulated by changing the repetition frequency (bursts/s) and the number of cycles per burst (cycles/burst x J/cycle = J/burst). Small power fluctuations are regulated by the repetition rate, while the number of cycles per burst is applied for power level setting. The ignition voltage is up to 100 kV, while the arc voltage is 8 kV peak-to-peak. Schematics and typical waveforms are given in Figs. 1, 2 and 3, respectively.

A few thousand Kelvin arc is produced in the gas phase of a borosilicate 800 mL glass beaker, partially filled with deionized water, typically 400 mL, see also Table 4. The arc is directed into the water vortex, propelled by a magnetic stirrer bar, in order to optimize plasma-water interaction and $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ gas-to-liquid phase mass transfer. The plasma reactor configuration features a DBD topology, the ground electrode situated underneath the glass beaker bottom. Figure 4 shows a long exposure photo of the arc in the vortex; a time-resolved CCD picture is given by Fig. 5 [24]. Additionally, a double wall 600 mL Duran glass beaker has been applied, conditioned at $12\,^{\circ }\hbox {C}$. Although PAW synthesis using tap water is equally possible, deionized water has been chosen for reasons of standardization in process and analytical conditions. The reactor is sealed and purged with filtered compressed air at ambient pressure, unless stated otherwise.

Experiments mainly comprise aqueous phase nitrate, nitrite and peroxide determination and potentiometry. Applied chemical analytical diagnostics are a Shimadzu LC-10Avp liquid chromatograph, Merck Pharo 300 UV–VIS spectrometer, Mettler Toledo S400 Bio pH/ORP meter, WTW Electrical Conductivity/pH/ORP meters and typical peroxide, nitrite and nitrate test strip kits with a combined colorimetric analyzer. Ion chromatography analysis, $\hbox {H}_2\hbox {O}_2$ related peroxotitanyl spectrometry and sample preparation have been performed according to the analytical procedures described by Lukeš [14]. Sample stabilization has been applied for reasons of analysis times inherent to large sample sets regarding both $\hbox {NO}_x^-$ chromatography and $\hbox {H}_2\hbox {O}_2$ spectrometry.

Fig. 1

VitalFluid PAW synthesizer pulsed power topology

Fig. 2

Characteristic voltage and current waveforms at 90 W RF power; burst repetition rate $\sim 23.5\, \hbox {kHz}$, duty cycle $\sim 0.51$ (Color figure online)

Fig. 3

Characteristic power burst waveform at 90 W RF power

Fig. 4

Typical arc-water vortex interaction; exposure time 1/40 s, aperture f/5

Fig. 5

Typical CCD arc image: $\hbox {V}_{{MCP}}$ = 760 V, gating time = $25 \,\mu \hbox {s}$, $\hbox {f}_{{rep}}$ = 40 kHz, $\hbox {f}_0$ = 750 kHz, f/4 aperture; the refraction area represents the optically inaccessible region of vortex upper part

Plasma Fundamental Considerations

The generation of a strong plasma is the key element for water activation [7]. In the atmospheric air plasma, nitrogen and oxygen molecules are ionized and dissociated. Atomic nitrogen, atomic oxygen, simple molecular radicals like NO and OH, and electrons and ions thus are precursors to $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ in both the gas and aqueous phase.

The plasma is excited by applying RF voltage bursts to the high voltage electrode over water. The counter electrode is underneath the glass vessel and is capacitively coupled to the stirred water phase.

The current and the applied voltage are out-of-phase, see Fig. 2. The water has a good conductance and most of the voltage is over the plasma. The applied voltage is in the range of 1–5 kV and the current is 0.1–0.3 A. The series capacitance in the RLC circuit explains the current, which is relatively small for thermal plasmas. It makes that the discharge is like a DBD discharge. Because of the moderate current, we expect a small plasma diameter, in the 0.3 mm range [25, 26]. Then there will be sufficient power density and resistance to create a near thermal atomic plasma. The dissipated energy has been determined from Fig. 3 and is about 2–4 mJ/burst. The repetition frequency of the power bursts is 25 kHz, the average power is then around 50–100 W.

Although arc dimensions seem to appear several millimeter diameter size according to Fig. 4, this observation is incorrect, because many moving small discharges are integrated over the long exposure time. Short exposure CCD images like Fig. 5 indeed reveal tiny channels, in particular close to the electrode, where the power density is at maximum. It indicates a sub-millimeter plasma, consistent with the observed moderate currents, moving through the wider channel, thus explaining the wider emission pattern taken with low time resolution. Considering the 0.3 mm arc diameter and a curved length of approximately 5 cm, the active arc volume is about $3\cdot 10^{-9}\, \hbox {m}^3$. Thus power densities range up to $10^{10}\, \hbox {W}/\hbox {m}^3$, which is sufficient to maintain a small-sized thermal plasma. The plasma density is expected in the range of $10^{21}-10^{22}$$\hbox {m}^{-3}$ [26] close to or even in the thermal plasma range. It indicates that in the arc channel, the plasma is atomic and that atomic ions dominate.

A rough estimate of the produced activity can be obtained by comparison of the dissipated energy with the energy needed for ionization and dissociation of the heated gas in the plasma core. Ionization produces first molecular ions, which undergo dissociative recombination and are again ionized. Thus, ionization is accompanied with dissocation and also direct dissociation occurs. As in atmospheric pressure plasmas the number of dissociations can be as high as 5–10 radicals per ion/electron production [27], we can assume around 20–40 eV per ionization. The produced radicals are mainly nitrogen and oxygen atoms resulting from ionization, dissociative recombination and re-ionization of the exited atomic radical. The plasma electron temperature is close to 2 eV [28]; electron-heavy particle energy transfer will heat both neutrals and ions, the hot plasma subsequently heating the gas and aqueous phase.

The produced flux of radicals, $\Phi _{rad}$, in particular N and O atoms, can be linked to the charged particle production by ionization $\Phi _{ion}$, see Eq. 1. The latter can be estimated from the consumed power $\textit{P}$ (J/s) and the energy needed to ionize the gas $\textit{IE}$ (ionization energy, expressed in eV/atom or J/mol), see Eq. 2.

$$\Phi _{rad}= \xi _{rad}\cdot \Phi _{ion}$$

(1)

$$\Phi _{ion}= \frac{1}{\xi _P}\cdot \frac{P}{IE}$$

(2)

Here the power factor $\xi _P$ (dimensionless) accounts for energy losses, as heat conduction and diffusion, $\frac{1}{\xi _P}$ indicates which part of the applied energy is used for ionization. Typically, the number of produced radicals is larger than the number of ions. The regular estimate for more developed arcs, higher current atmospheric plasmas is $\xi _P$$\sim \,3$ [27]. For the lower current present case, a larger value is expected, i.e. $\xi _P$$\sim$ 10–20, thus more other losses than for ionization.

$\xi _{rad}$ (also dimensionless) is the average radical yield per ion yield; a typical value $\xi _{rad}$$\sim 5$ has been assumed [27]. Finally, if a $10\%$ yield for NO formation from $\hbox {N}_2$ and $\hbox {O}_2$ is additionally taken into account [29, 30] an estimation of the amount of radicals available to enter the water can be obtained: $\Phi _{rad}$ [$\hbox {s}^{-1}$] $\sim 1.0\cdot 10^{16}$ P [W]. For P = 100 W and 20 min plasma operation, we obtain a total production of approximately $1.3\cdot 10^{21}$ radicals. If comparable product species quantities are assumed in plasma treated 400 mL solutions, the calculated number corresponds to order of magnitude millimol/L (mM) concentrations.

The generated flux of atoms and simple molecular radicals, mainly atomic nitrogen, atomic oxygen and $\hbox {NO}_x$ will approach the gas-liquid interface. In addition, electrons and ions will contribute to the plasma chemistry. Atomic hydrogen and hydroxyl radicals result from the plasma interaction with both the water surface and gas phase water vapour. H is of particular interest, as it diffuses faster than the heavier O and N atoms. However, the main contribution from the gaseous discharge will be N, O and simple molecular radicals formed in the periphery like NO and OH [31].

Also in the aqueous bulk phase, plasma chemistry is expected: O, H, OH, NO, HNO, $\hbox {H}_2$, $\hbox {H}_2\hbox {O}_2$ (as well as $\hbox {N}_2$, $\hbox {O}_2$, $\hbox {H}_2\hbox {O}$) are produced, the precursors to the aqueous phase RNS, i.e. $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ nitrogen oxoacids; the latter increase the electrical conductivity of the water, possibly thereby also influencing the plasma characteristics. How the current is conducted through the water film at the surface of the bottom of the vessel is not clear. It is possible that small transient current carrying plasmas are formed near the glass bottom, a dielectric barrier.

Considering timescales, the formation of ions, excited species, atomic and radicalar species is on sub-microsecond level, while the more stable species $\hbox {HNO}_3$, $\hbox {HNO}_2$, $\hbox {H}_2\hbox {O}_2$ and ONOOH evolve on millisecond level [9]. After plasma operation, post plasma reactions generally comprise decay of transient liquid and gas phase ROS and RNS (e.g. ONOOH typical half life in water $<1$ s [14], $\hbox {O}_2(\hbox {a}^1\Delta _g$) typical gas phase lifetime $\sim 2700 \hbox {s}$ [32]) and continued oxidation of residual RNS amounts by more stable ROS, eventually yielding stable aqueous solutions of $\hbox {HNO}_3$ and $\hbox {HNO}_2$ in thermodynamical equilibrium with an $\hbox {NO}_x$ based gas phase.

Results

Initial experiments directly indicated, that the applied generator synthesizes PAW at very high nitrite and nitrate levels and low hydrogen peroxide content. This is explained by the high arc temperature, enabling the strongly endothermic oxidation of air to $\hbox {NO}_x$, but without compromising the thermally fragile peroxide chemistry. In order to properly quantify $\hbox {H}_2\hbox {O}_2$ levels, azide recipe concentration for destruction of nitrite had to be dramatically increased, up to maximum allowable levels. Active cooling of PAW during synthesis was subsequently introduced and appeared to increase $\hbox {H}_2\hbox {O}_2$ levels at already impressive nitrite levels, and peroxynitrite chemistry presumably positively. The plasma-water interface, enabling mass transfer of $\hbox {NO}_x$ and $\hbox {H}_2\hbox {O}_2$, is defined by the water vortex and the arc point-of-attack in the vortex, thus fundamentally important for PAW batch production consistency. The PAW synthesizer protocol therefore is fully automated with regard to arc ignition, arc stabilization and stirring speed.

Energy Density

The applied plasma power P, treatment time $\Delta$t and treated deionized water volume $\hbox {V}_w$ can be merged into the energy density $\epsilon$, given by Eq. 3. Herewith the amount of process parameters is reduced and different experiments might be more easily compared mutually. Then, the assumption needs to be made, that the ratio of RONS formation energy to loss energy is independent of the applied power.

$$\epsilon \left[ \frac{J}{L}\right] = \frac{P[W] \cdot \Delta t[s]}{V_{w}[L]}$$

(3)

Figure 6 shows nitrite, nitrate and peroxide densities of freshly prepared PAW as a function of the energy density. During PAW synthesis, active reactor cooling has been applied at $12\,^{\circ }\hbox {C}$. Obviously, the endothermic $\hbox {NO}_x$ formation scales with the energy density, while hydrogen peroxide production shows a maximum: plasma-water interaction at low energy density is not able to produce relevant peroxide densities, while higher energy densities thermally destroy peroxide, irrespective of active cooling. The effect of non-cooling during synthesis is dramatic: beyond 288 kJ/L in 500 mL, PAW temperatures easily reach $54\,^{\circ }\hbox {C}$; RONS decomposition then is evident. The initial slopes of the double logarithmic plot clearly reveal proper linearity for hydrogen peroxide production and non-linearity for nitrite and nitrate production; the latter reflects the oxidation of nitrite to nitrate. Together with the nitrite, nitrite and peroxide measurements, PAW acidity, oxidation-reduction potential (ORP) and electrical conductivity (EC) have been recorded, see Fig. 7. The ORP value reflects the tendency of the PAW solution to withdraw (oxidizing agent specific) or donate (reducing agent specific) electrons, relative to a reference electrode. Like pH is an integral parameter for acidic species, the ORP comprises contributions from all redox species. It has appeared that acidity, ORP and EC increase as a function of the applied energy density.

Although this may be rather evident, some additional comments have to be made: the individual parameters, although easily experimentally accessible cannot quantify PAW activity on itself. At higher energy density the weak acid $\hbox {HNO}_2$ is gradually converted into the strong acid $\hbox {HNO}_3$, the latter contributing considerably more to the pH than the former does. The electrical conductivity reflects the overall solution conductivity, which is mainly determined by the $\hbox {H}_3\hbox {O}^+$ concentration (10$^{-pH}$), together with other ionic species with lower equivalent ion conductivity but at the same time impressive concentration: nitrate and nitrite.

Fig. 6

Hydrogen peroxide, nitrite and nitrate concentrations in PAW as a function of the energy density; multifold analysis applies

Fig. 7

Acidity, electrical conductivity and oxidation reduction potential of PAW solutions as a function of the energy density; multifold analysis applies

Nitrite, nitrate and peroxide production efficiency values have been determined from the ratio of observed species concentration and applied energy density, according to Eq. 4. Average efficiency values have been determined from the initial slopes of the linear plot version of Fig. 6 and are given in Table 1.

Also included in the table are observed maximum efficiencies, derived from additional reactor optimization experiments, not connected to Fig. 6; these comprise variation of air purge rate, air-to-water volume, high voltage electrode-water distance and water mixing speed.

It appears, that $\hbox {H}_2\hbox {O}_2$ production is unfavourable under hot-arc conditions; similarly, thermal decomposition of $\hbox {NO}_2$ might be an explanation for lower yields of nitrate compared to nitrite. Reported values are comparable with efficiency data from Machala [33].

$$\eta \left[ \frac{nmol}{J}\right] = \frac{C\left[ \frac{{\mu }mol}{L}\right] }{\epsilon \left[ \frac{kJ}{L}\right] }$$

(4)

Table 1 Observed average and maximum RONS production efficiencies

PAW synthesis data from other studies have been summarized in Table 2. It should be noted, that reported pH and EC values are also dependent on the initial water (aqueous ion) composition. Observed densities of nitrite, nitrate and peroxide are comparable and although these values scale with the applied energy density, the latter parameter and thus also production efficiencies are not generally reported. The diversity in applied plasma types is reflected by diversity in pH and EC values. This may suggest that PAW chemistry and connected PAW activity are well definable by precise plasma control, which offers an interesting future prospective for PAW applications.

Table 2 Different processes to generate ROS and RNS from air and water, maximum values are reported (except for pH, minimal values)

Kinetics

Freshly prepared PAW decays due to the transient RONS chemistry. A characteristic half life time for peroxynitrous acid has been determined to be less than 1 second [14]. Figures 8 and 9 show nitrite, nitrate and peroxide levels as a function of the shelf time, both for synthesis cooled and synthesis non-cooled PAW solutions, respectively.

Fig. 8

PAW main analytes decomposition kinetics for cooled synthesis ($12\,^{\circ }\hbox {C}$); sampling moments after end-of-synthesis; multifold analysis applies

Fig. 9

PAW main analytes decomposition kinetics for non-cooled synthesis; sampling moments after end-of-synthesis; multifold analysis applies

Non-cooled solutions are rich in nitrite and nitrate and lack peroxide, due to the Arrhenius temperature dependence of the reaction rates. Cooled solutions contain less but still impressive amounts of nitrite and nitrate and considerably more peroxide. Both for cooled and non-cooled preparation, nitrate levels slowly increase upon standing, with a positive effect of applied energy density. Nitrite is slowly converted then, while peroxide levels dramatically decrease with shelf time. Summarizing, when defining PAW activity by peroxynitrous acid presence (requiring nitrite, peroxide and acidic conditions), cold synthesized PAW exhibits a few minutes time scale activity. RONS decomposition not only is caused by enhanced temperatures, also energetic photons from gas discharges/daylight easily decompose hydrogen peroxide and nitrogen peroxoacids; catalytic activity from the high voltage electrode or sputtered electrode material may also play a role.

Titration

In order to resolve the composition of PAW solutions more extensively, dedicated recipies have been submitted to titration, classic wet-chemical analysis. Titration is a very mature, robust and accurate chemical diagnostic tool, despite a presumed vintage image, yet unmistakably valuable in both laboratory analysis and contemporary chemical process control. Applying titrimetry on PAW solutions is challenging. Several analytical approaches exist, i.e. freezing transient PAW chemistry before analysis by addition of quenching agents, measuring on near-equilibrium solutions or apply fast analysis directly after PAW synthesis. The latter approach has been chosen, in order to obtain approximate but unique insight, unbiased by additional chemistry or composition change over longer timescales.

Initially, the intention was to apply ORP based redox titration, where the oxidizing power of PAW due to different RONS is resolved by using a titrant with strong reducing power. The ORP value exhibits a logarithmic dependence on the concentrations³ of the oxidizing and reducing species (redox couples) present in PAW according to Nernst [39]. As example, Eq. 5 shows the reduction reaction half-cell electrode potential concerning the oxidizing hydroxyl radical species under acidic conditions; R and F represent the universal gas constant and Faraday constant, respectively. Like pH, ORP measurements generally use an Ag/AgCl electrode as electrode potential reference. Although ORP changes normally are small, its application is of particular significance in situations where the concentration of species will vanish, i.e. in redox titrimetry. Sodium azide $\hbox {NaN}_3$ was chosen being the strongest reducing agent applicable in aqueous solution. However, required concentrations to titrate the prepared PAW solutions eventually appeared not attainable, considering the intrinsic instability hazard of required aqueous $\hbox {NaN}_3$ solutions beyond 2 M.

$$\begin{aligned}&E=2.73 V -\frac{RT}{F}\ln \frac{1}{[OH] \cdot [H^{+}]}\\&OH + H^{+} + e^{-} \rightarrow H_{2}O\\ \end{aligned}$$

(5)

Thereupon, acid-base titration was performed using 2 M potassium hydroxide KOH titrant solutions. Now, RNS are resolved by intrinsic acidity $\hbox {pK}_a$, see Table 3 and Eq. 6, valid for a monoprotic acid ($\hbox {H}_2\hbox {O}_2$ is considered as weak monoprotic acid); the water autodissociation constant $\hbox {K}_w$ is derived accordingly, see Eq. 7. Note that the acid equilibrium constant and water autodissociation constant seem to bear units, respectively: $\hbox {K}_a\, [\mathrm{mol/L}]$ and $\hbox {K}_w$ [$\hbox {mol}^2/\hbox {L}^2$], although they are dimensionless. This apparent discrepancy is caused by the fact, that water as solvent is present in excess and therefore left out of the equilibrium quotient (set to unity) [39], see Eqs. 6 and 7. Simultaneous with pH, ORP was logged because titration might influence the aqueous $\hbox {NO}_x$ equilibrium concentration.

$$\begin{aligned}&HA + H_{2}O \rightleftharpoons H_{3}O^{+} + A^{-}\\&K_{a} = \frac{[H_{3}O^{+}]\cdot [A^{-}]}{[HA]\cdot [H_{2}O]} \equiv \frac{[H_{3}O^{+}]\cdot [A^{-}]}{[HA]} \quad \wedge \quad [H_{2}O]=constant \end{aligned}$$

(6)

$$\begin{aligned}&H_{2}O + H_{2}O \rightleftharpoons H_{3}O^{+} + OH^{-}\\&K_{w} = \frac{[H_{3}O^{+}]\cdot [OH^{-}]}{[H_{2}O]^{2}} \equiv [H_{3}O^{+}]\cdot [OH^{-}] \quad \wedge \quad [H_{2}O]=constant \end{aligned}$$

(7)

Table 3 Acid dissociation constants of basic PAW components, expressed as $\hbox {pK}_a$ = − $^{10}$log($\hbox {K}_a$); acidity decreases with increasing $\hbox {pK}_a$

Directly after synthesis, eighteen PAW recipies have been submitted to acid-base titration and simultaneous measurement of initial nitrate, nitrite and hydrogen peroxide concentration. Table 4 describes the applied experimental settings. Experiments have been performed at different plasma power, treatment time and exposed water volume; titration runs have been sorted by increasing applied energy density and power.

Also, the titration curves have been simulated using the titration equation for a mixture of monoprotic acids of different acidic strength with a single strong monoprotic base titrant (here KOH), according to Eq. 8 [43].

$$\begin{aligned}&\frac{ \sum _{}F_{a, HA}\cdot c_{HA}-\Delta }{c_{KOH} + \Delta } = \frac{V_{KOH}}{V_{PAW}} \\&F_{a, HA}=\frac{K_{a}}{[H_{3}O^{+}]+K_{a}}\\&\sum _{acid}F_{a, HA}\cdot c_{HA}=\frac{K_{a, HNO_3}\cdot c_{HNO_3}}{[H_{3}O^{+}]+K_{a, HNO_3}} + \frac{K_{a, HNO_2}\cdot c_{HNO_2}}{[H_{3}O^{+}]+K_{a, HNO_2}} + \frac{K_{a, H_2O_2}\cdot c_{H_2O_2}}{[H_{3}O^{+}]+K_{a, H_2O_2}} \\&\Delta =[H_{3}O^{+}]-\frac{K_{a, H_2O}}{[H_{3}O^{+}]} \\&pH=-^{10}log([H_{3}O^{+}]) \end{aligned}$$

(8)

$\hbox {c}_{{HA}}$ equals the monoprotic acid analytical concentration, $\hbox {F}_{a, HA}$ is the proton dissociation function for a monoprotic acid powered by the dissociation constant $\hbox {K}_a$, $\hbox {V}_{{KOH}}$ is the titrant volume ($<289\, \hbox {mL}$) at concentration $\hbox {c}_{{KOH}}$ (2 mM) and $\hbox {V}_{{PAW}}$ is the PAW sample volume (50 mL). Calculation of the pH implicit titration curves has been performed using a vpasolve based Matlab script to numerically solve equations [44]. PAW main components $\hbox {HNO}_3$, $\hbox {HNO}_2$, $\hbox {H}_2\hbox {O}_2$ (and $\hbox {H}_2\hbox {O}$) have been included in the simulation, omitting contributions from expected nanomole per liter order of magnitude peroxynitrite concentrations [14]. Figure 10 represents an overview graph of the titrated PAW solutions, characterized by the imposed energy density and observed Electrical Conductivity; Fig. 11 provides initial concentrations of nitrate $\hbox {NO}_{{3}}^{-}$, nitrite $\hbox {NO}_{{2}}^{-}$ and hydrogen peroxide $\hbox {H}_2\hbox {O}_2$, sampled prior to titration.

Table 4 Experimental settings for preparation of PAW titration recipies; temperature of the $12 \,^{\circ }\hbox {C}$ cooled solutions is within the range 19.2–21.8 $^{\circ }\hbox {C}$

Fig. 10

Titrated PAW solutions characterized by the imposed energy density and measured electrical conductivity; numbers refer to the titration run (marker bottom) and applied power (marker top). Colors indicate the degree of matching between observed and simulated curves: cyan = simulation precedes titration curve, yellow = simulation lags titration curve, red = non matching situation; titration nr. 15 lacks EC data (Color figure online)

Fig. 11

Initial nitrite, nitrate and peroxide concentrations of titrated PAW solutions; numbers refer to the titration run, see Table 4

Obviously, increasing the applied energy density introduces more RNS in the water, resulting in higher conductivity due to more $\hbox {H}_{{3}}\hbox {O}^{+}$, $\hbox {NO}_{{3}}^{-}$ and $\hbox {NO}_{{2}}^{-}$ ions. At higher energy densities, $\hbox {NO}_{{3}}^{-}$ levels further increase due to ROS induced $\hbox {NO}_{{2}}^{-}$ oxidation, again due to Arrhenius law-based acceleration of reaction kinetics; also thermal decomposition of $\hbox {H}_2\hbox {O}_2$ occurs. It appears that the sum of nitrate and nitrite concentrations exhibits a properly linear dependence on the applied energy density.

Although applied experimental parameters have been grouped by energy density, it is typical to observe that differences in applied power settings still remain visible; thus it is possible to indicate near to linear trend lines of EC versus $\epsilon$, see again Fig. 10. From a plasma fundamental point of view, referring to "Plasma Fundamental Considerations" section, the power factor at 120 W is lower than that at 90 W, implying a better radical production or higher plasma efficiency at 120 W.

Data points 8 and 11 seem outliers, but are likely explained by higher $\hbox {NO}_x$ and OH densities thus higher formation rates of nitrogen oxoacids; involved conditions namely comprise a closed/non-purged PAW reactor without $\hbox {NO}_x$ loss due to air purging and, additionally doubled mixing speeds and a larger gas-to-liquid phase volume. Conductivity therefore is considerably higher, then. Additionally, in a closed reactor a higher water vapour density exists; therefore the plasma produces a higher flux of atomic hydrogen, resulting in more arc contraction and consequently a higher arc power density. Finally, higher mixing speeds deepen the vortex, thereby extending the arc.

Electrical conductivity is directly connected to pH acidity, because the hydronium ion $\hbox {H}_3\hbox {O}^+$ has highest equivalent ion conductivity, followed by $\hbox {NO}_{{2}}^{-}$ and $\hbox {NO}_{{3}}^{-}$ ions [45]. Although EC cannot be deconvoluted into the contributions of different ions, pH actually comprises an $\hbox {H}_3\hbox {O}^+$ selective electrical conductivity measurement. It should also be noted, that pH values intrinsically are not convertible to EC values, because identity and concentration of the balancing negative ions, also contributing to conductivity, should be known. Figure 12 shows the observed inverse relationship, due to the negative logarithmic concentration dependence of the pH.

Fig. 12

Initial pH versus initial Electrical Conductivity for titrated PAW solutions; numbers refer to titrations, see Table 4. Datapoints 14 and 16 lack accurate pH data; marker colors: blue = 90 W, red = 120 W (Color figure online)

Figures 13, 14 and 15 illustrate a selection of measured and simulated titration curves. It has appeared that the match between simulated and measured curves generally is poor, but yet differences appear and titration data can be reasonably grouped into three clusters by a degree of matching. The first group comprises samples $1+2+3+4+5+16$ where the simulation curve generally precedes the measured titration curve; group two consisting of samples $6+9+10+12$ exhibits typical simulation curve matching beyond the measured titration curve; group three holding samples $7+8+11+13+14+15+17+18$ represents non-matching simulations. The degree of matching seems related to the degree of acidity or conductivity, thus applied energy density. In more detail, the composition of PAW solutions with approximately $\hbox {EC}>300$$\mu \hbox {S}/\hbox {cm}$ seems to strongly deviate from that of presumed model solutions at measured initial concentrations or the model solutions require additional components.

Fig. 13

Simulation (red) precedes the measured (blue) titration curve; graph titles comprise energy density “e” (kJ/L) and electrical conductivity “s” ($\upmu \hbox {S}/\hbox {cm}$) (Color figure online)

Fig. 14

Simulation (red) lags the measured (blue) titration curve; graph titles comprise energy density “e” (kJ/L) and electrical conductivity “s” ($\upmu \hbox {S}/\hbox {cm}$) (Color figure online)

This may be explained as follows. Determination of initial nitrate, nitrite and peroxide concentrations prior to titration occurs via strict and separate analytical protocols to inhibit further reactions after PAW synthesis, i.e. peroxide consumption by nitrite and acidic decomposition of nitrites [14]. However, titration proceeds with non-inhibited thus reactive PAW samples. Despite rapid starting of the titration after synthesis, the solution thus changes composition during titration, albeit initially most pronounced, but analysis times comprised 4–15 min. These typical timescales also have been observed in the kinetics experiments. It is expected that actual nitrite levels during titration are overall lower and consequently nitrate levels higher than initially measured, not mentioning transient RNS densities, thus accounting for discrepancies between measurements and simulation.

Another remarkable observation is, that the slope of all measured titration curves appears to be flatter than the simulated ones. Acid-base titration curve steepness is determined by the acid dissociation constant $\hbox {K}_a$. Weak acids, relative to strong acids, feature enhanced bonding of acidic hydrogen, implying a lower dissociation degree, i.e. higher $\hbox {pK}_a$ values and, deducible from the titration Eq. 8, flatter slopes.

Fig. 15

Non-matching simulations (red) and measurements (blue; graph titles comprise energy density “e” (kJ/L) and electrical conductivity “s” ($\mu \hbox {S}/\hbox {cm}$) (Color figure online)

In addition to nitric and nitrous acid, other nitrogen oxoacids $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ are known, which are weak to very weak acids and transient (reactive, unstable) RNS [40, 41]: oxohyponitrous or hyponitric acid $\hbox {H}_2\hbox {N}_2\hbox {O}_3$, nitroxyl HNO, peroxynitric acid $\hbox {O}_2\hbox {NOOH}$, peroxynitrous acid ONOOH and trans-hyponitrous acid $\hbox {H}_2\hbox {N}_2\hbox {O}_2$, see Table 5.

Table 5 Acid dissociation constants of some transient nitrogen based oxoacids, sorted on decreasing acid strength; also provided are nitrogen atom valency numbers

HNO is formed from atomic hydrogen and nitric oxide; it is a reactive intermediate and could be considered as precursor of the higher RNS. In aqueous solution, HNO partially dissociates to $\hbox {NO}^-$, which upon oxidation yields $\hbox {ONOO}^-$. HNO easily dimerizes to $\hbox {H}_2\hbox {N}_2\hbox {O}_2$ and also reacts with $\hbox {HNO}_2$ to $\hbox {H}_2\hbox {N}_2\hbox {O}_3$. $\hbox {H}_2\hbox {N}_2\hbox {O}_2$ is reported to have a remarkable half-life of about 16 days at pH = 1–3 and 25 $\,^{\circ }\hbox {C}$ [47]. $\hbox {ONOO}^-$ is reasonably stable in alkaline solution [19]. $\hbox {O}_2$NOOH exhibits only limited stability in non-concentrated aqueous solution at $\hbox {pH}<5$. $\hbox {H}_2\hbox {N}_2\hbox {O}_3$ is unstable and its decomposition to nitric oxide and water is catalyzed by nitrite. Finally to mention is the highly unstable nitroxylic or hydronitrous acid $\hbox {H}_4\hbox {N}_2\hbox {O}_4$ with -therefore- unknown acidity constant data, decomposing to nitrogen and water. Orthonitric $\hbox {H}_3\hbox {NO}_4$ free acid is unknown. Generally, these RNS decompose in aqueous solution via release of ROS (OH, $\hbox {HO}_2$, $^1\hbox {O}_2$), $\hbox {NO}_x$ and also $\hbox {N}_2\hbox {O}$, while acidic nitrite and nitrate solutions remain.

Discerning transient and more stable RNS, the former ones have a crucial role in PAW activity. Transient RNS generally exhibit high reactivity towards biological materials, both in molecular form and via their decomposition products, inducing e.g. DNA damage, lipid peroxidation, protein oxidation, antioxidant depletion, protein nitration, etching, inactivation of enzymes [48, 49]. Connecting reactivity and instability, in situ production of RONS is required to have full germicidal potential, while storage inevitably involves activity decline. Although very explainable from a theoretical point of view, direct analytical evidence for the presence of transient nitrogen oxoacids in PAW is hard to provide; their instable nature and low concentration actually exclude identification by primary analytical-chemical diagnostics like LC-MS, FTIR and Raman spectroscopy. However, $^{14}\hbox {N}$ NMR spectroscopy may be a suitable tool for resolving RNS structure, though under specific measurement conditions (solvent, temperature) and likely for high analyte concentrations [50]. Indirect evidence is easily obtained via detection of decomposition—originating radicalar species by ESR spectroscopy (using spin traps), as well as less structure specific UV–VIS absorbance spectroscopy.

Figure 16 shows simulated individual titration curves of aqueous solutions of $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ acids from Tables 3 and 5 at concentrations ranging from 100–1000 $\upmu \hbox {M}$.

Fig. 16

Simulated titration curves of aqueous solutions of $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ at concentration 100–1000$\,\upmu \hbox {M}$; the horizontal axis reflects the dosed KOH titrant quantity ($\mu \hbox {mol}$), the vertical axis equals the solution pH (−)

The diprotic oxo- and trans-hyponitrous acid require modification of the titration equation, using a more complex proton dissociation function $\hbox {F}_{a, H_2A}$, see Eq. 9. Although both $\hbox {pK}_a$ and concentration determine the titration curve course, titration curve steepness is mostly governed by the $\hbox {pK}_a$ value.

$$F_{a, H_{2}A}=\frac{K_{a,1}[H_{3}O^{+}]+2K_{a,1}K_{a,2} }{[H_{3}O^{+}]^{2}+K_{a,1}[H_{3}O^{+}]+K_{a,1}K_{a,2}}$$

(9)

Nitric acid, nitrous acid, oxyhyponitrous acid and nitroxyl appear not to account for the observed low degree of steepness, however the very weak acids do, according to the order trans-hyponitrous acid > peroxynitrous acid > peroxynitric acid. Also typical to mention and likely related to the presence of these weak acids is the fact that several titration curves exhibit a typical bend at the ramp onset, see Fig. 17. The bend seems to occur with higher titration experiment numbers, i.e. PAW solutions produced at higher energy density. It should be noted, that in a complex system of oxyacids as PAW is, the titration curve shape originates from more species than simulated, mutally coupled via the existing temperature dependent chemical equilibria, in addition to acid dissociation—also gas/liquid phase partitioning equilibria. And, despite reported $\hbox {pK}_a$ values, for unstable acidic species the titration curve validity range is limited.

Fig. 17

Detail of recorded titration curves, numbers refer to titrations, see Table 4; right down situated are curves 8 and 11, respectively

The individual contribution of $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ acids on the solution acidity as a function of the analytical (i.e. dosed) concentration is given by Fig. 18. These curves are derived from the titration Eq. 8, by setting $\hbox {V}_{{KOH}}==0\, \hbox {mL}$, respecting different proton dissociation functions for mono ($\hbox {F}_{a, HA}$) and diprotic ($\hbox {F}_{a, H_{2}A}$) acids, see Eqs. 8, 9 and 10. It is obvious, that PAW acidity is mainly determined by $\hbox {HNO}_3$ and $\hbox {HNO}_2$. Otherwise, to reach typical $\hbox {pH}\sim 3$ levels with the other weaker and also unstable acids, non-realistic or impossibly high concentrations would be needed.

$$F_{a}\cdot c_{a}-\Delta = 0$$

(10)

Fig. 18

Theoretical acidity of aqueous solutions of selected $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ acids as a function of their analytical concentration (Color figure online)

In order to further unravel the individual contribution of acids on solution pH, the acidic power has been defined as negative differential change of pH with the analytical concentration − $\frac{dpH}{dc}$ and derived as follows.

Departing from Eq. 10 for a monoprotic acid HA, Eq. 11 represents the analytical concentration as a function of [$\hbox {H}_3\hbox {O}^+$]. Subsequent differentiation by [$\hbox {H}_3\hbox {O}^+$] gives the differential Eq. 12. Inverting the latter, substituting [$\hbox {H}_{{3}}\hbox {O}^{+}$] by $10^{-pH}$ and d[$\hbox {H}_{{3}}\hbox {O}^{+}$] by -ln(10)$\cdot 10^{-pH}\cdot \hbox {dpH}$ yields Eq. 13, which after rearrangement yields the defined acidic power, Eq. 14.

$$c = \frac{[H_{3}O^{+}]^2}{K_a} + [H_{3}O^{+}] - \frac{K_{w}}{K_{a}} - \frac{K_{w}}{[H_{3}O^{+}]}$$

(11)

$$\frac{dc}{d[H_{3}O^{+}]} = \frac{2[H_{3}O^{+}]}{K_a} + 1 + \frac{K_{w}}{[H_{3}O^{+}]^{2}}$$

(12)

$$\frac{d[H_{3}O^{+}]}{dc} = \frac{-ln(10)\cdot 10^{-pH}\cdot dpH}{dc} = \frac{1}{ (\frac{2}{K_a} \cdot {10^{-pH}} + 1 + K_{w} \cdot 10^{2pH}) }$$

(13)

$$-\frac{dpH}{dc} = \frac{1}{ ln(10) \cdot (\frac{2}{K_a} \cdot {10^{-2pH}} + 10^{-pH} + K_{w} \cdot 10^{pH}) }$$

(14)

$$\begin{aligned}&c = \frac{ [H_{3}O^{+}]^3+K_{1}[H_{3}O^{+}]^{2}+K_{1}K_{2}[H_{3}O^{+}] }{K_1[H_{3}O^{+}]+K_{1}K_{2}}\nonumber \\&-\frac{ K_{w}[H_{3}O^{+}]^2+K_{1}K_{w}[H_{3}O^{+}]+K_{1}K_{2}K_{w} }{K_1[H_{3}O^{+}]^{2}+K_{1}K_{2}K_{w}} \end{aligned}$$

(15)

Deriving a simultaneous relationship for a diprotic acid like $\hbox {H}_2\hbox {N}_2\hbox {O}_2$ is much more complex. However, the analogue to Eq. 11, i.e. Eq. 15 already indicates, that Eq. 14 by approximation is also valid for a diprotic acid, if the dissociation constant products are negligibly small, which is true, here: $\hbox {K}_1\cdot \hbox {K}_2\approx 10^{-18.8}$ and $\hbox {K}_1\cdot \hbox {K}_2\cdot \hbox {K}_w$$\approx 10^{-32.8}$, then Eq. 15 reducing to Eq. 11.

Figure 19 shows the acidic power ranking of PAW acids as a function of the solution pH. At $\hbox {pH}<\sim 3.5$$\hbox {HNO}_3$ mostly contributes to pH, from $\hbox {pH}>\sim 3.5$$\hbox {H}_2\hbox {N}_2\hbox {O}_3$ equally contributes, while $\hbox {HNO}_2$ does from $\hbox {pH}>\sim 4.5$. The other weak RNS negligibly contribute to solution pH.

Fig. 19

Acidic power of PAW related $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ acids as a function of the pH (Color figure online)

Fast Analysis Tools

Parallel to the ion chromatography measurements, a number of spectrometric, indicator strip and pH-ORP measurements were performed in order to validate the extent of applicability of low access diagnostic tools for PAW characterization in situations, where no liquid chromatography or wet chemical laboratory facilities are available. For reasons of direct analysis, no additional sample stabilization has been applied.

The UV absorbance spectrum of PAW solutions exhibits some typical features [42]. A five-fold absorption band in the 325-390 nm range is attributed to the nitrite ion, while the absorbance peak at 300 nm is connected to nitrate. Peroxynitrite is reported to absorb at 302 nm, however this absorbance overlaps with nitrate absorbance and therefore is ambiguous. Generally, electronic transition related UV–VIS absorbance phenomena are not molecule unique like FTIR vibrational spectroscopy is, though certain features like conjugated systems and chromophoric functional groups induce characteristic absorption phenomena. However, the absorption region below 200 nm is non-specific at all.

Figures 20 and 21 show UV absorbance spectra of different PAW recipies. It has been observed that the nitrite absorbance indeed increases with the measured nitrite concentration. Additionally, cooled solutions exhibit stronger nitrite absorbance than non-cooled ones. Nitrate levels seem low, the absorption at 300 nm overruled by the strong nitrite background. Finally, note that energy density and nitrite levels not necessarily scale, the latter depending on integral process conditions.

Fig. 20

UV absorbance spectrum of cooled PAW solutions, energy density and nitrite concentration are provided in the legend (Color figure online)

Fig. 21

UV absorbance spectrum of non-cooled PAW solutions, energy density and nitrite concentration are provided in the legend (Color figure online)

The applicability of typical nitrite and hydrogen peroxide sensitive indicator strips combined with a colorimetric analyzer has been shortly investigated. Nitrate strips have not been considered, due to known strong cross-sensitivity with nitrite, already indicated by the manufacturer. Figures 22 and 23 show nitrite and peroxide levels determined by wet chemical analysis diagnostics and by the indicator strips. The nitrite strips seem to reasonably follow the actual nitrite levels, although with non-linear overestimation. The peroxide strips largely overestimate, perform unacceptably.

Fig. 22

PAW nitrite levels determined by Ion Chromatography and typical $\hbox {NO}_2^-$ indicator strips, as a function of the applied energy density

Fig. 23

PAW peroxide levels determined by peroxotitanyl spectrometry and typical $\hbox {H}_2\hbox {O}_2$ indicator strips, as a function of the applied energy density

Finally, observed ORP values during titration have been plotted in Fig. 24.⁴ It is typical, that the acid-base titration is accompanied by changes in redox chemistry, while no redox titrant is applied. This seems related to the pH-dependency of RONS reduction half reactions thus their-half cell voltage, as explained by Table 6 and the Nernst equation, see again Eq. 5.

Apart from this, RONS oxidizing power ranking is evident, the hydroxyl radical being the strongest practically applicable oxidizing species; an example is RONS cytotoxic activity through lipid cell membrane peroxidation by combined action of OH and $\hbox {O}_2$. Observed high ORP values are also due to high RONS concentrations. Eventually, oxidation power is connected to reaction spontaneity via the Gibbs free energy change $\Delta$G of the redox reaction, calculated from the half cell potential difference $\Delta$E of oxidizer and reducing species half reactions, the number of involved electrons $\textit{n}$ and the Faraday constant $\textit{F}$, see Eqs. 5 and 16. Typical deviations are visible with titrations 8 and 11, comprising highly acidic / high EC conditions, due to closed PAW reactor operation.

$$\Delta G = -n\cdot F \cdot \Delta E$$

(16)

Combining $\hbox {pH}=\hbox {f}_1$(KOH) (Fig. 17) and $\hbox {ORP}=\hbox {f}_2$(KOH) (Figure 24) titration data, a new relationship $\hbox {ORP}=\hbox {f}_3$(pH) has been derived that may provide novel insight with regard to resolving PAW activity, typical data are provided in Fig. 25. These curves comprise combined redox-acid chemistry information, that may discriminate the different PAW recipies.

As a function of the applied energy density, ORP and acidity increase, while acid-base titration of these recipies resolves nitrogen oxoacid densities and additionally influences the pH-dependent redox chemistry. More specifically, the area under the ORP versus pH curve (Volt units), between initial pH and equivalence point pH, might be related to RONS activity of the PAW solution. By replotting titrations 8 and 11, the ORP = $\hbox {f}_3$(pH) curves still reside in the higher ORP regions, but now seem to follow the general ORP versus pH trend during titration: a tailed maximum.

Fig. 24

Typical ORP versus KOH titration curves, the legend represents the titration run number according to Table 4 (Color figure online)

Fig. 25

Typical ORP versus pH titration curves, the legend represents the titration run number according to Table 4 (Color figure online)

Table 6 Standard reduction potentials of some PAW related RONS [20, 41, 51]

Conclusion

Hot-arc PAW contains impressive amounts of nitrate and nitrite. Using the laboratory scale PAW synthesizer, typically observed maximum efficiencies for production of nitrite, nitrate and peroxide are 23 nmol $\hbox {NO}_2^-$/J, 9 nmol $\hbox {NO}_3^-$/J and 2 nmol $\hbox {H}_2\hbox {O}_2$/J, corresponding to following energy requirements: 0.957 GJ/kg $\hbox {NO}_2^-$, 1.76 GJ/kg $\hbox {NO}_3^-$ and 14.2 GJ/kg $\hbox {H}_2\hbox {O}_2$. Fortunately, reported values exclude re-use of energy removed by process cooling and the electric efficiency of the considered PAW synthesizer is very high, i.e. 94–97%. Other efficiency improvements involve balanced $\hbox {NO}_x$ production, relative to liquid phase uptake. Closed reactor operation revealed dramatic increases of solution acidity, apparently the isolated air volume not yet being oxygen depleted; also, plasma fundamental phenomena seem involved with closed operating conditions.

While endothermic nitrogen fixation benefits from high arc temperatures, transient RONS synthesis requires low process temperatures. PAW synthesis for agricultural nutrition (nitrate) is not hampered by cooling precautions nor storage time, if no germicidal/conservation potential is required. On the other hand, PAW germicidal power strictly demands cooling, UV-daylight shielding and fresh preparation, the energetic decomposition of transient RONS accounting for its potency.

$\hbox {NO}_x^-$ ion chromatography and spectrometric $\hbox {H}_2\hbox {O}_2$ determination are reference diagnostics for characterizing PAW, but not always available and actually not suitable as fast diagnostic tool for PAW synthesis process feedback control or in-field PAW activity monitoring. On the other hand, no unique parameter exists to properly characterize PAW. It has appeared from this study, that a representative parameter set may comprise pH, EC and ORP. Also in-process UV absorbance spectrometry on nitrite and gas phase $\hbox {NO}_x$ seems a powerful tool, the latter of particular interest for balanced $\hbox {NO}_x$ production. Despite analyte concentration range availability, nitrite and peroxide indicator strips only seem to perform qualitatively in PAW analysis, that means only confirming the presence or absence of mentioned analytic species at given accuracy.

Acid-base titration resolved peculiar matching with simulations based on PAW base ingredients $\hbox {HNO}_3$, $\hbox {HNO}_2$ and $\hbox {H}_2\hbox {O}_2$, dependent on the applied energy density. Together with observed flat titration slopes and typical initial slope bends, it is apparent that other weaker acidic RNS are present in PAW. Although their identity cannot resolved by this technique, the typical phenomena observed with either acid-base or electrochemical titration, might be connectable to RONS potential. This would require additional experimental proof from synthesis-combined application experiments like germicidal/biochemical effect measurements. In addition to $\hbox {NO}_x$, $\hbox {N}_2\hbox {O}$ is formed from electric gas discharges in air. It also is a decomposition product of the potent RNS $\hbox {H}_2\hbox {N}_2\hbox {O}_2$ [40] and reduction product of NO and $\hbox {HNO}_2$ (Table 6). Although not applicable during synthesis, $\hbox {N}_2\hbox {O}$ might be an interesting marker for RONS activity during PAW storage.

Resuming, $\hbox {H}_a\hbox {N}_b\hbox {O}_c$ as part of the mystic family of interrelated $\hbox {NO}_y$ species, comprises diagnostically hard-accessible RNS members; their presence is observable through oxidizing-germicidal potential and explained by decomposition to ROS and more stable oxides and oxoacids of nitrogen.