Some Possible Dynamical Constraints for Life’s Origin

Abstract

Oscillating biochemical reactions are common in cell dynamics and could be closely related to the emergence of the life phenomenon itself. In this work, we study the dynamical features of some classical chemical or biochemical oscillators where the effect of cell volume changes is explicitly considered. Such analysis enables us to find some general conditions about the cell membrane to preserve such oscillatory patterns, of possible relevance to hypothetical primitive cells in which these structures first appeared.

Introduction

The beginning of life is one of the most amazing and intriguing facts of our Universe. Much work has been done on this subject since the famous results of Miller-Urey’s experiment in 1953, in a first attempt to explain how the basic building blocks of life were synthesized in a primordial atmosphere. However, the appearance of the first simple organisms in the early Earth is far from being a solved problem, since most of the main questions about it remain unanswered. How the transition between non-living and living matter took place? What is the essential difference between them? Today there are no definitive answers to these questions. The first problem arises with the life concept itself. The fact that we do not have an appropriate definition for the term, may be because its own essence remains unknown to us. Useful definitions such as “any chemical system or molecular assembly able to regenerate itself, replicate itself and is capable of evolving” or similar, see (Joyce and Orgel 1993) are descriptive or phenomenological statements, rather than firm first-principles starting points.

It is well-known that living beings display interesting features that could shed some light on the emergence of life phenomenon, mainly by helping to better define the frontier between living and non-living matter, even without having a precise definition of the term. Concepts such as homochirality (Plankensteiner et al. 2004), complex networks (Fell and Wagner 2000), oscillations and synchronization (Bier et al. 2000) and others, are distinctive features of all living beings, suggesting a much more intrinsic and deep connection with the life phenomenon itself.

In this work we focus mainly on only one of the former features: the oscillations. Initially introduced in chemistry to describe the oxidation transitions of ions Ce³⁺, BO ⁻₃ in acid solution in the Belousov-Zhabotinsky (BZ) reaction, the term oscillating reactions rapidly reached their best applications in biochemical and biological systems. Oscillations appear to be generic processes (McKane et al. 2007) in biological systems, with a very large number of them exhibiting some oscillatory degree in their dynamics. They are expected to form a key component of important cellular process such as metabolic network, reproduction and even signalization (Igoshin et al. 2004). One of the best examples is the periodic fluctuations exhibit by ATP and glucose during the glycolysis cycle.

Nowadays, the presence of biochemical oscillations can be understood at least in two ways, either as endogenous or as exogenous process. The first arise as result of inner complexities of metabolic network with multiple loops and feedback between the different components (metabolites, enzymes, etc) and structures (see Micheva and Roussel 2007). The models studied in this work basically belong to this group.

The second arise as the influence of forcing or fluctuating environmental parameters (illumination, temperature, pH, etc.) and the climate in general on organisms. Among them, the most important contributions appear to be closely related with the extension of the daily light–dark cycle, (from 15 h beginning the Archean to 24 h at present). Such influence appears decisive in the expansion of circadian rhythms in plants, animals and microorganisms such as cyanobacteria (for circadian rhythms see Mihalcescu et al. 2004; Lakin-Thomas and Brody 2004; Liebermeister 2005). Together with photosensitive proteins, circadian rhythms are believed to have originated in the earliest cells, with the purpose of protecting the replication of DNA from high doses of ultraviolet radiation during the daytime in Hadean or early Archean. Then, rhythm appears to be an important key in regulating biochemical processes within an individual, as in coordination with the fluctuating environment. Many other sources of ciclicity, (many of them astronomical) could have direct or indirect repercussion in the origin, distribution and evolution of life.

Based on the above considerations we may initially assume that oscillations are an inherited property of the living systems, and this assumption enable us in some (drastic) way to classify a simple system as alive (oscillating) or dead (non-oscillating). Actually this definition is known to be oversimplified for realistic modern organisms, but we believe it could be helpful to study and classify some simple systems, probably similar to the first “abiotic” expressions of life.

Another important feature of modern life is the presence of complex membrane boundary structure or cell wall separating the cell from the exterior world. A common property of these structures (membranes) is to be semi-permeable, restricting the passage of some specific molecules or metabolites. In modern cells the membrane is indispensable for cellular functioning, controlling the flow of water and selective species across the membrane and delimiting the effective cell dimensions. Besides, together with the incorporation of certain substances (pigments) they could give some additional protection to the inner cell structures against harmful environmental variables, such as the UV radiation.

It is not totally clear if the primitive cell ancestor had a cell wall but probably it is quite unlikely to reach the high organization and complexities of the modern organism without it. Some different compounds have been proposed as possible cell wall candidates for the primitive cells as amphiphiles products (Ourisson and Nakatani 1994, Deamer et al. 2002). Unfortunately there is not a clear alternative to this picture as yet, and the stability of the formed structures is known to be strongly dependent of environmental parameters as the pH of the medium. It is has also been argued in the last years, that many of the most important compounds to form theses structures could be particularly conditioned by the delivery of exogenous organic material from the outer space (Bernstein et al. 2001, 2002; Muñoz Caro et al. 2002; Dworkin et al. 2001).

On the other hand, given the elasticity of the membrane structure, the cell volume is a variable magnitude able to change for the different moments of the cell phase, or by changes in internal or external conditions such as concentration, pH, temperature, etc. At any given time, there is a dynamic balance between the osmotic potential across the membrane and cell volume, which is largely dependent on the intracellular metabolic flux and external cellular conditions. To minimize the effects of volume changes, modern cells exhibit several effective mechanisms to regulate the volume variations (Zonia and Munnik 2007). On the same fashion, our aim is to study how the volume changes could impose some restrictions on a cell wall for a very rough model of a primitive cell.

A (Fiducial) Brusselator Model

It is well known fact that the normal cells functioning imply volume changes. However, usually most biochemical systems studies in the literature neglect them, implicitly considering that the volume variations are not significant enough to induce notable changes in the biochemical dynamics. In order to take them into account (Pawłowski and Zielenkiewicz 2004) introduced a new term into the classical kinetics equations of the form $- {\text{x}}_{\text{idV}}/{\text{V}}_0$ where x_i is the modeled component, V₀ is an arbitrary volume unit and dV is the small variation of the volume experienced by the cell. In the original context, the authors considered Vas an explicit function of time (say, linear or exponential) to describe specific phases of the cell cycle. In this work, we assume an approach that diverges considerable from Pawłowski and Zielenkiewicz (2004). As our motivations differ, we prefer to infer our “volume variation law” from some simple thermodynamic criterion, rather than introducing the volume as an ad hoc explicit function of time. Let us consider a particular parameterization of the well-known Brusselator system as a first illustrative example. In this case the dynamics is set by the following two coupled differential equations, at fixed cell volume:

$$ \begin{array}{*{20}c} {dx/dt = a - \left( {b + 1} \right)~x + x^2 y} \\ {dy/dt = bx - x^2 y} \end{array} $$

(1)

where x and y are two arbitrary intermediary chemical species.

A variable volume Brusselator arises modifying the original system (1) as

$$ \begin{array}{*{20}c} {dx/dt = a - \left( {b + 1} \right)~x + x^2 y - x~dV/dt} \\ {dy/dt = bx - x^2 y - y~dV/dt} \end{array} $$

(2)

where the last terms are the explicit diluting factors associated to the volume changes. V is the volume of the cell in units of V ₀.

As a step to solve the system (2), we consider in our simplified scenario that the rate of volume variation dV/dt is mainly determined by the rate of change of all species concentrations into the cells. Specifically that means $dV/dt\sim dN/dt$ where N is the sum of different concentrations species for the original system (Eq. 1) and in our case $N = x + y$. The expression of dN/dt is easily derived as the sum of the two equations of the system (1) yielding

$$ dV/dt = r\left( {a - x} \right), $$

(3)

where a new proportionality parameter r ≥ 0 has been introduced (see below). The same procedure was extended to the other two studied systems (see next section).

It is important to note that the sign of dV/dt follows the dN/dt sign, for some times the volume increase or decrease according to the behavior of the total concentration N. The new parameter r represents some integrated structural characteristics of the cell membrane, rigidity, elasticity, and it could be further related to the velocity of diffusions of the solvent or specific metabolites across it. High r values imply high elasticity or high diffusion speed, where low values mean high rigidity or low diffusion rate. When r = 0 the stiffness reach the limit, corresponding to the classic situation when the volume is fixed.

In an alternative view, the additional dilution term, building in that way acts as some kind of stabilizer or buffer in a more chemical context. For instance, when both species concentration x and y are decreasing (dx/dt < 0 and (dy/dt < 0) in the system 2, the “dilution term” have the form (+dV/dt), against to the normal tendency. In this context, the parameter r acts as a measure of efficiency of the stabilizer.

With the above considerations, the volume is now self-consistently and inherently determined by the dynamics of the system with the additional advantage on the original approach followed by (Pawłowski and Zielenkiewicz 2004), explicitly dependent on the time, are now reduced to an autonomous system of differential Eq. (2).

Let us now discuss in more detail the viability of the assumptions. If we assume a semi permeable membrane, then the main volume dynamics can be driven by the imbalance of the chemical potential of the solvent (water in our case) at both side of the membrane, or osmotic pressure. The magnitude of water flux (J_solv) across the cell wall can be estimated by

$$ J_{solv} \sim P_{osm} \approx \Delta C_N \cdot R \cdot T $$

(4)

where P_osm is the osmotic pressure, ∆C_N is the difference of concentration inside and outside the cell, R = 8.314 J K⁻¹ mol⁻¹ is the universal gas constant and T is the temperature expressed in Kelvin degrees (K). In the expression we are assuming that the oscillating species are kept by the membrane mainly constraint into the cell, while the motion of the solvent and other possible species is not seriously limited (Fig. 1). A particular interesting situation could take place if the osmotic pressure increases over some threshold value. In this case the proportionality between J_solv ~ P_osm could be reduced to a limiting relation J_solv = J_max where J_max is a constant and expressed the diffusion-limited velocity. The magnitude of J_max is ultimately determined by the inner physical chemistry structure of the membrane and the existence or absence of specific transport channels.

Fig. 1

Effects of internal concentration change into the cell on the water fluxes supposing and oscillating behavior of N

The existence of J_max could be notable if the frequency of the oscillation is fast enough (short period). In this case, the equilibrium driven by (Eq. 4) does not have enough time to hold, and in practice the experimental value of r will be lower than the corresponding one for an equivalent system with longer period. It must be clear that in our analysis we are describing only passive membranes, in the sense that they are not directly coupled to the metabolism of the cell itself. Obviously, this is not the case of modern organisms where the membrane structures are continually regenerated and growing, but acceptable at the beginning, when their main role was to act as simple receptacles for the incipient “biochemical” process.

Additional Model Examples

We have also considered two other cases of well-known chemical/biochemical oscillators, besides the already introduced Brusselator (even if the latter does not represent exactly any specific system, the dynamics caught some basic properties of more realistic systems, with the additional advantage to be a simpler and well-studied case).

The first of these other examples is the minimal cascade mitotic oscillator based on (Goldbeter 1991)

$$ \begin{array}{*{20}c} {dC_1 /dt = v_i - v_d X\frac{{C_1 }}{{Kd + C_1 }} - Kd \cdot C_1 - C_1 \frac{dV}{dt}} \\ {dM/dt = V_1 \frac{{\left( {1 - M} \right)}}{{K_1 + \left( {1 - M} \right)}} - V_2 \frac{M}{{K_2 + M}} - M\frac{dV}{dt}} \\ {dX/dt = V_3 \frac{{\left( {1 - X} \right)}}{{K_3 + \left( {1 - X} \right)}} - V_4 \frac{X}{{K_4 + X}} - X\frac{dV}{dt}} \end{array} $$

(5)

$$ dV/dt = vi - C_1 K_d + \frac{{V_1 \left( {M - 1} \right)}}{{M - \left( {1 + K_1 } \right)}} - \frac{{V_2 M}}{{K_2 + M}} - \frac{{v_d C_1 X}}{{C_1 + K_d }} + \frac{{K_3 V_3 }}{{X - \left( {1 + K_3 } \right)}} - \frac{{V_4 X}}{k4 + X} $$

with $V_1 = \frac{{C_1 }}{{K_c + C_1 }}V_{M1}$ and V₃ = MV_M3, where C₁ is the cyclin concentration, M and X, the fraction of actives cdc2 kinase and cyclin protease respectively (see Appendix 1).

As our last example we considere the core of glycolytic model of synchronization proposed by (Bier et al. 2000), but as we are interested more in the inner cell dynamics than in the interaction between them, the coupling term was neglected focusing in the dynamics of only one cell. Now, the extended system is as follows

$$ \begin{array}{*{20}c} {dG/dt = V_{in} - k_1 G\;T - G\frac{dV}{dt}} \\ {dT/dt = 2K_1 G\;T - \frac{{k_p T}}{{K_m + T}} - T\frac{dV}{dt}} \\ {\frac{dV}{dt} = r (V_{in} + k_1 G\;T - \frac{{k_p T}}{{K_m + T}})} \end{array} $$

(6)

where G and T, denote the concentrations of glucose and ATP respectively, and the other quantities are kinetic parameters of the systems (see Appendix 1).

Results

Our basic program can be summarized in the following main steps:

• Identify a region of the parameters space in the original system (r = 0) consistent with oscillatory states.

• Explore, through a bifurcation diagram, the qualitative effects of increasing r values for each system, focusing mainly in the lost of oscillatory states and the emergence of asymptotic stables states (death states)

• Study explicitly the temporal effects on the dynamics for different values of the parameter r

Two different computer codes were used for the bifurcation analysis: AUTO (Doedel and Kernévez 1986) and Matcont (Dhooge et al. 2006). We have not studied in full detail the complete diagrams (in some cases highly complex), and limited ourselves to identify the regions for the r parameter consistent with stable oscillations (alive states) and their transitions commonly to non-oscillating states (dead states)

It is easy to show that the specific form of the additional dilution terms guarantee that all the steady states of the original system are also present in the extended system. For the Brusselator case the original system has only asymptotic solutions $x = a,y = b/a$. Such values automatically cancel the additionally term reducing the extended system to the original one. However, the extended systems would present additional steady states (new equilibrium branches) and the dynamical behavior in general would be essentiality different for the original system for determined values of our new parameter r. Even in the simplest case, is not an easy task to express these additionally asymptotic solutions in analytical form.

The Brusselator Case

The relative mathematical simplicity of the Brusselator enables us to perform some analytical treatment that is very difficult for larger and probably more realistic systems. Let us begin to find out the stationary solutions for our extended system. It is easy to show after some algebra that the following values are solutions of our system (2)

$$ \begin{array}{*{20}c} {x_0 = a} \\ {y_0 = b/a} \end{array} $$

(7)

The solution of system (7) is inherited from the original system (r = 0) and the additional ones, that only appear in the extended system are the roots of the cubic polynomial x_i

$$ \begin{array}{*{20}c} {\left[ {x^3 + \left( {\frac{{r^2 + 1}}{r}} \right) \cdot x^2 + \left( {a \cdot r + b + 1} \right) \cdot x - a = 0} \right]} \hfill \\ {y_i = \frac{{1 - r \cdot x_i }}{r}} \hfill \end{array} $$

(8)

It is interesting to see that from this point of view the implicit diffusion term could be seen as some kind of chemical reaction with molecularity equal to three. In general, a third order polynomial have three different roots, real or complex according the specific parameter values. We are only interested in positive real solutions; therefore we have two possibilities, only one real or three real solutions.

For the original Brusselator (r = 0) oscillating states always satisfy that the inner parameters a and b fulfill the constraint $a^2 + 1 < b < \left( {a + 1} \right)^2$, where the oscillations appear because the stable state lose stability through a Hopf bifurcation, just when the equality b = a² + 1 hold.

For our numerical test we chose to fix a = 1, b = 3 that are just inside the region of the oscillatory behavior for the original system. We study the influence of the parameter r based in the advantages of bifurcation analysis (see Fig. 2)

Fig. 2

The blue solid line is consistent with oscillating states (alive states), blue dashed and green lines are no stable and non-oscillatory states, red line represents stable states (dead states). The continuous straight line is consistent with oscillation states (alive states), dashed line and curve line above the lower limit point LP are not stable and non-oscillatory states, lower curve line (beginning in lower LP) represent stable states (death states)

The diagram shows that for a region of the parameters (a) and (b) where the original systems always oscillates (continues blue line), collapse with the new equilibrium branch (BP) for r = 0.25 losing stability. A new stability region emerges when the parameter r increases to around r = 0.212197 (solid red line) and all the solutions converge to either. The system does not present two alternative states or a bi-stability region between (0.212197 ≤ r ≤ 0.25). It can be easily checked numerically that just when the new stable branch emerge, the oscillatory state become unstable.

Figure 3 shows the explicit temporal behavior for increasing values of the parameter r. We find that both the period and amplitude are affected. For the first, as the r parameter increases the oscillation period increase (T₀ < T) and finally “dies” at r = 0.21 (solid red line). The system oscillates for values close to r = 0.21 but the periods in these cases are several times larger than the diagram scale. For the amplitude, we find that it increases slightly when the r parameter grows (A₀ < A)

Fig. 3

Effects of increasing the values of r values in the dynamics. The solid blue line represents the standard brusselator. The solid red line the stable or death state. Note that (T₀ < T) and (A₀ < A) in this case

Other numerical tests were performed with different values of the parameters a and b. No significant changes in the qualitative behavior were found. As a general rule, only a single new interesting equilibrium branch emerges from (Eq. 8), the others are being uninteresting negative or complex solutions.

The Mitotic Oscillator Case

In the case of mitotic oscillator model the bifurcation diagrams differs considerably from the previous case. Again, increasing r values (beyond r = 0.333) stabilize the system, but in this case, the oscillatory states collapse before the system reaches the branching point on the original equilibrium branch. Just at the point when the two equilibrium branches merge (usually called as branch point BP), the first branch loses stability (Fig. 4, dashed blue line) while the other additional branch is stabilized.

Fig. 4

Bifurcation diagram for the mitotic oscillator. Oscillatory states collapse (solid blue line) to a stable state (solid red line). Simple and dashed blue lines represent unstable non-oscillatory states

The temporal behavior of the cycling (C₁) shows that the period in this case decreases (T ₀ > T) in contrast with the Brusselator behavior discussed above. The oscillation amplitudes are now also decreasing (A ₀ > A) when r increases, giving to the system a new alternative to reach the equilibrium. This corresponds with slow attenuated oscillatory state (solid red line) to reach an asymptotic stable state (death state.) when the r parameter increases beyond r = 0.34 (Fig. 5)

Fig. 5

Temporal evolution of the cycling (C₁) for different values of r in the mitotic model (T₀ > T) and (A₀ > A)

The Glycolytic Oscillator Case

Glycolysis is present in almost all organisms as a main source of chemical energy and it is perhaps together with the tricarboxylic acid cycle the most ancient metabolic pathways (Fell and Wagner 2000). These features made it a particularly interesting process from the astrobiological point of view. The process itself consists in the step-by-step breakdown of glucose storing the release energy in the form of ATP molecules. It is well documented fact that during the process, the different metabolites (ATP, glucose) would exhibit periodic changes in their concentrations. Another interesting property of the glycolysis is the ability to synchronize the oscillation between different cells. Different kinetics models have been proposed to study and reproduce the oscillatory patterns and the synchronization mechanism. We considered the minimal version of the specific model proposed originally by (Bier et al. 2000) with the aim to explain the oscillatory and synchronization patterns in yeast cells in Eq. (6).

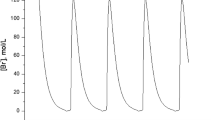
In this case, the emergence of several new equilibrium branches in the extended system becomes the bifurcation studies a highly intricate task. For that reason, we limit ourselves to study the numerical solutions for increasingly r values. Again, the additional term acts as a tendency to break the limit oscillation cycle to reach a non-oscillating stable state (dead state), but in this case the solutions have been found to be particularly sensitive to small increments of the parameter r. Details on temporal behavior are shown in Fig. 6.

Fig. 6

Oscillation patterns for different values of r for the the glycolitic oscillator model. Solid red line is the corresponding dead state. For this case (T₀ < T) and (A₀ > A)

Now, the behavior is in some way, a mixture of the previous systems, period increases (T ₀ < T) similarly to the Brusselator, while the amplitude decreases (A ₀ > A) as in the mitotic oscillator, but with a marked dependence in both cases. Note that the period dramatically increases for small increments of the parameter.

Conclusions

We have studied a class of models with variable volume changes (or the diffusion process driven directly by the evolving concentrations). We have found that in all cases, the temporal patterns are strongly dependent of the values of the r parameter. For the period (T) and amplitude (A) all the possible combinations were found in terms of the original values (T₀) and (A₀). The specific influence appears to be model dependent, but with a general tendency to lose their oscillatory character. There is always some threshold value r_c of the parameter, above which the oscillatory state collapse generally reaching directly a stable non-oscillating state.

The stabilization process reported in the three studied models are in consonance with the analysis done in the “A (Fiducial) Brusselator Model”. However the results could not be considered as trivial, because the particular way to reach a general non-oscillating stable state becomes to be highly dependent of the specificity of the model as we discussed in the formers sections.

At this point, there is another issue that must be clarified. The term “equilibrium state” used throughout this work is in the sense of dynamical systems theory and not in the thermodynamic ones. Living beings are open systems, far from thermodynamic equilibrium, with continuous energy and matter flows. In that sense both our “living” and “dead” states are alive. If our criteria make sense, livings being form a much more limited group into a more general class of thermodynamical systems out of equilibrium.

Although our analyses are far from being complete, the results suggest some interesting constraints to the primitive cell membrane candidates to support complex chemical patterns as oscillations. Beyond the obvious limitations of our model, it might give some hint to study an important fact that happened more than 3.5 billion of years ago, when life in it simplest form emerged.

Appendix 1

Parameters of the mitotic and glycolitic oscillators

The kinetics parameters for the mitotic oscillator and the glycolytic oscillator were taken from Pawłowski and Zielenkiewicz (2004) and read, respectively

Mitotic
Parameters	Values
C1(0)	0.01 μM
M(0)	0.01 μM
X(0)	0.01 μM
v i	0.025 μM/min
v d	0.25 μM/min
Kd	0.02 μM
Kc	0.5 μM
K1,K2, K3,K4	0.005
V2	1.5
V4	0.5
VM1	3
VM3	1
V0	1
Glycolytic
Parameters	Values [a.u.]
G(0)	10.5
T(0)	0.04
Vin	0.36
k1	0.02
kp	6
Km	13
V0	1